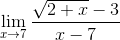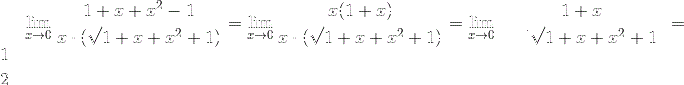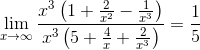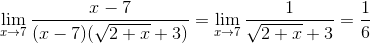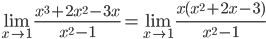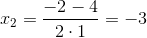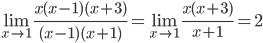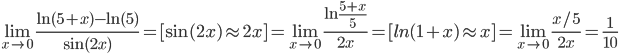Предел функции при ( x to x_0 )
Пусть функция ( f(x) ) определена на некотором множестве (X) и пусть точка ( x_0 in X ) или ( x_0 notin X )
Возьмем из (X) последовательность точек, отличных от (x_0) :
(x_1 ;, ; x_2 ;, ; x_3 ;, …, ; x_n ; , ; … tag{1} )
сходящуюся к (x^*).
Значения функции в точках этой последовательности также образуют числовую последовательность
( f(x_1) ;, ; f(x_2) ;, ; f(x_3) ;, …, ; f(x_n) ; , ; … tag{2} )
и можно ставить вопрос о существовании ее предела.
Определение. Число (A) называется пределом функции (f(x)) в точке ( x = x_0 ) (или при ( x to x_0 ) ), если для
любой сходящейся к (x_0) последовательности (1) значений аргумента (x), отличных от (x_0) соответствующая
последовательность (2) значений функции сходится к числу (A).
Символически это записывается так:
$$ lim_{xto x_0}{ f(x)} = A $$
Функция (f(x)) может иметь в точке (x_0) только один предел. Это следует из того, что последовательность ( left{ f(x_n) right} )
имеет только один предел.
Существует другое определение предела функции.
Определение Число (A) называется пределом функции (f(x)) в точке (x_0), если для любого числа ( varepsilon > 0 )
существует число ( delta > 0 ) такое, что для всех ( x in X, ; x neq x_0 ), удовлетворяющих неравенству ( |x-x_0| < delta ),
выполняется неравенство ( |f(x)-A| < varepsilon )
Используя логические символы, это определение можно записать в виде
( (forall varepsilon > 0) (exists delta > 0) (forall x in X, ; x neq x_0, ; |x-x_0| < delta): |f(x)-A| < varepsilon )
Отметим, что неравенства ( x neq x_0, ; |x-x_0| < delta ) можно записать в виде ( 0 < |x-x_0| < delta )
<>Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением
«на языке последовательностей».
Второе определение называют определением «на языке ( varepsilon — delta )».
Эти два определения предела функции эквивалентны и можно использовать любое из них в зависимости от того, какое более
удобно при решении той или иной задачи.
Заметим, что определение предела функции «на языке последовательностей» называют также определением предела функции по Гейне,
а определение предела функции «на языке ( varepsilon — delta )» — определением предела функции по Коши.
Предел функции при ( x to x_{0-} ) и при ( x to x_{0+} )
В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.
Определение Число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любой сходящейся
к (x_0) последовательности (1), элементы (x_n) которой больше (меньше) (x_0), соответствующая
последовательность (2) сходится к (A).
Символически это записывается так:
$$ lim_{x to x_{0+}} f(x) = A ; left( lim_{x to x_{0-}} f(x) = A right) $$
Можно дать равносильное определение односторонних пределов функции «на языке ( varepsilon — delta )»:
Определение число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любого
( varepsilon > 0 ) существует ( delta > 0 ) такое, что для всех (x), удовлетворяющих неравенствам
( x_0 < x < x_0 + delta ; (x_0 -delta < x < x_0 ) ) , выполняется неравенство ( |f(x)-A| < varepsilon ).
Символические записи:
( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 < x < x_0 + delta ): |f(x)-A| < varepsilon )
( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 -delta < x < x_0 ): |f(x)-A| < varepsilon )
Связь между односторонними пределами и пределом функции устанавливает следующая теорема.
Теорема
Функция (f(x)) имеет в точке (x_0) предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы,
и они равны. В этом случае предел функции равен односторонним пределам.
Предел функции при ( x to infty ), при ( x to -infty ) и при ( x to +infty )
Кроме рассмотренных понятий предела функции при ( x to x_0 ) и односторонних пределов существует также понятие предела функции
при стремлении аргумента к бесконечности.
Определение. Число (A) называется пределом функции (f(x)) при ( x to infty ), если для любой бесконечно большой
последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к (A).
Символическая запись:
$$ lim_{x to infty} f(x) = A $$
Определение. Число (A) называется пределом функции (f(x)) при ( x to +infty ; (x to -infty) ) , если для любой бесконечно
большой последовательности значений аргумента, элементы (x_n) которой положительны (отрицательны), соответствующая
последовательность значений функции сходится к (A).
Символическая запись:
$$ lim_{x to +infty} f(x) = A ; left( lim_{x to -infty} f(x) = A right) $$
Теоремы о пределах функций
Определение предела функции «на языке последовательностей» дает возможность перенести доказанные выше теоремы о пределах
последовательностей на функции. Покажем это на примере двух теорем.
Теорема. Пусть функции (f(x)) и (g(x)) имеют в точке (x_0) пределы (B) и (C). Тогда функции ( f(x) pm g(x) ; , ; f(x) cdot g(x) ) и
( frac{f(x)}{g(x)} ) (при ( C neq 0 ) ) имеют в точке (x_0) пределы, равные соответственно ( B pm C ; , ; B cdot C ), и ( frac{B}{C} ).
Теорема. Пусть функции ( f(x) ; , ; g(x) ) и ( h(x) ) определены в некоторой окрестности точки (x_0), за исключением, быть
может, самой точки (x_0), и функции ( f(x) ; , ; h(x) ) имеют в точке (x_0) предел, равный (A), т.е.
$$ lim_{x to x_0} f(x) = lim_{x to x_0} h(x) = A $$
Пусть, кроме того, выполняются неравенства ( f(x) leqslant g(x) leqslant h(x) ).
Тогда $$ lim_{x to x_0} g(x) = A $$
Теорема Лопиталя. Если $$ lim_{x to x_0} f(x) = lim_{x to x_0} g(x) = 0 $$ или (infty ), (f(x)) и (g(x))
дифференцируемы в окрестности (x_0) , и ( g'(x) neq 0 ) в окрестности (x_0) ,
и существует $$ lim_{x to x_0} frac{f'(x)}{g'(x)} $$ то существует $$ lim_{x to x_0} frac{f(x)}{g(x)} = lim_{x to x_0} frac{f'(x)}{g'(x)} $$
Т.е. теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя позволяет раскрывать неопределённости вида ( frac{0}{0} ) и ( frac{infty}{infty} ).
Первый замечательный предел
$$ lim_{x to 0} frac{sin x}{x} = 1 $$
Второй замечательный предел
$$ lim_{x to infty} left( 1+ frac{1}{x} right)^x = e $$
Постоянная называется пределом функции
при , если для любого числа
существует число
такое, что при всех , удовлетворяющих условию
выполняется неравенство
Для того чтобы вычислить предел необходимо знать основные правила вычисления пределов или воспользоваться нашим онлайн калькулятором.
Наш онлайн калькулятор способен вычислить пределы для очень многих математических выражений, калькулятор также генерирует подробное решение задачи.
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
lim_{xto 3}(frac{5x^2-8x-13}{x^2-5})
-
lim_{xto 2}(frac{x^2-4}{x-2})
-
lim_{xto infty}(2x^4-x^2-8x)
-
lim _{xto :0}(frac{sin (x)}{x})
-
lim_{xto 0}(xln(x))
-
lim _{xto infty :}(frac{sin (x)}{x})
-
lim_{(x,y)to (3,3)}(frac{x-y}{sqrt{x}-sqrt{y}})
-
lim_{(x,y)to (0,0)}(frac{3x^{3}y}{x^{4}+y^{4}})
- Показать больше
Описание
Поэтапное вычисление пределов
limit-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Advanced Math Solutions – Limits Calculator, Squeeze Theorem
What happens when algebraic manipulation does not work to find the limit? Give the squeeze theorem, also known…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Решение пределов
Число A называется пределом функции y=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Если выбрать вид предела, то подробное решение по шагам будет доступно в MS Word:
1. Не знаю
2. Пределы вида 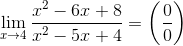
3. Вычислить предел, используя правило Лопиталя.
4. Пределы простейших иррациональности вида
5. Нахождение пределов, используя свойства первого замечательного предела ,
6. Нахождение пределов, используя свойства второго замечательного предела ,
,
Для нахождения предела слева
используйте знак -, справа
: +. Например, 0-, 1+
Примечание: число «пи» (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
Например, найти предел 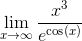
см. также нахождение пределов, используя свойства первого замечательного предела и второго замечательного предела.
Примеры.
Вычислить указанные пределы:
1. 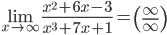
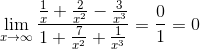
2. 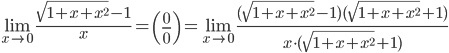
3. 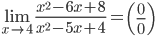
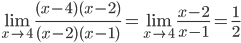
4. 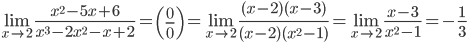
5. 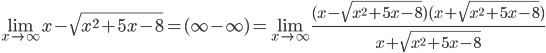
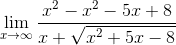
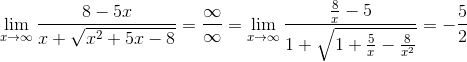
6. 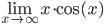
7. 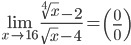
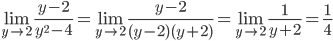
8. 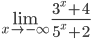
9. 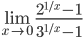
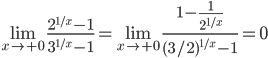
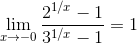
Следовательно, 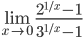
Найти пределы функции, не применяя правило Лопиталя.
а)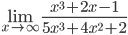
Ответ: 1/5
б) 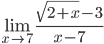
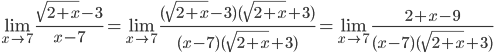
Ответ: 1/6
в) 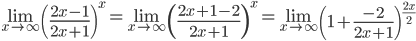
e-2/2 = e-1
Ответ: 1/e
г)
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-1).
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
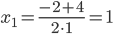
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
Ответ: 2
д) 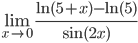
Ответ: 1/10
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Калькулятор для решения пределов
Данный онлайн калькулятор вычисляет предел функции. Программа не просто даёт ответ, она приводит пошаговое
и подробное решение.
Как пользоваться калькулятором для решения пределов онлайн:
- Введите математическое выражение с переменной $ x $ в выражении используйте стандартные
операции: + сложение, — вычитание, / деление, * умножение, ^ — возведение в степень, а
также математические
функции. - Введите значение, к которому стремится переменная икс.
- Нажмите кнопку — Вычислить предел.
- Через несколько секунд внизу отобразится пошаговое решение с подробными комментариями.
В качестве тренировки, можете нажать на любой из 3-х примеров внизу и все поля заполнятся автоматически, затем
нажмите на
«Найти предел» и вы получите подробное решение и ответ.
Также внизу страницы вы можете прочитать полные правила ввода данных, ответы на часто задаваемые вопросы и оставить
свой комментарий.
Другие онлайн калькуляторы
- Правило Лопиталя
- Теория про
пределы - Решение
производных - Решение
интегралов
Вы поняли, как решать? Нет?
- Правила
- Комментарии
- Ответы на вопросы
Последовательность ввода данных
- вводите функцию, предел которой хотите найти. Вот ссылка на правила
ввода функций; - нводите значение, к которому стремится переменная икс;
- нажимаете кнопку — Вычислить предел;
- смотрите решение, радуетесь, ставите лайки и рассказываете друзьям!
Что можно вводить
Простейшие математические операции: Сумма: + ; Вычитание: — ; Умножение: * ; Деление или дроби: / и
пробел.
Элементарные функции: x^n степень, sqrt(x) квадратный корень, log(a,x) логарифм, ln(x) натуральный
логарифм, exp() экспонента, sin(x) синус, cos(x) косинус, tg(x) тангенс и др.
Десятичные дроби можно вводить только через точку, то есть, пишем 0.7, а не 0,7 — полные правила
ввода функций.
Как вводить переменную икс
- выберите — вводить значение переменной самому или минус/плюс бесконечность;
- введите число, если выбрали вариант «Ввести самому»
Вопросов пока не поступало =))
Вопросы можете задавать в комментариях, мы обязательно на них ответим!
Рассчитайте цену решения ваших задач


Калькулятор
стоимости
Решение контрольной
от 300 рублей
*
* Точная стоимость будет определена после загрузки задания для исполнителя
+Загрузить файл
Файлы doc, pdf, xls, jpg, png не более 5 МБ.