Основные понятия
Углы установки колес – конструктивные параметры, определяющие их положение в режиме прямолинейного движения и в поворотах. Каждая модель автомобиля предусматривает индивидуальные значения углов, которые определяются устройством автомобильной подвески. В зависимости от ее конструкции одни углы могут быть регулируемыми, а другие – жестко фиксированными. Это относится как к передней, так и к задней осям автомобиля. Одним из важнейших свойств подвески является стабилизация управляемых колес, т.е. их способность устойчиво сохранять прямолинейное движение автомобиля и возвращаться к нему после поворота. Для улучшения стабилизации управляемых колес оси их поворота имеют наклоны как в в продольной, так и в поперечной плоскостях.
Рис. 1: Угол продольного (слева) и угол поперечного (справа) наклона оси поворота управляемого колеса отсчитываются не от продольной плоскости кузов, а от вертикали
Ось поворота колеса, или «шкворневая ось – это условная или виртуальная ось, вокруг которой осуществляется поворот управляемого колеса при вращении руля. Как правило, условная ось поворота проходит через центры опор поворотной стойки подвески или центры шаровых опор, но в ряде современных автомобилей, например, автомобильного концерна VAG, подвеска колес снабжена парой рычагов с шаровыми шарнирами как сверху, так и снизу. Поворот управляемого колеса происходит вокруг виртуальной оси, которая меняет свое положение в пространстве не только при повороте управляемых колес, но и в ходе сжатия отбоя подвески.
К углам установки колес относятся развал и схождение колес. За стабилизацию управляемых колес отвечают углы продольного и поперечного наклона оси поворота колеса.
Для убедительности, расскажу вначале о рулевой колонки и вилке переднего колеса велосипеда
Вы, наверняка, замечали, что ось поворота управляемого колеса велосипеда наклонена вперед, и что стоящий на месте велосипед почему-то поворачивает руль в сторону.
Если взять велосипед за седло и катить его вперед, то Вы почувствуете, как чутко реагирует велосипед на малейшие наклоны рамы велосипеда в стороны.
Если же, взявшись за седло, попробовать катить велосипед назад, то движения его руля станут непредсказуемыми. Удержать рули в прямолинейном положении не удастся!
Вы, наверняка, когда-либо ездили на велосипеде, и даже «без рук»! Велосипед чутко реагировал на любые, даже самые незначительные наклоны корпуса в сторону, ответно реагирую поворотом руля.
А Вы не пробовали на велосипеде ехать задним ходом? Как-то неустойчиво ведет себя велосипед, чтобы не упасть, все время приходится касаться ногами земли.
Отчего же это происходит, и зачем велосипеду необходим наклон рулевой колонки, и изогнутая форма вилки переднего колеса?
Геометрия передней вилки и Trail (выкат переднего колеса)
Проделаем эксперимент. Если поставить обычный велосипед вертикально на оба колеса, и, держа за раму, наклонить её в сторону, то и руль сам повернется в ту же сторону. Причина такого поведения кроется в конструкции передней вилки и рулевой колонки. Именно они определяют взаимное расположение двух важных точек. Точки A – места контакта переднего колеса с дорогой и точки B – пересечения оси рулевой колонки с той же дорогой. Взаимное положение этих точек задает не только направление, в какую сторону повернётся руль при наклоне велосипеда, но и его курсовую устойчивость, управляемость, строгость управления, стабильность на виражах и многое другое. Все велосипеды можно разделить на два типа: AB и BA. Тип AB – у которого точка контакта переднего колеса с дорогой расположена впереди точки B (рис. 2а). Тип BA – Точка A лежит позади точки B (рис. 2б).
Рис. 2: Формирование плеча действия боковой силы наклоном оси поворота управляемого колеса велосипеда + выносом сои вращения колеса относительно его оси поворота
При наклоне велосипеда типа АВ в одну сторону, его руль будет поворачиваться в другую сторону и по очень ясной причине – точка приложения силы трения A лежит впереди оси вращения колеса В. Велосипед, при повороте “без рук”, будет складываться пополам как ширма и с грохотом сыпаться на землю. Совсем иначе реагирует на наклон руль и переднее колесо велосипеда типа ВА, – они будут поворачиваться в сторону наклона велосипеда сами, и безо всяких рук. А при правильных размерах и углах, велосипед будет стремиться вернуться в вертикальное положение точно так, как будто его руль повернули руками – рулю надо только немного помочь, направить его в нужном направлении! По этой причине велосипеды типа АВ в магазинах не сыскать, их используют только в цирке, обученные артисты, которые ездят и вперед и назад, и на одном колесе…
Форма передней вилки
Рис. 3: Формы передних вилок оказывают существенное влияние на формирование плеча действия боковой силы
Варианты, изображенные на рисунках 3а) и 3б), иллюстрируют, что изгиб вилки оказывает существенное влияние на формирование плеча выката переднего управляемого колеса. Если сделать слишком большой выкат колеса (расстояние между точками B и A), это приведет к колоссальному стремлению руля повернуть в сторону при малых скоростях движения велосипеда, или при его остановке. Это обусловлено появлением поворотного момента, образованного вертикальной силой (весом велосипеда), прилагаемой к точке A. Вместе с тем, при движении велосипеда управляемое колесо будет стремиться занять положение, соответствующее прямолинейному движению. В этом случае продольная сила (сила трения между колесом и опорной поверхностью), прилагаемая к той же точке A, будет стремиться повернуть колесо прямо (эффект рояльного колесика).
Если же к точке A, будет приложена боковая сила, то эта сила будет стремиться повернуть руль в сторону. Плечо действия боковой силы определяется длиной перпендикуляра, опущенного из точки A на ось рулевой колонки (ось поворота управляемого колеса).
Кстати, боковая сила появляется при движении велосипеда, как только Вы отклоните руль от прямолинейного положения. Момент боковой силы, формируемый при движении велосипеда боковой силой, будет стремиться вернуть руль в положение, соответствующее прямолинейному движению.
Чтобы дать возможность велосипедисту двигаться как на малых, так и на больших скоростях, плечо AB делают короче, изгибая велосипедную вилку вперед (см. рис. 3в). Но, даже если вилка прямая, то меняют её наклон, относительно оси рулевой колонки, или петухи, в которых крепится переднее колесо, смещают вперед.
Расстояние между осью рулевой колонки и осью втулки переднего колеса, называют по-разному, и Rake и Fork Offset, а на русскоязычных сайтах можно встретить названия: выбег, смещение или вылет вилки. Величина вылета вилки R обычно находится в пределах от 30 до 50мм. Зная вылет вилки, угол наклона оси рулевой колонки и реальный диаметр (с учетом толщины и деформации шины) колеса, легко можно подсчитать расстояние между точками A и B. Это расстояние называется Trail или выкат (выбег) переднего колеса, иногда его можно найти в каталогах. Итак, зная Trail, можно подсчитать коэффициент устойчивости (управляемости) (Ку), который равен:
Где
Т (Trail) – выкат, или выбег переднего колеса;
G – межосевая база велосипеда.
У современных велосипедов Ку лежит в диапазоне от 5% до 7,5% и выбирается обычно значение близкое к границе устойчивости, по весьма прозрачной причине – таким велосипедом легче управлять.
Итак, мы определили, что плечо устойчивости велосипеда (вылет) передней вилки определяются по принципу: из центра переднего колеса опускают перпендикуляр к точке (B) на опорную поверхность, а ось вилки продолжают до пересечения с опорной поверхностью – до точки (A). Полученное расстояние (AB) между двумя точками и будет плечом устойчивости велосипеда.
Рис. 4: Форма вилки дорожного велосипеда, и плечо устойчивости АВ
Плечо устойчивости AB существенно влияет на устойчивость велосипеда и удобство его управлением. Для велосипеда очень важно сочетание этих двух свойств.
После того, как Вы ознакомились с конструкцией передней вилки велосипеда, можно приступить к изучению узла поворота управляемого колеса автомобиля.
Кастер
(Caster – англ.) – Продольный угол наклона оси поворота управляемого колеса.
Рис. 5: Угол продольного наклона оси поворота управляемого колеса (кастер) и плечо действия боковой силы (В)
Для обеспечения динамической стабилизации управляемых колес нам необходимо сформировать плечо устойчивости (Trail). Принцип формирования этого плеча подобен рассмотренному выше примеру с велосипедным колесом, однако изгиб передней вилки на автомобиле, конечно же, не применяют.
Рис 6: Формирование необходимой величины плеча действия боковой силы (плеча устойчивости) выносом оси вращения колеса относительно оси его поворота
К формированию необходимого значения плеча устойчивости подходят следующим образом:
- Определяют значение угла продольного наклона оси поворота управляемого колеса (τ = кастер);
- Определяют значение выноса оси вращения управляемого колеса по отношению к оси его поворота (nτ = вынос оси поворота);
- Расстояние от точки пересечения оси поворота управляемого колеса до точки пересечения перпендикуляра, опущенного из оси вращения колеса на опорную плоскость, и является плечом устойчивости управляемого колеса.
Угол наклона оси поворота управляемого колеса формирует весовую стабилизацию колеса. Если управляемого колесо поворачивать, например, на 90°, то точка 1, которой обозначена ось вращения колеса, займет место, определяемое точками 2. Причем два колеса управляемой оси при их взаимной повороте займут противоположные относительно точки 1 позиции. Это вызовет небольшой крен передней части автомобиля, так как одно колесо будет приподнимать переднюю часть, а противоположное колесо – опускать переднюю часть автомобиля.
Мы ранее упоминали, что при наличии угла наклона передней вилки неподвижного велосипеда будет наблюдаться стремление руля самостоятельно повернуть так, чтобы рама велосипеда заняла положение как можно ближнее к поверхности земли.
Рис 7: Плечо действия боковой силы na получено путем сложения продольного угла наклона (кастера) и отрицательного выноса (-nτ) оси вращения колеса. Параметр n’a – реальное плечо, формирующее совместно с боковой силой (1) поворотный момент управляемого колеса (момент стабилизации)
Принцип действия ясен из поведения рояльного колесика – при движении оно стремится оказаться позади ножки, то есть занять наиболее устойчивое положение.
Рис. 5: (дополнительно – ближе к тексту)
Чтобы получить тот же эффект на автомобиле с приводом на задние колеса, точка пересечения оси поворота с поверхностью дороги (с) должна быть впереди центра пятна контакта колеса с дорогой (d). Для этого ось поворота и наклоняют назад, как у велосипеда. Теперь при отклонении от прямолинейного движения в точке (d) будет возникать боковая сила, которая постараются вернуть колесо на место.
Если на автомобиль будет действовать боковая сила, формируемая, например, центробежной силой, возникающей при повороте автомобиля, управляемое колесо будет стремиться занять положение, соответствующее прямолинейному движению.
Более того, если на машину действует боковая сила, то кастер обеспечивает при случайно отпущенном руле плавный поворот машины по направлению этой силы, и не дает ей опрокинуться. На переднеприводном автомобиле при торможении динамическая стабилизация работает так же, как и на заднем приводе. Но при разгоне колесо уже не катится позади ножки, а толкает ее впереди себя, поэтому динамическая стабилизация не требуется.
Рис. 8: Формирование поворотного момента при качении колеса с наклоном плоскости его вращения
На этом значение кастера не заканчивается, при повороте руля он наклоняет оба колеса в сторону поворота. Когда колесо наклоняется, наружная окружность качения (1) становится больше внутренней (2), и соответственно проходит больший путь.
Рис 9: Образование угла продольного наклона оси поворота управляемого колеса (кастера)
1 – стойка типа McPherson; 2 – верхняя опора стойки; 3 – шаровая опора; 4 – ось поворота управляемого колеса; τ – угол продольного наклона оси поворота (кастер).
Но так как это одно и то же тело и не может разорваться, то внутренняя часть тормозит внешнюю и колесо стремится повернуть в сторону наклона. Это значит что кастер, наклоняя оба передних колеса в сторону поворота, увеличивает поворачиваемость при повернутом руле
Угол продольного наклона оси поворота управляемого колеса (кастер) можно измерить, если спроецировать на продольную перпендикулярную опорной поверхности плоскость автомобиля ось поворота управляемого колеса. Кастер – это угол между образовавшейся проекцией и вертикалью. Его будет видно, если смотреть на автомобиль сбоку (см. рис. 9). Кастер является одним из основных параметров геометрии подвески, которые обеспечивают стабилизацию управляемых колес в движении. Кастер считается положительным, если ось наклонена назад по ходу движения относительно вертикали. Однако стабилизацию управляемых колес автомобиля при движении формирует не сам кастер, а продольная сила, действующая на плече, которое на рисунке 7 обозначено, как na. Это плечо называют плечом действия боковой силы.
А теперь попытайтесь ответить сами себе.
Изменится ли плечо действия боковой силы, если на автомобиль установить нештатные колеса?
Кастер
Для управляемых колёс
Кастер (продольный угол наклона оси поворота колеса)
Кастор (английское – caster angle или castor angle) — угол продольного наклона оси поворота колеса автомобиля.
Кастер (или кастор) измеряется в градусах (угловых минутах) и представляет собой угол в продольной плоскости автомобиля между вертикальной линией и линией, проходящей через центры поворота колеса.
Эта линия проходит через шаровые опоры верхнего и нижнего рычагов подвески («классическая» двухрычажная подвеска), либо через верхнюю и нижнюю точки крепления амортизаторной стойки (подвеска типа McPherson) либо по оси шкворня (шкворневая подвеска) в продольной плоскости автомобиля. Кастор может быть как положительным, так и отрицательным.
Кастер или кастор (en:Caster angle) — угол между вертикалью и проекцией оси поворота колеса на продольную плоскость автомобиля. Продольный наклон обеспечивает самовыравнивание управляемых колёс за счёт скорости автомобиля. Другими словами: автомобиль выходит из поворота сам; руль, который отпущен и обладает свободным ходом, сам возвращается в положение прямолинейного движения (на ровной дороге, с отрегулированными механизмами). Это происходит, естественно, при положительном кастре. Например, кастер позволяет ездить на велосипеде, не держась за руль.
Патент Артура Кребса (1896) гласит: «Чтобы обеспечить устойчивость переднего моста, то есть, чтобы автоматически устанавливать оси колёс параллельно… передняя ось располагается на некотором расстоянии позади проекции оси рулевого механизма…»
На обычных автомобилях кастер превышает 6°. Спортсмены устанавливают данное значение на несколько градусов выше, что делает ход автомобиля устойчивее, а также повышается стремление авто к прямолинейному движению. И, наоборот, на цирковых велосипедах или на погрузчиках кастер часто равняется нулю, так как скорость перемещения сравнительно невелика, но при этом есть возможность повернуть по меньшему радиусу. Но автомобиль создается для большей скорости, поэтому требует лучшей управляемости.
Положительный кастер.
Кастер, или кастор — это продольный угол оси поворота колеса, взятый между ней и вертикалью.
На заднеприводных автомобилях оси поворота передних колёс всегда наклоняют назад (положительный кастер). При наклонённой назад оси поворота колесо во время движения само стремится занять положение позади этой оси, что создаёт динамическую стабилизацию. Это можно уподобить поведению колёсика рояля или офисного стула — при качении оно всегда само занимает положение позади своей оси (во многих европейских языках такое колёсико как раз и называется «кастером» или «кастором»). При движении в повороте боковые силы реакции дороги также стараются вернуть колесо в исходное положение, так как прикладываются позади оси его поворота.
По той же причине вилку переднего колеса на мотоциклах и велосипедах тоже всегда наклоняют назад.
Благодаря наличию положительного кастера заднеприводный автомобиль продолжает ехать прямо при отпущенном руле, даже несмотря на воздействие возмущающих сил — неровностей дороги, бокового ветра и так далее. Колесо, имеющее положительный кастер, старается занять положение, соответствующее прямолинейному движению, даже если лопнула одна из рулевых тяг.
Отсюда вытекает совершенная недопустимость при тюнинге заднеприводных автомобилей чрезмерно лифтовать заднюю подвеску — при этом кузов вместе с осью поворота передних колёс наклоняется вперёд, и кастер становится нулевым или даже отрицательным, при этом эффект динамической стабилизации передних колёс сменяется их динамической дестабилизацией, что значительно затрудняет управление автомобилем и делает его опасным. Большинство передних подвесок автомобилей имеют возможность регулировки кастера в небольших пределах для компенсации нормального износа в процессе эксплуатации.
Рис. 10: Изменение значения угла продольного наклона оси поворота управляемого колеса (кастера) при изменении положения кузова
Для переднеприводного автомобиля положительный кастер намного менее актуален, так как передние колёса уже не свободно катятся, а тянут машину за собой, и небольшое его положительное значение сохраняют лишь для большей устойчивости при торможении.
Влияние кастора на управляемость автомобиля
Кастор влияет на стабилизирующий момент и на изменение развала колес при повороте руля. Чем больше кастор, тем больше стабилизирующий эффект при вывернутых колёсах.
Из-за того, что точка контакта колеса (при положительном касторе) с поверхностью лежит несколько позади оси поворота, при отклонении колеса от прямолинейного движения возникают боковые силы, стремящиеся вернуть колесо в начальное положение.
Кроме того, если в начальный момент отклонения колес от нейтрального положения при прохождении поворота только внешнее колесо имеет необходимый отрицательный развал, то по мере увеличения отклонения колес в сторону поворота внешнее колесо приобретает ещё больший отрицательный развал, а отрицательный развал внутреннего колеса уменьшается или даже становится положительным. Таким образом, кастор благоприятно влияет на сцепление управляемых колес в поворотах.
При повороте в одну из сторон одно из колес стремится приподнять шасси, другое же само приподнимается. Таким образом, для поворота колес необходимо не только преодолеть силы трения, но и затратить некоторое количество энергии на приподнимание шасси. Благодаря этому и выше описанным боковым силам водитель может «чувствовать» автомобиль.
При дефектах кузова, после ударов, этот угол обычно изменяется неодинаково. Разница между этими углами на левом и правом колёсах обычно приводит к уводу автомобиля с прямой линии даже при идеально отрегулированных остальных углах и качественной резине.
Параметры кастера
Параметры кастера для легковых автомобилей
| Автомобиль | Значение кастера |
| ЗАЗ-965, ЗАЗ-965А | 2°31’ |
| ЗАЗ-966, ЗАЗ-966В | 2°30’ |
| ЗАЗ-968, ЗАЗ-968А, ЗАЗ-968М | 5°30’ |
| ЛуАЗ-969, ЛуАЗ-969М | 5°30’ |
| Москвич 407 | 1°…3° |
| Москвич-403, −408, −412, −2140, −2138, −2137, −2136 | 0°20’…1°20’ |
| ВАЗ-2101, −2102, −2105 | 3°30’…4°30’ |
| ВАЗ-2103, −2106, −2107 | 3°40’…4°20’ |
| ВАЗ-2121 | 3°00’…4°00’ |
| ГАЗ-21 | 1° |
| ГАЗ-24 | 0°…1° |
| ГАЗ-3110 | 3°…6° |
| ГАЗ-13, ГАЗ-14 | 0°…1° |
| ГАЗ-69, ГАЗ-69А | 3°30’±30’ |
| ЗИЛ-114, ЗИЛ-117, ЗИЛ-41047 | 0°45’±30’ |
| УАЗ-469, УАЗ-469Б | 3°30’ |
Параметры кастора для грузовых автомобилей
| Автомобиль | Значение кастера |
| ГАЗ-51 | 2°30’ |
| ГАЗ-52-03, ГАЗ-52-04 | 3° |
| ГАЗ-53, ГАЗ-53А | 2°30’ |
| ЗИЛ-164 | 1°30’ |
| ЗИЛ-130 | 2°30’ |
| ЗИЛ-157 | 2°30’ |
| МАЗ-500, −503, −504, −5335, −6422 | 2°30’ |
| Урал-375, Урал-377 | 2°10’ |
| КрАЗ-256, −257, −258 | 0° |
| КрАЗ-255Б, КрАЗ-260 | 5° |
5
2
голоса
Рейтинг статьи
МАШИНОСТРОЕНИЕ И ТРАНСПОРТ: ТЕОРИЯ, ТЕХНОЛОГИИ, ПРОИЗВОДСТВО
УДК 629.33
В.В. Беляков1, Ю.В. Палутин2, А.В. Тумасов1, Д.А. Бутин1, А.П. Трусов1
РАСЧЕТ УГЛОВ ПОВОРОТА УПРАВЛЯЕМЫХ КОЛЕС АВТОМОБИЛЯ
С УЧЕТОМ УВОДА
Нижегородский государственный технический университет им. Р.Е. Алексеева1 Нижегородская государственная сельскохозяйственная академия2
Представлен способ расчета углов поворота управляемых колес автомобиля, учитывающий угол увода шин управляемой оси. Различные известные теории на практике почти не используются в связи со сложностью вычислений, при этом геометрия рулевого управления основывается на опыте и анализе существующих автомобилей. Выявлено, что теория поворота управляемых колес Фиала наиболее адекватно описывает физические процессы, протекающие в контакте пневматической шины с опорной поверхностью. Предложенная методика отличается от ранее используемых значительным упрощением расчетов. В качестве данных, требуемых для расчета углов поворота управляемых колес, используются колесная база, высоты ЦТ, ширина колеи, масса на оси, коэффициент увода шин, боковое ускорение, радиус движения. Приведенный расчет зависимости поворота управляемых колес может быть использован на стадии проектирования автомобиля.
Ключевые слова: углы поворота управляемых колес, соотношение углов поворота направляющих колес, управляемые колеса, геометрия рулевого управления, схождение.
Введение
Зависимость поворота управляемых колес автомобиля влияет на износ шин, а также на управляемость и устойчивость движения в повороте. В различные периоды развития автомобилестроения выдвигались те или иные теории поворота управляемых колес с целью уменьшения износа шин и улучшения показателей управляемости при движении в поворот. На основании анализа работ П.В. Аксенова, Д.А. Антонова, С.В. Бахмутова, Л.Л. Гинцбурга, А. Дика, Р.П. Кушвида, Э.И. Григолюка, Н.Т. Катанаева, В.Н. Кравца, К.С. Колесникова, А.А. Полунгяна, В.Ф. Платонова, В.А. Петрушова, Д.Р. Эллиса, Е.О. Рыкова, Ю.В. Шемякина, Г.П. Антипова, Н.А. Алфутова, М.В. Гурьянова, В.М. Семенова, В.И. Кольцова, Я.Е. Фа-робина, W.F. Milliken, D.L. Millken, H.B. Pacejka [1-14] можно выделить четыре наиболее распространенные теории поворота управляемых колес:
• параллелограммная — углы поворота управляемых колес всегда равны друг другу;
• геометрическая — соотношение углов поворота определяется по условию Аккер-мана;
• система по Гауфу и Ширеру — углы бокового увода обоих передних колес должны быть по возможности малыми, что достигается при одинаковой величине их углов бокового увода;
• система Фиала [12,13] — соотношения уводов пропорционально перераспределенной нагрузке;
• система по Хассельгруберу [7,8] — мощность бокового трения, т.е. производная боковой силы при уводе и компонента скорости, перепендикулярной к плоскости вращения шины, должны быть одинаковыми для обоих передних колес.
© Беляков В.В., Палутин Ю.В., Тумасов А.В., Бутин Д.А., Трусов А.П.
Для выявления наиболее оптимальной концепции необходимо представление в теории движения автомобиля и работы пневматической шины. При движении в повороте у автомобиля происходит перераспределение нормальных реакций колес. Под действием бокового ускорения на центр тяжести, нагрузка на внешнее колесо увеличиваются, а на внутреннем — снижается, что представлено на схеме (рис. 1). Рулевое управление — так же, как и подвеска — должно обеспечивать оптимальное положение пневматических шин относительно опорной поверхности во время движения. Для определения оптимальных режимов работы пневматических шин передней оси необходимы данные о качении шины с уводом. На рис. 2. представлены графики, характеризующие качение шины с уводом для различных вертикальных нагрузок. Следует обратить внимание, как изменяется зависимость боковой силы от угла уводы при различных вертикальных силах. При уменьшении вертикальной силы уменьшается максимальная боковая сила, развиваемая колесом, пропорционально боковой силе снижается угол увода, при котором достигается максимальное ее значение. Из графиков видно, что при изменении вертикальной силы характеристика шины на линейном участке остается неизменной.
Ру Ру
внешн внутр
Рис. 1. Схема распределения сил Рис. 2. Диаграмма боковой силы
в управляемых колесах от угла увода
На основании данных о движении автомобиля в повороте и работы пневматической шины можно сделать выводы о теориях поворота управляемых колес. Так, теория закона Ак-кермана подходит для жестких не пневматических колес, катящихся без увода; система по Га-уфу и Ширеру неприемлема в связи с тем, что углы увода у внешнего и внутреннего колеса будут разными из-за различных вертикальных сил; система по Хассельгруберга также не состоятельна в связи с тем, что не возможно на шинах развивать одинаковое боковое усилие, при том, что у них различные вертикальные силы; по этому самой объективной и учитывающий работу пневматической шины является система Фиала.
Расчет распределения вертикальной силы между колесами управляемой оси
Распределение вертикальных сил на управляемых колесах от действия бокового ускорения, действующего при движении автомобиля в повороте, рассчитывается по формулам (1), (2). При таком подходе перераспределения нагрузок на передней оси не учитываются многие факторы: угловая жесткость подвесок, жесткость кузова на кручение. Также эти формулы подходят только для равномерного движения без продольного ускорения.
^внутр _ ^9,81Мрсь^ ^
¿твнешн _ ^9,81Мос^ | ^ДуЯцт^
г-»внутр гвнешн
где , ^2внешн — сила вертикальная на управляемом колесе внутреннем и внешнем соответственно, Н; Мось — масса на управляемой оси, кг; ау — боковое ускорение, м/с2; Нцт — высота центра тяжести, м; В — ширина колеи, м.
Боковые силы
Суммарная боковая сила, действующая на шины управляемой оси, рассчитывается по формуле (3). При этом расчете не учитываются переходный процесс установления кругового движения.
1 = Мось ■ . (3)
Боковые силы между внутренним и внешним колесом будут распределяться пропорционально вертикальным силам, согласно закону силы трения. Расчет боковых сил на внутреннем и внешнем колесе производится по формулам (4), (5).
внутр
рвнутр = I р • __(4)
У 9,81-Мось’ (4)
рвнешн
гв™ = I • -, (5)
^ У 9,81 •Мось’ 4 ‘
где /^шутр, /увнешн — сила боковая на управляемом колесе внутреннем и внешнем соответственно, Н.
Характеристика качения колеса с уводом
Характеристику качения шины с уводом можно описать формулой любого из авторов теории шин Пасейки, Щадрин, Эллис, Фуфаев и других. Как правило, это функции боковой силы от угла увода, но для решения нашей задачи необходима обратная функция угла увода от боковой силы. Поскольку вывод угла увода из функции не всегда возможен или затруднен для решения данной задачи, примем, что шина работает только в зоне упругой деформации. Допущение, что при небольших углах увода шин зависимость линейна, имеется у многих авторов и часто используется при решении задач. Это допущение сильно упрощает расчетную формулу, при этом погрешность остается в рамках допустимого на режимах качения шин без жесткого скольжения. Режим жесткого скольжения в рамках оптимизации поворота управляемых колес не рассматривается. Представив зависимость угла увода от боковой силы в виде линейной зависимости выражение примет элементарный вид (6), (7):
внутр
авнУтр= _У-, (6)
^увода
рвнешн
квнешн= -, (7)
^увода
где авнугр, авнешн — угол увода внутреннего и внешнего колеса, град; кувод — коэффициент увода шины от боковой силы, Н/град.
Поворот управляемых колес
На первом этапе рассчитывается угол поворота управляемых колес по закону Аккер-мана, потому что по этой траектории будут двигаться центры управляемых колес. Схема идеального поворота управляемых колес по закону Аккермана представлена на рис. 3
Рис. 3. Схема поворота управляемых колес
Расчет углов поворота по Аккерману производится без учета угла увода колес задней оси, а также радиус движения принимается до центра задней оси, приняв, что радиус движения ЦТ отличается не сильно, расчетные формулы (8) и (9).
0,
внутр идеал
идеал
= arctg (
—),
Я+(Б/2)/’
(8)
(9)
Действительные углы поворота управляемых колес вычисляются по сумме идеальных углов поворота и углов увода, представлены в формулах (10) и (11).
лвнУ’Р = лвнУ’Р .^внутр ^действ ^идеал ‘
двнешн _ двнешн I -„.внешн
^действ ^идеал
(10) (11)
Результаты
В качестве примера был проведен расчет оптимальных углов поворота колес по теории Фиала. Расчет был проведен для автомобиля с параметрами, представленными в табл. 1.
Таблица 1
Параметры автомобиля
Параметр Значение
Колесная база, м 3,145
Высота ЦТ, м 0,85
Ширина колеи передней оси, м 1,75
Масса на передней оси, кг 1273
Коэффициент увода шин, Н/град 1250
В результате расчета были получены углы поворота управляемых колес. Для наглядности зависимости поворота колес от параметров движения в повороте в табл. 2 приведены значения расхождения колес.
Таблица2
Расхождения углов поворота управляемых колес
Расхождение управляемых колес, град
Радиус движения, м Боковое ускорения, м/с2
1 2 3 4 5 6
10 3,41993 3,11739 2,61316 1,90723 0,99962 -0,1097
20 0,70897 0,40643 -0,0978 -0,80373 -1,7113 -2,8207
30 0,25372 -0,04882 -0,55305 -1,25897 -2,1666 -3,2759
40 0,09756 -0,20498 -0,70921 -1,41513 -2,3228 -3,4321
50 0,02583 -0,27671 -0,78094 -1,48687 -2,3945 -3,5038
По результатам расчета оптимальных углов поворота управляемых колес выявлено две зависимости: с уменьшением радиуса движения увеличивается расхождение колес; с увеличением бокового ускорения расхождение колес уменьшается.
Исследования А.С. Добрина выявили, что при эксплуатации среднестатистического автомобиля на дорогах общего пользования боковые ускорения не превышают 3 м/с2. Этот порог называют «порогом неприятных ощущений»: он вызывает чувства дискомфорта и опасности. Если принять этот фактор во внимание и сопоставить с результатами расчета оптимального расхождения колес, то видно, что от 0 до 3 м/с2 угол расхождения колес крайне мал и увеличивается лишь при маневрировании и движениями с радиусами менее 20 м. Если рассматривать режимы движения с ограниченным боковым ускорением и исключить режим маневрирования, оптимальные углы поворота колес настолько близки по значениям, что зависимость поворота колес можно принять параллельной.
Если в эксплуатации автомобиля значительную часть составляет маневрирование с минимальными радиусами поворота, то наиболее адекватным теоретической конструкцией является закон поворота управляемых колес по Аккерману. Данный расчет также подтверждает правильность использования в спортивных автомобилях класса «Формула 1» и «Формула 3» кинематики рулевого управления с зависимостью Анти-Аккермана. Автомобили, двигающиеся с большими боковыми ускорениями, при определенных конструктивных параметрах имеют оптимальные углы поворота управляемых колес в положительном схождении.
Вывод
В результате анализа теорий оптимального поворота управляемых колес в качестве наиболее адекватно описывающей физические процессы, протекающие в контакте пневматической шины с опорой поверхностью, была определена теория Фиала. Основанный на ней способ расчета оптимальных углов поворота, в силу ряда допущений (линейная зависимость
увода от боковой силы, увод колес задней оси) был сведен к инженерным формулам. Полученные результаты могут быть сопоставлены с геометриями рулевых управлений, используемых на автомобилях различных эксплуатаций. Приведенный расчет зависимости поворота управляемых колес может быть использован на стадии проектирования автомобиля.
Анализ рассчитанных величин углов поворота колес показывает, что для автомобилей, двигающихся с небольшими боковыми ускорениями до 1 м/с2, геометрия поворота управляемых колес схожа с геометрической теорией Аккермана, а при движении с боковыми ускорениями, близкими к потери динамической устойчивости, зависимость может быть описана по теории Анти-Аккермана.
Исследования выполнены при финансовой поддержке Министерства образования и науки РФ по договору № 02.G25.31.0193 от 27.04.2016 г. (постановление Правительства Российской Федерации от 9 апреля 2010 года № 218).
Экспериментальные исследования выполнены с использованием оборудования Центра коллективного пользования НГТУ «Транспортные системы».
Библиографический список
1. Чудаков, Е.А. О рациональной форме рулевой трапеции // Доклады АН СССР. — М.: Изд-во АН СССР. — 1952. — Т. 88. — № 4.
2. Фрикционный износ резин / Сборник статей под ред. д.т.н. В.Ф. Евстратова. — М.: Химия, 1964, -271 с.
3. Фаробин, Я.Е. О рациональной форме рулевой трапеции // Автомобильная промышленность. — Т. 2. — 1959. — С. 15-17.
4. Фаробин, Я.Е. Теория поворота транспортных машин / Я.Е. Фаробин. — М.: Машиностроение, 1970, — 176 с.
5. Стефанович, Ю.Г. Исследование рулевой трапеции автомобилей / Ю.Г. Стефанович: Дис. … канд. техн. наук. — М., 1954. — 147 с.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
6. Кушвид, Р.П. Исследование рулевого управления автомобиля (оптимизация по критерию минимума износа шин) / Р.П. Кушвид. — дисс. …канд. техн. наук. — М., 1978, — 202 с.
7. Hasselgruber, H. Veerhaiten eines Kraftfahrzeuges bei Kurveenfahrt Automobilitechn Z / H. Has-selgruber. — №7. — 1965.
8. Hasselgruber, H. Zweckmäbige Auslegung van Krafttahrzeugienkungen in Hinbick auf Kurven vehaiten ung Reifengchonung / H. Hasselgruber // Automob. Ind., — № 3 (1). — 1964.
9. Добрин, A.C. Исследование движения автомобиля по заданной траектории / А.С. Добрин. — М.: НАМИ, 1966. — С. 35-65.
10. Добрин, A.C. Устойчивость и управляемость автомобиля при неустановившемся движении // Автомобильная промышленность. 1968. — № 9. — С.29-35.
11.Schallamach, A. The theori of dynamie rubber friction / А. Schallamach. — Wear. — 1963. — v.6. — № 5.
12.Fiala, E. Kraftkorrigierte Lenkanggeometrie / E. Fiala // ATZ. — 1959. — № 2.
13.Fiala E. Zur Fahrdunamik des Stressenfahrzeges unter Berück gichtigung der Lenkwngelastizitet / E. Fiala // ATZ. — № 3. — 1960.
14.Тумасов, А.В. Способ расчета интенсивности износа шин для различных режимов движения автомобиля / А.В. Тумасов, Д.А. Бутин, А.А. Васильев // Беспилотные транспортные средства: проблемы и перспективы. Сборник материалов 94 международной научно-технической конференции Ассоциации автомобильных инженеров. — Н. Новгород: НГТУ им. Р.Е. Алексеева, 2016. — С. 123-129.
Дата поступления
в редакцию: 07.03.2019
V.V. Belyakov, Y.V. Palutin, A.V. Tumasov, D.A. Butin, A.P. Trusov
CALCULATION STEETING GEOMETRY OF THE CAR TAKING INTO ACCOUNT THE SLIP ANGLE TIRE
Nizhny Novgorod State Technical University n.a. R.E. Alekseev
Purpose: method for calculating the steering angle of the directive wheels of a car. Design/methodology/approach: The calculation is presented in the form of engineering formulas. Findings: The calculation results are comparable with the geometry of the steering controls of existing cars. Research limitations/implications: In calculating the slip of the tires of the driven axes adopted linear, and the slip of tires of the rear axle not included.
Originality/value: for the first time the theory of geometry of steering control of the car of the Fiala theory is presented in a simple mathematical form.
Key words: steering angles, steering angle difference, steering geometry, slip angle, toe in.
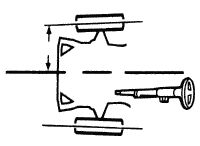
 Схождение колес
Схождение колес
Угол между плоскостью вращения колеса и осевой линией автомобиля (индивидуальное схождение каждого из колес). Также суммарное схождение — это сумма углов схождения левого и правого колеса.
Правильно отрегулированный статический угол суммарного схождения приведет к расположению колес параллельно при движении. Неправильно отрегулированное суммарное схождение приведет к повышенному износу шин, сопротивлению движению (и как следствие увеличенному расходу топлива).
В случае если суммарное схождение отрегулировано верно, но индивидуальные схождения двух колес не равны при горизонтально установленном рулевом колесе, на современных автомобилях возможны проблемы со вспомогательными системами (при наличии датчика положения рулевого колеса). Также при прямолинейном движении на любом автомобиле руль будет стоять не по уровню.
Схождение является наиболее важным углом установки колес, т.к. при отклонении от нормы всего на 15′ срок службы шины может упасть в два-три раза, в то время как допуск на углы развала и кастера у большинства производителей составляют от 30′ до 1 градуса. Также схождение передних колес является единственным углом поддающимся штатной регулировке абсолютно у всех автомобилей. Измеряется абсолютно всеми измерительными системами Hunter как для передней, так и для задней осей.
 Развал колес
Развал колес
Угол между плоскостью вращения колеса и вертикалью.
Уменьшает (при правильной установке) нагрузку на элементы рулевого управления и подвески, смягчает удары от дорожного покрытия. Способствует поддержанию прямолинейного движения, и увеличению срока службы шин.
Неверный угол развала вызывает увод автомобиля от прямолинейного движения и увеличенный износ шин. В отличие от схождения, в случае значительного отклонения от нормы развала неравномерный износ резины будет заметен только к концу службы шины.
Большинство автомобилей имеют штатную регулировку угла развала передних колес.
Измеряется абсолютно всеми измерительными системами Hunter как для передней, так и для задней осей.
 Угол продольного наклона шкворня (поворотной оси) или кастер
Угол продольного наклона шкворня (поворотной оси) или кастер
Обеспечивает стабильность движения при повороте транспортного средства. Неправильно отрегулированный угол продольного наклона оси поворота приведет к увеличению сопротивления рулевого колеса, вибрациям и уводу автомобиля от прямолинейного движения.
Многие автомобили не поддерживают регулировку кастера штатными средствами (например автомобили группы VAG) в этом случае угол кастера может использоваться для диагностики элементов подвески и кузова на наличие возможных повреждений.
Поскольку ось поворота во многих конструкциях подвески нематериальна, на нее невозможно установить какой-либо датчик. Поэтому кастер вычисляется по изменению схождения и развала колес при повороте на определенный угол (10 или 20 градусов).
Измеряется абсолютно всеми измерительными системами Hunter.
 Угол поперечного наклона шкворня (поворотной оси)
Угол поперечного наклона шкворня (поворотной оси)
Обеспечивает стабильность движения и используется для уменьшения нагрузки на элементы подвески и рулевого управления при ударах от дороги.
Неверно выставленный угол продольного наклона может привести к потере стабильности и недостаточной отдаче рулевого колеса.
Угол поперечного наклона не подлежит регулировке штатными методами и его значительное отклонение от нормы говорит о наличии повреждений подвески либо кузова автомобиля.
Измеряется тем же способом, что и кастер.
Измеряется абсолютно всеми измерительными системами Hunter.
 Смещение оси автомобиля
Смещение оси автомобиля
Смещение оси — расстояние между линиями проходящими через ось вращения колес и перпендикулярных осевой линии автомобиля.
Данный вспомогательный диагностический угол может быть использован для выявления неисправных элементов подвески или кузова.
В случае чрезмерного смещения, автомобиль теряет стабильность при движении и уменьшается отдача рулевого колеса.
Смещение передних колес измеряется всеми измерительными системами Hunter. Смещение задних колес измеряется всеми стендами использующими технологию 3D и только инфракрасными датчиками имеющими «замкнутый контур» (DSP708, DSP508, DSP308 или DSP258).
 Расстояние от колесной арки до оси вращения колеса — Ride Height
Расстояние от колесной арки до оси вращения колеса — Ride Height
Высота посадки используется как диагностическое средство для диагностики (пружин) подвески а также как требуемый параметр для определения углов установки колес в моделях автомобилей, где углы установки зависят от просадки пружин.
Стенды Hunter позволяют измерять высоту посадки несколькими способами.
Самый удобный способ — измерение с помощью дополнительного набора мишеней, устанавливаемых на крылья автомобилей. Функция поддерживается только 3D-стендами Hunter с премиум-консолью WA или 811.
Также высоту посадки можно измерить с помощью дополнительного инфракрасного пульта со встроенной электронной рулеткой 20-1885-1.
Также высота посадки у стендов Hunter традиционно измерялась инфракрасными датчиками DSP306/506 и DSP308/508 с помощью механического устройства (как показано на рисунке справа).
Доступно только для 811/WA консолей.
 Максимальный угол поворота каждого из колес
Максимальный угол поворота каждого из колес
Дополнительный диагностический угол позволяет провести диагностику элементов подвески и рулевой системы.
Позволяет выявить дефекты или неправильную установку релевого механизма, рулевых тяг и т.д.
Измеряется автоматически электронными поворотными пластинами или вручную по указателю на поворотных дисках (при наличии такого указателя).
Поддерживается всеми моделями компьютерных консолей Hunter (PA100 и WA100).
 Углы симметрии
Углы симметрии
Данная функция позволяет быстро определить наличие повреждений кузова или элементов подвески.
Позволяет оценить шансы на приведение всех углов установки колес в норму и объяснить клиенту почему на его автомобиле после окончания регулировки остались «красные» значения.
Внимание!
Данная функция не предназначена для серъезной диагностики состояния кузова, а только для экспресс анализа состояния кузова и подвески. Для правильной профессиональной диагностики состояния кузова требуется использовать профильное оборудование проводящее измерение контрольных точек кузова, а не взаимного положения колес.
 Измерение колесной базы и ширины колеи
Измерение колесной базы и ширины колеи
Дополнительная опция для диагностики кузова.
Доступно только для компьютерных консолей WA100/WA300.
Иногда применительно к автомобилям всплывают вопросы из математики и физики. В частности, одним из таких вопросов является угловая скорость. Она имеет отношение как к работе механизмов, так и к прохождению поворотов. Разберёмся же, как определить эту величину, в чём она измеряется и какими формулами тут нужно пользоваться.
Содержание
- Как определить угловую скорость: что это за величина?
- Формула времени, за которое вращается точка по окружности заданного радиуса
- Угол поворота и период обращения
- Чему равна угловая скорость в конкретных случаях?
- Связь угловой и линейной скоростей
- Ускорение, момент и связь их с массой
- Шарнир как пример передачи импульса
Как определить угловую скорость: что это за величина?
С физико-математической точки зрения эту величину можно определить следующим образом: это данные, которые показывают, как быстро некая точка осуществляет оборот вокруг центра окружности, по которой она движется.
ПОСМОТРЕТЬ ВИДЕО
Эта, казалось бы, чисто теоретическая величина, имеет немалое практическое значение при эксплуатации автомобиля. Вот лишь несколько примеров:
- Необходимо правильно соотносить движения, с которыми вращаются колёса при повороте. Угловая скорость колеса автомобиля, движущегося по внутренней части траектории, должна быть меньше, чем у внешнего.
- Требуется рассчитывать, насколько быстро в автомобиле вращается коленвал.
- Наконец, сама машина, проходя поворот, тоже имеет определённую величину параметров движения – и от них на практике зависит устойчивость автомобиля на трассе и вероятность опрокидывания.
Формула времени, за которое вращается точка по окружности заданного радиуса
Для того, чтобы рассчитывать угловую скорость, используется следующая формула:
ω = ∆φ /∆t
Где:
- ω (читается «омега») – собственно вычисляемая величина.
- ∆φ (читается «дельта фи») – угол поворота, разница между угловым положением точки в первый и последний момент времени измерения.
- ∆t
(читается «дельта тэ») – время, за которое произошло это самое смещение. Точнее, поскольку «дельта», это означает разницу между значениями времени в момент, когда было начато измерение и когда закончено.
Приведённая выше формула угловой скорости применяется лишь в общих случаях. Там же, где речь идёт о равномерно вращающихся объектах или о связи между движением точки на поверхности детали, радиусом и временем поворота, требуется использовать другие соотношения и методы. В частности, тут уже будет необходима формула частоты вращения.
Угловая скорость измеряется в самых разных единицах. В теории часто используется рад/с (радиан в секунду) или градус в секунду. Однако эта величина мало что означает на практике и использоваться может разве что в конструкторской работе. На практике же её больше измеряют в оборотах за секунду (или минуту, если речь идёт о медленных процессах). В этом плане она близка к частоте вращения.
Угол поворота и период обращения
Гораздо более часто, чем угол поворота, используется частота вращения, которая показывает, сколько оборотов делает объект за заданный период времени. Дело в том, что радиан, используемый для расчётов – это угол в окружности, когда длина дуги равна радиусу. Соответственно в целой окружности находится 2 π радианов. Число же π – иррациональное, и его нельзя свести ни к десятичной, ни к простой дроби. Поэтому в том случае, если происходит равномерное вращение, проще считать его в частоте. Она измеряется в об/мин – оборотах в минуту.
Если же дело касается не длительного промежутка времени, а лишь того, за который происходит один оборот, то здесь используется понятие периода обращения. Она показывает, как быстро совершается одно круговое движение. Единицей измерения здесь будет выступать секунда.
Связь угловой скорости и частоты вращения либо периода обращения показывает следующая формулы:
ω = 2 π / T = 2 π *f,
где:
- ω – угловая скорость в рад/с;
- T – период обращения;
- f – частота вращения.
Получить любую из этих трёх величин из другой можно с помощью правила пропорций, не забыв при этом перевести размерности в один формат (в минуты либо секунды)
Чему равна угловая скорость в конкретных случаях?
Приведём пример расчёта на основе приведённых выше формул. Допустим, имеется автомобиль. При движении на 100 км/ч его колесо, как показывает практика, делает в среднем 600 оборотов за минуту (f = 600 об/мин). Рассчитаем угловую скорость.
Для начала переведем об/мин в об/с. Для этого разделим 600 на 60 (число секунд в минуте) и получим 10 об/с . Попутно мы получили и период обращения: эта величина является обратной по отношению к частоте и при измерении в секундах 0,1 с.
Далее используем формулу:
ω = 2 π *f
Поскольку точно выразить π десятичными дробями невозможно, результат примерно равен будет 62,83 рад/с.
Связь угловой и линейной скоростей
На практике часто приходится проверять не только ту скорость, с какой изменяется угловое положение у вращающейся точки, но и скорость её самой применительно к линейному движению. В приведённом выше примере были сделаны расчёты для колеса – но колесо движется по дороге и либо вращается под действием скорости автомобиля, либо само ему эту скорость обеспечивает. Значит, каждая точка на поверхности колеса помимо угловой будет иметь и линейную скорость.
Рассчитать её проще всего через радиус. Поскольку скорость зависит от времени (которым будет период обращения) и пройденного расстояния (которым является длина окружности), то, учитывая приведённые выше формулы, угловая и линейная скорость будут соотноситься так:
V = ωR
Где:
- V – линейная скорость;
- R – радиус.
Из формулы очевидно, что чем больше радиус, тем выше и значение такой скорости. Применительно к колесу с самой большой скоростью будет двигаться точка на внешней поверхности протектора (R максимален), но вот точно в центре ступицы линейная скорость будет равна нулю.
Ускорение, момент и связь их с массой
Помимо приведённых выше величин, с вращением связано ещё несколько моментов. Учитывая же, сколько в автомобиле крутящихся деталей разного веса, их практическое значение нельзя не учесть.
Равномерное вращение – это важная вещь. Вот только нет ни одной детали, которая бы всё время крутилась равномерно. Число оборотов любого крутящегося узла, от коленвала до колеса, всегда в конечном итоге растёт, а затем падает. И та величина, которая показывает, насколько выросли обороты, называется угловым ускорением. Поскольку она производная от угловой скорости, измеряется она в радианах на секунду в квадрате (как линейное ускорение – в метрах на секунду в квадрате).
С движением и её изменением во времени связан и другой аспект – момент импульса. Если до этого момента мы могли рассматривать только чисто математические особенности движения, то здесь уже нужно учитывать то, что каждая деталь имеет массу, которая распределена вокруг оси. Он определяется соотношением начального положения точки с учётом направления движения – и импульса, то есть произведения массы на скорость. Зная момент импульса, возникающий при вращении, можно определить, какая нагрузка будет приходиться на каждую деталь при её взаимодействии с другой
Шарнир как пример передачи импульса
Характерным примером того, как применяются все перечисленные выше данные, является шарнир равных угловых скоростей (ШРУС) . Эта деталь используется прежде всего на переднеприводных автомобилях, где важно не только обеспечить разный темп вращения колёс при повороте – но и при этом их управляемость и передачу на них импульса от работы двигателя.
ПОСМОТРЕТЬ ВИДЕО
Конструкция этого узла как раз и предназначена для того, чтобы:
- уравнивать между собой, как быстро вращаются колёса;
- обеспечивать вращение в момент поворота;
- гарантировать независимость задней подвеске.
В результате все формулы, приведённые выше, учитываются в работе ШРУС.
Enter the wheelbase length and the turning angle of the front wheels into the calculator to determine the turning radius.
- Wheel Speed Calculator
- Piston Speed Calculator (mean)
- HP to Torque Calculator
- CC to HP Calculator
- GVWR (Gross Vehicle Weight Rating) Calculator
- Trailer Tongue Length Calculator
- Handwheel Diameter Calculator
- Aircraft Turn Radius Calculator
- MPH to G Force Calculator
Turning Radius Formula
The following formula is used to calculate the turning radius of a car.
TR = WB/tan(a)
- Where TR is the turning radius
- a is the angle of the turn
- WB is the wheelbase (distance between centers of the front and back wheels)
This formula assumes a perfect theoretical turning scenario. In real-world situations, this turning radius would vary depending on wheel tilt, friction, and many other factors.
Turning Radius Definition
What is a turning radius? A turning radius is a radius at which a car will rotate, or turn, given a certain wheelbase length and an angle of turn of the wheels.
Example Problem
How to calculate a turning radius?
- First, determine the wheel base.
This is the distance from the centers of the front and back wheels. For this example, the wheelbase is found to be 5 ft.
- Next, determine the turn angle.
This is the angle at which the front wheels are turned from their neutral position. in this problem, the angle of turn is 10 degrees.
- Finally, calculate the turn radius.
Using the formula, the turn radius is found to be: 5/tan(10)= 28.356 ft.
FAQ
What is a good turning radius?
Most common cars have a turning radius of 35′ so anything smaller than that would be considered good. This is the turning radius of the car assuming the wheels are turned as much as possible.
Do bigger tires affect the turning radius?
Typically larger wheels will increase the turning radius of a vehicle to more wheel tilt during turning.
Is a smaller or larger turning radius better?
A smaller turning radius is better for handling and cars that want to perform well on a track will want to try to decrease the turning radius as much as possible.
What is the turning radius?
The turning radius is the minimum radius of the path that a vehicle must follow in order to make a turn without skidding or losing control. It is defined as the distance from the center of the turning circle to the center of the vehicle.
How is turning radius calculated?
The turning radius can be calculated by dividing the wheelbase of the vehicle (the distance between the front and rear axles) by the tangent of the angle of the turn. The formula is: R = (WB) / tan (Θ), where R is the turning radius, WB is the wheelbase, and Θ is the angle of the turn.
What is the relationship between speed and turning radius?
The relationship between speed and turning radius is inversely proportional, meaning that as speed increases, the turning radius decreases. This is because at higher speeds, the vehicle must follow a tighter turning radius in order to maintain stability and control.
Why is turning radius important in vehicle design?
Turning radius is an important factor in vehicle design because it affects the maneuverability of the vehicle. A smaller turning radius allows a vehicle to make tighter turns, which can be useful in tight spaces, while a larger turning radius can make it more difficult to maneuver in tight spaces.
How does the weight of a vehicle affect its turning radius?
The weight of a vehicle affects its turning radius by increasing the forces acting on the tires during a turn. As a result, a heavier vehicle will require a larger turning radius in order to maintain stability and control.
How does the width of a vehicle affect its turning radius?
The width of a vehicle affects its turning radius by increasing the distance between the tires, which increases the forces acting on the tires during a turn. As a result, a wider vehicle will require a larger turning radius in order to maintain stability and control.
What is the relationship between tire size and turning radius?
The relationship between tire size and turning radius is indirect. Larger tires can increase the stability of a vehicle during a turn, but they also increase the distance between the tires, which can result in a larger turning radius.
How does the suspension of a vehicle affect its turning radius?
The suspension of a vehicle affects its turning radius by changing the way the vehicle handles during a turn. A softer suspension can increase the stability of the vehicle during a turn, but can also increase the turning radius. A stiffer suspension can reduce the turning radius, but can also decrease the stability of the vehicle during a turn.
How does the type of vehicle affect its turning radius?
The type of vehicle can greatly affect its turning radius. For example, larger vehicles like buses and trucks typically have a larger turning radius than smaller vehicles like cars, due to their increased length and width.
How is turning radius measured?
Turning radius can be measured by observing the path that a vehicle follows during a turn and measuring the distance from the center of the turning circle to the center of the vehicle. This measurement can be made using a variety of tools, including laser measuring devices or tape measures.











 Схождение колес
Схождение колес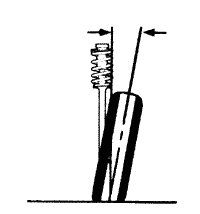 Развал колес
Развал колес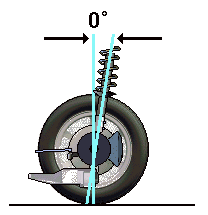 Угол продольного наклона шкворня (поворотной оси) или кастер
Угол продольного наклона шкворня (поворотной оси) или кастер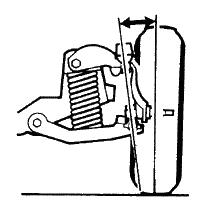 Угол поперечного наклона шкворня (поворотной оси)
Угол поперечного наклона шкворня (поворотной оси) Смещение оси автомобиля
Смещение оси автомобиля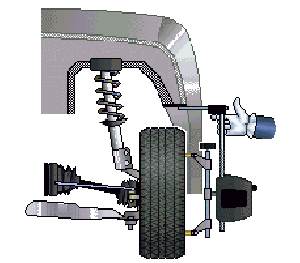 Расстояние от колесной арки до оси вращения колеса — Ride Height
Расстояние от колесной арки до оси вращения колеса — Ride Height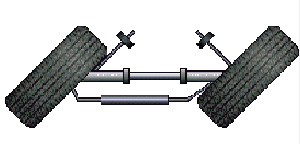 Максимальный угол поворота каждого из колес
Максимальный угол поворота каждого из колес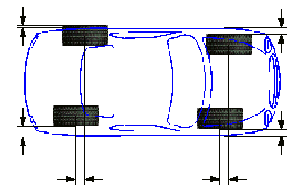 Углы симметрии
Углы симметрии Измерение колесной базы и ширины колеи
Измерение колесной базы и ширины колеи