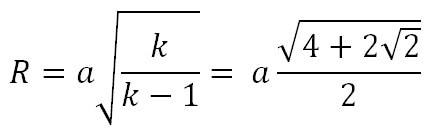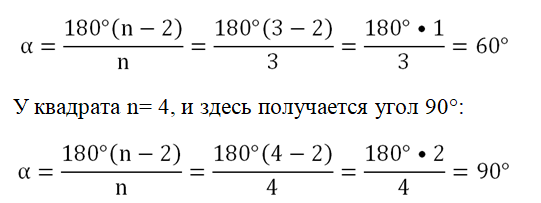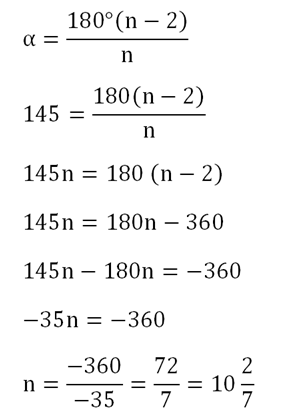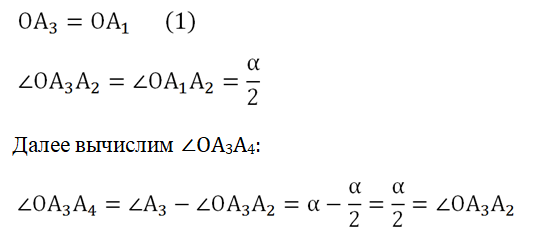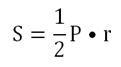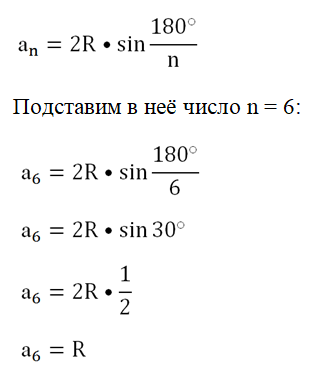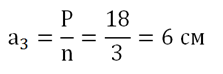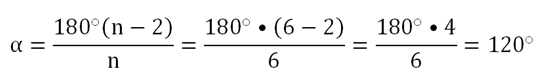В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
Решение:
Формула нахождения величины угла в правильном многоугольнике:
L=(180(n-2))/n
L — угол в многоугольнике.
n-количество сторон многоугольника.
Величина угла в восьмиугольнике равна:
n=8
∆ALB – равнобедренный т.к. AL=LB и углы LAB и LBA равны.
Найдем углы LAB и LBA из ∆ ALB:
Углы LAB= LBA=22,5
Угол LBA опирается на хорду LA.
LA сторона восьмиугольника, следовательно, LA=AC.
Углы LBA и ABC, т. к. опираются на равные хорды LA=AC
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Восьмиугольник вписанный в окружность найти угол
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
Решение:
Формула нахождения величины угла в правильном многоугольнике:
L=(180(n-2))/n
L — угол в многоугольнике.
n-количество сторон многоугольника.
Величина угла в восьмиугольнике равна:
n=8
∆ALB – равнобедренный т.к. AL=LB и углы LAB и LBA равны.
Найдем углы LAB и LBA из ∆ ALB:
Углы LAB= LBA=22,5
Угол LBA опирается на хорду LA.
LA сторона восьмиугольника, следовательно, LA=AC.
Углы LBA и ABC, т. к. опираются на равные хорды LA=AC
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Центральные и вписанные углы
О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
Нахождение угла восьмиугольника, вписанного в окружность
Условие задачи для наглядности изображается схематически на рисунке. Для начала определяется величина внутреннего угла равностороннего восьмиугольника, применяя формулу нахождения суммы всех углов n-угольника. Величина искомого угла АВС вычисляется как разность между величиной внутреннего угла восьмиугольника и величинами углов СВА и DBC. В ходе дальнейшего решения доказывается равенство углов CBA=DBC. Вычислив величину угла CBA, определяется величина искомого угла.
http://b4.cooksy.ru/articles/vosmiugolnik-vpisannyy-v-okruzhnost-nayti-ugol
http://www.virtualacademy.ru/lesson/1220/
Восьмиугольник, виды, свойства и формулы.
Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.
Восьмиугольник, выпуклый и невыпуклый восьмиугольник
Правильный восьмиугольник (понятие и определение)
Свойства правильного восьмиугольника
Формулы правильного восьмиугольника
Правильный восьмиугольник в природе, технике и культуре
Шестиугольник
Восьмиугольник, выпуклый и невыпуклый восьмиугольник:
Восьмиугольник – это многоугольник с восемью углами.
Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.
Восьмиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый восьмиугольник – это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый восьмиугольник
Рис. 2. Невыпуклый восьмиугольник
Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.
Правильный восьмиугольник (понятие и определение):
Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.
Рис. 3. Правильный восьмиугольник
Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.
Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.
Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Свойства правильного восьмиугольника:
1. Все стороны правильного восьмиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a7 = a8.
2. Все углы равны между собой и составляют 135°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = α8 = 135°.
Рис. 4. Правильный восьмиугольник
3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.
Рис. 5. Правильный восьмиугольник
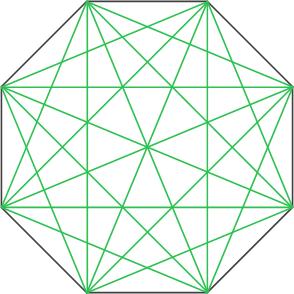
5. Количество диагоналей правильного восьмиугольника равно 20.
Рис. 6. Правильный восьмиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный восьмиугольник
Формулы правильного восьмиугольника:
Пусть a – сторона восьмиугольника, r – радиус окружности, вписанной в восьмиугольник, R – радиус описанной окружности восьмиугольника, k – константа восьмиугольника, P – периметр восьмиугольника, S – площадь восьмиугольника.
Формула константы правильного восьмиугольника:
Формула периметра правильного восьмиугольника:
Формулы площади правильного восьмиугольника:
Формулы радиуса окружности, вписанной в правильный восьмиугольник:
Формулы радиуса окружности, описанной вокруг правильного восьмиугольника:
Формулы стороны правильного восьмиугольника:
Правильный восьмиугольник в природе, технике и культуре:
В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного правильного восьмиугольника.
Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
7 181
An octagon is an eight-sided shape, such as a stop sign. Octagons can be regular or irregular. A regular octagon has sides that are congruent, or all equal. An irregular octagon has sides with different lengths. Once you have figured out the total number of degrees for all the angles, knowing whether the octagon is regular or irregular helps you determine the measure of any of the individual angles in the octagon. If you have an irregular octagon, you need to know the other seven angles to figure the unknown eighth angle.
Regular Octagons
Subtract two from the number of sides in an octagon. Since an octagon has eight sides, subtract two from eight to get six.
Multiply six by 180 to find the total number of degrees in an octagon equals 1,080.
Divide 1,080 by eight to find the measure of each interior angle if the octagon is regular. In a regular octagon, each angle measures 135 degrees.
Irregular Octagons
- Calculator
- Protractor
-
If you do not have the angles given to you, you can determine the angle measures with a protractor. To use a protractor, put the origin over the angle vertex and align the protractor with one of the angle sides. Then find the degree measure based on where the second side of the angle intersects the angle measurement on the protractor.
Subtract two from the number of sides in an octagon. Since an octagon has eight sides, subtract two from eight to get six.
Multiply six by 180 to find the total number of degrees in an octagon equals 1,080.
Add the angle measures of the seven known angles to find the sum of those angles. For example, if your seven known angles measure 100, 110, 120, 140, 150, 160 and 170, find the sum to be 950.
Subtract the measure of the seven known angles from 1,080 to find the measure of the unknown angle if you have an irregular polygon. Finishing the example, subtract 950 from 1,080 to find the unknown angle to be 130 degrees.
Things You’ll Need
Tips
План урока:
Понятие правильного многоугольника
Описанная и вписанная окружности правильного многоугольника
Формулы для правильного многоугольника
Построение правильных многоугольников
Понятие правильного многоугольника
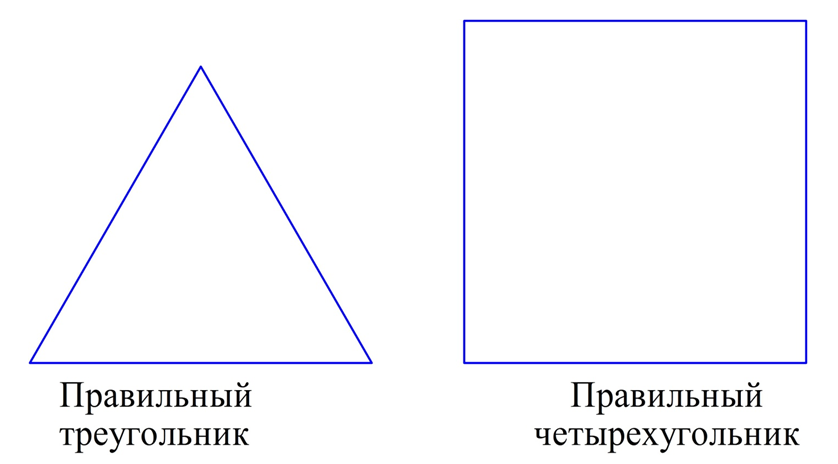
У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.
Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.
Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.
Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:
Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:
Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:
Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?
Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:
Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?
Решение. В формулу
Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?
Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:
Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.
Ответ: не может.
Описанная и вписанная окружности правильного многоугольника
Докажем важную теорему о правильном многоуг-ке.
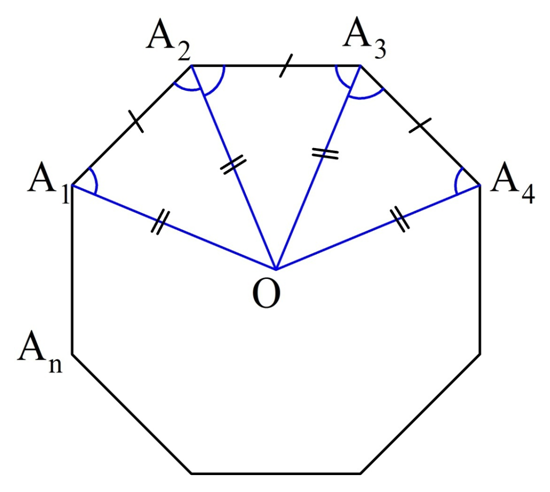
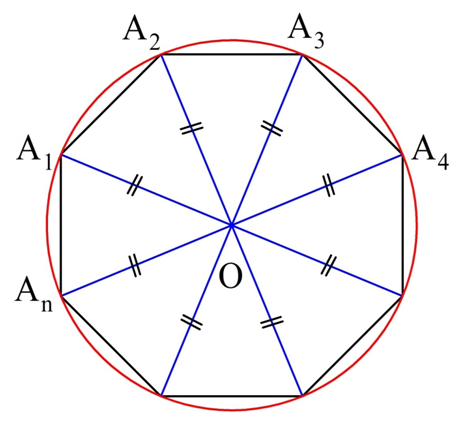
Для доказательства обозначим вершины произвольного правильного n-угольника буквами А1, А2, А3…Аn. Далее проведем биссектрисы углов ∠А1 и ∠А2. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА3, ОА4 и т. д.
∠А1 и ∠А2 одинаковы по определению правильного многоуг-ка:
Из этого факта вытекает два равенства:
Получается, что ОА3 – это также биссектриса ∠А3. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):
Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:
Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А1, А2 и А3, можно провести только одну окружность, ч. т. д.
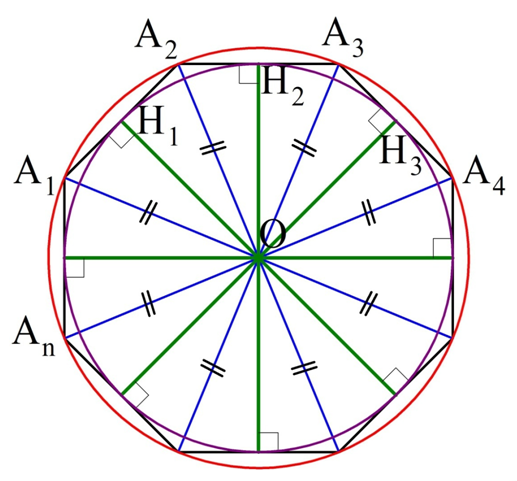
Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА1А2, ∆ОА2А3, ∆ОА3А4, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН1, ОН2, ОН3… на стороны многоуг-ка.
Так как высоты проведены в равных треуг-ках, то и сами они равны:
Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН1. Он должен будет пройти и через точки Н2, Н3, … Нn. Причем отрезки ОН1, ОН2, ОН3 окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:
Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А1, ∠А2, ∠А3, то есть в точке О. Так как расстояние от О до А1А2 – это отрезок ОН1, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.
Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.
Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН1, ОН2, ОН3,… проведены в равнобедренных треуг-ках∆ОА1А2, ∆ОА2А3, ∆ОА3А4,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н1, Н2, Н3,… – это середины сторон многоуг-ка.
Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?
Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.
Ответ: не могут.
Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.
Формулы для правильного многоугольника
Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой an, где n– число сторон у многоуг-ка. Например a4– это сторона квадрата, a6– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.
Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу
для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.
Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:
Теперь можно найти и ∠А1ОН1, рассмотрев ∆А1ОН1:
Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:
С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).
Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.
Решение. Запишем следующую формулу:
Это равенство как раз и надо было доказать в этом задании.
Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.
Решение. Запишем формулу:
Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.
Решение.
Найдем периметр шестиугольника:
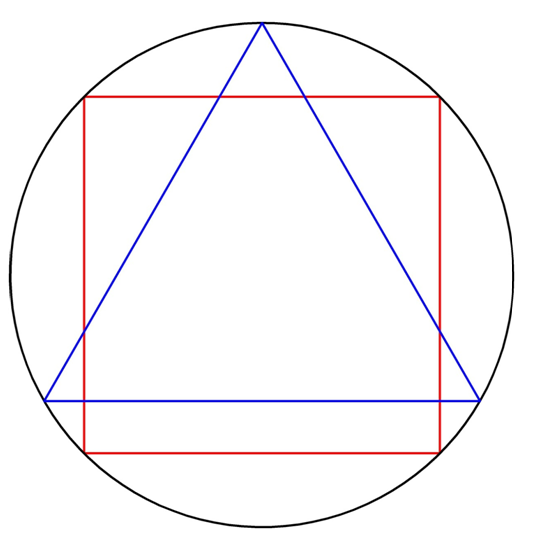
Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?
Решение. Зная периметр треуг-ка, легко найдем и его сторону:
Далее вычисляется радиус описанной около треугольника окружности:
Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?
Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:
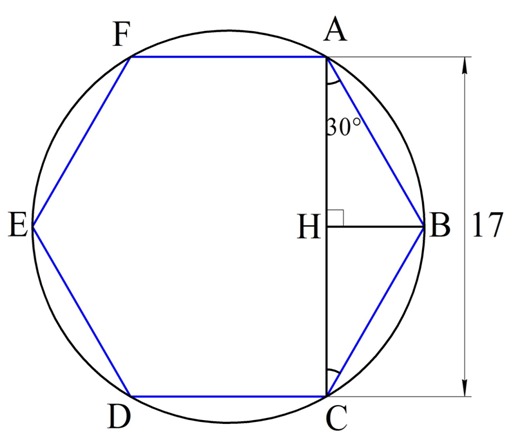
Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:
Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:
В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:
Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:
AC = 17 мм
∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:
AH = AC/2 = 17/2 = 8,5 мм
Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:
Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.
Ответ: 20 мм.
Построение правильных многоугольников
При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.
Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:
a6 = R
На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а6. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а6. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.
Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.
Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.
Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:
Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.
Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.
В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.
Содержание
- 1 Формулы расчёта параметров правильного восьмиугольника
- 2 Правильный восьмиугольник (понятие и определение):
- 3 Литература
- 4 Применение восьмиугольников
- 5 Построение
- 6 Признаки и свойства
- 7 Другие восемнадцатиугольники фигуры
- 8 Свойства
- 9 Площадь через квадрат
- 10 Симметрия
- 11 Формулы расчёта параметров правильного восьмиугольника[править | править код]
- 12 Площадь через квадрат[править | править код]
Формулы расчёта параметров правильного восьмиугольника
Пример:
- t — длина стороны восьмиугольника
- r — радиус вписанной окружности
- R — радиус описанной окружности
- S — площадь восьмиугольника
- k — константа, равная (1+2){displaystyle (1+{sqrt {2}})} ≈ 2,414213562373095
Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной kt{displaystyle kt}, радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:
Радиус вписанной окружности правильного восьмиугольника:
- r=k2t{displaystyle r={frac {k}{2}}t}
Радиус описанной окружности правильного восьмиугольника:
- R=tkk−1{displaystyle R=t{sqrt {frac {k}{k-1}}}}
Площадь правильного восьмиугольника:
Через сторону восьмиугольника
- S=2kt2=2(1+2)t2≃4.828t2.{displaystyle S=2kt^{2}=2(1+{sqrt {2}})t^{2}simeq 4.828,t^{2}.}
Через радиус описанной окружности
- S=4sinπ4R2=22R2≃2.828R2.{displaystyle S=4sin {frac {pi }{4}}R^{2}=2{sqrt {2}}R^{2}simeq 2.828,R^{2}.}
Через апофему (высоту)
- A=8tanπ8r2=8(2−1)r2≃3.314r2.{displaystyle A=8tan {frac {pi }{8}}r^{2}=8({sqrt {2}}-1)r^{2}simeq 3.314,r^{2}.}
Правильный восьмиугольник (понятие и определение):
Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.
Рис. 3. Правильный восьмиугольник
Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.
Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.
Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Литература
- Pierre Wantzel. Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas // Journal de Mathématiques. — 1837. — С. 366–372.
-
W. W. Rose Ball, H. S. M.Coxeter. Mathematical recreations and Essays. — Thirteenth edition. — New York: The MacMillan company, 1947. — С. 141.
Перевод: Математические эссе и развлечения / перевод Н.И. Плужниковой, А.С.Попова, Г.М. Цукерман, под редакцией И.М.Яглома. — Москва: «Мир», 1986. — С. 156.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — Chaim Goodman-Strauss, 2008. — С. 275—278. — ISBN 978-1-56881-220-5.
- Branko Grünbaum. Metamorphoses of polygons // The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History. — 1994.
- Jay Bonner. Islamic geometric pattens. — Springer, 2017. — ISBN 978-1-4419-0216-0.
- Nielsen D. Design & Nature V: Comparing Design in Nature with Science and Engineering // Fifth international conference on comapring design in nature with science engineering / Angelo Carpi, C. A. Brebbia. — WIT Press, 2010. — ISBN 978-1-84564-454-3.
- Вёрман К. История искусств всех времен и народов. — Москва, Берлин: Директ-медиа, 2015. — Т. 3 Книга2-3. — ISBN 978-5-4475-3827-9.
Применение восьмиугольников
Дорожный знак «Движение без остановки запрещено»
Восьмиугольный план Купола Скалы
В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.
Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и . Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.
Построение
Точное построение
Проводим большую окружность k₁ (будущую описанную окружность семнадцатиугольника) с центром O.
Проводим её диаметр AB.
Строим к нему перпендикуляр m, пересекающий k₁ в точках C и D.
Отмечаем точку E — середину DO.
Посередине EO отмечаем точку F и проводим отрезок FA.
Строим биссектрису w₁ угла ∠OFA.
Строим w₂ — биссектрису угла между m и w₁, которая пересекает AB в точке G.
Проводим s — перпендикуляр к w₂ из точки F.
Строим w₃ — биссектрису угла между s и w₂. Она пересекает AB в точке H.
Строим окружность Фалеса (k₂) на диаметре HA. Она пересекается с CD в точках J и K.
Проводим окружность k₃ с центром G через точки J и K. Она пересекается с AB в точках L и N
Здесь важно не перепутать N с M, они расположены очень близко.
Строим касательную к k₃ через N.
Точки пересечения этой касательной с исходной окружностью k₁ — это точки P₃ и P₁₄ искомого семнадцатиугольника. Если принять середину получившейся дуги за P₀ и отложить дугу P₀P₁₄ по окружности три раза, все вершины семнадцатиугольника будут построены.
Примерное построение
Следующее построение хоть и приблизительно, но гораздо более удобно.
- Ставим на плоскости точку M, строим вокруг неё окружность k и проводим её диаметр AB;
- Делим пополам радиус AM три раза по очереди по направлению к центру (точки C, D и E).
- Делим пополам отрезок EB (точка F).
- строим перпендикуляр к AB в точке F.
Вкратце: строим перпендикуляр к диаметру на расстоянии 9/16 диаметра от B.
Точки пересечения последнего перпендикуляра с окружностью являются хорошим приближением для точек P₃ и P₁₄.
При этом построении получается относительная ошибка в 0,83%. Углы и стороны получаются таким образом немного больше, чем нужно. При радиусе 332,4 мм сторона получается длиннее на 1 мм.
Признаки и свойства
Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:
Стороны равны между собой.
Любой угол правильного пятиугольника равен остальным его углам.
Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:
Равенство сторон.
Углы равны по 108 градусов.
Центры вписанной и описанной окружностей совпадают.
Сумма внутренних углов равна 180 * (5 – 2) = 540 (градусов), а внешних – 360.
Количество диагоналей соответствует 5.
Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.
Биссектрисы, проведенные через центр, равны.
Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.
Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.
Другие восемнадцатиугольники фигуры
Звёздчатые 18{displaystyle 18}-угольники имеют символы {18n}{displaystyle {18/n}}. Существует два правильных звёздчатых многоугольника: 185{displaystyle {18/5}} и {187}{displaystyle {18/7}}. Они используют те же самые вершины, но соединяют каждую пятую или седьмую вершину. Имеются также составные восемнадцатиугольники: {182}{displaystyle {18/2}} эквивалентен 2{9}{displaystyle 2{9}} (двум девятиугольникам), {183}{displaystyle {18/3}} эквивалентен 3{6}{displaystyle 3{6}} (трём шестиугольникам), {184}{displaystyle {18/4}} и {188}{displaystyle {18/8}} эквивалентны 2{92}{displaystyle 2{9/2}} и 2{94}{displaystyle 2{9/4}} (двум эннеаграммам), {186}{displaystyle {18/6}} эквивалентен 6{3}{displaystyle 6{3}} (6{displaystyle 6} равносторонним треугольникам), и, наконец, {189}{displaystyle {18/9}} эквивалентен 9{2}{displaystyle 9{2}} (девять двуугольников).
| Составные и звёздчатые многоугольники | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вид | Выпуклый многоугольник | Составные | Звёздчатый многоугольник | Составной | Звёздчатый многоугольник | Составной | |||
| Рисунок |
{181}{displaystyle {18/1}} = {18}{displaystyle {18}} |
{182}{displaystyle {18/2}} = 2{9}{displaystyle 2{9}} |
{183}{displaystyle {18/3}} = 3{6}{displaystyle 3{6}} |
{184}{displaystyle {18/4}} = 2{92}{displaystyle 2{9/2}} |
{185}{displaystyle {18/5}} |
{186}{displaystyle {18/6}} = 6{3}{displaystyle 6{3}} |
{187}{displaystyle {18/7}} |
{188}{displaystyle {18/8}} = 2{94}{displaystyle 2{9/4}} |
{189}{displaystyle {18/9}} = 9{2}{displaystyle 9{2}} |
| Внутренний угол | 160∘{displaystyle 160^{circ }} | 140∘{displaystyle 140^{circ }} | 120∘{displaystyle 120^{circ }} | 100∘{displaystyle 100^{circ }} | 80∘{displaystyle 80^{circ }} | 60∘{displaystyle 60^{circ }} | 40∘{displaystyle 40^{circ }} | 20∘{displaystyle 20^{circ }} | ∘{displaystyle 0^{circ }} |
Более глубокие усечения правильного многоугольника и правильной эннеаграммы дают равноугольные (вершинно-транзитивные) промежуточные восемнадцатиугольники с находящимися на равном расстоянии вершинами и двумя длинами сторон. Другие усечения дают двойное покрытие: t{98}={188}=2{94},t{94}={184}=2{92},t{92}={182}=2{9}{displaystyle mathrm {t} {9/8}={18/8}=2{9/4},;mathrm {t} {9/4}={18/4}=2{9/2},;mathrm {t} {9/2}={18/2}=2{9}}.
| Вершинно-транзитивные усечения девятиугольника и эннеаграмм | |||||
|---|---|---|---|---|---|
| Квазиправильные | Изогональные | КвазиправильныеДвойное покрытие | |||
|
t9=18{displaystyle mathrm {t} {9}={18}} |
t98=188{displaystyle mathrm {t} {9/8}={18/8}}=294{displaystyle =2{9/4}} |
||||
|
t95=185{displaystyle mathrm {t} {9/5}={18/5}} |
t94=184{displaystyle mathrm {t} {9/4}={18/4}}=292{displaystyle =2{9/2}} |
||||
|
t97=187{displaystyle mathrm {t} {9/7}={18/7}} |
t92=182{displaystyle mathrm {t} {9/2}={18/2}}=29{displaystyle =2{9}} |
Многоугольники Петри
Правильный восемнадцатиугольник является многоугольником Петри для ряда политопов, что показано в косоортогональных проекциях на :
| Восемнадцатиугольные многоугольники Петри | |||||||
|---|---|---|---|---|---|---|---|
| A17 | B9 | D10 | E7 | ||||
|
17-симплекс |
Эннеракт |
> |
Свойства
Координаты
Пусть xC{displaystyle x_{C}} и yC{displaystyle y_{C}} — координаты центра, а R{displaystyle R} — радиус описанной вокруг правильного многоугольника окружности, ϕ{displaystyle {phi }_{0}} — угловая координата первой вершины, тогда декартовы координаты вершин правильного n-угольника определяются формулами:
- xi=xC+Rcos(ϕ+2πin){displaystyle x_{i}=x_{C}+Rcos left({phi }_{0}+{frac {2pi i}{n}}right)}
- yi=yC+Rsin(ϕ+2πin){displaystyle y_{i}=y_{C}+Rsin left({phi }_{0}+{frac {2pi i}{n}}right)}
где i=…n−1{displaystyle i=0dots n-1}
Размеры
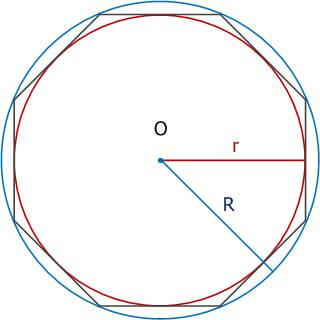
Правильный многоугольник, вписанный и описанный около окружности
Пусть R{displaystyle R} — радиус описанной вокруг правильного многоугольника окружности, тогда радиус вписанной окружности равен
- r=Rcosπn{displaystyle r=Rcos {frac {pi }{n}}},
а длина стороны многоугольника равна
- a=2Rsinπn=2rtgπn{displaystyle a=2Rsin {frac {pi }{n}}=2rmathop {mathrm {tg} } ,{frac {pi }{n}}}
Площадь
Площадь правильного многоугольника с числом сторон n{displaystyle n} и длиной стороны a{displaystyle a} составляет:
- S=n4 a2ctgπn{displaystyle S={frac {n}{4}} a^{2}mathop {mathrm {} } ,operatorname {ctg} {frac {pi }{n}}}.
Площадь правильного многоугольника с числом сторон n{displaystyle n}, вписанного в окружность радиуса R{displaystyle R}, составляет:
- S=n2R2sin2πn{displaystyle S={frac {n}{2}}R^{2}sin {frac {2pi }{n}}}.
Площадь правильного многоугольника с числом сторон n{displaystyle n}, описанного вокруг окружности радиуса r{displaystyle r}, составляет:
- S=nr2tgπn{displaystyle S=nr^{2}mathop {mathrm {tg} } ,{frac {pi }{n}}}(площадь основания n-угольной правильной призмы)
Площадь правильного многоугольника с числом сторон n{displaystyle n} равна
- S=nra2{displaystyle S={frac {nra}{2}}},
где r{displaystyle r} — расстояние от середины стороны до центра, a{displaystyle a} — длина стороны.
Площадь правильного многоугольника через периметр (P{displaystyle P}) и радиус вписанной окружности (r{displaystyle r}) составляет:
- S=12Pr{displaystyle S={frac {1}{2}}Pr}.
Периметр
Если нужно вычислить длину стороны an{displaystyle a_{n}} правильного n-угольника, вписанного в окружность, зная длину окружности L{displaystyle L} можно вычислить длину одной стороны многоугольника:
- an{displaystyle a_{n}} — длина стороны правильного n-угольника.
- an=sin180n⋅Lπ{displaystyle a_{n}=sin {frac {180}{n}}cdot {frac {L}{pi }}}
Периметр Pn{displaystyle P_{n}} равен
- Pn=an⋅n{displaystyle P_{n}=a_{n}cdot n}
где n{displaystyle n} — число сторон многоугольника.
Площадь через квадрат
Площадь правильного восьмиугольника можно вычислить как площадь усечённого квадрата.
Площадь можно также вычислить как усечение квадрата
- S=A2−a2,{displaystyle S=A^{2}-a^{2},}
где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.
Если задана сторона a, то длина A равна
- A=a2+a+a2=(1+2)a≈2.414a.{displaystyle A={frac {a}{sqrt {2}}}+a+{frac {a}{sqrt {2}}}=(1+{sqrt {2}})aapprox 2.414a.}
Тогда площадь равна:
- S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{displaystyle S=((1+{sqrt {2}})a)^{2}-a^{2}=2(1+{sqrt {2}})a^{2}approx 4.828a^{2}.}
Площадь через A (ширину восьмиугольника)
- S=2(2−1)A2≈0.828A2.{displaystyle S=2({sqrt {2}}-1)A^{2}approx 0.828A^{2}.}
Ещё одна простая формула площади:
- S=2aA.{displaystyle S=2aA.}
Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем
- a≈A2.414.{displaystyle aapprox A/2.414.}
Два катета углового треугольника можно получить по формуле
- e=(A−a)2.{displaystyle e=(A-a)/2.}
Симметрия
11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.
Правильный восьмиугольник имеет группу симметрии Dih8 порядка 16. Имеется 3 диэдральные подгруппы — Dih4, Dih2 и Dih1, а также 4 циклические подгруппы — Z8, Z4, Z2 и Z1. Последняя подгруппа подразумевает отсутствие симметрии.
Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 . Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.
|
r16 |
||
|---|---|---|
|
d8 |
g8 |
p8 |
|
d4 |
g4 |
p4 |
|
d2 |
g2 |
p2 |
|
a1 |
На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.
Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.
Формулы расчёта параметров правильного восьмиугольника[править | править код]
Пример:
- t — длина стороны восьмиугольника
- r — радиус вписанной окружности
- R — радиус описанной окружности
- S — площадь восьмиугольника
- k — константа, равная (1+2){displaystyle (1+{sqrt {2}})} ≈ 2,414213562373095
Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной kt{displaystyle kt}, радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:
Радиус вписанной окружности правильного восьмиугольника:
- r=k2t{displaystyle r={frac {k}{2}}t}
Радиус описанной окружности правильного восьмиугольника:
- R=tkk−1{displaystyle R=t{sqrt {frac {k}{k-1}}}}
Площадь правильного восьмиугольника:
Через сторону восьмиугольника
- S=2kt2=2(1+2)t2≃4.828t2.{displaystyle S=2kt^{2}=2(1+{sqrt {2}})t^{2}simeq 4.828,t^{2}.}
Через радиус описанной окружности
- S=4sinπ4R2=22R2≃2.828R2.{displaystyle S=4sin {frac {pi }{4}}R^{2}=2{sqrt {2}}R^{2}simeq 2.828,R^{2}.}
Через апофему (высоту)
- A=8tanπ8r2=8(2−1)r2≃3.314r2.{displaystyle A=8tan {frac {pi }{8}}r^{2}=8({sqrt {2}}-1)r^{2}simeq 3.314,r^{2}.}
Площадь через квадрат[править | править код]
Площадь правильного восьмиугольника можно вычислить как площадь усечённого квадрата.
Площадь можно также вычислить как усечение квадрата
- S=A2−a2,{displaystyle S=A^{2}-a^{2},}
где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.
Если задана сторона a, то длина A равна
- A=a2+a+a2=(1+2)a≈2.414a.{displaystyle A={frac {a}{sqrt {2}}}+a+{frac {a}{sqrt {2}}}=(1+{sqrt {2}})aapprox 2.414a.}
Тогда площадь равна:
- S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{displaystyle S=((1+{sqrt {2}})a)^{2}-a^{2}=2(1+{sqrt {2}})a^{2}approx 4.828a^{2}.}
Площадь через A (ширину восьмиугольника)
- S=2(2−1)A2≈0.828A2.{displaystyle S=2({sqrt {2}}-1)A^{2}approx 0.828A^{2}.}
Ещё одна простая формула площади:
- S=2aA.{displaystyle S=2aA.}
Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем
- a≈A2.414.{displaystyle aapprox A/2.414.}
Два катета углового треугольника можно получить по формуле
- e=(A−a)2.{displaystyle e=(A-a)/2.}