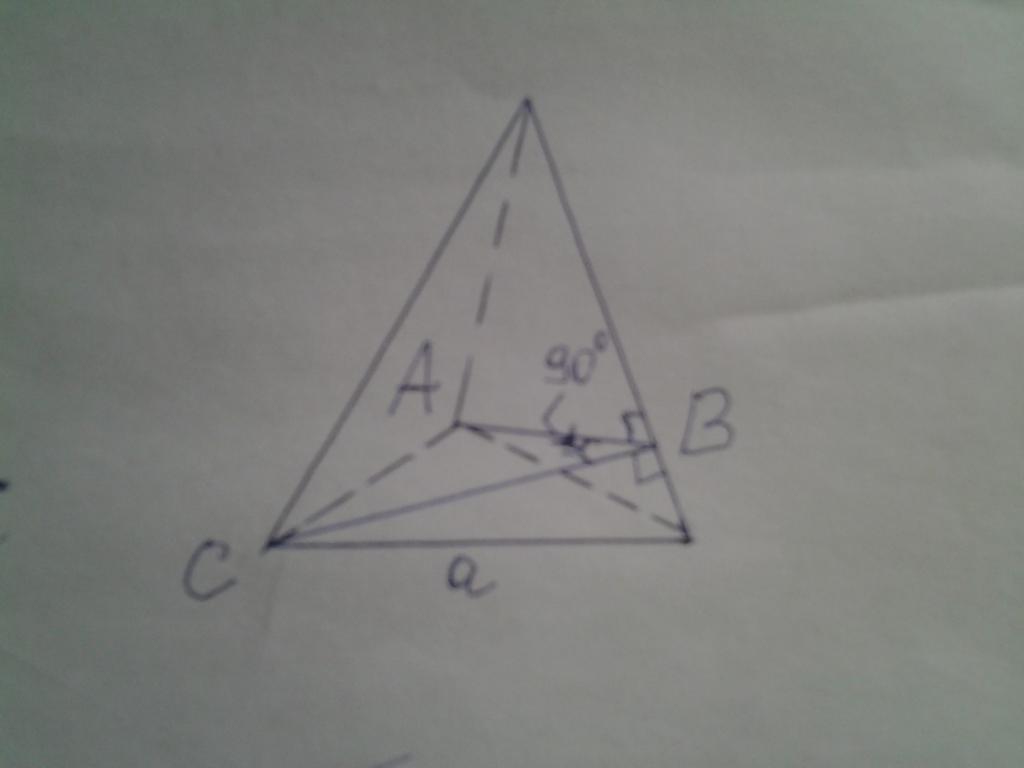Как найти угол в правильной шестиугольной пирамиде

Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.

Обозначения

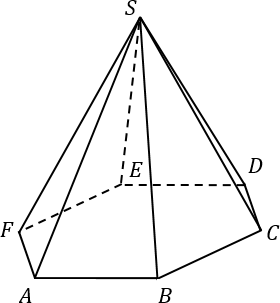
• $SABCDEF$ — правильная шестиугольная пирамида
• $O$ — центр основания пирамиды
• $a$ — длина стороны основания пирамиды
• $h$ — длина бокового ребра пирамиды
• $S_{text{осн.}}$ — площадь основания пирамиды
• $V_{text{пирамиды}}$ — объем пирамиды

Площадь основания пирамиды

В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$

Правильный шестиугольник в основании пирамиды

По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a, angle EOA=120^{circ}$. По свойствам равнобедренного треугольника $$ AE=acdotsqrt{2(1-cos EOA)}=sqrt{3}cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=sqrt{3}cdot a $, $FM=MO=frac{1}{2}cdot a$.

Находим $SO$

Прямая $SO$ является высотой пирамиды, поэтому $angle SOF=90^{circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a, FS=h$. По свойствам прямоугольного треугольника $$ SO=sqrt{FS^2-FO^2}=sqrt{h^2-a^2} $$

Объем пирамиды

Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{пирамиды}}=frac{1}{3}cdot S_{text{осн.}}cdot SO=frac{sqrt{3}}{2}cdot a^2 cdot sqrt{h^2-a^2} $$

Находим $ST$ и $TO$

Пусть точка $T$ является серединой ребра $AF$. Треугольник $AOF$ правильный, поэтому, по свойствам правильного треугольника $$ TO=frac{sqrt{3}}{2}cdot a $$ Треугольник $STO$ прямоугольный, высота $SO$ равна $sqrt{h^2-a^2}$. По теореме Пифагора $$ ST=sqrt{SO^2+TO^2}=sqrt{h^2-frac{1}{4}cdot a^2} $$

22 января 2014

Основная проблема всех стереометрических задач (и B13 в частности) — понять, где расположен линейный угол двугранного угла, либо просто угла между плоскостью и прямой.

Просто запомните: углы в стереометрии всегда связаны с перпендикулярами. Именно поэтому в задаче B13 так часто дается высота. Как ее использовать — смотрите в сегодняшнем видеоуроке.

Задача B13. Высота правильной шестиугольной пирамиды равна 42. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите боковое ребро пирамиды.

Практика показывает, что после небольшой тренировки большинство учеников начинают решать такие задачи вообще устно. Поэтому не поленитесь и прорешайте несколько аналогичных примеров.

Смотрите также:

1. Углы и отрезки в стереометрии — 2
2. Пример простейшего перехода
3. Тест к уроку «Что такое логарифм» (тяжелый)
4. Сводный тест по задачам B12 (1 вариант)
5. Как решать простейшие логарифмические уравнения
6. Задача B4: резка стекол

Очень просто. Для этого достаточно знать, что на любой окружности можно отметить

лишь 6 точек без остатка, на расстоянии равном радиусу этой оеружности.

Если эти точки соединить прямыми линиями — получим правильный вписанный шестиугольник сторона которого равна радиусу этой окружности.

Теперь, можем смело разрезать (рассечь) нашу призму, через вершину и две

противолежащие верщины шести угольника — в сечении получим треугольник

со сторонами 6м, 6м и основанием равным двум радиусам 3+3=6м.

В итоге выясняется, что все стороны треугла равны — а у равностороннего треугла,

из основ геометрии извесно, что все углы равны меж собой, и равны 60 градусам.

Отсюда и угол наклона ребра к основанию призмы = 60 градусам.

Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, — это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.

Пространственная фигура пирамида

Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово «пирамида». Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.

Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.

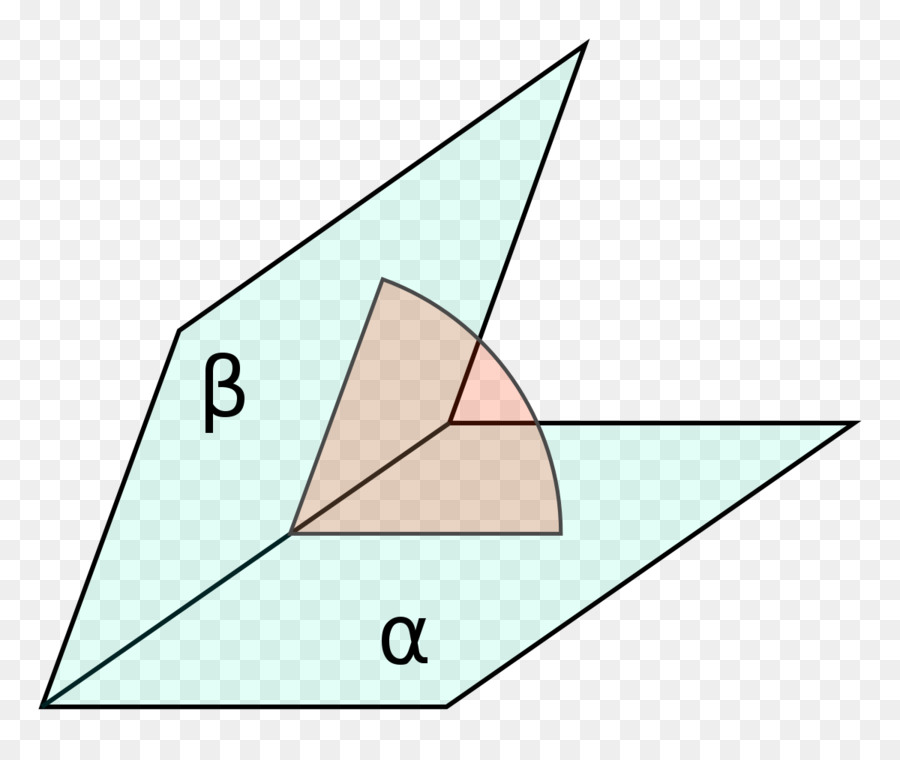
Двугранные углы фигуры

Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.

Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:

• При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n — число сторон многоугольника.
• Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.

Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип — на боковых ребрах.

Как рассчитать углы пирамиды?

Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.

В трехмерном пространстве плоскость задается следующим выражением:

A*x + B*y + C*z + D = 0

Где A, B, C, D — это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:

n¯ = [A; B; C]

Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.

Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:

n₁¯ = [A₁; B₁; C₁];

n₂¯ = [A₂; B₂; C₂]

Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:

φ = arccos(|(n₁¯*n₂¯)|/(|n₁¯|*|n₂¯|))

Или в координатной форме:

φ = arccos(|A₁*A₂ + B₁*B₂ + C₁*C₂|/(√(A₁² + B₁²+C₁²)*√(A₂² + B₂² + C₂²)))

Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.

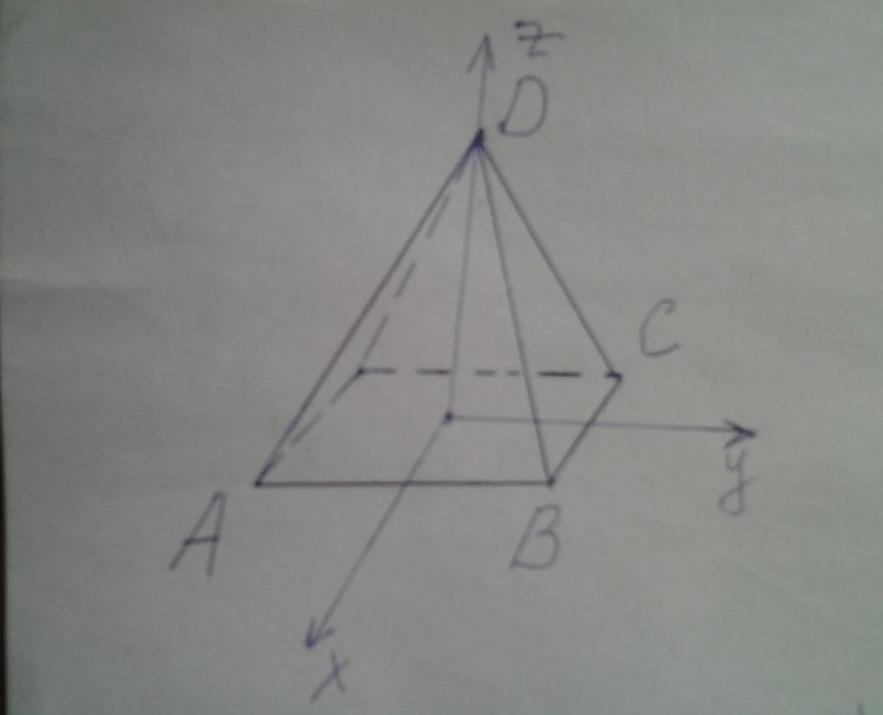
Углы правильной пирамиды четырехугольной

Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.

Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.

Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:

A(a/2; -a/2; 0);

B(a/2; a/2; 0);

C(-a/2; a/2; 0);

D(0; 0; h)

Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:

Для ABC:

AB¯ = (0; a; 0); AC¯ = (-a; a; 0); n₁¯ = [AB¯*AC¯] = (0; 0; a²)

Для ABD:

AB¯ = (0; a; 0); AD¯ = (-a/2; a/2; h); n₂¯ = [AB¯*AD¯] = (a*h; 0; a²/2)

Для BCD:

BC¯ = (-a; 0; 0); BD¯ = (-a/2; -a/2; h); n₃¯ = [BC¯*BD¯] = (0; a*h; a²/2)

Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:

Угол между ABC и ABD:

(n₁¯*n₂¯) = a⁴/2; |n₁¯| = a²; |n₂¯| = a*√(h² + a²/4);

φ = arccos(a⁴/2/(a²*a*√(h² + a²/4))) = arccos(a/(2*√(h² + a²/4))) = 67,38^o

Угол между ABD и BDC:

(n₂¯*n₃¯) = a⁴/4; |n₂¯| = a*√(h² + a²/4) ; |n₃¯| = a*√(h² + a²/4);

φ = arccos(a⁴/(4*a²*(h²+a²/4)) = arccos(a²/(4*(h²+a²/4))) = 81,49^o

Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.

Углы треугольной правильной пирамиды

На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.

Двугранный угол, равный 90^o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры — h, апофему — h_b и боковое ребро — b. Теперь можно записать следующие формулы:

S = 1/2*a*h_b;

b² = h_b² + a²/4;

b² = h² + a²/3

Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:

x = a/√2;

S = 1/2*b*a/√2

Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:

1/2*a*h_b = 1/2*b*a/√2 =>

h_b = b/√2;

b² = b ²/2 + a²/4 =>

b = a/√2;

a²/2 = h² + a²/3 =>

a = h*√6

Площадь равностороннего треугольника рассчитывается так:

S = √3/4*a² = 3*√3/2*h²

Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см².

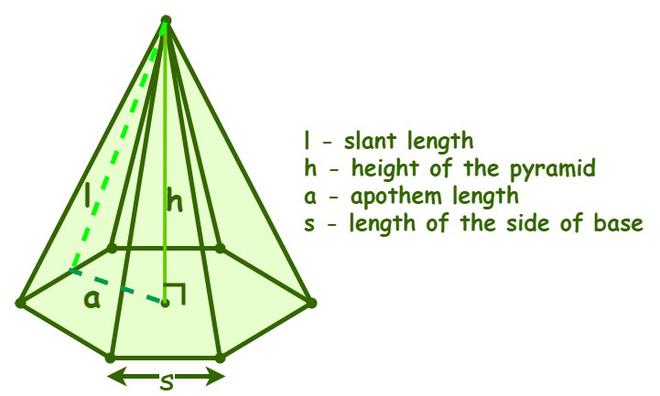
A hexagonal pyramid is a three-dimensional shaped pyramid that has a hexagonal base along with the sides or faces in the shape of isosceles triangles that meet at the apex or the top of the pyramid. A hexagonal pyramid is one of the different types of pyramids, which are classified based on the shape of the base of a pyramid. It is also known as a heptahedron since a hexagonal pyramid consists of 7 faces, which includes a hexagonal base and 6 isosceles triangular lateral faces. It has a total of seven faces, twelve edges, and seven vertices. One of the seven vertices is the apex, which is at the top, and the other six are at the base of the pyramid. Out of the twelve edges, six edges connect the triangle edges that meet at the apex, and the other six are the edges of the base.

 Regular Hexagonal Pyramid

A regular hexagonal pyramid is a pyramid whose hexagonal base is regular and the pyramid is straight, whereas an irregular hexagonal pyramid is a pyramid whose hexagonal base is irregular and the pyramid is oblique. A right regular pyramid is a hexagonal pyramid with a regular hexagonal base and, the apex of the pyramid is right above the center of the base, such that the apex forms a right angle with the center of the base and any other vertex.

Regular Hexagonal Pyramid formula

There are two formulas for a regular hexagonal pyramid, i.e., the surface area of a regular hexagonal pyramid and the volume of a regular hexagonal pyramid. To calculate the surface area or the volume of a regular hexagonal pyramid, we need to know its four major aspects, i.e., the length of the side of the base; the apothem, which is the distance from the center of the base to any point on the side of the base; the height of the pyramid, which is the perpendicular distance from the apex to the center of the base; and finally the slant height of the pyramid, which is the height of the triangular faces or the perpendicular distance from the apex to any point on the boundary of the base of the pyramid.

Lateral surface area (LSA)

The lateral surface area is the region occupied by the lateral surfaces or triangular faces of a regular hexagonal pyramid. The formula to determine the lateral surface area of the regular hexagonal pyramid (LSA) is given as follows,

The lateral surface area of the regular hexagonal pyramid = The sum of areas of the lateral surfaces (triangles) of the pyramid

= 6 × [½ × base × height] =3 (s × l)

Lateral surface area of the regular hexagonal pyramid = 3(s × l)

Where,

“s” is the side length of the base, and

“l” is the slant height of the pyramid. 

Total surface area (TSA)

The total surface area is the total region occupied by all the surfaces of a regular hexagonal pyramid, i.e., the area occupied by the lateral surfaces, or triangular faces, and also is hexagonal base. 

Total surface area of a pyramid (TSA) = Lateral surface area of the pyramid + Base area

The surface area of the hexagonal pyramid can be calculated when we have the slant height of the pyramid which is the height from the apex to any point on the boundary of the base of the pyramid. Hence, let us see both the formula of the hexagonal pyramid – base area and surface area.

Base area = 3as

Where,

“a” is the apothem length, and

“s” is the side length of the base.

TSA = LSA + Base area

TSA = 3sl + 3as

Hence,

Total surface area of the regular hexagonal pyramid (TSA) = 3sl + 3as

Where,

“s” is the side length of the base, 

“l” is the slant height, and 

“a” is the apothem length.

When the apothem of the regular hexagonal pyramid is not mentioned and the triangular faces are equilateral, there is another alternative formula to calculate its surface area, i.e.,

Total surface area of the hexagonal pyramid = 3(s × l) + 3√3/2 (s)²

Where, 

“s” is the side length of the base, and 

“l” is the slant height of the pyramid. 

Area of the hexagonal base = 3√3/2 (s)²

Volume of the regular hexagonal pyramid

The volume is the total space enclosed between all the faces of a regular hexagonal pyramid. The general formula for calculating the volume of a pyramid is equal to one-third of the product of the base area and the height of the pyramid.

Volume (V) = (1/3) × Base area × Height cubic units

Now, by substituting the values of the base area and the height, we get

Volume of the regular hexagonal pyramid = (a × s × h) cubic units

Where,

“a” is the apothem length,

“s” is the side length of the base, and

“h” is the height of the pyramid. 

When the apothem of the regular hexagonal pyramid is not mentioned and the triangular faces are equilateral, there is another alternative formula to calculate its volume, i.e.,

Volume of the regular hexagonal pyramid (V)= (√3/2) × s² × h cubic units

Where,

“s” is the side length of the base, and

“h” is the height of the pyramid. 

Practice Problems based on Regular Hexagonal Pyramid

Problem 1: What is the volume of a regular hexagonal pyramid whose apothem length is 5 cm, length of the side of the base is 10 cm, and height is 13 cm?

Solution: 

Given data,

Apothem length (a) = 5 cm

The length of the side of the base  = 10 cm,

The height of the pyramid = 13 cm

We know that,

The volume of a regular hexagonal pyramid (V) = (a × s × h) cubic units

V = 5 × 10 × 13

Volume = 650 cm³

Therefore, the volume of the given hexagonal pyramid is 650 cu. cm.

Problem 2: What is the surface area of a regular hexagonal pyramid if its apothem length is 6 inches, the length of the side of the base is 8 inches, and the slant height is 15 inches?

Solution: 

Given data,

Apothem length (a) = 6 inches

The length of the side of the base (s)  = 8 inches

The slant height of the pyramid (l) = 15 inches

We know that,

The surface area of the hexagonal pyramid = 3as + 3sl square units

= 3 × 6 × 8 + 3 × 8 × 15

= 144 + 360 = 504 sq. in

Therefore, the surface area of the given pyramid is 504 sq. in.

Problem 3: Find the height of a regular hexagonal pyramid if its volume is 576 cu. cm, the length of the side of the base is 8 cm, and the apothem length is 8 cm.

Solution:

Given data,

Apothem length (a) = 8 cm

The length of the side of the base (s) = 8 cm

Volume = 576 cu. cm

We know that,

The volume of a regular hexagonal pyramid (V) = (a × s × h) cubic units

⇒ 8 × 8 × h = 576

⇒ 64h = 576

⇒ h = 576/64 = 9 cm

Hence, the height of a regular hexagonal pyramid is 9 cm.

Problem 4: What is the volume of a regular hexagonal pyramid if the sides of a base are 7 cm each and the height of the pyramid is 14 cm?

Solution:

Given data,

Height of the pyramid (h) = 14 cm

The length of the side of the base (s) = 7 cm

Area of the hexagonal base (A) = 3√3/2 b² = 3√3/2 (7)² = 147√3/2 sq. cm

The volume of a regular hexagonal pyramid (V) = 1/3 × A × h

V = 1/3 × (147√3/2) × 14 = 594.09 cm³

Hence, the volume of the given pyramid is 594.09 cm³.

 Problem 5: Determine the lateral surface area of a regular hexagonal pyramid if the side length of the base is 15 inches and the pyramid’s slant height is 21 inches.

Solution:

Given data,

The length of the side of the base (s) = 15 inches, and

Slant height (l) = 21 inches

The perimeter of the square base (P) = 6s = 6(15) = 90 inches

We know that,

The lateral surface area (LSA) = (½) Pl

= (½ ) × (90) × 21 = 945 sq. in

Therefore, the lateral surface area of the given pyramid is 945 sq. in.

FAQs based on Regular Hexagonal Pyramid

Question 1: What is a Hexagonal Pyramid?

Answer:

A hexagonal pyramid is a 3D shape with hexagonal base combined with 6 triangles faces against each sides of the hexagonal base erected  in such a way to form a pyramid at its apex. These triangles may be either isosceles triangles or equilateral triangles and these triangles are called as lateral faces. A hexagonal pyramid contains 7 vertices, 7 faces, and 12 edges.

Question 2: What is the formula for finding the volume of the Hexagonal Pyramid?

Answer:

The formula for calculating the volume of the hexagonal pyramid is given by,

Volume of Hexagonal Pyramid(V) = (abh) cubic units

where,

a is the apothem of the pyramid,

b is the base, and h is the height.

Question 3: What is the formula for finding the Surface Area of a Hexagonal Pyramid?

Answer:

Formula for finding the surface area of a hexagonal pyramid is given by,

Surface Area of Hexagonal Pyramid (TSA)= (3ab + 3bs) square units,

where,

a is the apothem of the pyramid,

b is the base, and

s is the slant height of the pyramid.