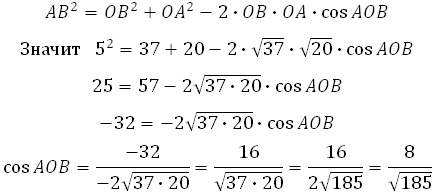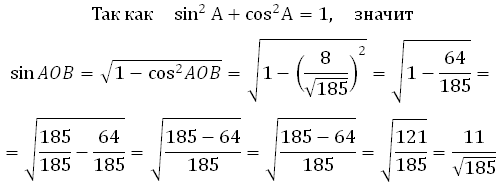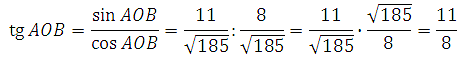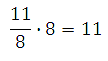Как найти угол синуса аов

Условие задачи

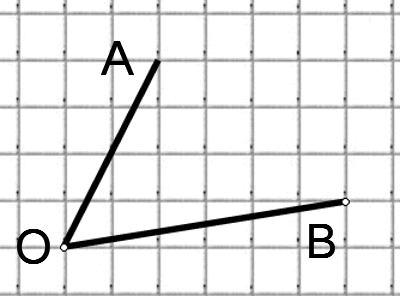
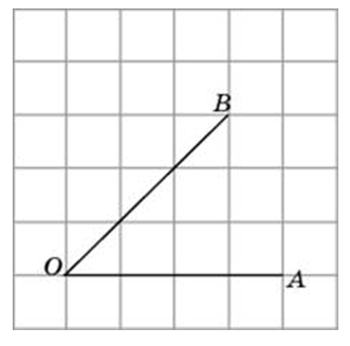
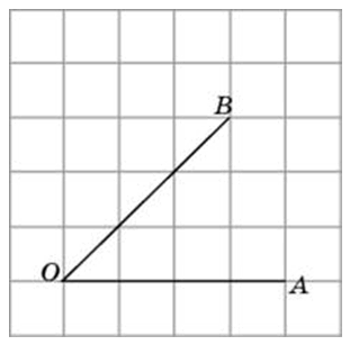
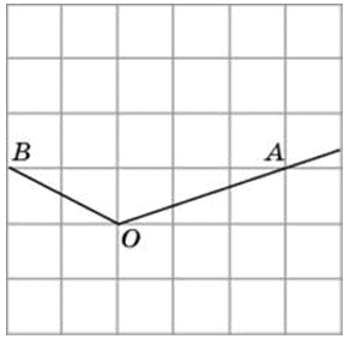
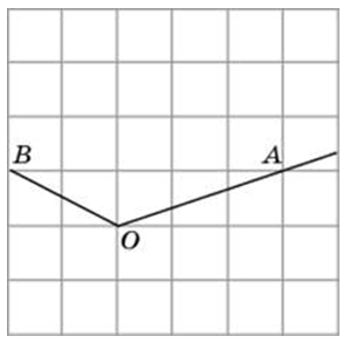
Найдите синус угла АОВ, изображённого на рисунке.

Решение

Опустим из точки В перпендикуляр на прямую ОА. Получим прямоугольный треугольник, катеты которого равны 3 и 4. По теореме Пифагора, его гипотенуза равна 5. Тогда синус угла АОВ равен Мы нашли синус угла как отношение противолежащего катета к гипотенузе.

Ответ:

0,6.

Найдите синус угла AOB изображенного на рисунке?

Геометрия | 5 — 9 классы

Найдите синус угла AOB изображенного на рисунке.

Рисунок во вложении.

Я просто не помню как делать.

Нам обьясняли что сначало нужно достроить до треугольника потом по теореме пифагора.

Ответ должен получится 0, 6.

ОА = 4 клетки, АВ = 3 клетки.

По теореме Пифагора : квадрат гипотенузы ОВ = квадрат катета ОА + квадрат катета АВ

Синус угла АОВ = АВ / ОВ = 3 / 5 = 0, 6.

Найдите синус угла ВАС треугольника АВС, изображенного на рисунке?

Найдите синус угла ВАС треугольника АВС, изображенного на рисунке.

Найдите синус угла ВАС треугольника АВС, изображенного на рисунке?

Найдите синус угла ВАС треугольника АВС, изображенного на рисунке.

Найдите косинус угла AOB, изображенного на рисунке?

Найдите косинус угла AOB, изображенного на рисунке.

ПОМОГИТЕ ПОЖАЛУЙСТА?

Найти синус угла AOB, изображенного на рисунке , ДОЛЖНО ПОЛУЧИТСЯ 0.

Найдите синус угла, изображенного на рисунке?

Найдите синус угла, изображенного на рисунке.

Определите углы треугольника со сторонами 1, корень из 3, 2 без синусов косинусов по теореме пифагора?

Определите углы треугольника со сторонами 1, корень из 3, 2 без синусов косинусов по теореме пифагора!

Найдите синус угла аов , изображенного на рисунке?

Найдите синус угла аов , изображенного на рисунке.

Найдите синус угла AOB изображенного на рисунке?

Найдите синус угла AOB изображенного на рисунке.

Найдите тангенс угла AOB, изображенного на рисунке?

Найдите тангенс угла AOB, изображенного на рисунке.

Найдите синус угла ВАС треуголника АВС, изображенного на рисунке?

Найдите синус угла ВАС треуголника АВС, изображенного на рисунке.

Вы перешли к вопросу Найдите синус угла AOB изображенного на рисунке?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Геометрия. Урок 1. Задания. Часть 2.

№8. Найдите тангенс угла A O B , изображенного на рисунке.

Решение:

Опустим перпендикуляр A H на сторону O B .

Рассмотрим прямоугольный △ A O H :

Тангенс угла – отношение противолежащего катета к прилежащему.

tg ∠ A O H = A H O H = 4 2 = 2

№9. Найдите тангенс угла A треугольника A B C б изображённого на рисунке.

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ B A C = B C A C = 2 5 = 0,4

№10. На рисунке изображена трапеция A B C D . Используя рисунок, найдите sin ∠ B A H .

Решение:

Рассмотрим прямоугольный △ A B H :

Синус угла – отношение противолежащего катета к гипотенузе.

sin ∠ A = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 3 2 + 4 2

A B 2 = 9 + 16 = 25

A B = ± 25 = [ − 5 не подходит 5 подходит

sin ∠ A = B H A B = 4 5 = 0,8

№11. На рисунке изображен ромб A B C D . Используя рисунок, найдите tg ∠ O B C .

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ O B C = O C B O = 3 4 = 0,75

№12. На рисунке изображена трапеция A B C D . Используя рисунок, найдите cos ∠ H B A .

Решение:

Рассмотрим прямоугольный △ A B H :

Косинус угла – отношение прилежащего катета к гипотенузе.

cos ∠ A B H = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 6 2 + 8 2

A B 2 = 36 + 64 = 100

A B = ± 100 = [ − 10 не подходит 10 подходит

cos ∠ A B H = B H A B = 8 10 = 0,8

№13. Найдите тангенс угла, изображенного на рисунке.

Решение:

tg β = tg ( 180 ° − α ) = − tg α

Рассмотрим прямоугольный △ B C H .

Тангенс угла – отношение противолежащего катета к прилежащему.

tg α = C H B H = 3 1

tg β = − tg α = − 3

№14. Найдите тангенс угла A O B .

Решение:

Опустим высоту B H на сторону O A .

Рассмотрим прямоугольный △ O B H :

Найдем B H и O H по теореме Пифагора:

B H 2 = 2 2 + 8 2 = = 4 + 64 = 68

B H = ± 68 = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит

O H 2 = 1 2 + 4 2 = 1 + 16 = 17

O H = ± 17 = [ − 17 не подходит 17 подходит

Синус угла. Таблица синусов.

Синус угла через градусы, минуты и секунды

Синус угла через десятичную запись угла

Как найти угол зная синус этого угла

У синуса есть обратная тригонометрическая функция — arcsin(y)=x

Пример sin(30°) = 1/2; arcsin(1/2) = 30°

Определение синуса

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

Периодичность синуса

Функция y = sin(x) периодична, с периодом 2π

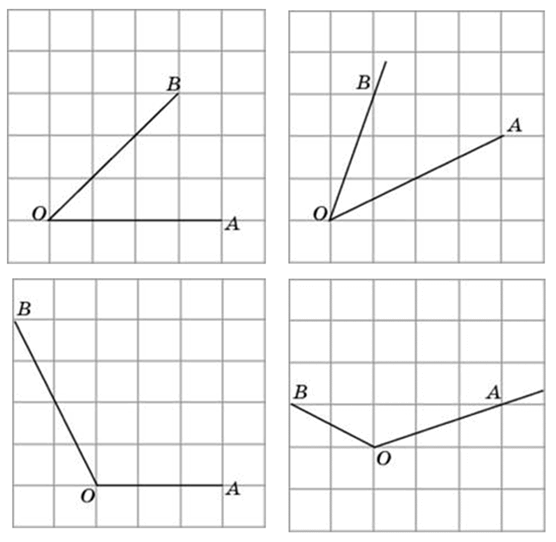
Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике. 

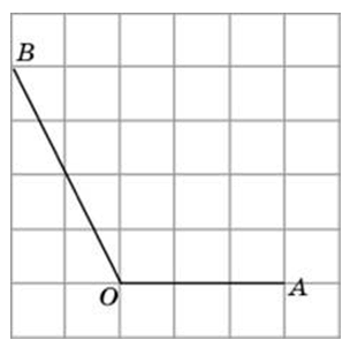
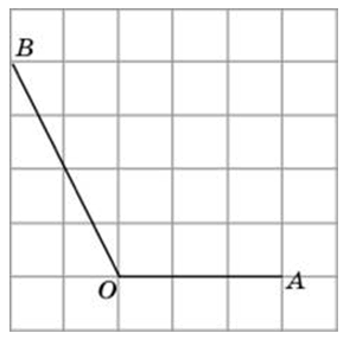
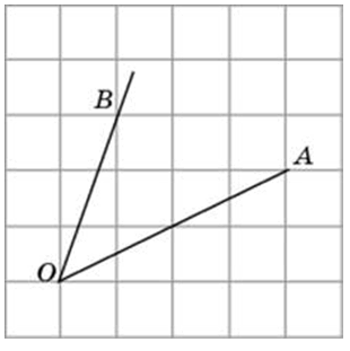
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):

Итак, рассмотрим задание:

Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.

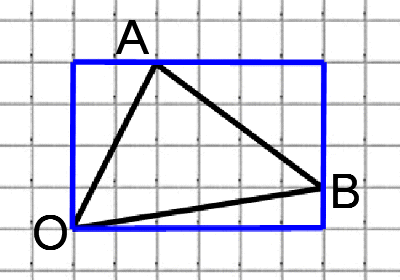
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.

Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).

АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,

ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1, 

OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,

По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус  угла между ними.

Из основного тригонометрического тождества можем найти sin AOB:

*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение. 

Теперь можем найти тангенс:

Умножим результат на 8 и запишем ответ:

Ответ: 11

Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.

Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.

Посмотреть решение

Найдите тангенс угла AOB.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.

Посмотреть решение

Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на  два корня из двух.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.

Посмотреть решение

Найдите тангенс угла AOB.

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите!

С уважением, Александр Крутицких.

*Делитесь информацией в социальных сетях )

Спрятать решение