Сдвиг фаз между током и напряжением в цепи переменного тока
Содержание
- 1 Определения и основные формулы
- 2 ПТ и активная нагрузка
- 3 Конденсатор в цепи ПТ
- 4 Индуктивность в цепи ПТ
- 5 Видео по теме
При транспортировке электрической энергии от мест её генерации (тепловые, атомные и гидроэлектростанции) до конечных потребителей необходимо неоднократно варьировать величину напряжения (понижать или повышать). С наибольшей эффективностью эти преобразования удаётся сделать, когда в линиях электропередачи используется переменное напряжение. При этом электрический ток, возникающий в результате действия переменного электрического поля, будет также переменным, изменяясь во времени периодически с такой же частотой. Если в сети присутствуют реактивные элементы (ёмкости, индуктивности), то возникает сдвиг фаз между переменным током и напряжением.
Определения и основные формулы
Переменным принято называть ток, изменяющийся с течением времени как по величине, так и по амплитуде. В английской технической литературе используется термин alternating current (AC). Он переводится как «чередующийся ток» или ток, изменяющий свою полярность.
Периодический переменный ток (ПТ) — это ток, который через идентичные интервалы времени принимает исходную величину, совершая таким образом циклический процесс, аналогичный гармоническому колебанию маятника. Гармонические колебания описываются с помощью синусоидальной функции:
Величина, которая определяется как произведение ω на t и имеет размерность угла (в радианах угол 90 градусов соответствует π/2 радиан), называется фазой синусоидальной переменной. В данном случае тока. Формула справедлива для случая, когда измерение тока стартует с точки отсчёта t = 0. В общем случае рабочая формула выглядит так:
Используя специальный измерительный прибор — осциллограф, можно наблюдать синусоиду напряжения на экране и определять её параметры.
ПТ и активная нагрузка
Если к источнику переменного тока подключено обычное сопротивление (резистор), то согласно закону Ома ток на резисторе, равен:
В приведенной выше формуле величина I0 = U0 / R — амплитуда ПТ. Видно, что ток в цепи с активным сопротивлением изменяется с течением времени абсолютно синхронно с напряжением.
Таким образом, на активной нагрузке угол сдвига фаз между током и напряжением равен нулю.
Конденсатор в цепи ПТ
Конструкция конденсатора препятствует протеканию постоянного тока, полностью его блокируя. Поочерёдно заряжаясь и разряжаясь конденсаторные пластины поддерживают ток в цепи, поскольку по определению ток I — это изменение заряда Q за единицу времени:
Ниже представлена картинка, объясняющая подключение конденсатора С к источнику переменного напряжения U.
Напряжение на конденсаторе в любой момент времени равно напряжению:
Тогда заряд Q(t) на обкладках конденсатора определим, используя выражение:
Пользуясь формулой для тока, получим первую производную от заряда по времени, которая равна ёмкостному току Ic(t):
Из графиков, представленных на картинке ниже, видно, что максимальная амплитуда тока наступает на четверть периода раньше, чем напряжения. Из этого следует, что фаза напряжения на π/2 радиан меньше фазы электротока. То есть, в цепи синусоидального тока существует отставание напряжения по фазе (фазовый сдвиг) на π/2.
Данное явление может быть объяснено по-другому. Из курса тригонометрии известно, что:
С помощью формул, приведенных выше, можно получить такое выражение:
Данное соотношение в явном виде показывает, что фазовый сдвиг равен π/2.
Индуктивность в цепи ПТ
Катушка индуктивности в цепях СПТ является реактивным элементом, поскольку ее активное сопротивление практически равно нулю. При подключении катушки также возникает фазовый сдвиг, но его причина несколько иная, чем в цепи с емкостью.
При практически нулевом омическом сопротивлении не может возникнуть короткое замыкание (резкий рост тока), поскольку переменный характер напряжения включает иной механизм сопротивления. Согласно закону, открытому британским учёным Майклом Фарадеем, в катушке появляется переменное магнитное поле, которое создает магнитный поток F, инициирующий появление электродвижущей силы (ЭДС самоиндукции) на концах катушки индуктивности:
В соответствии с законом Фарадея:
Откуда следует, что:
Используя данную формулу, находим определение для тока на индуктивности:
Как известно,
Следовательно, в идеальном индуктивном элементе угол сдвига фаз между напряжением и током равен π/2, причём ток отстаёт по фазе от напряжения.
Из графика видно, что максимум силы тока достигается на четверть периода позже, чем максимум напряжения, что соответствует отставанию по фазе на π/2.
От угла сдвига фаз зависит, какова будет реактивная мощность и, следовательно, коэффициент мощности, который выражается через cosφ и является очень важной характеристикой для оценки эффективности работы электрооборудования. Его значение может находиться в диапазоне от нуля до единицы. Если cosφ = 0, это означает, что в электроцепи присутствуют лишь реактивные токи. На практике такая ситуация невозможна, но чтобы потери мощности, связанные с реактивными токами, были меньше, используют компенсационные устройства.
Принцип действия таких устройств основывается на свойстве конденсаторов и катушек сдвигать фазу в противоположных направлениях. Компенсаторы зачастую используют в производственных цехах, где работает большое количество электрооборудования. Это приводит к ощутимым потерям электроэнергии и ухудшению качества электротока. Устройство компенсации решает подобные проблемы. Им успешно силу тока изменяют, если что-то сдвигают. Обычно такое устройство состоит из блоков конденсаторов довольно большой емкости, которые помещаются в отдельных шкафах.
Видео по теме
Рассмотрим
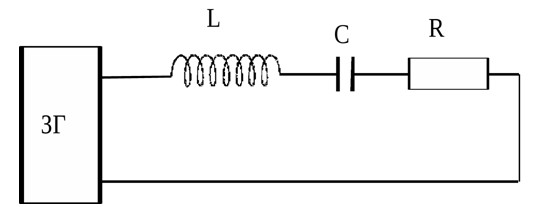
цепь переменного тока, состоящую из
последовательно соединенных сопротивления
R,
индуктивности L,
электроемкости С
и генератора
ЗГ (Рис.5). Пусть ЭДС генератора изменяется
по закону:
Тогда
сила тока в цепи будет изменяться по
тому же закону, но со сдвигом фазы:
.
Сдвиг
фазы можно определить теоретически
методом векторных диаграмм.
Известно,
что падение напряжения на активном
сопротивлении
совпадает
по фазе с током, падение напряжения на
индуктивности,опережает
ток на π/2, а падение напряжения на емкости,
отстает от тока на π/2.
Рис.5
Рис.6
Векторная
диаграмма напряжений для схемы,
изображенной на Рис. 5, показана на Рис.
6. Из рисунка видно, что разность фаз
междуи
(т.
е. между напряжением и током в цепи)
равна
(3).
Разность
фаз между током и напряжением в работе
создается с помощью фазовращающей
цепочки, которая состоит из последовательно
соединенных сопротивлений R
и емкости
С,
величины которых можно изменять в
процессе опыта (Рис. 5). В этом случае в
выражении (3) L=O
и для этой цели соотношение (3) упрощается,
и сдвиг фаз можно рассчитать по формуле:
(4),

v—
частота сигнала, снимаемого с генератора.
Для экспериментального определения
сдвига фаз используется основная фигура
Лиссажу — эллипс, который получается в
результате сложения напряжений одинаковой
частоты с генератора и с омического
сопротивления (см. Рис. 5).
Рис.7
Пусть
на Х-вход осциллографа подано напряжение,
изменяющееся со временем по закону:
а
на Y-вход — напряжение той же частоты, но
сдвинуто по фазе на φ0:
На
экране осциллографа будет наблюдаться
траектория движения электронного луча
в виде наклонного эллипса (см. Рис.5).
При х=О, получим
,
откуда
(5).
Таким
образом, для определения разности фаз
между током и напряжением достаточно
измерить максимальное отклонение луча
по вертикальной оси Y0
определить координату точки пересечения
эллипса с вертикальной осью Y и
воспользоваться формулой (5).
5Б. Проведение измерений по определению сдвига фаз.
Чтобы
создать сдвиг фаз между напряжениями,
подаваемыми на различные пластины,
пользуются фазовращающий цепочкой,
схема которой представлена на рис.7. В
такой цепочке падение потенциала на
омическом сопротивлении совпадает по
фазе, а падение потенциала на всей
цепочке отстает по фазе относительно
тока. Величина сдвига фазы определяется
постоянной времени цепочки =RС.
Измерение величины сдвига фазы
производится следующим образом.
Соберите
схему из звукового генератора, осциллографа
и фазовращающей цепочки согласно рис.
8. Частоту генератора сделайте равной
100 Гц,
а ручку «регул.
вых. сигн.»
поставьте посередине. Переключатели
осциллографа должны находиться в
положениях: «род
работы» — на
«усил.»,
«род
синхронизации»
— на «внешн.»,
«делитель»
1: К— 1: 100 или 1: 10.
Включите
генератор и осциллограф и, подобрав
разумную величину сигналов с помощью
ручек «синхронизация»
и «усиление
плавно»,
получите четкий эллипс. Ручками «смещение
X»
и «смещениеУ»
сместите
эллипс так, чтобы центр экрана совпадал
с пересечением осей эллипса. По сетке
шкалы экрана осциллографа замерьте
координату у
(при х
= 0) и амплитуду У0
и рассчитайте сдвиг фазы 0
(см. рис. 7).

Повторите
измерения для различных комбинаций R
и С,
в соответствии
со значениями, указанными на панели
фазовращающей цепочки.
Заполните табл. 2, затем выключите
генератор и осциллограф.
Необходимо
зарисовать в масштабе четыре положения
эллипса для рассмотренных комбинаций
RС.
Таблица №3.
|
№ |
С,Ф |
R,Ом |
Y |
Y0 |
|
|
|
|
|
1 |
||||||||
|
2 |
||||||||
|
3 |
||||||||
|
4 |
Соседние файлы в папке 19 27 72 74 75
- #
- #
- #
- #

Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.
Угол сдвига фаз находится при необходимости, тогда, если один из сигналов является опорным, а второй сигнал с фазой в самом начале совпадает с углом сдвига фаз.
Измерение угла сдвига фаз производится прибором, в котором присутствует нормированная погрешность.
Фазометр может производить измерение угла сдвига в границах от 0о до 360о в некоторых случаях от -180оС до +180оС, а диапазон измеряемых частот сигналов может колебаться от 20Гц до 20 ГГц. Измерение гарантируется в том случае если напряжение входного сигнала равно от 1 мВ до 100 В, если же напряжение входного сигнала превышает эти границы точность измерения не гарантируется.
Методы измерения угла сдвига фаз
Существует несколько способов измерения угла сдвига фаз, это:
- Использование двухлучевого или двухканального осциллографа.
- Компенсационный метод основан на сравнении измеряемого фазового сдвига, с фазовым сдвигом, который предоставляется образцовым фазовращателем.
- Суммарно-разностный метод, он заключается в использовании гармонических или сформированных прямоугольных сигналов.
- Преобразование сдвига фаз во временном интервале.
Как измеряется угол сдвига фаз осциллографом
Осциллографический способ можно отнести к самому простейшему с погрешностью в районе 5о. Определение сдвига осуществляется при помощи осциллограмм. Существует четыре осциллографических метода:
- Применение линейной развертки.
- Метод эллипса.
- Метод круговой развертки.
- Использование яркостных меток.
Определение угла сдвига фаз зависит от характера нагрузки. При определении фазного сдвига в первичной и вторичной цепях трансформатора, углы могут считаться равными и практически не отличаются друг от друга.
Угол сдвига фаз напряжений, измеряемый по эталонному источнику частоты и при использовании измерительного органа лает возможность обеспечить точность всех последующих измерений. Фазные напряжения и угол сдвига фаз зависят от нагрузки, так симметричная нагрузка обуславливает равенство фазного напряжения , токов нагрузки и угол фазного сдвига, также будет равна нагрузка по потребляемой мощности на всех фазах электроустановки.
Угол сдвига фаз между током и напряжением в несимметричных трехфазных цепях не равны друг другу. Для того чтобы вычислить угол сдвига фаз (угол φ) в цепь включают последовательно присоединенные сопротивления (резисторы), индуктивности и конденсаторы (емкости).
Рис. №1. Последовательное соединение сопротивления, индуктивности и емкости для вычисления угла сдвига фаз. В этом контуре протекает переменный ток, который способствует возникновению ЭДС.
Рис. №2. Схема проведения опыта по определению сдвига фаз между током и напряжением. Слева показаны схемы подключения конденсаторов, катушек индуктивности и резисторов, справа показаны результаты опыта.
Из результатов опыта можно определить, что сдвиг фаз между напряжением и током служит при определении нагрузки и не может зависеть от переменных величины тока и напряжения в электрической сети.
Как вывод, можно сказать, что:
- Составляющие элементы комплексного сопротивления, такие как резистор и емкость, а также проводимость не будут взаимообратными величинами.
- Отсутствие одного из элементов делает резистивные и реактивные значения, которые входят в состав комплексного сопротивления и проводимости и делают их величинами взаимообратными.
- Реактивные величины в комплексном сопротивлении и проводимости используются с противоположным знаком.
Угол сдвига фаз между напряжением и током всегда выражается, как главный аргументированный фактор комплексного сопротивления φ.
Сдвиг фаз переменного тока и напряжения
Мощность постоянного тока, как мы уже знаем, равна произведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При переменном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденсаторов и катушек индуктивности.
Для этого случая формула мощности
остается справедливой.
На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.
При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.
О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.
Представим себе, что при начале вращения радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.
Рассмотрим, как будут изменяйся при этом ток и напряжение. Из построенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.
Затем напряжение достигает своей наибольшей величины и начинает уже убывать, а ток хотя и становится положительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Действительно, если мы посмотрим на рисунок 2, то заметим, что синусоида тока сдвинута вправо относительно синусоиды напряжения. Так как по горизонтальной оси мы откладываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.
Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с направлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величины на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источником ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрицательной, тем, следовательно, меньше будет средняя мощность тока.
При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).
Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.
Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т. е. формулы
в этом случае будут неверны
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Фазовый сдвиг
При наличии в цепи индуктивного или емкостного сопротивлений
сдвиг по фазе между током и напряжением составляет +π/2.
Если цепь содержит еще и активное сопротивление (полностью устранить которое невозможно), то фазовый сдвиг лежит в пределах
[ frac{π}{2} > φ > -frac{π}{2} ]
Разность фаз φ между током и напряжением изображается на векторной диаграмме для этих величин.
На векторной диаграмме сопротивлений φ — это угол между активным и реактивным сопротивлениями или проводимостями.
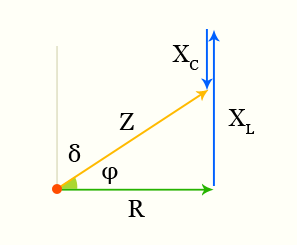
Фазовый сдвиг при последовательном соединении
В случае последовательного соединения R,С и L из формулы реактивного сопротивления следует
Фазовый сдвиг — векторная диаграмма сопротивлений для последовательного соединения
[ tg(φ) = frac{ωL — frac{1}{ωC}}{R} ]
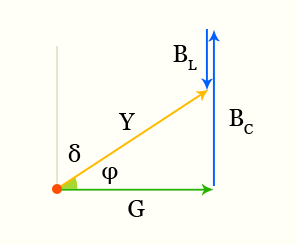
Фазовый сдвиг при параллельном соединении
В случае параллельного соединения R, С и L из формулы реактивного сопротивления следует
Фазовый сдвиг — векторная диаграмма сопротивлений для параллельного соединения
[ tg(φ) = R (ωC — frac{1}{ωL}) ]
Во многих случаях (например, при параллельном соединении большой емкости и большого активного сопротивления
или последовательном соединении большой индуктивности и очень малого активного сопротивления)
фазовый сдвиг оказывается близким к π/2 = 90°.
Из-за трудности определения φ в этих случаях пользуются углом потерь δ:
[ δ = 90° — φ ]
откуда
[ tg(δ) = frac{1}{tg(φ)} = ctg(φ) ]
Фазовый сдвиг |
стр. 692 |
|---|