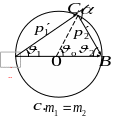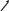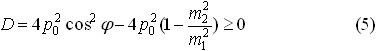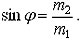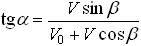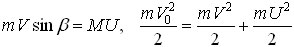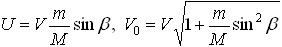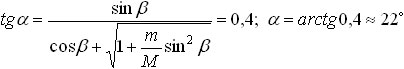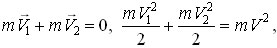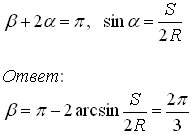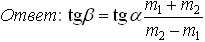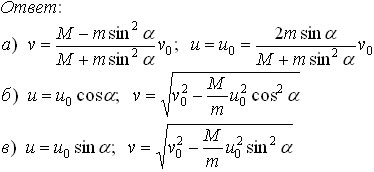Как найти угол разлета

2.5.2*. На покоящийся шар налетает шар такой же массы. Найдите угол разлета шаров после нецентрального упругого удара.

Решение.

Рассмотрим векторный треугольник импульсов тел (см. рис.)

$vec{p_0} = vec{p_1} + vec{p_2}$.

Воспользуемся теоремой косинусов

$p_1^2 + p_2^2 + 2p_1p_2cosalpha = p_0^2$. (1)

Здесь $p_0$ — модуль начального импульса шара до взаимодействия, $p_1, p_2$ — модули импульсов шаров после соударения, $alpha$ — угол разлета шаров.

Так как кинетическая энергия равна $E = frac{mv^2}{2}$, а импульс тела $p = mv$, то $E = frac{p^2}{2m}$. (2)

Воспользовавшись уравнение связи кинетической энергии и импульса тела (2) запишем закон сохранения кинетической энергии при упругом столкновении шаров:

$frac{p_0^2}{2m_1} = frac{p_1^2}{2m_1} + frac{p_2^2}{2m_2}$. (3)

По условию задачи $m_1 = m_2 = m$,

тогда уравнение (3) примет вид

$p_0^2 = p_1^2 + p_2^2$. (4)

Решая совместно уравнения (1) и (4) получаем

$2p_1p_2cosalpha = 0 Rightarrow cosalpha = 0 Rightarrow alpha = frac{pi}{2}$,

Ответ: угол разлета шаров после нецентрального упругого удара равен $frac{pi}{2}$

Столкновение двух
частиц называется упругим,
если оно не сопровождается изменением
их внутреннего состояния. Поэтому при
описании упругого соударения в законе
сохранения энергии внутреннюю энергию
тел можно не учитывать.

Выберем лабораторную
систему отсчета, где одна из частиц
обладает импульсом

,
а вторая покоится (
)
и запишем законы сохранения энергии и
импульса:

.

(14.17)

Выразим

из закона сохранения импульса и подставим
в закон сохранения энергии:

Введя угол

между векторами

и

,
выразим

:

.
(14.18)

Полученный
результат можно интерпретировать
геометрически с помощью векторных
диаграмм, построенных для различных
соотношений масс сталкивающихся частиц:

;

и

.

Обозначим

,
(14.19)

где

приведенная
масса,

скорость
налетающей частицы (вторая частица
покоится

),

и проведем окружность
радиусом

.

Построим вектор

.

Из (14.19) следует

.
(14.20)

Направленный
отрезок

на диаграмме изображает импульс

налетающей частицы до рассеяния. При
этом точка

лежит внутри
(если

),
вне
(если

)
или на
окружности
(если

).

Из (14.20) видно,
что

складывается из отрезков

и

,
пропорциональных массам сталкивающихся
частиц,

и

,
соответственно.

В свою очередь
из (14.18) следует, что диаметр окружности,
равный

,

будучи умноженным
на

,
дает вектор

(см. рисунок:

как
угол, вписанный в окружность).

Из уравнения
(14.17) следует, что вектору

на диаграмме соответствует отрезок,
направленный из точки

в точку

.
Тогда

угол
отклонения 1-ой частицы (налетающей) от
её первоначального направления движения
после столкновения.

Угол

угол разлета
1 и 2-ой частиц после столкновения.

Возможные
направления рассеяния первой частицы
определяются вращением вектора

вокруг точки

.
При этом конец вектора

(точка

)
всегда должен лежать на окружности
радиусом

.

При

угол рассеяния

может принимать значения от

до

,
а угол разлета

изменяется от

до

.

При

очевидно, что существует максимальный
угол отклонения налетающей частицы

,
определяемый точкой касания вектором

окружности:

.

угол разлета

в этом случае изменяется от

до

.

Угол

соответствует центральному удару, или
лобовому столкновению частиц.

При

все точки начала и конца векторов лежат
на

окружности. Угол

,
т.е. разлет частиц происходит под

прямым углом. В
этом случае

.

Исключением
является лобовое столкновение, при
котором

.

Тот же
результат можно получить аналитически,
решая

совместно
уравнения законов сохранения энергии
и импульса:

,

.

Возводя в
квадрат второе уравнение и сравнивая
с первым, легко убедиться, что совместно
эти уравнения могут быть удовлетворены
лишь при указанных значениях углов.

На всех рисунках
центральный угол

представляет собой угол поворота первой
частицы в системе центра инерции. Из
рисунков видно, что углы

и

связаны с углом

соотношениями:

,

.

Модули скоростей
частиц после столкновения выражаются
через угол

и скорость налетающей частицы следующим
образом:

,

,

где

.

1.15. Рассеяние
частиц.

15.1. Рассеяние
частицы на силовом центре.
Формула
Резерфорда.

Рассмотрим
снова рассеяние частицы на силовом
центре.

Если на налетающую
частицу действуют силы отталкивания,
то, как мы установили в § 13, её движение
всегда инфинитно, а траектория частицы
— гипербола.

Для
рассмотрения задачи введем

прицельное
расстояние – длина

перпендикуляра,
опущенного из

рассеивающего
центра на направление

касательной
к траектории (асимптоту гиперболы)

находящейся
на бесконечно большом удалении

от
центра частицы,

угол
рассеяния частицы,

масса
частицы,

скорость
налетающей частицы на

бесконечно
большом удалении от центра.

Угол

определяет наклон асимптот гиперболы,
по которой движется рассеиваемая частица
(см. рисунок и уравнение (13.17)), к оси

и связан с углом рассеяния

очевидным
соотношением

(15.1)

Значение угла

может быть найдено из уравнения (13.17),
если положить, что частица находится
на бесконечно большом удалении от
рассеивающего центра (
).
В этом случае уравнение (13.17) приводится
к виду:

и

.

(15.1а)

Тогда, с учетом
(15.1) и (15.1а),

.

Учитывая (13.5),
получаем

.
(15.2)

На бесконечно
большом расстоянии от рассеивающего
центра (
,

),
полная энергия и момент импульса частицы
равны

.
(15.3)

Подставляя эти
величины в выражение (15.2), получаем
формулу, связывающую угол рассеяния

с прицельным параметром

:

.

(15.4)

Заметим, что
при движении частицы в поле притяжения
(
)
связь между углом рассеяния и прицельным
параметром получается точно такой же,
т.е. также выражается формулой (15.4).

Задача о
рассеянии на силовом центре имеет важное
практическое значение. Однако, формулу
(15.4) не удается непосредственно
использовать для описания результатов
эксперимента, т.к. она написана для
определенного прицельного параметра

и определяет индивидуальное отклонение
частицы. В эксперименте же мы имеем дело
не с отдельной частицей, а наблюдаем
рассеяние целого пучка одинаковых
частиц, падающих на рассеивающий центр
с одинаковыми
скоростями

,
но с разными
значениями прицельного параметра

.
Следовательно, и рассеиваются частицы
под разными углами

.

Поэтому в физике
вводится другая, очень важная,
характеристика процесса рассеяния —
сечение
или эффективное
сечение.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задачи на непрямой упругий удар практически не рассматриваются в курсе школьной физики. В то же время такие задачи встречаются в заданиях олимпиад различного уровня, в том числе вузовских олимпиад, включаемых в перечень Министерства образования, призеры которых имеют право засчитывать свой результат как высший балл по ЕГЭ. В связи с этим представляется целесообразным рассматривать задачи на непрямой упругий удар на школьном факультативе по физике, что в течение ряда лет и делается в Лицее научно-инженерного профиля города Королева. Кроме того, на факультативе имеется возможность систематизировано изложить подходы к решению данных задач, разбросанных по различным задачникам и учебным пособиям. Представляется, что данная статья может быть полезной как для учителей физики школ с углубленным изучением предмета, так и для абитуриентов.

Задача 1. На покоящийся шар налетает шар такой же массы. Найдите угол разлета шаров после нецентрального упругого удара. [1,2]

Решение. Используя теорему косинусов для треугольника импульсов, представленного на рисунке, запишем закон сохранения импульса в виде:

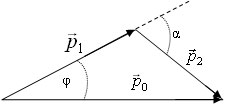
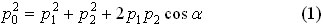
где p₀ – модуль импульс налетающего шара до удара, p₁ – модуль импульса налетающего шара после удара, p₂ – модуль импульса покоящегося шара после удара, α – угол разлета шаров. Закон сохранения энергии запишем также через импульсы шаров:

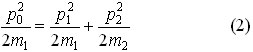
Если m₁ = m₂, то из уравнений (1) и (2) следует, что cosα = 0 и α = π/2.

Ответ: α = π/2.

Задача 2. Тяжелая частица массы m₁ сталкивается с покоящейся легкой частицей массы m₂. На какой наибольший угол может отклониться тяжелая частица в результате упругого удара? [1]

Решение. Запишем закон сохранения импульса в виде (рисунок к задаче 1):

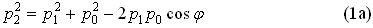
где p₀ – модуль импульса налетающей частицы до удара, p₁ – модуль импульса налетающей частицы после удара, p₂ – модуль импульса покоящейся частицы после удара, φ – искомый угол отклонения налетающей частицы. Закон сохранения энергии запишем также через импульсы частиц:

Из второго уравнения выразим

И подставим в (1а). Тогда

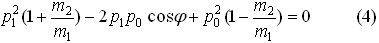
Детерминант уравнения (4) должен быть больше или равен нуля:

Отсюда получаем ограничение на угол отклонения налетающей частицы:

Максимальный угол отклонения имеет место, когда детерминант равен нулю. Для этого угла

Ответ:

Важным обстоятельством при упругом нецентральном ударе является то, что ввиду отсутствия сил трения, силы взаимодействия соударяющихся тел направлены по нормали к поверхности их соприкосновения.

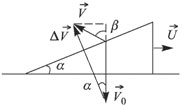
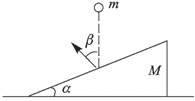
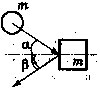
Задача 3. На горизонтальном столе покоится клин массой М = 4 кг. Сверху на клин падает шарик массой m = 1 кг. Определить угол при основании клина α, если известно, что после упругого удара о клин шарик отскочил под углом β = 45° к вертикали. Трением пренебречь.[3]

Решение. Поскольку смещения шарика и клина за время соударения пренебрежимо малы (удар, как обычно, считается мгновенным), а также из-за отсутствия трения, силы взаимодействия шарика и клина направлены по нормали к наклонной плоскости. Следовательно, изменение импульса шарика при ударе также будет направлено по нормали к наклонной плоскости клина (смотри рисунок, где через V₀ и V обозначены скорости шарика до и после удара соответственно, U — скорость клина после удара). Из рисунка видно, что

Используя закон сохранения импульса в проекции на горизонтальное направление и закон сохранения кинетической энергии при упругом ударе, получаем следующие равенства:

Отсюда

Объединяя записанные выражения, получаем ответ.

Ответ:

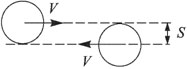
Задача 4. Два одинаковых шара радиусами R летят навстречу друг другу с одинаковыми скоростями как показано на рисунке. Расстояние между линиями движения центров шаров S = R. На какой угол β повернется вектор скорости каждого из шаров после удара? Удар считать упругим, шары – идеально гладкими. [3]

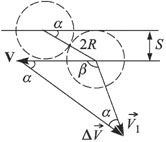
Решение. Обозначим через 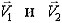 скорости шаров после удара. Используя законы сохранения импульса и энергии

находим, что V₁ = V₂ = V, т.е. модули скоростей шаров после удара останутся прежними. Из предположения о кратковременности удара вытекает, что приращение импульса каждого из шаров направлено по линии, соединяющей центры шаров в момент удара. Из рисунка видно, что

Задачи для самостоятельного решения.

1. [1] Частица массы m₁ налетает на шар массы m₂. Направление ее движения составляет угол α с нормалью к поверхности шара. Под каким углом к этой нормали отскочит от шара частица, если шар сначала покоился, а удар упругий?

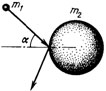
2. [1] При упругом столкновении налетающей частицы с покоящейся первая полетела под углом α к направлению первоначального движения, а вторая – под углом β. Найдите отношение масс этих частиц.

m₁ – масса налетающей частицы.

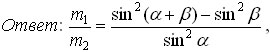
3. [1] Частица массы m₁ налетела со скоростью v на неподвижную частицу массы m₂, которая после упругого удара полетела под углом α к первоначальному направлению движения налетающей частицы. Определите скорость частицы массы m₂ после удара.

4. [2] По центру неподвижного кубика, лежащего на гладкой горизонтальной поверхности, наносят удар шариком той же массы, так, что начальная скорость шарика v направлена под углом α к оси симметрии кубика. Определить скорость v₁ и v₂ шарика и кубика после удара. Под каким углом β к оси симметрии кубика полетит шарик после удара?

Ответ: v₁ = v sinα; v₂ = v cosα; β = π/2

5. [2] Шариком массой m наносят удар по клину. Масса клина M, угол при основании α. Удар абсолютно упругий. Трением можно пренебречь. Определить скорость шарика v и скорость клина u после удара, если скорость шарика перед ударом равна v₀ и направлена: а) перпендикулярно поверхности клина; б) по вертикали; в) по горизонтали.

Литература:

1. Задачи по физике: Учеб. пособие/ И.И. Воробьев, П.И. Зубков, Г.А. Кутузова и др.; Под ред. О.Я. Савченко. − 2-е изд., перераб. − М.: Наука. Гл. ред. физ.-мат. лит. 1988. – 416 с.
2. Дмитриев С.Н., Васюков В.И., Струков Ю.А. Физика: Сборник задач для поступающих в вузы. Изд. 7-е, доп. М: Ориентир. 2005. – 312 с.
3. Драбович К.Н., Макаров В.А., Чесноков С.С. Физика. Практический курс для поступающих в университеты. – М.: ФИЗМАТЛИТ, 2006. – 544 с. – ISBN 5-9221-0652-Х.

2016-11-20   

На покоящийся гладкий шар налетает другой такой же шар. Удар абсолютно упругий, нецентральный. Найти угол разлета шаров. Внешними силами пренебречь.

Решение:

Запишем закон сохранения импульса для системы из двух шаров в начальном состоянии (до удара) и конечном (после удара):

$m vec{v}_{0} = m vec{v}_{1} + m vec{v}_{2}$, (1)

где обозначения указаны на рисунке. Запишем также закон сохранения полной механической энергии для тех же начального и конечного состояний системы

$frac{mv_{0}^{2}}{2} = frac{mv_{1}^{2}}{2} + frac{mv_{2}^{2}}{2}$. (2)

Умножим уравнение (1) скаляр но само на себя (или, что то лее самое, возведем обе части (1) в квадрат) и вычтем из получившегося равенства (2), предварительно сократив (1) на $m$, а (2) на $frac{m}{2}$. Получим:

$2v_{1} cdot v_{2} cdot cos alpha = 0$.

Поскольку $v_{1}$ и $v_{2}$ по условию задачи не равны нулю (удар нецентральный), то $cos alpha = 0$ или $alpha = frac{ pi}{2}$, то есть шары разлетаются под прямым углом.

Полученный результат остается в силе, если рассмотреть столкновение шаров на гладкой горизонтальной поверхности. Действительно, в этом случае сила тяжести и сила реакции со стороны поверхности, действующие на каждый шар, друг друга компенсируют (движения шаров по вертикали нет). Следовательно, (1, 2) имеют место.

Решение.
Полная энергия фотона и электрона до столкновения равна:

Е_ф +m∙с² = 3∙m∙с²   (1).

После столкновения электрон приобретает импульс p_е, и его полная энергия становится равной:

[ {{E}_{e}}=sqrt{p_{e}^{2}cdot {{c}^{2}}+{{m}^{2}}cdot {{c}^{4}}} (2). ]

Импульс рассеянного электрона может быть найден из закона сохранения энергии, полная энергия до столкновения равна полной энергии после столкновения:

[  sqrt{p_{e}^{2}cdot {{c}^{2}}+{{m}^{2}}cdot {{c}^{4}}} +mcdot {{c}^{2}} =3cdot mcdot {{c}^{2}}, {{p}_{e}} =sqrt{3}cdot mcdot c (3). ]

По условию задачи, энергия рассеянного фотона и импульс равны:

[ {{E}_{pPhi }}=frac{{{E}_{Phi }}}{2}=mcdot {{c}^{2}}, {{p}_{pPhi }}=frac{mcdot {{c}^{2}}}{c} =mcdot c (4). ]

По условию задачи, энергия фотона и импульс фотона равны:

[ {{E}_{Phi }}=2cdot mcdot {{c}^{2}}, {{p}_{Phi }}=frac{2cdot mcdot {{c}^{2}}}{c} =2cdot mcdot c (5). ]

Покажем рисунок. По теореме косинусов определим угол разлёта α между рассеянным фотоном и электроном отдачи.

[ p_{Phi }^{2}=p_{e}^{2}+p_{pPhi }^{2}+2cdot {{p}_{e}}cdot {{p}_{pPhi }}cdot cos alpha , cos alpha =frac{p_{Phi }^{2}-(p_{e}^{2}+p_{pPhi }^{2})}{2cdot {{p}_{e}}cdot {{p}_{pPhi }}}. ]

соsα = 0, α = 90°.