Как найти угол равнобедренного тупоугольного треугольника

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Равнобедренным называется треугольник, у которого две стороны равны.

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

Равнобедренный тупоугольный треугольник – основание, формула

Равнобедренный треугольник наиболее часто встречается в задачах по геометрии. Так сложилось, что равнобедренный треугольник не столь прост в решении, как правильный, но при этом обладает рядом интересных свойств, которые могут затруднить решение задачи.

Равнобедренный треугольник

Равнобедренным треугольником зовется треугольник, две стороны которого равны между собой. Тогда третья сторона зовется основанием, а равные стороны считаются боковыми.

Рис. 1. Равнобедренный треугольник.

Любой равнобедренный треугольник имеет ряд свойств:

• Углы при основании равнобедренного треугольника равны.
• Медиана, проведенная к основанию равнобедренного треугольника является биссектрисой и высотой.

Именно эти два свойства определяют специфические особенности равнобедренных треугольников. Как и произвольные треугольник, равнобедренные треугольники бывают 3 видов:

• Остроугольные
• Прямоугольные
• Тупоугольные.

Углы при основании равнобедренного треугольника равны, а сумма углов треугольника всегда равна 180 градусам. Поэтому в равнобедренном и тупоугольном треугольнике наибольший угол всегда лежит напротив основания. Если такой угол лежал бы при основании, то сумма углов превысила бы 180 градусов, а это невозможно.

Тупоугольный треугольник

Тупой угол это угол больше 90 градусов. Очень часто тупоугольный треугольник стараются изобразить так, чтобы тупой угол находился у основания треугольника. Такой подход облегчает восприятие фигуры.

Рис. 2. Тупоугольный треугольник.

В любой треугольник тупой угол добавляет несколько особенностей:

• Одна из высот треугольника будет проходить вне треугольника. Она упадет на продолжение одной из сторон.
• Ортоцентр, т.е. точка пересечения высот треугольника будет находится за пределами треугольника.
• Два других угла треугольника всегда будут острыми.

Равнобедренный тупоугольный треугольник

Равнобедренный треугольник это треугольник, который с одной стороны содержит в себе тупой угол, с другой имеет две равные между собой стороны.

Такой равнобедренный треугольник сложно воспринимать визуально. Дело в том, что с одной стороны тупоугольные треугольники ученики часто изображают так, чтобы тупой угол был при основании.

Но если тупой угол начертить в основании, то реальное основание тупоугольного равнобедренного треугольника будет визуально совпадать с боковой стороной. Такой подход очень часто приводит к ошибкам. Поэтому равнобедренный тупоугольный треугольник лучше рисовать с тупым углом напротив основания, а сам угол подписывать прямо на чертеже.

Рис. 3. Равнобедренный тупоугольный треугольник.

С другой стороны, этот подход не всегда помогает воспринимать фигуру именно как тупоугольный треугольник. Поэтому и нужно подписывать углы, а при решении доказывать или проверять условие на наличие доказательств существования тупого угла в треугольнике.

Что мы узнали?

Мы узнали, что такое тупоугольный равнобедренный треугольник и какими особенностями он обладает. Поговорили о том, как лучше начертить тупоугольный треугольник и выделили проблемы, которые могут возникнуть с этим вопросом при решении задач.

Равнобедренный тупоугольный треугольник

Средняя оценка: 4.8

Всего получено оценок: 199.

Средняя оценка: 4.8

Всего получено оценок: 199.

Равнобедренный треугольник наиболее часто встречается в задачах по геометрии. Так сложилось, что равнобедренный треугольник не столь прост в решении, как правильный, но при этом обладает рядом интересных свойств, которые могут затруднить решение задачи.

Равнобедренный треугольник

Равнобедренным треугольником называется треугольник, две стороны которого равны между собой. Тогда третья сторона называется основанием, а равные стороны считаются боковыми.

Рис. 1. Равнобедренный треугольник.

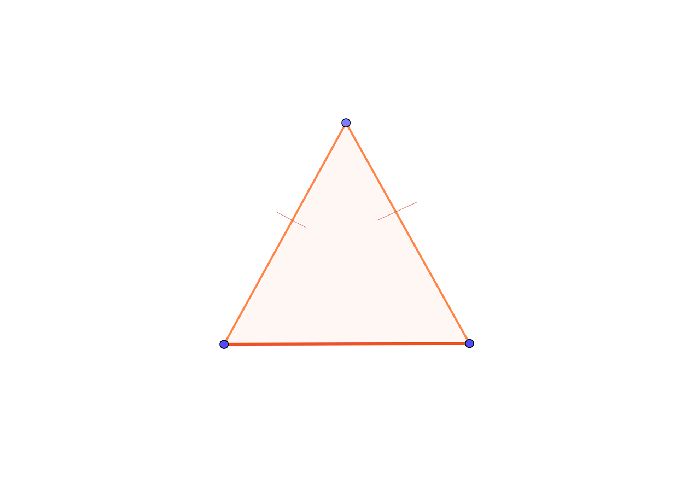
Любой равнобедренный треугольник имеет ряд свойств:

• Углы при основании равнобедренного треугольника равны.
• Медиана, проведенная к основанию равнобедренного треугольника является биссектрисой и высотой.

Именно эти два свойства определяют специфические особенности равнобедренных треугольников. Как и произвольные треугольник, равнобедренные треугольники бывают 3 видов:

• Остроугольные
• Прямоугольные
• Тупоугольные.

Углы при основании равнобедренного треугольника равны, а сумма углов треугольника всегда равна 180 градусам. Поэтому в равнобедренном и тупоугольном треугольнике наибольший угол всегда лежит напротив основания. Если такой угол лежал бы при основании, то сумма углов превысила бы 180 градусов, а это невозможно.

Тупоугольный треугольник

Тупой угол это угол больше 90 градусов. Очень часто тупоугольный треугольник стараются изобразить так, чтобы тупой угол находился у основания треугольника. Такой подход облегчает восприятие фигуры.

Рис. 2. Тупоугольный треугольник.

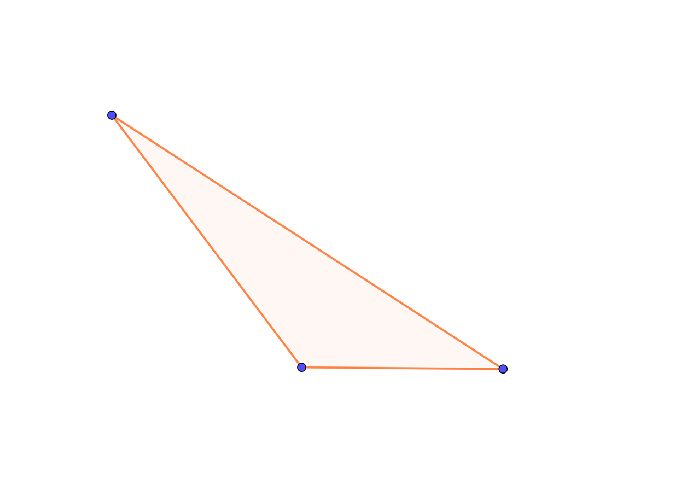
В любой треугольник тупой угол добавляет несколько особенностей:

• Две высоты тупоугольного треугольника будут проходить вне треугольника. Они падают на продолжение одной из сторон.
• Ортоцентр, т.е. точка пересечения высот треугольника будет находится за пределами треугольника.
• Два других угла треугольника всегда будут острыми.

Равнобедренный тупоугольный треугольник

Равнобедренный треугольник – это треугольник, который с одной стороны содержит в себе тупой угол, а с другой стороны имеет две равные между собой стороны.

Такой равнобедренный треугольник сложно воспринимать визуально. Дело в том, что с одной стороны тупоугольные треугольники ученики часто изображают так, чтобы тупой угол был при основании.

Но если тупой угол начертить в основании, то реальное основание тупоугольного равнобедренного треугольника будет визуально совпадать с боковой стороной. Такой подход очень часто приводит к ошибкам. Поэтому равнобедренный тупоугольный треугольник лучше рисовать с тупым углом напротив основания, а сам угол подписывать прямо на чертеже.

Рис. 3. Равнобедренный тупоугольный треугольник.

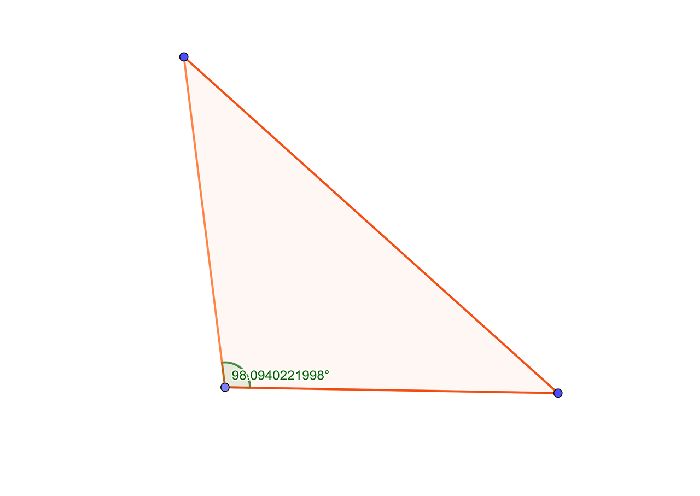
С другой стороны, этот подход не всегда помогает воспринимать фигуру именно как тупоугольный треугольник. Поэтому и нужно подписывать углы, а при решении доказывать или проверять условие на наличие доказательств существования тупого угла в треугольнике.

Что мы узнали?

Мы узнали, что такое тупоугольный равнобедренный треугольник и какими особенностями он обладает. Поговорили о том, как лучше начертить тупоугольный треугольник и выделили проблемы, которые могут возникнуть с этим вопросом при решении задач.

Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

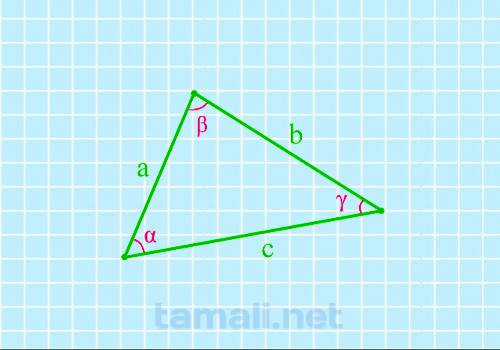
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

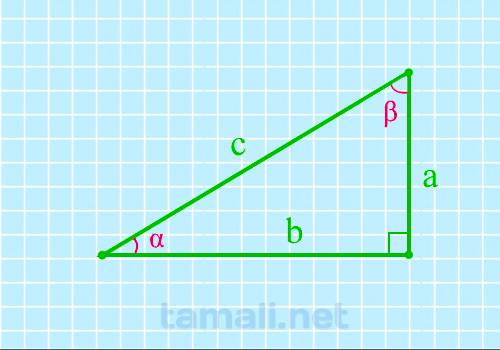
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

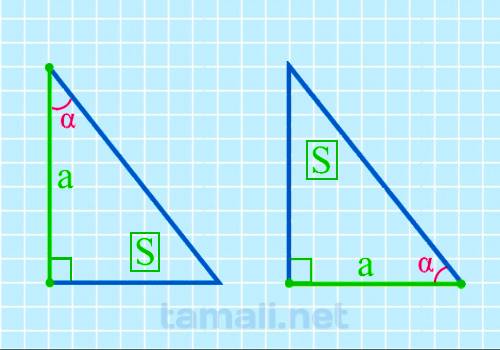
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

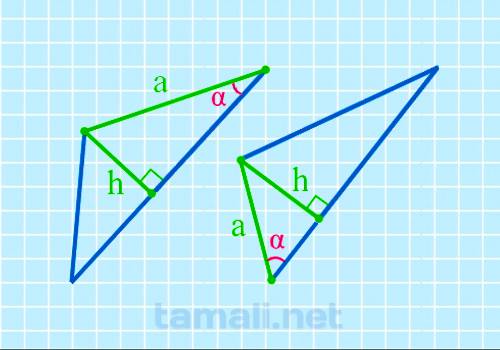
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

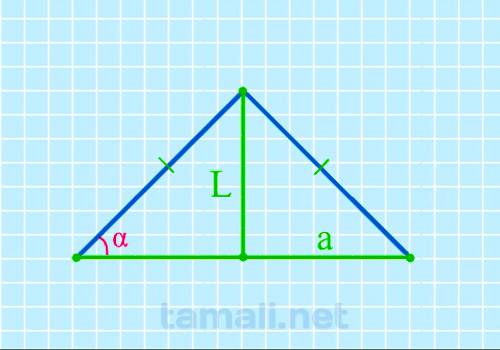
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

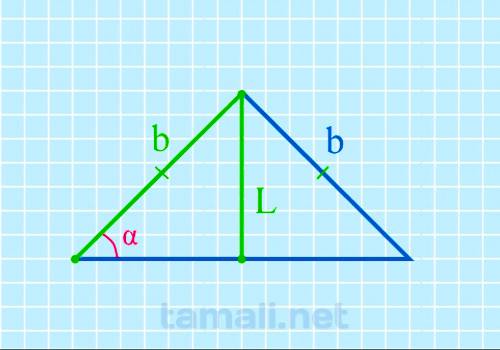
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

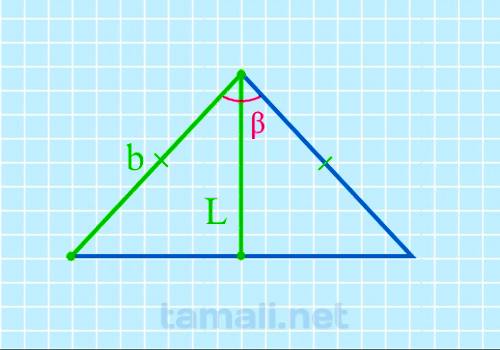
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

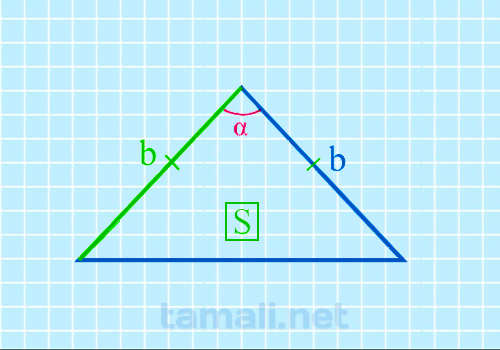
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.

Пусть Х градусов приходится на 1 часть ,
тогда 2х — приходятся на 2 части
5х- приходятся на 5 частей
Т к треугольник тупоугольный , то 5х — это величина тупого угла
2х- это величина угла при основании и таких углов два, т к треугольник равнобедренный , а в равнобедренном треугольнике углы при основании равны
Известно, что сумма внутренних углов треугольника равна 180 град
Составим уравнение :
2х+2х+5х=180
9х=180
Х=20 град — приходится на1 часть
2х=20*2=40 град — величина углов при основании
5х=20*5=100 град — величина тупого угла
Ответ: 40 град
40 град
100 град

Тупоугольный треугольник, элементы, свойства, признаки и формулы.

Тупоугольный треугольник – это треугольник, у которого один угол тупой.

Тупоугольный треугольник (понятие и определение)

Элементы тупоугольного треугольника

Свойства тупоугольного треугольника

Формулы тупоугольного треугольника

Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник

Тупоугольный треугольник (понятие и определение): 

Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.

Тупоугольный треугольник – это треугольник, у которого один угол тупой, а два других – острые. В свою очередь, тупой угол – это угол, градусная мера которого составляет 90° до 180°, а острый угол – это угол, градусная мера которого составляет менее 90 градусов

Рис. 1. Тупоугольный треугольник

∠ BАC– тупой угол треугольника,

∠ АВС, ∠ BСA – острые углы треугольника

По определению, тупоугольным треугольником не может быть правильный (равносторонний) треугольник, т.к. у него каждый угол составляет 60°.

Рис. 2. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника,

∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника 

По определению, тупоугольным треугольником не может быть прямоугольный треугольник , т.к. у него один угол составляет 90° и сумма двух других углов также составляет 90°.

Рис. 3. Прямоугольный треугольник

Тупоугольный треугольник также может быть одновременно равнобедренным треугольником. Но не всякий равнобедренный треугольник тупой.

Рис. 4. Равнобедренный треугольник

АВ = AС – боковые стороны, BС – основание,

∠ ВАС – вершинный угол, ∠ АBC и ∠ BСA – углы при основании

Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

∠ ВAD – острый угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Свойства тупоугольного треугольника:

Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 9. Тупоугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 10. Тупоугольный треугольник с равными боковыми сторонами

АВ = АС

3. Сумма углов тупоугольного треугольника равна 180°.

4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:

• • a < b + c;
  • a > b – c;
  • b < a + c,
  • b > a – c;
  • c < a + b;
  • c > a – b.

Квадрат

Овал

Остроугольный треугольник

Полукруг

Прямой угол

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Трапеция

Тупой угол

Тупоугольный треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
20 769