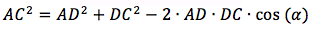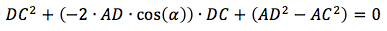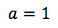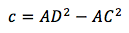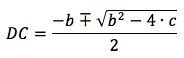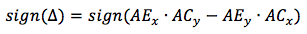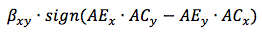Как найти угол прицеливания

Задачи по бомбометанию

1. Расчет угла прицеливания.

Задача решается
по формуле (рис. 58)

где
φ
— угол прицеливания;

W
—
путевая скорость;

Т —
время падения бомбы;

Н —
высота полета;

Δ —
отставание бомбы.

Порядок
решения
(шкалы 1,
2,
4
и 5):

— передвигая
движок, установить индекс
по шкале 1
на деление, соответствующее путевой
скорости W
(рис.
59);

— установить
визирку по шкале 2
на деление, соответствующее времени
падения бомбы Т;

— отсчитать
по визирке на шкале 1
значение величины S
= W·T;

— сдвинуть
визирку влево на величину Δ,т.е. установить
визирку по шкале 1
на деление, соответствующее разности
S
— Δ;

— передвигая
движок, установить индекс
по шкале 5 против деления, соответствующего
высоте полета Н;

— отсчитать
по визирке на шкале 4
угол прицеливания φ.

Примеры:
1)
Дано: Н = 2000 м;
W
= 680
км/час;
Т
= 22,65
сек.; Δ
= 1300
м.

Находим:
φ
= 56°,4.

2)
Дано: Н
= 7500
м;
W
= 800
км/час;
Т = 47,7
сек.; Δ = 4800 м.

Находим:
φ
= 37,7°.

2. Определение наклонной дальности сбрасывания бомб.

Задача решается
по формулам (рис. 60)

где
НД_С
— наклонная дальность сбрасывания
бомб;

Н —
высота сбрасывания;

φ
— угол прицеливания (обычно отрабатывается
решающим прибором оптического прицела).

Порядок
решения
(шкалы 3
и 5):

— установить
визирку по шкале 5
наделение, соответствующее высоте
полета самолета Н
(рис.
61);

— подвести
под визирку деление шкалы 3,
соответствующее значению угла (90°
— φ);

— отсчитать
по шкале 5
против индекса
искомую наклонную дальность сбрасывания

Пример.
Дано:
Н
= 9000
м;
φ
= 41°;
90° — φ
= 49°.

Находим:
НД_С
= 11 900 м.

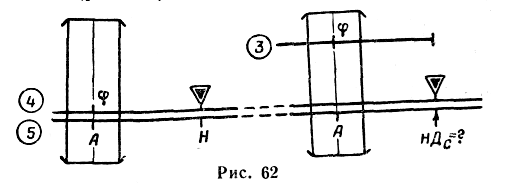
При
малых значениях углов φ
для
повышения точности расчета НД_С
определяют по второй формуле.

Порядок
решения
(шкалы 3,
4
и 5):

— передвигая
движок, установить индекс

на
деление шкалы 5,
соответствующее значению Н
(рис.
62);

— установить
визирку по шкале 4
на деление, соответствующее значению
φ (этим самым определяется величина
относа бомбы с заданной высоты А = Н·tg
φ
);

— передвигая
движок, подвести под визирку деление
шкалы 3,
соответствующее значению φ;

— отсчитать
по шкале 5
против индекса
искомое значение наклонной дальности
НД_С.

Пример.
Дано:
Н
=
12 000 м;
<?
= 26°. Находим: ЯД_С
= 13 400 м.

3. Определение величины сноса медленно падающего тела.

Задача
решается по формуле:

где
Z
— величина сноса в м;

Н —
высота сбрасывания в
м;

Ucp
— скорость среднего ветра в м/сек;

Vсн
— средняя скорость снижения в м/сек.

Порядок
решения
(шкалы 1
и 2
или 14
и 15):

— установить
визирку по шкале 1
на деление, соответствующее значению
Н;

— передвигая
движок, подвести под визирку деление
шкалы 2,
соответствующее значению V_СНУ;

— перевести
визирку по шкале 2
на деление, соответствующее значению
U_СР;

— отсчитать
по визирке на шкале 1
искомое значение сноса Z
(рис. 63).

Пример.
Н
= 800 м;
U_СР
= 14 м/сек;
V_СНcs
=
6 м/сек.

Находим:
Z
= 1860 м.

4. Определение высоты бомбометания по фотоснимкам

Задача решается
по формуле

где
W
—
путевая скорость в м/сек;

t
—
интервал между экспозициями в сек.;

а —
рабочая сторона снимка в см;

f—фокусное
расстояние объектива аэрофотоаппарата
в см.

Порядок
решения
(шкалы 1
и 2):

— передвигая
движок, установить индекс
против деления, соответствующего
значению W,
(рис. 64);

— установить
визирку по шкале 2
на деление, соответствующее времени t;

— передвигая
движок, установить под визирку деление
шкалы 2,
соответствующее значению a;

— перевести
визирку по шкале 2
на деление, соответствующее величине
f,
и по шкале 1
отсчитать искомое значение H.

Пример.
Дано:
W
= 730 км/час
=
202 м/сек;
t
— 18
сек.; а
= 30 см;
f
=
50 см.

Находим:
H
= 6080 м.

Примечание.
Аналогично можно определить минимально
допустимую высоту фотографирования
Н_мин,
если вместо t
взять t_МИН
т. е. минимальный интервал между
экспозициями, равный продолжительности
цикла аэрофотоаппарата.

Решение задачи прицеливания

• При стрельбе в воздухе движение всех объектов можно рассматривать либо относительно воздуха, либо относительно стреляющего самолета.

• Система координат, неподвижная относительно того слоя воздуха, в котором находится стреляющий самолет; называется абсолютной системой координат.

• Система координат, связанная со стреляющим самолетом и неподвижная относительно него, называется относительной системой координат.

Абсолютная система координат

• В абсолютной системе координат (рис.1) при стрельбе с самолета, летящего со скоростью V1, для попадания в цель, имеющую скорость Vц, необходимо построить в пространстве три угла (три треугольника):
  — угол прицеливания  (баллистический треугольник), учитывающий понижение траектории под действием силы тяжести;
  — угол относа  (треугольник скоростей), учитывающий влияние скорости стреляющего самолета на полет снаряда;
  — угол упреждения  (упредительный треугольник), учитывающий абсолютную скорость движения цели.

• 
  
  

  
  

• Упредительный треугольник OAoAy строится исходя из предположения, что вектор скорости цели является постоянным от момента выстрела до встречи снаряда с целью.

• Угол между вектором скорости Vц и начальной линией цели ОАо называется курсовым углом цели q.

• Путь цели за время полета снаряда от точки О до упрежденной точки Ауназывается линейным упреждением L.

• У
  гол между начальной и упрежденной линией цели называется углом упреждения , который равен:

или

где Рц — ракурс цели.

Относительная траектория снаряда и относительная скорость цели

• П
  ри решении задачи прицеливания в относительной системе координат приходится рассматривать относительную траекторию снаряда и учитывать относительную скорость цели.

• Относительной траекторией снаряда называется линия, описываемая центром тяжести снаряда, которую наблюдает стрелок, находящийся на стреляющем самолете.

• На рис.2 показана относительная траектория снаряда при стрельбе с бомбардировщика, двигающегося после выстрела равномерно, прямолинейно и без скольжения.

• Р
  асстояние, на которое снаряд отстает от относительной плоскости бросания, называется отставанием снаряда z:

• У
  гол, под которым видно отставание снаряда из точки вылета, называется углом отставания :

• где Dr— относительная дальность стрельбы.

• Л
  инейная скорость цели относительно стреляющего самолета называется относительной (линейной) скоростью цели Vr (рис.3):

• Направление относительного движения цели определяется относительным курсовым углом qr.

• Положение цели относительно стреляющего самолета характеризуется наклонным бортовым углом цели .

• С
  оставляющая вектора относительной скорости цели по направлению начальной линии цели называется скоростью изменения дальности VD и определяется из соотношения:

• С
  оставляющая вектора Vr по направлению, перпендикулярному к начальной линии цели, называется поперечной скоростью цели Vп :

• П
  ри определении Vп углы q и  следует отсчитывать от векторов V1 и Vц к линии цели от 0 до 180°; если отсчет ведется по часовой стрелке, угол считается положительным, если против часовой стрелки — отрицательным.
  При стрельбе с истребителя, атакующего бомбардировщик, Vп равна:

• где Vб — скорость бомбардировщика.

• П
  ри стрельбе с бомбардировщика по истребителю, летящему по кривой погони, Vп равна:

• Угловая относительная скорость линии цели wц равна:

Относительная система координат

• Для решения задачи прицеливания в относительной системе координат (рис.4) необходимо в пространстве построить три угла (три треугольника):
  — угол прицеливания ar (относительный баллистический треугольник), учитывающий понижение траектории под действием силы тяжести;
  — угол отставания  (треугольник отставания), учитывающий отставание снаряда z;
  — относительный угол упреждения yr (относительный упредительный треугольник), учитывающий о
  тносительную скорость полета цели.

• Относительный упредительный треугольник строится в предположении, что вектор относительной скорости цели является постоянным за время tr от момента выстрела до встречи снаряда с целью. Точка Ay, в которой по расчетам должны встретиться цель и снаряд, называется относительной упрежденной точкой, прямая ОАу — относительной упрежденной линией цели. Расстояние Dr oт точки вылета снаряда до относительной точки встречи, измеренное в момент выстрела, называется относительной дальностью стрельбы, расстояние AoAy = Lr— относительным линейным упреждением.

• У
  гол между начальной линией цели ОАo и относительной упрежденной линией цели ОАy называется относительным углом упреждения Yr, который определяется по следующей формуле:

и
ли 

• г
  де Tp — расчетное время полета снаряда, величина которого в общем случае зависит от принятого при стрельбе закона движения цели:

Стрельба из неподвижного оружия

• На рис.5 показана схема решения задачи прицеливания при стрельбе из неподвижного оружия истребителя или истребителя-бомбардировщика.

• С
  уммарная угловая поправка с учетом наличия в полете у самолета углов атаки а или скольжения bск равна:

• Угол упреждения при стрельбе с прицелом, имеющим подвижную сетку (прицел с зависимой линией визирования или радиолокационный прицел с начальной точкой) равен:

где

• 

• — угловая скорость цели, выраженная через угловую

скорость разворота истребителя 1 и скорость изменения угла упреждения ; k — коэффициент демпфирования, зависящий от конструкции прицела.

• У
  гловая поправка, учитывающая скольжение, равна:

где — угол относа, возникающий вследствие скольжения:

• y
  ск — угол, отрабатываемый гироузлом прицела вследствие скольжения:

• У
  гловая поправка aп, которую должен отработать прицел для учета понижения траектории, равна:

где a0 — угол прицеливания при стрельбе в горизонтальной плоскости.

• Составляющие угловой поправки aп: в плоскости симметрии самолета:

• в
  плоскости размаха крыльев:

где q — угол тангажа самолета; g — угол крена самолета.

• Угловые поправки, необходимые для решения задачи прицеливания в радиолокационных прицелах с упрежденной точкой (прицелы с независимой линией визирования), равны:

где  и  — угловые координаты цели; (Yсум)m — составляющая суммарной угловой поправки в плоскости симметрии самолета:

• (
  Yсум)n — составляющая суммарной угловой поправки в плоскости размаха крыльев:

Стрельба из смещенного оружия

• Н
  а рис.6 показана схема решения задачи прицеливания при стрельбе с самолета-бомбардировщика, где оружие смещено относительно прицела на некоторую величину, называемую параллаксом оружия.

• Поворотом в вертикальной и горизонтальной (или наклонной и вертикальной) плоскостях оружию можно придать любое положение.

• К
  аждая угловая поправка (Yr, , ) делится на две составляющие: вертикальную и горизонтальную (наклонную). Если оружие смещено относительно прицела, дополнительно вводятся поправки на параллаксП построением угла параллакса (или двух его составляющих по соответствующим плоскостям). Все составляющие в каждой плоскости суммируются, и на величину суммарной поправки оружие поворачивается относительно цели:

• где  и  — угол возвышения и бортовой угол линии визирования на цель (начальной линии цели); — суммарная поправка в вертикальной плоскости:

•  — суммарная поправка в горизонтальной плоскости:

Глава 9. Расчёт элементов пространственного маневра ЛА

Уравнение динамики полета

• При полете по маршруту после взлета и перед посадкой ВС выполняют различные маневры для занятия необходимого положения относительно оси воздушной трассы или аэродрома. Поэтому решение многих задач воздушной навигации связано с маневрированием, а аналитическое их решение требует знания законов движения ВС в пространстве. При расчетах элементов маневрирования используются только истинные значения воздушной скорости полета.

• П
  еремещение ВС, как и любого физического тела, характеризуется движением его центра масс относительно выбранной системы координат.

• В
  прямоугольной системе координат (рис.1), связанной с землей, самолет находится в точке М с координатами Хт, Ym, Zm. Перемещение его при отсутствии ветра будет характеризоваться уравнениями:

где c, q, g — углы крена, тангажа и курса ВС, отсчитываемые от оси;nx, ny — продольная и поперечная перегрузка ВС.

• В
  установившемся горизонтальном полете (q = 0) при расчете элементов пространственного маневра ВС пользуются следующими выражениями:

Продольное маневрирование

• Продольное маневрирование выполняется при необходимости изменения скорости полета как в горизонтальной плоскости (q = 0), так и при наборе (q > 0) высоты и снижении ( < 0). При условии постоянства продольной перегрузки nx = const продолжительность маневра и протяженность участка разгона (V_К > V_Н) от начальной V_Н до конечной V_К скорости или торможения (V_К <V_Н):

• В
  
  ыразив скорости в км/ч, пройденный путь в км, а время в мин., получим расчётные формулы:

Маневрирование в вертикальной плоскости

• Оно выполняется при необходимости изменения высоты полета. В процессе набора заданного эшелона после взлета и снижения до высоты круга происходит полет по некоторой пространственной траектории переменной кривизны. Это является следствием изменения вертикальной и истинной воздушной скоростей полета в широких пределах. Кроме того, изменяется и вектор ветра.

• Д
  ля набора высоты рекомендуются три режима: экономический, обеспечивающий наименьшие эксплуатационные расходы на рейс; максимальной дальности, соответствующий минимальному расходу топлива на весь полет; максимальной скороподъемности, соответствующий наименьшей продолжительности набора высоты.

• Вертикальные и приборные скорости полета устанавливаются в зависимости от полетной массы ВС, температуры и высоты полета. Они указываются в РЛЭ по типам ВС.

• Если принять средние значения воздушной, вертикальной скоростей и ветра, то продолжительность маневрирования и протяженность участка набора от начальной Нн до конечной Нк высоты рассчитываются по формулам:

Например, при наборе высоты от 600 до 9600 м с вертикальной скоростью 15 м/с на V_СР = 700 км/ч (195 м/с) и попутном эквивалентном ветре U_Э.СР = 72 км/ч (20 м/с) получаем t_наб = 10 мин, Sнаб = 129 км.

• И
  зменение скорости ветра приводит к увеличению Sнабпри попутном ветре и ее уменьшению при встречном. Характер изменения удаления рубежа набора заданного эшелона DSнаб в зависимости от Uэпоказан на рис.1.

• Набор высоты с 4000 м до 10 000 м при Uэ = -100 км/ч приводит к сокращению Sнаб на 23 км по сравнению с данными, РЛЭ.

• Е
  сли установлен определенный рубеж набора заданного эшелона Sнаб , то в зависимости от Uэ будет изменяться потребное значение вертикальной скорости:

• Д
  ля снижения с эшелона рекомендуются три режима полета: экономический, обеспечивающий наименьшие эксплуатационные расходы на рейс; минимального времени снижения; экстренного (аварийного) снижения, выполняемого с максимально возможной вертикальной скоростью.
  Время и путь, проходимый ВС в процессе снижения:

• Дополнительное время, возникающее при ограничениях, вводимых УВД, и при снижении до высоты круга, то есть с необходимостью установки аэродромного давления на высотомере:

Боковое маневрирование

• Оно выполняется при необходимости изменения направления полета для исправления пути и вывода самолета на новую ЛЗП.

• Э
  лементами разворота являются радиус R, время и путь, проходимый самолетом за время разворота на заданный угол. Если не учитывать переходный период ввода и вывода самолета из крена, то:

• Д
  
  ля плавного вписывания в ЛЗП очередного участка маршрута (рис.1) необходимо знать либо линейное (ЛУР), либо боковое (БУР) упреждения разворота:

• У
  чет влияния ветра на траекторию самолета в процессе разворота и вывода его на ЛЗП осуществляется вводом поправки DЛУР в линейное упреждение разворота:

• З
  нак DЛУР определяется знаком эквивалентного ветра, соответствующего полету на текущем участке маршрута. Порядок расчета DЛУР показан на номограмме пунктиром (рис.2).

• Расчет элементов разворота на обратный курс с точным выводом самолета на ЛЗП, смещенную на величину Ш, производится при навигационном обеспечении многих авиационных работ. Если смещение смежных маршрутов Ш < 2R, то необходимо выполнить специальный маневр с отворотом самолета на заданный угол (рис.3):

• П
  ри штиле:

• П
  ри ветре:

• г
  де Uб — боковая составляющая ветра. Знак «+» в формуле берется при смещении маршрутов «на ветер» и «—» «под ветер». Продолжительность маневрирования самолета:

• Если самолет Ан-2 необходимо вывести на новую ЛЗП, отстоящую от первой на 800м, при V = 200 км/ч (55.5 м/с), c= 15 град и безветрии, то R = 1174 м, a = 70 град, tраз = 118с = 1 мин. 58с.

• П
  ри наличии ветра в расчетное значение угла отворота вносится поправка на УС. Если смещение маршрутов производится в сторону, откуда дует ветер («на ветер»), то угол a увеличивается на величину УС и, наоборот, при смещении очередного участка маршрута по направлению ветра («под ветер») — уменьшается на величину УС. При этом знак УС не учитывается.
  Если в результате контроля пути было установлено уклонение самолета от заданного маршрута, то выполняется специальный маневр для вывода его на ЛЗП. Чаще всего производят выход на ближайший контрольный ориентир, лежащий на ЛЗП, или выполняют S-образный маневр.
  Вывод самолета на КО производится путем расчета поправки в курс (ПК) и изменения курса на этот угол (рис.4):

• Н
  аиболее быстрый способ вывода самолета на ЛЗП при наличии бокового уклонения Z (рис.5) является S-образный маневр, заключающийся в последовательном выполнении двух разворотов на угол a .

• Ц
  
  елесообразность его применения определяется условием Z < 2R. При этом:

• Путь и время маневрирования:

• Увеличение длины фактического пути в результате маневрирования:

• Если самолет ТУ-154 уклонился от ЛЗП на Z= 8 км, то V = 950 км/ч (263.8 м/с), c= 15 град. В результате R = 26.5 км, a = 32 град, Sман = 28 км, tман = 112с, DSман = 1.58 км.

Влияние ветра и динамики ЛА на участках разворота

• Найдем соответствующие зависимости с учетом ветра, а также времени ввода и вывода ЛА из разворота, которое для тяжелых машин может быть достаточно большим.

• Р
  ассмотрим траекторию движения центра масс ЛА в горизонтальной плоскости на этих участках для двух вариантов его ввода в разворот. Выберем связанную с землей прямоугольную систему координат хОz, совместив ее начало с точкой начала ввода ЛА в разворот (рис.1).

• Известно, что:

• г
  де b — угол крена (правый крен считается положительным). Умножим и разделим правую часть этой формулы на штилевой путь Ut, где 0<t<t1 — время ввода ЛА в разворот до крена b, переписав ее в виде:

• Если в этом выражении положить отношение (tg)/t величиной постоянной, характеризующей угловую скорость w создания крена при вводе ЛА в разворот, то данное соотношение будет уравнением клотоиды(спирали Корно):

• З
  апишем дифференциальные уравнения штилевой траектории движения ЛА в прямоугольной системе земных координат хОz (рис.1):

• г
  де g — курс ЛА , отсчитываемый от оси х. Вид траектории движения будет определяться законом изменения курса g на участке ввода ЛА в разворот. Учтем, что в общем случае угловая скорость w1 разворота в горизонтальной плоскости равна:

• П
  одставим в это соотношение значение радиуса R из (3). Тогда для текущего значения курса gна участке ввода ЛА в разворот получим:

• Следовательно, уравнения штилевой траектории будут иметь вид:

• П
  олученные уравнения (типа интегралов Френеля) решаются только численными методами, для чего имеются специальные программы. Хорошие результаты дает разложение подынтегральных функций в ряды, быстрая сходимость которых позволяет ограничиться двумя первыми членами разложения. Это приводит к уравнениям вида:

• З
  апишем из формулы (3) выражение для определения текущего значения угла  , которое будет иметь вид:

• Б
  олее сложные уравнения получаются, если угловую скоростьw ввода ЛА в крен считать постоянной. В этом случае w= db / dt = const и b= wt . Тогда, аналогично предыдущему случаю, найдем для текущего значения курса:

• П
  одставив это выражение в (4), получим уравнения штилевой траектории ЛА для этого условия ввода его в разворот:

• Записанные уравнения также приходится решать численными методами. Сопоставление результатов определения штилевых координат ЛА и других элементов его ввода в разворот, вычисленных по различным формулам, показывает, что расхождения в координатах точки окончания ввода ЛА в разворот не превышают единиц метров, крена — около одного градуса, и курса — десятые доли градуса. Поэтому в основу дальнейших вычислений положены уравнения (8). Нетрудно убедиться также, что за время ввода в разворот ЛА проходит штилевой путь с большой точностью равный Ut₁. При этом боковое смещение Z оказывается весьма незначительным, которым в большинстве случаев, по-видимому, можно пренебречь. Особенно мала величина его второго слагаемого, с которым можно не считаться.

• П
  ерепишем уравнения (8), учтя влияние ветра и считая его постоянным:

где 0<t<t1, U — скорость ветра,  — его направление.

• Для участка CD вывода ЛА из разворота за время t₂ , взяв за основу уравнения (11), получим следующие соотношения:

• где Dg= __ — изменение курса за время выполнения маневра;  — изменение путевого угла;₁ и ₂ — углы сноса до и после разворота. В этих соотношениях х_с , z_с -координаты точки окончания установившегося разворота, а время 0<t<t2.

• На участке разворота с постоянным креном штилевая траектория ЛА — окружность радиуса R. Относительно земной поверхности центр масс ЛА опишет циклоиду, уравнение которой имеет вид:

• где x_B, z_B — координаты точки окончания ввода ЛА в разворот, которые находятся из уравнений (11); 0<t<tур — время разворота с постоянным креном, равным заданному значению b .

• Для определения продолжительности tур установившегося разворота необходимо найти из рис.1 величину угла УР = ____, где _ и _ — величины изменения курса на участках ввода и вывода ЛАиз разворота.

• У
  гловая скорость разворота с постоянным креном и радиусом определяется формулой (5), поэтому время его выполнения будет следующим:

• Е
  сли окажется УР < 0, что может иметь место при малых углах  и/или большой продолжительности ввода и вывода ЛА из разворота, то участка установившегося разворота с постоянным углом крена не будет. В этом случае ₁___. Положив t₁ = t₂ , а значит, и __, с учетом (6) получим:

• С
  ледовательно, ЛА должен вводиться в разворот в течение следующего времени (до угла крена, определяемого формулой (9)):

Разворот на новый этап маршрута

• П
  редположим, что на предыдущем этапе Ох₁ ЛА точно следовал по маршруту. По окончании вывода из разворота он должен оказаться на линии пути КD второго этапа (в точке D на рис.1).

• В
  принятой земной системе координат хОz уравнения прямых ОК первого и КD второго этапов будут иметь вид:

• И
  сходя из условия, что точка D (x_D, z_D) вывода ЛА из разворота должна лежать на прямой второго этапа, нетрудно найти координаты точки К излома маршрута, а значит, и точки начала ввода ЛА в разворот. Подставив во второе соотношение значение, найденное из первого уравнения, получим:

• Разворот на второй этап часто начинают в момент нахождения ЛА от точки излома маршрута на расстоянии, равном величине штилевого линейного упреждения (ЛУР = L), определяемого по формуле:

L=R tg/2.

• Н
  етрудно получить зависимости для определения боковой Zб и продольной dn погрешности выхода на второй этап за счет влияния ветра, а также времени ввода и вывода ЛА из разворота. Учитывая, что ОК= S (рис.1), получим:

• г
  де x_E, z_E— координаты фактической точки окончания разворота, начатого на удалении штилевого ЛУР. Координаты точки N окончания разворота в штилевых условиях без учета ввода ЛА и выхода его из разворота равны:

• Тогда:

• Н
  апишем выражение для вспомогательного угла:

• П
  ри отрицательном значении и числителя и знаменателя в этой формуле к найденному значению угла  необходимо прибавить 180°. С учетом записанных соотношений получим окончательные выражения для определения боковой Zб и продольной dn погрешностей выхода на второй этап, если разворот на него начат на штилевом ЛУР без учета ветра, а также участков ввода и вывода ЛА из разворота:

• Напомним, что обе погрешности определены относительно штилевой точки N выхода на второй этап. Величина l при неизменных значениях максимального угла крена, а также времени ввода ЛА в разворот и вывода из него не остается постоянной. Она существенно изменяется в зависимости от направления ветра. Поэтому геометрическое место точек выхода ЛА на новый этап при постоянной скорости ветра, но различных направлениях его образуют близкую к эллипсу овальную кривую. Ее большая ось относительно направления второго этапа располагается под углом, равным половине угла излома маршрута. Такая закономерность позволяет выработать правило расчета точки начала разворота, уменьшающее погрешности выхода на второй этап маршрута.

• Возможен и второй вариант выхода на очередной этап маршрута, при котором после ввода ЛА в разворот траектория его полета относительно земли будет близка к окружности. Для этого воздушная траектория ЛА должна быть циклоидой. При расчете данного варианта необходимо, чтобы радиус кривизны клотоиды в момент окончания ввода ЛА в разворот был равен радиусу кривизны циклоиды в точке перехода на полет по этой штилевой траектории. Такое же условие должно быть соблюдено и в точке начала вывода ЛА из разворота. Это требует уточнения времени ввода и вывода из разворота. Чтобы между этими участками траектория движения ЛА относительно земли была близка к окружности, его крен должен изменяться в соответствии с изменением радиуса кривизны циклоиды. Строгое решение этой задачи связано с более громоздкими выражениями и усложнением вычислительных процедур.

• Записанные соотношения для определения параметров разворота на очередной этап маршрута можно рассматривать как кинематические алгоритмы выхода на цель с заданного направления, если к району цели подходить с пересекающим его курсом. Для этого достаточно ввести дополнительное условие, чтобы после окончания разворота на цель ЛА находился от нее на требуемом удалении.

• Полученные соотношения позволяют точно рассчитывать и другие виды маневров ЛА, например такие, как стандартные траектории захода на посадку, длина витка зоны ожидания и т. д.

• Учет динамики ЛА и ветра при наличии высокоточных средств навигации (к примеру, спутниковых) требует нового подхода к расчету и выдерживанию заданных траекторий движения ЛА.

• Приведенные кинематические алгоритмы выполнения маневров при решении рассмотренных навигационных задач целесообразно использовать для точного расчета программных траекторий в интересах более надежного управления воздушным движением в таких ответственных зонах полетов, как аэродромы посадки, полигоны и другие узловые диспетчерские районы. Отображение как на бортовых, так и наземных экранах предельных рубежей, а также расчетных траекторий маневра с учетом ветра и участков ввода и вывода ЛА из разворота позволит более обоснованно оценивать воздушную обстановку и точность соблюдения параметров движения, способствуя повышению безопасности полетов.

Целимся из пушки

В статье описан простой алгоритм наведения пушки, когда оси вращения не пересекаются с осью ствола. Быстро найти готовый не получилось – пришлось вспоминать школьные времена. Ну а раз вспомнил – грех не поделиться с остальными. А кто-то где-то, сэкономив время, использует его на создание еще чего-то полезного…

Результат приведенных расчетов используется в аркадной игре. За месяц промахов не было. Если вы разрабатываете симулятор, скорее всего, понадобится что-то более изощренное.

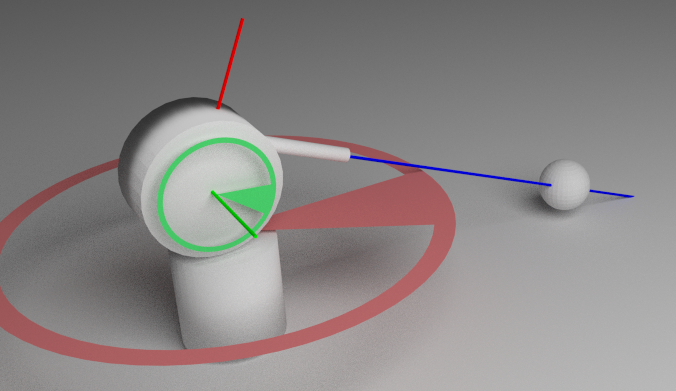
Итак, дана пушка. При наведении турель может поворачиваться в горизонтальной (красная ось вращения на рисунке) и вертикальной (зеленая ось) плоскостях.

Свойства модели пушки

1. Ось ствола (обозначена синим цветом) не пересекается с осями вращения.
2. Ось ствола параллельна оси X
3. Направление выстрела совпадает с положительным направлением X
4. Ось горизонтального поворота (красная) параллельна оси Z, или оси совпадают
5. Ось вертикального поворота (зеленая) параллельна оси Y, или оси совпадают
6. Верх модели соответствует положительному направлению оси Z

Для успешного наведения на цель требуется вычислить два угла поворота – горизонтальный и вертикальный

Благодаря заданным ограничениям модели (оси поворотов параллельны или совпадают с соответствующими осями координат), задачу нахождения углов наведения в трехмерном пространстве можно разбить на две в двухмерном:

1. Угол горизонтального поворота может быть найден с использованием проекции модели на плоскость XY (Z=0)
2. Угол вертикального поворота – ось XZ (Y=0)

Решаться обе подзадачи будут одинаково.

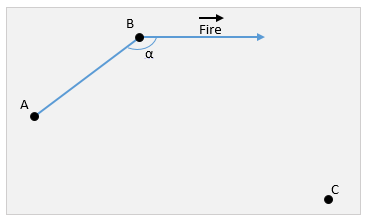
Для начала рассмотрим исходное положение

A – центр вращения. Результат проекции оси поворота на перпендикулярную плоскость.

B – точка вылета снаряда.

Fire – проекция вектора направления выстрела.

C – позиция цели

Определим угол между вектором выстрела и AB

Здесь и далее угловыми скобками будет обозначаться скалярное произведение векторов.

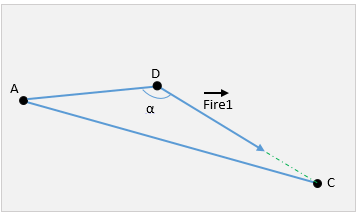
Теперь предположим, что наведение завершено. При повороте на цель точка B перешла в D, а вектор Fire стал Fire1

Отсюда можно найти длину отрезка DC, используя теорему косинусов.

Где

Перепишем формулу, чтобы она соответствовала общей форме квадратного уравнения

для неизвестного DC

тогда

из двух получившихся значений DC нам подходит положительное.

Если DC получается отрицательным, то цель находится в недоступной (при использовании этого алгоритма по крайней мере) для наведения позиции.

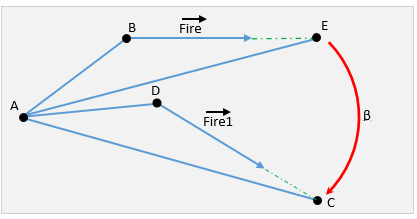
Теперь рассмотрим рисунок, на котором изображены положения системы до и после наведения

Красным обозначен искомый угол наведения.

Определим координату точки E. Это координата цели C, повернутая на угол прицеливания относительно центра A в противоположном направлении. Т.е это куда бы попала пушка, если бы выстрелила на правильное расстояние, забыв повернуться. Для этого нужно сдвинуть точку B в направлении вектора Fire на расстояние DC.

Тогда угол прицеливания – это угол между векторами AE и AC, который находится через скалярное произведение

Угол найден, но нужно помнить, что точка прицеливания может находиться где угодно, в том числе и «выше» направления выстрела. Т.е. нужно найти еще направление поворота.

Определим ориентацию векторов AE и AC. Двух векторов для этого недостаточно. Нужен третий вектор, перпендикулярный первым двум. Назовем его V. Именно его направление определяет позицию наблюдателя, который увидит поворот по или против часовой стрелки в зависимости от того, по какую сторону от плоскости с векторами AE и AC находится. Поскольку мы работаем с проекциями на координатные плоскости, искомый вектор будет параллелен третьей оси координат.

Для определенности рассмотрим пример проекции на ось XY. В этом случае перпендикулярный вектор будет иметь координаты (0, 0, z), где z не равно нулю. Со знаком z нужно определиться. При построении проекций я исходил из того, что нахожусь с положительной стороны по оси Z, поэтому z > 0

Ориентация векторов определяется по знаку определителя, составленного из координат. Первую строку составляют координаты поворачиваемого вектора, вторую – вектора, к которому поворачивается первый и третью – вектор V. Для нашего случая (AE поворачивается до совпадения с AC) это

Поскольку мы определились, что z будет строго положителен, на знак результата его значение не повлияет

Т.е окончательный угол поворота для случая проекции на ось XY, это

Аналогично рассчитывается направление поворота для проекции на ось XZ

Ну и последнее замечание. Полностью независимо друг от друга углы поворота рассчитывать нельзя. Башня может сделать полный поворот (от -180 до 180 градусов) вокруг горизонтальной оси, но вокруг вертикальной это обычно невозможно (будет выглядеть, как будто пушка оторвалась от основы и перевернулась. Вертикальный поворот логично ограничить диапазоном от -90 до 90 градусов.

Реализовать это проще всего так.

1. Находим угол горизонтального поворота
2. Поворачиваем цель на этот угол вокруг оси горизонтального поворота в противоположном направлении
3. Рассчитываем вертикальный угол наведения для новых координат цели.

Или (что, по сути, то же самое) можно сначала поворачивать башню горизонтально, а потом рассчитывать угол вертикального поворота.

Теперь пушка будет попадать.

ОПРЕДЕЛЕНИЕ ИСХОДНЫХ ДАННЫХ ДЛЯ СТРЕЛЬБЫ.

ПОНЯТИЕ ТЫСЯЧНОЙ

ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ПО УГЛОВЫМ ВЕЛИЧИНАМ

ОПРЕДЕЛЕНИЕ ДАЛЬНОСТИ ПО СЕТКЕ БИНОКЛЯ И ПЕРИСКОПА

БЫСТРОЕ ОПРЕДЕЛЕНИЕ ДИСТАНЦИИ ДО ЦЕЛИ ДАЛЬНОМЕРНОИ ШКАЛОЙ ПРИЦЕЛА ПСО-1

Как уже было сказано, прямой выстрел — тот, при котором траектория пули не поднимается выше цели на всей дистанции стрельбы. Дальность прямого выстрела зависит от высоты цели и определяется по таблицам превышения средних траекторий путем сравнивания высоты цели с высотой табличной траектории. Явление прямого выстрела используют в подвижных маневренных боевых действиях при дефиците времени, когда нужно все время двигаться, некогда крутить маховиками и выставлять прицел по дальности.

Прямой выстрел в обороне при отражении атаки наступающего противника обычно составляет по дальности 600 метров с прицелом «6» и точкой прицеливания все время по каблукам противника Почему так? Средний рост перебегающего в атаке пехотинца 150 см. Реально он различим метров на 600. По таблице превышения средних траекторий находим наиболее подходящую ее высоту, не превышающую высоту цели на дистанции 600 метров. Она будет равна на середине (вершине) траектории при дистанции 300 метров — 120 см с прицелом «6»; на 400 метров с тем же прицелом «6» — 120 см; на 500 метров с прицелом «6» — 82 см (схема).

Схема. Прямой выстрел

Следовательно, целясь в ноги наступающему пехотинцу с прицелом «6», начиная с дистанции 600 метров и ближе, по мере его приближения, можно стрелять без перестановки прицела. Противник будет поражен сначала в ноги, потом в живот, грудь, голову. По достижении дистанции 300 метров (вершины траектории) противник будет поражаться в грудь, голову, живот и снова в ноги.

Способ стрельбы прямым выстрелом удобен в обороне, при отражении атаки противника, когда некогда устанавливать прицел на постоянно меняющиеся дистанции стрельбы, и неважно, куда будет поражен противник (идущих на вас в атаку противников будет очень много), — важно, чтобы он до вас не дошел.

В данном случае целить в голову — ненужная роскошь. Важнее стрелять почаще, чтобы атака неприятеля быстрее захлебнулась. Если уж вы хотите «зацепить» противника «покруче», имейте в виду следующее: на дистанции 600 метров пуля упадет в точку прицеливания, то есть по каблукам, и поэтому на этой дистанции нужно целиться повыше, куда-то в область коленей или выше, в пояс, если хотите попасть по центру. Но ближе, на 500 метров, надо стрелять уже по каблукам — траектория сама выведет пулю куда надо. На близкой дистанции, 100 метров, пуля также будет уходить вниз (см. по табл. 8: превышение на такой дистанции будет 53 см), поэтому целиться нужно также выше колен и ниже пряжки, чтобы попасть в грудь. Но на всех остальных дистанциях, от 500 и до 100 метров, по мере приближения атакующего противника точку прицеливания нужно брать только по горизонту, «по каблукам», не меняя установку прицела по высоте.

При наступательных действиях при стрельбе легкой пулей из винтовок прямой выстрел получается:

по окопавшейся цели (высота 30 см) с прицелом «3 1/2» или постоянным «П» на дистанции до 350 метров;

по открыто лежащей цели (высота 50 см) с прицелом «4» на дистанции до 400 метров;

по перебегающей цели (высота 1,5 м) с прицелом «6» на дистанции до 600 метров.

На вышеуказанных дистанциях при вышеназванных установках прицелов стрельба производится с выбором точки прицеливания по горизонту поверхности грунта на уровне цели без изменения установки прицела при изменениях дистанции «ближе к противнику».

В целом правило назначения исходной установки прицела можно сформулировать так: в летних условиях на все дальности стрельбы прицел целесообразно назначать соответственно дальности до цели; зимой при стрельбе на расстояния свыше 400 м точку прицеливания следует выбирать на верхнем краю цели, а при низких температурах (ниже -25° С)-увеличивать прицел на одно деление.
Наиболее сильное влияние на траекторию пули в горизонтальной плоскости оказывает боковой ветер (см.таблицу). Поправки на боковой ветер вносятся с помощью целика, либо отсчитывают по фигурам цели.

ЯВЛЕНИЕ ДЕРИВАЦИИ

Расстояние                            Отклонение