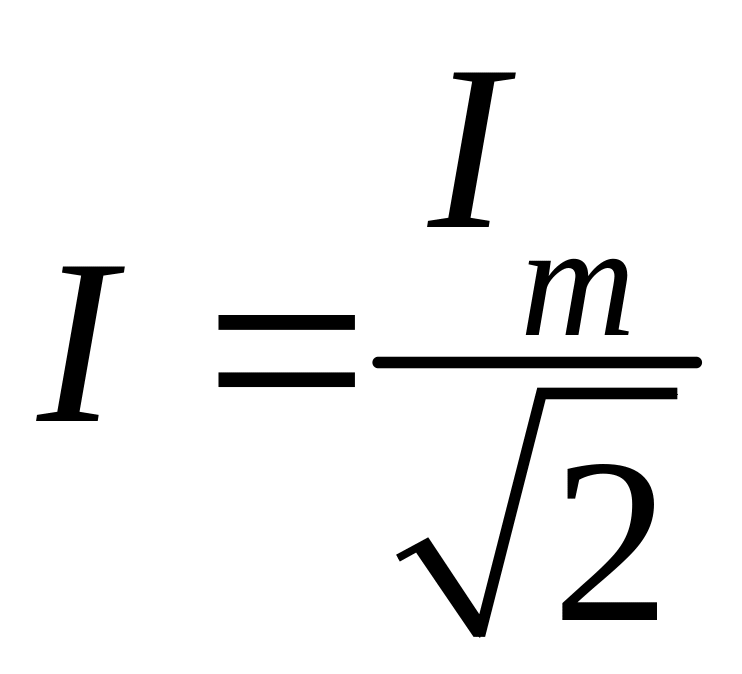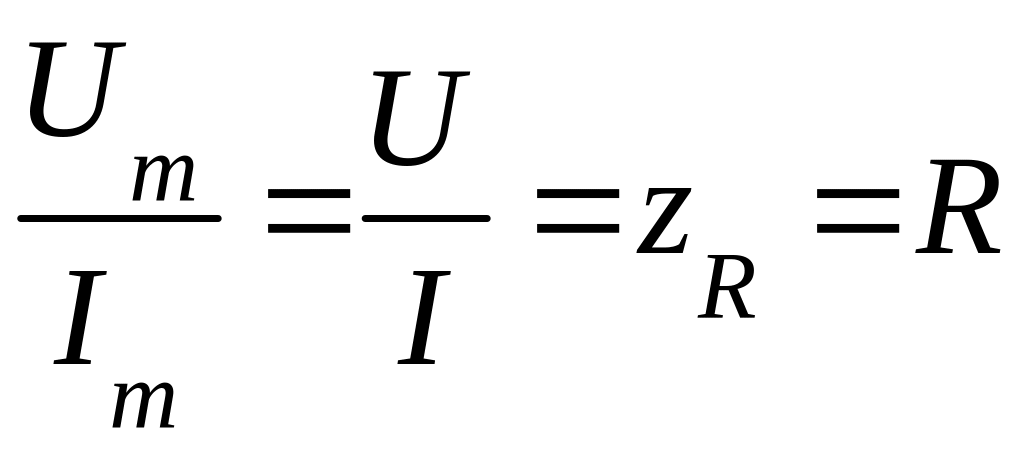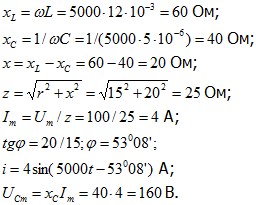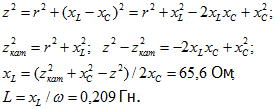Как найти угол отставания тока от напряжения

Сдвиг фаз переменного тока и напряжения

Мощность постоянного тока, как мы уже знаем, равна произведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При переменном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденсаторов и катушек индуктивности.

Для этого случая формула мощности

остается справедливой.

На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.

Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.

При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.

О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.

Представим себе, что при начале вращения радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.

Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.

Рассмотрим, как будут изменяйся при этом ток и напряжение. Из построенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.

Затем напряжение достигает своей наибольшей величины и начинает уже убывать, а ток хотя и становится положительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.

Действительно, если мы посмотрим на рисунок 2, то заметим, что синусоида тока сдвинута вправо относительно синусоиды напряжения. Так как по горизонтальной оси мы откладываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.

Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с направлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величины на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источником ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.

Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрицательной, тем, следовательно, меньше будет средняя мощность тока.

При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).

Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.

Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т. е. формулы

в этом случае будут неверны

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Сдвиг фаз между током и напряжением в цепи переменного тока

Содержание

1 Определения и основные формулы
2 ПТ и активная нагрузка
3 Конденсатор в цепи ПТ
4 Индуктивность в цепи ПТ
5 Видео по теме

При транспортировке электрической энергии от мест её генерации (тепловые, атомные и гидроэлектростанции) до конечных потребителей необходимо неоднократно варьировать величину напряжения (понижать или повышать). С наибольшей эффективностью эти преобразования удаётся сделать, когда в линиях электропередачи используется переменное напряжение. При этом электрический ток, возникающий в результате действия переменного электрического поля, будет также переменным, изменяясь во времени периодически с такой же частотой. Если в сети присутствуют реактивные элементы (ёмкости, индуктивности), то возникает сдвиг фаз между переменным током и напряжением.

Определения и основные формулы

Переменным принято называть ток, изменяющийся с течением времени как по величине, так и по амплитуде. В английской технической литературе используется термин alternating current (AC). Он переводится как «чередующийся ток» или ток, изменяющий свою полярность.

Периодический переменный ток (ПТ) — это ток, который через идентичные интервалы времени принимает исходную величину, совершая таким образом циклический процесс, аналогичный гармоническому колебанию маятника. Гармонические колебания описываются с помощью синусоидальной функции:

Величина, которая определяется как произведение ω на t и имеет размерность угла (в радианах угол 90 градусов соответствует π/2 радиан), называется фазой синусоидальной переменной. В данном случае тока. Формула справедлива для случая, когда измерение тока стартует с точки отсчёта t = 0. В общем случае рабочая формула выглядит так:

Используя специальный измерительный прибор — осциллограф, можно наблюдать синусоиду напряжения на экране и определять её параметры.

ПТ и активная нагрузка

Если к источнику переменного тока подключено обычное сопротивление (резистор), то согласно закону Ома ток на резисторе, равен:

В приведенной выше формуле величина I₀ = U₀/ R — амплитуда ПТ. Видно, что ток в цепи с активным сопротивлением изменяется с течением времени абсолютно синхронно с напряжением.

Таким образом, на активной нагрузке угол сдвига фаз между током и напряжением равен нулю.

Конденсатор в цепи ПТ

Конструкция конденсатора препятствует протеканию постоянного тока, полностью его блокируя. Поочерёдно заряжаясь и разряжаясь конденсаторные пластины поддерживают ток в цепи, поскольку по определению ток I — это изменение заряда Q за единицу времени:

Ниже представлена картинка, объясняющая подключение конденсатора С к источнику переменного напряжения U.

Напряжение на конденсаторе в любой момент времени равно напряжению:

Тогда заряд Q(t) на обкладках конденсатора определим, используя выражение:

Пользуясь формулой для тока, получим первую производную от заряда по времени, которая равна ёмкостному току I_c(t):

Из графиков, представленных на картинке ниже, видно, что максимальная амплитуда тока наступает на четверть периода раньше, чем напряжения. Из этого следует, что фаза напряжения на π/2 радиан меньше фазы электротока. То есть, в цепи синусоидального тока существует отставание напряжения по фазе (фазовый сдвиг) на π/2.

Данное явление может быть объяснено по-другому. Из курса тригонометрии известно, что:

С помощью формул, приведенных выше, можно получить такое выражение:

Данное соотношение в явном виде показывает, что фазовый сдвиг равен π/2.

Индуктивность в цепи ПТ

Катушка индуктивности в цепях СПТ является реактивным элементом, поскольку ее активное сопротивление практически равно нулю. При подключении катушки также возникает фазовый сдвиг, но его причина несколько иная, чем в цепи с емкостью.

При практически нулевом омическом сопротивлении не может возникнуть короткое замыкание (резкий рост тока), поскольку переменный характер напряжения включает иной механизм сопротивления. Согласно закону, открытому британским учёным Майклом Фарадеем, в катушке появляется переменное магнитное поле, которое создает магнитный поток F, инициирующий появление электродвижущей силы (ЭДС самоиндукции) на концах катушки индуктивности:

В соответствии с законом Фарадея:

Откуда следует, что:

Используя данную формулу, находим определение для тока на индуктивности:

Как известно,

Следовательно, в идеальном индуктивном элементе угол сдвига фаз между напряжением и током равен π/2, причём ток отстаёт по фазе от напряжения.

Из графика видно, что максимум силы тока достигается на четверть периода позже, чем максимум напряжения, что соответствует отставанию по фазе на π/2.

От угла сдвига фаз зависит, какова будет реактивная мощность и, следовательно, коэффициент мощности, который выражается через cosφ и является очень важной характеристикой для оценки эффективности работы электрооборудования. Его значение может находиться в диапазоне от нуля до единицы. Если cosφ = 0, это означает, что в электроцепи присутствуют лишь реактивные токи. На практике такая ситуация невозможна, но чтобы потери мощности, связанные с реактивными токами, были меньше, используют компенсационные устройства.

Принцип действия таких устройств основывается на свойстве конденсаторов и катушек сдвигать фазу в противоположных направлениях. Компенсаторы зачастую используют в производственных цехах, где работает большое количество электрооборудования. Это приводит к ощутимым потерям электроэнергии и ухудшению качества электротока. Устройство компенсации решает подобные проблемы. Им успешно силу тока изменяют, если что-то сдвигают. Обычно такое устройство состоит из блоков конденсаторов довольно большой емкости, которые помещаются в отдельных шкафах.

Видео по теме

Источник

Фазовые соотношения между током и напряжением цепи

Если
ток и напряжение одновременно достигают
нуля, то это означает, что они совпадают
по фазе (рис. 2.1). При этом

.
Если этого нет, то напряжение и ток
сдвинуты по фазе. Угол сдвига фаз между
напряжением и током принято определять
как разность начальных фаз напряжения
(
)
и тока (
).
Этот угол обозначают греческой буквой

(фи):

/
(2.3)

Угол
сдвига фаз 
любой электрической цепи не произвольная
величина. Он определяется соотношением
между параметрами R,
L
и C
для каждой конкретной цепи с постоянной
частотой f.

В
частности, в цепи с сопротивлением
R
ток и напряжение всегда совпадают по
фазе (
)
и угол сдвига фаз, см. формулу (2.3), 
= 0; в цепи с индуктивность L
ток всегда отстает по фазе от напряжения
на 90

и поэтому угол сдвига фаз

;
в цепи с емкостью C
ток всегда опережает напряжение по
фазе на 90

и
поэтому угол сдвига фаз

.

В энергетике широко
распространено понятие о коэффициенте
мощности цепи, под которым понимают
отношение ее активной мощности Р
к полной S:

.
(2.4)

Этот
коэффициент показывает, какая доля
полной мощности преобразуется в тепло
и другие виды энергии. Энергетики
стремятся эту долю свести к единице, т.
е. иметь P
= S
или cos 
= 1.

Фазовые
соотношения между током и напряжением
цепи исследуются с помощью двухлучевого
осциллографа, позволяющего получать
на экране одновременно две синусоиды:
тока и напряжения (рис. 2.4).

Амплитудные соотношения между током и напряжением цепи

Синусоидальные
напряжения и токи часто изображают
в виде векторов, длина которых равна
амплитуде, а угол между вектором и
произвольно выбранной осью отсчета
равен начальной фазе. При этом принято
положительные начальные фазы откладывать
от оси отсчета против часовой стрелки,
а отрицательные начальные фазы 
по часовой стрелке.

Совокупность
векторов тока и напряжений цепи
называется векторной диаграммой этой
цепи. Векторные диаграммы для цепей
с R,
L
и C
показаны на рис. 2.1, 2.2 и 2.3.

Рис.
2.4

Токи
и напряжения в электрических цепях
измеряют с помощью амперметров и
вольтметров. Обычно для этого применяют
приборы электромагнитной системы, шкалы
которых отградуированы не в амплитудных
значениях тока I_m
и напряжения U_m,
а в так называемых действующих значениях
тока и напряжения U.
Это основные расчетные величины
цепей синусоидального тока. Они меньше
амплитуд в

раз:

;

.
(2.5)

Между
амплитудами напряжения и тока (так
же, как и между их действующими
значениями) любой электрической
цепи существует однозначная связь,
определяемая соотношениями между
параметрами R,
L
и C.
Отношение амплитуд (или действующих
значений) напряжения и тока называется
полным сопротивлением цепи:

.

В
частности:

для
цепи с активным сопротивлением:

;

для
цепи с индуктивностью:

;
(2.6)

для
цепи с емкостью:

где
x_L

индуктивное, а x_C

емкостное сопротивления.

Индуктивное
и емкостное сопротивления принципиально
зависят от частоты напряжения:

;

.
(2.7)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Разность фаз напряжения и тока

Условимся под разностью фаз φ напряжения и тока всегда понимать разность начальных фаз напряжения и тока (а не наоборот):

Поэтому на векторной диаграмме угол φ отсчитывается в направлении от вектора I к вектору U (рис. 3.10). Именно при таком определении разности фаз угол φ равен аргументу комплексного сопротивления. Угол φ положителен при отстающем токе () и отрицателен при опережающем токе ().
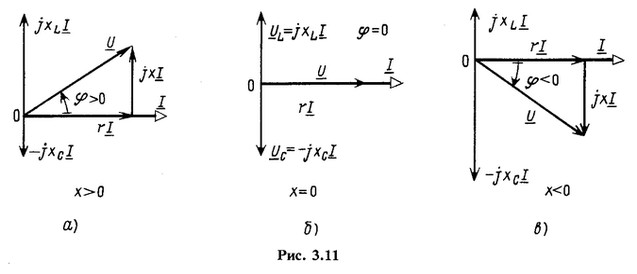
Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При имеем и ток отстает по фазе от напряжения, . При имеем , ток совпадает по фазе с напряжением, rLC-цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса в последовательном контуре. Наконец, при имеем , ток опережает по фазе напряжение.

Векторные диаграммы для трех возможных соотношений даны на рис. 3.11. При построении этих диаграмм начальная фаза тока ; принята равной нулю. Поэтому равны друг другу.
Рассматривая при заданной частоте цепь по рис. 3.8 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при как последовательное соединение сопротивления и индуктивности (), при как сопротивление r и при как последовательное соединение сопротивления и емкости (). При заданных L и С соотношение между зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
Выше, в разделе, было принято, что задан ток, а определялись напряжения на элементах и на входных выводах цепи. Однако часто бывает задано напряжение на выводах, а ищется ток. Решение такой задачи не представляет труда. Записав по заданным величинам комплексное напряжение U и комплексное сопротивление Z, определим комплексный ток

и тем самым действующий ток и начальную фазу тока.
Часто равной нулю принимается начальная фаза заданного напряжения: . В этом случае, как следует из раздела, начальная фаза тока ; равна и противоположна по знаку разности фаз φ, т. е .
Установленные выше соотношения между амплитудами и действующими токами и напряжениями, а также выражение для сдвига фаз ф позволяют вычислить ток и не прибегая к записи закона Ома в комплексной форме. Подробно этот путь решения показан в примере 3.4.

Пример 3.4.
К цепи, состоящей из последовательно соединенных конденсатора и катушки, приложено напряжение . Емкость конденсатора С=5 мкФ, сопротивление катушки r=15 Ом, индуктивность L=12 мГн. Найти мгновенные значения тока в цепи и напряжений на конденсаторе и на катушке.

Решение.
Схема замещения цепи показана на рис. 3.8.

Напряжение на емкости отстает от тока по фазе на 90°, следовательно,

Комплексное сопротивление катушки

Комплексная амплитуда напряжения на выводах катушки

Мгновенное напряжение на катушке

Пример 3.5.
В цепи, состоящей из последовательно соединенных конденсатора и катушки, ток I=2 А, его частота f=50 Гц. Напряжение на выводах цепи U=100 В, катушки U_кат =150 В и конденсатора U_с=200 В. Определить сопротивление и индуктивность катушки и емкость конденсатора.

Решение.

Полное сопротивление цепи z=U/I=50 Ом.
Полное сопротивление катушки zкат=Uкат/I=75 Ом;

Все страницы раздела «Цепи переменного тока» на websor

Источник

From Wikipedia, the free encyclopedia

Graph showing a voltage with a leading and lagging current, plotted against time.

Leading and lagging current are phenomena that occur as a result of alternating current. In a circuit with alternating current, the value of voltage and current vary sinusoidally. In this type of circuit, the terms lead, lag, and in phase are used to describe current with reference to voltage. Current is in phase with voltage when there is no phase shift between the sinusoids describing their time varying behavior. This generally occurs when the load drawing the current is resistive.

In electric power flow, it is important to know how much current is leading or lagging because it creates the reactive power in the system, as opposed to the active (real) power. It can also play an important role in the operation of three phase electric power systems.

Angle notation[edit]

Angle notation can easily describe leading and lagging current:

^[1]

In this equation, the value of theta is the important factor for leading and lagging current. As mentioned in the introduction above, leading or lagging current represents a time shift between the current and voltage sine curves, which is represented by the angle by which the curve is ahead or behind of where it would be initially. For example, if θ is zero, the curve will have amplitude zero at time zero.^[2] Using complex numbers is a way to simplify analyzing certain components in RLC circuits. For example, it is very easy to convert these between polar and rectangular coordinates. Starting from the polar notation, can represent either the vector or the rectangular notation $cos theta +jsin theta =e^{{jtheta }},,$ both of which have magnitudes of 1.

Lagging current[edit]

Lagging current can be formally defined with respect to “an alternating current that reaches its maximum value up to 90 degrees later than the voltage that produces it.” This means that current lags the voltage when beta , the angle of the current sine wave with respect to an arbitrarily chosen reference, is less than delta , the angle of the voltage sine wave with respect to the same reference. Therefore, current can quickly be identified as lagging if the angle theta is positive. For example, if the voltage angle delta is zero, current will be lagging if beta is negative. This is often the case because voltage is taken as the reference.

In circuits with primarily inductive loads, current lags the voltage. This happens because in an inductive load, it is the induced electromotive force that causes the current to flow. Note that in the definition above, the current is produced by the voltage. The induced electromotive force is caused by a change in the magnetic flux linking the coils of an inductor.

Leading current[edit]

Leading current can be formally defined as “an alternating current that reaches its maximum value up to 90 degrees ahead of the voltage that it produces.” This means that the current leads the voltage when beta , the angle of the current sine wave with respect to an arbitrarily chosen reference is greater than delta , the angle of the voltage sine wave with respect to the same reference. Therefore, current can quickly be identified as leading if the angle theta is negative. For example, if the voltage angle delta is zero, current will be leading if beta is positive. This is often the case because voltage is taken as the reference.

In circuits with primarily capacitive loads, current leads the voltage. This is true because current must first flow to the two plates of the capacitor, where charge is stored. Only after charge accumulates at the plates of a capacitor is a voltage difference established. The behavior of the voltage is thus dependent on the behavior current and on how much charge accumulates. This is why the formal definition states that the current produces the voltage.

Visualizing leading and lagging current[edit]

A simple phasor diagram with a two dimensional Cartesian coordinate system and phasors can be used to visualize leading and lagging current at a fixed moment in time. In the real-complex coordinate system, one
period of a sine wave corresponds to a full circle in the complex plane. Since
the voltage and current have the same frequency, at any moment in time those
quantities can be easily represented by stationary points on the circle, while
the arrows from the center of circle to those points are called phasors. Since
the relative time difference between functions is constant, they also have a
constant angle difference between them, represented by the angle between points
on the circle. ^[2]

Historical documents concerning leading and lagging currents[edit]

An early source of data is an article from the 1911 American Academy of Arts and Sciences by Arthur E. Kennelly. Kennelly uses conventional methods in solving vector diagrams for oscillating circuits, which can also include alternating current circuits as well.

Notes[edit]

References:

^ Nilsson p. 338
^ ^a ^b von Meier, Alexandra (2006). Electric Power Systems: A Conceptual Introduction. Wiley-Interscience. pp. 49–66.

References[edit]

Bowick, Chris, John Blyler, and Cheryl J. Ajluni. RF Circuit Design. 2nd ed. Amsterdam: Newnes/Elsevier, 2008. Print.
Gaydecki, Patrick. Foundations of Digital Signal Processing: Theory, Algorithms and Hardware Design. 2nd ed. London: Institution of Electrical Engineers, 2004. Print
Gilmore, Rowan, and Les Besser. Passive Circuits and Systems. Boston [u.a.: Artech House, 2003. Print.
Hayt, W. H., and J. E. Kemmerly. Engineering Circuit Analysis. 2nd ed. New York: McGraw-Hill, 1971. Print.
Kennelly, Arthur E. «Vector-Diagrams of Oscillating-Current Circuits.» American Academy of Arts & Sciences 46.17 (1911): 373-421. Jstor. ITHAKA. Web. 1 May 2012. <https://www.jstor.org/stable/20022665>.
«Lagging Current.» TheFreeDictionary.com. Web. 1 May 2012. (http://encyclopedia2.thefreedictionary.com/lagging_current)
«Leading Current.» TheFreeDictionary.com. Web. 1 May 2012. (http://encyclopedia2.thefreedictionary.com/leading_current)
Nilsson, James William; Riedel, Susan A. (2008). Electric circuits (8th ed.). Prentice Hall. p. 338. ISBN 0-13-198925-1, Chapter 9, page 338
Smith, Ralph J. Circuit Devices and Systems. 3rd ed. New York: John Wiley & Sons, 1976. Print.
Glover, Duncan J. Power System Analysis and Design. 5th ed. Cengage Learning, 2014.
Masters, G. Renewable and Efficient Electric Power Systems. 2nd ed. Wiley, 2004.

Источник

Сдвиг фаз переменного тока и напряжения

Похожие материалы:

Добавить комментарий

Сдвиг фаз между током и напряжением в цепи переменного тока

Определения и основные формулы

ПТ и активная нагрузка

Конденсатор в цепи ПТ

Индуктивность в цепи ПТ

Видео по теме

Фазовые соотношения между током и напряжением цепи

Амплитудные соотношения между током и напряжением цепи

Разность фаз напряжения и тока

Angle notation[edit]

Lagging current[edit]

Leading current[edit]

Visualizing leading and lagging current[edit]

Historical documents concerning leading and lagging currents[edit]

See also[edit]

Notes[edit]

References[edit]

Не пропустите также: