Как найти угол наклона плоскости к грани

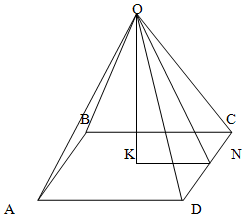
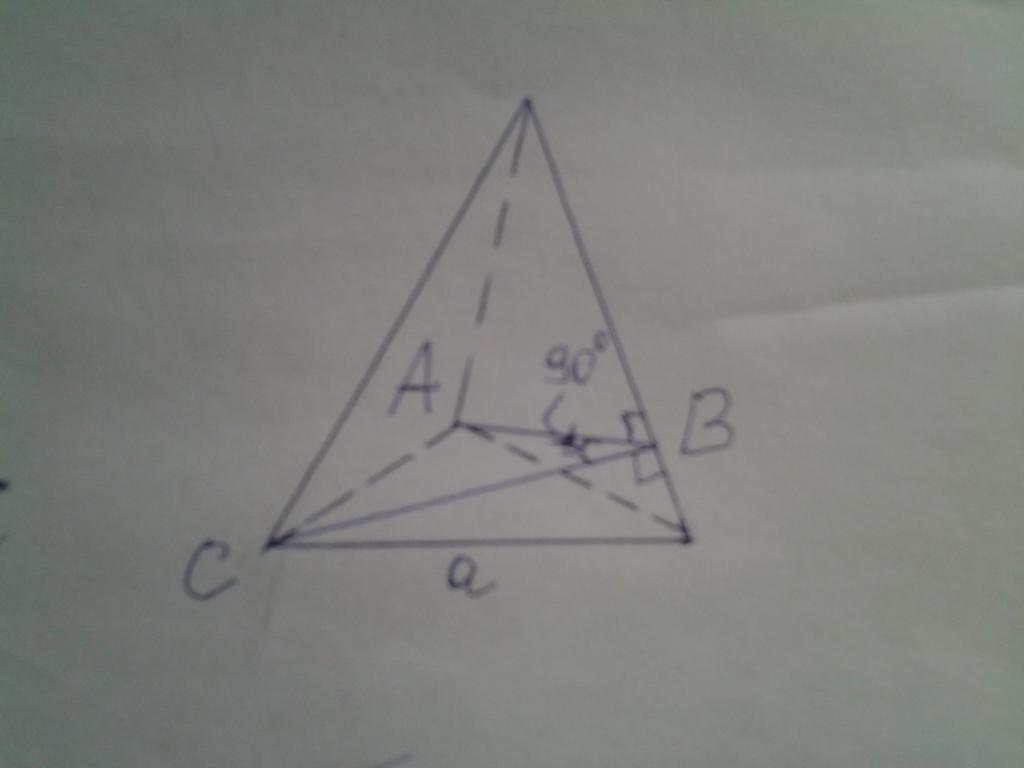Задача

В правильной четырёхугольной пирамиде сторона основания равна а, высота равна 3а.
Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.

Найдем угол наклона ребер к плоскости основания.
Поскольку в основании правильной пирамиды лежит правильный четырехугольник, то, в данном случае, это — квадрат. Поскольку высота пирамиды проецируется в центр основания, то это — точка пересечения диагоналей. Откуда KN = а/2

Треугольник OKN — прямоугольный, OK — высота, равная 3а.
Найдем тангенс угла KNO, обозначив его как α .

tg α = OK / KN
tg α = 3a / (a/2) = 6
α = arctg 6 ≈ 80.5377°

Найдем угол наклона ребра пирамиды.
Диагональ квадрата со стороной а равна а√2. Поскольку высота проецируется в центр основания, то в этой точке диагонали делятся пополам.

Таким образом, для прямоугольного треугольника OKC тангенс угла KCO (обозначим его как β ) равен

tg β = OK / KC
tg β = 3a / (а√2/2) = 6 / √2
β = arctg 6/√2 ≈ 76.7373°

Ответ: угол наклона граней arctg 6 ≈ 80.5377°; угол наклона ребер arctg 6/√2 ≈ 76.7373°

Двугранные углы пирамиды и методика их расчета

Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, — это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.

Пространственная фигура пирамида

Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово «пирамида». Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.

Вам будет интересно: Популяция людей: определение, виды, свойства и примеры

Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.

Двугранные углы фигуры

Вам будет интересно: «Дурачок» или «дурачек»: как не проспорить в Интернете из-за орфографии?

Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.

Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:

• При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n — число сторон многоугольника.
• Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.

Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип — на боковых ребрах.

Как рассчитать углы пирамиды?

Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.

В трехмерном пространстве плоскость задается следующим выражением:

A*x + B*y + C*z + D = 0

Где A, B, C, D — это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:

Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.

Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:

Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:

Или в координатной форме:

φ = arccos(|A1*A2 + B1*B2 + C1*C2|/(√(A12 + B12+C12)*√(A22 + B22 + C22)))

Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.

Углы правильной пирамиды четырехугольной

Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.

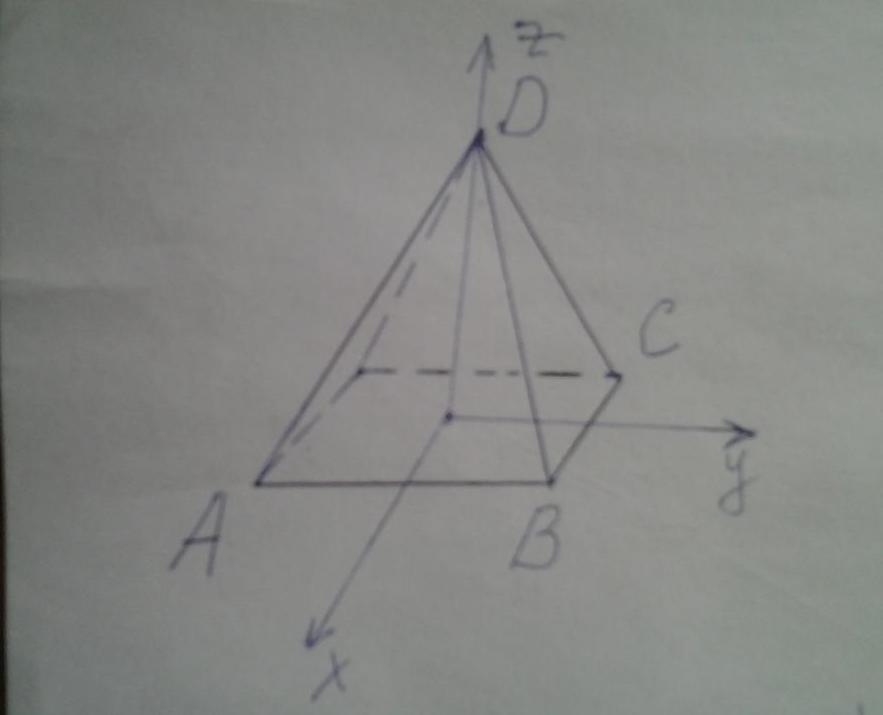
Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.

Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:

Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:

Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:

Угол между ABC и ABD:

Угол между ABD и BDC:

φ = arccos(a4/(4*a2*(h2+a2/4)) = arccos(a2/(4*(h2+a2/4))) = 81,49o

Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.

Углы треугольной правильной пирамиды

На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.

Двугранный угол, равный 90o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры — h, апофему — hb и боковое ребро — b. Теперь можно записать следующие формулы:

Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:

Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:

Площадь равностороннего треугольника рассчитывается так:

Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см2.

Пирамида и ее элементы

Здесь собраны основные сведения о пирамидах и связанных с ней формулах и понятиях. Все они изучаются с репетитором по математике при подготовке к ЕГЭ.

Рассмотрим плоскость , многоугольник , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки называются боковыми ребрами. Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.

Пирамида называется правильной, если правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.

Комментарий репетитора:
Не путайте понятие «правильная пирамида» и «правильный тетраэдр». У правильной пирамиды боковые ребра совсем не обязательно равны ребрам основания, а в правильном тетраэдре все 6 ребер ребра равные. Это его определение. Легко доказать, что из равенства следует совпадение центра P многоугольника с основанием высоты, поэтому правильный тетраэдр является правильной пирамидой.

Что такое апофема?
Апофемой пирамиды называется высота ее боковой грани. Если пирамида правильная, то все ее апофемы равны. Обратное неверно.

Репетитор по математике о своей терминологии: работа с пирамидами на 80% строится через два вида треугольников:
1) Содержащий апофему SK и высоту SP
2) Содержащий боковое ребро SA и его проекцию PA

Чтобы упростить ссылки на эти треугольники репетитору по математике удобнее называть первый из них апофемным, а второй реберным. К сожалению, этой терминологии вы не встретите ни в одном из учебников, и преподавателю приходится вводить ее в одностороннем порядке.

Формула объема пирамиды:
1) -высота пирамиды
2) – радиус вписанного шара, а – площадь полной поверхности пирамиды.
3) – площадь параллелограмма, образованного серединами четырех оставшихся ребер.

Свойство основания высоты пирамиды:

Точка P (смотри рисунок) совпадает с центром вписанной окружности в основание пирамиды, если выполняется одно из следующих условий:
1) Все апофемы равны
2) Все боковые грани одинаково наклонены к основанию
3) Все апофемы одинаково наклонены к высоте пирамиды
4) Высота пирамиды одинаково наклонена ко всем боковым граням

Комментарий репетитора по математике: обратите внимание, что все пункты объединяет одно общее свойство: так или иначе везде участвуют боковые грани (апофемы — это их элементы). Поэтому репетитор может предложить менее точную, но более удобную для заучивания формулировку: точка P совпадает с центром вписанной окружности основание пирамиды, если имеется любая равная информация о ее боковых гранях. Для доказательства достаточно показать, что все апофемные треугольники равны.

Точка P совпадает с центром описанной около основания пирамиды окружностью, если верно одно их трех условий:
1) Все боковые ребра равны
2) Все боковые ребра одинаково наклонены к основанию
3) Все боковые ребра одинаково наклонены к высоте

Комментарий репетитора. Аналогично предыдущему пункту текст можно упростить и вместо этих условий произнести : «если имеется любая равная информация о боковых ребрах». При этом все апофемные треугольники будут равны все проекции боковых ребер будет равны P будет равноудалена от всех вершин основания и поэтому окажется центром описанной окружности.

Площадь полной поверхности пирамиды:
Полощадью поверности пирамиды называется сумма площадей всех ее граней .
Если все апофемы равны (например в правильной пирамиде), то площадь ее боковой поверхности вычисляется по формуле , где p — полупериметр основания, а SK-апофема.

Правильная треугольная пирамида однозначно определяется двумя параметрами: один плоский, а другой пространственный: к плоскому я отношу любой элемент правильного треугольника (кроме угла), а к пространственному любой связующий параметр между основанием и точкой S: апофема, высота, углы наклона ребер, граней, объем, площадь поверхности и др. При наличие в условии задачи этих двух начальных данных репетитор с учеником может найти у такой пирамиды все что угодно.

Пирамида — обязательный пункт подготовки к ЕГЭ по математике. Програмный минимум по стереометрии включает в себя все вышеуказанные сведения, кроме третьей формулы вычисления объема пирамиды.

Колпаков Александр,
репетитор по математике в Москве. Строгино

Геометрия, 11 класс

Урок № 3. Координатный метод решения задач

Перечень вопросов, рассматриваемых в теме:

• специфика и преимущества решения задач в пространстве координатным методом;
• типы задач, решаемые координатным методом;
• этап решения задачи координатным методом;
• решение несложных задач методом координат.

Глоссарий по теме

Уравнение вида задает в пространстве плоскость α.

При этом вектор – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Очевидно, что нормалью является любой вектор, коллинеарный вектору .

Вектор и любой коллинеарный ему вектор называются направляющим векторами прямой и прямой соответственно.

Основная литература:

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 163-170.

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 353-260.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Работа по теме урока. Объяснение новой темы

Мы рассмотрели несложную задачу на применение метода координат в пространстве.

Векторы , угол между которыми мы искали, называются направляющими векторами прямой и прямой соответственно.

Рассмотрим этот метод более подробно.

Суть метода координат на плоскости и в пространстве заключается в следующем.

1. Ввести систему координат удобным образом (исходя их свойств заданной фигуры)
2. Записать условие задачи в координатах, определив во введенной системе координат координаты точек и/или векторов
3. Используя алгебраические преобразования, решить задачу
4. Интерпретировать полученный результат в соответствии с условием данной задачи

В рассмотренном нами примере, поскольку был дан куб, мы могли ввести систему координат с центром в любой его вершине.

В координатах удобно решать задачи, связанные с поиском расстояний и углов. Но для того чтобы его использовать, нужно знать некоторые формулы:

1. Угол между прямыми
2. Угол между прямой и плоскостью
3. Угол между плоскостями
4. Расстояние от точки до плоскости
5. Расстояние от точки до прямой в пространстве
6. Расстояние между скрещивающимися прямыми

Расстояние между параллельными плоскостями определяется как расстояние от точки, лежащей в одной плоскости, до другой плоскости.

Мы рассмотрим только первые четыре формулы.

Введем их.

Угол между прямыми

Если прямая задана двумя точками A и B, то известен направляющий вектор этой прямой с координатами {}. Пусть вторая прямая имеет направляющий вектор . Тогда угол между векторами вычисляется по формуле:

.

Дальше ищется арккосинус от найденного числа. Заметим, что если косинус получился отрицательным, то это значит, что угол между векторами тупой. Поэтому мы берем модуль получившегося числа.

Фактически мы уже рассмотрели пример вычисления угла между прямыми в пространстве.

Угол между прямой и плоскостью

Сначала рассмотрим уравнение плоскости, проходящей через три точки.

.

Вам известно, что в пространстве плоскость задается уравнением, аналогичным тому, которое на плоскости задает прямую.

Если линейное уравнение вида на плоскости задает прямую l, то уравнение вида задает в пространстве плоскость α. При этом вектор – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль.

Вам известно, что три точки в пространстве определяют единственную плоскость. Поэтому, если заданы три точки, то мы можем найти уравнение плоскости

Мы можем подставить координаты заданных точек в уравнение плоскости и решить систему из трех уравнений с тремя переменными:

В этой системе четыре неизвестных, однако, мы можем избавиться от одной, если разделим все уравнения на D:

.

Для изучения данного способа в 11 классе на базовом уровне введение понятий матрица, определитель матрицы не желателен, данные понятия не входят в базовый курс изучения геометрии.

Иногда эта система оказывается несложной. Но иногда бывает трудно ее решить, и тогда можно использовать следующую формулу:

Обозначение |M| означает определитель матрицы М.

В нашем случае матрица представляет собой таблицу 3х3 элемента. И определитель |M| вычисляется следующим образом:

.

Таким образом, уравнение плоскости будет записано так:

Пример 1:

Написать уравнение плоскости, проходящей через точки K(1; -2; 3), L (0; 1; 1), M (1; 0; 1).

Составим систему.

.

Решая ее, получим значения А, В и С: . То есть уравнение плоскости имеет вид:

.

Ответ: .

Теперь запишем формулу угла между прямой и плоскостью.

Пусть дано уравнение плоскости: и известен — направляющий вектор прямой.

Тогда – синус угла между прямой и плоскостью.

Пример 2:

Найдем угол между прямой и плоскостью. В качестве плоскости возьмем ту, уравнение которой мы только что написали:

Прямая проходит через точки Т(2; -1; 4) и Р(3; 2; 2).

Направляющий вектор прямой: .

Найдем синус угла между прямой и плоскостью:

.

Угол между прямой и плоскостью .

Ответ: .

Угол между плоскостями

Пусть:

уравнение первой плоскости:

уравнение второй плоскости:

Тогда — косинус угла между этими плоскостями.

Пример 3:

Найдем угол между плоскостями:

и .

Найдем косинус угла между плоскостями:

.

Угол между плоскостями:

Ответ:

Расстояние от точки до плоскости

Пусть координаты точки: , уравнение плоскости: .

Тогда Расстояние от точки до плоскости вычисляется по формуле: .

Пример 4.

Найдем расстояние от точки М(4; 3; 4) до плоскости .

.

Теперь рассмотрим решение задачи координатным методом с использованием рассмотренных формул.

Пример 5.

АВС…D1 – куб с ребром 4. Найти расстояние от точки А до плоскости ЕКС (Е – середина D1C1, K – середина C1B1)

Введем систему координат с началом в вершине А так, как показано на рисунке:

Интересующие нас точки будут иметь координаты:

A(0; 0; 0), C(4; 4; 0), E(4; 2; 4), K(2; 4; 4).

Напишем уравнение плоскости ЕКС:

.

Решая ее, получим значения А, В, С и D: .

Уравнение плоскости имеет вид:

Теперь найдем расстояние от точки А до плоскости ЕКС: .

Ответ: .

Рассмотрим задачу (№14 из варианта ЕГЭ).

В кубе ABC…D₁ все рёбра равны 4. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ построена плоскость α, параллельная прямой BD₁.

а) Докажите, что A₁P : PB₁ = 2 : 1, где P — точка пересечения плоскости α с ребром A₁B₁.

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

Решение:

Переформулируем первый пункт этой задачи таким образом:

Проведем плоскость через точки Р, K и C₁ и докажем, что она параллельна прямой BD₁.

Введем систему координат так, как показано на рисунке:

Найдем координаты точек :

Р(; 0; 4), К(4; 0; 3),(4; 4; 4).

Напишем уравнение плоскости :

;

Решая ее, получим значения А, В, С и D: .

— уравнение плоскости

Теперь докажем, что плоскость параллельна прямой BD₁.

Найдем угол между прямой BD₁ и плоскостью .

Точки В и D₁ имеют координаты: В (4; 0; 0), D₁ (0; 4; 4).

Направляющий вектор прямой BD₁ – это вектор .

Он имеет координаты .

Теперь найдем синус угла между вектором и плоскостью .

.

В этом случае нам не нужно считать знаменатель дроби. Так как числитель получился равен 0, то дробь равна 0, то есть синус угла между плоскостью и прямой равен 0, значит, плоскости параллельны или совпадают. Но, так как точка В, например, в плоскости, очевидно, не лежит, то плоскости параллельны.

Это значит, что плоскость, параллельная прямой BD₁ и проходящая через точки действительно пересекает ребро A₁B₁в точке Р так, что A₁P : PB₁ = 2 : 1. Что и требовалось доказать.

Теперь рассмотри второй пункт задачи. Уравнение плоскости у нас есть. Плоскость BB₁C₁ параллельна координатной плоскости YOZ и проходит через точку

В(4; 0; 0). Поэтому она имеет уравнение .

То есть ее коэффициенты .

Найдем угол между плоскостями, используя формулу

Ответ: .

Примечание. Это урок с решениями задачам по геометрии (раздел стереометрия, пирамида с четырехугольником в основании). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».

Задача

В правильной четырёхугольной пирамиде сторона основания равна а, высота равна 3а.

Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.

Решение.



Найдем угол наклона ребер к плоскости основания.

Поскольку в основании правильной пирамиды лежит правильный четырехугольник, то, в данном случае, это — квадрат. Поскольку высота пирамиды проецируется в центр основания, то это — точка пересечения диагоналей. Откуда KN = а/2

Треугольник OKN — прямоугольный, OK — высота, равная 3а.

Найдем тангенс угла KNO, обозначив его как

α.

tg

α = OK / KN

tg α = 3a / (a/2) = 6

α = arctg 6 ≈ 80.5377°

Найдем угол наклона ребра пирамиды.

Диагональ квадрата со стороной а равна а√2. Поскольку высота проецируется в центр основания, то в этой точке диагонали делятся пополам.

Таким образом, для прямоугольного треугольника OKC тангенс угла KCO (обозначим его как

β ) равен

tg

β = OK / KC

tg β = 3a / (а√2/2) = 6 / √2

β = arctg 6/√2 ≈ 76.7373°

Ответ: угол наклона граней arctg 6 ≈ 80.5377°; угол наклона ребер arctg 6/√2 ≈ 76.7373°

0
 

 Правильная пирамида с четырехугольником в основании (часть 3) |

Описание курса

| Нахождение величины наклона боковых граней правильной прамиды