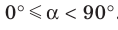Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.
Рис. (1). Дороги на земле и на эстакадах не пересекаются.
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).
Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.
Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD).
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:
Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.
Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
Содержание:
Перпендикулярность в пространстве
В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свойство ортогональной проекции многоугольника.
Угол между прямыми в пространстве
Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 
Угол между двумя параллельными прямыми считают равным 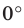
Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
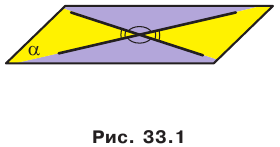
Пусть прямые 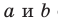
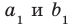
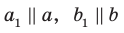
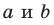
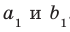
Возникает естественный вопрос: зависит ли угол между данными скрещивающимися прямыми 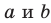
Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.
Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми 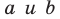
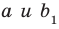
Например, на рисунке 33.3 изображена треугольная призма 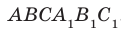
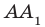
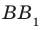
Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.
Если прямые 
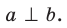
Например, ребра AD и 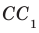
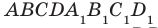
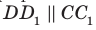
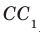
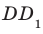
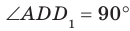
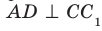
Пример:
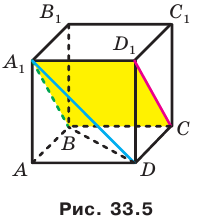
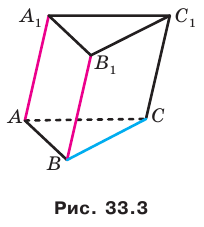
На рисунке 33.5 изображен куб 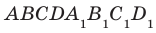
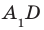
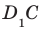
Решение:
Соединим точки 
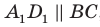
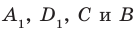
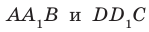
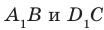
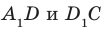
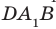
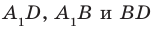
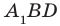
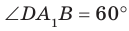
Перпендикулярность прямой и плоскости
В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.


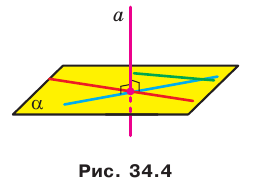
Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).
Если прямая 
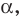
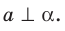
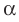
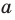
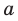
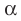
Из определения следует, что если прямая 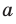
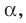
Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.
Например, интуитивно понятно, что ребро 
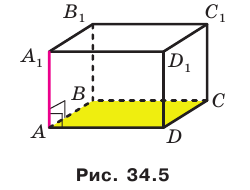
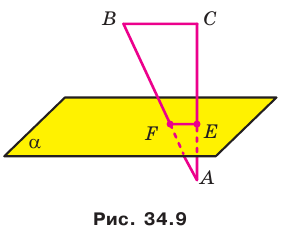
Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
На рисунке 34.5 прямая 
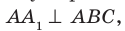
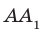
Теорему 34.1 часто используют на практике. Например, подставка для новогодней елки имеет форму крестовины. Если елку установить так, чтобы ее ствол был перпендикулярен направлениям крестовины, то елка будет стоять перпендикулярно плоскости пола (рис. 34.6).
Приведем теорему, которую можно рассматривать как еще один признак перпендикулярности прямой и плоскости.
Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).
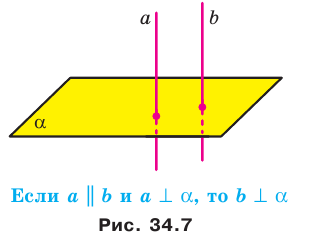
Например, на рисунке 34.5 прямая 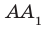
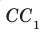
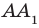
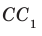
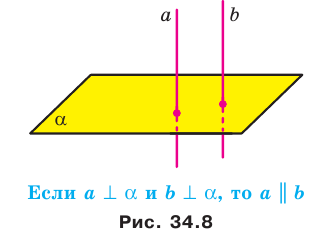
Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.
Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Пример:
Плоскость 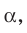
Решение:
Поскольку прямая АС перпендикулярна плоскости 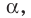

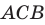
Перпендикуляр и наклонная
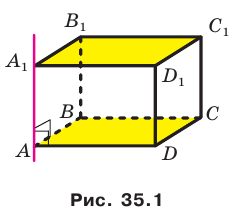
Пусть фигура 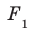
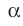
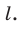
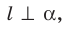
Например, основание ABCD прямоугольного параллелепипеда 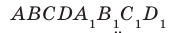
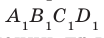
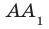
В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.
Пусть даны плоскость 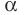
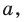
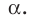
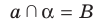
Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость 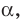
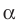
Отметим на плоскости 
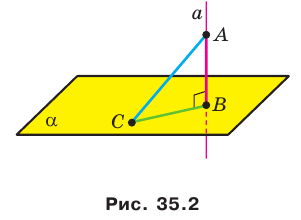
Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.
Пример:
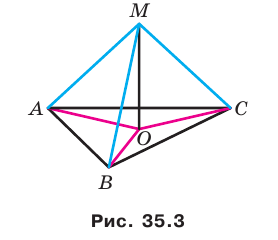
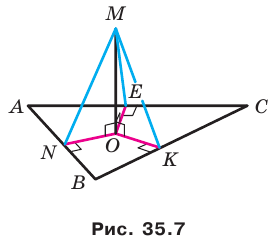
Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку 
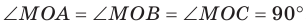
Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.
Определение. Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Пример:
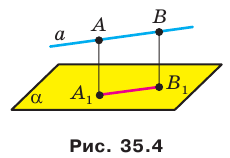
Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.
Решение:
Пусть А и В — две произвольные точки прямой 
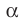
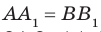
По теореме 34.3 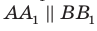
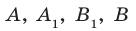
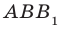
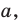
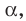
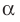
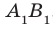
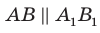
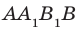
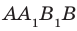
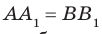
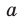
Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.
Пример:
Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Результаты, полученные в ключевых задачах 2 и 3, часто используют в практической деятельности, например в строительстве (рис. 35.5).

Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Доказательство. Докажем первую часть теоремы.Пусть прямая 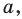
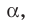
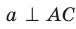
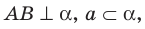
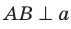
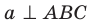
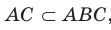
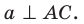
Пример:
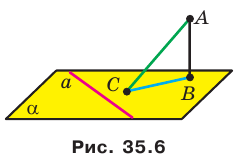
Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.
Отрезок ON является проекцией наклонной MN на плоскость АВС. По построению 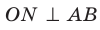
Аналогично можно доказать, что 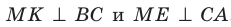
В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.
Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.
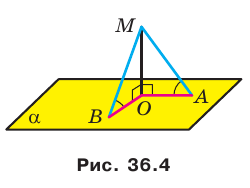
Угол между прямой и плоскостью
Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.
Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.
Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.
Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 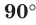
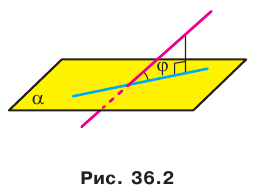
Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).
Из определения следует, что если 
Также принято говорить, что прямая образует угол 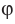
Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.
Например, рассмотрим куб 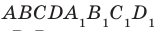
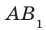
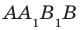
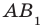
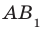
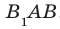
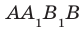
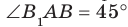
Пример:
Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.
Решение:
Пусть МЛ и М В — наклонные, образующие с плоскостью 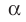
Прямая ОА является проекцией прямой МА на плоскость 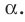
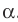
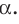
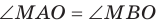
Поскольку 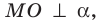
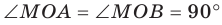
- Заказать решение задач по высшей математике
Двугранный угол. Угол между плоскостями
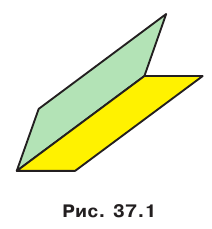
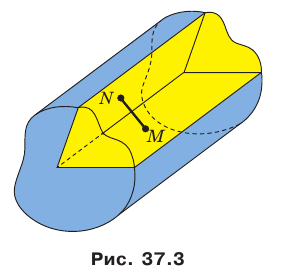
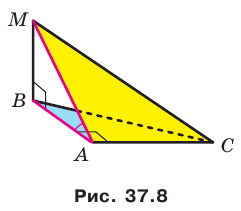
На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугранным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).
Отрезок MN принадлежит «желтому» двугранному углу, а «синему» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).
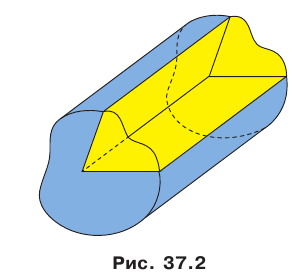
Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).
Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.
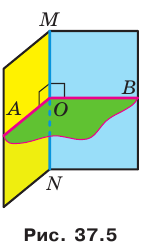
Отметим на ребре MN двугранного угла произвольную точку О. Через точку О в гранях двугранного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугранного угла. Поскольку 
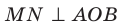
Определение. Величиной двугранного угла называют величину его линейного угла.
Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.
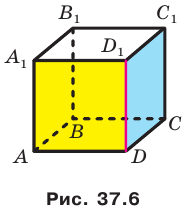
Например, рассмотрим куб 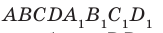
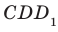
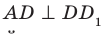
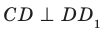
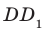
Угол ADC прямой.
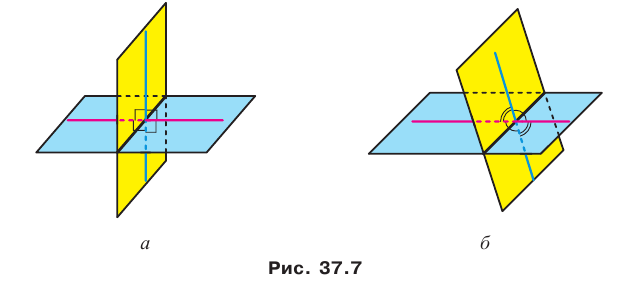
При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:
- все четыре двугранных угла прямые (рис. 37.7, а);
- из четырех двугранных углов два равных угла острые и два равных угла тупые (рис. 37.7, б).
В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.
Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.
Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.
Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.
Пример:
Прямоугольные треугольники 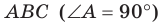
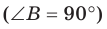
Решение:
Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как 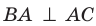
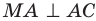
Для стороны AM прямоугольного треугольника АМС можно записать: 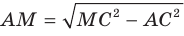
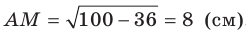
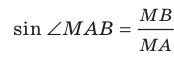
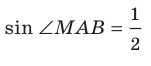
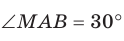
Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.
Теорема 37.1 (площадь ортогональной проекции многоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где 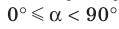
Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Если плоскости 
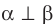
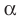
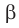
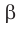
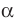
Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).
Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).
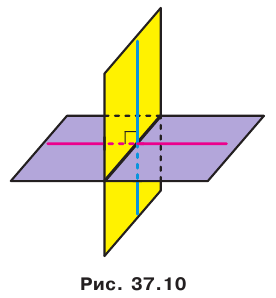
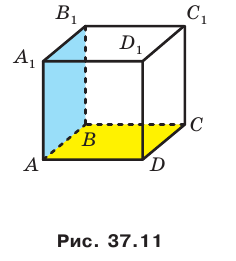
Теорема 37.2 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Например, плоскость грани 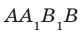
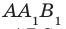
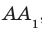

Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Перпендикулярность прямой и плоскости
- Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
- Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
- Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
- Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
- Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Ортогональная проекция фигуры
Пусть фигура 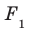
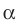
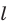
Расстояние от точки до плоскости
Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Расстояние от прямой до параллельной ей плоскости
Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями
Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Теорема о трех перпендикулярах
Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Угол между прямой и плоскостью
- Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между такой прямой и плоскостью равен 0°.
- Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 90°.
- Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.
Величина двугранного угла
Величиной двугранного угла называют величину его линейного угла.
Угол между двумя пересекающимися плоскостями
Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.
Площадь ортогональной проекции многоугольника
Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где
Перпендикулярные плоскости
Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Признак перпендикулярности плоскостей
Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Векторы и координаты в пространстве
- Множества
- Рациональные уравнения
- Рациональные неравенства и их системы
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
- Параллельность в пространстве
Угол между скрещивающимися прямыми и расстояние между ними. Расстояние от точки до плоскости и от прямой до параллельной ей плоскости
Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость невозможно.
Часто в задачах требуется найти угол между скрещивающимися прямыми. Как это сделать?
Угол между прямыми, лежащими в одной плоскости, найти нетрудно. Можно измерить его транспортиром. Можно найти из какого-нибудь треугольника по теореме синусов или косинусов.
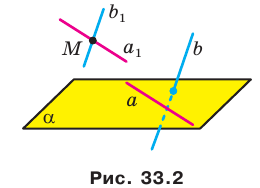
Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях α и β . Проведем в плоскости β прямую с, параллельную прямой а. Угол между прямыми а и b равен углу между прямыми b и с.
Можно сказать, что угол между скрещивающимися прямыми — это угол между параллельными им прямыми, лежащими в одной плоскости.
Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
Другими словами, расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат.
Дадим еще два полезных определения.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.
Расстояние от прямой до параллельной ей плоскости — длина перпендикуляра, опущенного на плоскость из любой точки этой прямой.
Заметим, что расстояние от точки до плоскости или угол между скрещивающимися прямыми иногда проще найти с помощью координатно-векторного метода.
Читаем дальше: Теорема о трех перпендикулярах.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Угол между скрещивающимися прямыми и расстояние между ними. Расстояние от точки до плоскости и от прямой до параллельной ей плоскости» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Учебник
Геометрия, 10 класс
Угол между скрещивающимися прямыми в пространстве
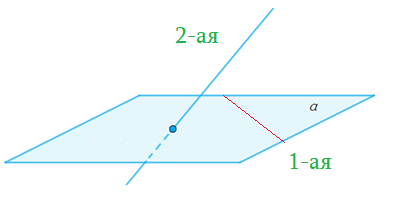
Скрещивающиеся прямые — не параллельны, не имеют общих точек, не пересекаются.
Признаки Скрещивающихся прямых
- 1-ая прямая лежит в плоскости, а 2-ая пересекает плоскость в точке не из 1-ой, то прямые скрещивающиеся.
- Через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой. Единственная.
- Скрещивающиеся $a$ и $b$ : есть пара пареллельных плоскостей $alpha$ и $beta$, таких что $ain alpha$, $bin beta$
Задача 1: В прямоугольном параллелепипеде $ABCDMNKL$ найти угол между
скрещивающимися прямыми $AN$ и $BK$, если известны ребра $BA=36$, $BN=15$, $BC=20$
- Как находить угол между двумя стереометрическими объектами? по алгоритму параллельных переносов, совмещений.
- Свойство инвариантности углов при параллельном переносе стереометрических объектов — прямых, плоскостей:
- Если объекты $A$ и $B$ параллельны соответственно $A’$ и $B’$, то углы между парами равные: $angle left(A;Bright)=angle left(A’;B’right)$
- В нашем случае, $BKparallel AL$, поэтому равны углы $angle left(AN;BKright)=angle left(AN;ALright)=angle NAL$
- Перетащим $BK$ по плоскости $BKLA$ вдоль $BA$ до совмещения с точкой $A$. Тогда $BK$ совметится с отрезком $AL$.
- Итак, мы ищем угол $angle NAL$. Найдем его через теорему косинусов в треугольнике $ANL$ для угла $angle NAL$ :
- *** $NL^2=AN^2+AL^2-2cdot ANcdot NLcdot cos angle NAL$
- Стороны $AN$, $NL$ и $AL$ можем признать диагоналями граней — прямоугольников, значит, найти их по теоремам Пифагора.
- Решение: $AN=sqrt{36^2+15^2}=39$ $AL=sqrt{20^2+15^2}=25$ $NL=sqrt{36^2+20^2}=4cdot sqrt{106}$
- Из теоремы косинусов $cos angle NAL=frac{AN^2+AL^2-NL^2}{2cdot ANcdot AL}=frac{39^2+25^2-16cdot 106}{2cdot 39cdot 25}=frac{450}{1950}=frac{3}{13}$ Ответ: $angle NAL=arccos frac{3}{13}$
- Признак: $NAL$ — плоскость угла: $ANin NAL$ и $BKparallel NAL$
case I 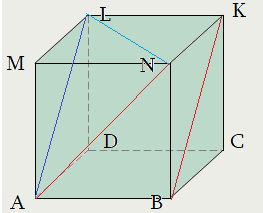
Алгоритм: нахождение угла между прямыми путем параллельного переноса (демонстрация по II, прямые $AN$, $BK$ ):
1-ый шаг: Выбираем точку, в которой хотим совместить прямые. Например, точку $Z$ — середину отрезка $BK$.
2-ой шаг: Для прямой $AN$ определим плоскость «скольжения» — плоскость, содержащая эту прямую и точку $Z$. Это $ANC$
3-ий шаг: Двинем прямую $AN$ по плоскости $ANC$ оставаясь параллельно «как стержень». Она совместится с отрезком $ZX$.
4-ый шаг: Что за точка $X$ ? угол $angle XZB$ — именно то, что нам нужно: $angle XZB=angle left(XZ;BKright)=angle left(AN;BKright)$.
Признак: — увидеть ту главную плоскость угла , которая параллельна обеим скрещивающимся прямым. Здесь это $XZB$.
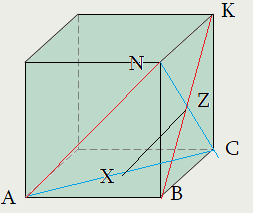
Задача 2: В правильной треугольной призме все ребра 1. Найти косинус угла $angle left(AB;CMright)$
- $ABCMNK$ правильная призма: в основании правильный $bigtriangleup ABC$ , ребро $BN$ перпендикулярно основанию.
- Нужен угол между $AB$ и $CM$. Выберем Точкой совмещения $M$. Прямая $CM$ уже проходит через нее.
- Прямая $AB$ и точка $M$ лежат в плоскости $ABNM$. Значит, $ABNM$ — плоскость сколжения. $AB$ перейдет в $MN$.
- Путем параллельного совмещения $AB$ с $MN$ мы устоновили, что искомый угол — это $angle CMN$.
- Косинус угла $angle CMN$ можно найти по теореме косинусов треугольника $CMN$: $cos angle CMN=frac{CM^2+MN^2-CN^2}{2cdot CMcdot MN}$
- Признак: $CMN$ — плоскость угла: $ABparallel CMN$ и $MCin CMN$
k задачe 2 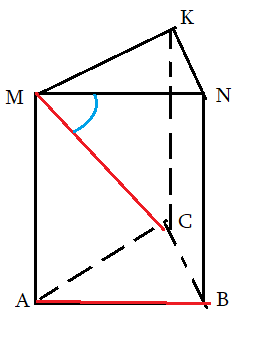
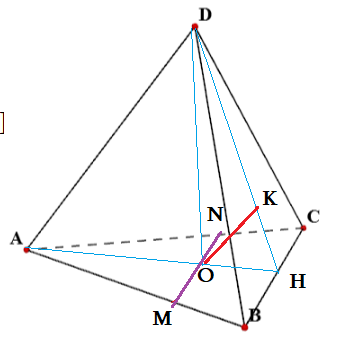
Задача 3: В правильном тетраэдре $DABC$ все ребра 1 см. Найти угол между $AD$ и $BC$.
- Для нахождения угла, совместим «движениями» наши прямые в точку $O$ — основание высоты $DO$ .
- В правильном тетраэдре в основании равносторонный треугольник $DABC$, высота пирамиды попадает в центр окружностей.
- Точка $O$ — пересечение высот, медиан, биссектрис. $O$ лежит на высоте $AH$ , $DH$ — высота грани $BDC$.
- В точке $O$ проведем прямую параллельную прямой $BC$. Им будет линия $MN$
- В точке $O$ проведем прямую $OK$, параллельную $AD$. Она будет лежат в плоскости $ADH$ Значит, $Kin DH$.
- Итак, «взамен» наших $AD$ и $BC$ мы получили прямые $OK$ и $MN$ : $OKparallel AD$, $MNparallel BC$
- по свойству углов при параллельном переносе $angle left(AD;BCright)=angle left(OK;MNright)=angle MOK$
- Найти $angle MOK$ ? Легко! учтите, что у нас правильный тетраэдр и находите.
- Признак: $MONK$ — плоскость угла: $ADparallel MONK$ и $BCparallel MONK$
Алгоритм: вычисление угла в пространстве или плоскости
- В каком треугольнике этот угол? узнать стороны треугольника и найти угол по теореме косинусов.
- Если треугольник окажется равнобедренным, то провести высоту и найти угол прямоугольного треугольника.
- А если треугольник прямоугольный, то написать cos или sin или tg этого угла и найти как arc !
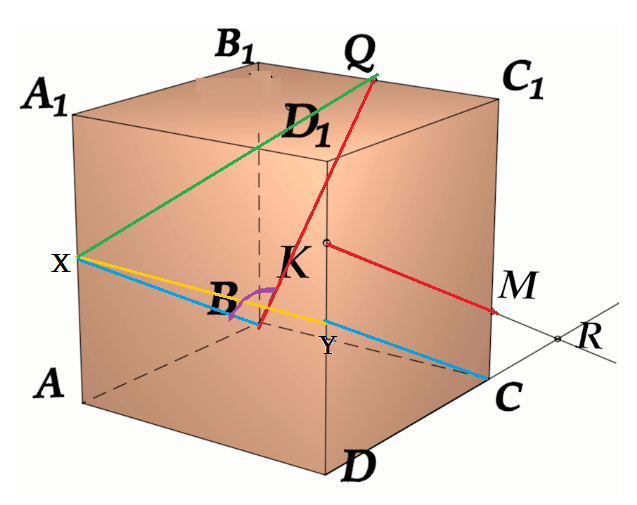
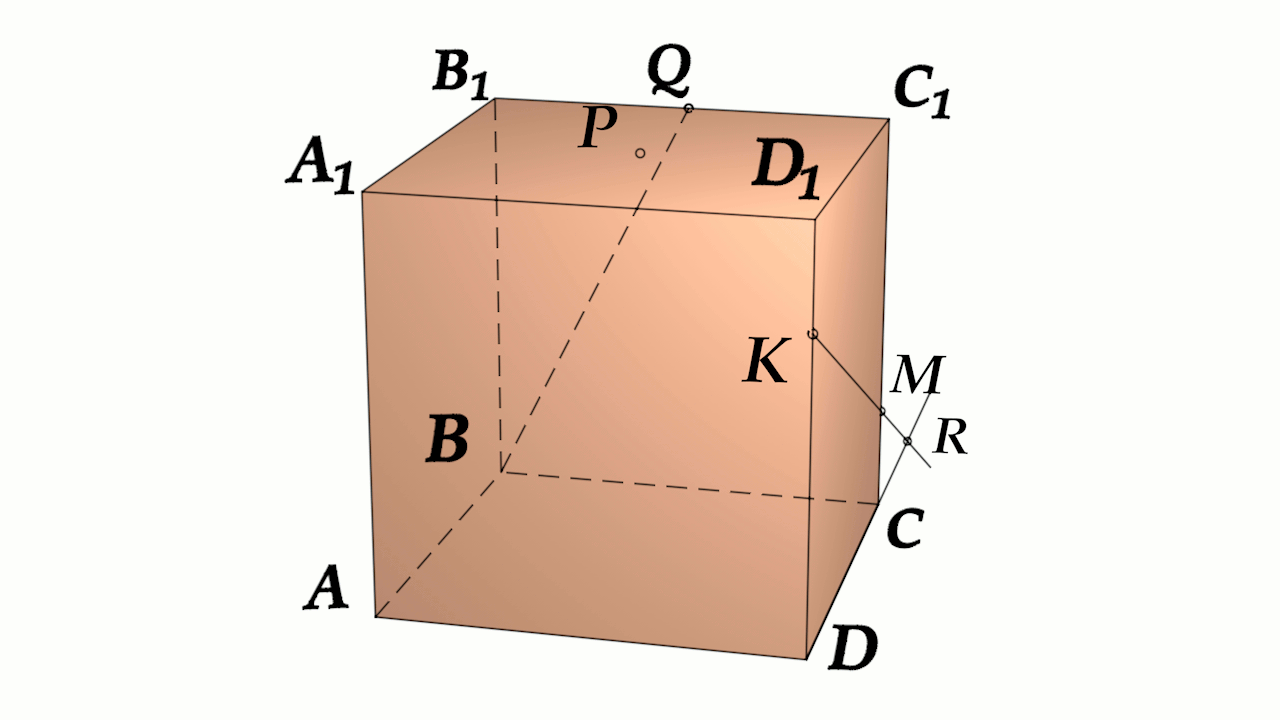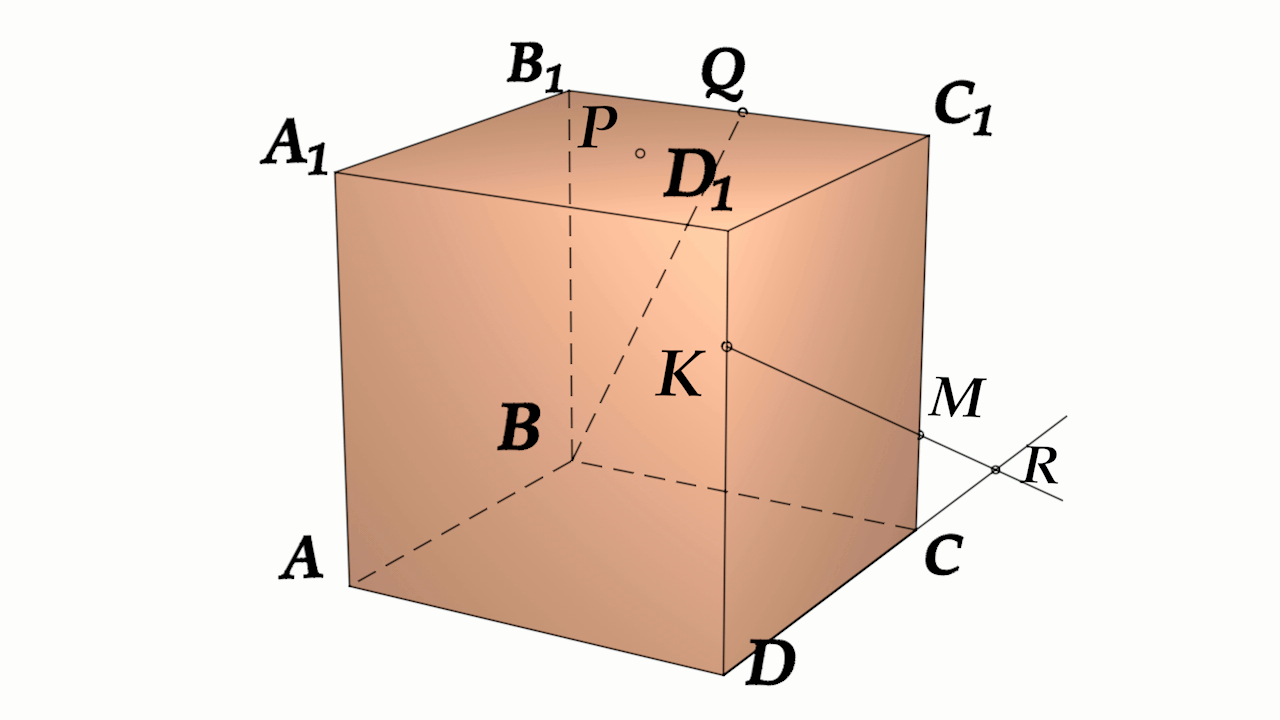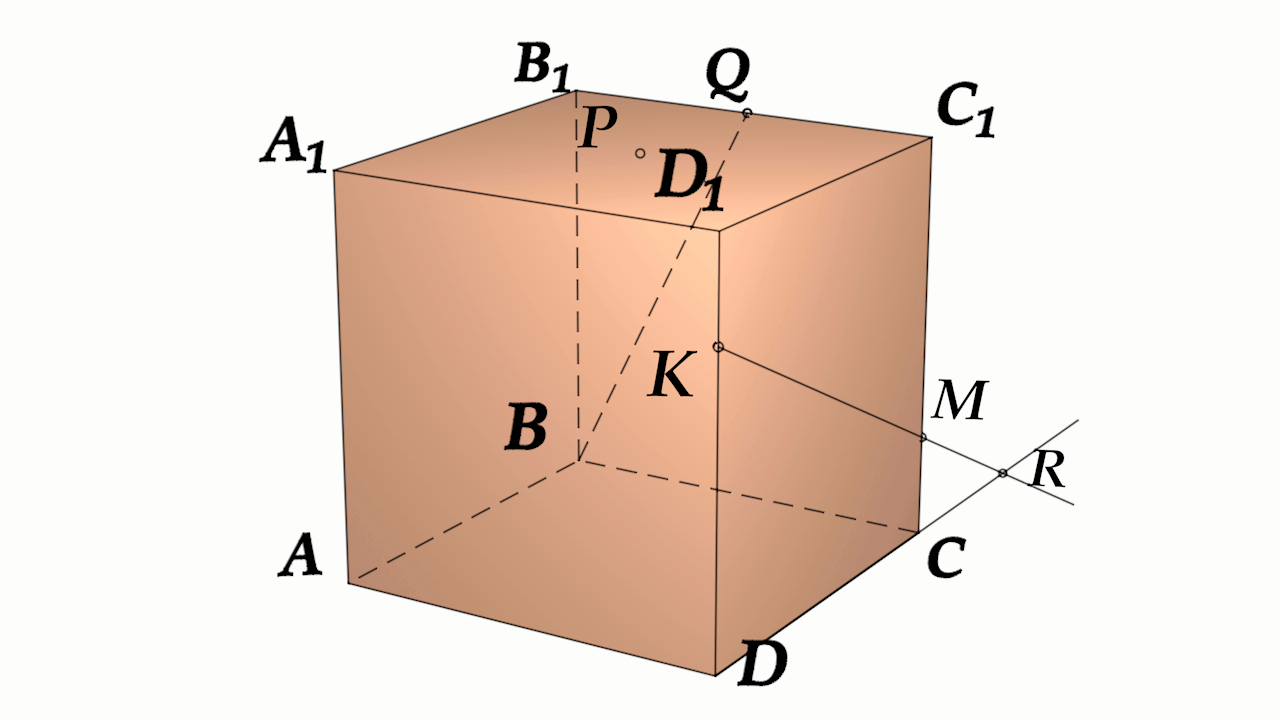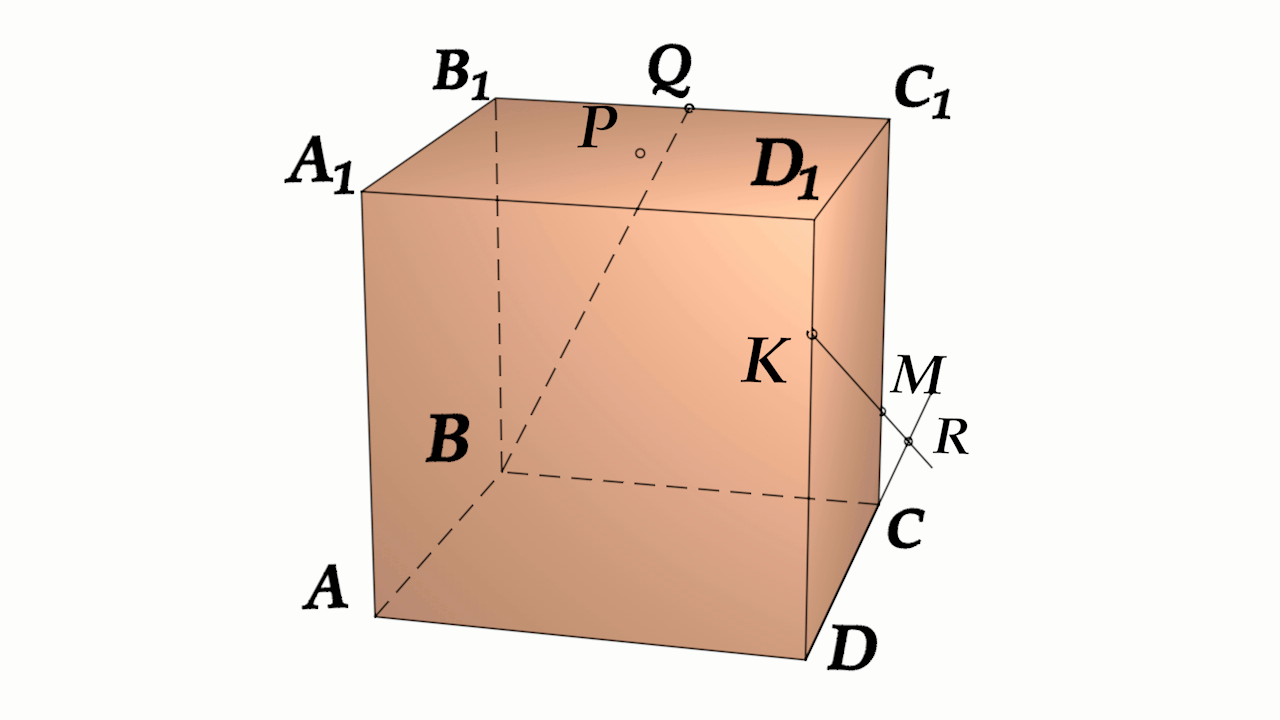
Задача 4: В кубе $ABCD{A_1}{B_1}{C_1}{D_1}$ все ребра равны 1. Точка $Q$ — середина ребра . Точка $K$
делит ребро $D_1D$ в соотношении 1 : 3 считая от вершины $D_1$, а точка $M$ делит $C_1C$ в соотношении
5 : 2 считая от вершины $C_1$. Найти угол между скрещивающимися прямыми $BQ$ и $KM$ .

- Параллельными переносами добъемся совмещения в точке $B$. Для этого, перенесем $KM$ в два этапа.
- Сперва соскользим $KM$ по грани $DD_1C_1C$ вдоль $C_1C$ до вершины $C$. Получим отрезок $CYparallel MK$
- Затем, $CY$ протащим параллельно себе вдоль пути $CB$ и перейдем к отрезку $BXparallel CY$.
- В итоге получили то, что надо: $KM$ параллельна $BX$, потому как $MKparallel CYparallel BX$.
- Требуемый угол $angle left(MK;BQright)=angle left(BX;BQright)=angle XBQ$. Найдем его через треугольник $bigtriangleup XBQ$
- В теореме косинусов нам нужны стороны этого треугольника. Вычислим постепенно, шаг за шагом, зная ребро куба 1:
- Из отношения $frac{D_1K}{DK}=frac{1}{3}Rightarrow D_1K=frac{1}{4} DK=frac{3}{4}$. Из отношения $frac{C_1K}{CM}=frac{5}{2}Rightarrow C_1M=frac{5}{7} CM=frac{2}{7}$
- $MKparallel CYRightarrow KY=MC$ отрезок $DY=D_1D-D_1K-KY=1-frac{1}{4}-frac{2}{7}=frac{13}{28}$
- $BXparallel CYRightarrow BX=DY=frac{13}{28}$. По условию задачи $B_1Q=frac{1}{2}$.
- Нужные нам стороны треугольника $bigtriangleup XBQ$ являются гипотенузами прямоугольных треугольников.
- Зная все катеты, как части ребер, по теореме Пифагора найдем стороны $XB$, $BQ$, $XQ$.
- Нужный угол $angle XBQ$ вычислим из теоремы косинусов $XQ^2=XB^2+BQ^2-2cdot XBcdot BQcdot cos angle XBQ$
- наконец: $cos angle XBQ=frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$ $angle XBQ=arccos frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$
- Признак: $XBQ$ — плоскость угла: $KMparallel XBQ$ и $BQin XBQ$
Задача 5: В правильной треугольной призме $ABCMNK$ все ребра равны 2. Точка $D$ делит
ребро $MN$ в отношении 3 : 2 считая от вершины $M$. Найдите угол между прямыми $AD$ и $BK$.
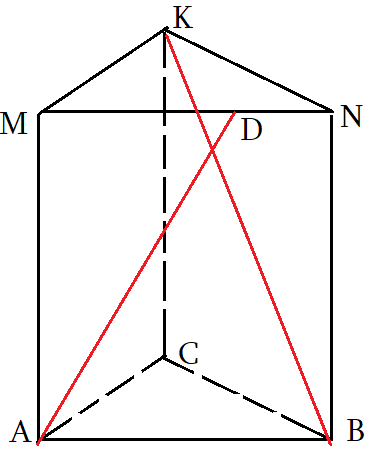
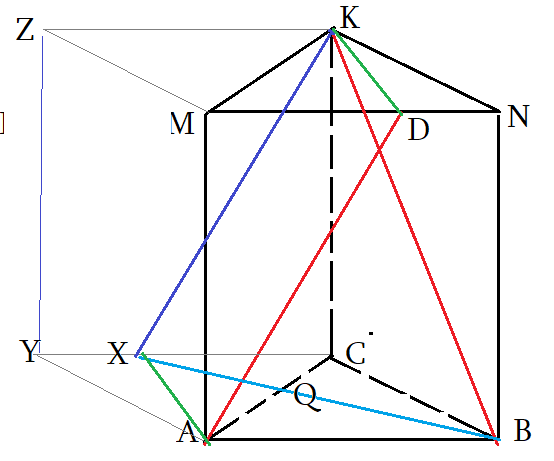
- Чтоб найти угол между скрещивающимися прямыми, нужно «подвигать параллельно» $AD$ и $BK$ до совмещения.
- Если двинуть $AD$ так, чтоб точка $D$ совпала с $K$ — т.е. скользить по плоскости $ADK$, но тогда другой конец $D$ вне рисунка.
- Достроим призму до параллелепипеда $ABCYMNKZ$ и все нужные отрезки, «движения», плоскости будут внутри!
- $AD$ скользит по плоскости $ADK$ и совпадет с $XK$. Точка $X$, конечно, окажется на ребре $YC$
- по построению: $Xin CDK$ плоскости; $ADparallel XK$ , $XCparallel AB$ . Значит, $XK$ параллельна $AD$
- Угол между прямыми $angle left(AD;BKright)=angle left(XK;BKright)=angle XKB$. Надо найти угол $angle XKB$.
- Угол $XKB$ ищем , как обычно, через треугольник $bigtriangleup XKB$, с помощью теоремы косинусов.
- Для этого надо найти стороны этого треугольника. Сторону $BK$ найдем по Пифагору для треугольника $bigtriangleup BKC$.
- $XC=MD$, найдем $MD$ из отношения 3 : 2 для $MN$ . Затем, по Пифагору $bigtriangleup XKC$ найдем $XK$.
- С вычислением $XB$ придется повозится через теорему косинусов треугольника $bigtriangleup XBC$, две его стороны известны.
- А что с углом $angle XCB$? по условию $bigtriangleup ABC$ равносторонный, значит в параллелограмме $angle YCB=120$ градусов.
- Ну и финально: как только найдем все стороны $bigtriangleup XKB$, мы найдем и его угол $angle XKB$ — то что надо!
- Признак: $XKB$ — плоскость угла: $ADparallel XKB$ и $BKin XKB$
Упражнения: