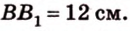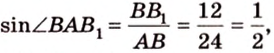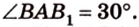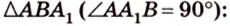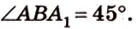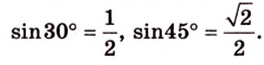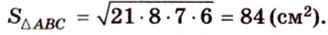В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания – точка С1, причём СС1 – образующая цилиндра, а АС – диаметр основания. Известно, что ∠АСВ = 30°, АВ = √2, СС1 = 4.
а) Докажите, что угол между прямыми АС1 и ВС равен 60°
б) Найдите площадь боковой поверхности цилиндра
Решение:
- a) Проведём B1C1 параллельно ВС, тогда ∠(АС1;ВС) = ∠(AC1;B1C1) = ∠AC1B1
△ABC – прямоугольный, так как АС – диаметр окружности
△АВС: sin∠ACB = AB/AC → 1/2 = √2/AC → AC = 2√2 → AO = CO = r = √2
cos∠ACB = BC/AC → √3/2 = BC/(2√2) → BC = √6 = B1C1
△ACC1: AC1² = AC²+CC1² = 8+16 = 24 → AC1 = 2√6
△AA1B1: AB1² = AA1²+A1B1² = 16+2 = 18→ AB1 = 3√2
△AB1C1: AB1² = AC1²+B1C1²-2·AC1·B1C1·cos∠AC1B1
18 = 24+6-2·2√6·√6·cos∠AC1B1
cos∠AC1B1 = 1/2 → ∠AC1B1 = ∠(АС1;ВС) = 60°
б) Пусть площадь боковой поверхности = S
S = 2·π·r·h, где r – радиус окружности, h – высота цилиндра
S = 2·π·√2·4 = 8√2·π = 8√2π
Ответ: б) 8√2π
Цели и задачи урока:
- Знакомство учащихся со
стереометрическими задачами на применение
свойств цилиндра и скрещивающихся прямых. - Способствовать формированию и развитию у
учащихся пространственных представлений;
повторить определения, свойства цилиндра и
скрещивающихся прямых при решении
комбинированных задач на нахождение
расстояния, угла между двумя скрещивающихся
прямыми в прямом круговом цилиндре. - Формировать умения анализировать,
устанавливать связь между элементами содержания
ранее изученного материала, способность к
самоанализу, рефлексии. - Содействовать развитию интереса к оперированию
геометрическими понятиями и образами,
личностной активности учащихся; создать условия
для творческой самореализации личности.
Оборудование: 16 персональных
компьютеров для учащихся, персональный
компьютер учителя, проектор, раздаточный
материал в виде готовых чертежей с задачами,
листы для отчета о проделанной работе, модели
цилиндра и призмы. Презентации учителя к
уроку .
ХОД УРОКА
1. Организационный момент (2 мин.)
После проверки готовности класса к уроку,
учитель сообщает тему, цели и задачи практикума и
отмечает, что урок проходит с использованием
компьютерной презентации, выполненной в Power Point.
Учитель проводит инструктирование учащихся по
технике безопасности при работе в компьютерном
классе.
2. Актуализация опорных знаний и умений
учащихся (10 мин.)
Тестирование с самопроверкой
Для диагностики и коррекции основных понятий и
формул, необходимых на уроке учитель предлагает
учащимся ответить на вопросы теста. С условиями
заданий теста учащиеся знакомятся с помощью
слайдов презентации. Оценивает ответы учащихся
компьютер. Максимальная оценка 3 балла – за три
правильных ответа. На каждом слайде необходимо
нажать кнопку с номером ответа. Неверно
выбранный ответ откроет слайд решение задачи или
напомнит теоретический материал.
1. Дан куб. Угол между прямыми A1D1 и BC1
равен …
1) 90°; 2) 45°; 3) 60°.
2. Дан куб . Угол между прямыми A D1 и BD равен …
1) 90°; 2) 45°; 3) 60°.
3. На основании цилиндра взяты две
непараллельные друг другу хорды AN и BM, не
проходящие через центры оснований. Тогда
расстояние между хордами…
1) равно образующей цилиндра ; 2) больше
высоты цилиндра 3) меньше образующей
цилиндра
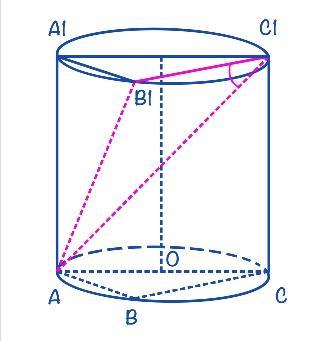
4. Концы отрезка AB лежат на окружностях
оснований цилиндра AB и OQ не
параллельные друг другу отрезки. Тогда
расстояние между прямой AB и осью цилиндра OQ
неравно длине отрезка …
1) MN; 2) QK ; 3) OA.
5 Высота цилиндра 8 см, радиус основания 5 см.
Цилиндр пересечен плоскостью параллельно оси
так, что в сечении получился квадрат. Тогда
расстояние от этого сечения до оси цилиндра
равно…
см ; 2) 4 см ;
3) 3 см
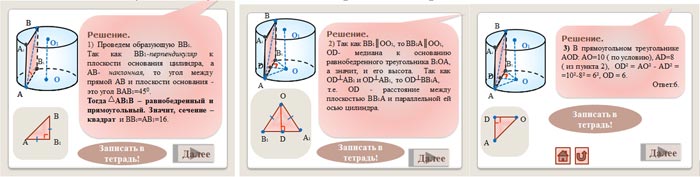
3. Решение задачи №1 (8 мин.)
Учитель предлагает вниманию учащихся задачу:
Концы отрезка AB лежат на окружностях оснований
цилиндра. Высота цилиндра равна 16, радиус
основания равен 10, а угол между прямой AB и
плоскостью основания цилиндра равен 45°. Найдите
расстояние между осью цилиндра и параллельной ей
плоскостью, проходящей через точки A и B.
Вопросы для обсуждения:
- Назовите угол между прямой AB и плоскостью
основания цилиндра. Ответ обоснуйте. - Каким четырехугольником является сечение
цилиндра AA1BB1? - Какое взаимное расположение прямых AB и OO1 в
пространстве? - Как найти расстояние между осью цилиндра и
параллельной ей плоскостью, проходящей через
точки A и B?
Далее в ходе обсуждения условия задачи,
приходим к решению задачи.
Отмечаем какой теоретический материал
использовался при решении задачи:
- Прямой круговой цилиндр
- Определение скрещивающихся прямых
- Расстояние между двумя скрещивающихся прямыми
- Угол между наклонной и плоскостью
- Терема Пифагора
- Тригонометрические функции острых углов
- Решение прямоугольных треугольников
- Свойства равнобедренного треугольника
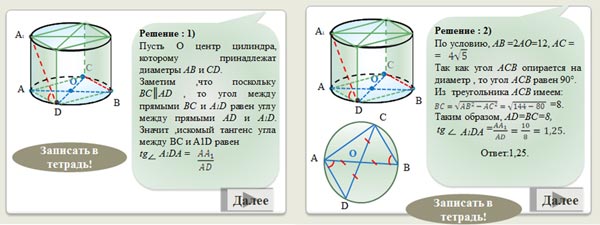
4. Решение задачи №2 (8 мин.)
Учитель предлагает вниманию учащихся задачу:
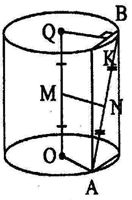
Радиус основания цилиндра равен 6, высота равна
10. Отрезки AB и CD – диаметры одного из оснований
цилиндра, AC =
Отрезок AA1 – образующая цилиндра. Найдите
тангенс угла между прямыми BC и A1D
Вопросы для обсуждения:
- Какое взаимное расположение прямых BCи
A1D в пространстве? - Как найти угол между прямыми BC и A1D?
- Угол ACB опирается на диаметр окружности.
Что можно сказать о его величине?
Далее в ходе обсуждения условия задачи,
приходим к решению задачи.
Отмечаем какой теоретический материал
использовался при решении задачи
- Прямой круговой цилиндр
- Определение скрещивающихся прямых
- Угол между двумя скрещивающихся прямыми
- Терема Пифагора
- Вписанный угол, опирающийся на диаметр
- Тригонометрические функции острых углов
- Решение прямоугольных треугольников
5. Самостоятельная работа по решению
задач с использованием готовых чертежей и
последующей проверкой или самопроверкой (10 мин.)
Учащиеся получают тексты задач по вариантам в
печатном виде и на слайдах презентации. Учитель
контролирует работу учащихся, определяет
степень усвоения изученного материала. Через
определенное время краткое решение задач можно
проверить, используя слайды презентации.
Вариант №1
- Концы отрезка AB лежат на окружностях оснований
цилиндра. Радиус основания цилиндра равен 15,
длина отрезка AB равна, а угол между прямой AB и плоскостью
основания цилиндра равен 30?. Найдите расстояние
между осью цилиндра и параллельной ей
плоскостью, проходящей через точки A и B. - Радиус основания цилиндра равен 1, высота равна
Отрезки AB и CD
– диаметры одного из оснований цилиндра. Отрезок
AA1 – образующая цилиндра, AD =. Найдите косинус угла между
прямыми BD и A1C
6. Отчёт о проделанной на уроке работе
(5 мин.)
В конце занятия учащимся заполняют бланк
отчета о проделанной на уроке работе.
Тестирование с самопроверкой.
Приложение 1
Скрещивающиеся прямые
Как определяется угол между скрещивающимися прямыми?
Ты можешь спросить, а чего тут определять? Угол, он и в Африке (то есть в пространстве) – угол!
И действительно, если прямые лежат в одной плоскости, то угол между ними ищется так же, как и на плоскости:
Наименьший из двух углов, образованных при пересечении.
Но что же делать, если прямые совсем не пересекаются?
Читай эту статью и всё узнаешь!
Скрещивающиеся прямые — коротко о главном
Если прямые лежат в разных плоскостях (т.е. не пересекаются), нужно через произвольную точку на одной прямой (например, прямая ????) провести прямую, параллельную другой прямой (например, прямую ????′, где ????′||????.
Скрещивающиеся прямые — подробнее
Как найти угол, если прямые не пересекаются?
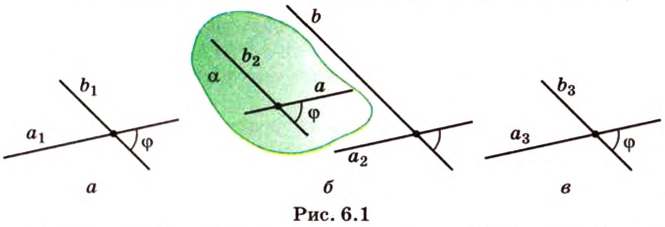
Вот, например: прямые ( displaystyle a) и ( displaystyle b) скрещиваются. Какой угол между ними?
Чтобы это определить, делаем так: через произвольную точку одной прямой (например ( displaystyle b)), нужно провести прямую ( displaystyle {a}’||a).
И тогда угол между ( displaystyle a) и ( displaystyle b) будет равен (по определению!) углу между ( displaystyle {{a}’}) и ( displaystyle b).
Да, но как это применить в задачах? Давай посмотрим.
Решение задач на угол между скрещивающимися прямыми
В кубе ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) найти угол между ( displaystyle AC) и ( displaystyle D{{C}_{1}}).
Решаем:
Прямые ( displaystyle AC) и ( displaystyle D{{C}_{1}}) не пересекаются, но нужно как-то найти угол между ними.
Пользуемся правилом: через точку ( displaystyle {{C}_{1}}) проведем прямую ( displaystyle {{A}_{1}}{{C}_{1}}). Она будет параллельна ( displaystyle AC).
Значит, угол между ( displaystyle AC) и ( displaystyle D{{C}_{1}}) равен углу между ( displaystyle {{A}_{1}}{{C}_{1}}) и ( displaystyle D{{C}_{1}}). Осталось его найти.
Смотри: ( displaystyle {{A}_{1}}{{C}_{1}}), ( displaystyle {{A}_{1}}D) и ( displaystyle D{{C}_{1}}) – диагонали граней куба, поэтому ( displaystyle {{A}_{1}}{{C}_{1}}={{C}_{1}}D={{A}_{1}}D), то есть ( displaystyle Delta {{A}_{1}}{{C}_{1}}D) – равносторонний.
Поэтому ( displaystyle angle {{A}_{1}}{{C}_{1}}D=60{}^circ ).
Ответ: ( displaystyle 60{}^circ ).
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
Задачи на скрещивающиеся прямые и углы между ними попадаются сплошь и рядом в этом вебинаре.
ЕГЭ 8. Куб. Параллелепипед. Призма – расстояния и углы в пространстве
На этом уроке мы на примере самых простых объемных фигур научимся находить важнейшие вещи в стереометрии — расстояния и углы в пространстве.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Координаты вектора
Вектор – отрезок, имеющий длину и указывающий направление.
На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.
Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$
Скрещивающиеся прямые
И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$
Уравнение плоскости
В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.
Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
Например, пусть даны три точки:
$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$
Подставим координаты точек в общее уравнение плоскости:
$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$
Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.
Теперь у нас есть три уравнения и три неизвестные – можем решить систему:
Пример 3
Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$
Расстояние от точки до плоскости
Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$
Пример 4
Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$
Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).
Пример 5
Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.
Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) — середина ребра (CE).
- Докажите, что прямые (AD) и (BG) перпендикулярны.
- Найдите расстояние между прямыми (AD) и (BG).
Решение:
Решим задачу полностью методом координат.
Нарисуем рисунок и выберем декартову систему координат. (Рис 5).
Содержание:
В планиметрии угол — это геометрическая фигура, образованная двумя лучами, которые выходят из одной точки — вершины угла (лучи — стороны угла). Такое определение понятия угла переносится и в стереометрию. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Опишем и определим каждый из этих случаев.
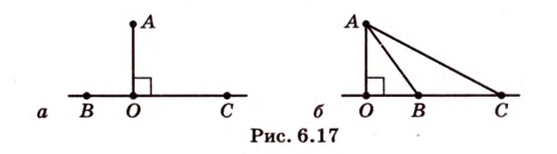
Угол между двумя прямыми в пространстве
Две прямые, лежащие в одной плоскости, при пересечении образуют смежные и вертикальные углы. В модуле 1 мы повторили все свойства таких углов (вертикальные углы равны, а смежные — дополняют друг друга до 180°). В пространстве (аналогично планиметрии) также сохраняются все названия и понятия об углах и их величинах. Меньший из углов, образованных двумя пересекающимися прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Считают, что параллельные прямые также образуют угол, равный 0°. В стереометрии рассматривают угол между скрещивающимися прямыми. Пусть даны скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 
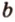
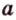
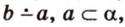
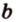
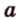
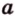
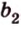
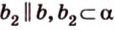
Итак,
Если 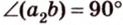
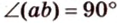
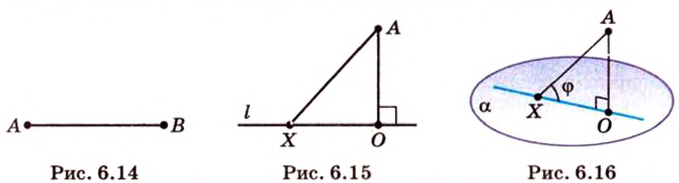
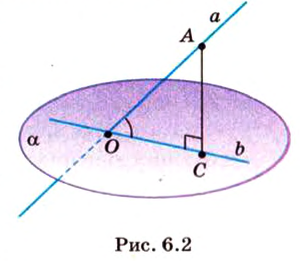
Угол между прямой и плоскостью в пространстве
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 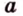
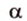
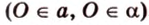
- выбирают точку
прямой
;
- проводят из точки
перпендикуляр к плоскости
;
- проводят через точки плоскости
и
прямую
.
Прямую 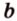
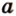
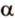
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая 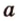
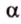
Угол между прямой 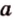
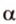
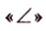
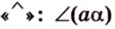
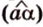
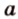
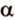
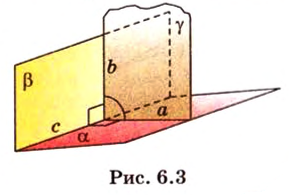
Угол между двумя плоскостями, пространства
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например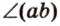
Пересекающиеся плоскости образуют четыре угла. Чтобы определить угол между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между двумя пересекающимися плоскостями — это угол между двумя прямыми, которые принадлежат этим плоскостям и перпендикулярны прямой их пересечения.
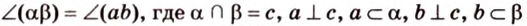
Если линейный угол — 90°, то плоскости перпендикулярны. Если плоскости параллельны, то угол между ними равен 0°.
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Доказательство:
Выберем точки 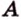
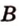
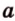
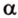
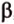
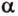
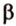
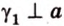
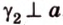
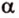
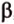
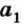
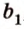
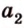
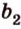
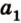
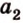
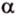
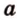
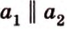
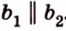
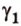
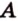
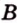
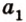
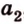
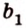
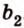
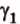
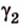
Пример №1
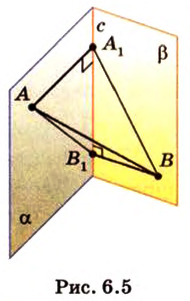
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 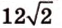
Дано: 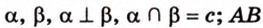

Найти: углы, образованные отрезком 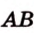
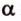
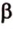
Решение:
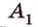
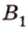
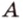
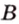
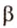
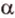
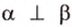
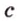
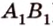
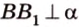
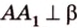
Итак, 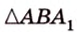
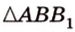
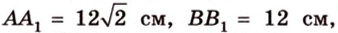
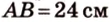
Из 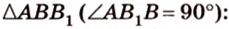
Из 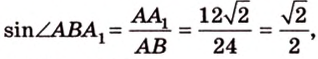
Ответ. 30°; 45°.
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
Расстояния в пространстве
Одним из ключевых понятий геометрии является длина отрезка. Через него вводится много других понятий, связанных с понятием расстояния. Как известно, расстоянием между двумя точками 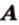
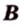
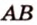
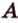
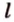
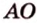
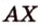
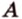
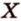
Рассмотрим плоскость 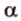
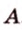
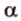
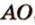
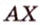
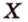
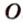
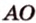
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
Расстояние от точки 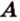
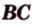
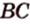
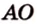

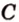
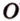
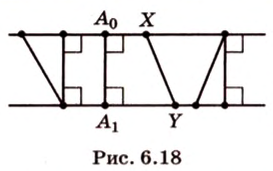
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 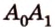
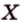
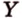
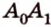
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
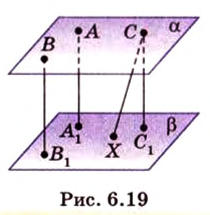
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
Доказательство:
Пусть имеем две параллельные плоскости 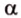
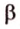
и второй, то перпендикуляр 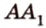
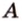
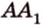
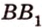
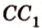
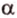
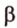
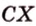
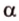
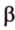
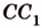
А это вытекает из того, что перпендикуляр 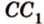
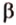
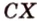
Понятие расстояния между точками широко применяется в разнообразных сферах жизни человека — от науки до быта и досуга. Используется оно в тех случаях, когда размерами реальных объектов, расстояние между которыми вычисляется, в данных условиях можно пренебречь. Так мы говорим о расстоянии между звездами, планетами, передатчиками и принима-телями информации, населенными пунктами, ядрами атома и электронами на его орбите и т.п.
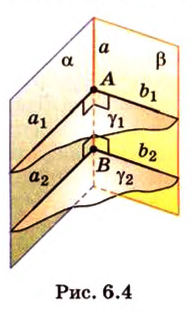
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
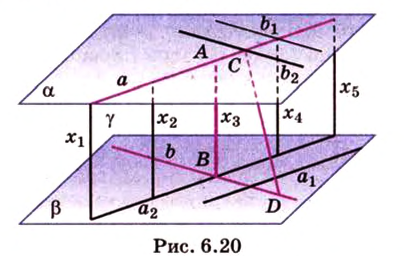
Теорема 4
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
Доказательство:
Действительно, пусть 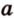
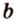
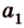
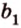
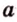
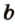
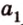
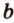
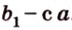
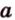
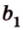
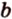
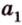
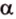
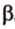
Плоскости 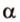
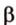
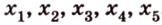
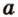
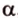
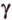
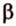
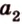
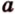
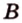
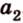
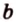
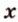
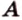
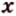
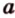
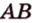
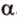
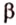
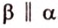
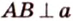
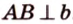
Отрезок 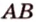
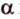
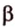
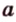
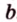
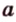
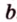
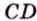
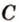
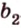
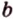

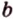
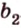
Поскольку она перпендикулярна прямым 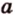
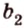

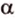




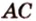
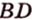
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
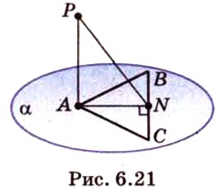
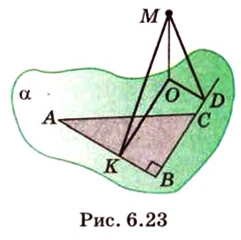
Пример №2
Отрезок 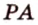
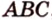
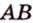
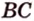
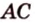
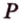
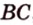
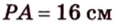
Решение:
Пусть 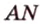
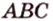
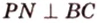
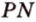
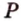
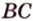
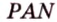
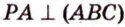
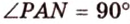
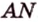
Из формулы для площади треугольника 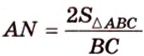
Необходимую площадь определим по формуле Герона:
Тогда 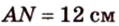
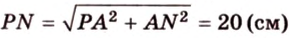
Ответ. 20 см.
Пример №3
Прямая 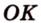
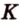
Доказательство:
Пусть 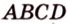
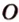
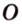
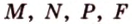
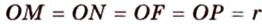
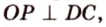
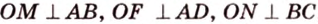
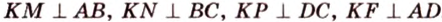
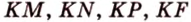
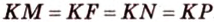
Пример №4
Точка 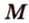
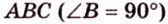
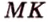
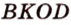
Доказательство:
Поскольку отрезки 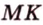
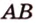
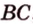
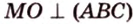
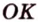
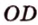
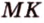
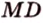
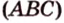
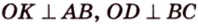
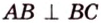
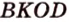
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы

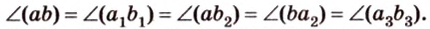
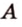 прямой
прямой 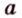
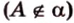 ;
;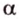
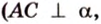
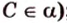 ;
;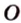 и
и 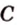 прямую
прямую 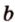 .
.