Как найти угол между прямыми шестиугольной призмы - AvtoShod.ru

Угол между прямыми в призме

Угол между прямыми в призме. Для вас очередной материал – мы рассмотрим пару задач с призмами. Требуется определить угол между прямыми проходящими через указанные вершины призмы. Дело в том, что эти прямые не лежат в одной плоскости. Такие прямые называют скрещивающимися.

Если вы с ними уже знакомы, то задачки решите сразу сходу после построения эскиза без всяких вычислений. Если нет, то посмотрите соответствующую теорию, можете посмотреть информацию здесь, материал подан достаточно наглядно.

Принцип прост – необходимо одну из прямых переместить до пересечения со второй параллельным переносом. Либо установить — имеется ли параллельная ей прямая в одной плоскости со второй прямой. Рассмотрим задачи:

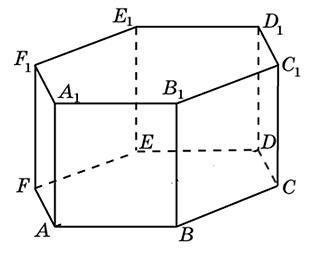
316553. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра которой равны 8, найдите угол между прямыми FA и D₁Е₁. Ответ дайте в градусах.

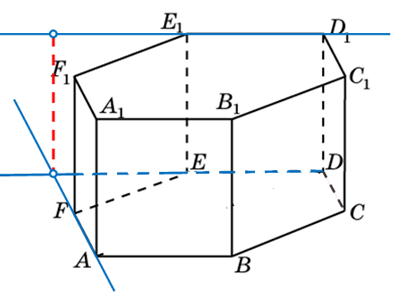
Построим прямые, переместим параллельным переносом прямую D₁Е₁ до пересечения с прямой AF. Полученная прямая будет проходить через DE:

Зная свойства правильного шестиугольника, а именно, то что углы при его вершинах равны 120 градусам, мы уже можем записать ответ. Угол между указанными прямыми равен 60⁰. Если посмотреть на призму сверху, то эскиз будет выглядеть так:

*Как видим, на самом деле, чему равна длина ребра не имеет значения.

Ответ: 60

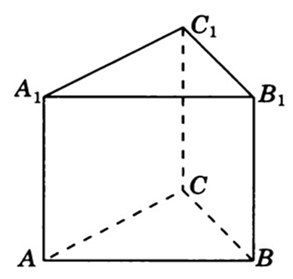
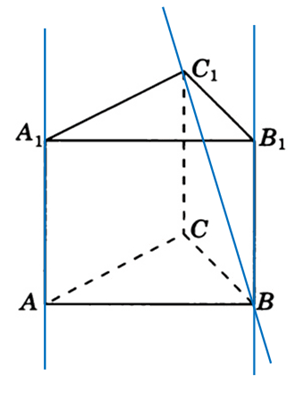
316558. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 3, найдите угол между прямыми AA₁и BC₁. Ответ дайте в градусах.

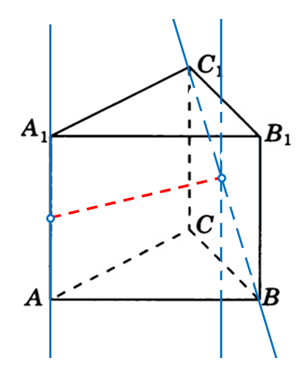
Построим указанные прямые и параллельным переносом «передвинем» прямую AA₁ до грани BCC₁B₁ через которую проходит BC₁:

Так как в условии сказано, что все рёбра равны 3, то это значит что грань BCC₁B₁ является квадратом. Прямая BC₁ является диагональю этого квадрата и она пересекает все прямые параллельные боковым рёбрам под углом 45 градусов. Наглядно это можно увидеть на проекции призмы:

*Небольшая оговорка. В обеих задачах мы перемещали прямые как бы «стягивая» их по соединяющему их перпендикуляру (обозначен красным пунктиром). Необязательно это делать именно так. Важно, чтобы одна из прямых была перемещена до пересечения с другой именно параллельным сдвигом. Во второй задаче это можно было сделать и так:

На этом закончим. Так что если встретите скрещивающиеся прямые на ЕГЭ в задаче кратким ответом, не пугайтесь, решаются они устно. Важно понимать, каким образом переместить прямую до пересечения с другой. А уж угол найти, как говорится, это дело техники.

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2Углы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В правильной шестиугольной призме, все рёбра которой равны, найдите угол между прямыми, отмеченными на рисунке:

Аналоги к заданию № 398: 399 Все

Аналоги к заданию № 400: 401 Все

Пройти тестирование по этим заданиям

Источник

Задача 1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна а площадь поверхности равна

Решение: + показать

Задача 2. В правильной четырёхугольной призме известно, что Найдите угол между диагоналями и Ответ дайте в градусах.

Решение: + показать

Задача 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и боковое ребро равно Найдите объем призмы.

Решение: + показать

Задача 4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и высота призмы равна Найдите площадь ее поверхности.

Решение: + показать

Задача 5. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и Площадь ее поверхности равна . Найдите высоту призмы.

Решение: + показать

Задача 6. Площадь поверхности правильной треугольной призмы равна Какой будет площадь поверхности призмы, если все ее ребра увеличить в два раза?

Решение: + показать

Задача 7. В правильной треугольной призме , все ребра которой равны найдите угол между прямыми и . Ответ дайте в градусах.

Решение: + показать

Задача 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными и и боковым ребром, равным

Решение: + показать

Задача 9. Гранью параллелепипеда является ромб со стороной и острым углом $60^{circ}.$ Одно из ребер параллелепипеда составляет с этой гранью угол в $60^{circ}$ и равно Найдите объем параллелепипеда.

Решение: + показать

Задача 10. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна а высота —

Решение: + показать

Задача 11. Найдите объем правильной шестиугольной призмы, стороны основания которой равны а боковые ребра равны

Решение: + показать

Задача 12. В правильной шестиугольной призме все ребра равны . Найдите расстояние между точками и .

Решение: + показать

Задача 13. В правильной шестиугольной призме все ребра равны Найдите угол . Ответ дайте в градусах.

Решение: + показать

Задача 14. В правильной шестиугольной призме , все ребра которой равны найдите угол между прямыми и . Ответ дайте в градусах.

Решение: + показать

Задача 15. В правильной шестиугольной призме все ребра равны Найдите тангенс угла

Решение: + показать

Задача 16. В сосуд, имеющий форму правильной треугольной призмы, налили см воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки см до отметки см. Найдите объем детали. Ответ выразите в см

Решение: + показать

Задача 17. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.

Решение: + показать

Задача 18. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 26, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

Решение: + показать

Задача 19. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен Найдите объем исходной призмы.

Решение: + показать

Задача 20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Задача 21. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами а боковые ребра равны и наклонены к плоскости основания под углом $30^{circ}.$

Решение: + показать

Задача 22. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно и отстоит от других боковых ребер на и Найдите площадь боковой поверхности этой призмы.

Решение: + показать

Задача 23. В правильной треугольной призме стороны оснований равны боковые рёбра равны Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер , и и точку

Решение: + показать

Задача 24. В правильной треугольной призме стороны оснований равны боковые рёбра равны Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер и

Решение: + показать

Задача 25. Объём куба равен Построено сечение проходящее через середины рёбер и и параллельное ребру Найдите объём треугольной призмы

Решение: + показать

Задача 26. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 27. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 28. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 29. Найдите объём многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Вы можете пройти тест «Призма»

Источник

Решение:

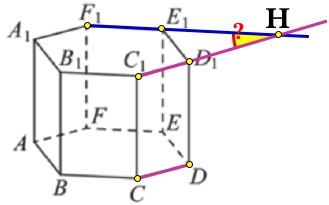
Прямые CD и E₁F₁лежат в разных плоскостях, вместо прямой CD возьмём параллельную ей прямую C₁D₁ и продолжим их до пересечения:

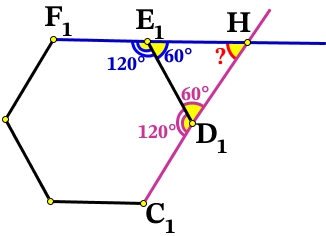
Рассмотрим верхнее основание, которое является равносторонним шестиугольником, а значит в нём все углы равны 120°:

Найдём смежные к ним углы, их сумма равна 180°, тогда:

∠НE₁D₁ = 180° – 120° = 60°
∠E₁D₁H = 180° – 120° = 60°

В ΔE₁HD₁ знаем два угла, сумма углов любого треугольника равна 180°, найдём 3-й угол:

∠Н = 180° – ∠НE₁D₁ – ∠E₁D₁H = 180° – 60° – 60° = 60°

Ответ: 60.

Источник

Конспект урока по теме «Нахождение углов в
призме»

Тема. Нахождение углов в призме

Цель: повторить и обобщить материал на
нахождение углов между прямыми и плоскостями при решении задач по теме
«Призма».

Задачи:

Образовательные – научить использовать
методы решения задач, применяемые для куба, на призме.

Развивающие – развить
мышления через формирование умений анализировать, сравнивать; формирование
логического, абстрактного мышления;

Воспитательные – воспитать
самостоятельность, настойчивость, положительное эмоциональное отношение к
математике.

Тип урока – урок повторения.

Оборудование: доска, карточка с
заданиями.

Структура урока:

1.
Организационный
момент (2)

2.
Актуализация
знаний (10)

3.
Решение
задач (25)

4.
Информация
о домашнем задании(3)

Ход урока.

I Организационный момент

Здравствуйте! Садитесь! На
прошлых уроках вы вспомнили, как находить углы и расстояния между различными
элементами куба. Сегодня мы вспомним, как находит углы в призме.

II Актуализация опорных знаний

Для актуализации учащимся раздаются
карточки с заданиями (таблица 9).

Карточка с заданием

Укажите искомый угол между
скрещивающимися прямыми и	прямой и плоскостью	двумя плоскостями и