Как найти угол между двумя графиками

Углом
между двумя кривыми
у
= f₁(x)
и у
= f₂(x)
в точке их пересечения М₀(х₀,
у₀)
называется угол между касательными к
этим кривым в точке М₀.
Этот угол определяется по формуле

=

.

Пример.
Найти угол между параболами

у
= 8 – х²
и у
= х².

□ Для
нахождения координат точек пересечения
заданных кривых решим систему уравнений

В
результате получим А(2;
4) и В(−2;
4). Продифференцируем уравнения парабол:

= −2х,

= 2х.
Найдем значения

и

для точки А(2;
4):

= −4,

= 4. Следовательно,

=

=

и

=


.

Аналогично
определяется угол между кривыми в точке
В(−2;
4):

=

.
■

§ 21. Формула тейлора

Теорема.
Пусть функция f(x)
имеет в точке а
и некоторой ее окрестности производные
порядка п
+ 1. Пусть х
– любое значение аргумента из указанной
окрестности, х
≠ а.
Тогда между точками а
и х
найдется точка

такая, что справедлива формула:

f(x)
= f(а)
+

(х
– а)
+
(х
– а)²+
…+

(х
– а)^п
+

+
(х
– а)^п+1.

Эту
формулу называют формулой
Тейлора.

Выражение

R_n+1(x)
=

(х
– а)^п+1

называют
остаточным
членом

формулы Тейлора.

Запишем остаточный
член в другом виде:

так
как

(а,
х),
то найдется число

,
0 <

< 1, что

= а
+

(х
– а)
и тогда

R_n+1(x)
=

(х
– а)^п+1,
0 <

< 1.

Эта
форма остаточного члена наиболее
употребительна в приложениях.

Если
в формуле Тейлора а
= 0, то получим формулу
Маклорена:

f(x)
= f(0)
+

х
+

х²
+
… +

х^п
+
R_n+1(x)

с
остаточным членом

R_n+1(x)
=

х^п+1,
0 <

< 1.

Разложение
некоторых элементарных функций по
формуле Маклорена

1.
f(x)
= е^х.

Так как

f(x)
=

=

= … = f
^п+1(x)
= е^х,

f(0)
=

=

= … = f
^п+1(0)
= 1,

то
формула Маклорена имеет вид

е^х
= 1 +

+

+

+…+

+ R_n+1(x),

где

R_n+1(x)
=

х^п+1,
0 <

< 1.

Аналогично
можно разложить по формуле Маклорена
следующие функции:

2.
f(x)
=

.

= х
−

+

−

+
…+ (−1)^т+1

+ R_2т(x),

где
R_2т(x)
= (−1)^т
·
,
0 <

< 1.

3.
f(x)
=

.

= 1
−

+

−

+
…+ (−1)^т

+ R_2т+1(x),

где
R_2т+1(x)
= (−1)^т+1
·
,
0 <

< 1.

4.
f(x)
= (1 + х)^т.

(1
+ х)^т
=1+
х+
х²+

х³+…+

+

х^п
+R_n+1(x),

где

R_n+1(x)=

х^п+1(1
+

)^т—п-1,
0 <

< 1.

Пример.
Вычислить число е.

□ Запишем
разложение е^х
по формуле Маклорена:

е^х

= 1+

+

+

+…+

+
х^п+1,
0 <

< 1.

Если
заменить функцию е^х
ее многочленом Тейлора степени п
(отбросим остаточный член), то получим
приближенное равенство

е^х

1 +

+

+

+…+

,
(1)

абсолютная
погрешность которого

| R_n+1(x)
| =

| х
|^п+1,
0 <

< 1.

Если
рассматривать функцию е^х
для −1 ≤ х
≤ 1, то

|
R_n+1(x)
| ≤

<

.

Полагая
в (1) х
= 1, получаем приближенное значение числа

е
≈ 1+

+

+

+ …+

.

При
этом | R_n+1(x)
| <

.

Если
требуется вычислить значение е
с точностью

= 0,001, то число п
определяется из неравенства

< 0,001, или (п
+ 1)! > 3000,

которое
выполняется при п
= 6. Следовательно,

е
≈ 1+

+

+

+ …+

.

Вычисляя
с четырьмя знаками после запятой, получим

е
≈ 2,7180.

Три
знака после запятой гарантированы.
■

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

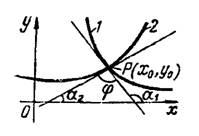
Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (рис. 1) по формуле

где и — угловые коэффициенты касательных к кривым в точке их пересечения ,
т. е. частные значения в точке производных от по из уравнений этих кривых:

Рис.1

Пример 1. Найти углы, под которыми пересекаются следующие линии:
1) прямая и парабола ;
2) эллипс и парабола ;
3) синусоида и косинусоида .
Решение.
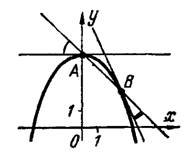
1) Совместно решая уравнения параболы и прямой, находим, что они пересекаются в двух точках: и , рис.2.

Рис.2

Далее находим производную от по из уравнения параболы: и определяем угловые коэффициенты касательных к параболе в точках и , как частные значения этой производной:

Угловой коэффициент прямой один и тот же во всех ее точках; у данной прямой он равен — 1.
Согласно формуле (2) получим

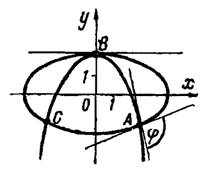
2) Решая совместно уравнения кривых, находим их общие точки: и рис.3. Затем определяем угловые коэффициенты и касательных в любой точке эллипса и параболы как производные от по из их уравнений

Рис.3

Подставляя координаты точки , получим и . Следовательно, в точке :

Под таким же углом кривые пересекаются и в точке вследствие их симметричности относительно оси .
В точке имеем: , следовательно, в точке кривые имеют общую касательную, т. е. касаются друг друга. В этой точке угол между кривыми равен нулю.
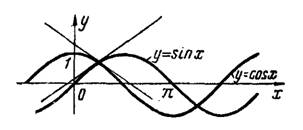
3) Абсциссы точек пересечения кривых (рис.4) определяются уравнением , решая которое, получим

Дифференцированием находим угловые коэффициенты касательных к синусоиде и косинусоиде:

Рис.4

Искомый угол между кривыми определяем по общей формуле (2)

Положительному знаку соответствует острый угол , отрицательному — тупой, смежный с ним угол .

Задание. Найти тангенс угла между кривыми $y=x^2-1$ и
$y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.

Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:

$$begin{array}{c}
left{begin{array}{l}
y_{1}=x^{2}-1 \
y_{2}=x^{3}-1
end{array} Rightarrow x^{2}-1=x^{3}-1 Rightarrow x^{3}-x^{2}=0 Rightarrowright. \
Rightarrow x_{1,2}=0, x_{3}=1
end{array}$$

Таким образом, искомая точка $x=1$.

Далее находим производные заданных функций в найденной точке:

$$begin{array}{c}
y_{1}^{prime}=left(x^{2}-1right)^{prime}=left(x^{2}right)^{prime}-(1)^{prime}=2 x-0=2 x, y_{1}^{prime}(1)=2 \
y_{2}^{prime}=left(x^{3}-1right)^{prime}=left(x^{3}right)^{prime}-(1)^{prime}=3 x^{2}-0=3 x^{2}, y_{2}^{prime}(1)=3
end{array}$$

Итак, искомый тангенс:

$$operatorname{tg} phi=frac{3-2}{1+2 cdot 3}=frac{1}{7}$$

Ответ. $operatorname{tg} phi=frac{1}{7}$

угол между графиками в точке их пересечения равен углу между касательными, проведенными в данной точке.

для начала найдем саму точку пересечения.
f(x) = g(x)

x^3 -6x = 27/x
x=+-3
например для x=3

уравнение касательной в точке x=3 для f(x)
y-9 = 21(x-3) , угловой коэффициент k1=21
Для g(x)
y-9 = -3(x-3) ; угловой коэффициент k2=-3

тангенс угла между двумя прямыми
tg(φ)=(k2-k1)/(1+k1*k2)

Угол между касательными.

В этой статье мы рассмотрим, как решать задачи на нахождение угла между касательными.

Угол между касательными.

Пусть дана функция и через точку к графику этой функции проведены две касательные. Найти тангенс угла между прямыми:

Угол между прямыми — это меньший из двух углов, образованных этими прямыми. В нашем случае это угол .

Чтобы найти угол рассмотрим треугольник :

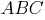
В треугольнике 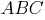угол — внешний угол треугольника, он равен сумме двух углов, не смежных с ним: . Отсюда

Но угол — это угол между касательной и положительным направлением оси , следовательно, :

Угол — это угол между касательной и положительным направлением оси , следовательно, :

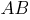
Итак,

Мы помним, что угол между прямыми всегда острый, и его тангенс должен быть больше нуля. В общем случае вполне может быть отрицательным, поэтому

формула для нахождения тангенса угла между касательными и выглядит так

Решим задачу:

Найти тангенс большего угла между касательными, проведенными из точки  к параболе .

Заметим, что в этой задаче нужно найти тангенс большего угла между касательными, то есть тангенс тупого угла. Тангенсы смежных углов равны по модулю, но противоположны по знаку. Следовательно, нам нужно найти тангенс угла между касательными, и в ответе записать это значение со знаком «-«.

Нужно найти коэффициенты наклона касательных, проведенных к параболе из точки . Но сначала найдем абсциссы точек касания и .

Вспомним, как находить уравнение касательной, проведенной к графику функции из данной точки, не принадлежащей графику.

Пусть — абсцисса точки касания.

Уравнение касательной, проведенной из точки имеет вид:

Подставим выражения для и в уравнение касательной. Получим уравнение относительно :

Решим это уравнение. Упростим правую часть:

Итак, мы нашли абсциссы точек касания:

Найдем коэффициенты наклона касательных, проведенных к параболе . Для этого найдем, чему равны значения производной функции в точках касания.

Тангенс большего угла между касательными равен

Ответ: -4

И.В. Фельдман, репетитор по математике.