Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 57287 Площадь основания цилиндра относится с…
Условие
5f6cf18a347ae046112d5363
22.01.2021 19:33:09
Площадь основания цилиндра относится с площадью осевого сечения как pi : 4. Вычислите значения угла между диагоналями осевого сечения.
математика 10-11 класс
1828
Решение
5f3eaa23faf909182968dde0
22.01.2021 20:03:30
★

Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Смотрим рисунок.
Площадь основания цилиндра — это площадь круга:
Sосн = Pi*R^2
Осевое сечение — это прямоугольник ABCD, у которого одна сторона равна высоте цилиндра H, а другая диаметру D = 2R.
Sсеч = 2RH
И они относятся друг к другу как 3 : 4.
(Pi*R^2) : (2RH) = 3 : 4
По правилу пропорции произведение крайних членов равно произведению средних:
4Pi*R^2 = 3*2RH
Делим всё на 2R:
2Pi*R = 3H
Pi*D = 3H
H/D = Pi/3
Из треугольника ABD получаем:
ctg α = AB/AD = H/D = Pi/3
Сумма углов треугольника AOB равна 180°, углы A = B = α, поэтому:
AOB = β = 180° — 2α = 180° — 2*arcctg (H/D) = 180° — 2*arcctg(Pi/3)
Но здесь надо понимать, что Pi/3 ≈ 3,1416/3 = 1,0472
Это просто число, а ни в коем случае не угол 60°.
Поэтому я специально в формуле угла β написал 180°, а не Pi, чтобы не путаться.
Ответ: Угол между диагоналями AOB = 180° — 2*arcctg(Pi/3)
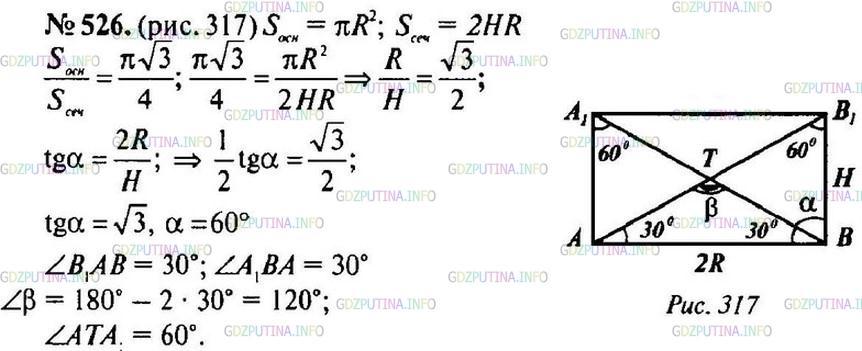
ГДЗ (готовое домашние задание из решебника) на Номер №526 по учебнику Геометрия. 10-11 классы: учебник для общеобразовательных учреждений : базовый и профильный уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. — 22-е изд. — Просвещение, 2013-2019г
Условие
Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите: а) угол между диагональю осевого сечения цилиндра и плоскостью основания; б) угол между диагоналями осевого сечения.
Решение 1
Решение 2
Решение 3
Решение 4
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Найди верный ответ на вопрос ✅ «Помогите решить задачу. Площадь основания цилиндра относится к площади осевого сечения, как пи: 4. Найти угол между диагоналями осевого …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Геометрия » Помогите решить задачу. Площадь основания цилиндра относится к площади осевого сечения, как пи: 4. Найти угол между диагоналями осевого сечения
Геометрия,
вопрос задал ГОСТЬ2014,
6 лет назад
помогите решить задачу. Площадь основания цилиндра относится к площади осевого сечения, как  Найти угол между диагоналями осевого сечения
Найти угол между диагоналями осевого сечения
Ответы на вопрос
Площадь основания цилиндра — это площадь круга радиуса r.
S=πr²
Площадь осевого сечения цилиндра — площадь прямоугольника, одна из сторон которого равна диаметру основания, вторая — высоте цилиндра.
S цил= 2r•h
По условию πr²:2r•h=π:4, откуда находим h=2r.
Следовательно, сечение цилиндра — квадрат.
Диагонали квадрата пересекаются под прямым углом.
Приложения:

Новые вопросы
сообщение про Египет в котором должно быть указана сталица,плоцадь,соседнии страны,насиление,язык,численность насиления,религия,климат,внутренние воды,природные зоны,рельев,полезные ископаемые…