Углы в окружности, центральный и вписанный. Свойства и способы нахождения
Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?
Что такое центральный угол?
Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).
Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.
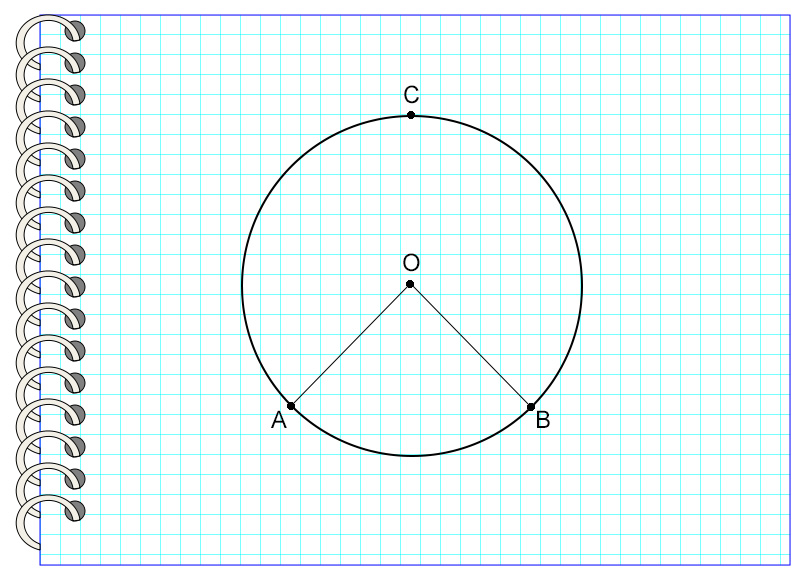
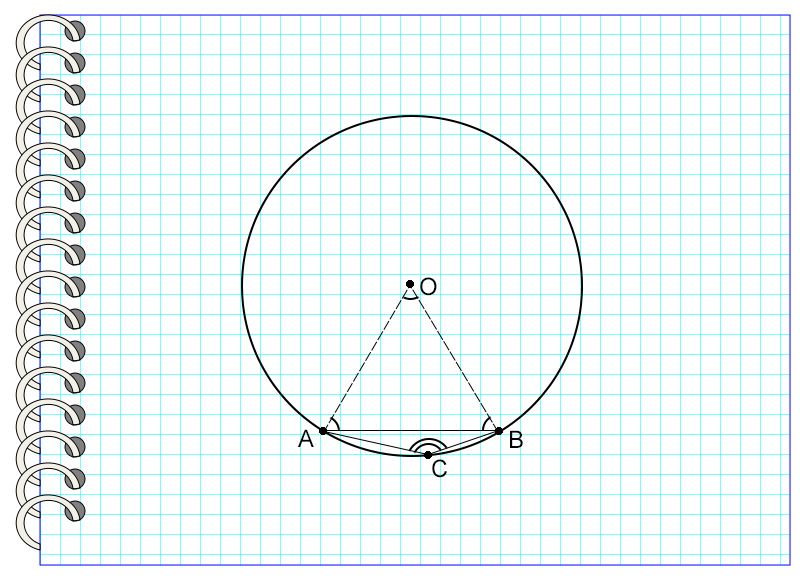
Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.
Рассмотрим пример №1.
На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.
Чем вписанный угол отличается от центрального?
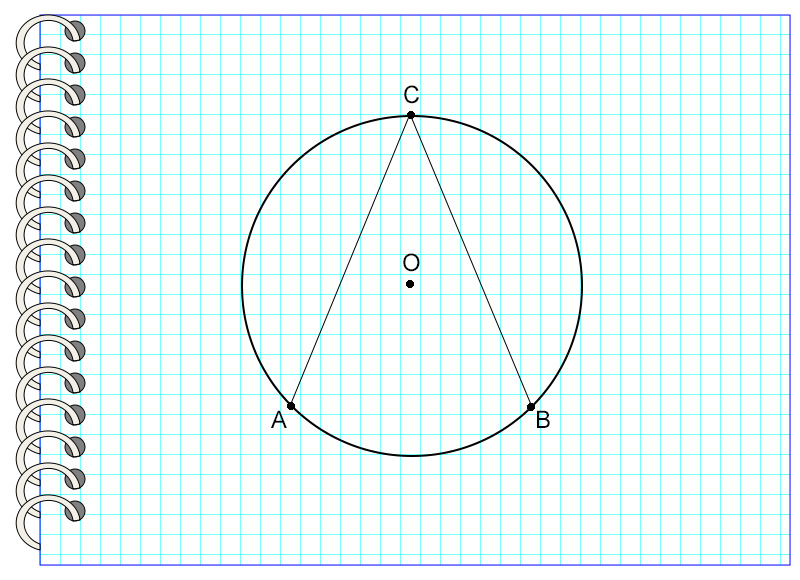
Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.
Приведем следующий пример.
Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.
Чему равен центральный угол
Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.
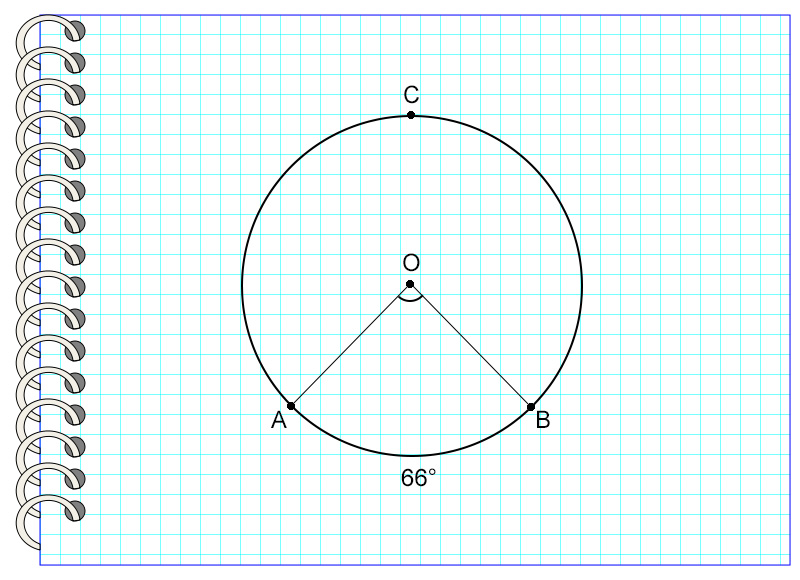
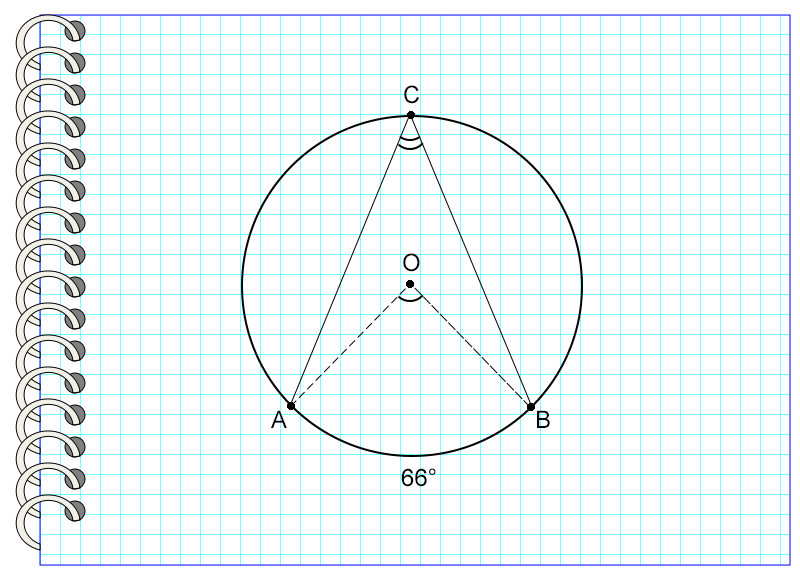
Итак, центральный угол равен градусной мере дуги, на которую он опирается.
На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.
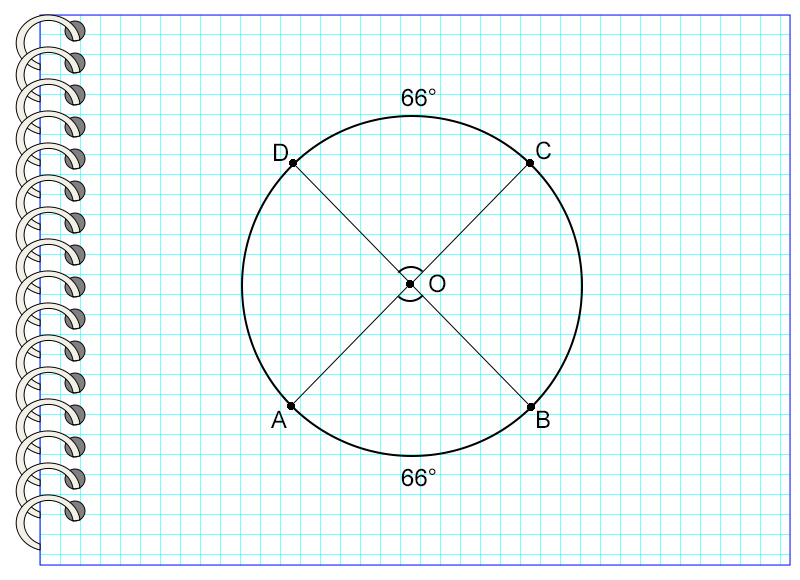
Таким образом, центральные углы, опирающиеся на равные дуги, равны.
На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.
Как найти вписанный угол
Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?
Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.
Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.
Значит, угол АСВ = 66° : 2 = 33°
Рассмотрим некоторые следствия из этой теоремы.
- Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
- Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
- Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
- Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.
Где могут встретиться задачи на эту тему? Их виды и способы решения
Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.
Углы, опирающиеся на одну дугу
Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.
Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.
Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла — общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,
1) АОВ = 54° : 2 = 27°.
Углы, опирающиеся на разные дуги одной окружности
Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.
В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.
Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.
Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.
Точно так же угол АОВ опирается на дугу АВ.
Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.
ВС = 360° — АС — АВ
ВС = 360° — 120° — 30° = 210°
Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.
Угол САВ = 210° : 2 = 110°
Задачи, основанные на соотношении дуг
Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.
Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.
Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.
АВ = 360° — 60° = 300°
Угол АВС = 300° : 2 = 150°
В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.
Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.
По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.
Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°
В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги — 50. Вычислите длину большей дуги.
Для того чтобы вычислить длину большей дуги, нужно составить пропорцию — как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.
Большая дуга равна 360° — 60° = 300°.
Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.
Большая дуга = 50 * 5 = 250
Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.
Центральные и вписанные углы
О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
Углы, связанные с окружностью
Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.
| Фигура | Рисунок | Теорема |
| Вписанный угол |  |
|
| Вписанный угол |  |
Вписанные углы, опирающиеся на одну и ту же дугу равны. |
| Вписанный угол |  |
Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
| Вписанный угол |  |
Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды |
| Вписанный угол |  |
Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |  |
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды
Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.
Теоремы об углах, образованных хордами, касательными и секущими
| Вписанный угол |
| Окружность, описанная около прямоугольного треугольника |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |
 |
|
| Угол, образованный секущими, которые пересекаются вне круга |  |
 |
|
| Угол, образованный касательной и хордой, проходящей через точку касания |  |
 |
|
| Угол, образованный касательной и секущей |  |
 |
|
| Угол, образованный двумя касательными к окружности |  |
 |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
|
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
|
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
|
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство источники: http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly http://www.resolventa.ru/spr/planimetry/cangle.htm |
Ответ:
∠β=82°
Решение:
Для удобства поставим буквы.
Так как с и d перпендикуляры к а, то ∠А=∠Д=90°.
По свойству четырёхугольников сумма 4 углов =360°:
∠А+∠β+∠С+∠Д=360°;
90°+∠β+90°+68°=360°;
∠β=360°-278°=82°
2 ВАРИАНТ
Если с и d перпендикуляры к а, то с║d ( по свойству параллельных прямых), следовательно данная фигура — прямоугольная трапеция с основами с и d (Трапецией называется четырехугольник, у которого две пары противоположных сторон параллельны. Трапеция, у которой при одной боковой стороне прямые углы называется прямоугольной. )
Сумма углов трапеции, прилежащих к боковой стороне, равна 180°
∠β=180-98°=82°
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
flamewow |
Заголовок сообщения: Найти Углы альфа,бета и гамма
|
||
|
даны длины отрезков(подписаны) a,b,c Вложение:
|
||
| Вернуться к началу |
|
||
|
flamewow |
Заголовок сообщения: Re: Найти Углы альфа,бета и гамма
|
||
|
забыл добавить, так же известны координаты точки Х и У.
|
|||
| Вернуться к началу |
|
||
|
flamewow |
Заголовок сообщения: Re: Найти Углы альфа,бета и гамма
|
|
подразумевается, как найти группы решения, тут же не одно только будет, что б добраться до данной точки можно выбирать разные комбинации углов ( будет «дуга» выгнута вниз, а не вверх, например)
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Если углы альфа бета и гамма углы треугольника то докажите н
в форуме Геометрия |
mdauletiyarov |
8 |
373 |
23 дек 2021, 12:48 |
|
Найти порядок малости альфа от Х относительно бета от Х
в форуме Пределы числовых последовательностей и функций, Исследования функций |
RomaFed |
4 |
842 |
12 ноя 2014, 02:14 |
|
Гамма- Бета функций в КА??
в форуме Комплексный анализ и Операционное исчисление |
kroluk |
0 |
320 |
22 май 2015, 11:34 |
|
Выбор подстановки в гамма и бета функциях
в форуме Интегральное исчисление |
brom |
0 |
215 |
22 ноя 2018, 17:15 |
|
Найти альфа
в форуме Тригонометрия |
sable102 |
4 |
376 |
25 фев 2016, 21:27 |
|
Найти параметр альфа
в форуме Теория вероятностей |
183jpg |
1 |
212 |
15 дек 2018, 18:53 |
|
Метод скорейшего спуска (Как найти альфа)?
в форуме Исследование операций и Задачи оптимизации |
Evgenii123456 |
7 |
283 |
30 ноя 2021, 02:35 |
|
Найти углы треугольника
в форуме Геометрия |
dikarka2004 |
7 |
161 |
10 ноя 2021, 15:41 |
|
Найти углы треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
nadezhda8369 |
5 |
474 |
19 апр 2014, 16:09 |
|
Найти углы треугольника
в форуме Геометрия |
sfanter |
6 |
466 |
08 апр 2015, 14:56 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
АГ
Александр Горемыкин
Бета пишется через одну т.
И если дан только угол альфа — то никак; из теоремы косинусов можно получить, что угол бета зависит от альфы и отношения помеченных сторон; но поскольку для этих сторон дана только теорема Пифагора с одной неизвестной, они могут иметь практически любое отношение.
Определение
Геометрия — это раздел математики, который занимается изучением форм и их измерений. Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Определение угла в математике
Определение
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла – точка, из которой выходят лучи (О).
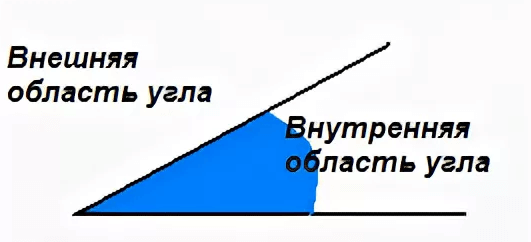
Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
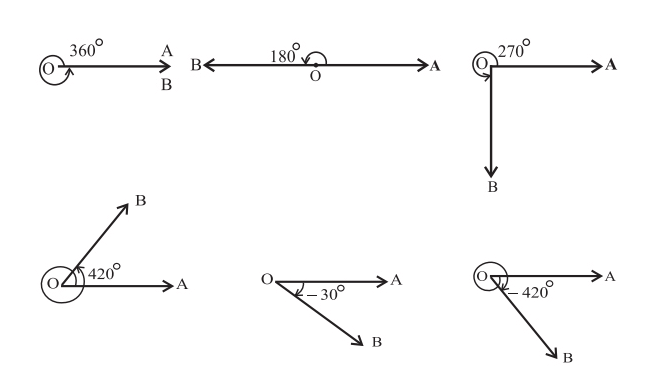
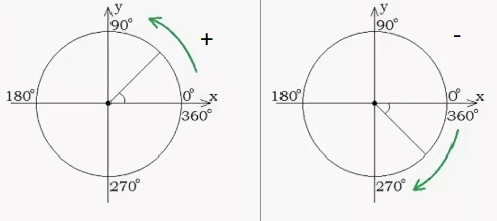
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.
Как обозначить углы?
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
- Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д. - Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
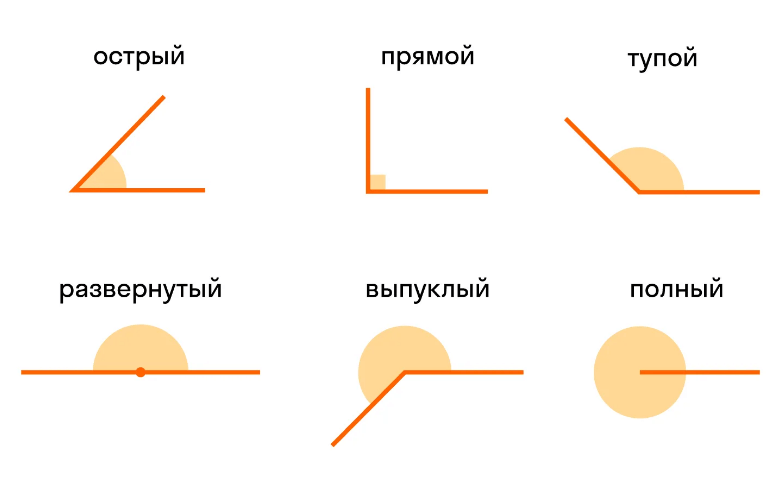
Типы углов
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
- Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
Прямой угол можно легко наблюдать, так как он образует форму буквы L. - Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
это тупой угол. - Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.
Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Углы образованные при пересечении двух прямых
При пересечении двух прямых образуются два вида углов:
- смежные;
- вертикальные.
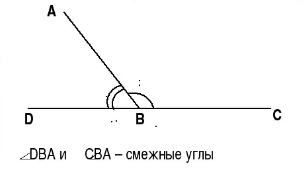
Смежные углы
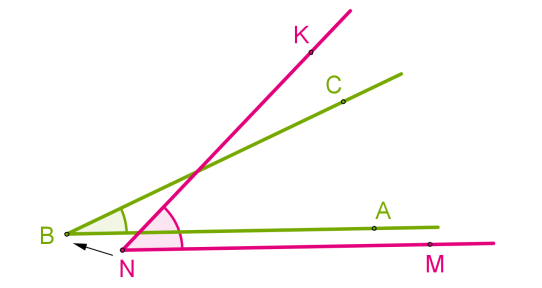
Определение
Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.
Свойства смежных углов
- Сумма смежных углов равна 180°
- Если оба смежных угла равны между собой, то они являются прямыми.
- В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
- Синусы смежных углов равны.
- Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
Вертикальные углы
Определение
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
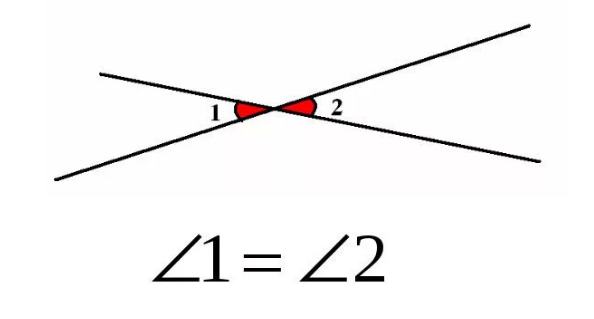
Пример:
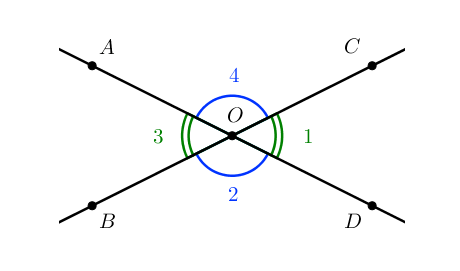
Пары углов 1 и 3; 2 и 4 – являются вертикальными
По свойству вертикальных углов:
[angle C O D=angle A O B]
[angle B O D=angle A O C]
Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными
По свойству смежных углов:
[angle C O D+angle D O B=180^{circ}]
[angle D O B+angle B O A=180^{circ}]
[angle B O A+angle A O C=180^{circ}]
[angle A O C+angle C O D=180^{circ}]
| Смежные углы | Вертикальные углы |
| Два угла с общей стороной и вершиной называются смежными. | Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами. |
| Имеют общую сторону и общую вершину. | Имеют общую вершину, но не имеют общую сторону |
| Смежные углы не всегда равны по величине | Вертикально противоположные углы равны по величине |
Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
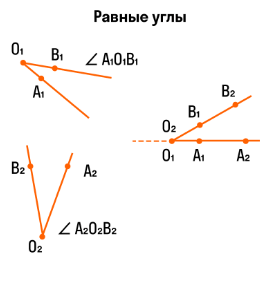
[angle A_{1} O_{1} B_{1}] и [angle A_{2} O_{2} B_{2}] полностью совмещаются при наложении следовательно: [angle A_{1} O_{1} B_{1}=angle A_{2} O_{2} B_{2}]
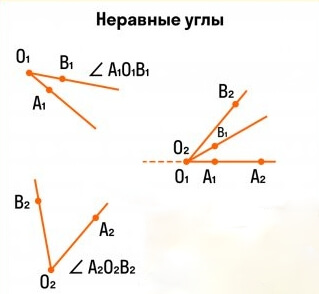
[angle A_{1} O_{1} B_{1}] и [ angle A_{2} O_{2} B_{2}] не совмещаются при наложении: [angle A_{1} O_{1} B_{1} neq angle A_{2} O_{2} B_{2}]
Причем: [angle A_{1} O_{1} B_{1}<angle A_{2} O_{2} B_{2}]
При этом развернутые углы всегда являются равными.
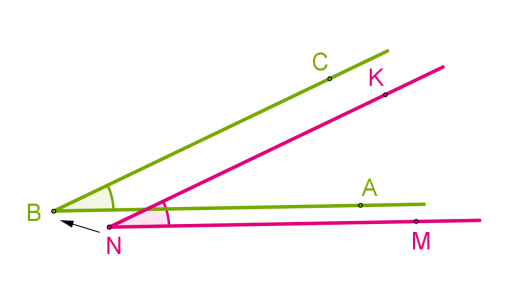
Совмещение углов [angle A B C] и [angle M N K] происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:
Градусная мера
Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет [left(frac{1}{360}right)] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.
Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов
- 1 градус = 60 минут, обозначаемый как 1° = 60′.
- 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.
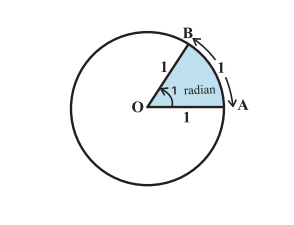
Радианная мера
Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица. Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
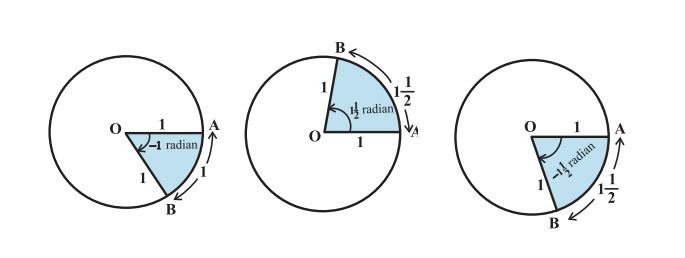
Вот еще несколько примеров углов: -1 радиан, радиан, [1 frac{1}{2}] радиан, [-1 frac{1}{2}] радиан.
Длина окружности = [2 pi r ldots] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна [2 pi]. Следовательно, один полный оборот начальной стороны образует в центре угол [2 pi] радиан. Обобщая это, имеем:
В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = [frac{l}{r}] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:
[theta=frac{l}{r}]
[l=r theta]
Связь между степенью и радианными мерами
По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:
- 360° – по градусной мере
- [2 pi] радиан — в радианах
Следовательно, [2 pi] радиан = 360° ⇒ [pi] радиан = 180°. Теперь подставим приблизительное значение [pi] как [frac{22}{7}] в уравнении выше и получить, 1 радиан [frac{180^{circ}}{pi}=57^{circ} 16^{prime}]. Кроме того, [1^{0}=frac{pi}{180^{circ}}] радиан = 0,01746 радиан примерно. Ниже таблица, изображающая соотношение между градусами и радианами некоторых распространенных углов:
| Градусы | [30^{circ}] | [45^{circ}] | [60^{circ}] | [90^{circ}] | [180^{circ}] | [270^{circ}] | [360^{circ}] |
| Радианы | [frac{pi}{6}] | [frac{pi}{4}] | [frac{pi}{3}] | [frac{pi}{2}] | [pi] | [frac{3pi}{2}] | [2pi] |
Пример
Преобразуйте 40° 20′ в радианы.
Решение: мы знаем, что 1° = 60′, следовательно, 20′ = [frac{1^{0}}{3}].
Следовательно,
[40^{circ} 20^{prime}=40 frac{1}{3}=frac{121}{3}];
Кроме того, мы знаем, что
радианная мера = [frac{pi}{180^{0}} x] градусную меру
Следовательно, радианная мера [40^{circ} 20^{prime}=frac{pi}{180} times frac{121}{3}=frac{121 pi}{540}] радиан.
Нет времени решать самому?
Наши эксперты помогут!
Как измерить угол
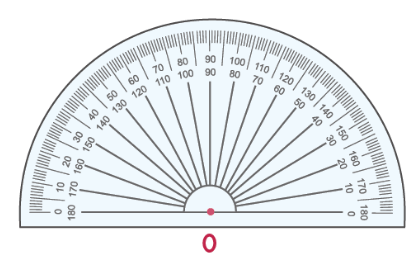
Для измерения углов используется транспортир:
Попробуем измерить угол [angle A O B]
Шаги для измерения угла [angle mathrm{AOB}].
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
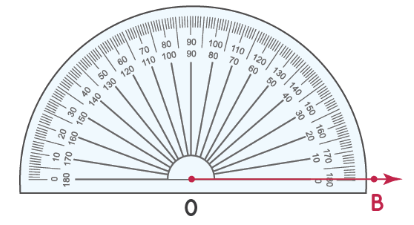
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
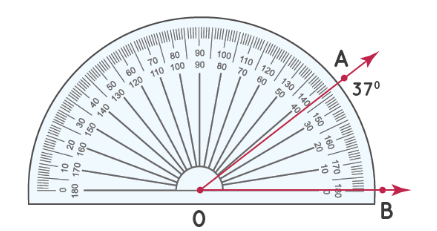
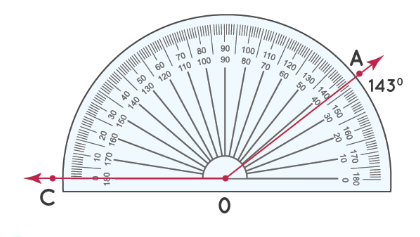
Далее попробуем измерить этот ∠AOC:
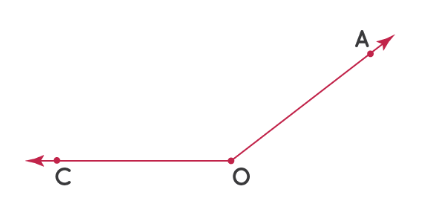
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
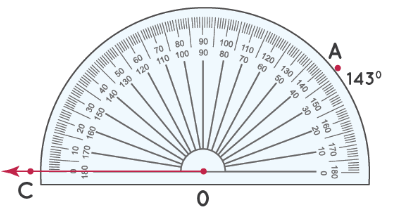
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°
Как построить углы
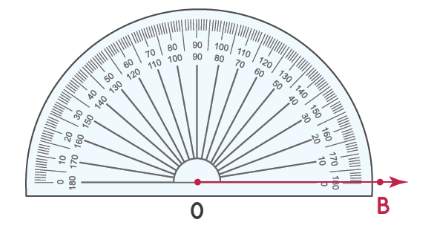
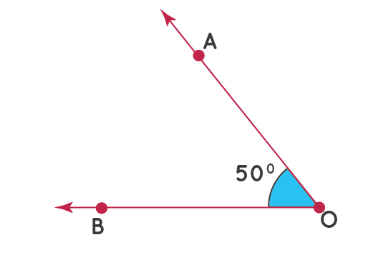
Используем транспортир для построения углов. Нарисуем угол 50°.
Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.
Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.
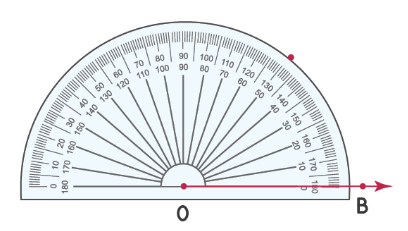
Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.

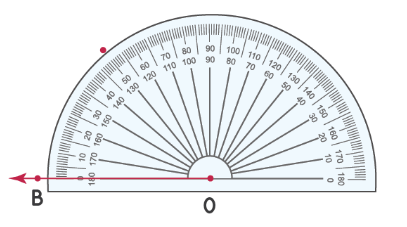
Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.
На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.
Обозначение углов на чертеже
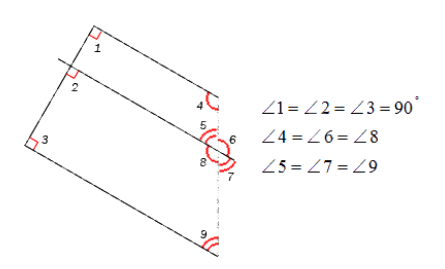
Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.
На чертеже запечатлено корректное обозначение острых, равных и неравных углов.
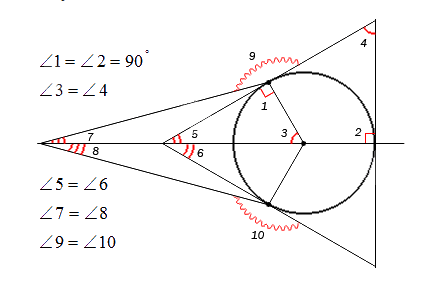
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.