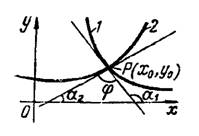
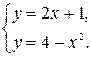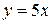Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (рис. 1) по формуле
где и
— угловые коэффициенты касательных к кривым в точке их пересечения
,
т. е. частные значения в точке производных от
по
из уравнений этих кривых:
Рис.1
Пример 1. Найти углы, под которыми пересекаются следующие линии:
1) прямая и парабола
;
2) эллипс и парабола
;
3) синусоида и косинусоида
.
Решение.
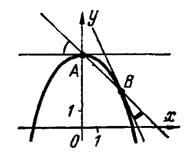
1) Совместно решая уравнения параболы и прямой, находим, что они пересекаются в двух точках: и
, рис.2.
Рис.2
Далее находим производную от по
из уравнения параболы:
и определяем угловые коэффициенты касательных к параболе в точках
и
, как частные значения этой производной:
Угловой коэффициент прямой один и тот же во всех ее точках; у данной прямой он равен — 1.
Согласно формуле (2) получим
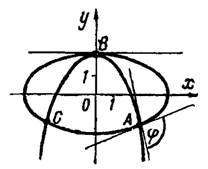
2) Решая совместно уравнения кривых, находим их общие точки: и
рис.3. Затем определяем угловые коэффициенты
и
касательных в любой точке эллипса и параболы как производные от
по
из их уравнений
Рис.3
Подставляя координаты точки , получим
и
. Следовательно, в точке
:
Под таким же углом кривые пересекаются и в точке вследствие их симметричности относительно оси
.
В точке имеем:
, следовательно, в точке
кривые имеют общую касательную, т. е. касаются друг друга. В этой точке угол между кривыми равен нулю.
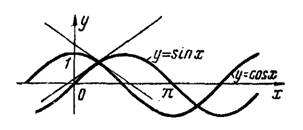
3) Абсциссы точек пересечения кривых (рис.4) определяются уравнением , решая которое, получим
Дифференцированием находим угловые коэффициенты касательных к синусоиде и косинусоиде:
Рис.4
Искомый угол между кривыми определяем по общей формуле (2)
Положительному знаку соответствует острый угол , отрицательному — тупой, смежный с ним угол
.
Углом
между двумя кривыми
у
= f1(x)
и у
= f2(x)
в точке их пересечения М0(х0,
у0)
называется угол между касательными к
этим кривым в точке М0.
Этот угол определяется по формуле
=
.
Пример.
Найти угол между параболами
у
= 8 – х2
и у
= х2.
□ Для
нахождения координат точек пересечения
заданных кривых решим систему уравнений
В
результате получим А(2;
4) и В(−2;
4). Продифференцируем уравнения парабол:
= −2х,
= 2х.
Найдем значения
и
для точки А(2;
4):
= −4,
= 4. Следовательно,
=
=
и
=
.
Аналогично
определяется угол между кривыми в точке
В(−2;
4):
=
.
■
§ 21. Формула тейлора
Теорема.
Пусть функция f(x)
имеет в точке а
и некоторой ее окрестности производные
порядка п
+ 1. Пусть х
– любое значение аргумента из указанной
окрестности, х
≠ а.
Тогда между точками а
и х
найдется точка
такая, что справедлива формула:
f(x)
= f(а)
+
(х
– а)
+
(х
– а)2+
…+
(х
– а)п
+
+
(х
– а)п+1.
Эту
формулу называют формулой
Тейлора.
Выражение
Rn+1(x)
=
(х
– а)п+1
называют
остаточным
членом
формулы Тейлора.
Запишем остаточный
член в другом виде:
так
как
(а,
х),
то найдется число
,
0 <
< 1, что
= а
+
(х
– а)
и тогда
Rn+1(x)
=
(х
– а)п+1,
0 <
< 1.
Эта
форма остаточного члена наиболее
употребительна в приложениях.
Если
в формуле Тейлора а
= 0, то получим формулу
Маклорена:
f(x)
= f(0)
+
х
+
х2
+
… +
хп
+
Rn+1(x)
с
остаточным членом
Rn+1(x)
=
хп+1,
0 <
< 1.
Разложение
некоторых элементарных функций по
формуле Маклорена
1.
f(x)
= ех.
Так как
f(x)
=
=
= … = f
п+1(x)
= ех,
f(0)
=
=
= … = f
п+1(0)
= 1,
то
формула Маклорена имеет вид
ех
= 1 +
+
+
+…+
+ Rn+1(x),
где
Rn+1(x)
=
хп+1,
0 <
< 1.
Аналогично
можно разложить по формуле Маклорена
следующие функции:
2.
f(x)
=
.
= х
−
+
−
+
…+ (−1)т+1
+ R2т(x),
где
R2т(x)
= (−1)т
·
,
0 <
< 1.
3.
f(x)
=
.
= 1
−
+
−
+
…+ (−1)т
+ R2т+1(x),
где
R2т+1(x)
= (−1)т+1
·
,
0 <
< 1.
4.
f(x)
= (1 + х)т.
(1
+ х)т
=1+
х+
х2+
х3+…+
+
хп
+Rn+1(x),
где
Rn+1(x)=
хп+1(1
+
)т—п-1,
0 <
< 1.
Пример.
Вычислить число е.
□ Запишем
разложение ех
по формуле Маклорена:
ех
= 1+
+
+
+…+
+
хп+1,
0 <
< 1.
Если
заменить функцию ех
ее многочленом Тейлора степени п
(отбросим остаточный член), то получим
приближенное равенство
ех
1 +
+
+
+…+
,
(1)
абсолютная
погрешность которого
| Rn+1(x)
| =
| х
|п+1,
0 <
< 1.
Если
рассматривать функцию ех
для −1 ≤ х
≤ 1, то
|
Rn+1(x)
| ≤
<
.
Полагая
в (1) х
= 1, получаем приближенное значение числа
е
≈ 1+
+
+
+ …+
.
При
этом | Rn+1(x)
| <
.
Если
требуется вычислить значение е
с точностью
= 0,001, то число п
определяется из неравенства
< 0,001, или (п
+ 1)! > 3000,
которое
выполняется при п
= 6. Следовательно,
е
≈ 1+
+
+
+ …+
.
Вычисляя
с четырьмя знаками после запятой, получим
е
≈ 2,7180.
Три
знака после запятой гарантированы.
■
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лучший ответ
|
|
 |
|
Как найти угол под которым пересекаются кривые
Читайте также:
- II. Операционная стратегия на примере отдельного предприятия.
- PEST-анализ и пример его использования
- SWOT-анализ и пример его использования
- VI. ПРИМЕРНЫЙ ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ ВОПРОСОВ ПО ПОДГОТОВКЕ К ЭКЗАМЕНУ
- А Примерный перечень вопросов, рассматриваемых на практических занятиях
- А. Работа переписчиков на Руси. Причины и примеры порчи текста в древнеславянских рукописях библейских книг.
- А.2. Пример описания объекта
- Анализ примера
- Аппаратная поддержка мультипрограммирования на примере процессора Pentium 1 страница
- Аппаратная поддержка мультипрограммирования на примере процессора Pentium 2 страница
- Аппаратная поддержка мультипрограммирования на примере процессора Pentium 3 страница
- Аппаратная поддержка мультипрограммирования на примере процессора Pentium 4 страница
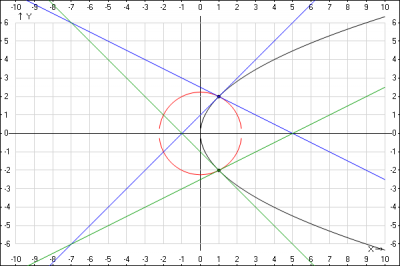
Решение.Найдем точки пересечения кривых, решив систему уравнений
Отсюда имеем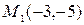 
, 
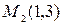
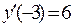
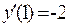
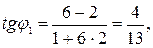
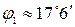
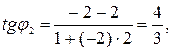
. Далее, определим угловые коэффициенты касательных к параболе в точках 
и 
.Соответственно имеем 
, 
. Угловой коэффициент прямой во всех точках один и тот же и равен в нашем случае 2. Далее находим углы 
,
.
Пример 3.Определить в каких точках заданной линии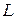 
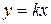
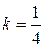
касательная к этой линии параллельна прямой 
и написать уравнение этой касательной
, 
.
Решение. Находим производную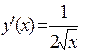 
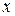
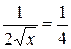
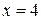
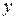
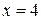
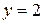
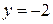
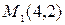
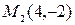
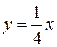
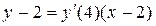
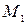
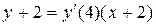
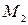
. Далее находим значение 
из уравнения 
. Имеем, 
.Значения функции 
при есть 
и 
. Отсюда имеем, 
и 
точки заданной линии в которых касательная к этой линии параллельна данной прямой 
. Найдем теперь уравнения этих касательных. Используя формулу (1), получим
-уравнение касательной в точке ,
-уравнение касательной в точке .
Контрольные вопросы.
1.Геометрический смысл производной.
2.Касательная и нормаль к кривой.
3.Угол между двумя кривыми.
4.Другие приложения производной.
Задания.
1.Найти углы, под которыми пересекаются эллипс и парабола
, 
.
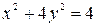
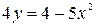
2. Определить в каких точках заданной линии касательная к этой линии параллельна прямой и написать уравнение этой касательной
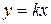
1) 
, 
; 2) 
, 
; 3) 
, 
.
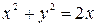
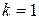
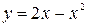
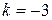
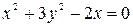
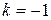
3.Найти угол между кривой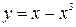 
и прямой 
Дата добавления: 2014-12-16 ; Просмотров: 3162 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Планиметрические задачи
Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если:
Решение. Уравнение касательной будем искать по формуле ; уравнение нормали — по формуле По условию, .
Подставляем все найденные значения в уравнение касательной:
Теперь находим уравнение нормали:
Ответ: уравнение касательной:; уравнение нормали:
Задача 2.Написать уравнения касательной и нормали в точке
Подставим полученные решения в равенство
Найдем производную функции, заданной параметрически .
Подставляем все найденные значение в уравнение касательной:
Теперь находим уравнение нормали:
Ответ: уравнение касательной: уравнение нормали: .
Задача 3. Найти углы, под которыми пересекаются заданные кривые:
Решение. Угол между кривыми находится по формуле
Найдем координаты точки пересечения заданных кривых. Решаем систему уравнений:
Таким образом, кривые пересекаются в точках .
Далее найдем значения производных заданных функций в точках пересечения.
производный дифференцирование уравнение планиметрический
Подставляем найденные значение в формулу нахождения угла:
Ответ: в точке угол равен 0 (т.е. касательные совпадают), в точке угол равен .
Задача 4. Задан прямоугольник с периметром 56 см. Каковы должны быть его стороны, чтобы площадь была наибольшей [7]?
Обозначим одну из сторон за, тогда вторая сторона:
Площадь такого прямоугольника составит:
Требуется найти максимум функции .
Это квадратичная функция, ее график — парабола, ветви которой направлены вниз.
Определим критические точки: .
Так, — точка экстремума, слева от нее производная положительна, а справа — отрицательна.
Очевидно, что — точка максимума. В таком случае площадь прямоугольника максимальна, когда его стороны равны 14 см, то есть когда он является квадратом.
Ответ: площадь максимальна, когда стороны прямоугольника равны 14 см.
Задача 5. Площадь прямоугольника составляет . Каковы должны быть его размеры этого прямоугольника, чтобы периметр был минимальным?[7]
Пусть стороны прямоугольника равны . Тогда:
Периметр такого прямоугольника составит:
Требуется найти минимум данной функции. Найдём производную:
Найдем точки экстремума:
Очевидно, что , поэтому нас интересует точка .Слева от нее производная отрицательна, а справа — положительна.
Так, — точка минимума.
Ответ: чтобы периметр прямоугольника был минимальным, его стороны должны составить 4 см.
Задача 6. Две стороны параллелограмма лежат на сторонах заданного треугольника, а одна из его вершин принадлежит третьей стороне. Найти условия, при которых площадь параллелограмма является наибольшей [2].
Пусть треугольник определяется двумя сторонами и углом между ними (рис.4). Построим параллелограмм в соответствии с условиями задачи. Обозначим стороны параллелограмма Площадь параллелограмма определяется формулой
Выразим через и стороны треугольника . Из подобия треугольников и следует, что
В результате площадь записывается как функция:
Отсюда видно, что экстремум функциисуществует в следующей точке:
При переходе через эту точку производная меняет свой знак с плюса на минус, то есть эта точка является точкой максимума. Другая сторона параллелограмма при этом равна
Итак, вписанный в треугольник параллелограмм со сторонами имеет наибольшую площадь при условии
где стороны треугольника. Интересно, что результат не зависит от угла между сторонами треугольника.
Ответ: площадь параллелограмма является наибольшей при условии
где стороны треугольника.
Задача 7.Среди всех равнобедренных треугольников, вписанных в данную окружность, найти треугольник с наибольшим периметром [2].
Пусть треугольник вписан в окружность данного радиуса ,
(независимая переменная) (рис.5). Выразим периметр треугольника как функцию . По теореме синусов:
. Найдем, при каком значении функция принимает наибольшее значение на данном интервале
следовательно, точка максимума, в которой функция принимает наибольшее значение на заданном промежутке. Таким образом, наибольший периметр имеет равносторонний треугольник.
Ответ: среди всех равнобедренных треугольник, вписанных в данную окружность, с наибольшим периметром является равносторонний треугольник.
Задача 8.Окно имеет форму прямоугольника, ограниченного сверху полукругом.
Периметр окна равен . Определить радиус полукруга , при котором площадь окна является наибольшей (рис.6) [2].
Очевидно, что одна сторона прямоугольника равна . Другую сторону обозначим через . Периметр всего окна выражается формулой
Площадь окна составляет:
Полученное выражение представляет собой функцию . Исследуем ее на экстремум. Находим производную:
Определяем стационарные точки:
Поскольку вторая производная отрицательна:
то найденная точка является точкой максимума, т.е. при этом значении площадь окна будет наибольшей.
Само максимальное значение площади составляет
Ответ: радиус полукруга , при котором площадь является наибольшей.
Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.
Информация
© admin
reshak.ru
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Значение производной $f'(x_0)$ функции $y=f(x)$ в точке $x_0$ равно угловому коэффициенту $k=tgvarphi$ касательной $TT’$ к графику этой функции, проведенной через точку $M_0(x_0, y_0),$ где $y_0=f(x_0)$ (геометрический смысл производной).
Прямая $NN’,$ проходящая через точку касания $M_0$ перпендикулярно к касательной, называется нормалью к графику функции $y=f(x)$ в этой точке. Уравнение нормали $$(x-x_0)+f'(x_0)(y-y_0)=0.$$Уравнение касательной $TT’$ к графику функции $y=f(x)$ в его точке $M_0(x_0, y_0)$ имеет вид $$y-y_0=f'(x_0)(x-x_0)$$
Углом $omega$ между кривыми $y=f_1(x)$ и $y=f_2(x)$ в их общей точке $M_0(x_0, y_0)$ называется угол между касательными к этим кривым в точке $M_0.$ Его можно вычислить по формуле $$tg,omega=frac{f_2′(x_0)-f’_1(x_0)}{1+f’_1(x_0)f’_2(x_0)}.$$
Примеры.
Написать уравнения касательной и нормали к графику функции $y=f(x)$ в данной точке, если:
5.235. $y=x^2-5x+4,$ $x_0=-1.$
Решение.
Уравнение касательной будем искать по формуле $y-y_0=f'(x_0)(x-x_0);$ уравнение нормали — по формуле $(x-x_0)+f'(x_0)(y-y_0)=0.$
По условию, $x_0=-1.$
$y_0=y(x_0)=(-1)^2-5cdot(-1)+4=1+5+4=10.$
$y'(x)=2x-5Rightarrow y'(x_0)=y'(-1)=2cdot (-1)-5=-2-5=-7.$
Подставляем все найденные значения в уравнение касательной:
$y-10=-7(x+1)Rightarrow 7x+y-3=0.$
Теперь находим уравнение нормали:
$(x+1)-7(y-10)=0Rightarrow x-7y+71=0.$
Ответ: Уравнение касательной: $7x+y-3=0;$ уравнение нормали: $ x-7y+71=0.$
5.237. $y=sqrt x,$ $x_0=4.$
Решение.
Уравнение касательной будем искать по формуле $y-y_0=f'(x_0)(x-x_0);$ уравнение нормали — по формуле $(x-x_0)+f'(x_0)(y-y_0)=0.$
По условию, $x_0=4.$
$y_0=y(x_0)=sqrt 4=2.$
$y'(x)=frac{1}{2}x^{-frac{1}{2}}=frac{1}{2sqrt x}Rightarrow y'(x_0)=y'(4)=frac{1}{2sqrt 4}=frac{1}{4}.$
Подставляем все найденные значения в уравнение касательной:
$y-2=frac{1}{4}(x-4)Rightarrow 4(y-2)=x-4Rightarrow 4y-8=x-4Rightarrow x-4y+4=0.$
Теперь находим уравнение нормали:
$(x-4)+frac{1}{4}(y-2)=0Rightarrow 4(x-4)+(y-2)=0Rightarrow 4x+y-18=0.$
Ответ: Уравнение касательной: $x-4y+4=0;$ уравнение нормали: $4x+y-18=0.$
5.241. Написать уравнения касательной и нормали в точке $M_0(2, 2)$ к кривой $x=frac{1+t}{t^3},$ $y=frac{3}{2t^2}+frac{1}{2t},,, tneq 0.$
Решение.
Найдем значение $t_0,$ подставляя координаты точки $M_0$ в уравнение кривой: $2=frac{1+t}{t^3},$ $2=frac{3}{2t^2}+frac{1}{2t}.$
$left{begin{array}{rcl} 2=frac{1+t}{t^3},\ 2=frac{3}{2t^2}+frac{1}{2t},end{array}right.Rightarrow$ $2=frac{1+t}{t^3}=frac{3}{2t^2}+frac{1}{2t}$
Решим уравнение
$frac{1+t}{t^3}=frac{3}{2t^2}+frac{1}{2t}$
$2(1+t)=3t+t^2Rightarrow$
$t^2+t-2=0Rightarrow t_1=1, t_2=-2.$
Подставим полученные решения в равенство $frac{1+t}{t^3}=frac{3}{2t^2}+frac{1}{2t}:$
$t_1=1: frac{1+1}{1}=frac{3}{2}+frac{1}{2}=2$
$t_2=-2: frac{1-2}{-8}=frac{3}{8}-frac{1}{4}=frac{1}{8}neq 2$ — не удовлетворяет нашей системе.
Найдем производную функции, заданной параметрически $y’_x.$
$y’_t=left(frac{3}{2}t^{-2}+frac{1}{2}t^{-1}right)’=frac{3}{2}cdot (-2)t^{-3}+frac{1}{2}cdot (-1)t^{-2}=-3t^{-3}-frac{1}{2}t^{-2}$
$y’_t|_{t=1}=-3-1/2=-3,5;$
$x’_t=left(frac{1+t}{t^3}right)’=frac{(1+t)’t^3-(1+t)(t^3)’}{t^6}=frac{t^3-(1+t)3t^2}{t^6}=frac{t^3-3t^2-3t^3}{t^6}=frac{-3t^2-2t^3}{t^6}.$
$x’_t|_{t=1}=-3-2=-5;$
$y’_x=frac{y’_t}{x_t}.$
$y’_x|_{t=1}=frac{-3,5}{-5}=frac{7}{10}.$
Подставляем все найденные значения в уравнение касательной:
$y-y_0=f'(x_0)(x-x_0)Rightarrow$ $y-2=frac{7}{10}(x-2)Rightarrow 10(y-2)=7(x-2)Rightarrow 10y-20=7x-14Rightarrow$ $7x-10y+6=0.$
Теперь находим уравнение нормали:
$(x-x_0)+f'(x_0)(y-y_0)=0Rightarrow$ $(x-2)+frac{7}{10}(y-2)=0Rightarrow 10(x-2)+7(y-2)=0Rightarrow 10x+7y-34=0.$
Ответ: Уравнение касательной: $7x-10y+6=0;$ уравнение нормали: $10x+7y-34=0.$
Найти углы, под которыми пересекаются заданные кривые:
5.254. $y=x^2$ и $y=x^3.$
Решение.
Угол между кривыми находим по формуле $$tg,omega=frac{f_2′(x_0)-f’_1(x_0)}{1+f’_1(x_0)f’_2(x_0)}.$$
Найдем координаты точки пересечения заданных кривых. Решаем систему уравнений:
$left{begin{array}{rcl} y=x^2,\ y=x^3,end{array}right.Rightarrow$ $left{begin{array}{rcl} y=x^2,\ x^2=x^3,end{array}right.Rightarrow$ $left{begin{array}{rcl} y=x^2,\ x_1=0\x_2=1,end{array}right.$ Таким образом, кривые пересекаются в точках $M_1(0, 0)$ и $M_2(1, 1).$
Далее найдем значения производных заданых функций в точках пересечения.
$f_1(x)=x^2Rightarrow f_1′(x)=2x$
$f_2(x)=x^3Rightarrow f_2′(x)=3x^2$
$f_1′(0)=0;$
$f_2′(0)=0;$
$f_1′(1)=2;$
$f_2′(1)=3.$
Подставляем найденные значения, в формулу нахождения угла:
$$tg,omega_1=frac{f_2′(0)-f’_1(0)}{1+f’_1(0)f’_2(0)}=frac{0-0}{1+0}=0.$$
Следовательно, $omega_1=0.$
$$tg,omega_2=frac{f_2′(1)-f’_1(1)}{1+f’_1(1)f’_2(1)}=frac{3-2}{1+2cdot 3}=frac{1}{7}.$$
Следовательно, $omega_2=arctgfrac{1}{7}.$
Ответ: В точке $M_1(0, 0)$ угол равен 0. (т.е. касательные совпадают), в точке $M_2(1, 1)$ угол равен $arctgfrac{1}{7}.$
Домашнее задание.
Написать уравнения касательной и нормали к графику функции $y=f(x)$ в данной точке, если:
5.236. $y=x^3+2x^2-4x-3,$ $x_0=-2.$
Ответ: Уравнение касательной: $y-5=0;$ уравнение нормали: $x+2=0.$
5.238. $y=tg 2x,,,, x_0=0.$
Ответ: Уравнение касательной: $y-2x=0;$ уравнение нормали: $2y+x=0.$
5.239. $y=ln x,,,, x_0=1.$
Ответ: Уравнение касательной: $x-y-1=0;$ уравнение нормали: $x+y-1=0.$
5.242. Написать уравнения касательных к кривой $$x=tcos t, ,,, y=tsin t,,,, tin(-infty,,, +infty),$$ в начале координат и в точке $t=pi/4.$
Ответ: $y=0,$ $(pi+4)x+(pi-4)y-pi^2frac{sqrt 2}{4}=0$
5.244. Написать уравнения касательной к кривой $$x^5+y^5-2xy=0 в точке $M_0(1, 1).$
Ответ: $ x+y-2=0.$
Найти углы,под которыми пересекаются заданные кривые:
5.255. $y=(x-2)^2$ и $y=4x-x^2+4.$
Ответ: $arctgfrac{8}{15}.$
5.256. $y=sin x$ и $y=cos x,,, xin[0, 2pi].$
Ответ: $arctg2sqrt 2.$
5.260. Найти расстояние от начала координат до нормали к линии $y=e^{2x}+x^2,$ проведенной в точке с абсциссой $x=0.$
Ответ: $frac{2}{sqrt 5}.$