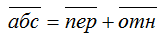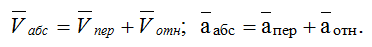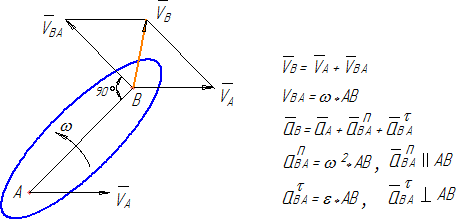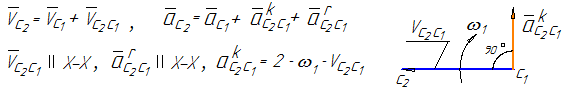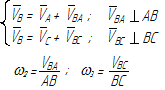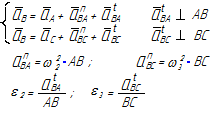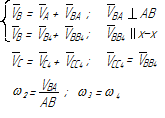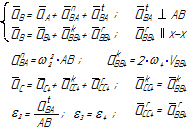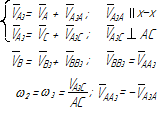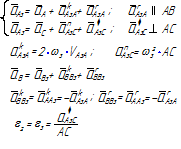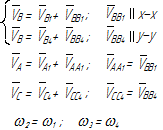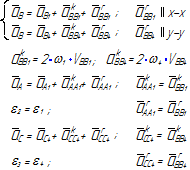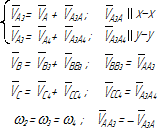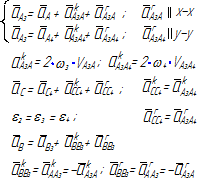Для
положения 6
Определим угловые скорости звеньев. Угловые скорости звеньев определяются из следующих соотношений:
.
Подставим
найденное значение относительной
линейной скорости
и известную длину звена механизма
в
записанную формулу:
.
Примечание:
за положительное направление вращения
принято вращение кривошипа.
Для
положения 0
Угловые скорости звеньев определяются из следующих соотношений:
.
Подставим
найденное значение относительной
линейной скорости
и известную длину звена механизма
в
записанную формулу:
.
Таблица
1.3.
Значения
линейных скоростей точек и угловых
скоростей звеньев для 6-го и
0-го
положений механизма.
|
положение |
Отрезки мм |
Линейные м/с |
Угловые |
||||||||||||||||||||
|
Pvc2 |
Pvs |
Pvd2 |
Pve |
Pvd45 |
bс2 |
bs |
bd2 |
be |
d2d45 |
VB |
VC2 |
VC2 |
VC3 |
VC0 |
VA |
VS |
VD2 |
VE |
VD45/D2 |
VD45=VN |
1 |
2=3= |
|
|
6 |
40,5 |
44 |
49 |
57,5 |
28 |
37 |
18,5 |
63,21 |
76,47 |
32 |
1,36 |
0,925 |
1,012 |
0 |
0 |
0 |
1,1 |
1,225 |
1,44 |
0,8 |
0,7 |
13,6 |
3,1 |
|
0 |
54,4 |
54,4 |
54,4 |
54,4 |
0 |
0 |
0 |
0 |
0 |
54,4 |
1,36 |
0 |
1,36 |
0 |
0 |
0 |
1,36 |
1,36 |
1,36 |
1,36 |
0 |
13,6 |
0 |
-
Определение линейных ускорений всех характерных точек механизма
(для
положения 6)
Найдем
ускорение точки B.
Так как ω1=const,
то угловое ускорение 1=0
и тангенциальное ускорение
=0.
Полное
ускорение точки В будет равно нормальному
ускорению:
.
Вектор
нормального ускорения
//АB
и направлен к центру вращения звена 1.
Примем
масштаб построения плана ускорений:
.
На
плане ускорений:
.
Выбираем
точку-полюс плана ускорений Ра,
проводим вектор
//АB.
Определим
ускорение точки С2.
Ускорение
точки С2
определим из совместного решения 2-х
уравнений:
-
— Для звена 2.
-
— Для звена 3.
Решим
первое уравнение:
=
,
где
=
и
//ВС;
=
=
и
ВС.
Решим
второе уравнение:
=
,
где
=
;
=
=
.
Для
определения направления ускорения
нужно
вектор относительной скорости
повернуть на угол 900
по направлению ω2.
—
релятивное ускорение, оно всегда
направлено по кулисе (векторы
и
всегда
взаимно перпендикулярны).
Из
плана получим:
;
;
.
Найдем
ускорения точек S,
D2,
E.
Ускорение
точек найдём так же как и скорость на
основании свойства и пропорциональности
отрезков bc2,
bs, bd2,
be на плане ускорений и размеров звеньев
lBC,
lBS,
lBD,
lBE.
Получим
следующее отношение:
.
Отсюда
находим:
;
;
.
Построив
план с сохранением того же порядка
обхода букв получим:
;
;
.
Найдем
ускорения точек D45,
M,
N.
Точки
D45,
M,
N
принадлежат одному звену, а значит
движутся в одном направлении:
.
Причем,
звенья
2 и 4 образуют поступательную кинематическую
пару:
;
=
.
На
плане отложим
вектор Кориолисова ускорения. Для
определения его направления повернём
вектор скорости
на
900
в сторону мгновенного вращения.
=
=
.
Из
плана:
;
.
Релятивное
ускорение всегда направлено вдоль
кулисы.
«К
построению плана ускорений»
(для
«мертвого» положения механизма)
Анализ
проведем в той же последовательности
Найдем
ускорение точки B.
.
Примем
масштаб построения плана ускорений:
.
На
плане ускорений:
.
Выбираем
точку-полюс плана ускорений Ра,
проводим вектор
//АB.
Определим
ускорение точки С2.
Ускорение
точки С2
определим из совместного решения 2-х
уравнений:
1.
=
— для звена 2.
2.
=
—
для звена 3.
В
мертвом положении ω2=0,
следовательно:
=0
м/с2;
=0
м/с2.
Получаем:
=
;
=
.
Из
плана получим:
;
;
.
Найдем
ускорения точек S,
D2,
E.
Ускорение
точек найдём из отношения:
.
Отсюда
находим:
;
;
;
Построив
план с сохранением того же порядка
обхода букв получим:
;
;
.
Найдем
ускорения точек D45,
M,
N.
.
В
мертвом положении ω5=0,
следовательно:
;
.
Из
плана:
;
.
Соседние файлы в папке 2 рычаги и 13 зубы
- #
- #
- #
- #
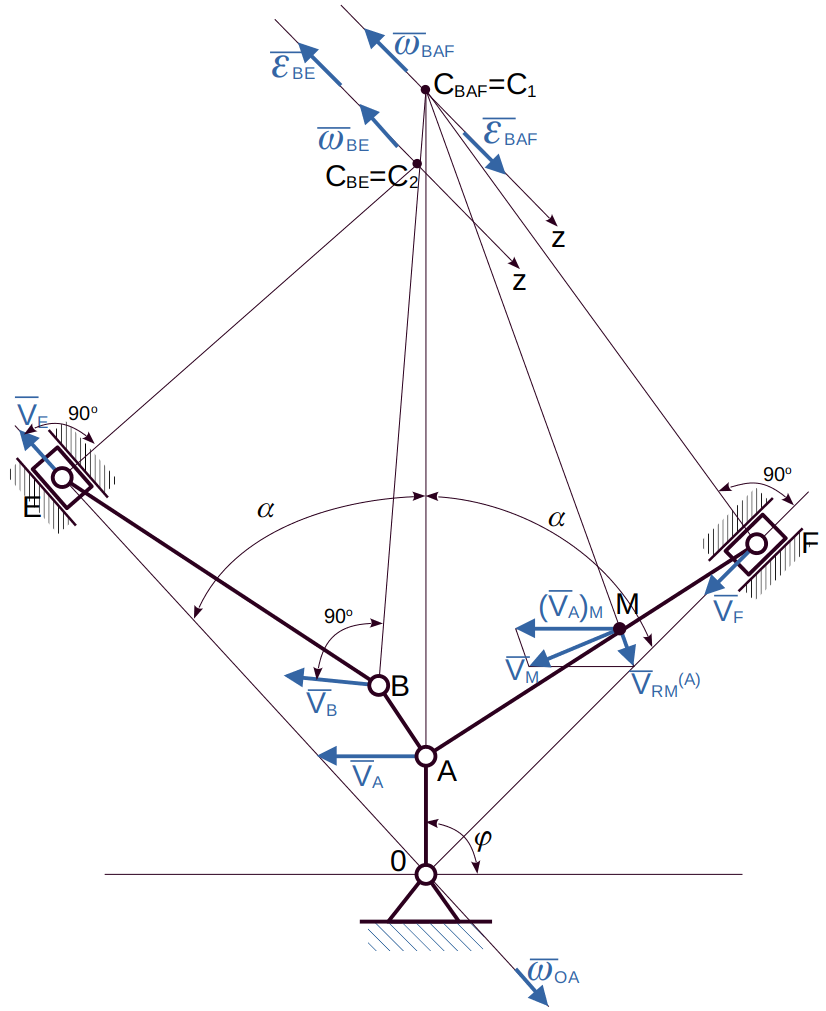
Рис.1
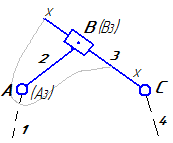
В положении механизма, указанном на рис.1, определить аналитически и построить на чертеже :
- положение мгновенных центров скоростей всех звеньев, совершающих плоское движение;
- скорости всех, точек механизма, расположенных в местах соединения звеньев (шарнирах);
- угловые скорости всех звеньев;
- ускорение точки А;
- ускорений других точек механизма методом полюса;
- угловые ускорения звеньев;
- касательное и нормальное ускорения точки В;
- установить характер движения точки В (ускоренное, замедленное, мгновенная остановка).
Дано:
= 30 об./мин.
Определить:
1) = ?
2) = ?
3) = ?
4) = ?
Решение:
I. Определим скорости точек и угловые скорости звеньев механизма (метод мгновенного центра скоростей, мцс)
1.1 Определим угловую скорость ведущего кривошипа OA:
C1: вектор оси
— оси вращения кривошипа OA (см. рис.1),
1.2 Рассмотрим кривошип OA:
C2: в сторону вращения кривошипа OA (см. рис.1)
1.3 рассмотрим уголковый шатун BAF
Точка — мгновенный центр скоростей шатуна BAF
ось — мгновенная ось вращения шатуна BAF.
(1)
Примечание: Так как на Рис.1 звенья механизма изображены в масштабе, то величины (размеры) мгновенных радиусов точек, а именно: и
берутся с рисунка.
C3: вектор скорости по направляющей в сторону поворота шатуна (вниз).
Определим скорость точки B
Угловая скорость шатуна BAF:
(2)
C4: Вектор , т.к. шатун относительно оси
поворачивается по часовой стрелке.
(3)
Примечание: Величина так-же берётся с Рис.1.
Из (3) получаем
C5: вектор и направлен в сторону вращения шатуна BAF.
1.4 Рассмотрим шатун «BE»
Точка — мгновенный центр скоростей шатуна «BE»
Ось — мгновенная ось вращения шатуна «BE»
(4)
Из (4) получаем:
C6: Вектор и направлен по направляющей вверх (см. Рис.1).
Угловая скорость шатуна BE:
(5)
Примечание: Величину берём из рис. 1 с учётом масштаба.
C7: вектор угловой скорости шатуна BE (от нас),
т.к. «отсюда» видим вращение по часовой стрелке относительно оси
1.5 Определим скорость точки M:
а) метод «мгновенного центра скоростей»:
Точка M шатуну BAF, точка
— мгновенный центр скоростей BAF,
— мгновенный радиус точки M.
(6)
Из (6) получаем:
C8: Вектор скорости и направлен в сторону вращения шатуна BAF
б) метод «полюса»: точка А — полюс
(7)
Где — вращательная скорость точки M относительно «полюса» A, вектор направлен перпендикулярно
= 0.342 (величина угла взята с рис.1)
Сравним = 0.68 m/c (мцс) и «метод полюса»
= 0.73 m/c : погрешность расчёта составляет
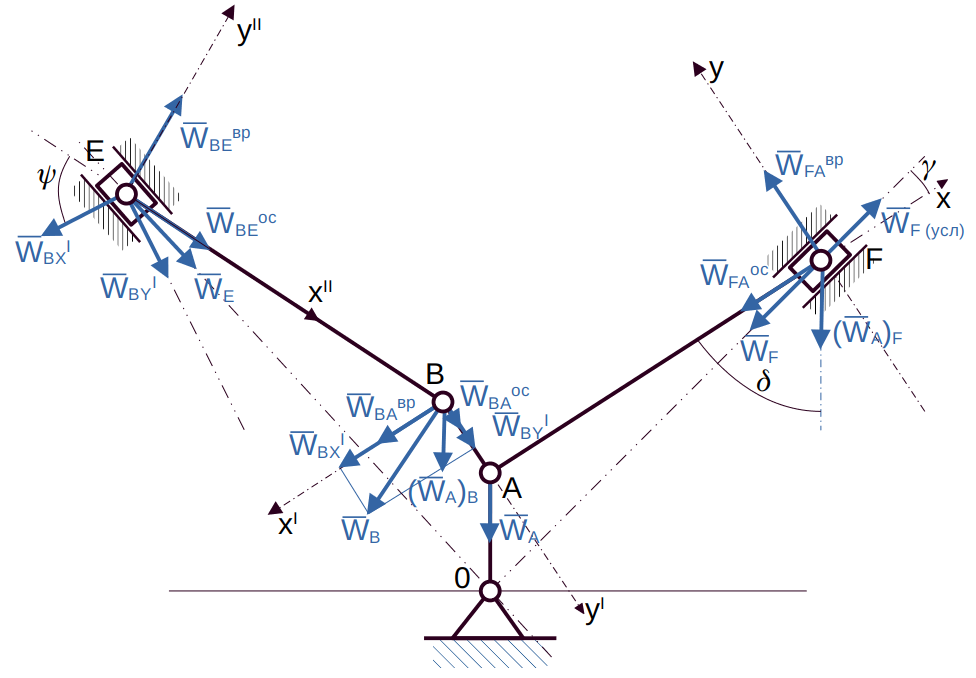
II. Определение ускорений точек и угловых ускорений звеньев механизма. (методом «полюса»)
2.1 Ускорение точки A, принадлежащей кривошипу OA, который вращается вокруг неподвижной оси 
(8)
(9)
где и
— вращательное и осестремительное ускорения точки A около оси
соответственно.
(10)
С учётом (9) и (10) из (8) получим:
(11)
(12)
тогда их (11) с учётом (12) получим
Рис.2
C9: направлен из точки A к оси
(см.рис.2).
2.2 Рассмотрим шатун BAF
а) определяем ускорение точки F
(13)
где и
— вращательное и осестремительное ускорения точки F вокруг «полюса» A, соответственно.
(14)
C10: Вектор осестремительного ускорения направлен от точки F к «полюсу» A (см.рис.2)
C11: Для вектора вращательного ускорения известна только линия действия (л.д.),
(направление также выбираем условно см.рис.2)
C12: Для вектора — (ускорения «ползуна» F) известна только линия действия (л.д.) — направляющая «OF» (направление также выберем условно)
(15)
Спроектируем векторное равенство (13) на оси координат «XFY»:
на ось :
(16)
на ось :
(17)
C13: (см.рис.2)
, где величину этих углов берём с чертежа (см.рис.2)
Далее перепишем (16) и (17), подставляя числовые значения:
(18)
(19)
Из уравнения (16) получим:
C14: Получили, что , следовательно, условное направление надо поменять на противоположное (см.рис.2)
Из уравнения (17) получим:
C15: Так как , то условное направление верно! (см.рис.2).
Определим угловое ускорение шатуна BAF:
(20)
Направление определяем из векторного произведения
(см.рис.2)
C16: Вектор и, так как
, то шатун «BAF» вращается замедленно ! (см.рис.1)
б) Определим ускорение точки  (метод «полюса»):
(метод «полюса»):
(21)
где (см. пункт I.)
C17: Вектор направлен по
от точки B к «полюсу» A (см.рис.2).
С учётом (20) получим, что:
(22)
C18: Вектор (см.рис.2).
Спроектируем векторное равенство (21) на оси :
на ось
(23)
на ось
(24)
угол берём с чертежа (см.рис.2).
Перепишем (23) и (24), подставляя числовые значения:
(25)
(26)
Далее находим абсолютную величину ускорения точки B:
(27)
Направление вектора определяется направляющими косинусами по отношению к осям BXY.
(28)
Соотношение (27) и (28) представляют вектор по величине (27) и направлению (28)
2.3 Рассмотрим шатун «BE»
Запишем для — вектора ускорения точки
шатуну «BE» (по методу «полюса») векторное равенство:
(29)
Спроецируем (29) на оси координат и
(см. рис.2)
(30)
(31)
Далее перепишем (30) и (31), подставляя числовые значения, получим
(32)
(33)
Здесь также значение угла берём с чертежа (см.рис.2)
Из (32) определим величину вектора ускорения точки E
Из (33) определим величину вектора вращательного ускорения точки «E» около «полюса» B:
(34)
Определим величину углового ускорения шатуна BE с учётом (34)
Направление вектора определим из векторного произведения:
(35)
C19: Так как получили (34), что , то следует условное направление вектора изменить на противоположное (рис.2), тогда чтобы удовлетворить векторное произведение (35), вектор
(см. рис.1), а поскольку получили, что
, то, значит, характер вращения шатуна «BE» — ускоренный.
Ответ:
Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов в теории механизмов и машин.
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное — движение данной точки относительно той, движение которой принято за переносное:
Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:
Планы скоростей и ускорений обладают следующими свойствами:
- на плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана. На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает;
- отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек. Вектор относительной скорости направлен на плане к той точке, которая в индексе скорости стоит на первом месте;
- фигуры, образованные точками одного и того же жесткого звена на плане и на механизме, подобны. Поэтому, если на звене известны скорости и ускорения двух точек, то скорость и ускорение любой третьей точки этого же звена можно найти по подобию;
- имея план скоростей, можно найти угловую скорость любого звена механизма. Для определения угловой скорости исследуемого звена надо взять относительную скорость двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
- имея план ускорений, можно найти угловое ускорение любого звена механизма. Для определения углового ускорения исследуемого звена надо взять тангенциальную составляющую относительного ускорения двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
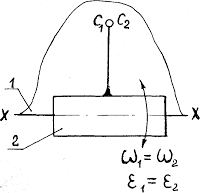
- звенья, соединенные в поступательную кинематическую пару, имеют одинаковые угловые скорости и одинаковые угловые ускорения.
При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:
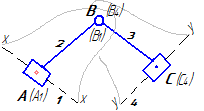
1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).
В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.
Рисунок 13
Для примера, приведенного на рисунке 13, нормальное ускорение точки В относительно точки А будет направлено вдоль радиуса ВА к точке А. Тангенциальное – перпендикулярно этому радиусу;
2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей (рисунок 14).
Рисунок 14
Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С1, принадлежащей этой направляющей.
Движение точки С1 принимается в качестве переносного. Движение точки С2, принадлежащей ползуну, относительно точки С1 получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С1 и С2 совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).
Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится.
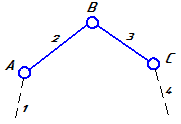
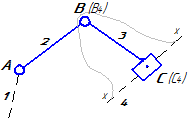
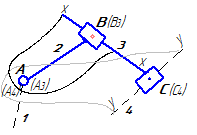
Уравнения планов для групп Ассура второго класса приведены в таблице 3.1.
Таблица 3.1 – Кинематический анализ групп Ассура II класса методом планов
| Вид группы | Конфигурация группы | Уравнения для построения планов скоростей и для определения угловых скоростей | Уравнения для построения планов ускорений и для определения угловых ускорений |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
Аналитический метод кинематического исследования >
Курсовой проект по ТММ >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее