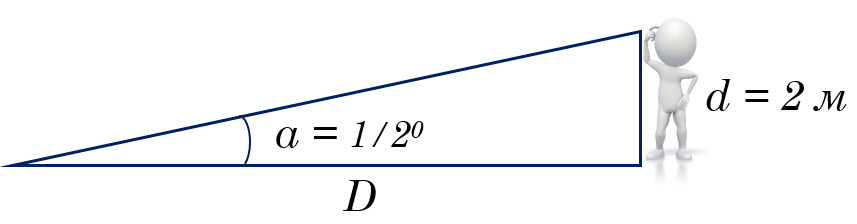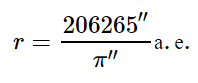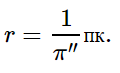Как найти угловой размер звезды

From Wikipedia, the free encyclopedia

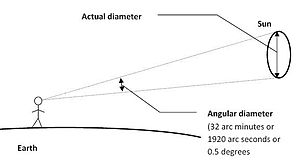
The angular diameter, angular size, apparent diameter, or apparent size is an angular distance describing how large a sphere or circle appears from a given point of view. In the vision sciences, it is called the visual angle, and in optics, it is the angular aperture (of a lens). The angular diameter can alternatively be thought of as the angular displacement through which an eye or camera must rotate to look from one side of an apparent circle to the opposite side. Humans can resolve with their naked eyes diameters of up to about 1 arcminute (approximately 0.017° or 0.0003 radians).^[1] This corresponds to 0.3 m at a 1 km distance, or to perceiving Venus as a disk under optimal conditions.

Formula[edit]

The angular diameter of a circle whose plane is perpendicular to the displacement vector between the point of view and the center of said circle can be calculated using the formula^[2]

in which is the angular diameter in degrees, and is the actual diameter of the object, and is the distance to the object. When , we have , and the result obtained is in radians.

For a spherical object whose actual diameter equals and where is the distance to the center of the sphere, the angular diameter can be found by the formula

The difference is due to the fact that the apparent edges of a sphere are its tangent points, which are closer to the observer than the center of the sphere. The difference is significant only for spherical objects of large angular diameter, since the following small-angle approximations hold for small values of :^[3]

Estimating angular diameter using the hand[edit]

Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.^[4][5][6]

Use in astronomy[edit]

In astronomy, the sizes of celestial objects are often given in terms of their angular diameter as seen from Earth, rather than their actual sizes. Since these angular diameters are typically small, it is common to present them in arcseconds (″). An arcsecond is 1/3600th of one degree (1°) and a radian is 180/π degrees. So one radian equals 3,600 × 180/ arcseconds, which is about 206,265 arcseconds (1 rad ≈ 206,264.806247″). Therefore, the angular diameter of an object with physical diameter d at a distance D, expressed in arcseconds, is given by:^[7]

.

These objects have an angular diameter of 1″:

• an object of diameter 1 cm at a distance of 2.06 km
• an object of diameter 725.27 km at a distance of 1 astronomical unit (AU)
• an object of diameter 45 866 916 km at 1 light-year
• an object of diameter 1 AU (149 597 871 km) at a distance of 1 parsec (pc)

Thus, the angular diameter of Earth’s orbit around the Sun as viewed from a distance of 1 pc is 2″, as 1 AU is the mean radius of Earth’s orbit.

The angular diameter of the Sun, from a distance of one light-year, is 0.03″, and that of Earth 0.0003″. The angular diameter 0.03″ of the Sun given above is approximately the same as that of a human body at a distance of the diameter of Earth.

This table shows the angular sizes of noteworthy celestial bodies as seen from Earth:

Celestial object	Angular diameter or size	Relative size
Magellanic Stream	over 100°
Gum Nebula	36°
Milky Way	30° (by 360°)
Width of spread out hand with arm streched out	20°	353 meter at 1 km distance
Serpens-Aquila Rift	20° by 10°
Canis Major Overdensity	12° by 12°
Smith’s Cloud	11°
Large Magellanic Cloud	10.75° by 9.17°	Note: brightest galaxy, other than the Milky Way, in the night sky (0.9 apparent magnitude (V))
Barnard’s loop	10°
Zeta Ophiuchi Sh2-27 nebula	10°
Width of fist with arm streched out	10°	175 meter at 1 km distance
Sagittarius Dwarf Spheroidal Galaxy	7.5° by 3.6°
Northern Coalsack Nebula	7° by 5°[8]
Coalsack nebula	7° by 5°
Cygnus OB7	4° by 7°[9]
Rho Ophiuchi cloud complex	4.5° by 6.5°
Hyades	5°30′	Note: brightest star cluster in the night sky, 0.5 apparent magnitude (V)
Small Magellanic Cloud	5°20′ by 3°5′
Andromeda Galaxy	3°10′ by 1°	About six times the size of the Sun or the Moon. Only the much smaller core is visible without long-exposure photography.
Veil Nebula	3°
Heart Nebula	2.5° by 2.5°
Westerhout 5	2.3° by 1.25°
Sh2-54	2.3°
Carina Nebula	2° by 2°	Note: brightest nebula in the night sky, 1.0 apparent magnitude (V)
North America Nebula	2° by 100′
In the Moon’s sky the apparent size of Earth	2° — 1°48′[10]	Appearing about three to four times larger than the Moon in Earth’s sky
Orion Nebula	1°5′ by 1°
Width of little finger with arm streched out	1°	17.5 meter at 1 km distance
Moon	34′6″ – 29′20″	32.5–28 times the maximum value for Venus (orange bar below) / 2046–1760″ the Moon has a diameter of 3,474 km
Sun	32′32″ – 31′27″	31–30 times the maximum value for Venus (orange bar below) / 1952–1887″ the Sun has a diameter of 1,391,400 km
Angular size of the distance between Earth and the Moon as viewed from Mars, at inferior conjunction	about 25′
Helix Nebula	about 16′ by 28′
Spire in Eagle Nebula	4′40″	length is 280″
Venus	1′6″ – 0′9.7″
International Space Station (ISS)	1′3″	;[11] the ISS has a width of about 108 m
Maximum resolvable diameter by the human eye	1′	;[12] 0.3 meter at 1 km distance[13]
About 100 km on the surface of the Moon	1′	Comparable to the size of features like large lunar craters, such as the Copernicus crater, a prominent bright spot in the eastern part of Oceanus Procellarum on the waning side, or the Tycho crater within a bright area in the south, of the lunar near side.
Jupiter	50.1″ – 29.8″
Maximum resolvable point/gap by the human eye	40″	;[12] at close view the width of a 0.04 mm very thin hair[13]
Mars	25.1″ – 3.5″
Saturn	20.1″ – 14.5″
Mercury	13.0″ – 4.5″
Uranus	4.1″ – 3.3″
Neptune	2.4″ – 2.2″
Ganymede	1.8″ – 1.2″	Ganymede has a diameter of 5,268 km
An astronaut (~1.7 m) at a distance of 350 km, the average altitude of the ISS	1″
Maximum resolvable diameter by Galileo Galilei’s largest 38mm refracting telescopes	~1″	;[14] Note: 30x[15] magnification, comparable to very strong contemporary terrestrial binoculars
Ceres	0.84″ – 0.33″
Vesta	0.64″ – 0.20″
Pluto	0.11″ – 0.06″
Eris	0.089″ – 0.034″
R Doradus	0.062″ – 0.052″	Note: R Doradus is thought to be the extrasolar star with the largest apparent size as viewed from Earth
Betelgeuse	0.060″ – 0.049″
Alphard	0.00909″
Rho Cassiopeiae	0.0072″
Alpha Centauri A	0.007″
Canopus	0.006″
Sirius	0.005936″
Altair	0.003″
Deneb	0.002″
Proxima Centauri	0.001″
Alnitak	0.0005″
Proxima Centauri b	0.00008″
Event horizon of black hole M87* at center of the M87 galaxy, imaged by the Event Horizon Telescope in 2019.	0.000025″ (2.5×10−5)	Comparable to a tennis ball on the Moon
A star like Alnitak at a distance where the Hubble Space Telescope would just be able to see it[16]	6×10−10 arcsec

The table shows that the angular diameter of Sun, when seen from Earth is approximately 32′ (1920″ or 0.53°), as illustrated above.

Thus the angular diameter of the Sun is about 250,000 times that of Sirius. (Sirius has twice the diameter and its distance is 500,000 times as much; the Sun is 10¹⁰ times as bright, corresponding to an angular diameter ratio of 10⁵, so Sirius is roughly 6 times as bright per unit solid angle.)

The angular diameter of the Sun is also about 250,000 times that of Alpha Centauri A (it has about the same diameter and the distance is 250,000 times as much; the Sun is 4×10¹⁰ times as bright, corresponding to an angular diameter ratio of 200,000, so Alpha Centauri A is a little brighter per unit solid angle).

The angular diameter of the Sun is about the same as that of the Moon. (The Sun’s diameter is 400 times as large and its distance also; the Sun is 200,000 to 500,000 times as bright as the full Moon (figures vary), corresponding to an angular diameter ratio of 450 to 700, so a celestial body with a diameter of 2.5–4″ and the same brightness per unit solid angle would have the same brightness as the full Moon.)

Even though Pluto is physically larger than Ceres, when viewed from Earth (e.g., through the Hubble Space Telescope) Ceres has a much larger apparent size.

Angular sizes measured in degrees are useful for larger patches of sky. (For example, the three stars of the Belt cover about 4.5° of angular size.) However, much finer units are needed to measure the angular sizes of galaxies, nebulae, or other objects of the night sky.

Degrees, therefore, are subdivided as follows:

• 360 degrees (°) in a full circle
• 60 arc-minutes (′) in one degree
• 60 arc-seconds (″) in one arc-minute

To put this in perspective, the full Moon as viewed from Earth is about 1⁄2°, or 30′ (or 1800″). The Moon’s motion across the sky can be measured in angular size: approximately 15° every hour, or 15″ per second. A one-mile-long line painted on the face of the Moon would appear from Earth to be about 1″ in length.

In astronomy, it is typically difficult to directly measure the distance to an object, yet the object may have a known physical size (perhaps it is similar to a closer object with known distance) and a measurable angular diameter. In that case, the angular diameter formula can be inverted to yield the angular diameter distance to distant objects as

In non-Euclidean space, such as our expanding universe, the angular diameter distance is only one of several definitions of distance, so that there can be different «distances» to the same object. See Distance measures (cosmology).

Non-circular objects[edit]

Many deep-sky objects such as galaxies and nebulae appear non-circular and are thus typically given two measures of diameter: major axis and minor axis. For example, the Small Magellanic Cloud has a visual apparent diameter of 5° 20′ × 3° 5′.

Defect of illumination[edit]

Defect of illumination is the maximum angular width of the unilluminated part of a celestial body seen by a given observer. For example, if an object is 40″ of arc across and is 75% illuminated, the defect of illumination is 10″.

See also[edit]

• Angular diameter distance
• Angular resolution
• Solid angle
• Visual acuity
• Visual angle
• Perceived visual angle
• List of stars with resolved images
• Apparent magnitude

References[edit]

External links[edit]

• Small-Angle Formula
• Visual Aid to the Apparent Size of the Planets

Почему так трудно определить размеры небесных объектов и расстояния до них? Все дело в том, что размеры удаленных объектов мы можем определить только по сравнению размерами известных объектов, а на небе нам не с чем сравнивать. Мы видим на небе множество светящихся точек, но яркость точки может определяться как ее размером, абсолютной светимостью, так и расстоянием до нее.

Поэтому в астрономии практически невозможно определить оптическими методами линейный размер удаленного объекта, можно определить только его угловой размер.

Древние греки изобрели тригонометрию, которая позволяет определить количественные соотношения между углами, линейными размерами и линейными расстояниями. С помощью простых математических соотношений, включающих базовую тригонометрию, мы можем вычислить расстояния до удаленных объектов, размеры которых известны (или размеры, если расстояния известны).

Уравнение малых углов

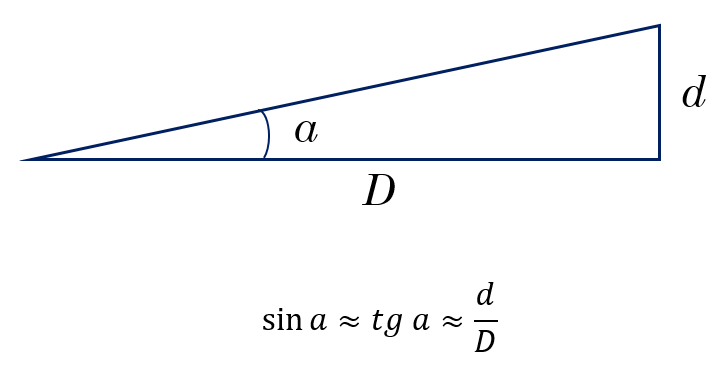
Если углы малые, то синус угла примерно равен тангенсу, который, в свою очередь примерно равен самому углу в радианной мере. 

Уравнение малых углов включает в себя угловой размер объекта, его линейный размер и расстояние. Если известны какие-либо две из этих величин, можно вычислить третью. Обратимся к угловому размеру с символом a, выраженному в секундах дуги. Обозначим диаметр объекта как d, а расстояние до него как D. Тогда уравнение малого угла

a / 206 265 = d / D

Число 206 265 называется константой пропорциональности. Число 206 265 на самом деле является числом секунд дуги в угле 57,3°, который является специальным углом, называемым радианом. Радиан определяется как центральный угол дуги, длина которой равна радиусу окружности. Длина окружности равна 2πr, Радиан равен 360° / 2 π = 57,3° или около шестой части полного круга. 

Вот пример использования уравнения малого угла. Предположим, что ваш друг ростом в 2 метра стоит через поле от вас, где он виден под углом ½°, или 1800″. Как он далеко от вас? Мы хотим найти расстояние D, выразим эту величину из уранения:

D = 206 265 d / a

Используя метрические единицы, найдем

D = (2.1 x 10⁵ x 2) / (1.8 x 10³) = 2.3 х 10² метра = 230 метров

Если ваш друг имеет рост 2 метра и угловой размер его составляет ½ ° (или 1800 угловых секунд), расстояние D составляет 230 метров. Обратите внимание, что мы округляем все наши оценки до двух значащих цифр, потому что измерение угла вряд ли будет очень точным.

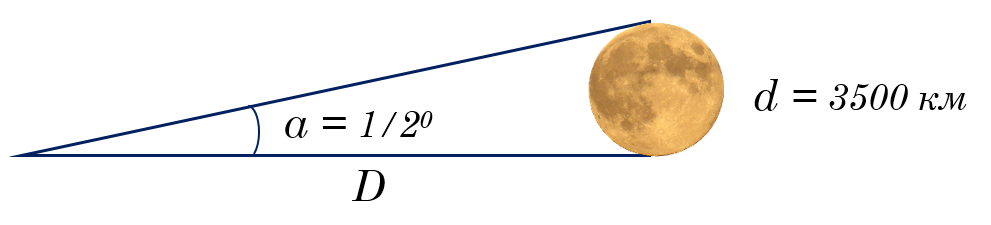
Как поняли древние греки, уравнение малого угла можно использовать для определения астрономических расстояний. Они не могли точно измерить диаметр Луны, но они знали ее угловой размер a, который также составляет примерно ½°, или 1800″.

Если мы используем современные знания о том, что диаметр Луны составляет около 3500 километров, мы можем оценить расстояние до нее так же, как мы это сделали для расстояния друга выше. В метрических единицах d будет 3,5 × 10⁶ метров. Уравнение будет гласить:

D = (2.1 × 10⁵ × 3.5 × 10⁶) / (1.8 × 10³) ≈ 4 х 10⁸ метров ≈ 4 x 10⁵ километров.

Реальное среднее расстояние до Луны 384 000 км. Неплохая точность!

Методы определения расстояний до звезд

Годичный параллакс

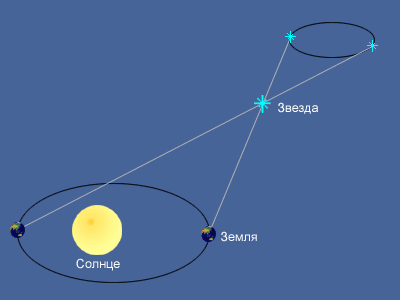
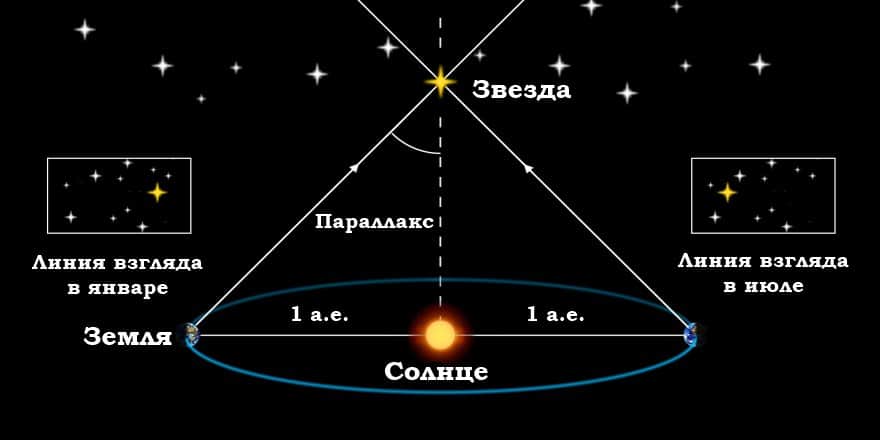
Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом (π).

Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.

Если CT = a есть средний радиус земной орбиты, SC = r — расстояние до звезды S от Солнца C, а угол π — годичный параллакс звезды, то

Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′, то расстояние до звезды можно определить из соотношения

При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины — парсек (пк), название которой происходит от слов «параллакс» и «секунда».

Парсек — это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.

1 пк = 206 265 а. е. = 3,086 · 10¹³ км.

Таким образом, расстояние до звезд в парсеках будет определяться выражением

В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках (1 кпк = 10³ пк) и мегапарсеках (1 Мпк = 10⁶ пк), а также в световых годах (1 св. г. = 9,46 · 10¹² км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г.).

Световой год — расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.

Источник

Фотометрический метод определения расстояний

Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m — видимая, M — абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний r_ф(пк):

Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.

Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5^m. Эта погрешность соответствует относительной погрешности 30%.

Цефеиды (стандартные свечи)

Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном свойстве переменных звезд — цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5^m. Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.

Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).

     

В начале 1610 г. Галилей навел на небо только что построенный им телескоп. В первые же ночи наблюдений он увидел много интересного: увидел, что Луна имеет горы и равнины, что планеты имеют заметные диски, открыл четырех спутников Юпитера, смог различить фазы Меркурия и Венеры, подобные фазам Луны, а на дисках Юпитера и Марса мог заметить даже некоторые детали. Но, направив телескоп на звезды, Галилей, вероятно, был несколько разочарован. Правда, звезды в телескоп были видны более яркими, их стало больше, но каждая звезда осталась такой же точкой, как была видна глазом, и даже наоборот: яркие звезды стали как бы меньше, они потеряли те лучи, которые окружали их при рассматривании невооруженным глазом.

С тех пор прошло 300 лет. Современные телескопы неизмеримо превосходят и по величине и по качеству оптики первый телескоп Галилея, однако до сих пор никто не видел в телескоп диск звезды. Правда, звезда при рассматривании в телескоп, особенно при сильном увеличении, кажется кружочком, но диаметры этих кружочков одинаковы для всех звезд, чего не могло бы быть, если бы мы видели реальный диск звезды, — ведь звезды различны по величине и находятся на различных расстояниях от нас. К тому же при увеличении диаметра объектива телескопа диаметр этих кружочков уменьшается, звезды становятся ярче, но меньше.

В оптике доказывается, что видимые нами диски звезд ничего общего с действительными размерами звезд не имеют и являются следствием самой природы света, получаются вследствие «дифракции» света. Границу видимости в телескоп ставит сам свет.

Но, как часто бывает в науке, те же самые свойства света, умело использованные, дали возможность измерить действительные диаметры звезд.

Немного о свойствах света

Электромагнитная теория света учит, что световой луч можно рассматривать как совокупность электромагнитных колебаний — волн, распространяющихся в пространстве с колоссальной скоростью — 300 000 км/сек. Колебания имеют определенную периодичность во времени и в пространстве. Это значит, во-первых, что они совершаются с определенной частотой — порядка 600 биллионов раз в секунду для видимого света, во-вторых. что имеются точки вдоль луча на некотором определенном расстоянии друг от друга, которые находятся в одинаковом состоянии. Расстояние между двумя такими точками называется длиной волны и для видимого света составляет около 0,0005 мм. Частота и длина волны определяют цвет луча.

Чтобы лучше понять дальнейшие явления, представим себе волны на поверхности воды. Они бьют о берег определенное число раз в минуту, — это их частота; гребень за гребнем идет на некотором постоянном расстояния,— это длина волны. И так же, как посредине между двумя гребнями на воде лежит впадина, — между двумя точками луча, разделенными расстоянием в одну длину волны, расположится точка, отклонение которой от состояния равновесия будет противоположно отклонению двух первых точек. Принято говорить, что две точки на расстоянии длины волны находятся в одинаковых фазах, а на расстоянии полуволны — в противоположных фазах, как гребень и впадина волн на воде (фазой называется величина, характеризующая состояние колеблющейся точки в данный момент). Нужно помнить, что сходство снеговых воли и волн на воде относится лишь к закономерностям, определяющим то и другое явление, и не пытаться представать себе световой луч как механическое «дрожание» какого-то вещества, — такое расширение аналогии было незаконно и неверно.

Если на пути водяных воли лежит какое-нибудь препятствие, например камень, то можно заметить (рис. 1), что волны как бы огибают его края и заходят за камень. То же происходит и со световыми волнами. Встречая какое-либо препятствие, волны света огибают его края, отклоняясь от прямолинейного распространения; однако, так как величина препятствия всегда во много раз больше длины волны, заметить эти «загнувшиеся» лучи не так легко. Они и дают явление дифракции света — появление света там, где его не могло бы быть, если бы луч был геометрической прямой линией. Так, смотря в микроскоп на тень от острого края экрана, можно заметить светлые и темные полосы, в центре тени от маленького кружочка можно увидеть светлую точку, образованную световыми волнами, обогнувшими края кружка, и т. д.

Дифракция происходит и с лучами света звезды, входящими в объектив телескопа. Крайние лучи пучка испытывают отклонение («загибание») на краю оправы объектива и дают в фокусе телескопа маленький диск, тем меньший, чем больше диаметр объектива при данном его фокусном расстоянии. Следовательно, если источник света даже геометрическая точка в полном смысле слова, то телескоп из-за дифракции всегда покажет его в виде маленького кружочка. И эти «дифракционные диски» не дают возможности видеть действительные диски звезд.

Второе явление, существенное для нас,— интерференция света. Представим себе, что в берег бьют две системы волн равной силы и одинаковой частоты, например волны, разбегающиеся от двух орошенных в воду камней. В некоторые точки берега гребни обеих волн будут приходить одновременно, волны сложатся, и колебание воды будет сильным; в другие, наоборот, гребень одной волны будет приходить одновременно с впадиной другой, волны уничтожат друг друга, и вода останется спокойной. В промежуточных точках волны будут в разной степени усиливаться и ослабляться.

То же явление, только более осложненное, будет происходить и с световыми волнами. При некоторых определенных условиях, освещая белый экран двумя лучами одного и того же цвета, можно получить «интерференцию» света. В тех точках, где колебания приходят в одинаковых фазах, они должны складываться, и яркость света повышаться; в других точках экрана, где волны обоих лучей приходят в противоположных фазах, с разностью в полволны, они взаимно уничтожатся, и два луча, сложившись, дадут темноту.

Такой опыт сделал около 1820 г. французский физик Френель. Он поставил стеклянную призму Р (рис. 2) с очень тупым углом между источником света S и белым экраном Е. На экране вместо ровного освещения получилась картина, состоящая из чередующихся светлых и темных полос. Произошло это потому, что призма разделила пучок лучей на два одинаковых по составу пучка, как бы идущих от двух воображаемых источников, S1 и S2. Точка а находится на равном расстоянии от обоих этих источников, «гребни» и «впадины» (говоря чисто условно, пользуясь аналогией с волнами воды) в обоих лучах совпадают, колебания складываются и усиливают друг друга; будет наблюдаться яркий свет. Иначе обстоит дело в точке b: она на половину длины волны ближе к S2, чем к S1, колебания приходят в противоположных фазах, «гребни», накладываясь на «впадины», взаимно уничтожаются, колебаний нет, и наблюдается темная полоса. Рассуждая так же, найдем, что по обе стороны светлой центральной полосы а будут чередоваться светлые и темные полосы, что и подтверждается на опыте.

Так будет наблюдаться явление в том случае, если все лучи источника света имеют одну и ту же длину волны. Обычный белый свет состоит из смеси лучей различных цветов, т. е. с разными длинами волн. Лучи каждого цвета дадут свою систему светлых и темных полос, системы эти наложатся друг на друга, и на экране по обе стороны от центральной белой полосы расположатся полосы, окрашенные в разные цвета.

Каковы же диаметры звезд?

Представьте себе, что вы смотрите на шарик диаметром в 1 мм с расстояния 206 м. Рассмотреть его, конечно, не удается, диаметр шарика будет виден под углом в одну секунду дуги.

Современные большие телескопы могут при большом увеличении показать отдельно две светящиеся точки на угловом расстоянии в десятые доли секунды. Можно рассчитать, что диаметр дифракционного диска звезды у наибольшего в мире 2,5-метрового рефлектора (отражательный телескоп с диаметром главного зеркала 2,5 м), находящегося на обсерватории Моунт-Вильсон (США, Калифорния) равен теоретически О’’45. И так как даже в этот телескоп все звезды кажутся одинаковыми, — реальные угловые диски их, очевидно, еще меньше.

Угловой диаметр звезд можно оценить косвенными методами. Есть звезды, меняющие свою яркость строго периодически, вследствие того что эти звезды двойные и более яркая затмевается менее яркий спутником при каждом обороте пары вокруг общего центра тяжести. Исследование закона изменения яркости этих звезд в соединении с спектроскопическими наблюдениями скоростей их движения дает возможность определить линейные размеры обеих звезд, а отсюда, если известно расстояние до звезды, — вычислить ее угловой диаметр.

Исследуя распределение энергии в звездном спектре, можно узнать температуру звезды; измерив полное излучение, приходящее от звезды на Землю, можно вычислить угол, под которым виден диаметр звезды, даже и не зная его расстояния.

Оказалось, что видимые диаметры даже самых больших звезд всего около 0″,05,— того же размера, что и дифракционный диск у 2,5-метрового рефлектора. Поэтому-то даже в величайший телескоп мира все звезды кажутся одинаковыми. Лишь с новым гигантским телескопом, который строится сейчас в Америке и будет иметь главное зеркало диаметром 5 м, можно будет увидеть, что некоторые звезды больше других, увидеть реальные диски звезд.

Дифракционный диск этого телескопа будет иметь диаметр 0″,022.

Но еще 70 лет тому назад, в 1868 г., Физо указал на возможность применения явления интерференции света к измерению диаметров звезд. Основная идея метода очень проста. Представим себе, что перед призмой Френеля (рис. 2) расположен не один, а два источника света. Каждый из них дает свою систему светлых и темных полос на экране. Передвигая источники света, можно расположить их так, что светлые полосы от одного источника лягут на темные полосы от другого, и наоборот. На экране получится ровное освещение. Зная данные взятой для опыта установки, можно вычислить угол, под которым видно из центра экрана расстояние между источниками в момент исчезновения полос.

Подобным образом можно поступить и с телескопом. Если на объектив телескопа одеть крышку с двумя отверстиями (рис. 3), то лучи света, пройдя объектив, дадут прежде всего обычное изображение звезды, дифракционный диск. Но, кроме того лучи идущие от обоих отверстий, встречаясь в главном фокусе телескопа, будут интерферировать, как лучи за призмой Френеля и дадут полосы на диске звезды. Закрыв одно из отверстий, увидим, что диск останется, но полосы на нем исчезнут. Расстояния между полосами тем меньше, чем дальше друг от друга отверстия в диафрагме. Такой прибор называется звездным интерферометром.

Предположим теперь, что звезда двойная, т. е. на самом деле там две, расположенные настолько близко, что они даже в телескоп видны как одна. Каждая из звезд даст свою систему полос на диске; системы эти наложатся одна на другую, Меняя расстояние между отверстиями в диафрагме, можно подобрать его так, что полосы на диске перестанут быть видимыми: светлые полосы, даваемые одной звездой, совпадут с темными, даваемыми другой, и диск будет освещен равномерно. Зная расстояние между отверстиями в диафрагме и фокусное расстояние телескопа, можно будет вычислить угол, под которым видно расстояние между составляющими двойной звезды, хотя различить их отдельно и не удастся.

Физо сделал и следующий шаг. Рассуждения его, на самом деле несколько более сложные, можно упрощенно изложить так: если звезда не точка, а маленький диск, то ее можно представить себе как бы состоящей из двух «полудисков» и рассматривать далее каждый из них как самостоятельный источник света, дающий свою систему полос. Тогда, меняя расстояние между отверстиями в диафрагме телескопа, можно добиться исчезновения полос, равномерного освещения дифракционного диска звезды. По расстоянию отверстий в диафрагме можно вычислить расстояние между «центрами тяжести» обоих «полудисков», а отсюда по формулам геометрии найти диаметр звезды.

Идеи Физо были использованы Стефеном.

На 80-сантиметровом рефракторе обсерватории в Марселе он наблюдал интерференционные полосы от многих звезд, но ни разу не смог добиться их исчезновения. Затем работы Физо и Стефена были забыты.

Идеи эти высказал снова в 1890 г. известный американский физик Майкельсон. Пользуясь различными телескопами, он показал, что с помощью интерференции можно измерять расстояния между составляющими очень тесных двойных звезд, диаметры спутников Юпитера и т. д. Результаты хорошо совпадали с результатами обычных измерений точным микрометром. Однако астрономы не сразу обратили внимание на результаты Майкельсона. Лишь около 1920 г. эти опыты были повторены на обсерватории Моунт-Вильсон, сначала на полутораметровом, а затем на 2,5-метровом рефлекторах. Удалось измерить расстояния в некоторых очень тесных звездных парах, например расстояние между составляющими двойной звезды Капеллы, равное всего 0»,045.

Но обнаружилось, что даже при расположении отверстий диафрагмы на краях 2,5-метрового зеркала полосы на дифракционных дисках звезд не исчезают, — расстояние это еще слишком мало. Объектива или зеркала диаметром более 2,5 м тогда не существовало, нет еще и сейчас, и, казалось бы, дальше идти некуда.

Однако Майкельсон чрезвычайно просто и остроумно решил задачу, как бы искусственно увеличив размеры 2,5-метрового зеркала еще в 2,5 раза. На рис. 4 показан ход лучей в звездном интерферометре Майкельсона, расположенном на главном телескопе обсерватории Моунт-Вильсон. На стальной балке длиною 6 м, укрепленной на конце рефлектора, расположены два плоских зеркала 1 под углом 45° к оси телескопа. Лучи от этих зеркал идут к двум плоским зеркалам 2, главному вогнутому зеркалу рефлектора 3 и после отражения от выпуклого зеркала 4 и плоского 5 в окуляр 6. Встречаясь в фокусе телескопа, лучи дают ту же картину, что и при двух отверстиях в крышке на объективе, т. е. дифракционный диск и систему полос на нем. Расстояние между зеркалами может меняться от 2,5 до 6 м.

13 декабря 1920 г. давно поставленная цель была достигнута. Первой звездой, для которой удалось добиться исчезновения полос (рис. 7) при расстоянии между зеркалами интерферометра в 3 м, была альфа Ориона (Бетельгейзе). Для ее диаметра получилась величина 0″,047, в хорошем согласия с теоретическими подсчетами. Тем же интерферометром были измерены видимые диаметры еще нескольких звезд.

Но даже расстояние 6 м между зеркалами интерферометра слишком мало для огромного большинства звезд. Так как для измерения диаметров звезд не важно, чтобы главное зеркало телескопа имело максимальный диаметр, а существенно расстояние между подвижными зеркалами, — в 1930 г. был построен новый интерферометр с главным зеркалом диаметром 100 см и балкой длиной 15 м (рис. 8). Этот интерферометр уже является не насадкой на телескоп, а вполне самостоятельным инструментом. С ним при помощи улучшенной методики наблюдений (наблюдалось не только расстояние, при котором полосы исчезают, но и оценивалась степень видимости полос при других расстояниях между зеркалами путем сравнения с искусственными полосами) удалось измерить диаметры довольно большого числа звезд. Часть результатов этих измерений приведена в табличке. Можно заметить, что согласие между наблюденными и вычисленными теоретически диаметрами звезд очень хорошее.

Разумеется, что сейчас могут быть измерены диаметры лишь наиболее близких к нам и очень больших звезд, — диаметры остальных звезд значительно меньше и недоступны даже 15-метровому интерферометру. В последней строке таблицы приведена Вега, одна из наиболее ярких звезд нашего северного неба. Чтобы измерить ее диаметр, пришлось бы раздвинуть зеркала интерферометра на 50 м.

В последнем столбце таблички приведены действительные диаметры звезд, причем диаметр Солнца принят за единицу. Действительные размеры звезды легко вычислить если известен ее угловой диаметр и расстояние до нее. Из этого столбца видно, как огромны некоторые звезды. Если бы, например, Антарес оказался на месте нашего Солнца, то не только орбита Земли, но и орбита Марса лежала бы внутри него (рис. 9); Марс, среднее расстояние которого от Солнца равно 228 млн. км, двигался бы внутри Антареса. Зная размеры Антареса и его массу, можно вычислить среднюю плотность его вещества. И оказывается что плотность эта в три миллиона раз меньше плотности вещества нашего Солнца.

Для Бетельгейзе в табличке приведены два значения величины измеренного диаметра, из которых одно в 1,5 раза более другого. Это не ошибка в измерениях. Уже давно известно, что Бетельгейзе — переменная звезда, меняющая яркость и цвет Измерения показывают, что, по-видимому, меняется и ее диаметр — звезда «пульсирует» то сжимаясь, то расширяясь. Но для полной разгадки происходящих на этой звезде явлений необходимы длительные и тщательные наблюдения.

Спросите Итана: почему звёзды бывают разных размеров?

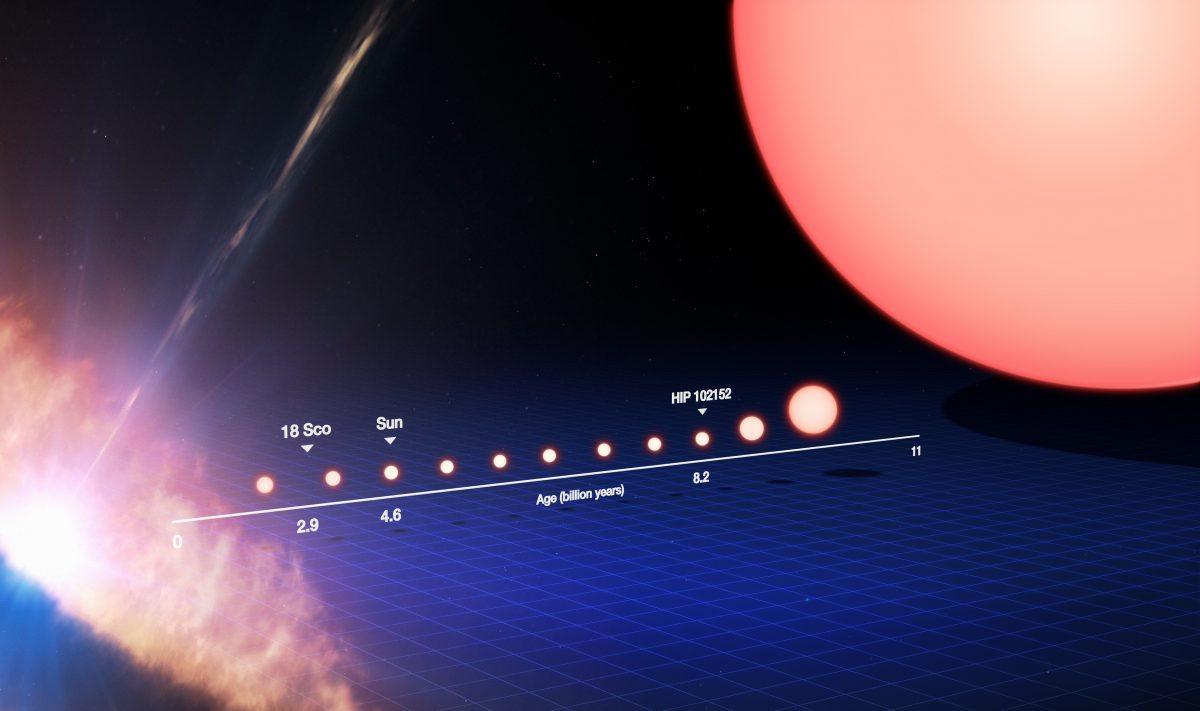
Даже единственная звезда, например, наше Солнце, в течение своей жизни будет сильно менять размер. Чем объяснить огромное разнообразие звёздных размеров, наблюдаемых нами сегодня?

Если сравнить планету Земля с Солнцем, окажется, что необходимо поставить 109 земель одну на другую, чтобы заполнить Солнце с одной стороны до другой. Однако же существуют звёзды, по размеру гораздо меньшие, чем Земля — и гораздо большие, чем даже орбита Земли вокруг Солнца! Как это возможно, и что именно определяет размер звезды? Наш читатель задаёт вопрос на эту тему:

Почему звёзды могут вырастать до разных размеров? От размеров чуть больше Юпитера до размеров, превышающих орбиту Юпитера?

Вопрос этот сложнее, чем кажется, поскольку, по большей части размеры звёзд нам не видны.

Изображение с телескопа, полученное в результате глубокого сканирования, на котором видны звёзды в ночном небе, демонстрирует нам звёзды разных цветов и яркости, но все видимые звёзды кажутся там точками. Разница в их размерах — это лишь оптические иллюзии, появляющиеся из-за особенностей работы камер.

Даже в телескоп большая часть звёзд кажется точками света из-за невероятных расстояний от нас до них. Их различия в цвете и яркости легко увидеть, но размер — это совершенно другое дело. Объект определённого размера на определённом расстоянии будет иметь, что называется, определённый угловой диаметр: видимый размер, занимаемый им на небе. Ближайшая солнцеподобная звезда, Альфа Центавра А, расположена всего в 4,3 световых годах от нас, и на 22% больше Солнца по радиусу.

Две похожие на Солнце звезды, Альфа Центавра А и В, расположены в 4,37 световых годах от нас, и вращаются друг вокруг друга на расстоянии, находящемся где-то между радиусами орбит Сатурна и Нептуна. Но даже на фото с Хаббла они выглядят просто как перенасыщенные источники света — диска не видно.

Однако же для нас она имеет угловой диаметр в 0,007″ (угловых секунд), с учётом того, что одна угловая минута вмещает 60 угловых секунд, 1 угловой градус — 60 угловых минут, а полный круг — 360°. Даже у телескопа типа Хаббла максимальное разрешение составляет порядка 0,05″; мало какие звёзды Вселенной можно детально рассмотреть при таком разрешении. Обычно это расположенные близко гиганты вроде Бетельгейзе или R Золотой Рыбы, одни из самых крупных звёзд по угловому диаметру на всём небосводе.

Радиоизображение очень большой звезды, Бетельгейзе, на которое наложен размер оптического диска. Это одна из очень немногих звёзд, которую с Земли можно увидеть не просто, как точечный источник света

К счастью, существуют непрямые измерения, позволяющие нам подсчитывать физические размеры звёзд — причём очень надёжные. Если взять сферический объект, раскалённый до такого состояния, что он начинает испускать излучение, то общее количество испущенного звездой излучения определяется только двумя параметрами: температурой объекта и его физическим размером. Причиной этому то, что единственное место звезды, излучающее свет во Вселенную — это его поверхность, а поверхность сферы всегда вычисляется по формуле 4 π r², где r — радиус. Если можно измерить расстояние до звезды, её температуру и видимую яркость, можно узнать её радиус (и, следовательно, размер), просто применив законы физики.

g
Увеличенное изображение красного гиганта UY Щита, в телескопе обсерватории Резерфорда. В большинство телескопов её видно только как яркую точку, но это — крупнейшая из известных человечеству звёзд на сегодня

Осуществляя наблюдения, мы видим, что некоторые звёзды имеют размер в десятки километров, а другие могут в 1500 раз превышать по размеру Солнце. Из сверхгигантских звёзд самой крупной будет UY Щита, с диаметром в 2,4 млрд км, что больше, чем орбита Юпитера вокруг Солнца. Но такие экстремальные примеры звёзд не относятся к звёздам, похожим на Солнце. Конечно, самым распространенным типом звезды будет звезда из главной последовательности, такая, как наше Солнце: звезда, состоящая в основном из водорода, получающего энергию при помощи синтеза гелия из водорода в своём ядре. И у таких звёзд тоже встречается огромное разнообразие размеров, определяемой их массой.

Молодой регион звёздного формирования в нашем Млечном пути. При гравитационном коллапсе газовых облаков протозвёзды разогреваются и становятся плотнее, а в итоге в их ядре запускается синтез

Когда формируется звезда, гравитационное сжатие превращает потенциальную эенергию в кинетическую энергию движения частиц в ядре звезды. Если массы достаточно, температура может вырасти до значений, позволяющих запустить ядерный синтез во внутренних частях звезды, и водород начнёт путём цепной реакции превращаться в гелий. В звезде небольшой массы только небольшая часть в самом центре перейдёт этот рубеж в 4 000 000 K и займётся синтезом, и то с очень малой скоростью. С другой стороны, крупные звёзды могут в сотни раз превышать по массе Солнце, и достигать температур в десятки миллионов градусов в ядре, синтезируя гелий из водорода со скоростями, в миллионы раз превышающей те, что свойственны Солнцу.

Современная спектральная классификация звёзд Моргана-Кинана, с температурными режимами, указанными сверху в кельвинах. Большая часть (75%) звёзд принадлежит к классу М, и только 1 из 800 достаточно тяжёлая для того, чтобы стать сверхновой

У наименьших звёзд будут наименьшие исходящие потоки и давление излучения, а у наикрупнейших они будут самыми крупными. Это исходящее излучение и энергия удерживают звезду против гравитационного схлопывания, но вас может удивить, что диапазон этих значений довольно узок. У самых лёгких звёзд, например, Проксима Центавра или Вольф 1055 В, размер не превышает 10% от солнечного — они немного больше Юпитера. А самая массивная из известных звёзд, голубой гигант R136a1, в 250 раз больше Солнца по массе — и лишь в 30 раз больше его по диаметру. Если звезда занимается синтезом гелия из водорода, то её размер не будет сильно варьироваться.

Скопление RMC 136 в центре туманности Тарантул в соседней галактике Большое Магелланово Облако, содержит самые массивные из известных звёзд

Но не всякая звезда производит синтез гелия из водорода! Самые мелкие звёзды вообще не занимаются синтезом, а самые крупные находятся на гораздо более энергетической фазе своей жизни. Типы звёзд можно разбить по размерам, и таким образом мы можем получить пять общих классов:

• Нейтронные звёзды: масса этих остатков сверхновых будет равна от одной до трёх солнечных, но по сути они сжаты в гигантское атомное ядро. Они испускают излучение, но в крохотных количествах из-за небольшого размера. Размер типичной нейтронной звезды — 20-100 км.
• Белые карлики: формируются, когда у солнцеподобных звёзд заканчивается в ядре гелиевое топливо, и внешние слои разлетаются, а внутренние — сжимаются. Обычно масса белого карлика составляет от 0,5 до 1,4 массы Солнца, но размером они с Землю: порядка 10000 км в поперечнике, и состоят из сильно сжатых атомов.
• Звёзды главной последовательности: сюда входят красные карлики, звёзды солнечного типа, голубые гиганты, о которых мы уже говорили. Их размер варьируется от 100 000 км до 30 000 000 км, у них довольно большой разброс размеров, но даже самая крупная из них на месте Солнца не поглотила бы и Меркурий.
• Красные гиганты: что происходит, когда в ядре кончается водород? Если звезда — не красный карлик (а в этом случае она просто превратится в белого карлика), гравитационное сжатие разогреет ядро так сильно, что в нём начнётся синтез углерода из гелия. А этот процесс выделяет гораздо больше энергии, чем синтез с участием водорода, из-за чего звезда чрезвычайно разбухает. Простая физика в том, что сила, действующая наружу (излучение) на краю звезды должна сбалансировать силу, действующую внутрь (гравитацию), чтобы поддерживать её в стабильном состоянии — так что с гораздо большей силой, действующей наружу, размер звезды просто сильно увеличится. В диаметре красные гиганты обычно бывают от 100 до 150 млн км: достаточно большие для того, чтобы поглотить Меркурий, Венеру, и, возможно, Землю.
• Сверхгиганты: самые массивные звёзды проходят дальше, за пределы синтеза гелия, и начинают синтезировать ещё более тяжёлые элементы, такие, как углерод, кислород и даже кремний и серу. Судьбой им предначертано стать сверхновыми и/или чёрными дырами, но до этого они разбухают до огромных размеров, и могут простираться на миллиард километров и более. Это самые крупные звёзды, как, например, Бетельгейзе, и, заменив Солнце, они поглотили бы все скалистые планеты и пояс астероидов, а крупнейшие поглотили бы даже Юпитер.

Сегодня Солнце весьма мало по сравнению с гигантами, но вырастет до размеров Арктура в фазе красного гиганта. Но до чудовищного сверхгиганта типа Антареса Солнцу никогда не добраться

Такие мелкие остатки крупных звёзд, как нейтронные звёзды и белые карлики, светят так ярко и так долго потому, что заключённая в них энергия может убежать только через их крохотную поверхность. Но размер других звёзд определяется простым балансом: сила от исходящего излучения на поверхности должна сравняться с давлением гравитации. Увеличение силы излучения раздувает звёзды до большего размера, а самые крупные звёзды раздуваются до миллиардов километров.

Если расчёты верны, Солнце, когда оно раздуется до красного гиганта, не должно поглотить Землю. Но она всё равно очень сильно разогреется.

По мере старения Солнца его ядро разогревается, и со временем оно расширяется и становится горячее. Через пару миллиардов лет оно станет достаточно горячим для того, чтобы вскипятить океаны Земли — если мы не предпримем что-нибудь, чтобы мигрировать нашу планету на безопасную удалённую орбиту. За достаточно большой промежуток времени и Солнце раздуется до красного гиганта. На несколько сотен миллионов лет оно станет больше и ярче, чем некоторые из самых массивных звёзд. Но не обманывайтесь этим впечатляющим фактом: в астрономии размер имеет значение, но это не единственный параметр. Как самые мелкие нейтронные звёзды, так и самые крупные сверхгиганты, а также как и многие белые карлики и звёзды главной последовательности всё равно будут более массивными, чем Солнце в виде красного гиганта!

Итан Сигель – астрофизик, популяризатор науки, автор блога Starts With A Bang! Написал книги «За пределами галактики» [Beyond The Galaxy], и «Трекнология: наука Звёздного пути» [Treknology].

ЧаВо: если Вселенная расширяется, почему не расширяемся мы; почему возраст Вселенной не совпадает с радиусом наблюдаемой её части .

В интерференционном опыте Юнга (см. 16) источниками света служат две щели, освещаемые некоторым источником света, т. е. схема опыта в существенных своих чертах совпадает со схемой рис. 4.20. Если разность хода сравнительно невелика, так что наблюдаются полосы низкого порядка, то контрастность интерференционных полос будет определяться главным образом степенью пространственной когерентности освещения щелей. Аналогично положение и в случае звездного интерферометра Майкельсона (см. 45), где частичная пространственная когерентность освещения щелей интерферометра служит средством для измерения угловых размеров звезд.  [c.105]

Ответ. I) 500 м/с Дх КбХ =10 м, где 6 = 3,8-105 км — среднее расстояние до Луны. Метод пригоден, когда угловые размеры звезд лежат примерно в интервале от 10 до 10″ угловой секунды.  [c.287]

Угловые размеры звезд 486  [c.571]

Проведенные до сих пор рассуждения относятся к наблюдению протяженных объектов. Наблюдение точечных источников света связано с некоторыми особенностями. Типичный пример точечного источника — звезда. Угловые размеры звезд настолько малы, что даже при большом увеличении а < 1. При любом  [c.127]

Майкельсон применил интерферометрическое наблюдение для оценки малых угловых расстояний между двойными звездами, а также для оценки углового диаметра звезд. Метод Майкельсона, равно как и применение его к определению размеров субмикроскопических частичек, будет изложен ниже (см. 45). Наконец, понятно, что интерференционные методы, позволяющие с огромной точностью определять длину волны, могут служить для самых тонких спектроскопических исследований (тонкая структура спектральных линий, исследование формы и ширины спектральных линий, ничтожные изменения в строении спектральных линий). Интерференционные спектроскопы, их достоинства и недостатки будут обсуждены вместе с другими спектральными приборами (дифракционная решетка, призма) в 50.  [c.149]

Во всяком реальном опыте источник имеет конечные размеры. Допустим, что угловой размер источника равен 2а. Это значит, что если мы производим опыт с удаленным источником (звезда. Солнце), то 2а есть угловой размер его, наблюдаемый из точки,  [c.179]

Э своем параллактическом движении должна описывать эллипс, угловые размеры которого тем больше, чем меньше расстояние до звезды.  [c.420]

Возвращаясь к снижению видности полос, вызванному увеличением размера источника, заметим, что этот эффект служит основой измерения с помощью звездного интерферометра Майкельсона угловых диаметров звезд, слишком малых для измерений обычным способом на телескопе. Этот метод описывается в гл. 6, где показано также, каким образом изменения видности полос в зависимости от расстояния между двумя апертурами позволяют получить информацию о распределении яркости источника.  [c.18]

Сразу же становится очевидным пример возникновений этой картины при получении изображения звезды с помощью астрономического телескопа, и Эри исследовал ее детали именно для такого случая. Фактически для земного наблюдателя звезда находится на бесконечности, и поэтому ее изображение образуется в задней фокальной плоскости объектива телескопа, где оно изучается с помощью окуляра. Поскольку ее угловой размер (угол, под которым ее диаметр виден с Земли) чрезвычайно мал, ее изображение должно быть близким к точечному. Однако фронты световых волн от звезды прерываются апертурой  [c.32]

Чтобы создать представление об использовании интерференции как непрямого способа применения телескопа для измерения угловых размеров астрономических объектов, рассмотрим рис. 6.1, а. На нем представлен апертурный экран, имеющий две щели, перпендикулярные рисунку и размещенные перед линзами телескопа (аналогичную схему нетрудно осуществить и для отражательного телескопа). Волновые фронты поступают от всех точек видимой части поверхности звезды, имеющей угловой диаметр фо (стягиваемый ею угол с вершиной у Земли). На рисунке показаны только граничные фронты волн Wi, испущенный на одном краю диска, и Wj от противоположного края. В фокальной плоскости линз образуется непрерывная система интерференционных полос типа os (источник считается некогерентным) от полос, вызываемых Wj, до полос, определяемых W2. Окончательным результатом является картина, показанная на рис. 6.1,6 с видностью < 1. Отметим, что расстояние между полосами остается таким же, как если бы источник был точечным, а именно A=fk/D [уравнение (1.11)]. На практике интенсивность картины полос снижается с той и другой стороны от оси (ср. с выборкой на дифракционной картине от одиночной щели в разд. 2.4). Мы можем пренебречь этим понижением, если щели узкие и, в частности, если наблюдения, как случается на практике, ограничены центральной областью картины полос.  [c.123]

Таким образом, идея состояла в том, что если флуктуации интенсивности на двух близких антеннах коррелировали, то уменьшение корреляции (отсюда корреляционный интерферометр) с увеличением базы позволяло бы определять угловой размер источника (это был бы аналог метода Майкельсона, использующий интенсивности для измерения диаметров оптически видимых звезд). Тогда трудность, связанная с взаимной нестабильностью далеко разнесенных гетеродинов, была бы преодолена. (В то время не были разработаны атомные часы, которые сейчас используются в интерферометрии с длинными базами.)  [c.160]

Угловые размеры почти всех звезд много меньше углового разрешения даже самых больших телескопов. Поэтому, как уже отмечалось выше, изображение звезды в фокальной плоскости объектива неотличимо от изображения точечного источника и представляет собой дифракционный кружок. Диаметр этого кружка настолько мал, что при использовании нормального увеличения он, как и сама звезда, для глаза неотличим от точечного источника. Это значит, что размер дифракционного пятна на сетчатке глаза не зависит от того, наблюдается ли звезда в телескоп или непосредственно. Но световой поток, приходящийся на это дифракционное пятно, и, следовательно, освещенность изображения при наблюдении в телескоп во столько раз больше, чем при наблюдении невооруженным глазом, во сколько раз площадь отверстия объектива больше площади зрачка глаза. В то же время освещенность изображения протяженных предметов (фона), как было показано в 7.5, не изменяется. Этим объясняется, почему в телескоп звезды на фоне неба видны и днем.  [c.370]

Имеется глубокая физическая аналогия между парными корреляциями тождественных частиц, образуемых в ядерных взаимодействиях, и корреляциями фотонов, испускаемых оптическими источниками (в частности звездами), позволяющими измерить их угловые размеры.  [c.98]

Из астрономических наблюдений хорошо известно, что планеты мерцают слабее звезд, находящихся на том же зенитном расстоянии. Этот эффект во многом схож с ослаблением мерцания за счет усредняющего действия объектива. Обозначим через 7 угловой размер планеты. Тогда в точку наблюдения приходит пучок плоских волн от различных точек диска с угловым размером у. На границе преломляющей атмосферы расстояние между  [c.378]

Из астрономических данных хорошо известно, что планеты, имеющие в отличие от звезд конечный угловой размер, мерцают слабее, чем звезды. Различные точки диска планеты можно рассматривать как не-  [c.603]

Пусть d — расстояние двойной звезды тогда видимый угловой размер а большой полуоси орбиты определяется как  [c.448]

Следующие данные характеризуют двойную систему Геркулеса орбитальный период 34,4 года, параллакс 0,10, угловой размер большой полуоси относительной орбиты 1,35, угловой размер большой полуоси орбиты главной звезды относительно центра масс 0,57″. Вычислите массы обоих компонентов в единицах массы Солнца.  [c.476]

Изложите идею опыта Брауна—Твисса по интерференции интенсивностей. Как таким методом можно оценить время когерентности и угловые размеры звезд  [c.457]

Принимая звезду за равномерно светящийся диск, можно теоретически рассчитать распределение освещенности в дифракционной картине. Сравнивая его с распределением освещенности, найденным экспериментально, можно опреде-л 1ть угловой диаметр звезды, что и было фактически выполнено в 1946 г. Уайт-Я ордом для четырех звезд на стодюймовом рефлекторе Маунт-Вильсоновской обсерватории. Оценить угловые размеры звезд, для которых может быть пригоден этот метод.  [c.287]

Угловые размеры бф, даваемые формулами -<60,2) и (60.3), совпадают с разрешаемым расстоянием телескопа. Однако, если угловой размер звезды порядка (60.2) или (60.3), то ее изображение в телескопе настолько мало отличается от изображения точечного источника, что непосредственное измерение диаметра звезд с помощью телескопа становится практически непригодным. Интерференционный же метод дает в этом случае еще хорошую точность. Однако, чтобы интерференционные полосы исчезли, а это необходимо по идее самого интерферен-иионного метода, нужен телескоп с большим диаметром объектива, Физо указал  [c.381]

Для иллюстрации этого основного положения остановимся на интересных исследованиях, целью которых было определение угловых размеров некоторых звезд ( красных гигантов и др.). История развития этих исследований восходит к созданию Май-кельсоном звездного интерферометра . Рассмотрим идею этого классического опыта и последующих исследований.  [c.335]

Для звезд, лежащих в плоскости эклиптики, этот эллипс вырождается в прямую, а для звезд у полюса — в окружность. Брадлей действительно обнаружил подобное смещение. Но большая ось эллипса оказалась для всех звезд имеющей одни и те же угловые размеры, а именно 2а = 40″,9, что значительно больше ожидаемого параллактического смещения даже для ближайшей к.Солнцу звезды наконец, направление наблюденного смещения оказалось перпендикулярным к ожидаемому вследствие параллакса (см. рис. 20.2, б). Брадлей объяснил (1728 г.) наблюденное явление, названное им аберрацией света, конечностью скорости распространения света и использовал его для определения этой скорости. Годичный параллакс, гораздо менее значительный и зависящий от расстояния до  [c.420]

В общем случае, когда звезда расположена на угловом расстоянии б от плоскости эклиптики, аберрационная траектория звезды представляет собой эллипс, большая полуось которого имеет угловые размеры с д, а малая — осц sin б. Именно такой характер и носило кажущееся смещение звезд по наблюдению Брадлея. Определив из наблюдений ад и зная Но, можно найти с. БраДлей нашел с = 308000 км/с. В. Я- Струве (1845 г.) значительно улучшил точность наблюдений и получил ао = 20″,445. Самые последние определения дают а = = 20″,470, чему соответствует с = 299 900 км/с.  [c.422]

В 1725—1728 гг. Брадлей произвел измерения годичного параллакса неподвижных звезд. Наблюдая за одной из звезд в созвездии Дракона, Брадлей обнаружил, что ее положение менялось в течение года. За это время она описала небольшую окружность, угловые размеры которой были равны 40,9″. В общем случае в результате движения Земли по орбите звезда описывает эллипс, большая ось которого имеет те же угловые размеры. Для звезд, лежащих в плоскости эклиптики ), эллипс вырождается в прямую, а для звезд у полюса — в окружность.  [c.198]

В то время мы знали лишь то, что их угловые размеры не превышают существенно несколько минут дуги, но не располагали никакими данными о том, насколько они могут быть малы. Если, как полагали некоторые, они оказались бы такими же малыми, как видимые звезды, то для метровых волн потребовалось бы разместить приемные станции на противоположных концах Земли. Можно ли создать радиоинтерферометр с базой, которая при необходимости могла бы простираться на десятки, сотни или даже тысячи километров Непосредственная техническая трудность в реализации существующих решений была связана с обеспечением когерентности гетеродинов в двух удаленных точках, и я начал размьпплять, действительно ли это условие необходимо. Может быть, принимаемые в двух точках волны удастся сравнивать каким-ли-бо другим способом Для примера я вообразил простой детектор, который демодулирует волны от источника и отображает их в виде обыч-  [c.159]

Прибором, принципиально пригоднь1м ддя этой цели, является интерферометр Рэлея (рис. 118, а). Из плоской волны, идущей от отдаленной звезды, в Аг и Аг выделяются два параллельных пучка света, которые, выйдя из прибора, дают в фокальной плоскости Р линзы Ь дифракционную картину, позволяющую измерить угловой размф источника. Однако применить йнтерферометр Рэлея для измерения угловых размеров астрономических объектов оказалось невозможным. Интер- ференционные полосы получаются очень узкими и проводить измерение трудно. Большие осложнения также связаны с обеспечением точности взаимного положения трубок на больших расстояниях между ними.  [c.167]

Первой звездой, угловой размф которой был измерен таким способов была Бетельгей (ф = 0,047″). Расстояние до этой звезды было известно по земному параллаксу. По известным угловым размерам и расстоянию «можно рассчитать линейные размеры звезды. Диаметр Бетельгейзе оказался примерно в 300 раз больше диаметра Солнца. Так же были измерены диаметры некоторых других звезд и объектов Солнечной системы.  [c.168]

ХОДИТ разрешающую силу глаза в 6000/4 = 1500 раз. Теоретическое разрешаемое расстояние составляет 35″/1500 = 0,023″. Для второго по величине телескопа-рефлектора Маунт-Паломарской обсерватории с диаметром зеркала 5 м теоретическое разрешаемое расстояние равно 0,028″. Разрешающей способности таких гигантских телескопов достаточно, чтобы изображения звезд с наибольшими угловыми размерами получадись уже в виде дисков, подобно изображениям планет.  [c.364]

Надо отметить, что с увеличением базы возрастают технические трудности, обусловленные внесением нерегулярно меняющейся разности фаз на пути от антенн к детектору. Для устранения этого недостатка в радиоинтерферометре Брауна и Твисса сигналы, принятые антеннами, детектируются независимо. Измеряется корреляция флуктуирующих интенсивностей этих сигналов в зависимости от расстояния между антеннами. По этим данным находятся угловые размеры ио точника. Браун и Твисс показали, что аналогичное устройство может работать также и в видимой области спектра. Свет от звезды фокусируется двумя вогнутыми зеркалами на два фотоэлемента. Измеряется корреляция флуктуирующих фототоков, возбуждающихся в фотоэлементах, в зависимости от расстояния между зеркалами. Без особых осложнений расстояние между зеркалами может быть сделано большим и достигнута высокая разрешаю1дая способность прибора,  [c.384]

Если мы хотим, чтобы при перефокусировке угловой размер изображения звезды изменялся со скоростью » сек, то линейная  [c.406]

Рассчитайте динамический параллакс визуальной двойной звезды, зная, что период обращения компонентов 67,4 года, угловой размер большой полуосн орбиты 3,14, видимый блеск компонентов 4,1-5 » и 6,35 «.  [c.476]

---