Перейти к контенту
Условие задачи:
Найти удлинение буксирного троса с жесткостью 100 кН/м при буксировке автомобиля массой 2 т с ускорением 0,5 м/с2. Трением пренебречь.
Задача №2.6.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(k=100) кН/м, (m=2) т, (a=0,5) м/с2, (x-?)
Решение задачи:
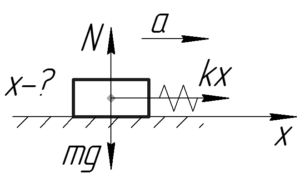
[kx = ma]
Значит удлинение (деформацию) троса можно определить по такой формуле:
[x = frac{{ma}}{k}]
Переведем некоторые данные задачи в систему СИ:
[100;кН/м = {10^5}; Н/м]
[2;т = 2000;кг]
Теперь приступим к расчету численного ответа.
[x = frac{{2000 cdot 0,5}}{{{{10}^5}}} = 0,01; м = 1; см]
Ответ: 1 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.6.7 Каков коэффициент жесткости буксировочного троса, если при буксировке автомобиля
2.6.9 Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины
2.6.10 Тело массой 2 кг тянут по горизонтальной поверхности с помощью пружины, которая
( 19 оценок, среднее 4.53 из 5 )
Вестник науки и образования Северо-Запада России
http://vestnik-nauki.ru/ ——-
2016, Т. 2, №1
УДК 531:639.2
ЭМПИРИЧЕСКАЯ ФОРМУЛА ДЛЯ РАСЧЕТА УДЛИНЕНИЯ СИНТЕТИЧЕСКИХ КАНАТОВ
И.М. Ахмедов
THE EMPIRICAL FORMULA FOR CALCULATING ELONGATION
SYNTHETIC ROPES I.M. Ahmedov
Аннотация. Проведен анализ результатов испытаний статической прочности синтетических канатов. С увеличением диаметра 3-прядных канатов из изученных синтетических материалов коэффициент относительной прочности уменьшается. Методом наименьших квадратов по опытным данным для отдельных материалов канатов были подобраны параметры степенной эмпирической зависимости нагрузка-удлинение. Среднеквадратическое отклонение результатов расчетов от опытных данных не превышает 8 %. Среди испытанных образцов наибольшей эластичностью обладают канаты из нейлона; упругие характеристики канатов из полистила и из полипропилена мало различаются.
Ключевые слова: синтетические канаты; разрывное усилие; испытания; относительное удлинение; эмпирическая формула.
Abstract. The analysis of the tests results of synthetic ropes static strength was performed. With increasing diameter, 3-strand ropes from synthetic materials studied, the coefficient of the relative strength decreases. The parameters empirical power-law dependence of the rope load-elongation were selected by the method of least squares on experimental data for certain materials. The standard deviation of calculated results from experimental data does not exceed 8 %. Among the samples tested have the highest elasticity of ropes of nylon. Elastic characteristics of ropes made of polysteel and polypropylene differ little
Keywords: synthetic ropes; breaking strength; test; elongation; empirical formula.
Введение
Синтетические канаты широко используются в самых разных отраслях промышленности и на транспорте. При решении многих прикладных задач необходимо учитывать упругие свойства канатов [1-5]. Практиков, в первую очередь, интересуют инженерные методы определения натяжения и формы канатных систем. Ф.И Баранов [6] на основе анализа проведенных опытов предложил зависимость для удлинения испытанного сухого образца пенькового каната:
s = 0,005 -4Т , (1)
где Т — сила натяжения в кгс (килограмм силы — техническая единица измерения усилия). Формула (1) использована в [7, 8] для расчета равновесия канатной части орудий рыболовства, причем не только из растительных материалов. Разумеется, зависимость (1) не является универсальной, справедлива только для условий проведения опытов.
В [9] нами была выдвинута гипотеза, что зависимость удлинения синтетических канатов от относительной нагрузки является степенной:
£ = Л, -вщ = A, ■(T/P1 )щ, (2)
http://vestnik-nauki.ru/
где в — отношение усилия в канате Т к разрывному усилию Р; Л/ , п^ — эмпирические параметры зависимости для /-го типа канатов.
Из формулы (2) следует, что предварительно необходимо исследовать разрывное усилие синтетических канатов Р, так как в многочисленных экспериментальных исследованиях именно к нему относят усилие в канате Т. В данной статье проанализированы опубликованные данные по разрывному усилию синтетических канатов [10-12] и подобраны эмпирические константы в зависимости (2) для некоторых из них.
Эмпирическая зависимость разрывного усилия от диаметра каната
Прочность синтетических канатов зависит от многих факторов: материала, из которых они изготовлены, соблюдения технологии при его изготовлении, типа (конструкции), износа каната, условий эксплуатации (воздействие температуры, химических веществ, ультрафиолетового излучения, ударных нагрузок). В [13] предпринята попытка сравнения прочностных характеристик канатов из различных полимерных материалов без учета их конструкции. В данной статье остановимся на прочностных характеристиках широко используемых в промышленности синтетических 3-прядных крученых кантов.
Все крупные производители синтетических канатов, как российские, так и зарубежные, имеют стенды (разрывные машины) для испытания прочности и эластичности своих изделий. Последние несколько лет для привлечения потенциальных покупателей они публикуют результаты испытаний прочности канатов [14-16]. В этих испытаниях увеличение силы натяжения происходит достаточно медленно, чтобы разрывное усилие можно было считать статическим.
Была выдвинута гипотеза [10, 11], что зависимость Р(ё) является степенной:
Р(ё) = Вг • ёт
(3)
где Р[ — статическое разрывное усилие 1-го типа канатов, кН; ё — диаметр каната, мм; В/ , т/ -эмпирические коэффициенты.
Были проанализированы результаты испытаний канатов, изготовленных ООО «Севзапканат» [14]. Методом наименьших квадратов были найдены значения эмпирических коэффициентов в формуле (3) для 3-х прядных канатов (табл. 1). На рис. 1 представлено сравнение результатов расчетов с данными испытаний. Среднее квадратическое отклонение опытных данных от зависимости (3) не превышает 1,2 %
Таблица 1 — Параметры характеристик разрывная нагрузка-диаметр каната
Параметр
Полипропилен
Материал канатов
Полистил
3
«Силвер» (полистил+полиэстер)
Полиамид
В
0,211
0,250
0,223
0,272
т
1,865
1,860
1,911
1,902
с.к.о., %
0,
0,9
0,
1,2
1
2
4
Зависимость (3) остается справедливой и при стремлении диаметра к нулю, так как величина Р тоже будет стремиться к нулю. Наименьшее разрывное усилие получилось у канатов, изготовленных ООО «Севзапканат» из полипропилена, наибольшее — из полиамида. Показатели степени для всех материалов меньше двух. Значит, разрывное напряжение в материале канатов будет уменьшаться с увеличением их диаметра.
http://vestnik-nauki.ru/
Р кН
250 200 150 100 50
0
У
у у У
-< У*У У
10
15
20
25
30
35
40
мы
Рисунок 1 — Зависимость разрывного усилия 3-х прядных канатов от диаметра: 1 — полипропиленовые; 2 — полистиловые; 3 — «Силвер» (полистил+полиэстер); 4 — полиамидные. Точки — опытные данные [14]; линии — расчет по формуле (3)
Для сравнения характеристик канатов из различных материалов используют коэффициент относительной прочности К [13,15]:
К = Pg/n,
(4)
где Pg — разрывное усилие, кгс (килограмм силы), Pg= 1000Р/9,8; щ — линейная плотность каната, кг/км (г/м).
На рис. 2 представлена зависимость коэффициента относительной прочности 3-прядных канатов от их диаметра. Видно, что коэффициент относительной прочности канатов монотонно уменьшается с увеличением их диаметра.
К
кгс г/м 40
38 36 34 32 30 28
1^2
V,
ч к
•ч
__ А 4
0
10
15
20
25
30
35
40 им
Рисунок 2 — Коэффициент относительной прочности 3-прядных канатов. Точки — данные [14]; линии — расчет по формуле (4). Обозначения, как на рис. 1
Анализ результатов испытаний эластичности синтетических канатов
В [15] приведены в безразмерной форме графики нагрузка-удлинение синтетических канатов, полученные опытным путем. Удлинение отнесено к первоначальному (перед опытом) размеру образца, а усилие — к разрывному усилию каната. Опубликованные графики обобщенные (скорее всего, осредненные, но это не указано в [15]), справедливые для всех размеров канатов, но различаются в зависимости от материала. Отдельно представлены графики по новым канатам и по бывшим в употреблении. Также не различаются
http://vestnik-nauki.ru/
прочностные и упругие характеристики 3-прядных крученых канатов и 4-прядных плетеных. Что подтверждается и нашими исследованиями.
Методом наименьших квадратов по опытным данным [15] были подобраны параметры степенной эмпирической зависимости (2). Они показаны в табл. 2.
Таблица 2 — Параметры характеристик нагрузка-удлинение
Параметр Материал канатов
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
1 2 3 4 5
Полипропилен «Малтитекс» Нейлон Полистил «Мастер»
Новые канаты
А 0,155 0,255 0,357 0,180 0,195
N 0,487 0,551 0,582 0,618 0,438
с.к.о., % 7,2 5,2 7,9 4,9 18,2
Поработавшие канаты
А 0,115 0,184 0,255 0,118 0,156
п 0,534 0,544 0,601 0,613 0,475
с.к.о., % 7,8 3,7 5,7 5,3 15,1
Сравнение результатов расчетов с опытными данными представлено на рис. 3-5. Среднеквадратическое отклонение опытных данных от кривых не превышает 8 %, только в одном случае выше (см. табл. 2). По рис. 5 видно, что наибольшей эластичностью обладают канаты из нейлона; упругие характеристики канатов из полистила и из полипропилена мало различаются.
€ 0.12 0.08 0.04 0
О 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 О Рисунок 3 — Зависимость относительного удлинения каната из полипропилена от безразмерной нагрузки: 1 — новые канаты, 2 — поработавшие. Точки -опытные данные [15], линии — результаты расчета по формуле (2)
€ 0.3 0.2 0.1
0
Рисунок 4 — Зависимость относительного удлинения каната из нейлона от безразмерной нагрузки. Обозначения, как на рис. 3
.1* 2 У ™
* с- .9*
«Г* 1″
1
Л ш * 2 4-*
*** ^ А
•
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 О
http://vestnik-nauki.ru/
Рисунок 5 — Зависимость относительного удлинения поработавших канатов от безразмерной нагрузки: 1 — нейлон; 2 — «Малтитекс»; 3 -«Мастер»; 4 — полистил; 5 — полипропилен
Заключение
Проведенный анализ показал, с увеличением диаметра 3-прядных канатов из изученных синтетических материалов коэффициент относительной прочности уменьшается.
Методом наименьших квадратов по опытным данным для отдельных материалов канатов были подобраны параметры степенной эмпирической зависимости нагрузка-удлинение. Среднеквадратическое отклонение опытных данных от кривых не превышает 8 %, кроме одного случая. Однако при 0 < 0,1 характер изменения опытных данных несколько отличается от зависимости (2). Возможно, модель, основанная на формуле (2), нуждается в дальнейшем уточнении.
Разрывные нагрузки и упругие характеристики устанавливаются производителями для сухих канатов; во влажных условиях разрывные нагрузки будут ниже. Для определения прочностных и эластичных свойств канатов в воде необходимо проведение соответствующих экспериментов.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Михайлов В.В. Предварительно напряженные и вантовые конструкции: учебное пособие. М.: Изд-во АСВ, 2002. 255 с.
2. Великанов Н.Л., Наумов В.А. Гидродинамическое сопротивление систем из стержней и нитей: монография. Калининград: Изд-во ФГОУ ВПО «КГТУ», 2015. 192 с.
3. Наумов В. А., Ахмедов И.М. Численный метод решения трехмерной задачи равновесия сферического тела на тросе в потоке // Известия КГТУ. 2015. № 37. С. 63-72.
4. Наумов В.А., Ахмедов И.М. Равновесие криволинейной нити, закрепленной в двух точках в однородном потоке // Материалы III Балтийского международного морского форума. Калининград: Изд-во БГАРФ, 2015. С. 299-304.
5. Наумов В.А., Ахмедов И.М. Пространственная задача равновесия сферического тела, закрепленного канатом на дне, в потоке // Материалы III Балтийского международного морского форума. Калининград: Изд-во БГАРФ, 2015. С. 591-598.
6. Баранов Ф.И. Техника промышленного рыболовства: учебник. М.: Пищепромиздат, 1960. 695 с.
7. Фридман А.Л. Теория и проектирование орудий промышленного рыболовства: учебник. М.: Легкая и пищевая промышленность, 1981. 238 с.
8. Розенштейн М.М., Недоступ А. А. Механика орудий рыболовства: учебник. М.: Моркнига, 2012. 527 с.
Вестник науки и образования Северо-Запада России
http://vestnik-nauki.ru/ ——-
2016, Т. 2, №1
9. Наумов В.А., Ахмедов И.М. Упругие свойства синтетических канатов // Наука в современном мире: Сборник статей Международной научно-практической конференции (19 февраля 2015 г.). Стерлитамак: РИЦ АМИ, 2015. — С. 180-182.
10. Ахмедов И.М., Наумов В.А. Зависимость разрывного усилия синтетических канатов от их диаметра // Водопользование и задачи гидромеханики: Сборник научных трудов. Калининград: Изд-во ФГБОУ ВПО «КГТУ», 2015. С. 15-20.
11. Наумов В. А., Ахмедова Н.Р., Ахмедов И.М. Анализ результатов испытания прочности трехпрядных канатов из полимерных материалов // Известия КГТУ. 2015. № 36. С. 43-51.
12. Наумов В.А., Ахмедов И.М. Статистический анализ результатов испытаний прочности синтетических канатов // Сборник статей Международной научно-практической конференции «Инновационное развитие современной науки» (7 февраля 2015 г.). Уфа: РИО МцИи «Омега сайнс», 2015. С. 51-53.
13. Евсеева С. С. Сравнительный анализ технических характеристик синтетических канатов // Вестник АГТУ. Промышленное рыболовство, 2008. № 3. С. 90-92.
14. Текстильные канаты, Севзапканат. [Электронный ресурс]. URL: http://www.sevzapkanat.com/index.php?newsid=409 (дата обращения 04.11.2015).
15. LANEX. Marine ropes [Электронный ресурс]. URL: http://www.lanex.cz/en/ marine-ropes-technical-parameters (дата обращения 31.12.2014).
16. Агни-Прогресс. Канаты, сети, шнуры [Электронный ресурс]. URL: http://www.agniprogress.ru/company.html (дата обращения 04.11.2015).
ИНФОРМАЦИЯ ОБ АВТОРЕ
Ахмедов Исфендияр Махмуд-оглы ФГБОУ ВПО «Калининградский государственный технический университет», г. Калининград, Россия, аспирант кафедры водных ресурсов и водопользования E-mail: isfendi@mail.ru
Ahmedov Isfendiar Mahmud-oglu FSEI HPE «Kaliningrad State Technical University», Kaliningrad, Russia, the post-graduate student of The Water Resources Department E-mail: isfendi@mail.ru
Корреспондентский почтовый адрес и телефон для контактов с автором статьи: 236022, Калининград, Советский пр., 1, КГТУ, ГУК, каб. 322. Ахмедов И.М.
8(4012)99-53-37
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Исходные данные: k (жесткость буксирного троса) = 100 кН/м = 100 * 10^3 Н/м; m (масса буксируемого автомобиля) = 2 т = 2000 кг; a (ускорение, с которым буксируется автомобиль) = 0,5 м/с^2.
Удлинение буксирного троса определим из равенства: F = Fупр.: m * a = k * Δl, откуда Δl = m * a / k.
Выполним расчет: Δl = 2000 * 0,5 / (100 * 10^3) = 0,01 м или 1 см.
Ответ: Удлинение буксирного троса составляет 1 сантиметр.
Силы упругости: пружины, канаты и нити
В задачах в этой статьи рассмотрены случаи, когда тело поднимают или опускают с ускорением. При этом натяжение нити, на которой подвешен груз, разное. Даны примеры составления уравнений по второму закону Ньютона в проекциях на оси.
Задача 1.
Грузовик взял на буксир легковой автомобиль массой т и, двигаясь равноускоренно, за
с проехал
м. На сколько при этом удлиняется трос, соединяющий автомобили, если его жесткость
Н/м? Трение не учитывать.
Удлинение троса можно найти, зная силу упругости:
Так как трение учитывать не нужно, то по второму закону Ньютона
Следовательно,
Определим ускорение грузовика:
Окончательно для удлинения троса получаем:
Ответ получен в метрах, можно записать его в мм: 0,64 мм.
Задача 2.
На нити, выдерживающей натяжение Н, поднимают груз массой
кг из состояния покоя вертикально вверх. Считая движение равноускоренным, найти предельную высоту
, на которую можно поднять груз за
с так, чтобы нить не оборвалась.
К задаче 2
Запишем второй закон Ньютона в проекция на вертикальную ось:
Тогда ускорение равно:
Высота, на которую тело можно поднять с таким ускорением, равна
Ответ: 5 м
Задача 3.
Веревка выдерживает груз массой кг при вертикальном подъеме его с некоторым ускорением и груз массой
кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза
, который можно поднимать или опускать на этой веревке с постоянной скоростью?
К задаче 3
Запишем уравнения по второму закону как для подъема, так и для спуска тела. Направим ось вверх, тогда при подъеме:
При спуске:
Ускорение по условию одно и то же, тогда:
Или
Приравняв, можем найти силу натяжения веревки, которую она выдерживает:
Если бы груз массой просто висел на такой веревке, то мы бы записали
Следовательно,
Ответ: 190 кг
Задача 4.
Груз массой кг подвешен к пружине жесткостью
Н/м. Длина пружины в нерастянутом состоянии
м. Найти длину пружины
, когда на ней висит груз. Какой будет длина пружины, если пружина с грузом будет находиться в лифте, движущемся с ускорением
м/с
, направленным а) вверх; б) вниз?
К задаче 4
Если груз повешен на пружину, ее длина увеличивается:
При движении лифта вверх запишем второй закон (ось направлена вверх):
Тогда длина пружины в этом случае:
При движении лифта вниз запишем второй закон (ось направлена вверх):
Тогда длина пружины в этом случае:
Ответ: ,
,
.
Задача 5.
Четырьмя натянутыми нитями груз закреплен на тележке. Силы натяжения горизонтальных нитей соответственно и
, а вертикальных —
и
. С каким ускорением движется тележка по горизонтальной плоскости?
К задаче 5
Запишем уравнения по второму закону в проекциях на оси, которые расположим традиционно: ось вправо, ось
— вверх. Тогда, если тележка движется вправо, по оси, имеем:
Из второго уравнения найдем массу груза:
Тогда ускорение тележки (и груза) равно:
Если же тележка движется влево (против оси), то изменится только первое уравнение:
Тогда ускорение тележки (и груза) равно:




