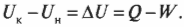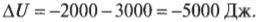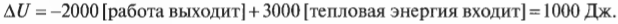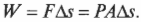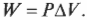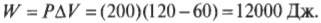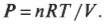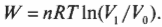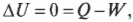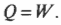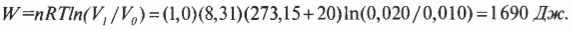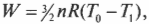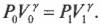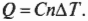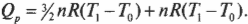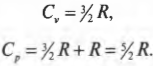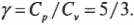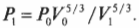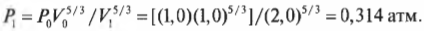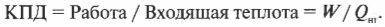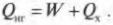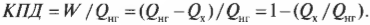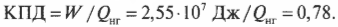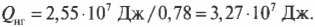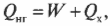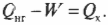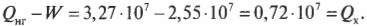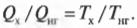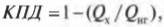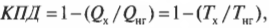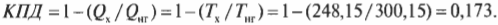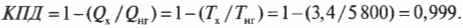Как найти удельную теплоемкость через мощность - AvtoShod.ru

Удельная теплоемкость вещества

Это физическая величина, выражающая количество тепла, необходимое веществу на единицу массы для повышения температуры на одну единицу.

Таким образом, удельная теплоёмкость является свойством вещества, поскольку его значение является репрезентативным для каждого вещества, каждое из которых, в свою очередь, имеет различные значения в зависимости от того, в каком состоянии оно находится (жидкое, твердое или газообразное).

Удельная теплоёмкость обозначается маленькой буквой c и измеряется в Дж/кг∗°С, представляет собой коэффициент повышения температуры в одной единице всей системы или всей массы вещества.

Кроме того, удельная теплоёмкость меняется в зависимости от физического состояния вещества, особенно в случае твердых частиц и газов, поскольку его молекулярная структура влияет на теплопередачу в системе частиц. То же самое относится и к условиям атмосферного давления: чем выше давление, тем ниже удельное тепло.

Основной состав удельной теплоты вещества должен быть с = С/m, т. е. удельная теплота равна соотношению калорийности и массы.

Однако когда это применяется к данному изменению температуры, говорят о средней удельной теплоемкости, которая рассчитывается на основе следующей формулы:

Q — передача тепловой энергии между системой и средой (Дж);

m — масса системы (кг);

Δt или (t2 — t1) — повышение температуры, которой она подвергается (°C).

Формула для нахождения количества теплоты Q:

Q = c∗m(t2— t1)

Чем выше удельная теплоёмкость вещества, тем больше тепловой энергии потребуется, чтобы его температура повысилась. Например, для нагрева воды (своды = 4200 Дж/кг∗°С) потребуется больше тепловой энергии, чем для нагрева свинца (ссвинца = 140 Дж/кг∗°С).

Уравнение теплового баланса:

Q отданное + Q полученное = 0.

Ниже представлена таблица значений удельной теплоёмкости некоторых веществ:

Примеры решения задач

Следующие задачи покажут примеры расчета необходимого количества теплоты.

Задача №1

Сколько теплоты нужно, чтобы изо льда массой 2 кг, взятого при температуре -10°С, получить пар при 100°С?

Ответ: чтобы изо льда массой 2 кг, взятого при температуре -10°С, получить пар при 100°С, нужно взять 6,162 мегаджоулей теплоты.

Задача №2

В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100°С?

Начнем решение и отметим, что нагреваться будет и котёл, и вода. Разница температур составит 100 0 С — 10 0 С = 90 0 С. Т. е. и температура котла изменится на 90 градусов, и температура воды также изменится на 90 градусов.

Количества теплоты, которые получили оба объекта (Q1 – для котла и Q2 — для воды), не будут одинаковыми. Мы найдем общее количество теплоты по формуле теплового баланса Q = Q1 + Q2.

Источник

О тепловой энергии простым языком!

Человечеству известно немного видов энергии – механическая энергия (кинетическая и потенциальная), внутренняя энергия (тепловая), энергия полей (гравитационная, электромагнитная и ядерная), химическая. Отдельно стоит выделить энергию взрыва,…

…энергию вакуума и еще существующую только в теории – темную энергию. В этой статье, первой в рубрике «Теплотехника», я попытаюсь на простом и доступном языке, используя практический пример, рассказать о важнейшем виде энергии в жизни людей — о тепловой энергии и о рождающей ее во времени тепловой мощности.

Несколько слов для понимания места теплотехники, как раздела науки о получении, передаче и применении тепловой энергии. Современная теплотехника выделилась из общей термодинамики, которая в свою очередь является одним из разделов физики. Термодинамика – это дословно «теплый» плюс «силовой». Таким образом, термодинамика – это наука об «изменении температуры» системы.

Воздействие на систему извне, при котором изменяется ее внутренняя энергия, может являться результатом теплообмена. Тепловая энергия, которая приобретается или теряется системой в результате такого взаимодействия с окружающей средой, называется количеством теплоты и измеряется в системе СИ в Джоулях.

Если вы не инженер-теплотехник, и ежедневно не занимаетесь теплотехническими вопросами, то вам, столкнувшись с ними, иногда без опыта бывает очень трудно быстро в них разобраться. Трудно без наличия опыта представить даже размерность искомых значений количества теплоты и тепловой мощности. Сколько Джоулей энергии необходимо чтобы нагреть 1000 метров кубических воздуха от температуры -37˚С до +18˚С. Какая нужна мощность источника тепла, чтобы сделать это за 1 час. На эти не самые сложные вопросы способны сегодня ответить «сходу» далеко не все инженеры. Иногда специалисты даже помнят формулы, но применить их на практике могут лишь единицы!

Прочитав до конца эту статью, вы сможете легко решать реальные производственные и бытовые задачи, связанные с нагревом и охлаждением различных материалов. Понимание физической сути процессов теплопередачи и знание простых основных формул – это главные блоки в фундаменте знаний по теплотехнике!

Количество теплоты при различных физических процессах.

Большинство известных веществ могут при разных температуре и давлении находиться в твердом, жидком, газообразном или плазменном состояниях. Переход из одного агрегатного состояния в другое происходит при постоянной температуре (при условии, что не меняются давление и другие параметры окружающей среды) и сопровождается поглощением или выделением тепловой энергии. Не смотря на то, что во Вселенной 99% вещества находится в состоянии плазмы, мы в этой статье не будем рассматривать это агрегатное состояние.

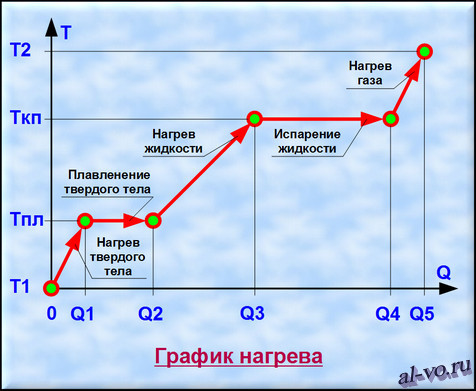
Рассмотрим график, представленный на рисунке. На нем изображена зависимость температуры вещества Т от количества теплоты Q, подведенного к некой закрытой системе, содержащей определенную массу какого-то конкретного вещества.

1. Твердое тело, имеющее температуру T1, нагреваем до температуры Tпл, затрачивая на этот процесс количество теплоты равное Q1.

2. Далее начинается процесс плавления, который происходит при постоянной температуре Тпл (температуре плавления). Для расплавления всей массы твердого тела необходимо затратить тепловой энергии в количестве Q2—Q1.

Главные формулы теплопередачи.

Формулы очень просты.

Количество теплоты Q в Дж рассчитывается по формулам:

1. Со стороны потребления тепла, то есть со стороны нагрузки:

1.1. При нагревании (охлаждении):

m – масса вещества в кг

с – удельная теплоемкость вещества в Дж/(кг*К)

1.2. При плавлении (замерзании):

λ – удельная теплота плавления и кристаллизации вещества в Дж/кг

1.3. При кипении, испарении (конденсации):

r – удельная теплота газообразования и конденсации вещества в Дж/кг

2. Со стороны производства тепла, то есть со стороны источника:

2.1. При сгорании топлива:

q – удельная теплота сгорания топлива в Дж/кг

2.2. При превращении электроэнергии в тепловую энергию (закон Джоуля — Ленца):

I – действующее значение тока в А

U – действующее значение напряжения в В

R – сопротивление нагрузки в Ом

Делаем вывод – количество теплоты прямо пропорционально массе вещества при всех фазовых превращениях и при нагреве дополнительно прямо пропорционально разности температур. Коэффициенты пропорциональности ( c, λ , r , q ) для каждого вещества имеют свои значения и определены опытным путем (берутся из справочников).

Тепловая мощность N в Вт – это количество теплоты переданное системе за определенное время:

Чем быстрее мы хотим нагреть тело до определенной температуры, тем большей мощности должен быть источник тепловой энергии – все логично.

Формулы для количества теплоты через мощность

Тепловое действие тока
Прохождение тока через проводник вызывает его нагрев. Это явление широко используется в различных областях. Например, всем хорошо знакомы такие бытовые приборы, как лампа накаливания, электрокипятильник, электрочайник, электрообогреватель, паяльник, утюг и другие приборы.

Также часто можно замечать, что провода, идущие к какому-то мощному электроприбору, нагреваются. Нагреваются и другие устройства, например, телевизоры, компьютеры и т.д.

Тепловое действие тока может быть как полезным (например в случае кипятильника или обогревателя), так и вредным (в случае нагрева проводов). Поэтому необходимо знать, сколько тепла выделяется в том или ином случае, чтобы создать наиболее эффективное нагревающее устройство или, наоборот, избежать чрезмерного нагрева.

Единицей количества теплоты является 1 Джоуль (иногда используют другую единицу – калорию). Количество теплоты, выделившееся на проводнике можно рассчитать по следующей формуле:

Где P – мощность, выраженная в Ваттах, t – время, выраженное в секундах, Q – количество тепла, выраженное в Джоулях.

Пример.

Пусть обогреватель, имеющий мощность 1000 Ватт, работает в течение 1 часа (в одном часе 3600 секунд). Вычислим, сколько тепла выделится на этом обогревателе. Подставив имеющиеся данные в вышеприведённую формулу, получим: Q = Pt =1000*3600=3600000 Джоулей или 3,6 МегаДжоуля (МДж).

Можно вычислить на сколько градусов повысится температура воды в электрочайнике, имеющего нагревательный элемент определённой мощности и включённого в течение определённого времени.

Число градусов Цельсия, на которое повысится температура вещества, выражается по следующей формуле:

где С – теплоёмкость. Для воды С=4200 Дж/кг*градус. m – масса вещества в килограммах.

Пример . Пусть электрочайник имеет мощность 2000 Ватт. В него налито 2 литра (2 кг) воды. Вычислим на сколько градусов Цельсия поднимется температура воды в чайнике, если он будет включён в течении 5 минут (300 секунд).

Решение. За 5 минут (300 секунд) нагревательный элемент выделит количество теплоты, равное Q = Pt =2000*300=600000 Дж. Это тепло передано двум литрам воды, следовательно, повышение температуры воды составит:

∆ T = Q mC = 600 000 2 ∙ 4200 =71 градус Цельсия

Итак, нам известна формула для расчета количества теплоты:

где P – мощность. Нам также известна формула для расчёта мощности:

где I –ток, U – напряжение. По закону Ома U = IR , где R – сопротивление, поэтому

Следовательно, формулу для расчёта количества теплоты можно записать следующим образом:

Таким образом, зная, какой ток течёт через проводник, сопротивление проводника и время, в течение которого протекал ток, можно вычислить количество теплоты, выделившееся на проводнике.

Пример. Пусть имеется два резистора, соединённых последовательно. Через них течёт один и тот же ток, пускай 0,1 Ампера. Допустим, что сопротивление одного резистора 10 Ом, а другого 1000 Ом (Рис.1). Вычислим, сколько тепла выделилось на резисторах, если через них протекал ток в течение 1 минуты.

Из расчётов видно, что сильнее нагревается тот проводник, сопротивление которого больше.

Разные провода имеют разное сопротивление. Оно зависит от толщины провода.

Пусть вам понадобилось увеличить длину провода, при помощи которого утюг включается в сеть. Для этого вы можете воспользоваться удлинителем. Очень часто старые удлинители имеют относительно тонкий провод (тоньше, чем провод утюга), поэтому сопротивление провода удлинителя будет больше, чем сопротивление провода утюга. Значит, существует опасность, что провод удлинителя будет чрезмерно нагреваться, что может привести к замыканию или пожару.

Следовательно, мощные электроприборы, необходимо подключать к сети только при помощи провода достаточной толщины. Если провод слишком тонкий он может загореться.

На вилках и розетках всегда пишется, какой максимальный ток может через них течь. Старые розетки могут выдержать ток не более 6 Ампер. Некоторые современные приборы потребляют значительно больше. Например, через чайник мощностью 2200 Ватт течёт ток 10 Ампер. Поэтому его ни в коем случае не следует подключать в старые розетки, даже через переходник!

Источник

Как рассчитать тепловую мощность конвекторов, обогревателей и прочих отопительных приборов

Теплотехнический расчет – это вычисление требуемой толщины перекрытий в соответствии теплоизоляционных характеристик материалов и мощности нагревательных приборов. Любое помещение для создания комфортных условий в холодное время года требует определенного количества тепла, и неважно проектируется отопительная система частного дома или требуется обогреть только одну комнату – расчеты необходимы.

Все отопительные приборы независимо от типа устройства (конвекторы, радиаторные батареи, обогреватели, тепловые пушки и т.д.) и типа теплоносителя (водяные, газовые, электрические) отапливают помещения и производимое ими тепло называется тепловой мощностью. Именно эта характеристика имеет важнейшее значение при выборе обогревательного прибора.

Например невозможно обогреть мастерскую площадью 20 м 2 и построенную без теплоизоляции при -15 0 С электрическим обогревателем мощностью 1 кВт, а небольшую ванную комнату, расположенную в центре кирпичного дома запросто.

Количество тепла, которое требуется помещению для обогрева, измеряется в килокалориях, а мощности приборов в ваттах, поэтому для перевода одного значения в другое нужно килокалории поделить на 860 и получатся кВт.

Все производители отопительного оборудования обязательно указывают тепловую мощность прибора в паспорте или инструкции. Однако, следует учитывать, что указанная мощность достигается при соблюдении всех условий эксплуатации т.е. для водяных конвекторов или радиаторов имеет значение температура теплоносители, а для газовых приборов давление газа.

Поэтому помимо мощности отопления производители указывают, для каких условий эксплуатации предназначено оборудование.

Например, если у вас старая система центрального отопления с температурой нагрева 40-50 0 С, рекомендуется приобретать конвекторы для низкотемпературных систем отопления.

Для чего нужен тепловой расчет?

Теплотехнический расчёт позволяет строить наиболее оптимально. Материалов берётся ни больше – ни меньше, а ровно столько, сколько нужно. Сокращаются габариты строения и расходы на его возведение.

Вычисление точки росы позволяет строить так, чтобы материалы не портились как можно дольше.

Для определения необходимой мощности котла также не обойтись без расчётов. Суммарная мощность его складывается из затрат энергии на обогрев комнат, нагрев горячей воды для хозяйственных нужд, и способности перекрывать теплопотери от вентиляции и кондиционирования. Прибавляется запас мощности, на время пиковых холодов.

При газификации объекта требуется согласование со службами. Рассчитывается годовой расход газа на отопление и общая мощность тепловых источников в гигакалориях.

Нужны расчёты при подборе элементов отопительной системы. Обсчитывается система труб и радиаторов – можно узнать, какова должна быть их протяжённость, площадь поверхности. Учитывается потеря мощности при поворотах трубопровода, на стыках и прохождении арматуры.

При расчетах затрат тепловой энергии могут пригодиться знания, как перевести Гкал в Квт и обратно. В следующей статье подробно рассмотрена эта тема с примерами расчета.

Полный расчет теплого водяного пола приведен в этом примере.

Знаете ли вы, что количество секций радиаторов отопления не берется “с потолка”? Слишком малое их количество приведет к тому, что в доме будет холодно, а чрезмерно больше создаст жару и приведет к чрезмерной сухости воздуха. По ссылке приведены примеры правильного расчета радиаторов.

Простейший расчет тепловой мощности обогревателя

Существует общепринятый стандарт расчета тепловой мощности обогревателя при высоте помещения не более 3 м. На 10 метров квадратных площади устанавливается 1 кВт мощности прибора.

Эта формула неплохо работает при расчетах электрических отопительных приборов в помещениях с идеальными условиями — высокой теплоизоляцией, минимальной теплопотерей и одним окном с утепленным стеклопакетом. Но существует и примитивный вариант расчета, позволяющий учитывать и высоту комнат.

Простой расчет тепловой нагрузки (Q) помещения:

V (объем помещения/м3) х 40 Вт/1000 = Q (кВт/ч)

Эта формула не позволяет допустить ошибок, связанных с грубым расчетом по принципу 1 кВт на 10 м 2 т.к., учитывает объем комнаты включая высоту потолков. Однако и при таком расчёте легко совершить оплошность и приобрести «слабый» прибор — не учтено много важных факторов.

Пример расчетов

Вводные данные: гостиная в частном доме, ВхШхД – 4х5х6 м.

По первой формуле мы выясняем площадь помещения – 5х6 = 30 м 2 и умножаем на 1 кВт. Получается, что нам потребуется обогреватель на 3 кВт.

Но эти расчеты не гарантируют, что, купив обогреватель мощностью 3 кВт, вы получите комфортную температуру в помещении — в столь примитивном расчете даже не учитывается температура за окном. Если в средней полосе 3 кВт могут и справится с отоплением такой гостиной, но на севере с -35 за окном можете не сомневаться, разочарование от покупки и стучащие зубы вам обеспечены.

По второй формуле мы выясняем объем помещения – 4х5х6 = 120 м 3 .

V х 40 Вт/1000 = 120 х 40 / 1000 = 4,8 кВт

Как можно видеть вторая формула более точно отражает необходимую потребность помещения в тепле. Кроме того учитывайте, что эти расчеты обычно применяются в электрических обогревателях, а с прибором мощностью 5 кВт в час вы разоритесь на счетах за электроэнергию, да и далеко не вся проводка выдержит подобную нагрузку.

Что такое тепловой расчет?

Если говорить просто, тепловой расчёт помогает точно узнать, сколько тепла хранит и теряет здание, и сколько энергии должно вырабатывать отопление, чтобы поддерживать в жилье комфортные условия.

Оценивая теплопотери и степень теплоснабжения, учитываются следующие факторы:

Какой это объект: сколько в нём этажей, наличие угловых комнат, жилой он или производственный и т. д.
Сколько человек будет «обитать» в здании.
Важная деталь – это площадь остекления. И размеры кровли, стен, пола, дверей, высота потолков и т. д.
Какова продолжительность отопительного сезона, климатические характеристики региона.
По СНиПам определяют нормы температур, которые должны быть в помещениях.
Толщина стен, перекрытий, выбранные теплоизоляторы и их свойства.

Могут учитываться и другие условия и особенности, например, для производственных объектов считаются рабочие и выходные дни, мощность и тип вентиляции, ориентация жилья по сторонам света и др.

Формула расчета тепловой нагрузки с учетом разницы температур

Для более точного определения требуемой тепловой мощности обогревателя или конвектора рекомендуем воспользоваться следующими формулой.

V (объем помещения) х T (разница температур) х φ (коэффициент теплопотери) = ккал/ч

V – это упоминаемый выше объем комнаты: ширина * длину * высоты.
Т (разница температур) – в зависимости от климатической зоны температура на улице может составлять и -5 0 С и -30 0 С. Поэтому в формулу введен параметр выражающий разницу между средней зимней температурой на улице и желаемой температурой в помещении. Пример: среднее зимнее значение на улице составляет -15 0 С, а в комнате требуется 25 0 С – получается Т = 40 0 С.
φ – коэффициент теплопотерь помещений в зависимости от конструкции и изоляции. 3-4 – отсутствие теплоизоляции. Простые деревянные или металлические строения без изоляции.
2-2,9 – низкая теплоизоляция. Кладка в один кирпич, упрощенная конструкция строений, одинарные окна.
1-1,9 – средняя теплоизоляция. Строения с кладкой в два кирпича, стандартные здания, обычная кровля, небольшое количество окон.
0,6-0,9 — высокая теплоизоляция. Мало окон, сдвоенные рамы, кирпичные стены, двойная теплоизоляция, утепленная крыша и толстое основание пола.

Что еще необходимо учесть при расчете

Предыдущие расчеты не дают точной оценки мощности котельной, необходимо учитывать и приготовление горячей воды. Мощность котлов необходимо увеличить примерно на 20% — столько тепла тратится на нагревание воды. Для частного дома лучше приобретать автоматические двухконтурные отопительные установки — они экономят потребляемое топливо, работают на обогрев помещения и на подготовку горячей воды.

Географическое расположение отапливаемого помещения тоже принимается во внимание. Для этого существуют карты с обозначением средних температур в разные времена года для разных местностей

К расчетной цифре, установленной ранее, прибавляется взятый из карты коэффициент. Для климата средней полосы России он равен 1, для северных районов — от 1,5 до 2. На этот коэффициент умножается цифра, полученная при измерении площади и объема отапливаемого помещения. Результатом будет мощность котлов, необходимая для данного региона.

Пример расчета потребления тепла в кирпичном доме в Сыктывкаре:

дом высотой 3 м;
площадь 100 м².

Вычисляем объем: 100 м² умножаем на 3 м, получаем 300 м³. 34 Вт умножаем на 300 м³, получаем 10,2 кВт. Населенный пункт находится в северной зоне, поэтому последнее число умножается на коэффициент 2. Результат — 20,4. К этому числу добавляется еще 20% на нагрев воды и 25% резервной мощности. Чтобы не допустить преждевременного износа оборудования, прибавляют еще 10% мощности. В результате получают полную мощность котельной.

Если отапливается несколько домов, нужно посчитать затрачиваемую энергию для каждого из них и сложить полученные значения. Эта сумма будет обозначать необходимую тепловую мощность.

Для более точного расчета специалисты пользуются формулами, которые включают в себя:

коэффициенты теплопотерь;
количество людей в помещении;
виды теплоизоляционных материалов;
разность наружных и внутренних температур.

Формула расчета тепловой мощности с учетом дополнительных факторов

Несмотря на введение коэффициента потерь тепла предыдущая формула не способна отразить всевозможные нюансы помещений. Наример теплопотери квартиры расположенной на 5 этаже в центре девятиэтажного здания ниже, чем у угловой квартиры на последнем этаже. Для получения более точных данных рекомендуем воспользоваться формулой:

Q = (100 Вт/м 2 х S х φ 1 х φ 2 х φ 3 х φ 4 х φ 5 х φ 6 х φ 7)/1000

S – площадь помещения в м 2 .
φ 1 – потери тепла через окна: 0,85 – тройной стеклопакет;
1 – двойной стеклопакет;
1,27 – одинарный стеклопакет (стандартный).

φ 2 – утепление стен (теплоизоляция):

0,854 – высокое;

1 – кладка в два кирпича;

1,27 – низкое.

φ 3 – соотношение общей площади окон к площади пола помещения в %:

1,2 – 50%;

1,1 – 40%;

1 – 30%;

0,9 – 20%;

0,8 – 10%.

φ 4 – коэффициент умножения в зависимости от температуры внешней среды в минусовых значениях 0 С:

1,5 – -35 0 С;

1,3 – -25 0 С;

1,1 – -20 0 С;

0,9 – -15 0 С;

0,7 – -10 0 С.

φ 5 – сколько стен имеют контакт со внешней средой (выходят на улицу):

1,4 -4;

1,3 -3;

1,2 -2;

1,1 -1.

φ 6 – теплоизоляция помещения находящегося сверху над расчетным:

0,8 – обогреваемое;

0,9 – утеплённое, но не отапливаемое;

1 — холодный чердак или крыша.

φ 7 – высота в метрах:

1,2 – 4,5м;

1,15 – 4м;

1,1 – 3,5м;

1,05 – 3м;

1 – 2,5м.

Как видите в формуле расчета тепловой мощности обогревательного оборудования учтено значительно больше значений влияющих на теплопотери.

Пример расчета

Вводные данные: гостиная в частном доме, ВхШхД – 4х5х6 м. Дом построен кладкой в два кирпича, на утепленном фундаменте с большим панорамным окном, со стандартным остеклением, занимающим 50% от площади пола. Средняя температура зимой -15 0 С. На втором этаже отапливаемые спальни, две стены выходят на улицу.

Выясняем требуемые значения и коэффициенты:

S – 30м 2 .
φ 1 – 1,27.
φ 2 – 1.
φ 3 – 1,2.
φ 4 – 0,9.
φ 5 – 1,2.
φ 6 – 0,8.
φ 7 – 1,15.

Подставляем значения в формулу:

Q = (100 Вт/м 2 х S х φ 1 х φ 2 х φ 3 х φ 4 х φ 5 х φ 6 х φ 7)/1000

Q = (100 Вт/м 2 х 30 х 1,27 х 1 х 1,2 х 0,9 х 1,2 х 0,8 х 1,15)/1000 = 4,543 кВт

Исходя из этого уточненного расчета, получается, что нам нужно организовать отопление на 4,5-5 кВт.

Эта формула предпочтительна для расчета тепловой мощности отопительных систем, причем она подходит для расчета отопления в небольших жилых помещениях и в организации отопления промышленных объектов.

Важно! Для увеличения срока службы теплового оборудования и для учета непредвиденных ситуаций, рекомендуется добавлять небольшой запас в 10-15 %.к полученной тепловой мощности.

Расчет для прибора

Как выполнить расчет тепловой мощности радиаторов отопления при известном количестве секций?

Все просто: количество секций умножается на тепловой поток от одной секции. Этот параметр обычно можно найти на сайте производителя.

Если вас привлекла необычно низкая цена радиаторов неизвестного производителя — тоже не беда. В этом случае можно ориентироваться на следующие усредненные значения:

Тип радиатора	Тепловой поток на секцию стандартного (500 мм по центрам ниппелей) размера
Чугунный	140-160
Биметаллический	180-190
Алюминиевый	190 — 200

На фото — алюминиевый радиатор, рекордсмен по теплоотдаче на одну секцию.

Если вы выбрали конвектор или панельный радиатор, единственным источником информации для вас могут стать данные производителя.

Данные для панельных радиаторов Керми с сайта производителя.

Выполняя расчет тепловой мощности радиатора своими руками, учтите одну тонкость: производители обычно приводят данные для перепада температур между водой в батарее и воздухом в отапливаемом помещении в 70С. Она достигается, например, при комнатной температуре +20 и температуре радиатора +90.

Уменьшение дельты ведет к пропорциональному уменьшению тепловой мощности; так, при температурах теплоносителя и воздуха 60 и 25С соответственно мощность прибора уменьшится ровно вдвое.

Температурный график отопления. Большую часть отопительного сезона поступающая в батареи смесь (темно-синяя линия на графике) холоднее 90С.

Давайте обратимся к нашему примеру и выясним, сколько чугунных секций может обеспечить тепловую мощность в 6,6 КВт в идеальных условиях — при нагретом до 90С теплоносителе и комнатной температуре в +20. 6600/160=41 (с округлением) секция. Очевидно, что батареи такого размера придется разнести как минимум по двум стоякам.

При большом количестве секций используйте диагональное двухстороннее подключение к подводке. Тогда батарея будет равномерно прогрета по всей длине.

Особый случай

Системы отопления частных домов и гаражей нередко оборудуют самодельными приборами из соединенных перемычками труб — регистрами. Как подсчитать тепловую мощность стального регистра известных размеров?

Трубчатый стальной радиатор, или регистр.

Для одной секции (одной горизонтальной трубы) она вычисляется по формуле Q=Pi*D*L*K*Dt.

В ней:

Q -мощность. Результат будет получен в ваттах;
Pi — число «пи», его округленно берут равным 3,14;
D — наружный диаметр трубы в метрах;
L — длина секции (опять-таки в метрах);
K — коэффициент, соответствующий теплопроводности металла (у стали он равен 11,63);
Dt — разность температур между воздухом и водой в регистре.

При расчете мощности многосекционного регистра первая снизу секция рассчитывается по этой формуле, а для последующих, поскольку они будут находиться в восходящем теплом потоке (что влияет на Dt), результат умножается на 0,9.

Четырехсекционный регистр. Верхние секции попадают в восходящий теплый поток от нижней.

Приведу пример расчета. Одна секция диаметром 108 мм и длиной 3 метра при комнатной температуре +25 и температуре теплоносителя +70 будет отдавать 3,14*0,108*3*11,63*(70-25)=532 ватта. Четырехсекционный регистр из таких же секций отдаст 523+(532*0,9*3)=1968 ватт.

Источник

О тепловой энергии простым языком!

Опубликовано 13 Окт 2013
Рубрика: Теплотехника | 117 комментариев

…энергию вакуума и еще существующую только в теории – темную энергию. В этой статье, первой в рубрике «Теплотехника», я попытаюсь на простом и доступном языке, используя практический пример, рассказать о важнейшем виде энергии в жизни людей — о тепловой энергии и о рождающей ее во времени тепловой мощности.

Воздействие на систему извне, при котором изменяется ее внутренняя энергия, может являться результатом теплообмена. Тепловая энергия, которая приобретается или теряется системой в результате такого взаимодействия с окружающей средой, называется количеством теплоты и измеряется в системе СИ в Джоулях.

Если вы не инженер-теплотехник, и ежедневно не занимаетесь теплотехническими вопросами, то вам, столкнувшись с ними, иногда без опыта бывает очень трудно быстро в них разобраться. Трудно без наличия опыта представить даже размерность искомых значений количества теплоты и тепловой мощности. Сколько Джоулей энергии необходимо чтобы нагреть 1000 метров кубических воздуха от температуры -37˚С до +18˚С?.. Какая нужна мощность источника тепла, чтобы сделать это за 1 час?.. На эти не самые сложные вопросы способны сегодня ответить «сходу» далеко не все инженеры. Иногда специалисты даже помнят формулы, но применить их на практике могут лишь единицы!

Количество теплоты при различных физических процессах.

Большинство известных веществ могут при разных температуре и давлении находиться в твердом, жидком, газообразном или плазменном состояниях. Переход из одного агрегатного состояния в другое происходит при постоянной температуре (при условии, что не меняются давление и другие параметры окружающей среды) и сопровождается поглощением или выделением тепловой энергии. Не смотря на то, что во Вселенной 99% вещества находится в состоянии плазмы, мы в этой статье не будем рассматривать это агрегатное состояние.

1. Твердое тело, имеющее температуру T1, нагреваем до температуры Tпл, затрачивая на этот процесс количество теплоты равное Q1.

2. Далее начинается процесс плавления, который происходит при постоянной температуре Тпл (температуре плавления). Для расплавления всей массы твердого тела необходимо затратить тепловой энергии в количестве Q2— Q1.

3. Далее жидкость, получившаяся в результате плавления твердого тела, нагреваем до температуры кипения (газообразования) Ткп, затрачивая на это количество теплоты равное Q3—Q2.

4. Теперь при неизменной температуре кипения Ткп жидкость кипит и испаряется, превращаясь в газ. Для перехода всей массы жидкости в газ необходимо затратить тепловую энергию в количестве Q4—Q3.

5. На последнем этапе происходит нагрев газа от температуры Ткп до некоторой температуры Т2. При этом затраты количества теплоты составят Q5—Q4. (Если нагреем газ до температуры ионизации, то газ превратится в плазму.)

Таким образом, нагревая исходное твердое тело от температуры Т1 до температуры Т2 мы затратили тепловую энергию в количестве Q5, переводя вещество через три агрегатных состояния.

Двигаясь в обратном направлении, мы отведем от вещества то же количество тепла Q5, пройдя этапы конденсации, кристаллизации и остывания от температуры Т2 до температуры Т1. Разумеется, мы рассматриваем замкнутую систему без потерь энергии во внешнюю среду.

Заметим, что возможен переход из твердого состояния в газообразное состояние, минуя жидкую фазу. Такой процесс именуется возгонкой, а обратный ему процесс – десублимацией.

Итак, уяснили, что процессы переходов между агрегатными состояниями вещества характеризуются потреблением энергии при неизменной температуре. При нагреве вещества, находящегося в одном неизменном агрегатном состоянии, повышается температура и также расходуется тепловая энергия.

Главные формулы теплопередачи.

Формулы очень просты.

Количество теплоты Q в Дж рассчитывается по формулам:

1. Со стороны потребления тепла, то есть со стороны нагрузки:

1.1. При нагревании (охлаждении):

Q=m*c*(Т2—Т1)

Здесь и далее:

m – масса вещества в кг

с – удельная теплоемкость вещества в Дж/(кг*К)

1.2. При плавлении (замерзании):

Q=m*λ

λ – удельная теплота плавления и кристаллизации вещества в Дж/кг

1.3. При кипении, испарении (конденсации):

Q=m*r

r – удельная теплота газообразования и конденсации вещества в Дж/кг

2. Со стороны производства тепла, то есть со стороны источника:

2.1. При сгорании топлива:

Q=m*q

q – удельная теплота сгорания топлива в Дж/кг

2.2. При превращении электроэнергии в тепловую энергию (закон Джоуля — Ленца):

Q=t*I*U=t*R*I^2=(t/R)*U^2

t – время в с

I – действующее значение тока в А

U – действующее значение напряжения в В

R – сопротивление нагрузки в Ом

Делаем вывод – количество теплоты прямо пропорционально массе вещества при всех фазовых превращениях и при нагреве дополнительно прямо пропорционально разности температур. Коэффициенты пропорциональности (c, λ, r, q) для каждого вещества имеют свои значения и определены опытным путем (берутся из справочников).

Тепловая мощность N в Вт – это количество теплоты переданное системе за определенное время:

N=Q/t

В жизни бывает часто необходимо сделать быстрый оценочный расчет, чтобы понять – имеет ли смысл продолжать изучение темы, делая проект и развернутые точные трудоемкие расчеты. Сделав за несколько минут расчет даже с точностью ±30%, можно принять важное управленческое решение, которое будет в 100 раз более дешевым и в 1000 раз более оперативным и в итоге в 100000 раз более эффективным, чем выполнение точного расчета в течение недели, а то и месяца, группой дорогостоящих специалистов…

Условия задачи:

В помещение цеха подготовки металлопроката размерами 24м х 15м х 7м завозим со склада на улице металлопрокат в количестве 3т. На металлопрокате есть лед общей массой 20кг. На улице -37˚С. Какое количество теплоты необходимо, чтобы нагреть металл до +18˚С; нагреть лед, растопить его и нагреть воду до +18˚С; нагреть весь объем воздуха в помещении, если предположить, что до этого отопление было полностью отключено? Какую мощность должна иметь система отопления, если все вышесказанное необходимо выполнить за 1час? (Очень жесткие и почти не реальные условия – особенно касающиеся воздуха!)

Расчет выполним в программе MS Excel или в программе OOo Calc.

С цветовым форматированием ячеек и шрифтов ознакомьтесь на странице «О блоге».

Исходные данные:

1. Названия веществ пишем:

в ячейку D3: Сталь

в ячейку E3: Лед

в ячейку F3: Лед/вода

в ячейку G3: Вода

в ячейку G3: Воздух

2. Названия процессов заносим:

в ячейки D4, E4, G4, G4: нагрев

в ячейку F4: таяние

3. Удельную теплоемкость веществ c в Дж/(кг*К) пишем для стали, льда, воды и воздуха соответственно

в ячейку D5: 460

в ячейку E5: 2110

в ячейку G5: 4190

в ячейку H5: 1005

4. Удельную теплоту плавления льда λ в Дж/кг вписываем

в ячейку F6: 330000

5. Массу веществ m в кг вписываем соответственно для стали и льда

в ячейку D7: 3000

в ячейку E7: 20

Так как при превращении льда в воду масса не изменяется, то

в ячейках F7 и G7: =E7=20

Массу воздуха находим произведением объема помещения на удельный вес

в ячейке H7: =24*15*7*1,23=3100

6. Время процессов t в мин пишем только один раз для стали

в ячейку D8: 60

Значения времени для нагрева льда, его плавления и нагрева получившейся воды рассчитываются из условия, что все эти три процесса должны уложиться в сумме за такое же время, какое отведено на нагрев металла. Считываем соответственно

в ячейке E8: =E12/(($E$12+$F$12+$G$12)/D8)=9,7

в ячейке F8: =F12/(($E$12+$F$12+$G$12)/D8)=41,0

в ячейке G8: =G12/(($E$12+$F$12+$G$12)/D8)=9,4

Воздух также должен прогреться за это же самое отведенное время, читаем

в ячейке H8: =D8=60,0

7. Начальную температуру всех веществ T1 в ˚C заносим

в ячейку D9: -37

в ячейку E9: -37

в ячейку F9: 0

в ячейку G9: 0

в ячейку H9: -37

8. Конечную температуру всех веществ T2 в ˚C заносим

в ячейку D10: 18

в ячейку E10: 0

в ячейку F10: 0

в ячейку G10: 18

в ячейку H10: 18

Думаю, вопросов по п.7 и п.8 быть недолжно.

Результаты расчетов:

9. Количество теплоты Q в КДж, необходимое для каждого из процессов рассчитываем

для нагрева стали в ячейке D12: =D7*D5*(D10-D9)/1000=75900

для нагрева льда в ячейке E12: =E7*E5*(E10-E9)/1000= 1561

для плавления льда в ячейке F12: =F7*F6/1000= 6600

для нагрева воды в ячейке G12: =G7*G5*(G10-G9)/1000= 1508

для нагрева воздуха в ячейке H12: =H7*H5*(H10-H9)/1000= 171330

Общее количество необходимой для всех процессов тепловой энергии считываем

в объединенной ячейке D13E13F13G13H13: =СУММ(D12:H12) = 256900

В ячейках D14, E14, F14, G14, H14, и объединенной ячейке D15E15F15G15H15 количество теплоты приведено в дугой единице измерения – в ГКал (в гигакалориях).

10. Тепловая мощность N в КВт, необходимая для каждого из процессов рассчитывается

для нагрева стали в ячейке D16: =D12/(D8*60)=21,083

для нагрева льда в ячейке E16: =E12/(E8*60)= 2,686

для плавления льда в ячейке F16: =F12/(F8*60)= 2,686

для нагрева воды в ячейке G16: =G12/(G8*60)= 2,686

для нагрева воздуха в ячейке H16: =H12/(H8*60)= 47,592

Суммарная тепловая мощность необходимая для выполнения всех процессов за время t рассчитывается

в объединенной ячейке D17E17F17G17H17: =D13/(D8*60) = 71,361

В ячейках D18, E18, F18, G18, H18, и объединенной ячейке D19E19F19G19H19 тепловая мощность приведена в дугой единице измерения – в Гкал/час.

На этом расчет в Excel завершен.

Выводы:

Обратите внимание, что для нагрева воздуха необходимо более чем в два раза больше затратить энергии, чем для нагрева такой же массы стали.

При нагреве воды затраты энергии в два раза больше, чем при нагреве льда. Процесс плавления многократно больше потребляет энергии, чем процесс нагрева (при небольшой разности температур).

Нагрев воды в десять раз затрачивает больше тепловой энергии, чем нагрев стали и в четыре раза больше, чем нагрев воздуха.

Мы вспомнили понятия «количество теплоты» и «тепловая мощность», рассмотрели фундаментальные формулы теплопередачи, разобрали практический пример. Надеюсь, что мой язык был прост и понятен.

Ссылка на скачивание файла: raschet-teplovoy-moshchnosti (xls 19,5KB).

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Источник

Загрузить PDF

Удельная теплоемкость — это энергия, необходимая для того, чтобы поднять температуру одного грамма чистого вещества на один градус Цельсия. Удельная теплоемкость вещества зависит от его химического состава и агрегатного состояния. Открытие удельной теплоемкости подстегнуло развитие термодинамики, науки о переходах энергии, касающейся теплоты и работы системы. Удельная теплоемкость и термодинамика широко используются в химии, ядерной инженерии и аэродинамики, а также в повседневной жизни для радиаторов и систем охлаждения автомобилей. Если вы хотите узнать, как вычислить удельную теплоемкость, следуйте приведенной ниже инструкции.

1
Ознакомьтесь с величинами, которые используются для расчета удельной теплоемкости. Очень важно знать величины, которые используются для расчета удельной теплоемкости. Вы должны знать, как выглядит символ каждой величины, и понимать, что он означает. Далее приведены величины, которые обычно используются в выражении для расчета удельной теплоемкости вещества:
- Дельта, или символ «Δ», подразумевает изменение величины.
  - Например, если ваша первая температура (T1) составляет 150 ºC, а вторая (T2) составляет 20 ºC, тогда ΔT, или изменение температуры, составит 150 ºC — 20 ºC = 130 ºC.
- Масса образца обозначается буквой «m».
- Количество теплоты обозначается буквой «Q». Единица измерения количества теплоты — «Дж», или Джоуль.
- «T» — это температура вещества.
- Удельная теплоемкость обозначается буквой «C_p».
2
Освойте выражение для определения удельной теплоемкости. Ознакомившись с величинами, которые используются для вычисления удельной теплоемкости, вы должны выучить уравнение для определения удельной теплоемкости вещества. Формула имеет вид: C_p = Q/mΔT.
- Вы можете оперировать этой формулой, если хотите узнать изменение количества теплоты вместо удельной теплоемкости. Вот как это будет выглядеть:
  - ΔQ = mC_pΔT
Реклама

1

Изучите формулу. Сначала вам нужно изучить выражение для того, чтобы понять, что вам нужно сделать, чтобы найти удельную теплоемкость. Давайте рассмотрим следующую задачу: Определите удельную теплоемкость 350 г неизвестного вещества, если при сообщении ему 34 700 дж теплоты его температура поднялась с 22 до 173 ºC без фазовых переходов.
2
Запишите известные и неизвестные факторы. Разобравшись с задачей, вы можете записать все известные и неизвестные переменные, чтобы лучше понять, с чем вы имеете дело. Вот как это делается:
- m = 350 г
- Q = 34 700 Дж
- ΔT = 173 ºC — 22 ºC = 151 ºC
- C_p = неизвестно
3
Подставьте неизвестные факторы в уравнение. Известны все значения за исключением «C_pc», поэтому необходимо подставить в исходное уравнение все остальные факторы и найти «C_p». Делать это нужно так:
- Исходное уравнение: C_p = Q/mΔT
- c = 34 700 Дж/(350 г x 151 ºC)
4
Найдите ответ. Теперь, после того как вы подставили известные величины в выражение, вам осталось выполнить несколько простейших арифметических действий, чтобы узнать ответ. Удельная теплоемкость — окончательный ответ — составляет 0,65657521286 Дж/(г x ºC).
- C_p = 34,700 Дж/(350 г x 151 ºC)
- C_p = 34,700 Дж/(52850 г x ºC)
- C_p = 0,65657521286 Дж/(г x ºC)
Реклама

Советы

Металл нагревается быстрее воды из-за низкой удельной теплоемкости.
При нахождении удельной теплоемкости сокращайте единицы измерения тогда, когда это возможно.
Удельную теплоемкость многих материалов можно найти в интернете для проверки вашего ответа.
Иногда для изучения процессе теплопередачи в процессе физических или химических превращений может использоваться калориметр.
Изменение температуры при прочих равных условиях значительнее для материалов с низкой удельной теплоемкостью.
Системная единица СИ (Международная система единиц измерения) удельной теплоемкости — джоуль на градус Цельсия на грамм. В странах с британской системой мер она измеряется в калориях на градус Фаренгейта на фунт.
Изучите формулу расчета удельной теплоемкости пищевых продуктов C_p = 4,180 x w + 1,711 x p + 1,928 x f + 1,547 x c + 0,908 x a — это уравнение для нахождения удельной теплоемкости, где «w» — процентное содержание воды в продукте, «p» — процентное содержание белков, «f» — процентное содержание жиров, «c» — процентное содержание углеводов и «a» — процентное содержание неорганических компонентов. Уравнение учитывает массовую долю (x) всех твердых веществ, которые составляют пищу. Расчет удельной теплоемкости приведен в кДж/(кг х K).

Об этой статье

Эту страницу просматривали 112 744 раза.

Была ли эта статья полезной?

Источник

Удельная теплоёмкость — это энергия, которая требуется для увеличения температуры 1 грамма чистого вещества на 1°. Параметр зависит от его химического состава и агрегатного состояния: газообразное, жидкое или твёрдое тело. После его открытия начался новый виток развития термодинамики, науки о переходных процессах энергии, которые касаются теплоты и функционирования системы.

Как правило, удельная теплоёмкость и основы термодинамики используются при изготовлении радиаторов и систем, предназначенных для охлаждения автомобилей, а также в химии, ядерной инженерии и аэродинамике. Если вы хотите узнать, как рассчитывается удельная теплоёмкость, то ознакомьтесь с предложенной статьёй.

Содержание:

Формула
Инструкция по расчёту параметра
Расчёт
Как рассчитать теплоемкость продуктов питания
Полезные советы
Видео

Формула

Перед тем, как приступить к непосредственному расчёту параметра следует ознакомиться с формулой и её компонентами.

Формула для расчёта удельной теплоёмкости имеет следующий вид:

с = Q/(m*∆T)

Знание величин и их символических обозначений, использующихся при расчёте, крайне важно. Однако необходимо не только знать их визуальный вид, но и чётко представлять значение каждого из них. Расчёт удельной теплоёмкости вещества представлен следующими компонентами:

ΔT – символ, означающий постепенное изменение температуры вещества. Символ «Δ» произносится как дельта.

ΔT можно рассчитать по формуле:

ΔT = t2–t1, где

t1 – первичная температура;
t2 – конечная температура после изменения.

m – масса вещества используемого при нагреве (гр).

Q – количество теплоты (Дж/J)

На основании Цр можно вывести и другие уравнения:

Q = m*цp*ΔT – количество теплоты ;
m = Q/цр*(t2 — t1) – массы вещества;
t1 = t2–(Q/цp*m) – первичной температуры;
t2 = t1+(Q/цp*m) – конечной температуры.

Инструкция по расчёту параметра

Рассчитать с вещества достаточно просто и чтобы это сделать нужно, выполнить следующие шаги:

Взять расчётную формулу: Теплоемкость = Q/(m*∆T)
Выписать исходные данные.
Подставить их в формулу.
Провести расчёт и получим результат.

В качестве примера произведём расчёт неизвестного вещества массой 480 грамм обладающего температурой 15ºC, которая в результате нагрева (подвода 35 тыс. Дж) увеличилась до 250º.

Согласно инструкции приведённой выше производим следующие действия:

Выписываем исходные данные:

Q = 35 тыс. Дж;
m = 480 г;
ΔT = t2–t1 =250–15 = 235 ºC.

Берём формулу, подставляем значения и решаем:

с=Q/(m*∆T)=35тыс.Дж/(480 г*235º)=35тыс.Дж/(112800 г*º)=0,31 Дж/г*º.

Расчёт

Выполним расчёт C_P воды и олова при следующих условиях:

m = 500 грамм;
t1 =24ºC и t2 = 80ºC – для воды;
t1 =20ºC и t2 =180ºC – для олова;
Q = 28 тыс. Дж.

Для начала определяем ΔT для воды и олова соответственно:

ΔТв = t2–t1 = 80–24 = 56ºC
ΔТо = t2–t1 = 180–20 =160ºC

Затем находим удельную теплоёмкость:

с=Q/(m*ΔТв)= 28 тыс. Дж/(500 г *56ºC) = 28 тыс.Дж/(28 тыс.г*ºC) = 1 Дж/г*ºC.
с=Q/(m*ΔТо)=28тыс.Дж/(500 гр*160ºC)=28 тыс.Дж/(80 тыс.г*ºC)=0,35 Дж/г*ºC.

Таким образом, удельная теплоемкость воды составила 1 Дж/г *ºC, а олова 0,35 Дж/г*ºC. Отсюда можно сделать вывод о том, что при равном значении подводимого тепла в 28 тыс. Дж олово нагрется быстрее воды, поскольку его теплоёмкость меньше.

Теплоёмкостью обладают не только газы, жидкости и твёрдые тела, но и продукты питания.

Как рассчитать теплоемкость продуктов питания

При расчёте емкости питания уравнение примет следующий вид:

с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908 *a), где:

w – количество воды в продукте;
p – количество белков в продукте;
f – процентное содержание жиров;
c – процентное содержание углеводов;
a – процентное содержание неорганических компонентов.

Определим теплоемкость плавленого сливочного сыра Viola. Для этого выписываем нужные значения из состава продукта (масса 140 грамм):

вода – 35 г;
белки – 12,9 г;
жиры – 25,8 г;
углеводы – 6,96 г;
неорганические компоненты – 21 г.

Затем находим с:

с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908*a)=(4.180*35)+(1.711*12,9)+(1.928*25,8) + (1.547*6,96)+(0.908*21)=146,3+22,1+49,7+10,8+19,1=248 кДж /кг*ºC.

Полезные советы

Всегда помните, что:

процесс нагревания металла проходит быстрее, чем у воды, так как он обладает C_P в 2,5 раза меньше;
по возможности преобразуйте полученные результаты в более высокий порядок, если позволяют условия;
в целях проверки результатов можно воспользоваться интернетом и посмотреть с для расчётного вещества;
при равных экспериментальных условиях более значительные температурные изменения будут наблюдаться у материалов с низкой удельной теплоёмкостью.

Видео

Разобраться в этой теме вам поможет видео урок.

Источник

В этой главе…

Достигаем теплового равновесия
Сохраняем тепловую энергию при различных условиях
Повышаем эффективность тепловых двигателей
Падаем почти до абсолютного нуля

Каждому, кому когда-либо приходилось работать летом на открытом воздухе, хорошо известны понятия “тепло” и “работа”, связь между которыми изучает термодинамика. В данной главе, наконец-то, встречаются эти два незабвенных понятия, о которых подробно рассказывается в главе 8 (о работе) и в главе 13 (о тепле, теплоте и тепловой энергии). В термодинамике имеется три закона, а точнее начала, которые также важны для термодинамики, как и законы Ньютона для механики. Кроме того, уж в одном отношении они даже превосходят законы Ньютона, а именно в том, что в термодинамике имеется еще и нулевой закон, который чаще называют нулевым началом термодинамики. В этой главе рассказывается о термодинамическом равновесии (нулевое начало), сохранении энергии (первое начало), о тепловых потоках (второе начало) и недостижимости абсолютного нуля (третье начало). Итак, самое время обратиться к термодинамике.

Содержание

Стремимся к тепловому равновесию: нулевое начало термодинамики
Сохраняем энергию: первое начало термодинамики
- Применяем закон сохранения энергии
- Изучаем изобарические, изохорические, изотермические и адиабатические процессы
  - Постоянное давление: изобарический процесс
  - Постоянный объем: изохорический процесс
  - Постоянная температура: изотермический процесс
  - Постоянная энергия: адиабатический процесс
- Вычисляем удельную теплоемкость
Передаем тепловую энергию: второе начало термодинамики
- Заставим тепловую энергию работать: тепловые двигатели
- Оцениваем эффективность работы: КПД теплового двигателя
- Как сказал Карно: нельзя все тепло превратить в работу
  - Построение двигателя Карно
  - Используем формулу Карно
Охлаждаемся: третье (и абсолютно последнее) начало термодинамики

Стремимся к тепловому равновесию: нулевое начало термодинамики

Основные законы термодинамики начинаются с нулевого начала. Возможно, эта нумерация покажется странной, ведь мало какой набор вещей из повседневной жизни начинается подобным образом (“Будь осторожен на нулевой ступеньке…”), но, знаете ли, физикам нравятся их традиции. Так вот, нулевое начало термодинамики гласит, что два тела находятся в тепловом равновесии, если они могут передавать друг другу теплоту, но не делают этого. (В русскоязычной научной литературе нулевое начало термодинамики называют также общим началом термодинамики. — Примеч. ред.)

Например, если у вас и у воды в плавательном бассейне, в котором вы находитесь, одна и та же температура, то никакое тепло от вас к воде или от воды к вам не передается (хотя такая передача возможна). Ваше тело и бассейн находятся в тепловом равновесии. Однако, если вы прыгнете в бассейн зимой, проломив при этом его ледяную корку, то первое время вряд ли будете в тепловом равновесии с его водой. Впрочем, вы и не захотите этого. (Не пытайтесь проделать этот физический опыт дома!)

Чтобы обнаружить тепловое равновесие (особенно в замерзших бассейнах, куда вы собираетесь прыгнуть), надо использовать термометр. Измерьте с его помощью температуру воды в бассейне, а затем — свою температуру. Если обе температуры совпадают (другими словами, наблюдается тепловое равновесие: ваше — с термометром, а термометра — с водой в бассейне), то в таком случае вы находитесь в тепловом равновесии с водой бассейна.

Использование термометра показывает: два тела, находящиеся в тепловом равновесии с третьим, также находятся в тепловом равновесии друг с другом; вот вам еще одна формулировка нулевого начала.

Кроме всего прочего, нулевое начало содержит идею, что температура — это индикатор теплового равновесия. То, что два тела, упомянутые в нулевом законе, находятся в тепловом равновесии с третьим, дает все нужное дая задания температурной шкалы, например шкалы Кельвина. Ну а с физической точки зрения нулевой закон устанавливает точку отсчета, утверждая, что между двумя телами, имеющими одинаковую температуру, тепловой поток в целом отсутствует.

Сохраняем энергию: первое начало термодинамики

Первое начало термодинамики — это, попросту говоря, закон сохранения энергии. Он утверждает, что энергия никуда не исчезает. Когда системой поглощается или высвобождается тепловая энергия ( Q ), а сама система выполняет над окружающими телами работу ( W ) (или, наоборот, окружающие тела выполняют работу над ней), то внутренняя энергия системы, имевшая начальное значение ( U_н ), становится равной ( U_к ) следующим образом:

В главе 8 немало говорится о сохранении механической энергии. Там показано, что общая механическая энергия (сумма потенциальной и кинетической энергии) сохраняется. Чтобы утверждать такое, надо было работать с системами, где энергия не тратится на нагревание, — например, когда отсутствует трение. Теперь все изменилось. Тепловая энергия, наконец-то, учитывается нами (как вы, вероятно, поняли из рассуждений), и теперь общую энергию системы можно рассматривать с учетом передачи тепловой энергии, проделанной работы и внутренней энергии системы.

На основании комбинации этих трех величин (тепловой энергии, работы и внутренней энергии) определяется общая энергия системы, которая в целом сохраняется. Если передать системе количество тепловой энергии, равное ( Q ), то при отсутствии работы ее количество внутренней энергии, обозначаемое как ( U ), изменится на ( Q ). Система может терять энергию, выполняя работу над окружающими телами, например, когда машина поднимает груз, висящий на конце каната. Так вот, когда система выполняет работу над окружающими телами и никакой тепловой энергии не тратит, ее внутренняя энергия ( U ) изменится на ( W ). Иначе говоря, если учитывать тепловую энергию, то с учетом всех этих трех величин (тепловой энергии, работы и внутренней энергии) общая энергия системы сохраняется.

Польза первого начала термодинамики состоит в том, что оно связывает все три основные величины: тепловую энергию, работу и внутреннюю энергию. Зная две из них, всегда можно определить третью.

Применяем закон сохранения энергии

Величина передаваемой тепловой энергии ( Q ) является положительной или отрицательной, когда система, соответственно, поглощает или высвобождает тепловую энергию. Величина работы ( W ) является положительной или отрицательной, когда работа, соответственно, выполняется системой над окружающими телами или окружающими телами над системой.

Новички часто путаются, пытаясь определить, являются ли значения каждой из величин положительными или отрицательными. Чтобы не запутаться, при работе с первым началом термодинамики рекомендуется исходить из общей идеи сохранения энергии. Допустим, что мотор выполняет над окружающими телами работу в 2000 Дж, высвобождая при этом 3000 Дж тепловой энергии. Насколько меняется его внутренняя энергия? В данном случае известно, что мотор выполняет над окружающими телами работу в 2000 Дж, поэтому ясно, что его внутренняя энергия уменьшается на 2000 Дж. Кроме того, выполняя работу, он еще высвобождает 3000 Дж тепловой энергии, так что внутренняя энергия мотора уменьшается еще на 3000 Дж.

Значения работы и передаваемой тепловой энергии следует считать отрицательными. Тогда в предыдущем примере получим такое изменение внутренней энергии:

Внутренняя энергия системы уменьшается на 5000 Дж, что определенно имеет смысл, ведь система выполняет над окружающими телами работу в 2000 Дж и высвобождает 3000 Дж тепловой энергии. С другой стороны, а что если система, выполняя над окружающими телами работу в 2000 Дж, поглощает 3000 Дж их тепловой энергии? В таком случае получилось бы 2000 Дж входящей и 3000 Дж исходящей энергии. Теперь понятно, какими должны быть знаки:

В данном случае общее изменение внутренней энергии системы равно +1000 Дж. Отрицательное значение работа принимает, когда она выполняется над системой окружающими телами. Например, система поглощает 3000 Дж, в то время как окружающие тела выполняют над ней работу в 4000 Дж. Это значит, что внутренняя энергия системы увеличивается на 3000 Дж + 4000 Дж = 7000 Дж. А если нужно все просчитать, то воспользуйтесь следующей формулой:

а затем обратите внимание, что поскольку окружающие тела выполняют работу над системой, значение ( W ) считается отрицательным. Таким образом, получаем:

Изучаем изобарические, изохорические, изотермические и адиабатические процессы

В этой главе рассматриваются процессы, при анализе которых приходится работать с такими параметрами, как объем, давление, температура и энергия. Причем полученные результаты очень сильно зависят от того, как эти величины меняются. Например, если газ выполняет работу, сохраняя свой объем постоянным, то этот процесс будет отличаться от того, при котором остается постоянным не объем, а давление газа.

В термодинамике обычно рассматривают четыре стандартных режима, которые отличаются постоянством одного из вышеперечисленных параметров (давление, объем, температура и энергия).

Обратите внимание, что изменения в процессах, описанных в последующих разделах, называются квазистатическими, т.е. эти изменения проходят достаточно медленно, позволяя давлению и температуре оставаться одинаковыми в любом месте системы.

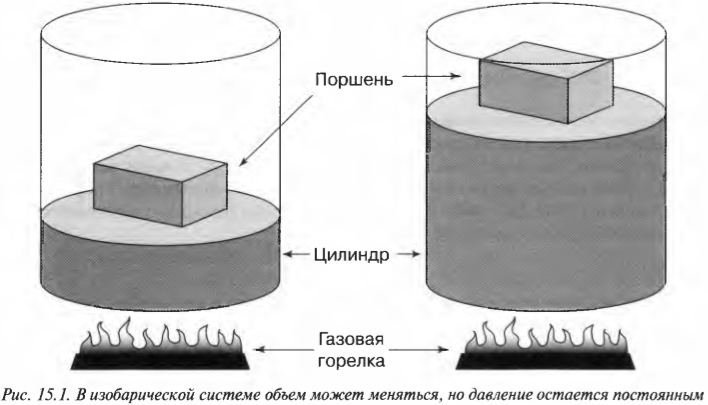
Постоянное давление: изобарический процесс

Процесс, в котором давление остается постоянным, называется изобарическим (“барический” означает “относящийся к давлению”). На рис. 15.1 показан цилиндр с поршнем, поднимаемым некоторым количеством газа, когда этот газ нагревается. Объем газа меняется, но утяжеленный поршень сохраняет давление постоянным.

Какую работу выполняет система при расширении газа? Работа равна произведению ( F ) на ( s ), означающих, соответственно, силу и перемещение. Кроме того, сила равна произведению ( P ) на ( A ), означающих, соответственно, давление и площадь. Это значит, что:

Но произведение площади ( A ) и перемещения ( s ) равно изменению объема ( Delta!V ). Таким образом:

Изобарический процесс можно показать в виде графика (как на рис. 15.2), на котором видно, что объем меняется, в то время как давление остается постоянным. Так как ( W=PDelta!V ), то работа — это площадь, ограниченная графиком.

Допустим, имеется 60 м³ идеального газа под давлением в 200 Па (см. главу 2), который нагревается до тех пор, пока он не расширится до объема в 120 м³ (( PV= nRT ), где ( n ), ( R ) и ( Т ) означают, соответственно, количество молей, универсальную газовую постоянную (8,31) и температуру; см. главу 14). Какую работу выполняет газ? Все, что вам нужно, — это подставить в формулу численные значения:

Расширяясь при постоянном давлении, газ выполняет работу в 12000 Дж.

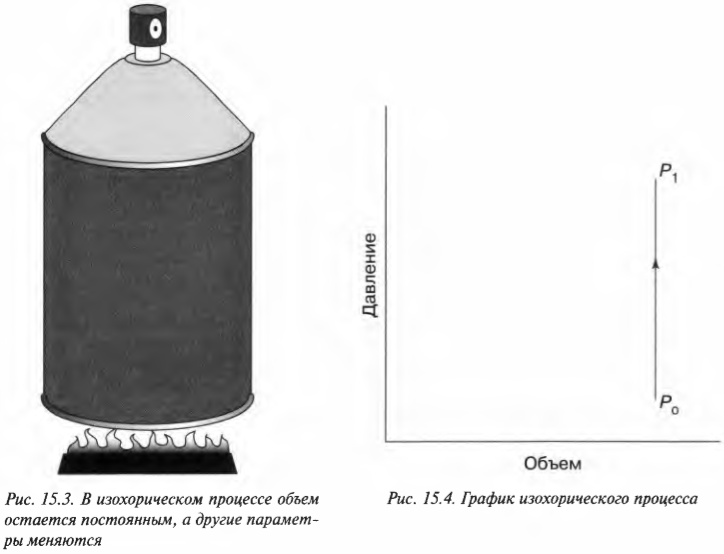
Постоянный объем: изохорический процесс

А что если давление в системе не постоянно? В конце концов, не так уж и часто попадаются устройства с утяжеленным поршнем, как на рис. 15.1. Чаще всего приходится иметь дело с простым замкнутым сосудом, как на рис. 15.3, где показан баллончик с дезодорантом, кем-то неосторожно брошенный в огонь. В этом случае объем остается постоянным, а такой процесс называется изохорическим. По мере того как газ внутри баллончика нагревается, его давление возрастает, но объем остается постоянным (если, конечно, баллончик не взорвется).

Какая работа выполняется с баллончиком распылителя? Посмотрите на график (рис. 15.4). В данном случае объем постоянный, поэтому ( Fs ) (произведение силы и перемещения) равно нулю. Никакая работа не выполняется — площадь под графиком равна нулю.

Постоянная температура: изотермический процесс

В изотермическом процессе температура остается постоянной, в то время как другие величины меняются. Посмотрите, какой замечательный аппарат показан на рис. 15.5. Этот аппарат специально предназначен для того, чтобы сохранять температуру газа постоянной, причем даже при подъеме поршня. При добавлении к системе (или отводе от системы) тепловой энергии поршень медленно поднимается (или медленно опускается) таким образом, чтобы произведение давления и объема сохранялось постоянным. Так как ( PV= nRT ) (см. главу 14), то температура также остается постоянной.

Какая работа выполняется при изменении объема? Поскольку ( PV= nRT ), то получается такое отношение между ( P ) и ( V ):

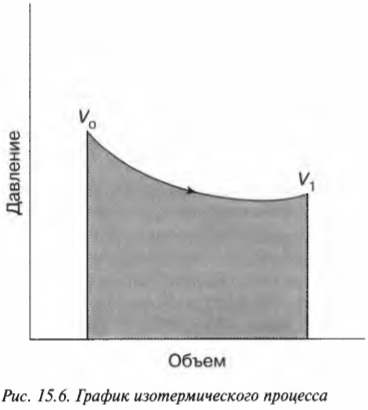
Эту формулу иллюстрирует график, показанный на рис. 15.6.

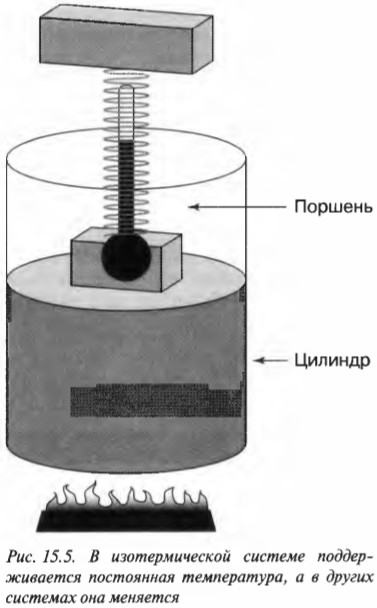
Выполненную работу “показывает” область, лежащая под графиком. Но какова же площадь этой области? Выполненная работа определяется следующей формулой, где ( ln ) — натуральный логарифм, ( R ) — газовая постоянная (8,31), ( V_1 ) и ( V_0 ) означают, соответственно, конечный и начальный объем:

Так как при изотермическом процессе температура остается постоянной, а внутренняя энергия идеального газа равна ( (3/2)nRT ) (см. главу 14), то эта энергия не меняется. Таким образом:

другими словами:

Итак, что произойдет, если цилиндр, показанный на рис. 15.5, погрузить в горячую ванну? В аппарат должна перейти тепловая энергия ( Q ), а поскольку температура газа остается постоянной, вся эта тепловая энергия должна превратиться в работу, выполненную системой. Скажем, к примеру, у вас имеется моль гелия при температуре 20°С, и, забавы ради, вы решили увеличить его объем с ( V_0 ) = 0,010 м³ до ( V_1 ) = 0,020 м³. Какую работу выполнит газ при расширении? Все, что вам нужно, — это подставить в формулу численные значения:

Работа, выполняемая газом, равна 1690 Дж. Изменение его внутренней энергии равно 0 Дж, как всегда при изотермическом процессе. А так как ( Q=W ), то добавляемая к газу тепловая энергия также равна 1690 Дж.

Постоянная энергия: адиабатический процесс

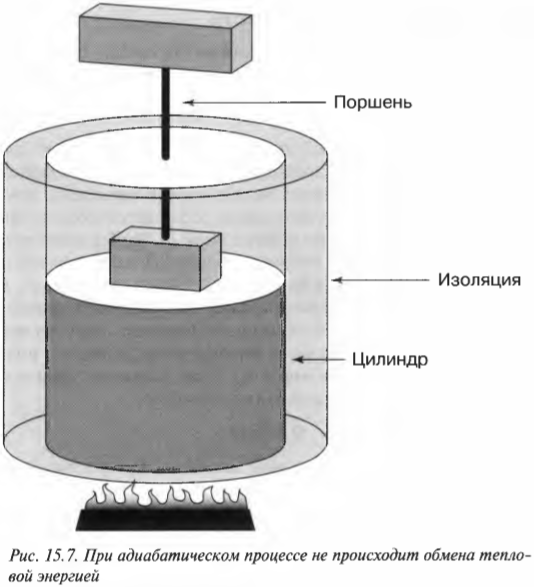
При адиабатическом процессе общая тепловая энергия системы остается постоянной. Посмотрите на рис. 15.7, где показан цилиндр, окруженный изоляционным материалом. Тепловая энергия из системы никуда не уходит, поэтому если происходит изменение, то оно является адиабатическим.

Вычисляя работу, выполняемую при адиабатическом процессе, вы можете сказать, что ( Q ) = 0, таким образом:

Так как внутренняя энергия ( U ) идеального газа равна ( (3/2)nRT ) (см. главу 14), то выполняется работа:

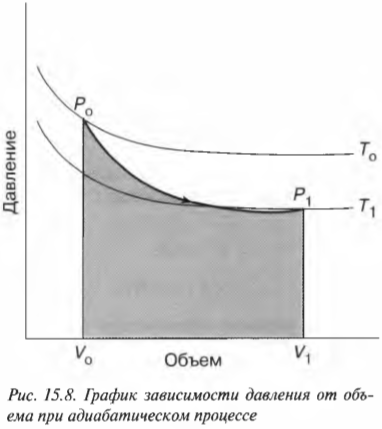
где ( T_0 ) и ( T_1 ) означают, соответственно, начальную и конечную температуру. Таким образом, если газ выполняет работу, то это происходит благодаря изменению температуры — при падении температуры газ выполняет работу над окружающими телами. На рис. 15.8 показан график зависимости давления от объема при адиабатическом процессе. Адиабатическая кривая, показанная на этом рисунке, так называемая адиабата, отличается от изотермических кривых, так называемых изотерм. Работа, выполненная, когда общая тепловая энергия системы постоянна, — это область под адиабатой (см. рис. 15.8).

Вычисляем удельную теплоемкость

Начальные значения давления и объема можно так связать с их конечными значениями по следующей формуле:

Что такое ( gamma )? Это отношение ( C_p/C_v ) двух удельных теплоемкостей идеального газа: в числителе — теплоемкость при постоянном давлении ( C_p ), а в знаменателе — теплоемкость при постоянном объеме ( C_v ). Удельной теплоемкостью называется отношение тепловой энергии, полученной телом единичной массы, к соответствующему приращению его температуры; подробнее об этом можно узнать в главе 13. Чтобы вычислить удельную теплоемкость, надо найти количество тепловой энергии ( Q ), необходимой для изменения температуры тела единичной массы на величину ( Delta T ), т.е. ( c=Q/mDelta T ), где ( c ), ( m ) и ( Delta T ) означают, соответственно, удельную теплоемкость, массу и изменение температуры. Впрочем, сейчас удобнее использовать молярную удельную теплоемкость, которая определяется как и удельная, но только рассчитывается не на единицу массу, а на один моль. Она обозначается символом ( C ) и измеряется в Дж/(моль·К). Итак, молярная удельная теплоемкость используется вместе с количеством молей ( n ), а не массой ( m ):

Как найти ( C )? Надо вычислить две разные величины: ( C_mathrm{p} ) (при постоянном давлении) и ( C_mathrm{v} ) (при постоянном объеме). Согласно первому началу термодинамики (см. предыдущий раздел этой главы), ( Q=Delta U+W ). Поэтому достаточно только выразить ( Delta U ) через ( T ). Выполняемая работа ( W ) равна ( PDelta!V ), тогда при постоянном объеме ( W ) = 0. А изменение внутренней энергии идеального газа равно ( (3/2)nRDelta T ) (см. главу 14), поэтому ( Q ) при постоянном объеме выражается следующей формулой:

При постоянном давлении работа ( W ) равна ( PDelta!V ). А поскольку ( PV= nRT ), то ( W=P(V_1-V_0)=nR(T_1-T_0) ). Поэтому ( Q ) при постоянном давлении выражается следующей формулой:

Каким образом можно получить из всего этого значения молярных удельных теплоемкостей? Как уже нам известно, ( Q=CnDelta T ), поэтому ( C=Q/nDelta T ). Деля предыдущие две формулы на ( nDelta T ), получаем:

Теперь вы имеете молярные удельные теплоемкости идеального газа. Нужное вам отношение ( gamma ) равно отношению этих двух формул:

Связать давление и объем в любых двух точках адиабаты (см. предыдущий раздел об адиабатическом процессе) можно таким образом:

Например, если сначала 1 л газа находился под давлением 1 атм, а после адиабатического изменения (когда обмена тепловой энергией нет), объем газа стал 2 л, то каким должно быть новое давление ( P_1 )? Путем простой алгебраической операции деления на ( V_1^{5/3} ) оставляем в левой части равенства только ( P_1 ) и получаем:

Подставив в эту формулу численные значения, получим:

Итак, новое давление должно быть равно 0,314 атмосферы.

Передаем тепловую энергию: второе начало термодинамики

Формально говоря, второе начало термодинамики гласит, что тепловая энергия естественно переходит из тела с более высокой температурой в тело с более низкой температурой, но не в обратном направлении.

Это начало, конечно же, появилось в результате простых наблюдений: приходилось ли вам когда-либо видеть, чтобы тело само становилось холоднее окружающих его тел, если только другое тело не проделало над ним определенной работы? Путем определенной работы можно заставить теплоту переходить из тела, когда естественно ожидать перехода тепловой энергии в тело (вспомните холодильники или кондиционеры), но такое явление само по себе не происходит.

Заставим тепловую энергию работать: тепловые двигатели

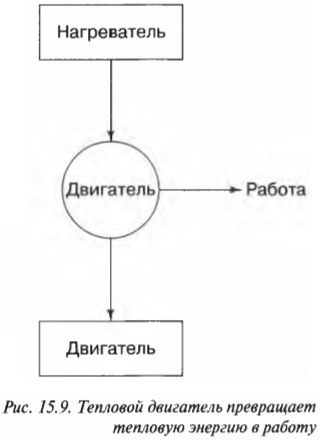
Имеется много способов заставить тепловую энергию работать. Возможно, у вас имеется, например, паровая машина с котлом и поршнями или атомный реактор, производящий перегретый пар, который может вращать турбину. Двигатели, выполняющие работу благодаря источнику тепловой энергии, называются тепловыми. Как они это делают, можно увидеть на рис. 15.9. Тепловая энергия идет от нагревателя к двигателю, который выполняет работу, а неизрасходованная тепловая энергия отправляется в холодильник. Им может быть, например, окружающий воздух или наполненный водой радиатор. Если температура холодильника меньше температуры нагревателя, то тепловой двигатель может работать — хотя бы теоретически.

Оцениваем эффективность работы: КПД теплового двигателя

Тепловая энергия, подаваемая нагревателем, обозначается как ( Q_{нг} ), а отправляемая в холодильник (см. предыдущий раздел) — как ( Q_{mathrm{x}} ). Путем некоторых вычислений можно найти коэффициент полезного действия (КПД) теплового двигателя. Он равен отношению работы ( W ), выполняемой двигателем, к входящей тепловой энергии — иными словами, это та доля входящей тепловой энергии, которую двигатель превращает в работу:

Когда вся входящая тепловая энергия превращается в работу, КПД равен 1. Если никакая входящая тепловая энергия не превращается в работу, КПД равен 0. Часто КПД выражается в виде процентов, поэтому только что названные значения можно представить как 100% и 0%. Поскольку общая энергия сохраняется, то тепловая энергия, входящая в двигатель, должна быть равна сумме выполняемой работы и тепловой энергии, отправляемой в холодильник, то есть:

Это значит, что для записи КПД достаточно использовать ( Q_{нг} ) и ( Q_{mathrm{x}} ):

Допустим, что имеется тепловой двигатель с КПД, равным 78%. Этот двигатель производит работу величиной 2,55·10⁷ Дж. Сколько тепловой энергии он использует, а сколько выбрасывает? Известно, что ( W ) = 2,55·10⁷ Дж и

Это значит, что:

Количество входящей тепловой энергии равно 3,27·10⁷ Дж. А сколько тепловой энергии ( Q_{mathrm{x}} ) остается неизрасходованной и отправляется в холодильник? Как известно:

поэтому:

Подставив в эту формулу численные значения, получим:

Количество тепловой энергии, отправляемое в холодильник, равно 0,72·10⁷ Дж.

Как сказал Карно: нельзя все тепло превратить в работу

Зная работу и КПД теплового двигателя, можно вычислить количество входящей и исходящей тепловой энергии (тут нам, конечно, поможет закон сохранения энергии, связывающий друг с другом работу, входящую и исходящую тепловую энергию; см. главу 8). А как насчет создания тепловых двигателей со 100%-ным КПД? С точки зрения производительности было бы прекрасно превращать в работу всю тепловую энергию, какая поступает в тепловой двигатель, но это невозможно. Кроме того, в реально работающих тепловых двигателях неизбежны определенные потери, например, из-за трения поршней в паровом двигателе. В XIX веке эту проблему изучал один инженер, которого звали Сади Карно, и он пришел к выводу: в сущности, лучшее, что можно сделать, — это попытаться изобрести двигатель, не имеющий таких потерь.

А если в двигателе нет потерь, то система будет возвращаться в то же состояние, что и перед началом процесса. Такой процесс называется обратимым. Например, если тепловой двигатель тратит энергию на преодоление трения, то обратимым процесс назвать нельзя, так как он не заканчивается в том же состоянии, в каком был сначала. При каких условиях работы тепловой двигатель будет иметь самый высокий КПД? Когда работа двигателя обратима (т.е. в системе нет потерь). Сегодня физики называют это принципом Карно. Итак, принцип Карно гласит, что ни у одного необратимого двигателя не будет такого же высокого КПД, как у обратимого, а все обратимые двигатели, работающие в промежутке между одинаковыми максимальными и одинаковыми минимальными температурами, имеют один и тот же КПД.

Построение двигателя Карно

Карно предложил свою идею двигателя — двигателя Карно. Этот двигатель должен работать обратимо, что не может быть ни в одном реально работающем двигателе, поэтому он представляет собой нечто идеальное. В двигателе Карно тепловая энергия идет от нагревателя, имеющего постоянную температуру ( T_{нг} ). А отработанная тепловая энергия уходит в холодильник, имеющий постоянную температуру ( T_{х} ). Поскольку температуры нагревателя и холодильника никогда не меняются, то можно сказать, что отношение подаваемой и отводимой тепловой энергии равно отношению их температур (в кельвинах):

А так как КПД теплового двигателя вычисляется по следующей формуле:

то получается такая формула для вычисления КПД двигателя Карно:

где температура выражается в кельвинах.

В этой формуле показан максимально возможный КПД теплового двигателя. И лучшего результата достичь нельзя. А как гласит третье начало термодинамики (в последнем разделе этой главы), абсолютного нуля достичь нельзя, т.е. ( T_{х} ) никогда не будет равна нулю, следовательно, невозможно получить тепловой двигатель со 100%-ным КПД.

Используем формулу Карно

Формулу максимально возможного КПД (см. предыдущий раздел) использовать довольно легко. Предположим, сделано потрясающее новое изобретение: машина Карно, в которой самолет совершает работу, причем земная поверхность играет роль нагревателя (с температурой примерно 27°С), а воздух на высоте 10000 м — роль холодильника (с температурой примерно -27°С). Какой максимальный КПД такой машины? Преобразуем значения температуры в кельвины и подставив их в формулу машины Карно:

Итак, КПД такой машины Карно равен всего 17,3%. Результат, скажем, не очень. А теперь представим, что в качестве нагревателя используется поверхность Солнца (примерно 5800 К), а в качестве холодильника — межзвездное пространство (примерно 3,4 К), совсем как в научно-фантастических рассказах. Тогда совсем другое дело:

Итак, в таких научно-фантастических условиях для машины Карно можно получить КПД, равный 99,9% и близкий к теоретически максимальному значению.

Охлаждаемся: третье (и абсолютно последнее) начало термодинамики

Третье начало термодинамики достаточно просто формулируется: нельзя достичь абсолютного нуля с помощью любого процесса, состоящего из конечного числа этапов, к нему можно лишь бесконечно приближаться. Иначе говоря, никогда нельзя достичь абсолютного нуля. Каждое действие по понижению температуры физического тела до абсолютного нуля может немного приблизить к цели, но достигнуть ее нельзя, если не выполнить бесконечного числа действий, что невозможно.

Странные явления вблизи абсолютного нуля

Хотя до абсолютного нуля нельзя добраться с помощью какого-либо известного конечного процесса, но к нему можно приблизиться. Причем, имея очень дорогое оборудование, вблизи абсолютного нуля можно столкнуться с множеством странных физических явлений и фактов. Один мой приятель изучает поведение жидкого гелия при очень низких температурах. Например, гелий становится таким эксцентричным, что может самостоятельно выбраться из любого сосуда, в котором он находится. За открытие и исследования этого явления сверхтекучести гелия и некоторые другие наблюдения кое-кто получил Нобелевскую премию. Везет же людям!

(Сверхтекучесть жидкого гелия-4 была открыта в 1938 году П. Л. Капицей, за что он был удостоен Нобелевской премии по физике за 1978 год. Теория сверхтекучего гелия-Н была разработана Л. Д. Ландау, за что он был удостоен Нобелевской премии по физике за 1962 год. — Примеч. ред.)

Глава 15. Тепловая энергия и работа: начала термодинамики

3.1 (62.86%) 7 votes

Источник

Удельная теплоемкость вещества

Примеры решения задач

Задача №1

Задача №2

О тепловой энергии простым языком!

Количество теплоты при различных физических процессах.

Главные формулы теплопередачи.

Формулы для количества теплоты через мощность

Как рассчитать тепловую мощность конвекторов, обогревателей и прочих отопительных приборов

Для чего нужен тепловой расчет?

Простейший расчет тепловой мощности обогревателя

Пример расчетов

Что такое тепловой расчет?

Формула расчета тепловой нагрузки с учетом разницы температур

Что еще необходимо учесть при расчете

Формула расчета тепловой мощности с учетом дополнительных факторов

Пример расчета

Расчет для прибора

Особый случай

О тепловой энергии простым языком!

Количество теплоты при различных физических процессах.

Главные формулы теплопередачи.

Условия задачи:

Исходные данные:

Результаты расчетов:

Выводы:

Статьи с близкой тематикой

Отзывы

Советы

Об этой статье

Была ли эта статья полезной?

Формула

Инструкция по расчёту параметра

Расчёт

Как рассчитать теплоемкость продуктов питания

Полезные советы

Видео

Стремимся к тепловому равновесию: нулевое начало термодинамики

Сохраняем энергию: первое начало термодинамики

Применяем закон сохранения энергии

Изучаем изобарические, изохорические, изотермические и адиабатические процессы

Постоянное давление: изобарический процесс

Постоянный объем: изохорический процесс

Постоянная температура: изотермический процесс

Постоянная энергия: адиабатический процесс

Вычисляем удельную теплоемкость

Передаем тепловую энергию: второе начало термодинамики

Заставим тепловую энергию работать: тепловые двигатели

Оцениваем эффективность работы: КПД теплового двигателя

Как сказал Карно: нельзя все тепло превратить в работу

Построение двигателя Карно

Используем формулу Карно

Охлаждаемся: третье (и абсолютно последнее) начало термодинамики

Не пропустите также: