
Электрическое сопротивление – физическая величина, характеризующая способность проводника препятствовать прохождению по нему электрического тока.
Сопротивление часто обозначается через R или r и в Международной системе единиц (СИ) измеряется в Омах.
В зависимости от среды проводника и носителей зарядов, физическая природа сопротивления может отличаться. Так, например, в металле движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решетки, теряют свой импульс, и энергия их движения преобразуется во внутреннюю энергию кристаллической решетки (то есть становится меньше).
Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он выполнен.
Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и определяется согласно зависимости
где ρ – удельное сопротивление вещества проводника, Ом·м, l — длина проводника, м, а S — площадь сечения, мм².
Удельное сопротивление ρ – скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади сечения (рисунок 1). При расчетах это значение выбирается из таблицы.
Сопротивление проводника R зависит от внешнего фактора – температуры T, но для разных групп веществ эта зависимость имеет различные зависимости. Так, при снижении температуры металлов их сопротивление снижается (то есть способность проводить ток увеличивается). Если температура металла достигает низких значений, он переходит в состояние так называемой свехрпроводимости и его сопротивление R стремится к 0. Поведение полупроводников под воздействием температур обратное – при снижении температуры T сопротивление R растет, а при его росте наоборот падает (рисунок 2).
Закон Ома
В 1826 году немецкий физик Георг Ом открыл важный в электронике закон, названный впоследствии его фамилией. Закон Ома определяет количественную зависимость между электрическим током и свойствами проводника, характеризующими его способность противостоять электрическому току.
Существует несколько интерпретаций закона Ома.
Закон Ома для участка цепи (рисунок 3) определяет величину электрического тока I в проводнике как отношение напряжения на концах проводника U и его сопротивления R
Интерпретировать закон Ома для участка цепи можно следующим образом: если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 В, тогда величина тока I в проводнике будет равна 1 А
На представленном выше простом примере разберем физическую интерпретацию закона Ома, используя аналогию электрического тока и воды. В качестве аналога проводника электрического тока возьмем воронку, сужение в которой возникает из-за наличие в проводнике сопротивления R (рисунок 4). Пусть в воронку из некоторого источника поступает вода, которая просачивается через узкое горлышко. Усилить поток воды на выходе горлышка воронки можно за счет давления на воду, например, силой поршня. В аналогии с электричеством, поршень будет являться аналогом напряжения – чем сильнее на воду давит поршень (то есть чем больше значение напряжения), тем сильнее будет поток воды на выходе из воронки (тем больше будет значение силы тока).
Закон Ома может быть применен не всегда, а лишь в ограниченном числе случаев. Так закон Ома «не работает» при расчете напряжения и тока в полупроводниковых или электровакуумных приборов, содержащих нелинейные элементы. В этом случае зависимость тока и напряжения можно определить только с помощью построение так называемой вольтамперной характеристики (ВАХ). К категории нелинейных элементов относятся все без исключения полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.), а также электронные лампы.
Проводимость
Величина обратная сопротивлению, называется проводимостью:
G = 1/R.
Единица проводимости называется сименс (См): G, (g) = 1/Ом = См.
#1. Формула закона для участка цепи Ома
R = I/U
I = U/R
I = R/U
#2. Найдите сопротивление участка цепи использую закон Ома, если к концам проводника приложено U = 12 В, и в нем протекает ток I = 6 А.
2 Ом.
5 Ом.
72 Ом.
Закон Ома гласит I=U/R, следовательно R = U/I = 12/6 = 2 Ом.
#3. В чем измеряется удельное сопротивление?
Ом
Ом*м
Ом*мм
#4. Сопротивление участка цепи равно 10 Ом. Найдите проводимость участка.
10 См.
5 См.
0,1 См.
Величина обратная сопротивлению, называется проводимостью:
G = 1/R.
Так как сопротивление участка цепи R = 10 Ом, следовательно G = 1/10 = 0,1 См.
Результат
Отлично!
Попытайтесь снова(
Почему медь проводит электричество лучше, чем вода? Прочитав эту статью, вы больше не будете задавать себе больше этот вопрос. Далее мы обсудим электропроводность и рассмотрим формулы, которые описывают это понятие. Наконец, вы можете проверить свои знания на двух примерах.
Простое объяснение.
Электропроводность — это физическая величина, которая описывает насколько хорошо определенный материал проводит электричество.
Формулы
Существует три различных формульных обозначения удельной электропроводности σ (греч. сигма), k (каппа) и γ (гамма). В дальнейшем мы будем использовать σ. Формула электропроводности, также называемой удельной электропроводностью, описывается формулой:
σ = 1 / ρ .
Здесь ρ называется удельным сопротивлением. Вы можете рассчитать электрическое сопротивление R проводника с учетом его параметров следующим образом: R = ( ρ * l ) / S .
Таким образом, сопротивление R равно удельному сопротивлению ρ , умноженному на длину проводника l, деленному на площадь поперечного сечения S. Если теперь вы хотите выразить эту формулу через удельную электропроводность σ = 1 / ρ , полезно знать, что электрическая проводимость G проводника выражается следующим образом: G = 1 / R .
Если в верхнюю формулу подставить удельную электропроводность σ и электрическую проводимость G, то получится следующее: 1 / G = ( 1 / σ ) * ( l / S ) .
Путем дальнейшего преобразования можно получить выражение: G = σ * S / l .
С помощью электропроводности можно также описать важную зависимость между плотностью электрического тока и напряженностью электрического поля с помощью выражения: J = σ * E .
Единица измерения
Единицей удельной электропроводности σ в СИ является: [ σ ] = 1 См/м ( Сименс на метр ).
Эти единицы определяются по формуле G = σ * S / l . Если решить эту формулу в соответствии с σ, то получим σ = G * l / S .
Единица измерения электрической проводимости G задается как: [ G ] = 1 / σ = 1 См ( Сименс, международное обозначение: S ).
Если теперь ввести в формулу все единицы измерения, то получится:
[ σ ] = 1 См * 1 м / м2 = 1 См / м .
Вы также будете чаще использовать единицы измерения См / см , м / Ом * мм2 или См * м / мм2 . Вы можете преобразовать отдельные измеряемые переменные так: См / см = См / 10-2 м и так: м / Ом * мм2 = См * м / мм2 = См * м / 10-3 м * 10-3 м = 106 См / м .
Электропроводность металлов
В зависимости от количества свободно перемещающихся электронов один материал проводит лучше, чем другой. В принципе, любой материал является проводящим, но в изоляторах, например, протекающий электрический ток ничтожно мал, поэтому здесь мы говорим о непроводниках.
В металлических связях валентные электроны, т.е. крайние электроны в атоме, свободно подвижны. Они расположены в так называемой полосе проводимости. Находящиеся там электроны образуют так называемый электронный газ. Соответственно, металлы являются сравнительно хорошими проводниками. Если теперь подать электрическое напряжение на металл, валентные электроны медленно движутся к положительному полюсу, потому что он их притягивает.
На рисунке 1 видно, что некоторые электроны не могут быть притянуты непосредственно к положительному полюсу, потому что на пути стоит, так сказать, твердое атомное ядро. Там они замедляются и в некоторой степени отклоняются. Именно поэтому электроны не могут ускоряться в металле бесконечно, и именно так возникает удельное сопротивление или электропроводность.
Теперь вы также можете измерить удельную электропроводность в металле с помощью следующей формулы: σ = ( n * e2 * τ ) / m .
В этой формуле n означает число электронов, e — заряд электрона, m — массу электрона, а τ — среднее время полета электрона между двумя столкновениями.
Таблица удельной электропроводности
Для большинства веществ уже известны значения удельной электропроводности. Некоторые из них вы можете найти в следующей таблице ниже. Все значения в этой таблице действительны для комнатной температуры, т.е. 25°C.
| Вещество | Удельная электропроводность в См / м |
| Серебро | 62 · 106 |
| Медь | 58 · 106 |
| Золото | 45,2 · 106 |
| Алюминий | 37,7 · 106 |
| Вольфрам | 19 · 106 |
| Латунь | 15,5 · 106 |
| Железо | 9,93 · 106 |
| Нержавеющая сталь (WNr. 1,4301) | 1,36 · 106 |
| Германий (легирование <10-9) | 2 |
| Кремний (легирование <10-12) | 0,5 · 10-3 |
| Морская вода | примерно 5 |
| Водопроводная вода | примерно 0,05 |
| Дистиллированная вода | 5 · 10-6 |
| Изолятор | обычно <10-8 |
Удельная электропроводность сильно зависит от температуры, поэтому указанные значения применимы только при 25°C. При повышении температуры вибрация решетки в веществе становится выше. Это нарушает поток электронов, и поэтому электропроводность уменьшается с ростом температуры.
Из таблицы видно, что медь имеет вторую по величине электропроводность, поэтому медные кабели очень часто используются в электротехнике. Серебро обладает еще более высокой проводимостью, но стоит намного дороже меди.
Интересно также сравнение между морской и дистиллированной водой. Здесь электропроводность возникает благодаря растворенным в воде ионам. Морская вода имеет очень высокую долю соли, которая растворяется в воде. Эти ионы передают электрический ток. В дистиллированной воде нет растворенных ионов, поэтому в ней практически не может протекать электрический ток. Поэтому электропроводность морской воды намного выше, чем дистиллированной.
Примеры задач
Для более детального рассмотрения приведём два примера расчетов.
Задача 1.
В первой задаче представьте, что у вас есть провод длиной 2 м с поперечным сечением 0,5 мм2. Электрическое сопротивление провода при комнатной температуре составляет 106 мОм. Из какого материала изготовлен провод?
Решение.
Решение данной задачи можно найти с помощью формулы: R = ( 1 / σ ) * ( l / S ). Из этой формулы найдём σ = l / ( S * R ) .
Теперь вы можете вставить заданные значения, убедившись, что вы перевели сечение в м2.
σ = l / ( S * R ) = 2 м / ( ( 0,5 * 10-6 м2 ) * ( 1 / 106 * 10-3 Ом ) ) = 37, 7 * 106 См / м .
Наконец, вы ищите в таблице, какой материал имеет удельную электропроводность σ = 37, 7 * 106 См / м и приходите к выводу, что провод сделан из алюминия.
Задача 2.
В задаче 2 вам дано только удельное сопротивление образца с 735 * 10-9 Ом * м. Из какого материла изготовлен образец?
Решение.
Вы можете использовать формулу σ = 1 / ρ для расчёта удельной электропроводности. После подстановки значений в эту формулу вы получите: σ = 1 / ρ = 1 / 735 * 10-9 Ом * м = 1,36 * 106 См / м .
Если вы снова заглянете в таблицу, то обнаружите, что образец должен быть изготовлен из нержавеющей стали.
This article is about electrical conductivity in general. For other types of conductivity, see Conductivity. For specific applications in electrical elements, see Electrical resistance and conductance.
| Resistivity | |
|---|---|
|
Common symbols |
ρ |
| SI unit | ohm metre (Ω⋅m) |
| In SI base units | kg⋅m3⋅s−3⋅A−2 |
|
Derivations from |
 |
| Dimension |  |
| Conductivity | |
|---|---|
|
Common symbols |
σ, κ, γ |
| SI unit | siemens per metre (S/m) |
| In SI base units | kg−1⋅m−3⋅s3⋅A2 |
|
Derivations from |
 |
| Dimension |  |
Electrical resistivity (also called specific electrical resistance or volume resistivity) is a fundamental property of a material that measures how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-meter (Ω⋅m).[1][2][3] For example, if a 1 m3 solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is 1 Ω, then the resistivity of the material is 1 Ω⋅m.
Electrical conductivity (or specific conductance) is the reciprocal of electrical resistivity. It represents a material’s ability to conduct electric current. It is commonly signified by the Greek letter σ (sigma), but κ (kappa) (especially in electrical engineering) and γ (gamma) are sometimes used. The SI unit of electrical conductivity is siemens per metre (S/m). Resistivity and conductivity are intensive properties of materials, giving the opposition of a standard cube of material to current. Electrical resistance and conductance are corresponding extensive properties that give the opposition of a specific object to electric current.
Definition[edit]
Ideal case[edit]
A piece of resistive material with electrical contacts on both ends.
In an ideal case, cross-section and physical composition of the examined material are uniform across the sample, and the electric field and current density are both parallel and constant everywhere. Many resistors and conductors do in fact have a uniform cross section with a uniform flow of electric current, and are made of a single material, so that this is a good model. (See the adjacent diagram.) When this is the case, the resistance of the conductor is directly proportional to its length and inversely proportional to its cross-sectional area, where the electrical resistivity ρ (Greek: rho) is the constant of proportionality. This is written as:
where
The resistivity can be expressed using the SI unit ohm metre (Ω⋅m) — i.e. ohms multiplied by square metres (for the cross-sectional area) then divided by metres (for the length).
Both resistance and resistivity describe how difficult it is to make electrical current flow through a material, but unlike resistance, resistivity is an intrinsic property and doesn’t depend on geometric properties of a material. This means that all pure copper (Cu) wires (which have not been subjected to distortion of their crystalline structure etc.), irrespective of their shape and size, have the same resistivity, but a long, thin copper wire has a much larger resistance than a thick, short copper wire. Every material has its own characteristic resistivity. For example, rubber has a far larger resistivity than copper.
In a hydraulic analogy, passing current through a high-resistivity material is like pushing water through a pipe full of sand — while passing current through a low-resistivity material is like pushing water through an empty pipe. If the pipes are the same size and shape, the pipe full of sand has higher resistance to flow. Resistance, however, is not solely determined by the presence or absence of sand. It also depends on the length and width of the pipe: short or wide pipes have lower resistance than narrow or long pipes.
The above equation can be transposed to get Pouillet’s law (named after Claude Pouillet):
The resistance of a given element is proportional to the length, but inversely proportional to the cross-sectional area. For example, if A = 1 m2, 
Conductivity, σ, is the inverse of resistivity:
Conductivity has SI units of siemens per metre (S/m).
General scalar quantities[edit]
For less ideal cases, such as more complicated geometry, or when the current and electric field vary in different parts of the material, it is necessary to use a more general expression in which the resistivity at a particular point is defined as the ratio of the electric field to the density of the current it creates at that point:
where
in which 

Conductivity is the inverse (reciprocal) of resistivity. Here, it is given by:
For example, rubber is a material with large ρ and small σ — because even a very large electric field in rubber makes almost no current flow through it. On the other hand, copper is a material with small ρ and large σ — because even a small electric field pulls a lot of current through it.
As shown below, this expression simplifies to a single number when the electric field and current density are constant in the material.
-
Derivation from general definition of resistivity There are three equations to be combined here. The first is the resistivity for parallel current and electric field: If the electric field is constant, the electric field is given by the total voltage V across the conductor divided by length ℓ of the conductor:
If the current density is constant, it is equal to the total current divided by the cross sectional area:
Plugging in the values of E and J into the first expression, we obtain:
Finally, we apply Ohm’s law, V/I = R:
Tensor resistivity[edit]
When the resistivity of a material has a directional component, the most general definition of resistivity must be used. It starts from the tensor-vector form of Ohm’s law, which relates the electric field inside a material to the electric current flow. This equation is completely general, meaning it is valid in all cases, including those mentioned above. However, this definition is the most complicated, so it is only directly used in anisotropic cases, where the more simple definitions cannot be applied. If the material is not anisotropic, it is safe to ignore the tensor-vector definition, and use a simpler expression instead.
Here, anisotropic means that the material has different properties in different directions. For example, a crystal of graphite consists microscopically of a stack of sheets, and current flows very easily through each sheet, but much less easily from one sheet to the adjacent one.[4] In such cases, the current does not flow in exactly the same direction as the electric field. Thus, the appropriate equations are generalized to the three-dimensional tensor form:[5][6]
where the conductivity σ and resistivity ρ are rank-2 tensors, and electric field E and current density J are vectors. These tensors can be represented by 3×3 matrices, the vectors with 3×1 matrices, with matrix multiplication used on the right side of these equations. In matrix form, the resistivity relation is given by:
where
Equivalently, resistivity can be given in the more compact Einstein notation:
In either case, the resulting expression for each electric field component is:
Since the choice of the coordinate system is free, the usual convention is to simplify the expression by choosing an x-axis parallel to the current direction, so Jy = Jz = 0. This leaves:
Conductivity is defined similarly:[7]
or
both resulting in:
Looking at the two expressions, 




If the electric field is parallel to the applied current, 



Conductivity and current carriers[edit]
Relation between current density and electric current velocity[edit]
Electric current is the ordered movement of electric charges.[2]
Causes of conductivity[edit]
Band theory simplified[edit]
According to elementary quantum mechanics, an electron in an atom or crystal can only have certain precise energy levels; energies between these levels are impossible. When a large number of such allowed levels have close-spaced energy values – i.e. have energies that differ only minutely – those close energy levels in combination are called an «energy band». There can be many such energy bands in a material, depending on the atomic number of the constituent atoms[a] and their distribution within the crystal.[b]
The material’s electrons seek to minimize the total energy in the material by settling into low energy states; however, the Pauli exclusion principle means that only one can exist in each such state. So the electrons «fill up» the band structure starting from the bottom. The characteristic energy level up to which the electrons have filled is called the Fermi level. The position of the Fermi level with respect to the band structure is very important for electrical conduction: Only electrons in energy levels near or above the Fermi level are free to move within the broader material structure, since the electrons can easily jump among the partially occupied states in that region. In contrast, the low energy states are completely filled with a fixed limit on the number of electrons at all times, and the high energy states are empty of electrons at all times.
Electric current consists of a flow of electrons. In metals there are many electron energy levels near the Fermi level, so there are many electrons available to move. This is what causes the high electronic conductivity of metals.
An important part of band theory is that there may be forbidden bands of energy: energy intervals that contain no energy levels. In insulators and semiconductors, the number of electrons is just the right amount to fill a certain integer number of low energy bands, exactly to the boundary. In this case, the Fermi level falls within a band gap. Since there are no available states near the Fermi level, and the electrons are not freely movable, the electronic conductivity is very low.
In metals[edit]
Like balls in a Newton’s cradle, electrons in a metal quickly transfer energy from one terminal to another, despite their own negligible movement.
A metal consists of a lattice of atoms, each with an outer shell of electrons that freely dissociate from their parent atoms and travel through the lattice. This is also known as a positive ionic lattice.[9] This ‘sea’ of dissociable electrons allows the metal to conduct electric current. When an electrical potential difference (a voltage) is applied across the metal, the resulting electric field causes electrons to drift towards the positive terminal. The actual drift velocity of electrons is typically small, on the order of magnitude of metres per hour. However, due to the sheer number of moving electrons, even a slow drift velocity results in a large current density.[10] The mechanism is similar to transfer of momentum of balls in a Newton’s cradle[11] but the rapid propagation of an electric energy along a wire is not due to the mechanical forces, but the propagation of an energy-carrying electromagnetic field guided by the wire.
Most metals have electrical resistance. In simpler models (non quantum mechanical models) this can be explained by replacing electrons and the crystal lattice by a wave-like structure. When the electron wave travels through the lattice, the waves interfere, which causes resistance. The more regular the lattice is, the less disturbance happens and thus the less resistance. The amount of resistance is thus mainly caused by two factors. First, it is caused by the temperature and thus amount of vibration of the crystal lattice. Higher temperatures cause bigger vibrations, which act as irregularities in the lattice. Second, the purity of the metal is relevant as a mixture of different ions is also an irregularity.[12][13] The small decrease in conductivity on melting of pure metals is due to the loss of long range crystalline order. The short range order remains and strong correlation between positions of ions results in coherence between waves diffracted by adjacent ions.[14]
In semiconductors and insulators[edit]
In metals, the Fermi level lies in the conduction band (see Band Theory, above) giving rise to free conduction electrons. However, in semiconductors the position of the Fermi level is within the band gap, about halfway between the conduction band minimum (the bottom of the first band of unfilled electron energy levels) and the valence band maximum (the top of the band below the conduction band, of filled electron energy levels). That applies for intrinsic (undoped) semiconductors. This means that at absolute zero temperature, there would be no free conduction electrons, and the resistance is infinite. However, the resistance decreases as the charge carrier density (i.e., without introducing further complications, the density of electrons) in the conduction band increases. In extrinsic (doped) semiconductors, dopant atoms increase the majority charge carrier concentration by donating electrons to the conduction band or producing holes in the valence band. (A «hole» is a position where an electron is missing; such holes can behave in a similar way to electrons.) For both types of donor or acceptor atoms, increasing dopant density reduces resistance. Hence, highly doped semiconductors behave metallically. At very high temperatures, the contribution of thermally generated carriers dominates over the contribution from dopant atoms, and the resistance decreases exponentially with temperature.
In ionic liquids/electrolytes[edit]
In electrolytes, electrical conduction happens not by band electrons or holes, but by full atomic species (ions) traveling, each carrying an electrical charge. The resistivity of ionic solutions (electrolytes) varies tremendously with concentration – while distilled water is almost an insulator, salt water is a reasonable electrical conductor. Conduction in ionic liquids is also controlled by the movement of ions, but here we are talking about molten salts rather than solvated ions. In biological membranes, currents are carried by ionic salts. Small holes in cell membranes, called ion channels, are selective to specific ions and determine the membrane resistance.
The concentration of ions in a liquid (e.g., in an aqueous solution) depends on the degree of dissociation of the dissolved substance, characterized by a dissociation coefficient 


The specific electrical conductivity (
where 




Superconductivity[edit]
Original data from the 1911 experiment by Heike Kamerlingh Onnes showing the resistance of a mercury wire as a function of temperature. The abrupt drop in resistance is the superconducting transition.
The electrical resistivity of a metallic conductor decreases gradually as temperature is lowered. In normal (that is, non-superconducting) conductors, such as copper or silver, this decrease is limited by impurities and other defects. Even near absolute zero, a real sample of a normal conductor shows some resistance. In a superconductor, the resistance drops abruptly to zero when the material is cooled below its critical temperature. In a normal conductor, the current is driven by a voltage gradient, whereas in a superconductor, there is no voltage gradient and the current is instead related to the phase gradient of the superconducting order parameter.[15] A consequence of this is that an electric current flowing in a loop of superconducting wire can persist indefinitely with no power source.[16]
In a class of superconductors known as type II superconductors, including all known high-temperature superconductors, an extremely low but nonzero resistivity appears at temperatures not too far below the nominal superconducting transition when an electric current is applied in conjunction with a strong magnetic field, which may be caused by the electric current. This is due to the motion of magnetic vortices in the electronic superfluid, which dissipates some of the energy carried by the current. The resistance due to this effect is tiny compared with that of non-superconducting materials, but must be taken into account in sensitive experiments. However, as the temperature decreases far enough below the nominal superconducting transition, these vortices can become frozen so that the resistance of the material becomes truly zero.
Plasma[edit]
Lightning is an example of plasma present at Earth’s surface. Typically, lightning discharges 30,000 amperes at up to 100 million volts, and emits light, radio waves, and X-rays.[17] Plasma temperatures in lightning might approach 30,000 kelvin (29,727 °C) (53,540 °F), or five times hotter than the temperature at the sun surface, and electron densities may exceed 1024 m−3.
Plasmas are very good conductors and electric potentials play an important role.
The potential as it exists on average in the space between charged particles, independent of the question of how it can be measured, is called the plasma potential, or space potential. If an electrode is inserted into a plasma, its potential generally lies considerably below the plasma potential, due to what is termed a Debye sheath. The good electrical conductivity of plasmas makes their electric fields very small. This results in the important concept of quasineutrality, which says the density of negative charges is approximately equal to the density of positive charges over large volumes of the plasma (ne = ⟨Z⟩>ni), but on the scale of the Debye length there can be charge imbalance. In the special case that double layers are formed, the charge separation can extend some tens of Debye lengths.
The magnitude of the potentials and electric fields must be determined by means other than simply finding the net charge density. A common example is to assume that the electrons satisfy the Boltzmann relation:
Differentiating this relation provides a means to calculate the electric field from the density:
(∇ is the vector gradient operator; see nabla symbol and gradient for more information.)
It is possible to produce a plasma that is not quasineutral. An electron beam, for example, has only negative charges. The density of a non-neutral plasma must generally be very low, or it must be very small. Otherwise, the repulsive electrostatic force dissipates it.
In astrophysical plasmas, Debye screening prevents electric fields from directly affecting the plasma over large distances, i.e., greater than the Debye length. However, the existence of charged particles causes the plasma to generate, and be affected by, magnetic fields. This can and does cause extremely complex behavior, such as the generation of plasma double layers, an object that separates charge over a few tens of Debye lengths. The dynamics of plasmas interacting with external and self-generated magnetic fields are studied in the academic discipline of magnetohydrodynamics.
Plasma is often called the fourth state of matter after solid, liquids and gases.[18][19] It is distinct from these and other lower-energy states of matter. Although it is closely related to the gas phase in that it also has no definite form or volume, it differs in a number of ways, including the following:
| Property | Gas | Plasma |
|---|---|---|
| Electrical conductivity | Very low: air is an excellent insulator until it breaks down into plasma at electric field strengths above 30 kilovolts per centimetre.[20] | Usually very high: for many purposes, the conductivity of a plasma may be treated as infinite. |
| Independently acting species | One: all gas particles behave in a similar way, influenced by gravity and by collisions with one another. | Two or three: electrons, ions, protons and neutrons can be distinguished by the sign and value of their charge so that they behave independently in many circumstances, with different bulk velocities and temperatures, allowing phenomena such as new types of waves and instabilities. |
| Velocity distribution | Maxwellian: collisions usually lead to a Maxwellian velocity distribution of all gas particles, with very few relatively fast particles. | Often non-Maxwellian: collisional interactions are often weak in hot plasmas and external forcing can drive the plasma far from local equilibrium and lead to a significant population of unusually fast particles. |
| Interactions | Binary: two-particle collisions are the rule, three-body collisions extremely rare. | Collective: waves, or organized motion of plasma, are very important because the particles can interact at long ranges through the electric and magnetic forces. |
Resistivity and conductivity of various materials[edit]
- A conductor such as a metal has high conductivity and a low resistivity.
- An insulator like glass has low conductivity and a high resistivity.
- The conductivity of a semiconductor is generally intermediate, but varies widely under different conditions, such as exposure of the material to electric fields or specific frequencies of light, and, most important, with temperature and composition of the semiconductor material.
The degree of semiconductors doping makes a large difference in conductivity. To a point, more doping leads to higher conductivity. The conductivity of a water/aqueous solution is highly dependent on its concentration of dissolved salts, and other chemical species that ionize in the solution. Electrical conductivity of water samples is used as an indicator of how salt-free, ion-free, or impurity-free the sample is; the purer the water, the lower the conductivity (the higher the resistivity). Conductivity measurements in water are often reported as specific conductance, relative to the conductivity of pure water at 25 °C. An EC meter is normally used to measure conductivity in a solution. A rough summary is as follows:
This table shows the resistivity (ρ), conductivity and temperature coefficient of various materials at 20 °C (68 °F; 293 K).
The effective temperature coefficient varies with temperature and purity level of the material. The 20 °C value is only an approximation when used at other temperatures. For example, the coefficient becomes lower at higher temperatures for copper, and the value 0.00427 is commonly specified at 0 °C.[52]
The extremely low resistivity (high conductivity) of silver is characteristic of metals. George Gamow tidily summed up the nature of the metals’ dealings with electrons in his popular science book One, Two, Three…Infinity (1947):
The metallic substances differ from all other materials by the fact that the outer shells of their atoms are bound rather loosely, and often let one of their electrons go free. Thus the interior of a metal is filled up with a large number of unattached electrons that travel aimlessly around like a crowd of displaced persons. When a metal wire is subjected to electric force applied on its opposite ends, these free electrons rush in the direction of the force, thus forming what we call an electric current.
More technically, the free electron model gives a basic description of electron flow in metals.
Wood is widely regarded as an extremely good insulator, but its resistivity is sensitively dependent on moisture content, with damp wood being a factor of at least 1010 worse insulator than oven-dry.[45] In any case, a sufficiently high voltage – such as that in lightning strikes or some high-tension power lines – can lead to insulation breakdown and electrocution risk even with apparently dry wood.[citation needed]
Temperature dependence[edit]
Linear approximation[edit]
The electrical resistivity of most materials changes with temperature. If the temperature T does not vary too much, a linear approximation is typically used:
where 








Metals[edit]
In general, electrical resistivity of metals increases with temperature. Electron–phonon interactions can play a key role. At high temperatures, the resistance of a metal increases linearly with temperature. As the temperature of a metal is reduced, the temperature dependence of resistivity follows a power law function of temperature. Mathematically the temperature dependence of the resistivity ρ of a metal can be approximated through the Bloch–Grüneisen formula:[54]
where 

- n = 5 implies that the resistance is due to scattering of electrons by phonons (as it is for simple metals)
- n = 3 implies that the resistance is due to s-d electron scattering (as is the case for transition metals)
- n = 2 implies that the resistance is due to electron–electron interaction.
The Bloch–Grüneisen formula is an approximation obtained assuming that the studied metal has spherical Fermi surface inscribed within the first Brillouin zone and a Debye phonon spectrum.[55]
If more than one source of scattering is simultaneously present, Matthiessen’s rule (first formulated by Augustus Matthiessen in the 1860s)[56][57] states that the total resistance can be approximated by adding up several different terms, each with the appropriate value of n.
As the temperature of the metal is sufficiently reduced (so as to ‘freeze’ all the phonons), the resistivity usually reaches a constant value, known as the residual resistivity. This value depends not only on the type of metal, but on its purity and thermal history. The value of the residual resistivity of a metal is decided by its impurity concentration. Some materials lose all electrical resistivity at sufficiently low temperatures, due to an effect known as superconductivity.
An investigation of the low-temperature resistivity of metals was the motivation to Heike Kamerlingh Onnes’s experiments that led in 1911 to discovery of superconductivity. For details see History of superconductivity.
Wiedemann–Franz law[edit]
The Wiedemann–Franz law states that for materials where heat and charge transport is dominated by electrons, the ratio of thermal to electrical conductivity is proportional to the temperature:
where 




Semiconductors[edit]
In general, intrinsic semiconductor resistivity decreases with increasing temperature. The electrons are bumped to the conduction energy band by thermal energy, where they flow freely, and in doing so leave behind holes in the valence band, which also flow freely. The electric resistance of a typical intrinsic (non doped) semiconductor decreases exponentially with temperature:
An even better approximation of the temperature dependence of the resistivity of a semiconductor is given by the Steinhart–Hart equation:
where A, B and C are the so-called Steinhart–Hart coefficients.
This equation is used to calibrate thermistors.
Extrinsic (doped) semiconductors have a far more complicated temperature profile. As temperature increases starting from absolute zero they first decrease steeply in resistance as the carriers leave the donors or acceptors. After most of the donors or acceptors have lost their carriers, the resistance starts to increase again slightly due to the reducing mobility of carriers (much as in a metal). At higher temperatures, they behave like intrinsic semiconductors as the carriers from the donors/acceptors become insignificant compared to the thermally generated carriers.[58]
In non-crystalline semiconductors, conduction can occur by charges quantum tunnelling from one localised site to another. This is known as variable range hopping and has the characteristic form of
where n = 2, 3, 4, depending on the dimensionality of the system.
Complex resistivity and conductivity[edit]
When analyzing the response of materials to alternating electric fields (dielectric spectroscopy),[59] in applications such as electrical impedance tomography,[60] it is convenient to replace resistivity with a complex quantity called impedivity (in analogy to electrical impedance). Impedivity is the sum of a real component, the resistivity, and an imaginary component, the reactivity (in analogy to reactance). The magnitude of impedivity is the square root of sum of squares of magnitudes of resistivity and reactivity.
Conversely, in such cases the conductivity must be expressed as a complex number (or even as a matrix of complex numbers, in the case of anisotropic materials) called the admittivity. Admittivity is the sum of a real component called the conductivity and an imaginary component called the susceptivity.
An alternative description of the response to alternating currents uses a real (but frequency-dependent) conductivity, along with a real permittivity. The larger the conductivity is, the more quickly the alternating-current signal is absorbed by the material (i.e., the more opaque the material is). For details, see Mathematical descriptions of opacity.
Resistance versus resistivity in complicated geometries[edit]
Even if the material’s resistivity is known, calculating the resistance of something made from it may, in some cases, be much more complicated than the formula 
In cases like this, the formulas
must be replaced with
where E and J are now vector fields. This equation, along with the continuity equation for J and the Poisson’s equation for E, form a set of partial differential equations. In special cases, an exact or approximate solution to these equations can be worked out by hand, but for very accurate answers in complex cases, computer methods like finite element analysis may be required.
Resistivity-density product[edit]
In some applications where the weight of an item is very important, the product of resistivity and density is more important than absolute low resistivity – it is often possible to make the conductor thicker to make up for a higher resistivity; and then a low-resistivity-density-product material (or equivalently a high conductivity-to-density ratio) is desirable. For example, for long-distance overhead power lines, aluminium is frequently used rather than copper (Cu) because it is lighter for the same conductance.
Silver, although it is the least resistive metal known, has a high density and performs similarly to copper by this measure, but is much more expensive. Calcium and the alkali metals have the best resistivity-density products, but are rarely used for conductors due to their high reactivity with water and oxygen (and lack of physical strength). Aluminium is far more stable. Toxicity excludes the choice of beryllium.[61] (Pure beryllium is also brittle.) Thus, aluminium is usually the metal of choice when the weight or cost of a conductor is the driving consideration.
See also[edit]
- Charge transport mechanisms
- Chemiresistor
- Classification of materials based on permittivity
- Conductivity near the percolation threshold
- Contact resistance
- Electrical resistivities of the elements (data page)
- Electrical resistivity tomography
- Sheet resistance
- SI electromagnetism units
- Skin effect
- Spitzer resistivity
- Dielectric strength
Notes[edit]
- ^ The atomic number is the count of electrons in an atom that is electrically neutral – has no net electric charge.
- ^ Other relevant factors that are specifically not considered are the size of the whole crystal and external factors of the surrounding environment that modify the energy bands, such as imposed electric or magnetic fields.
- ^ The numbers in this column increase or decrease the significand portion of the resistivity. For example, at 30 °C (303 K), the resistivity of silver is 1.65×10−8. This is calculated as Δρ = α ΔT ρ0 where ρ0 is the resistivity at 20 °C (in this case) and α is the temperature coefficient.
- ^ The conductivity of metallic silver is not significantly better than metallic copper for most practical purposes – the difference between the two can be easily compensated for by thickening the copper wire by only 3%. However silver is preferred for exposed electrical contact points because corroded silver is a tolerable conductor, but corroded copper is a fairly good insulator, like most corroded metals.
- ^ Copper is widely used in electrical equipment, building wiring, and telecommunication cables.
- ^ Referred to as 100% IACS or International Annealed Copper Standard. The unit for expressing the conductivity of nonmagnetic materials by testing using the eddy current method. Generally used for temper and alloy verification of aluminium.
- ^ Despite being less conductive than copper, gold is commonly used in electrical contacts because it does not easily corrode.
- ^ Commonly used for overhead power line with steel reinforced (ACSR)
- ^ a b Cobalt and ruthenium are considered to replace copper in integrated circuits fabricated in advanced nodes[29]
- ^ 18% chromium and 8% nickel austenitic stainless steel
- ^ Nickel-iron-chromium alloy commonly used in heating elements.
- ^ Graphite is strongly anisotropic.
- ^ a b The resistivity of semiconductors depends strongly on the presence of impurities in the material.
- ^ Corresponds to an average salinity of 35 g/kg at 20 °C.
- ^ The pH should be around 8.4 and the conductivity in the range of 2.5–3 mS/cm. The lower value is appropriate for freshly prepared water. The conductivity is used for the determination of TDS (total dissolved particles).
- ^ This value range is typical of high quality drinking water and not an indicator of water quality
- ^ Conductivity is lowest with monatomic gases present; changes to 12×10−5 upon complete de-gassing, or to 7.5×10−5 upon equilibration to the atmosphere due to dissolved CO2
References[edit]
- ^ Lowrie, William (2007). Fundamentals of Geophysics. Cambridge University Press. pp. 254–55. ISBN 978-05-2185-902-8. Retrieved March 24, 2019.
- ^ a b Kumar, Narinder (2003). Comprehensive Physics for Class XII. New Delhi: Laxmi Publications. pp. 280–84. ISBN 978-81-7008-592-8. Retrieved March 24, 2019.
- ^ Bogatin, Eric (2004). Signal Integrity: Simplified. Prentice Hall Professional. p. 114. ISBN 978-0-13-066946-9. Retrieved March 24, 2019.
- ^ a b c Hugh O. Pierson, Handbook of carbon, graphite, diamond, and fullerenes: properties, processing, and applications, p. 61, William Andrew, 1993 ISBN 0-8155-1339-9.
- ^ J.R. Tyldesley (1975) An introduction to Tensor Analysis: For Engineers and Applied Scientists, Longman, ISBN 0-582-44355-5
- ^ G. Woan (2010) The Cambridge Handbook of Physics Formulas, Cambridge University Press, ISBN 978-0-521-57507-2
- ^ Josef Pek, Tomas Verner (3 Apr 2007). «Finite‐difference modelling of magnetotelluric fields in two‐dimensional anisotropic media». Geophysical Journal International. 128 (3): 505–521. doi:10.1111/j.1365-246X.1997.tb05314.x.
- ^ David Tong (Jan 2016). «The Quantum Hall Effect: TIFR Infosys Lectures» (PDF). Retrieved 14 Sep 2018.
- ^ Bonding (sl). ibchem.com
- ^ «Current versus Drift Speed». The physics classroom. Retrieved 20 August 2014.
- ^ Lowe, Doug (2012). Electronics All-in-One For Dummies. John Wiley & Sons. ISBN 978-0-470-14704-7.
- ^ Keith Welch. «Questions & Answers – How do you explain electrical resistance?». Thomas Jefferson National Accelerator Facility. Retrieved 28 April 2017.
- ^ «Electromigration : What is electromigration?». Middle East Technical University. Retrieved 31 July 2017.
When electrons are conducted through a metal, they interact with imperfections in the lattice and scatter. […] Thermal energy produces scattering by causing atoms to vibrate. This is the source of resistance of metals.
- ^ Faber, T.E. (1972). Introduction to the Theory of Liquid Metals. Cambridge University Press. ISBN 9780521154499.
- ^
«The Feynman Lectures in Physics, Vol. III, Chapter 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity». Retrieved 26 December 2021. - ^
John C. Gallop (1990). SQUIDS, the Josephson Effects and Superconducting Electronics. CRC Press. pp. 3, 20. ISBN 978-0-7503-0051-3. - ^ See Flashes in the Sky: Earth’s Gamma-Ray Bursts Triggered by Lightning
- ^ Yaffa Eliezer, Shalom Eliezer, The Fourth State of Matter: An Introduction to the Physics of Plasma, Publisher: Adam Hilger, 1989, ISBN 978-0-85274-164-1, 226 pages, page 5
- ^ Bittencourt, J.A. (2004). Fundamentals of Plasma Physics. Springer. p. 1. ISBN 9780387209753.
- ^ Hong, Alice (2000). «Dielectric Strength of Air». The Physics Factbook.
- ^ a b c d e f g h i j k l m n o Raymond A. Serway (1998). Principles of Physics (2nd ed.). Fort Worth, Texas; London: Saunders College Pub. p. 602. ISBN 978-0-03-020457-9.
- ^ a b c David Griffiths (1999) [1981]. «7 Electrodynamics». In Alison Reeves (ed.). Introduction to Electrodynamics (3rd ed.). Upper Saddle River, New Jersey: Prentice Hall. p. 286. ISBN 978-0-13-805326-0. OCLC 40251748.
- ^ Matula, R.A. (1979). «Electrical resistivity of copper, gold, palladium, and silver». Journal of Physical and Chemical Reference Data. 8 (4): 1147. Bibcode:1979JPCRD…8.1147M. doi:10.1063/1.555614. S2CID 95005999.
- ^ Douglas Giancoli (2009) [1984]. «25 Electric Currents and Resistance». In Jocelyn Phillips (ed.). Physics for Scientists and Engineers with Modern Physics (4th ed.). Upper Saddle River, New Jersey: Prentice Hall. p. 658. ISBN 978-0-13-149508-1.
- ^ «Copper wire tables». United States National Bureau of Standards. Retrieved 3 February 2014 – via Internet Archive — archive.org (archived 2001-03-10).
- ^ [1]. (Calculated as «56% conductivity of pure copper» (5.96E-7)). Retrieved on 2023-1-12.
- ^ Physical constants. (PDF format; see page 2, table in the right lower corner). Retrieved on 2011-12-17.
- ^ [2]. (Calculated as «28% conductivity of pure copper» (5.96E-7)). Retrieved on 2023-1-12.
- ^ IITC – Imec Presents Copper, Cobalt and Ruthenium Interconnect Results
- ^ «Temperature Coefficient of Resistance | Electronics Notes».
- ^ [3]. (Calculated as «15% conductivity of pure copper» (5.96E-7)). Retrieved on 2023-1-12.
- ^ Material properties of niobium.
- ^ AISI 1010 Steel, cold drawn. Matweb
- ^ Karcher, Ch.; Kocourek, V. (December 2007). «Free-surface instabilities during electromagnetic shaping of liquid metals». Proceedings in Applied Mathematics and Mechanics. 7 (1): 4140009–4140010. doi:10.1002/pamm.200700645. ISSN 1617-7061.
- ^ «JFE steel» (PDF). Retrieved 2012-10-20.
- ^ a b Douglas C. Giancoli (1995). Physics: Principles with Applications (4th ed.). London: Prentice Hall. ISBN 978-0-13-102153-2.
(see also Table of Resistivity. hyperphysics.phy-astr.gsu.edu) - ^ John O’Malley (1992) Schaum’s outline of theory and problems of basic circuit analysis, p. 19, McGraw-Hill Professional, ISBN 0-07-047824-4
- ^ Glenn Elert (ed.), «Resistivity of steel», The Physics Factbook, retrieved and archived 16 June 2011.
- ^ Probably, the metal with highest value of electrical resistivity.
- ^ Y. Pauleau, Péter B. Barna, P. B. Barna (1997) Protective coatings and thin films: synthesis, characterization, and applications, p. 215, Springer, ISBN 0-7923-4380-8.
- ^ Milton Ohring (1995). Engineering materials science, Volume 1 (3rd ed.). Academic Press. p. 561. ISBN 978-0125249959.
- ^ Physical properties of sea water Archived 2018-01-18 at the Wayback Machine. Kayelaby.npl.co.uk. Retrieved on 2011-12-17.
- ^ [4]. chemistry.stackexchange.com
- ^ Eranna, Golla (2014). Crystal Growth and Evaluation of Silicon for VLSI and ULSI. CRC Press. p. 7. ISBN 978-1-4822-3281-3.
- ^ a b c Transmission Lines data. Transmission-line.net. Retrieved on 2014-02-03.
- ^ R. M. Pashley; M. Rzechowicz; L. R. Pashley; M. J. Francis (2005). «De-Gassed Water is a Better Cleaning Agent». The Journal of Physical Chemistry B. 109 (3): 1231–8. doi:10.1021/jp045975a. PMID 16851085.
- ^ ASTM D1125 Standard Test Methods for Electrical Conductivity and Resistivity of Water
- ^ ASTM D5391 Standard Test Method for Electrical Conductivity and Resistivity of a Flowing High Purity Water Sample
- ^ Lawrence S. Pan, Don R. Kania, Diamond: electronic properties and applications, p. 140, Springer, 1994 ISBN 0-7923-9524-7.
- ^ S. D. Pawar; P. Murugavel; D. M. Lal (2009). «Effect of relative humidity and sea level pressure on electrical conductivity of air over Indian Ocean». Journal of Geophysical Research. 114 (D2): D02205. Bibcode:2009JGRD..114.2205P. doi:10.1029/2007JD009716.
- ^ E. Seran; M. Godefroy; E. Pili (2016). «What we can learn from measurements of air electric conductivity in 222Rn ‐ rich atmosphere». Earth and Space Science. 4 (2): 91–106. Bibcode:2017E&SS….4…91S. doi:10.1002/2016EA000241.
- ^ Copper Wire Tables Archived 2010-08-21 at the Wayback Machine. US Dep. of Commerce. National Bureau of Standards Handbook. February 21, 1966
- ^ Ward, Malcolm R. (1971). Electrical engineering science. McGraw-Hill technical education. Maidenhead, UK: McGraw-Hill. pp. 36–40. ISBN 9780070942554.
- ^ Grüneisen, E. (1933). «Die Abhängigkeit des elektrischen Widerstandes reiner Metalle von der Temperatur». Annalen der Physik. 408 (5): 530–540. Bibcode:1933AnP…408..530G. doi:10.1002/andp.19334080504. ISSN 1521-3889.
- ^ Quantum theory of real materials. James R. Chelikowsky, Steven G. Louie. Boston: Kluwer Academic Publishers. 1996. pp. 219–250. ISBN 0-7923-9666-9. OCLC 33335083.
{{cite book}}: CS1 maint: others (link) - ^ A. Matthiessen, Rep. Brit. Ass. 32, 144 (1862)
- ^ A. Matthiessen, Progg. Anallen, 122, 47 (1864)
- ^ J. Seymour (1972) Physical Electronics, chapter 2, Pitman
- ^ Stephenson, C.; Hubler, A. (2015). «Stability and conductivity of self-assembled wires in a transverse electric field». Sci. Rep. 5: 15044. Bibcode:2015NatSR…515044S. doi:10.1038/srep15044. PMC 4604515. PMID 26463476.
- ^ Otto H. Schmitt, University of Minnesota Mutual Impedivity Spectrometry and the Feasibility of its Incorporation into Tissue-Diagnostic Anatomical Reconstruction and Multivariate Time-Coherent Physiological Measurements. otto-schmitt.org. Retrieved on 2011-12-17.
- ^ «Berryllium (Be) — Chemical properties, Health and Environmental effects».
Further reading[edit]
- Paul Tipler (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 978-0-7167-0810-0.
- Measuring Electrical Resistivity and Conductivity
External links[edit]
- «Electrical Conductivity». Sixty Symbols. Brady Haran for the University of Nottingham. 2010.
- Comparison of the electrical conductivity of various elements in WolframAlpha
- Partial and total conductivity. «Electrical conductivity» (PDF).
-
Электрическая проводимость растворов электролитов
Мерой
способности веществ проводить
электрический ток является электрическая
проводимость L
– величина обратная электрическому
сопротивлению проводника
R:
.
(3.15)
Так как
, (3.16)
то
, (3.17)
где
ρ
– удельное сопротивление, Ом·м (Ом·см);
S
– поперечное сечение, м2
(см2);
– длина проводника, м (см);
–удельная
электрическая проводимость, Ом-1·м-1
(Ом-1·см-1).
Удельная
электрическая проводимость
(χ)
раствора – это электрическая проводимость
объема раствора, заключенного между
двумя параллельными электродами,
имеющими площадь по 1м2
(1 см2)
и расположенными на расстоянии 1м (1 см)
друг от друга.
Сопротивление
раствора связано с удельной электрической
проводимостью соотношением:
, 3.18)
где
– постоянная измерительной ячейки.
Если
известна величина К,
то по измеренному сопротивлению раствора
можно рассчитать значение удельной
электрической проводимости:
(3.19)
Эквивалентная
(мольная) электрическая проводимость
λv
численно
равна электрической проводимости такого
объема V
(м3,
л, см3)
раствора данной концентрации, в котором
содержится 1г-экв (1 моль) растворенного
вещества. Условно, это электрическая
проводимость объема V
раствора,
заключенного между двумя параллельными
электродами, с расстоянием между
электродами 1м (1 см), причем каждый
электрод имеет такую площадь, чтобы в
этом объеме содержался 1г-экв (1моль)
электролита.
Эквивалентная
(мольная) электрическая проводимость
и удельная электрическая проводимость
связаны соотношением:
. (3.20)
Если
концентрация выражена в г-экв/л (моль/л),
а удельная электрическая проводимость
в Ом-1 ·
см-1,
то
, (3.21)
или с
учетом (3.5):
. (3.22)
Эквивалентная
электрическая проводимость при
бесконечном разбавлении в соответствии
с законом
Кольрауша
(законом
независимого движения ионов)
равна:
, (3.23)
где
– электрические проводимости
(электрические подвижности) катиона и
аниона, их значения приводятся в
справочниках.
Степень
диссоциации слабого электролита α
и коэффициент
электрической проводимости
растворов сильных электролитов f
(характеризует степень межионного
взаимодействия) могут быть рассчитаны
по формулам:
(3.24)
(3.25)
П
р и м е р 3.4. Какой объем раствора
электролита нормальной концентрации
CN
= 0,5 г-экв/л
нужно залить
в ячейку с электродами, расстояние между
которыми 1 см, чтобы измеренная
электропроводность была эквивалентной
электропроводностью этого раствора?
Р е ш е
н и е
Эквивалентная
электропроводность – это электропроводность
раствора, содержащего 1 г-экв электролита.
В 1 л исходного раствора содержится 0,5
г-экв, поэтому
V
= 1/CN
= 1/0,5 = 2 л,
то
есть следует залить 2 л раствора, чтобы
в нем находилось нужное количество
электролита.
П
р и м е р 3.5. Рассчитать удельную и
эквивалентную электрические проводимости
раствора хлорида калия KCl
с концентрацией 0,02 г-экв/л, если удельное
сопротивление ρ
составляет 354,61 Ом·см.
Р е ш е
н и е
Найдем удельную электрическую
проводимость:
Определим эквивалентную электрическую
проводимость:
П
р и м е р 3.6. Рассчитать эквивалентную
электрическую проводимость раствора
концентрации 0,075 г-экв/л, помещенного в
ячейку с расстоянием между электродами
1,2 см и поверхностью каждого электрода
0,8 см2,
если сопротивление раствора составляет
950 Ом.
Р е ш е
н и е
Сопротивление раствора:
;
отсюда
удельная электрическая проводимость:
;
Ом-1·
см-1Ом-1·
м-1.
Зная
,
рассчитываем эквивалентную электрическую
проводимость:
;
;
Ом-1
· г-экв–1
· м2.
П
р и м е р 3.7. Определить постоянную
измерительной ячейки K,
если раствор концентрации 0,005 г-экв/л
имеет эквивалентную электрическую
проводимость 400 Ом-1
·г-экв–1
·см2,
а сопротивление этого раствора составляет
290 Ом.
Р е ш е
н и е
Находим удельную электрическую
проводимость раствора:
Ом-1см-1.
Сопротивление раствора:
,
отсюда
;
см-1.
П
р и м е р 3.8. Сопротивление раствора
концентрации 0,015 г-экв/л составляет 1800
Ом. Постоянная измерительной ячейки
равна 2,5 см-1.
Рассчитать эквивалентную электрическую
проводимость раствора.
Р е ш е
н и е
По
уравнению (3.19):
Находим эквивалентную электрическую
проводимость:
П
р и м е р 3.9. Определить степень диссоциации
и константу диссоциации одно-одновалентного
слабого электролита, если при разведении
V
= 16 л удельная электрическая проводимость
раствора составляет 1,312·10-3
Ом-1см-1,
а
232,6
Ом-1см2/г-экв.
Р е ш е н и е
Находим
эквивалентную электрическую проводимость
по уравнению (3.22):
;
Ом-1см2/г-экв.
Находим степень диссоциации электролита
по формуле (3.24):
Рассчитываем константу диссоциации по
уравнению Оствальда (3.6):
г-экв/л
П
р и м е р 3.10. Определить количество AgCl
(г),
содержащегося в 1 л раствора, если
удельная электрическая проводимость
насыщенного водного раствора AgCl
составляет 1,259·10-6
Ом-1см-1.
Подвижности ионов:
Ом-1см2/г-ион;
Ом-1см2/г-ион.
Р е ш е
н и е
Так как хлорид серебра является
малорастворимым соединением, то
Из уравнения:
,
может быть выражена концентрация
раствора:
или
в г/л:
где
143,38 – эквивалент хлорида серебра, равный
его молярной массе.
Соседние файлы в папке физическая химия 1
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мера способности вещества сопротивляться или проводить электрический ток
Удельное электрическое сопротивление (также называемое удельное электрическое сопротивление или объемное удельное сопротивление ) и его обратная, электрическая проводимость, является фундаментальным свойством материала, которое количественно определяет, насколько сильно он сопротивляется или проводит электрический ток. Низкое удельное сопротивление указывает на материал, который легко пропускает электрический ток. Удельное сопротивление обычно обозначается греческой буквой ρ (rho ). Единица измерения удельного электрического сопротивления SI — это Ом — метр (Ом⋅м). Например, если твердый куб материала размером 1 м × 1 м × 1 м имеет контакты листов на двух противоположных гранях, а сопротивление между этими контактами составляет 1 Ом, то удельное сопротивление материала составляет 1 Ом · м.
Электропроводность или удельная проводимость обратно пропорциональна удельному электрическому сопротивлению. Он представляет собой способность материала проводить электрический ток. Обычно обозначается греческой буквой σ (сигма ), но иногда используются κ (каппа ) (особенно в электротехнике) и γ (гамма ).. Единица измерения электрической проводимости в системе СИ — сименс на метр (См / м).
Содержание
- 1 Определение
- 1.1 Идеальный случай
- 1.2 Общие скалярные величины
- 1.3 Тензорное удельное сопротивление
- 2 Проводимость и носители тока
- 2.1 Связь между плотностью тока и скоростью электрического тока
- 3 Причины проводимости
- 3.1 Упрощение зонной теории
- 3.2 В металлах
- 3.3 В полупроводниках и изоляторах
- 3.4 В ионных жидкостях / электролитах
- 3.5 Сверхпроводимость
- 3.6 Плазма
- 4 Удельное сопротивление и проводимость различных материалов
- 5 Температурная зависимость
- 5.1 Линейное приближение
- 5.2 Металлы
- 5.2.1 Закон Видемана-Франца
- 5.3 Полупроводники
- 6 Комплексное удельное сопротивление и проводимость
- 7 Сопротивление по сравнению с удельным сопротивлением в сложных геометрических формах
- 8 Произведение удельного сопротивления
- 9 См. также
- 10 Примечания
- 11 Ссылки
- 12 Дополнительная литература
- 13 Внешние ссылки
Определение
Идеальный случай

В идеальном случае поперечное сечение и физический состав части исследуемого материала однородны по всему образцу, а электрическое поле и плотность тока везде параллельны и постоянны. Многие резисторы и проводники на самом деле имеют однородное поперечное сечение с равномерным течением электрического тока и изготовлены из одного материала, так что это хорошая модель. (См. Диаграмму рядом.) В этом случае удельное электрическое сопротивление ρ (греч.: rho ) можно рассчитать следующим образом:
- ρ = RA ℓ, { displaystyle rho = R { frac {A} { ell}}, , !}
где
- R { displaystyle R}
— электрическое сопротивление однородного образца материал
- ℓ { displaystyle ell}
— это длина образца
- A { displaystyle A}
— крест -площадь сечения образца
Как сопротивление, так и удельное сопротивление описывают, насколько сложно заставить электрический ток течь через материал, но, в отличие от сопротивления, удельное сопротивление является внутренним свойством. Это означает, что все провода из чистой меди (которые не подвергались искажению своей кристаллической структуры и т. Д.), Независимо от их формы и размера, имеют одинаковое удельное сопротивление, но длинный тонкий медный провод имеет гораздо большее сопротивление, чем толстый, провод медный короткий. Каждый материал имеет свое собственное удельное сопротивление. Например, резина имеет гораздо большее удельное сопротивление, чем медь.
В гидравлической аналогии, прохождение тока через материал с высоким удельным сопротивлением похоже на проталкивание воды через трубу, полную песка, а пропускание тока через материал с низким удельным сопротивлением — как проталкивание воды через пустая труба. Если трубы одинакового размера и формы, у трубы, заполненной песком, будет более высокое сопротивление потоку. Однако сопротивление определяется не только наличием или отсутствием песка. Это также зависит от длины и ширины трубы: короткие или широкие трубы имеют меньшее сопротивление, чем узкие или длинные.
Приведенное выше уравнение можно транспонировать, чтобы получить закон Пуйе (названный в честь Клода Пуйе ):
- R = ρ ℓ A. { displaystyle R = rho { frac { ell} {A}}. , !}
Сопротивление данного материала пропорционально длине, но обратно пропорционально площади поперечного сечения. Таким образом, удельное сопротивление может быть выражено с помощью единицы SI «ом метр » (Ом⋅м) — то есть омы, разделенные на метры (для длины), а затем умноженные на квадратные метры (по площади поперечного сечения).
Например, если A = 1 м, ℓ { displaystyle ell}
Проводимость σ является обратной величиной удельного сопротивления:
- σ = 1 ρ. { displaystyle sigma = { frac {1} { rho}}. , !}
В единицах системы СИ сименс на метр (См / м).
Общие скалярные величины
Для менее идеальных случаев, таких как более сложная геометрия, или когда ток и электрическое поле изменяются в разных частях материала, необходимо использовать более общее выражение в котором удельное сопротивление в конкретной точке определяется как отношение электрического поля к плотности тока, который он создает в этой точке:
- ρ = EJ, { displaystyle rho = { frac {E} {J}}, , !}
где
- ρ { displaystyle rho}
— удельное сопротивление материала проводника,
- E { displaystyle E}
— величина электрического поля,
- J { displaystyle J}
— величина плотность тока,
, в которой E { displaystyle E}

Электропроводность — это величина, обратная (обратной) величине удельного сопротивления. Здесь это определяется как:
- σ = 1 ρ = J E. { displaystyle sigma = { frac {1} { rho}} = { frac {J} {E}}. , !}
Например, резина — это материал с большим ρ и малым σ — потому что даже очень большое электрическое поле в резине почти не пропускает ток. С другой стороны, медь — это материал с малым ρ и большим σ, потому что даже небольшое электрическое поле пропускает через него большой ток.
Как показано ниже, это выражение упрощается до одного числа, когда электрическое поле и плотность тока в материале постоянны.
-
Вывод из общего определения удельного сопротивления Здесь необходимо объединить три уравнения. Первый — это удельное сопротивление для параллельного тока и электрического поля: - ρ = EJ, { displaystyle rho = { frac {E} {J}}, , !}
Если электрическое поле постоянно, электрическое поле определяется как полное напряжение V на проводнике, деленное на длину ℓ проводника:
- E = V ℓ { displaystyle E = { frac {V} { ell}}}
Если плотность тока постоянна, она равна полному току, деленному на площадь поперечного сечения:
- J = IA { displaystyle J = { frac {I} {A}}}
Подсоединение значений E и J в первое выражение, мы получаем:
- ρ = VAI ℓ { displaystyle rho = { frac {VA} {I ell}}}
Наконец, мы применяем закон Ома, V / I = R.
- ρ = RA ℓ { displaystyle rho = R { frac {A} { ell}}}
- ρ = EJ, { displaystyle rho = { frac {E} {J}}, , !}
Тензорное удельное сопротивление
Когда удельное сопротивление материала имеет направленную составляющую, необходимо использовать самое общее определение удельного сопротивления. Он начинается с тензорно-векторной формы закона Ома, который связывает электрическое поле внутри материала с потоком электрического тока. Это уравнение является полностью общим, то есть справедливо во всех случаях, включая упомянутые выше. Однако это определение является наиболее сложным, поэтому оно напрямую используется только в анизотропных случаях, когда более простые определения не могут применяться. Если материал не является анизотропным, можно проигнорировать определение вектора тензора и вместо этого использовать более простое выражение.
Здесь анизотропный означает, что материал имеет разные свойства в разных направлениях. Например, кристалл графита микроскопически состоит из стопки листов, и ток очень легко течет через каждый лист, но гораздо труднее от одного листа к соседнему. В таких случаях ток не течет точно в том же направлении, что и электрическое поле. Таким образом, соответствующие уравнения обобщаются до трехмерной тензорной формы:
- J = σ E ⇌ E = ρ J { displaystyle mathbf {J} = { boldsymbol { sigma}} mathbf {E} , , rightleftharpoons , , mathbf {E} = { boldsymbol { rho}} mathbf {J} , !}
, где проводимость σ и удельное сопротивление ρ — тензоры ранга 2, а электрическое поле E и плотность тока J — векторы. Эти тензоры могут быть представлены матрицами 3 × 3, векторами с матрицами 3 × 1, с умножением матриц , используемым в правой части этих уравнений. В матричной форме соотношение удельных сопротивлений определяется следующим образом:
- [E x E y E z] = [ρ xx ρ xy ρ xz ρ yx ρ yy ρ yz ρ zx ρ zy ρ zz] [J x J y J z ] { displaystyle { begin {bmatrix} E_ {x} \ E_ {y} \ E_ {z} end {bmatrix}} = { begin {bmatrix} rho _ {xx} rho _ { xy} rho _ {xz} \ rho _ {yx} rho _ {yy} rho _ {yz} \ rho _ {zx} rho _ {zy} rho _ {zz} end {bmatrix}} { begin {bmatrix} J_ {x} \ J_ {y} \ J_ {z} end {bmatrix}}}
где
- E { displaystyle mathbf {E}}
— вектор электрического поля с компонентами (E x, E y, E z).
- ρ { displaystyle { boldsymbol { rho}}}
— тензор удельного сопротивления, обычно матрица три на три.
- J { displaystyle mathbf {J}}
— вектор плотности электрического тока, с компонентами (J x, J y, J z)
Эквивалентно, удельное сопротивление может быть задано в более компактной нотации Эйнштейна :
- E i = ρ ij J j { displaystyle mathbf {E} _ {i} = { boldsymbol { rho}} _ {ij} mathbf {J} _ {j}}
В любом случае результат Значение сопротивления для каждой компоненты электрического поля составляет:
- E x = ρ x x J x + ρ x y J y + ρ x z J z. { Displaystyle E_ {x} = rho _ {xx} J_ {x} + rho _ {xy} J_ {y} + rho _ {xz} J_ {z}.}
- E y = ρ yx J x + ρ yy J y + ρ yz J z. { Displaystyle E_ {y} = rho _ {yx} J_ {x} + rho _ {yy} J_ {y} + rho _ {yz} J_ {z}.}
- E z = ρ zx J x + ρ zy J y + ρ zz J z. { displaystyle E_ {z} = rho _ {zx} J_ {x} + rho _ {zy} J_ {y} + rho _ {zz} J_ {z}.}
Поскольку выбор система координат свободна, обычное соглашение состоит в том, чтобы упростить выражение, выбрав ось x, параллельную текущему направлению, поэтому J y = J z = 0. Это оставляет:
- ρ xx = E x J x, ρ yx = E y J x и ρ zx = E z J x. { displaystyle rho _ {xx} = { frac {E_ {x}} {J_ {x}}}, quad rho _ {yx} = { frac {E_ {y}} {J_ {x} }}, { text {and}} rho _ {zx} = { frac {E_ {z}} {J_ {x}}}.}
Проводимость определяется аналогично:
- [J x J Y J Z] знак равно [σ xx σ xy σ xz σ yx σ yy σ yz σ zx σ zy σ zz] [E x E y E z] { displaystyle { begin {bmatrix} J_ {x} \ J_ { y} \ J_ {z} end {bmatrix}} = { begin {bmatrix} sigma _ {xx} sigma _ {xy} sigma _ {xz} \ sigma _ {yx} sigma _ {yy} sigma _ {yz} \ sigma _ {zx} sigma _ {zy} sigma _ {zz} end {bmatrix}} { begin {bmatrix} E_ {x } \ E_ {y} \ E_ {z} end {bmatrix}}}
или
- J i = σ ij E j { displaystyle mathbf {J} _ {i} = { boldsymbol { sigma}} _ {ij} mathbf {E} _ {j}}
Оба результата дают:
- J x = σ xx E x + σ xy E y + σ xz E z { displaystyle J_ {x} = sigma _ {xx} E_ {x} + sigma _ {xy} E_ {y} + sigma _ {xz} E_ {z}}
- J y = σ yx E x + σ yy E y + σ yz E Z { displaystyle J_ {y} = sigma _ {yx} E_ {x} + sigma _ {yy} E_ {y} + sigma _ {yz} E_ {z}}
- J Z знак равно σ zx E Икс + σ zy E Y + σ zz E Z { Displaystyle J_ {z} = sigma _ {zx} E_ {x} + sig ma _ {zy} E_ {y} + sigma _ {zz} E_ {z}}
Глядя на два выражения, ρ { displaystyle { boldsymbol { rho}}}




- σ xx = ρ xx ρ xx 2 + ρ xy 2, σ xy = — ρ xy ρ xx 2 + ρ xy 2 { displaystyle sigma _ {xx} = { frac { rho _ {xx}} { rho _ {xx} ^ { 2} + rho _ {xy} ^ {2}}}, quad sigma _ {xy} = { frac {- rho _ {xy}} { rho _ {xx} ^ {2} + rho _ {xy} ^ {2}}}}
Если электрическое поле параллельно приложенному току, ρ xy { displaystyle rho _ {xy}}



Проводимость и носители тока
Связь между плотностью тока и скоростью электрического тока
Электрический ток — это упорядоченное движение электрических зарядов. Эти расходы называются носителями тока. В металлах и полупроводниках, электроны являются носителями тока; в электролитах и ионизированных газах, положительных и отрицательных ионах. В общем случае плотность тока одного носителя определяется по формуле:
- j → = qn υ → a { displaystyle { vec {j}} = qn { vec { upsilon}} _ {a }}
,
где 𝑛 — плотность носителей заряда (количество носителей в единице объема), 𝑞 — заряд одного носителя, υ → a { displaystyle { vec { upsilon}} _ {a}}
- j → = ∑ jji { displaystyle { vec {j}} = sum _ {j} j_ {i}}
.
, где ji { displaystyle j_ {i}}

Причины проводимости
Упрощенная зонная теория

Согласно элементарной квантовой механике, электрон в атоме или кристалл может иметь только определенные точные уровни энергии; энергии между этими уровнями невозможны. Когда большое количество таких разрешенных уровней имеют близкорасположенные значения энергии, то есть имеют энергии, которые отличаются лишь незначительно, эти близкие энергетические уровни в комбинации называются «энергетической зоной». В материале может быть много таких энергетических зон, в зависимости от атомного номера составляющих атомов и их распределения в кристалле.
Электроны материала стремятся минимизировать общую энергию в материале за счет перехода в низкоэнергетические состояния; однако принцип исключения Паули означает, что только один может существовать в каждом таком состоянии. Таким образом, электроны «заполняют» зонную структуру, начиная снизу. Характерный уровень энергии, до которого заполнились электроны, называется уровнем Ферми . Положение уровня Ферми по отношению к зонной структуре очень важно для электропроводности: только электроны на энергетических уровнях около или выше уровня Ферми могут свободно перемещаться в более широкой структуре материала, поскольку электроны могут легко перепрыгивать между частично занятыми государствами в этом регионе. Напротив, состояния с низкой энергией полностью заполнены с фиксированным пределом на количество электронов в любое время, а состояния с высокой энергией всегда пусты от электронов.
Электрический ток состоит из потока электронов. В металлах есть много уровней энергии электронов вблизи уровня Ферми, поэтому существует много электронов, которые могут двигаться. Это причина высокой электронной проводимости металлов.
Важной частью теории зон является то, что могут существовать запрещенные зоны энергии: интервалы энергии, которые не содержат уровней энергии. В изоляторах и полупроводниках количество электронов является правильным, чтобы заполнить определенное целое число низкоэнергетических зон точно до границы. В этом случае уровень Ферми попадает в запрещенную зону. Поскольку вблизи уровня Ферми нет доступных состояний, а электроны не могут свободно перемещаться, электронная проводимость очень мала.
В металлах

A металл состоит из решетки из атомов, каждый из которых имеет внешнюю оболочку из электронов, которые свободно отделяются от своих родительских атомов и проходят через решетку. Это также известно как положительная ионная решетка. Это «море» диссоциируемых электронов позволяет металлу проводить электрический ток. Когда к металлу прикладывается разность электрических потенциалов (напряжение ), возникающее электрическое поле заставляет электроны дрейфовать к положительному выводу. Фактическая скорость дрейфа электронов обычно мала, порядка метров в час. Однако из-за огромного количества движущихся электронов даже низкая скорость дрейфа приводит к большой плотности тока. Механизм аналогичен передаче количества движения шарикам в колыбели Ньютона, но быстрое распространение электрической энергии по проводу происходит не из-за механических сил, а из-за распространения несущего энергию электромагнитного поля. по проводам.
Большинство металлов обладают электрическим сопротивлением. В более простых моделях (неквантово-механических моделях) это можно объяснить заменой электронов и кристаллической решетки волнообразной структурой. Когда электронная волна проходит через решетку, волны интерферируют, что вызывает сопротивление. Чем более правильная решетка, тем меньше возмущений и, следовательно, меньше сопротивления. Таким образом, сопротивление в основном обусловлено двумя факторами. Во-первых, это вызвано температурой и, следовательно, количеством колебаний кристаллической решетки. Более высокие температуры вызывают более сильные вибрации, которые действуют как неровности решетки. Во-вторых, важна чистота металла, поскольку смесь различных ионов также является неоднородностью. Небольшое уменьшение проводимости при плавлении чистых металлов связано с потерей дальнего кристаллического порядка. Сохраняется ближний порядок, и сильная корреляция между положениями ионов приводит к когерентности между волнами, дифрагированными на соседних ионах.
В полупроводниках и изоляторах
В металлах уровень Ферми находится в зоне проводимости (см. Теорию зон выше), что приводит к свободному электроны проводимости. Однако в полупроводниках положение уровня Ферми находится внутри запрещенной зоны, примерно на полпути между минимумом зоны проводимости (нижняя часть первой зоны незаполненных электронных уровней энергии) и максимумом валентной зоны (верхняя часть зоны ниже зоны проводимости заполненных уровней энергии электронов). Это применимо к собственным (нелегированным) полупроводникам. Это означает, что при абсолютном нуле температуры не было бы свободных электронов проводимости, а сопротивление бесконечно. Однако сопротивление уменьшается по мере увеличения плотности носителей заряда (то есть, без дополнительных осложнений, плотности электронов) в зоне проводимости. В примесных (легированных) полупроводниках легирующие атомы увеличивают концентрацию основных носителей заряда, отдавая электроны зоне проводимости или создавая дырки в валентной зоне. («Дырка» — это положение, в котором отсутствует электрон; такие дырки могут вести себя аналогично электронам.) Для обоих типов донорных и акцепторных атомов увеличение плотности примеси снижает сопротивление. Следовательно, высоколегированные полупроводники ведут себя металлически. При очень высоких температурах вклад термически генерируемых носителей преобладает над вкладом атомов примеси, а сопротивление экспоненциально уменьшается с температурой.
В ионных жидкостях / электролитах
В электролитах электрическая проводимость осуществляется не зонными электронами или дырками, а полностью атомарными частицами (ионами ) путешествующие, каждый из которых несет электрический заряд. Удельное сопротивление ионных растворов (электролитов) сильно зависит от концентрации — в то время как дистиллированная вода является почти изолятором, соленая вода является разумным проводником электричества. Проводимость в ионных жидкостях также контролируется движением ионов, но здесь мы говорим о расплавленных солях, а не о сольватированных ионах. В биологических мембранах токи переносятся ионными солями. Небольшие отверстия в клеточных мембранах, называемые ионными каналами, избирательны по отношению к определенным ионам и определяют сопротивление мембраны.
Концентрация ионов в жидкости (например, в водном растворе) зависит от степени диссоциации растворенного вещества, характеризующейся коэффициентом диссоциации α { displaystyle alpha}


- N = α N 0 { displaystyle N = alpha N_ {0}}
.
Удельная электрическая проводимость (σ { displaystyle sigma}
- σ = q (b + + b -) α N 0 { displaystyle sigma = q left (b ^ {+} + b ^ {-} right) alpha N_ {0}}
,
где q { displaystyle q}




Сверхпроводимость
Удельное электрическое сопротивление металлического проводника постепенно уменьшается при понижении температуры. В обычных проводниках, таких как медь или серебро, это уменьшение ограничено примесями и другими дефектами. Даже около абсолютного нуля реальный образец нормального проводника показывает некоторое сопротивление. В сверхпроводнике сопротивление резко падает до нуля, когда материал охлаждается ниже критической температуры. Электрический ток, протекающий в петле из сверхпроводящего провода, может сохраняться бесконечно без источника питания.
В 1986 году исследователи обнаружили, что некоторые купрат — перовскит керамические материалы имеют гораздо более высокие критические температуры, и в 1987 году был произведен один материал с критической температурой выше 90 К (-183 ° C). Такая высокая температура перехода теоретически невозможна для обычного сверхпроводника , поэтому исследователи назвали эти проводники высокотемпературными сверхпроводниками. Жидкий азот кипит при 77 К, достаточно холодном, чтобы активировать высокотемпературные сверхпроводники, но не достаточно холодном для обычных сверхпроводников. В обычных сверхпроводниках электроны удерживаются вместе парами за счет притяжения, связанного с решеточными фононами. Лучшая доступная модель высокотемпературной сверхпроводимости все еще остается грубой. Существует гипотеза, что спаривание электронов в высокотемпературных сверхпроводниках обеспечивается короткодействующими спиновыми волнами, известными как парамагноны.
Плазма

Плазма — очень хорошие проводники и электрические потенциалы. играть важную роль.
Потенциал, существующий в среднем в пространстве между заряженными частицами, независимо от того, как его можно измерить, называется потенциалом плазмы или космическим потенциалом. Если электрод вставлен в плазму, его потенциал обычно значительно ниже потенциала плазмы из-за того, что называется оболочкой Дебая. Хорошая электропроводность плазмы делает ее электрические поля очень маленькими. Это приводит к важной концепции квазинейтральности, согласно которой плотность отрицательных зарядов примерно равна плотности положительных зарядов в больших объемах плазмы (n e = ⟨Z⟩>n i), но на шкале длины Дебая может быть дисбаланс заряда. В особом случае, когда образуются двойные слои , разделение зарядов может увеличиваться на несколько десятков длин Дебая.
Величина потенциалов и электрических полей должна определяться другими способами, кроме простого нахождения чистой плотности заряда. Типичным примером является предположение, что электроны удовлетворяют соотношению Больцмана :
- n e ∝ e e Φ / k B T e. { displaystyle n _ { text {e}} propto e ^ {e Phi / k _ { text {B}} T _ { text {e}}}.}
Дифференциация этого отношения дает средства для вычисления электрическое поле от плотности:
- E = — k BT ee ∇ nene. { displaystyle mathbf {E} = — { frac {k _ { text {B}} T _ { text {e}}} {e}} { frac { nabla n _ { text {e}}} {n _ { text {e}}}}.}
(∇ — оператор векторного градиента; дополнительную информацию см. в символе набла и gradient.)
Возможно создание не квазинейтральной плазмы. Электронный луч, например, имеет только отрицательные заряды. Плотность ненейтральной плазмы обычно должна быть очень низкой или очень маленькой. В противном случае отталкивающая электростатическая сила рассеивает его.
В астрофизической плазме экранирование Дебая предотвращает непосредственное воздействие электрических полей на плазму на больших расстояниях, то есть больше, чем длина Дебая. Однако наличие заряженных частиц заставляет плазму генерировать магнитные поля и воздействовать на них. Это может вызвать и вызывает чрезвычайно сложное поведение, такое как образование двойных слоев плазмы, объекта, который разделяет заряд на несколько десятков длин Дебая. Динамика взаимодействия плазмы с внешними и самогенерируемыми магнитными полями изучается в академической дисциплине магнитогидродинамика.
Плазму часто называют четвертым состоянием вещества после твердого тела, жидкостей и газов. Оно отличается от этих и других низкоэнергетических состояний материи. Хотя он тесно связан с газовой фазой в том смысле, что он также не имеет определенной формы или объема, он отличается по ряду причин, включая следующее:
| Свойство | Газ | Плазма |
|---|---|---|
| Электропроводность | Очень низкая: воздух является отличным изолятором, пока не распадется на плазму при напряженности электрического поля выше 30 киловольт на сантиметр. | Обычно очень высокая: для многих целей проводимость плазмы можно считать бесконечной. |
| Независимо действующие частицы | Один: все частицы газа ведут себя одинаково, под влиянием гравитации и столкновений друг с другом. | Два или три: электроны, ионы, протоны и нейтроны можно различить по знаку и значению их заряжают, так что они ведут себя независимо во многих обстоятельствах, с разными объемными скоростями и температурами, что допускает такие явления, как новые типы волн и нестабильности. |
| Распределение скоростей | Максвелловский : столкновения обычно приводят к максвелловскому распределению скоростей всех частиц газа с очень небольшим количеством относительно быстрых частиц. | Часто не максвелловские: столкновительные взаимодействия часто бывают слабыми в горячей плазме, и внешнее воздействие может увести плазму далеко от локального равновесия и привести к значительной популяции необычно быстрых частиц. |
| Взаимодействия | Двоичные: столкновения двух частиц — правило, столкновения трех тел — крайне редко. | Коллективный: волны или организованное движение плазмы очень важны, потому что частицы могут взаимодействовать на больших расстояниях посредством электрических и магнитных сил. |
Удельное сопротивление и проводимость различных материалов
- Проводник, такой как металл, имеет высокую проводимость и низкое удельное сопротивление.
- Изолятор , такой как стекло, имеет низкое проводимость и высокое удельное сопротивление.
- Электропроводность полупроводника обычно является промежуточной, но сильно варьируется в различных условиях, таких как воздействие на материал электрических полей или определенных частот свет, и, что наиболее важно, с температурой и составом полупроводникового материала.
Степень легирования полупроводников имеет большое значение для проводимости. В некотором смысле, большее количество легирования приводит к более высокой проводимости. Электропроводность раствора воды воды в значительной степени зависит от его концентрации растворенных солей и других химических веществ, которые ионизируют в растворе. Электропроводность образцов воды используется как индикатор того, насколько образец не содержит соли, ионов или примесей; чем чище вода, тем ниже проводимость (тем выше удельное сопротивление). Измерения проводимости воды часто выражаются как удельная проводимость по отношению к проводимости чистой воды при 25 ° C. EC-метр обычно используется для измерения проводимости в растворе. Приблизительное резюме выглядит следующим образом:
| Материал | Удельное сопротивление, ρ (Ом · м) |
|---|---|
| Сверхпроводники | 0 |
| Металлы | 10 |
| Полупроводники | Переменная |
| Электролиты | Переменная |
| Изоляторы | 10 |
| Суперизоляторы | ∞ |
В этой таблице показаны удельное сопротивление (ρ), проводимость и температурный коэффициент различных материалов при 20 ° C (68 ° F, 293 K )
| Материал | Удельное сопротивление, ρ,. при 20 ° C (Ом · м) | Проводимость, σ,. при 20 ° C (S / m) | Temperature. coefficient (K) | Reference |
|---|---|---|---|---|
| Silver | 1.59×10 | 6.30×10 | 0.00380 | |
| Copper | 1.68×10 | 5.96×10 | 0.00404 | |
| Annealed copper | 1.72×10 | 5.80× 10 | 0.00393 | |
| Gold | 2.44×10 | 4.11×10 | 0.00340 | |
| Aluminium | 2.65×10 | 3.77×10 | 0.00390 | |
| Calcium | 3.36×10 | 2.98×10 | 0.00410 | |
| Tungsten | 5.60×10 | 1.79×10 | 0.00450 | |
| Zinc | 5.90×10 | 1.69×10 | 0. 00370 | |
| Cobalt | 6.24×10 | 1.60×10 | 0.007 | |
| Nickel | 6.99×10 | 1.43×10 | 0.006 | |
| Ruthenium | 7.10×10 | 1.41×10 | ||
| Lithium | 9.28×10 | 1.08×10 | 0.006 | |
| Iron | 9.70×10 | 10 | 0.005 | |
| Platinum | 1.06×10 | 9.43×10 | 0.00392 | |
| Tin | 1.09×10 | 9.17×10 | 0.00450 | |
| Gallium | 1.40×10 | 7.10×10 | 0.004 | |
| Niobium | 1.40×10 | 7.00×10 | ||
| Carbon steel (1010) | 1.43×10 | 6.99×10 | ||
| Lead | 2.20×10 | 4.55×10 | 0.0039 | |
| Galinstan | 2.89×10 | 3.46×10 | ||
| Titanium | 4.20×10 | 2.38×10 | 0.0038 | |
| Grain oriented electrical steel | 4.60×10 | 2.17×10 | ||
| Manganin | 4.82×10 | 2.07×10 | 0.000002 | |
| Constantan | 4.90×10 | 2.04×10 | 0.000008 | |
| Stainless steel | 6.90×10 | 1.45×10 | 0.00094 | |
| Mercury | 9.80×10 | 1.02×10 | 0.00090 | |
| Mangane se | 1.44×10 | 6.94×10 | ||
| Nichrome | 1.10×10 | 6.70×10. | 0.0004 | |
| Carbon (amorphous) | 5×10 to 8×10 | 1.25×10 to 2.00×10 | −0.0005 | |
| Carbon (graphite). parallel to. basal plane | 2.5×10 to 5.0×10 | 2×10 to 3×10. | ||
| Carbon (graphite). perpendicular to. basal plane | 3×10 | 3.3×10 | ||
| GaAs | 10 to 10 | 10 to 10 | ||
| Germanium | 4.6×10 | 2.17 | −0.048 | |
| Sea water | 2.0×10 | 4.8 | ||
| Swimming pool water | 3.3×10 to 4.0×10 | 0.25 to 0.30 | ||
| Drinking water | 2×10 to 2×10 | 5×10 to 5×10 | ||
| Silicon | 2.3×10 | 4.35×10 | −0.075 | |
| Wood (damp) | 10 to 10 | 10 to 10 | ||
| Deionized water | 1.8×10 | 5. 5 × 10 | ||
| Стекло | от 10 до 10 | от 10 до 10 | ? | |
| Углерод (алмаз) | 10 | ~ 10 | ||
| Твердая резина | 10 | 10 | ? | |
| Воздух | от 10 до 10 | ~ 10 до 10 | ||
| Древесина (высушенная в печи) | 10-10 | 10-10 | ||
| Сера | 10 | 10 | ? | |
| плавленый кварц | 7,5 × 10 | 1,3 × 10 | ? | |
| ПЭТ | 10 | 10 | ? | |
| Тефлон | от 10 до 10 | от 10 до 10 | ? |
Эффективный температурный коэффициент зависит от температуры и уровня чистоты материала. Значение 20 ° C является приблизительным при использовании при других температурах. Например, для меди коэффициент становится ниже при более высоких температурах, и значение 0,00427 обычно указывается при 0 ° C.
Чрезвычайно низкое удельное сопротивление (высокая проводимость) серебра характерно для металлов. Джордж Гамов аккуратно резюмировал природу взаимодействия металлов с электронами в своей научно-популярной книге «Один, два, три… бесконечность» (1947):
Металлические вещества отличаются от всех других материалов тем, что тот факт, что внешние оболочки их атомов связаны довольно слабо и часто позволяют одному из своих электронов уйти на свободу. Таким образом, внутренняя часть металла заполнена большим количеством непривязанных электронов, которые бесцельно путешествуют, как толпа перемещенных лиц. Когда на металлическую проволоку действует электрическая сила, приложенная к ее противоположным концам, эти свободные электроны устремляются в направлении силы, образуя так называемый электрический ток.
С технической точки зрения, модель свободных электронов дает базовое описание электронного потока в металлах.
Древесина широко считается чрезвычайно хорошим изолятором, но ее удельное сопротивление сильно зависит от содержания влаги, при этом влажная древесина как минимум в 10 раз хуже изолирует, чем высушенная в печи. В любом случае достаточно высокое напряжение — например, при ударах молнии или в некоторых высоковольтных линиях электропередачи — может привести к риску пробоя изоляции электрического тока даже для явно сухой древесины.
Температурная зависимость
Линейное приближение
Удельное электрическое сопротивление материала изменяется в зависимости от температуры. Если температура T не меняется слишком сильно, обычно используется линейное приближение :
- ρ (T) = ρ 0 [1 + α (T — T 0)] { displaystyle rho (T) = rho _ {0} [1+ alpha (T-T_ {0})]}
где α { displaystyle alpha}







Металлы
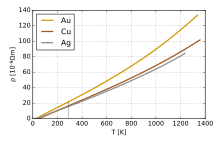
В общем, удельное электрическое сопротивление металлов увеличивается с температурой. Взаимодействия — фонон могут играть ключевую роль. При высоких температурах сопротивления металла линейно увеличивается с температурой. При понижении температуры металла температурная зависимость удельного сопротивления подчиняется степенной функции температуры. Математически температурная зависимость удельного сопротивления металла ρ определяетсялой Блоха — Грюнайзена:
- ρ (T) = ρ (0) + A (T Θ R) n ∫ 0 Θ RT xn (ex — 1) (1 — е — Икс) dx { Displaystyle rho (T) = rho (0) + A left ({ frac {T} { Theta _ {R}}} right) ^ {n} int _ {0} ^ { frac { Theta _ {R}} {T}} { frac {x ^ {n}} { left (e ^ {x} -1 right) left (1- e ^ {- x} right)}} , dx}
где ρ (0) { displaystyle rho (0)}

- n = 5 означает, что сопротивление вызвано рассеянием электронов на фононах (как в случае простых металлов).
- n = 3 означает, что сопротивление возникает из-за sd-рассеяния электронов (как в случае с переходными металлами)
- n = 2 означает, что сопротивление вызывает электрон-электронным взаимодействием.
. значение n.
Температура металла достаточно снижена (чтобы «заморозить» все фононы), удельное сопротивление обычно постоянное значение, известное как остаточное сопротивление . Это значение не только от типа металла, но и от его чистоты и термической истории. Величина остаточного сопротивления металла определяется концентрацией его примесей. Некоторые материалы теряют все электрическое сопротивление при достаточно низких температурах из-за эффекта, известного как сверхпроводимость.
Исследование низкотемпературного сопротивления металлов было мотивацией для экспериментов Хайке Камерлинг-Оннес что привело в 1911 году к открытию сверхпроводимости. Подробнее см. История сверхпроводимости.
Закон Видемана — Франца
Закон Видемана — Франца гласит, что коэффициент электропроводности металлов при нормальных температурах обратно пропорционален температура:
- σ ∼ 1 T { displaystyle sigma Thicksim {1 over T}}
.
При высоких температурах металла закон Видемана-Франца выполнен:
- K σ = π 2 3 (ke) 2 T { Displaystyle {K over sigma} = { pi ^ {2} over 3} left ({ frac {k} {e}} right) ^ {2} T}
,
где K { displaystyle K}




Полупроводники
В общем, собственное удельное сопротивление полупроводника уменьшается с повышением температуры. Электроны попадают в зону энергии проводимости тепловая энергия, где они свободно текут, и при этом оставляют после себя дырки в валентной зоне, которая также течь свободно. Электрическое сопротивление типичного собственного (нелегированного) полупроводника уменьшается экспоненциально с температурой:
- ρ = ρ 0 e — a T { displaystyle rho = rho _ {0} e ^ {- aT} ,}
Еще лучшее приближение температурной зависимости удельного сопротивления полупроводника дается уравнением Стейнхарта — Харта :
- 1 T Знак равно A + В пер ρ + С (пер ρ) 3 { Displaystyle { гидроразрыва {1} {T}} = A + B ln rho + C ( ln rho) ^ {3} ,}
где A, B и C — так называемые коэффициенты Стейнхарта — Харта .
Это уравнение используется для калибровки термисторов.
Внешние (легированные) полупроводники имеют намного больше сложный температурный профиль. При повышении температуры, начиная с абсолютного нуля, их сопротивление сначала резко падает, поскольку носители покидают доноры или акцепторы. После большинства доноров или акцепторов потеряли своих носителей сопротивление снова начинает немного увеличиваться из-за уменьшения подвижности носителей (как в металле). При более высоких температурах они ведут себя как собственные полупроводники, поскольку носители от доноров / акцепторов становятся незначительными по сравнению с термически генерируемыми носителями.
В некристаллических полупроводниках проводимость может происходить за счет зарядов квантовое туннелирование с одного локализованного сайта на другой. Это известно как скачкообразное изменение диапазона и имеет характерную форму
- ρ = A exp (T — 1 n), { displaystyle rho = A exp left (T ^ {- { frac {1} {n}}} right),}
где n = 2, 3, 4, в зависимости от размерности системы.
Комплексное сопротивление и проводимость
При реакции материалов на переменные электрические поля (электрический спектроскопия ) в таких приложениях, как томография электрического импеданса, удобно заменить удельное сопротивление на комплексную определяемую импедансом (по аналогии с электрическим импедансом ). Импедивность — это сумма реальной составляющей, удельного сопротивления и мнимой составляющей, реактивности (по аналогии с реактивным сопротивлением ). Величина импеданса — это квадратный корень из суммы квадратов значений удельного сопротивления и реактивности.
И наоборот, в таких случаях проводимость должна быть выражена в виде комплексного числа (или даже в виде матрицы комплексных чисел в случае анизотропных материалов), называемых допустимость. Адмиттивная способность — сумма проводимой составляющей, называемой способностию, и мнимой составляющей, называемой восприимчивостью.
. В альтернативном описании реакции на переменные токи используется реальная (но частотно-зависимая) проводимость, а также реальная диэлектрическая проницаемость. Чем больше проводимость, тем быстрее сигнал переменного тока поглощается (т.е. тем более непрозрачным является материалом). Подробнее см. Математическое описание непрозрачности.
Сопротивление в зависимости от формы сопротивления в геометрических формах
Даже если сопротивление материала известно, расчет сопротивления чего-либо, сделанного из него, в некоторых случаях может быть значительным. сложнее, чем формула R = ρ ℓ / A { displaystyle R = rho ell / A}
В подобных случаях формулы
- J = σ E ⇌ E = ρ J { displaystyle J = sigma E , , rightleftharpoons , , E = rho J , !}
необходимо заменить на
- J (r) = σ (r) E (r) ⇌ E (r) = ρ (r) J (r), { displaystyle mathbf {J} ( mathbf {r }) = sigma ( mathbf {r}) mathbf {E} ( mathbf {r}) , , rightleftharpoons , , mathbf {E} ( mathbf {r}) = rho ( mathbf {r}) mathbf {J} ( mathbf {r}), , !}
где E и J теперь присутствует поля. Это уравнение, вместе с уравнением неразрывности для J и уравнением Пуассона для E, образуют набор частных производных уравнений. «В особых точных или приближенных решениях» таких как анализ конечных элементов.
Произведение удельного сопротивления на плотность
В некоторых приложениях, где вес объекта очень важен, произведение удельного сопротивления и плотности более важно, чем абсолютно низкое удельное сопротивление — часто можно сделать проводник толще, чтобы компенсировать более высокое удельное сопротивление; и тогда желателен продукт с низким удельным сопротивлением и плотностью (или, что эквивалентно, с высоким отношением к плотности). Например, для междугородных воздушных линий электропередачи часто используется алюминий, а не медь (Cu), поскольку он легче при той же проводимости.
Серебро, хотя и является наименования резистивным из известных металлов, высокая плотность и по своим характеристикам аналогично меди, но намного дороже. Кальций и щелочные металлы используют лучшие произведения удельного сопротивления, но редко используются для проводников из-за их высокой реакционной способности с водой и кислородом (и прочности физической). Алюминий гораздо более устойчиво. Токсичность исключает выбор бериллия. (Чистый бериллий также является хрупким.) Таким образом, алюминий обычно является предпочтительным металлом, когда решающим фактором является вес или стоимость проводника.
| Материал | Удельное сопротивление. (нОм · м) | Плотность. (г / см) | Удельное сопротивление × плотность | …, Относительно Cu, что дает. такую же проводимость | Приблизительная цена, на. 9 декабря 2018 г. | |||
|---|---|---|---|---|---|---|---|---|
| (г · мОм / м) | Относительно. к Cu | Объем | Масса | (долл. США за кг) | относительно Cu | |||
| натрия | 47,7 | 0,97 | 46 | 31% | 2,843 | 0,31 | ||
| Литий | 92,8 | 0,53 | 49 | 33% | 5,531 | 0,33 | ||
| Кальций | 33,6 | 1,55 | 52 | 35% | 2,002 | 0,35 | ||
| Калий | 72,0 | 0,89 | 64 | 43% | 4,291 | 0,43 | ||
| Бериллий | 35,6 | 1,85 | 66 | 44% | 2,122 | 0,44 | ||
| Алюминий | 26,50 | 2,70 | 72 | 48% | 1,5792 | 0,48 | 2,0 | 0,16 |
| Магний | 43,90 | 1,74 | 7 6 | 51% | 2,616 | 0,51 | ||
| Медь | 16,78 | 8,96 | 150 | 100% | 1 | 1 | 6,0 | 1 |
| Серебро | 15,87 | 10,49 | 166 | 111% | 0, 946 | 1,11 | 456 | 84 |
| Золото | 22,14 | 19,30 | 427 | 285% | 1,319 | 2,85 | 39000 | 19000 |
| Железо | 96,1 | 7,874 | 757 | 505% | 5,727 | 5,05 |
См.
Примечания
Ссылки
Дополнительная литература
- Типлер (2004). Физика для ученых и инженеров: электричество, магнетизм, свет и элементарная современная физика (5-е изд.). В. Х. Фриман. ISBN 978-0-7167-0810-0.
- Измерение удельного электрического сопротивления и проводимости


































![{displaystyle rho (T)=rho _{0}[1+alpha (T-T_{0})],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4124cbfa1149d902f84b2b13f1ccbad6c188fad3)









 — электрическое сопротивление однородного образца материал
— электрическое сопротивление однородного образца материал — крест -площадь сечения образца
— крест -площадь сечения образца








 — вектор электрического поля с компонентами (E x, E y, E z).
— вектор электрического поля с компонентами (E x, E y, E z). — вектор плотности электрического тока, с компонентами (J x, J y, J z)
— вектор плотности электрического тока, с компонентами (J x, J y, J z)








 ,
, .
. .
. ,
,
![{ displaystyle rho (T) = rho _ {0} [1+ альфа (T-T_ {0})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f0d28efd73ce74b1399b50c01300a171066e9be)

 .
. ,
,


