Как найти удельную энергию связи ядра изотопа - AvtoShod.ru

Рассчитайте удельную энергию связи ядра изотопа кислорода

O
. Масса протона 1,0073 а.е. м., масса нейтрона 1,0087 а.е. м., масса изотопа кислорода 15,99491 а. е. м., масса электрона 0,00055 а. е. м.

reshalka.com

ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Радиоактивность. Строение атомного ядра. Энергия связи. Ядерные реакции. Номер №2056

Решение

Дано:

O
;

=
1
,
0073
а.е. м.;

=
1
,
0087
а.е. м.;

=
0
,
00055
а.е. м.;

m = 15,99491 а.е. м.

c
=
3
∗

м/с.
Найти:

− ?
Решение:
Найдем дефект массы ядра:

m
=
(
Z

+
N

)
−
m
;

Z = 8;

N = A − Z = 16 − 8 = 8;
Изотоп кислорода состоит из 8 протонов, 8 нейтронов.

Δm = (8 * 1,0073 + 8 * 1,0087) − 15,99491 = 0,13309 а.е.м.;

1

.
=
1
,
6605
∗

−
27

кг;

Δm =
1
,
6605
∗

−
27

∗
0
,
13309
=
0
,
22
∗

−
27

кг;
Найдем удельную энергию связи:

E
=

;

E
A

0
,
22
∗

−
27

∗
(
3
∗

)

=
0
,
12
∗

−
11

Дж;

1

1
,
6
∗

−
13

;

0
,
12
∗

−
11

1
,
6
∗

−
13

=
7
,
5
МэВ/нуклон.
или
Найдем дефект массы ядра:

m
=
(
Z

+
N

)
−
m
;

Z = 8;

N = A − Z = 16 − 8 = 8;
Изотоп кислорода состоит из 8 протонов, 8 нейтронов.

Δm = (8 * 1,0073 + 8 * 1,0087) − 15,99491 = 0,13309 а.е.м.;

=
931
,
5

;
Найдем удельную энергию связи:

E
=

;

E
A

;

0
,
13309
∗
931
,
5

=
7
,
5
МэВ/нуклон.
Ответ: 7,5 МэВ/нуклон.

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,663
гуманитарные
33,654
юридические
17,917
школьный раздел
611,987
разное
16,906

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

Энергия связи ядра.

Ядерные силы.
Атомная единица массы.
Дефект массы и энергия связи.
Удельная энергия связи.
Насыщение ядерных сил.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев.

Темы кодификатора ЕГЭ: энергия связи нуклонов в ядре, ядерные силы.

Атомное ядро, согласно нуклонной модели, состоит из нуклонов — протонов и нейтронов. Но какие силы удерживают нуклоны внутри ядра?

За счёт чего, например, держатся вместе два протона и два нейтрона внутри ядра атома гелия? Ведь протоны, отталкиваясь друг от друга электрическими силами, должны были бы разлететься в разные стороны! Может быть, это гравитационное притяжение нуклонов друг к другу не даёт ядру распасться?

Давайте проверим. Пусть два протона находятся на некотором расстоянии друг от друга. Найдём отношение силы $F_{el}$ их электрического отталкивания к силе $F_{gr}$ их гравитационного притяжения:

$frac{displaystyle F_{displaystyle el}}{displaystyle F_{displaystyle gr}}=frac{displaystyle ke^{2}/displaystyle r^{2}}{displaystyle Gm^{2}/displaystyle r^{2}}=frac{displaystyle ke^{2}}{displaystyle Gm^{2}}.$

Заряд протона $e=1.6 cdot 10^{-19}$ Кл, масса протона $m approx 1,7 cdot 10^{-27}$ кг, поэтому имеем:

$frac{displaystyle F_{displaystyle el}}{displaystyle F_{displaystyle gr}}=frac{9cdot 10^{9}cdot 1,6^{2}cdot 10^{-38}}{6,67cdot 10^{-11}cdot 1,7^{2}cdot 10^{-54}}sim 10^{36}.$

Какое чудовищное превосходство электрической силы! Гравитационное притяжение протонов не то что не обеспечивает устойчивость ядра — оно вообще не заметно на фоне их взаимного электрического отталкивания.

Следовательно, существуют иные силы притяжения, которые скрепляют нуклоны внутри ядра и превосходят по величине силу электрического отталкивания протонов. Это — так называемые ядерные силы.

к оглавлению ▴

Ядерные силы.

До сих пор мы знали два типа взаимодействий в природе — гравитационные и электромагнитные. Ядерные силы служат проявлением нового, третьего по счёту типа взаимодействий — сильного взаимодействия. Мы не будем вдаваться в механизм возникновения ядерных сил, а лишь перечислим их наиболее важные свойства.

1. Ядерные силы действуют между любыми двумя нуклонами: протоном и протоном, протоном и нейтроном, нейтроном и нейтроном.
2. Ядерные силы притяжения протонов внутри ядра примерно в 100 раз превосходят силу электрического отталкивания протонов. Более мощных сил, чем ядерные, в природе не наблюдается.
3. Ядерные силы притяжения являются короткодействующими: радиус их действия составляет около $10^{-15}$ м. Это и есть размер ядра — именно на таком расстоянии друг от друга нуклоны удерживаются ядерными силами. При увеличении расстояния ядерные силы очень быстро убывают; если расстояние между нуклонами станет равным $2cdot 10^{-15}$ м, ядерные силы почти полностью исчезнут.

На расстояниях, меньших $10^{-15}$ м, ядерные силы становятся силами отталкивания.

Сильное взаимодействие относится к числу фундаментальных — его нельзя объяснить на основе каких-то других типов взаимодействий. Способность к сильным взаимодействиям оказалась свойственной не только протонам и нейтронам, но и некоторым другим элементарным частицам; все такие частицы получили название адронов. Электроны и фотоны к адронам не относятся — они в сильных взаимодействиях не участвуют.

к оглавлению ▴

Атомная единица массы.

Массы атомов и элементарных частиц чрезвычайно малы, и измерять их в килограммах неудобно. Поэтому в атомной и ядерной физике часто применяется куда более мелкая единица — так
называемая атомная единица массы (сокращённо а. е. м.).

По определению, атомная единица массы есть 1/12 массы атома углерода $_{}^{12}textrm{C}$ . Вот её значение с точностью до пяти знаков после запятой в стандартной записи:

а. е. м. $=1,66054cdot 10^{-27}$ кг $=1,66054cdot 10^{-24}$ г.

(Такая точность нам впоследствии понадобится для вычисления одной очень важной величины, постоянно применяющейся в расчётах энергии ядер и ядерных реакций.)

Оказывается, что 1 а. е. м., выраженная в граммах, численно равна величине, обратной к постоянной Авогадро $N_{a}=1,602214cdot 10^{23}$ моль $^{-1}$ :

$frac{1}{N_{A}}=frac{1}{6,02214cdot 10^{23}}=1,66054cdot 10^{-24}$ моль.

Почему так получается? Вспомним, что число Авогадро есть число атомов в 12г углерода. Кроме того, масса $m_{C}$ атома углерода равна 12 а. е. м. Отсюда имеем:

г $=N_{a}m_{C}=N_{A}cdot 12$ а. е. м.,

поэтому $N_{A}cdot 1$ а. е. м.=г, что и требовалось.

Как вы помните, любое тело массы m обладает энергией покоя E, которая выражается формулой Эйнштейна:

$E=mc^{2}$ . (1)

Выясним, какая энергия заключена в одной атомной единице массы. Нам надо будет провести вычисления с достаточно высокой точностью, поэтому берём скорость света с пятью знаками после запятой:

$c=2,99792cdot 10^{8}$ м/с.

Итак, для массы $m_{1}=1$ а. е. м. имеем соответствующую энергию покоя $E_{1}$ :

$E_{1}=m_{1} c^{2}=1,66054 cdot 10^{-27} cdot 2,99792^{2} cdot 10^{16}=1,49241cdot 10^{-10}$ Дж. (2)

В случае малых частиц пользоваться джоулями неудобно — по той же причине, что и килограммами. Существует гораздо более мелкая единица измерения энергии — электронвольт (сокращённо эВ).

По определению, 1 эВ есть энергия, приобретаемая электроном при прохождении ускоряющей разности потенциалов 1 вольт:

эВ $=eV=1,60218cdot 10^{-19}$ Кл cdot 1 В $=1,60218cdot 10^{-19}$ Дж. (3)

(вы помните, что в задачах достаточно использовать величину элементарного заряда в виде $e=1,6cdot 10^{-19}$ Кл, но здесь нам нужны более точные вычисления).

И вот теперь, наконец, мы готовы вычислить обещанную выше очень важную величину — энергетический эквивалент атомной единицы массы, выраженный в МэВ. Из (2) и (3) получаем:

$E_{1}=frac{1,49241cdot 10^{-10}}{1,60218cdot 10^{-19}}=0,93149cdot 10^{9}$ эВ =931,5 . (4)

Итак, запоминаем: энергия покоя одной а. е. м. равна 931,5 МэВ. Этот факт вам неоднократно встретится при решении задач.

В дальнейшем нам понадобятся массы и энергии покоя протона, нейтрона и электрона. Приведём их с точностью, достаточной для решения задач.

$m_{p}=1,00728$ а. е. м., $E_{p}=938,3$ МэВ;
$m_{n}=1,00867$ а. е. м., $E_{n}=939,6$ МэВ;
$m_{e}=5,468cdot 10^{-4}$ а. е. м., $E_{e}=0,511$ МэВ.

к оглавлению ▴

Дефект массы и энергия связи.

Мы привыкли, что масса тела равна сумме масс частей, из которых оно состоит. В ядерной физике от этой простой мысли приходится отвыкать.

Давайте начнём с примера и возьмём хорошо знакомую нам alpha -частицу ядро $_{2}^{4}textrm{He}$ . В таблице (например, в задачнике Рымкевича) имеется значение массы нейтрального атома гелия: она равна 4,00260 а. е. м. Для нахождения массы M ядра гелия нужно из массы нейтрального атома вычесть массу двух электронов, находящихся в атоме:

а. е. м.

В то же время, суммарная масса двух протонов и двух нейтронов, из которых состоит ядро гелия, равна:

$2m_{p}+2m_{n}=2 cdot 1,00728+2 cdot 1,00867=4,03190$ а. е. м.

Мы видим, что сумма масс нуклонов, составляющих ядро, превышает массу ядра на

$Delta m= 2m_{p}+2m_{n}-M=4,03190-4,00150=0,0304$ а. е. м.

Величина Delta m называется дефектом массы. В силу формулы Эйнштейна (1) дефекту массы отвечает изменение энергии:

$Delta E=Delta mc^{2}=0,0304cdot 931,5approx 28$ МэВ:

Величина Delta E обозначается также $E_{CB}$ и называется энергией связи ядра $_{2}^{4}textrm{He}$ . Таким образом, энергия связи alpha -частицы составляет приблизительно 28 МэВ.

Каков же физический смысл энергии связи (и, стало быть, дефекта масс)?

Чтобы расщепить ядро на составляющие его протоны и нейтроны, нужно совершить работу против действия ядерных сил. Эта работа не меньше определённой величины $A_{min}$ ; минимальная работа $A_{min}$ по разрушению ядра совершается в случае, когда высвободившиеся протоны и нейтроны покоятся.

Ну а если над системой совершается работа, то энергия системы возрастает на величину совершённой работы. Поэтому суммарная энергия покоя нуклонов, составляющих ядро и взятых по отдельности, оказывается больше энергии покоя ядра на величину $A_{min}$ .

Следовательно, и суммарная масса нуклонов, из которых состоит ядро, будет больше массы самого ядра. Вот почему возникает дефект массы.

В нашем примере с alpha -частицей суммарная энергия покоя двух протонов и двух нейтронов больше энергии покоя ядра гелия на 28 МэВ. Это значит, что для расщепления ядра $_{2}^{4}textrm{He}$ на составляющие его нуклоны нужно совершить работу, равную как минимум 28 МэВ. Эту величину мы и назвали энергией связи ядра.

Итак, энергия связи ядра — это минимальная работа, которую необходимо совершить для расщепления ядра на составляющие его нуклоны.

Энергия связи ядра есть разность энергий покоя нуклонов ядра, взятых по отдельности, и энергии покоя самого ядра. Если ядро массы состоит из протонов и нейтронов, то для энергии связи $E_{CB}$ имеем:

$E_{CB}=(Zm_{p}+Nm_{n})c^{2}-Mc^{2}=(Zm_{p}+Nm_{n}-M)c^{2}$ .

Величина $Delta m=Zm_{p}+Nm_{n}-M$ , как мы уже знаем, называется дефектом массы.

к оглавлению ▴

Удельная энергия связи.

Важной характеристикой прочности ядра является его удельная энергия связи, равная отношению энергии связи к числу нуклонов:

$varepsilon =frac{E_{CB}}{A}$ .

Удельная энергия связи есть энергия связи, приходящаяся на один нуклон, и имеет смысл средней работы, которую необходимо совершить для удаления нуклона из ядра.

На рис. 1 представлена зависимость удельной энергии связи естественных (то есть встречающихся в природе 1) изотопов химических элементов от массового числа A.

Рис. 1. Удельная энергия связи естественных изотопов

Элементы с массовыми числами 210–231, 233, 236, 237 в естественных условиях не встречаются. Этим объясняются пробелы в конце графика.

У лёгких элементов удельная энергия связи возрастает с ростом , достигая максимального значения 8,8 МэВ/нуклон в окрестности железа $_{26}^{56}textrm{Fe}$ (то есть в диапазоне изменения примерно от 50 до 65). Затем она плавно убывает до величины 7,6 МэВ/нуклон у урана $_{92}^{238}textrm{U}$ .

Такой характер зависимости удельной энергии связи от числа нуклонов объясняется совместным действием двух разнонаправленных факторов.

Первый фактор — поверхностные эффекты. Если нуклонов в ядре мало, то значительная их часть находится на поверхности ядра. Эти поверхностные нуклоны окружены меньшим числом соседей, чем внутренние нуклоны, и, соответственно, взаимодействуют с меньшим числом соседних нуклонов. При увеличении доля внутренних нуклонов растёт, а доля поверхностных нуклонов — падает; поэтому работа, которую нужно совершить для удаления одного нуклона из ядра, в среднем должна увеличиваться с ростом .

Однако с возрастанием числа нуклонов начинает проявляться второй фактор — кулоновское отталкивание протонов. Ведь чем больше протонов в ядре, тем большие электрические силы отталкивания стремятся разорвать ядро; иными словами, тем сильнее каждый протон отталкивается от остальных протонов. Поэтому работа, необходимая для удаления нуклона из ядра, в среднем должна уменьшаться с ростом .

Пока нуклонов мало, первый фактор доминирует над вторым, и потому удельная энергия связи возрастает.

В окрестности железа действия обоих факторов сравниваются друг с другом, в результате чего удельная энергия связи выходит на максимум. Это область наиболее устойчивых, прочных ядер.

Затем второй фактор начинает перевешивать, и под действием всё возрастающих сил кулоновского отталкивания, распирающих ядро, удельная энергия связи убывает.

к оглавлению ▴

Насыщение ядерных сил.

Тот факт, что второй фактор доминирует у тяжёлых ядер, говорит об одной интересной особенности ядерных сил: они обладают свойством насыщения. Это означает, что каждый нуклон в большом ядре связан ядерными силами не со всеми остальными нуклонами, а лишь с небольшим числом своих соседей, и число это не зависит от размеров ядра.

Действительно, если бы такого насыщения не было, удельная энергия связи продолжала бы возрастать с увеличением — ведь тогда каждый нуклон скреплялся бы ядерными силами со всё большим числом нуклонов ядра, так что первый фактор неизменно доминировал бы над вторым. У кулоновских сил отталкивания не было бы никаких шансов переломить ситуацию в свою пользу!

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Энергия связи ядра.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Решение.
Для нахождения энергии связи используем формулу:

[ {{E}_{0}}=(Zcdot {{m}_{p}}+Ncdot {{m}_{n}}-{{m}_{j}})cdot 931,5 MeB (1). ]

Где: Z – количество протонов в ядре, N – количество нейтронов в ядре,

N = А – Z (2),

Z (⁴₂Не) = 2, N(⁴₂Не) = 4 – 2 = 2,
Z (¹²₆С) = 6, N(¹²₆С) = 12 – 6 = 6,
m_р – масса протона, m_р = 1,007825 а.е.м. m_n – масса нейтрона, m_n = 1,008665 а.е.м. m_j– масса ядра. m_j ( ⁴₂Не) = 4,0026 а.е.м, m _j ( ¹²₆С)= 12,000 а.е.м.
Подставим значения в формулу (1) и определим удельную энергию энергию связи.

[ begin{align}
& {{E}_{0}}(_{2}^{4}He)=(2cdot 1,007825+2cdot 1,008665-4,0026)cdot 931,5=28,29897. \
& {{E}_{y}}(_{2}^{4}He)=frac{{{E}_{0}}(_{2}^{4}He)}{A}=frac{28,29897}{4}=7,075. \
& {{E}_{0}}(_{6}^{12}C)=(6cdot 1,007825+6cdot 1,008665-12,000)cdot 931,5=92,16261. \
& {{E}_{y}}(_{6}^{12}C)=frac{{{E}_{0}}(_{6}^{12}Ce)}{A}=frac{92,16261}{12}=7,68. \
end{align}
]

Ответ: Е_у(⁴₂Не) = 7,075 МэВ/нуклон. Е_у(¹²₆С) = 7,68 МэВ/нуклон.

Источник

epachatons

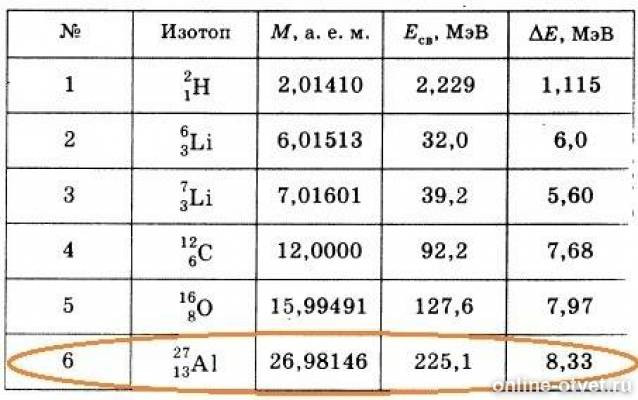
Рассмотрим строение ядра изотопа алюминия:
Al ₁₃²⁷

1)
В ядре 13 протонов.
Находим массу всех протонов:
mp = 1,00728*13 = 13,09464 а.е.м

2)
В ядре (27-13) = 14 нейтронов.
Находим массу всех нейтронов:
mn = 1,00866*14 = 14,12124 а.е.м

3)
Находим суммарную массу нуклонов:
m = mp+mn = 27,11588 а.е.м

4)
Находим дефект масс:
Δm = m — mя = 27,11588 — 26,97430 = 0,24158 а.е.м

5)
Находим энергию связи:
Eсв = с²*Δm = 931,4 * 0,24158 ≈ 225,1 МэВ
6)
Количество нуклонов равно 27, значит энергия связи на один нуклон (удельная энергия связи):
Ecв / 27 = 225 / 27 ≈ 8,33 МэВ/нуклон

Иногда после решения задачи полезно заглянуть в справочник.
Мы еще раз убеждаемся, что задача решена абсолютно правильно!!!