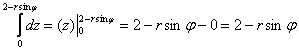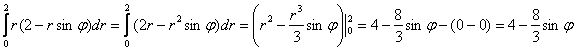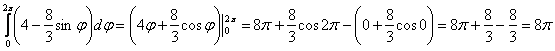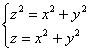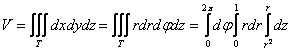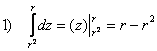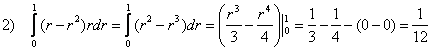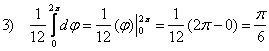Как найти тройной интеграл цилиндра

2.3. Тройной интеграл в цилиндрических координатах

Цилиндрические координаты – это, по сути, полярные координаты в пространстве. В цилиндрической системе

координат положение произвольной точки  пространства определяется полярными координатами  и  точки  – проекции точки  на плоскость  и аппликатой  самой точки .

Переход от трёхмерной декартовой системы к цилиндрической системе координат

осуществляется по следующим формулам:

Применительно к нашей теме преобразование выглядит следующим образом:

И, соответственно, в упрощённом случае, который мы рассматриваем сейчас:

Главное, не забывать про дополнительный множитель «эр» и правильно расставлять полярные пределы интегрирования при

обходе проекции:

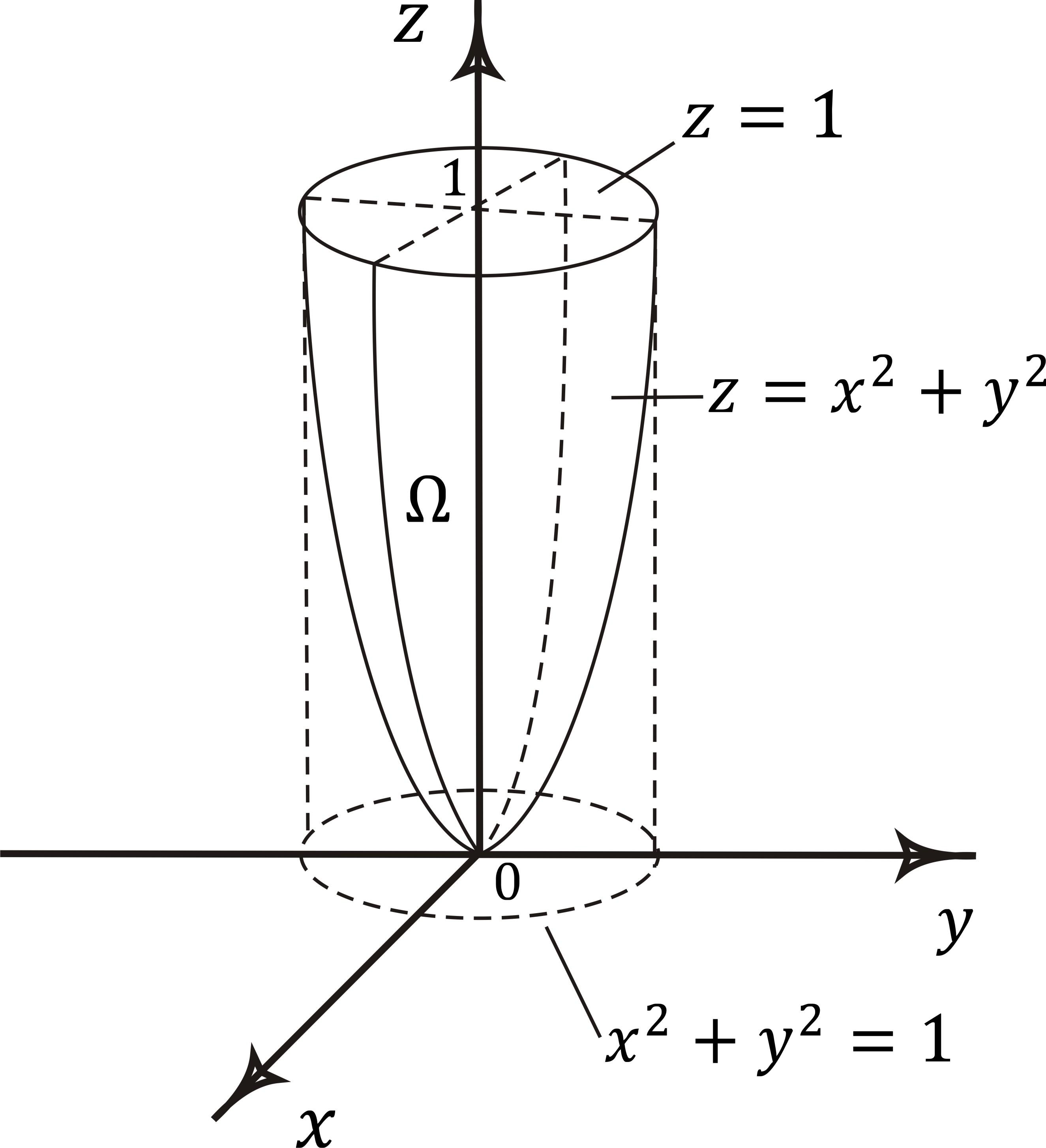
Пример 38

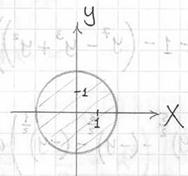
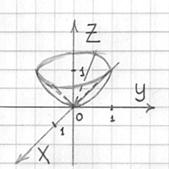
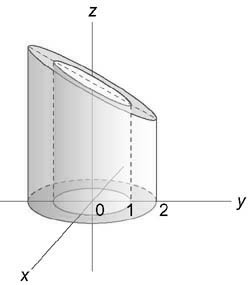
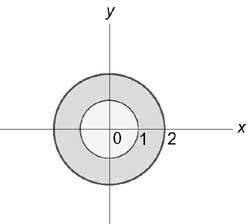
С помощью тройного интеграла вычислить объём тела, ограниченного поверхностями . Выполнить чертёж данного тела и его проекции на плоскость .

Решение: придерживаемся того же порядка действий: в первую очередь рассматриваем уравнения, в которых

отсутствует переменная «зет». Оно здесь одно. Проекция  цилиндрической поверхности  на плоскость  представляет собой одноимённую окружность . Плоскости  ограничивают искомое тело снизу и сверху и проецируются в круг :

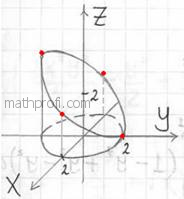
На очереди трёхмерный чертёж. Основная трудность состоит в построении плоскости , которая пересекает цилиндр  под «косым» углом, в результате чего получается эллипс. Уточним

данное сечение аналитически: для этого перепишем уравнение плоскости в функциональном виде  и вычислим значения функции («высоту») в напрашивающихся точках , которые лежат на границе проекции:  . Отмечаем найденные точки на чертеже и аккуратно (а  не так, как я =))

соединяем их линией:

Проекция тела на плоскость  представляет собой круг, и это весомый аргумент в пользу перехода к

цилиндрической системе координат по формулам .

Найдём уравнения поверхностей в цилиндрических координатах:

Теперь нужно выяснить порядок обхода тела. Сначала разберёмся с проекцией. Как определить её порядок обхода? ТОЧНО

ТАК ЖЕ, как и при вычислении двойных интегралов в полярных координатах. Здесь он

элементарен:

«Вертикальные» пределы интегрирования тоже очевидны – входим в тело через плоскость  и выходим из него через плоскость :

Перейдём к повторным интегралам:
, при этом множитель «эр» сразу ставим в

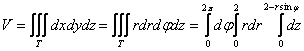
«свой» интеграл. Веник как обычно ломаем по прутикам:

1)

2) Сносим результат в следующий интеграл, не забывая, что там уже есть «эр»:

И ещё не забываем, что «фи» считается константой. Но это до поры до времени:
3)

Ответ:

Похожее задание для самостоятельного решения:

Пример 39

Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями . Выполнить чертёж данного тела и его проекции на плоскость .

Примерный образец чистового оформления в конце книги.

Обратите внимание, что в условиях задач ни слова не сказано о переходе к цилиндрической системе координат, и несведущий

человек будет «бодаться» с трудными интегралами в декартовых координатах. …А может и не будет – ведь есть третий, исконно

русский способ решения проблем =) …Но не после прочтения этой книги!

Пример 40

С помощью тройного интеграла найти объем тела, ограниченного поверхностями

Скромно и со вкусом.

Решение: данное тело ограничено конической поверхностью  и эллиптическим параболоидом .  Подготовленный читатель уже представил, как выглядит тело, но на практике

часто встречаются более сложные случаи, поэтому я проведу подробное аналитическое рассуждение. Сначала найдём линии, по

которым пересекаются поверхности. Составим и решим соответствующую систему:

Из 1-го уравнения почленно вычтем второе:

В результате получено два корня:

Подставим найденное значение  в любое

уравнение системы:
, откуда следует, что .

Таким образом, корню  соответствует

единственная точка – начало координат. Естественно – ведь вершины рассматриваемых поверхностей совпадают.

Теперь подставим второй корень  – тоже в

любое уравнение системы:

Каков геометрический смысл полученного результата? «На высоте»  (в плоскости ) параболоид и конус пересекаются по окружности

 – единичного радиуса с центром в точке . При этом «чаша» параболоида вмещает в себя «воронку»

конуса, следовательно, образующие конической поверхности следует прочертить пунктиром (за исключением фрагмента

дальней от нас образующей, который виден с данного ракурса):

Проекцией тела на плоскость  является

круг  с центром в начале координат

радиуса 1, который я даже не удосужился изобразить ввиду очевидности данного факта. Кстати, и в двух предыдущих задачах можно

было обойтись без двухмерного чертежа, но там его требовало условие.

При переходе к цилиндрическим координатам по формулам  неравенство  запишется в простейшем виде  и с порядком обхода проекции никаких

проблем:

Найдём уравнения поверхностей в цилиндрической системе координат.

С параболоидом проблем нет вообще:

И с конусом их тоже нет. Так как в задаче рассматривается его верхняя часть, то из уравнения  выражаем:

«Сканируем тело» вертикально, строго снизу вверх. Лучи света входят в него через эллиптический

параболоид  и выходят через

коническую поверхность . Таким

образом, «вертикальный» порядок обхода тела:

В результате:
Остальное – дело несложной техники:

Ответ:
Не редкость, когда тело задаётся не ограничивающими его поверхностями, а множеством неравенств:

Пример 41

С помощью тройного интеграла вычислить объём заданного тела:
, где  – произвольное положительное число.
Данная задача хоть и содержит параметр, но допускает выполнение точного чертежа, отражающего принципиальный вид тела.

Подумайте, как выполнить построение. Краткое решение и ответ – в конце книги.

2.4. Как вычислить произвольный тройной интеграл?

2.2. Как вычислить объём тела с помощью тройного интеграла?

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Для тройных
интегралов, как и для двойных, имеют
место формулы замены переменных при
переходе от прямоугольных координат к
новым системам координат, наиболее
употребительными из которых являются
цилиндрические и сферические координаты.

Переход от
прямоугольных координат
кцилиндрическим
координатам
(рис. 6.8),
связанным с
соотношениями

,

осуществляется
по формуле

.

Выражение
называют элементом объема в цилиндрических
координатах.

Название
«цилиндрические координаты» связано
с тем, что координатная поверхность
(т.е. поверхность, все точки которой
имеют одну и ту же координатуr)
является цилиндром, прямолинейные
образующие которого параллельны оси
.

Рис. 6.8. Цилиндрические
(слева) и сферические (справа) координаты

Переход от
прямоугольных координат
ксферическим
координатам
(рис. 6.8),
связанным с
соотношениями

,

осуществляется
по формуле

.

Выражение
называют элементом объема в сферических
координатах.

Название «сферические
координаты» связано с тем, что координатная
поверхность
(т.е. поверхность, все точки которой
имеют одну и ту же координату)
является сферой с центром в начале
координат.

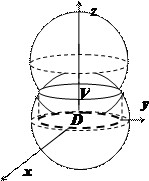
Пример.
Вычислить
тройной интеграл

,

где
– область,
ограниченная поверхностями
и(рис. 6.9).

Рис. 6.9. Пример
вычисления тройного интеграла в
цилиндрических координатах

В
данном примере удобно перейти от
прямоугольных к цилиндрическим
координатам.

Так как область
проектируется на плоскостьв круг,
то уголизменяется в пределах от 0 до,
радиус-векторr
изменяется
в пределах от 0 до 1. Координата z
изменяется от значений для точек, лежащих
на параболоиде
,
до значений для точек, лежащих на
плоскости,
т.е..

Применяя формулу
для вычисления тройного интеграла в
цилиндрических координатах, получаем

.

7 Криволинейные интегралы

7.1 Криволинейный интеграл первого рода

Пусть функция
определена и непрерывна на некоторой
кривойAB
в плоскости
.

Разобьем кривую
AB
произвольным образом на n
частей
точками

,

выберем на каждой
из частичных дуг
произвольную точку(рис. 7.1) и составим сумму

,

где
– длина дуги.
Данная сумма называетсяинтегральной
суммой для
функции
по кривойAB.
Обозначим через
наибольшую из длин частичных дуг:

.

Рис. 7.1. Разбиение
кривой AB
на частичные дуги в случае

криволинейного
интеграла первого рода

Определение.
Криволинейным
интегралом первого рода от
функции
по кривойAB
называется предел интегральных сумм
при
,
если этот предел существует и не зависит
ни от способа разбиения кривойAB
на частичные
дуги
,
ни от выбора в каждой из них точки:

или в другой записи:

.

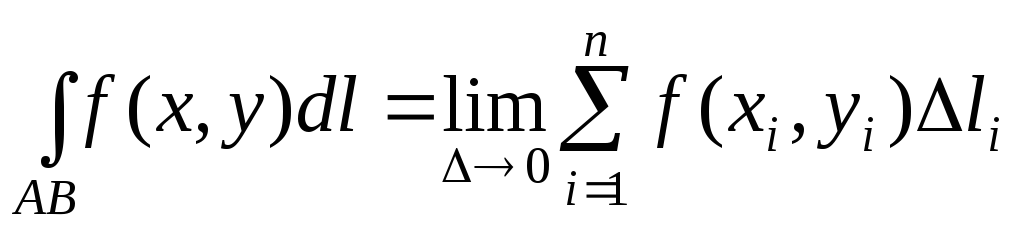
Функция
называетсяинтегрируемой
по (вдоль)
кривой AB,
сама кривая AB
– контуром
интегрирования,
A
– начальной, а B
– конечной точками интегрирования.

Определение.
Кривая,
заданная параметрически уравнениями

,

называется гладкой,
если функции
инепрерывны и имеют непрерывные производныеи,
не обращающиеся в нуль одновременно
(тем самым кривая в каждой точке имеет
касательную).

Непрерывная
кривая, составленная из конечного числа
гладких кусков, называется кусочно-гладкой.

Кривая, заданная
явно уравнением
,
будет гладкой, если функцияи ее производнаянепрерывны на отрезке.

Теорема
7.1 (существования криволинейного
интеграла первого рода) (без доказательства).
Функция
,
непрерывная вдоль кусочно-гладкой
кривойAB,
интегрируема по этой кривой.

Замечание.
Если положить
всюду на кривойAB,
то из определения криволинейного
интеграла первого рода легко получить
формулу для вычисления длины дуги l
кривой AB
с помощью криволинейного интеграла
первого рода:

или

.

Основные
свойства криволинейного интеграла
первого рода аналогичны
соответствующим свойствам определенного
интеграла.

Свойство
1. Постоянный
множитель можно выносить за знак
интеграла:

.

Свойство
2. Интеграл
от алгебраической суммы функций равен
алгебраической сумме интегралов от
этих функций:

.

Свойство
3. Если
кривую AB
разбить на две кривые AC
и
CB,
то интеграл по всей кривой AB
будет равен сумме интегралов по кривым
AC
и
CB:

.

Свойство 4
(Теорема о среднем).
Если функция

непрерывна вдоль гладкой кривойAB,
то на этой кривой существует такая точка
,
что справедлива формула

,

где l
– длина кривой AB.

Свойство
5. При
изменении направления интегрирования
величина интеграла не изменяется:

.

Вычисление
криволинейного интеграла первого рода
сводится к вычислению определенного
интеграла следующими способами.

Если кривая AB
задана параметрически уравнениями
,
то

.

Если кривая AB
задана явно уравнением
,
то

.

Если кривая AB
задана явно уравнением
,
то

.

Замечание. Для
пространственной кривой AB,
заданной параметрически уравнениями
,
формула для вычисления криволинейного
интеграла первого рода имеет вид

,

аналогичный
соответствующей формуле для плоской
кривой.

Пример.
Вычислить
криволинейный интеграл первого рода

,

где AB
– отрезок
прямой
от точкидо
точки.

Имеем

.

По формуле
вычисления криволинейного интеграла
первого рода получаем

.

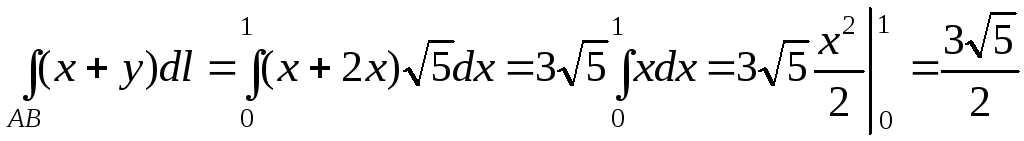
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Примеры применения цилиндрических и сферических координат

Как и в случае перехода к полярным координатам в двойном интеграле, дать однозначный рецепт того, когда следует применять цилиндрические или сферические координаты, нельзя, это дело опыта. Можно попробовать применить цилиндрические координаты, если подынтегральная функция и/или уравнения поверхностей, ограничивающих объём $mathbf { textit { V } } $, зависят от комбинации $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } =mathbf { textit { r } } ^ { 2 } $; сферические — если эти уравнения зависят от $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { r } } ^ { 2 } $. Рассмотрим ряд примеров.

Пример 1

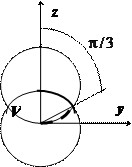
Найти объём $mathbf { textit { V } } $ общей части двух шаров, ограниченных сферами

$mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { R } } ^ { 2 } $, $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } $ = 2$mathbf { textit { Rz } } ^ { } $.

Решение:

Пересечение сфер находится на уровне $2Rz=R^2Rightarrow z=R/2$ и представляет собой круг радиуса $Rfrac { sqrt 3 } { 2 } $. Объём $mathbf { textit { V } } $ограничен сверху поверхностью $z=sqrt { R^2-x^2-y^2 } $, снизу — поверхностью $z=R-sqrt { R^2-x^2-y^2 } $. Вычисления в декартовых координатах дают $V=iiintlimits_V { dv } =iiintlimits_V { dxdydz } =intlimits_ { -Rfrac { sqrt 3 } { 2 } } ^ { Rfrac { sqrt 3 } { 2 } } { dxintlimits_ { -sqrt { frac { 3 } { 4 } R^2-x^2 } } ^ { sqrt { frac { 3 } { 4 } R^2-x^2 } } { dyintlimits_ { R-sqrt { R^2-x^2-y^2 } } ^ { sqrt { R^2-x^2-y^2 } } { dz } } } $ — достаточно громоздкие выкладки.

В цилиндрических координатах объём $mathbf { textit { V } } $ ограничен сверху поверхностью $z=sqrt { R^2-r^2 } $, снизу — поверхностью $z=R-sqrt { R^2-r^2 } $, поэтому

$V=iiintlimits_V { dv } =iiintlimits_V { rdrdvarphi dz } =intlimits_0^ { 2pi } { dvarphi intlimits_0^ { Rfrac { sqrt 3 } { 2 } } { rdrintlimits_ { R-sqrt { R^2-r^2 } } ^ { sqrt { R^2-r^2 } } { dz } } } =2pi intlimits_0^ { Rfrac { sqrt 3 } { 2 } } { left[ { 2sqrt { R^2-r^2 } -R }right]rdr } =$ $ =2pi left. { left[ { -frac { 2 } { 3 } sqrt { left( { R^2-r^2 }right)^3 } -Rfrac { r^2 } { 2 } }right] }right|_0^ { Rfrac { sqrt 3 } { 2 } } =2pi left[ { frac { 2 } { 3 } R^3-frac { 2 } { 3 } sqrt { left( { R^2/4 }right)^3 } -frac { 3R^3 } { 8 } }right]=2pi R^3left( { frac { 2 } { 3 } -frac { 2 } { 24 } -frac { 3 } { 8 } }right)=frac { 5 } { 12 } pi R^3. $

В сферических координатах уравнение нижней сферы принимает вид $r=R$, верхней — $r^2=2Rrcos theta Rightarrow r=2Rcos theta $, их пересечение соответствует значению $cos theta =1/2Rightarrow theta =pi /3$. В интервале $0leqslant theta leqslant pi /3 quad mathbf { textit { r } } $ меняется от $0$ до $mathbf { textit { R } } $, в интервале $pi /3leqslant theta leqslant pi /2 quad mathbf { textit { r } } $ меняется от $0$ до $2Rcos theta $, поэтому

$V=iiintlimits_V { dv } =iiintlimits_V { r^ { 2 } sintheta drdvarphi dtheta } = int_0^ { 2pi } d phi int_0^ { pi/3 } sin theta dtheta int_0^R r^2 dr + int_0^ { 2pi } d phi int_ { pi/3 } ^ { pi/2 } sin theta dtheta int_0^ { 2Rcos theta } r^2 dr = 2pi frac { R^3 } { 3 } (-costheta) =\ =2pi frac { R^3 } { 3 } left. { left( { -cos theta }right) }right|_0^ { frac { pi } { 3 } } +2pi frac { 8R^3 } { 3 } intlimits_ { frac { pi } { 3 } } ^ { frac { pi } { 2 } } { cos ^3theta sin theta dtheta } =frac { pi R^3 } { 3 } -frac { 16pi R^3 } { 3 } cdot left. { frac { cos ^4theta } { 4 } }right|_ { frac { pi } { 3 } } ^ { frac { pi } { 2 } } = $ $ =frac { pi R^3 } { 3 } +frac { pi R^3 } { 3cdot 4 } =frac { 5pi R^3 } { 12 } . $

В этом примере трудоёмкость вычислений в цилиндрических и сферических координатах примерно одинакова.

Пример 2

$I=iiintlimits_V { (x+y+z)dxdydz } ;quad V:left[{ begin{array} { l } x=2-y^2-z^2, \ x^2=y^2+z^2,;xgeqslant 0. \ end{array} }right.$

Решение:

Параболоид и конус пересекаются в плоскости $x=2-x^2Rightarrow x=1$ по кругу радиуса 1. Осью симметрии объёма $mathbf { textit { V } } $ служит ось $mathbf { textit { Ох } } $, поэтому цилиндрические координаты вводим формулами $x=x,quad y=rcos varphi ,quad z=rsin varphi ; quad I=iiintlimits_V { (x+y+z)dxdydz } =iiintlimits_V { (x+rcos varphi +rsin varphi )rdxdrdvarphi } =intlimits_0^ { 2pi } { dvarphi intlimits_0^1 { rdrintlimits_r^ { 2-r^2 } { (x+rcos varphi +rsin varphi )dx } } } =$ $ =intlimits_0^ { 2pi } { dvarphi intlimits_0^1 { left. { frac { x^2 } { 2 } }right|_r^ { 2-r^2 } rdr } } +intlimits_0^ { 2pi } { (cos varphi +sin varphi )dvarphi intlimits_0^1 { left. x right|_r^ { 2-r^2 } r^2dr } } =pi intlimits_0^1 { left( { 4-5r^2+r^4 }right)dr } =frac { 38pi } { 15 } . $ Применение сферических координат в этом примере нецелесообразно { громоздкое уравнение для параболоида } .

Пример 3

$I=iiintlimits_V { sqrt { x^2+y^2+z^2 } dxdydz } ;quad V:left[{ x^2+y^2+z^2=z. }right.$

Решение:

Здесь область интегрирования — шар радиуса 1/2, сдвинутый по оси $mathbf { textit { Оz } } $ на 1/2 единицы, подынтегральная функция зависит от выражения $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } $, поэтому применим сферические координаты. Уравнение сферы $x^2+y^2+z^2=zRightarrow r^2=rcos theta Rightarrow r=cos theta left( { Rightarrow 0leqslant theta leqslant pi /2 }right)$ , поэтому $I=iiintlimits_V { sqrt { x^2+y^2+z^2 } dxdydz } =iiintlimits_V { rcdot r^2sin theta drdvarphi dtheta } =intlimits_0^ { 2pi } { dvarphi intlimits_0^ { pi /2 } { sin theta dtheta } intlimits_0^ { cos theta } { r^3dr } } =frac { 2pi } { 4 } intlimits_0^ { pi /2 } { left. { r^4 }right|_0^ { cos theta } sin theta dtheta } = \ =frac { 2pi } { 4 } intlimits_0^ { pi /2 } { cos ^4theta sin theta dtheta } =-frac { 2pi } { 4cdot 5 } left. { cos ^5theta }right|_0^ { pi /2 } =frac { pi } { 10 } $.

Пример 4

Вычислить объём тела, ограниченного поверхностью $left( { x^2+y^2+z^2 }right)^ { ,2 } =a^3z,;a=const>0$

Решение:

Здесь тоже для того, чтобы понять, как устроено тело, и найти его объём, надо перейти к сферическим координатам { на это указывает комбинация $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { r } } ^ { 2 } )$. Уравнение поверхности $left( { x^2+y^2+z^2 }right)^ { ,2 } =a^3zRightarrow r^4=a^3rcos vartheta Rightarrow r=asqrt[3] { cos vartheta } ;left( { Rightarrow 0leqslant theta leqslant pi /2 }right)$. По этому уравнению поверхность построить уже можно; отсутствие координаты $varphi $ в уравнении показывает, что это — тело вращения вокруг оси $mathbf { textit { Oz } } $. Находим объём: $ V=iiintlimits_V { r^2sin theta drdvarphi dtheta } =intlimits_0^ { 2pi } { dvarphi intlimits_0^ { pi /2 } { sin } } theta dtheta intlimits_0^ { asqrt[3] { cos theta } } { r^2dr } =frac { 2pi } { 3 } intlimits_0^ { pi /2 } { left. { r^3 }right|_0^ { asqrt[3] { cos theta } } sin theta dtheta = } $ $ =frac { 2pi a^3 } { 3 } intlimits_0^ { pi /2 } { cos theta sin theta dtheta = } frac { pi a^3 } { 3 } . $

Пример 5

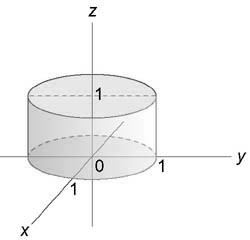
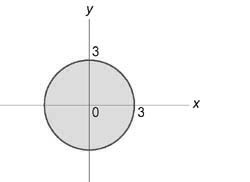
Вычислить интеграл $iiintlimits_U { left( { { x^4 } + 2 { x^2 } { y^2 } + { y^4 } }right)dxdydz } ,$ где область (U) ограничена поверхностью ( { x^2 } + { y^2 } le 1) и плоскостями (z = 0,) (z = 1).

Решение:

Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость (Oxy) представляет собой круг ( { x^2 } + { y^2 } le 1) или (0 le rho le 1).

Заметим, что подынтегральное выражение записывается в виде $ { left( { { x^4 } + 2 { x^2 } { y^2 } + { y^4 } }right) } = { { left( { { x^2 } + { y^2 } }right)^2 } } = { { left( { { rho ^2 } }right)^2 } = { rho ^4 } } $

Тогда интеграл будет равен $I = intlimits_0^ { 2pi } { dvarphi } intlimits_0^1 { { rho ^4 } rho drho } intlimits_0^1 { dz } .$

Здесь во втором интеграле добавлен множитель (rho) якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга.

В результате тройной интеграл легко вычисляется: $ { I = intlimits_0^ { 2pi } { dvarphi } intlimits_0^1 { { rho ^4 } rho drho } intlimits_0^1 { dz } } = { 2pi intlimits_0^1 { { rho ^5 } drho } intlimits_0^1 { dz } } = { 2pi cdot 1 cdot intlimits_0^1 { { rho ^5 } drho } } = { 2pi left. { left( { frac { { { rho ^6 } } } { 6 } }right) }right|_0^1 } = { 2pi cdot frac { 1 } { 6 } = frac { pi } { 3 } . } $

Пример 6

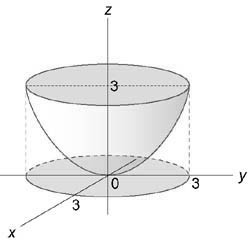
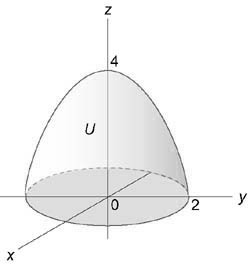
Вычислить интеграл $iiintlimits_U { left( { { x^2 } + { y^2 } }right)dxdydz } ,$ где область (U) ограничена поверхностями ( { x^2 } + { y^2 } = 3z,) (z = 3)

Решение:

Область интегрирования изображена на рисунке

Для вычисления интеграла перейдем к цилиндрическим координатам: $ { x = rho cos varphi , } ;; { y = rho sin varphi , } ;; { z = z. } $ Дифференциал при этом равен $dxdydz = rho drho dvarphi dz;;left( { rho — text { якобиан } }right).$

Уравнение параболической поверхности принимает вид: $ { rho ^2 } { cos ^2 } varphi + { rho ^2 } { sin^2 } varphi = 3z;;text { или } ;; { rho ^2 } = 3z.$ Проекция области интегрирования (U) на плоскость (Oxy) представляет собой окружность ( { x^2 } + { y^2 } le 9) радиусом (rho = 3).

Координата (rho) изменяется в пределах от (0) до (3,) угол (varphi) от (0) до (2pi) и координата (z) от (largefrac { { { rho ^2 } } } { 3 } normalsize) до (3.)

В результате интеграл будет равен $ { I = iiintlimits_U { left( { { x^2 } + { y^2 } }right)dxdydz } } = { iiintlimits_ { U’ } { { rho ^2 } cdot rho drho dvarphi dz } } = { intlimits_0^ { 2pi } { dvarphi } intlimits_0^3 { { rho ^3 } drho } intlimits_ { frac { { { rho ^2 } } } { 3 } } ^3 { dz } } = { intlimits_0^ { 2pi } { dvarphi } intlimits_0^3 { { rho ^3 } drho } cdot left[ { left. z right|_ { frac { { { rho ^2 } } } { 3 } } ^3 }right] } = { intlimits_0^ { 2pi } { dvarphi } intlimits_0^3 { { rho ^3 } left( { 3 — frac { { { rho ^2 } } } { 3 } }right)drho } } = \ = { intlimits_0^ { 2pi } { dvarphi } intlimits_0^3 { left( { 3 { rho ^3 } — frac { { { rho ^5 } } } { 3 } }right)drho } } = { intlimits_0^ { 2pi } { dvarphi } cdot left[ { left. { left( { frac { { 3 { rho ^4 } } } { 4 } — frac { { { rho ^6 } } } { { 18 } } }right) }right|_0^3 }right] } = { left( { frac { { 3 cdot 81 } } { 4 } — frac { { 729 } } { { 18 } } }right)intlimits_0^ { 2pi } { dvarphi } } = { frac { { 81 } } { 4 } cdot 2pi = frac { { 81pi } } { 2 } . } $

Пример 7

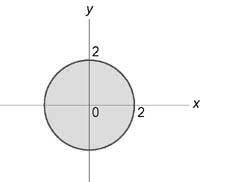
Используя цилиндрические координаты, найти значение интеграла $ I = intlimits_ { — 2 } ^2 { dx } intlimits_ { — sqrt { 4 — { x^2 } } } ^ { sqrt { 4 — { x^2 } } } { dy } intlimits_0^ { 4 — { x^2 } — { y^2 } } { { y^2 } dz } $

Решение:

Область интегрирования (U) изображена на рисунке:

Ее проекция на плоскость (Oxy) представляет собой круг ( { x^2 } + { y^2 } = { 2^2 } ):

Новые переменные в цилиндрических координатах будут изменяться в пределах $ { 0 le rho le 2, } ;; { 0 le varphi le 2pi , } ;; { 0 le z le 4 — { rho ^2 } . } $

Подставляя (x = rho cos varphi ) и (x = rho sin varphi,) найдем значение интеграла: $ { I = intlimits_ { — 2 } ^2 { dx } intlimits_ { — sqrt { 4 — { x^2 } } } ^ { sqrt { 4 — { x^2 } } } { dy } intlimits_0^ { 4 — { x^2 } — { y^2 } } { { y^2 } dz } } = { iiintlimits_U { { y^2 } dxdydz } } = { iiintlimits_ { U’ } { { { left( { rho sin varphi }right) } ^2 } rho drho dvarphi dz } } = { iiintlimits_ { U’ } { { rho ^3 } { { sin } ^2 } varphi drho dvarphi dz } } = { intlimits_0^ { 2pi } { { { sin } ^2 } varphi dvarphi } intlimits_0^2 { { rho ^3 } left( { 4 — { rho ^2 } }right)drho } } = \ = { intlimits_0^ { 2pi } { { { sin } ^2 } varphi dvarphi } intlimits_0^2 { left( { 4 { rho ^3 } — { rho ^5 } }right)drho } } = { intlimits_0^ { 2pi } { { { sin } ^2 } varphi dvarphi } cdot left[ { left. { left( { frac { { 4 { rho ^4 } } } { 4 } — frac { { { rho ^6 } } } { 6 } }right) }right|_0^2 }right] } = { left( { { 2^4 } — frac { { { 2^6 } } } { 6 } }right)intlimits_0^ { 2pi } { { { sin } ^2 } varphi dvarphi } } = { frac { { 16 } } { 3 } intlimits_0^ { 2pi } { { { sin } ^2 } varphi dvarphi } } = { frac { { 16 } } { 3 } intlimits_0^ { 2pi } { frac { { 1 — cos 2varphi } } { 2 } dvarphi } } = \ = { frac { 8 } { 3 } intlimits_0^ { 2pi } { left( { 1 — cos 2varphi }right)dvarphi } } = { frac { 8 } { 3 } left[ { left. { left( { varphi — frac { { sin 2varphi } } { 2 } }right) }right|_0^ { 2pi } }right] } = { frac { 8 } { 3 } cdot 2pi = frac { { 16pi } } { 3 } . } $

Пример 8

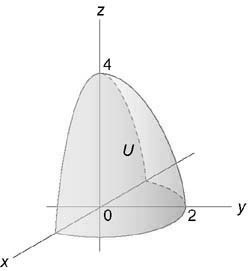
Вычислить интеграл, используя цилиндрические координаты: $iiintlimits_U { sqrt { { x^2 } + { y^2 } } dxdydz } .$ Область (U) ограничена параболоидом (z = 4 — { x^2 } — { y^2 } ,) цилиндром ( { x^2 } + { y^2 } = 4) и плоскостями (y = 0,) (z = 0)

Решение:

Изобразив схематически область интегрирования (U,) находим, что ее проекция на плоскость (Oxy) { область (D) } представляет собой полукруг радиусом (rho = 2).

Перейдем к цилиндрическим координатам, применяя подстановки $ { x = rho cos varphi , } ;; { y = rho sin varphi , } ;; { z = z, } ;; { dxdydz = rho drho dvarphi dz. } $

Новые переменные будут изменяться в пределах $ { 0 le rho le 2, } ;; { 0 le varphi le pi , } ;; { 0 le z le 4 — { rho ^2 } . } $

Теперь вычисляем интеграл: $ { I = iiintlimits_U { sqrt { { x^2 } + { y^2 } } dxdydz } } = { iiintlimits_ { U’ } { rho cdot rho drho dvarphi dz } } = { iiintlimits_ { U’ } { { rho ^2 } drho dvarphi dz } } = { intlimits_0^pi { dvarphi } intlimits_0^2 { { rho ^2 } drho } intlimits_0^ { 4 — { rho ^2 } } { dz } } = { intlimits_0^pi { dvarphi } intlimits_0^2 { { rho ^2 } drho } cdot left[ { left. z right|_0^ { 4 — { rho ^2 } } }right] } = { intlimits_0^pi { dvarphi } intlimits_0^2 { { rho ^2 } left( { 4 — { rho ^2 } }right)drho } } = \ = { intlimits_0^pi { dvarphi } intlimits_0^2 { left( { 4 { rho ^2 } — { rho ^4 } }right)drho } } = { intlimits_0^pi { dvarphi } left[ { left. { left( { frac { { 4 { rho ^3 } } } { 3 } — frac { { { rho ^5 } } } { 5 } }right) }right|_0^2 }right] } = { left( { frac { 4 } { 3 } cdot { 2^3 } — frac { { { 2^5 } } } { 5 } }right)intlimits_0^pi { dvarphi } } = { frac { { 64 } } { { 15 } } intlimits_0^pi { dvarphi } } = { frac { { 64 } } { { 15 } } cdot left[ { left. varphi right|_0^pi }right] = frac { { 64pi } } { { 15 } } . } $

Пример 9

Найти интеграл $iiintlimits_U { ydxdydz } ,$ где область (U) ограничена плоскостями (z = x + 1,) (z = 0) и цилиндрическими поверхностями ( { x^2 } + { y^2 } = 1,) ( { x^2 } + { y^2 } = 4)

Решение:

Вычислим данный интеграл в цилиндрических координатах. Из условия $0 le z le x + 1$ следует, что $0 le z le rho cos varphi + 1.$ Область интегрирования в плоскости (Oxy) представляет собой кольцо, ограниченное окружностями ( { x^2 } + { y^2 } = 1) и ( { x^2 } + { y^2 } = 4)

Следовательно, переменные (rho) и (varphi) изменяются в интервале $1 le rho le 2,;;0 le varphi le 2pi .$

Находим интеграл: $ { I = iiintlimits_U { ydxdydz } } = { iiintlimits_ { U’ } { rho sin varphi cdot rho drho dvarphi dz } } = { iiintlimits_ { U’ } { { rho ^2 } sin varphi drho dvarphi dz } } = { intlimits_0^ { 2pi } { sin varphi dvarphi } intlimits_0^2 { { rho ^2 } drho } intlimits_0^ { rho cos varphi + 1 } { dz } } = { intlimits_0^ { 2pi } { sin varphi dvarphi } intlimits_0^2 { { rho ^2 } drho } cdot left[ { left. z right|_0^ { rho cos varphi + 1 } }right] } = \ = { intlimits_0^ { 2pi } { sin varphi dvarphi } intlimits_0^2 { { rho ^2 } left( { rho cos varphi + 1 }right)drho } } = { intlimits_0^ { 2pi } { sin varphi dvarphi } intlimits_0^2 { left( { { rho ^3 } cos varphi + { rho ^2 } }right)drho } } = { intlimits_0^ { 2pi } { sin varphi dvarphi } cdot left[ { left. { left( { frac { { { rho ^4 } } } { 4 } cos varphi + frac { { { rho ^3 } } } { 3 } }right) }right|_ { rho = 1 } ^ { rho = 2 } }right] } = \ = { intlimits_0^ { 2pi } { sin varphi left[ { left( { 4cos varphi + frac { 8 } { 3 } }right) — left( { frac { { cos varphi } } { 4 } + frac { 1 } { 3 } }right) }right]dvarphi } } = { intlimits_0^ { 2pi } { sin varphi left( { frac { { 15 } } { 4 } cos varphi + frac { 7 } { 3 } }right)dvarphi } } = { intlimits_0^ { 2pi } { left( { frac { { 15 } } { 4 } sin varphi cos varphi + frac { 7 } { 3 } sin varphi }right)dvarphi } } = \ = { intlimits_0^ { 2pi } { left( { frac { { 15 } } { 8 } sin 2varphi + frac { 7 } { 3 } sin varphi }right)dvarphi } } = { left. { left( { — frac { { 15 } } { { 16 } } cos 2varphi — frac { 7 } { 3 } cos varphi }right) }right|_0^ { 2pi } = 0. } $

Этот результат закономерен, поскольку область (U) симметрична относительно плоскости (Oxz,) а подынтегральная функция является четной.

Пример 10

Найти интеграл (iiintlimits_U { sqrt { { x^2 } + { y^2 } + { z^2 } } dxdydz } ,) где область интегрирования (U) шар, заданный уравнением ( { { x^2 } + { y^2 } + { z^2 } } = 25.)

Решение:

Поскольку область (U) представляет собой шар, и к тому же подынтегральное выражение является функцией, зависящей от $fleft( { { x^2 } + { y^2 } + { z^2 } }right),$ то перейдем к сферическим координатам.

Сделаем замену: $ { x = rho cos varphi sin theta , } ;; { y = rho sin varphi sin theta , } ;; { z = rho cos theta , } $ Новые переменные изменяются в пределах: $ { 0 le rho le 5, } ;; { 0 le varphi le 2pi , } ;; { 0 le theta le pi . } $

Учитывая якобиан ( { rho ^2 } sin theta,) записываем интеграл в виде: $ { I = iiintlimits_U { sqrt { { x^2 } + { y^2 } + { z^2 } } dxdydz } } = { iiintlimits_ { U’ } { rho cdot { rho ^2 } sin theta drho dvarphi dtheta } } = { intlimits_0^ { 2pi } { dvarphi } intlimits_0^5 { { rho ^3 } drho } intlimits_0^pi { sin theta dtheta } } = { intlimits_0^ { 2pi } { dvarphi } intlimits_0^5 { { rho ^3 } drho } left[ { left. { left( { — cos theta }right) }right|_0^pi }right] } = \ = { intlimits_0^ { 2pi } { dvarphi } intlimits_0^5 { { rho ^3 } drho } left( { — cos pi + cos 0 }right) } = { 2intlimits_0^ { 2pi } { dvarphi } intlimits_0^5 { { rho ^3 } drho } } = { 2intlimits_0^ { 2pi } { dvarphi } cdot left[ { left. { left( { frac { { { rho ^4 } } } { 4 } }right) }right|_0^5 }right] } = \ = { 2intlimits_0^ { 2pi } { dvarphi } cdot frac { { { 5^4 } } } { 4 } } = { frac { { 625 } } { 2 } intlimits_0^ { 2pi } { dvarphi } } = { frac { { 625 } } { 2 } cdot 2pi = 625pi . } $

Пример 11

Вычислить интеграл $iiintlimits_U { { e^ { { { left( { { x^2 } + { y^2 } + { z^2 } }right) } ^ { frac { 3 } { 2 } } } } } dxdydz } ,$ где область (U) представляет собой единичный шар ( { { x^2 } + { y^2 } + { z^2 } } le 1.)

Решение:

Центр данного шара расположен в начале координат. Следовательно, в сферических координатах область интегрирования (U) описывается неравенствами $ { 0 le rho le 1, } ;; { 0 le varphi le 2pi , } ;; { 0 le theta le pi . } $

Записывая интеграл в сферических координатах, получаем $ { I = iiintlimits_U { { e^ { { { left( { { x^2 } + { y^2 } + { z^2 } }right) } ^ { frac { 3 } { 2 } } } } } dxdydz } } = { iiintlimits_ { U’ } { { e^ { { { left( { { rho ^2 } }right) } ^ { frac { 3 } { 2 } } } } } { rho ^2 } sin theta drho dvarphi dtheta } } = { iiintlimits_ { U’ } { { e^ { { rho ^3 } } } { rho ^2 } sin theta drho dvarphi dtheta } } = { intlimits_0^ { 2pi } { dvarphi } intlimits_0^1 { { e^ { { rho ^3 } } } { rho ^2 } drho } intlimits_0^pi { sin theta dtheta } . } $

Как видно, тройной интеграл вырождается в произведение трех однократных интегралов, каждый из которых вычисляется независимо. В результате находим $ { I = intlimits_0^ { 2pi } { dvarphi } intlimits_0^1 { { e^ { { rho ^3 } } } { rho ^2 } drho } intlimits_0^pi { sin theta dtheta } } = { left[ { left. varphi right|_0^ { 2pi } }right] cdot intlimits_0^1 { left( { { e^ { { rho ^3 } } } cdot frac { 1 } { 3 } d { rho ^3 } }right) } cdot left[ { left. { left( { — cos theta }right) }right|_0^pi }right] } = { 2pi cdot frac { 1 } { 3 } left[ { left. { left( { { e^ { { rho ^3 } } } }right) }right|_ { { rho ^3 } = 0 } ^ { { rho ^3 } = 1 } }right] cdot left( { — cos pi + cos 0 }right) } = { frac { { 2pi } } { 3 } cdot left( { e — 1 }right) cdot 2 } = { frac { { 4pi } } { 3 } left( { e — 1 }right). } $

Пример 12

Вычислить интеграл (iiintlimits_U { xyzdxdydz } ,) где область (U) представляет собой часть шара ( { x^2 } + { y^2 } + { z^2 } le { R^2 } ,) расположенную в первом октанте (x ge 0, y ge 0, z ge 0.)

Решение:

Перейдем к сферическим координатам. Сделаем замену переменных: $ { x = rho cos varphi sin theta , } ;; { y = rho sin varphi sin theta , } ;; { z = rho cos theta , } ;; { dxdydz = { rho ^2 } sin theta drho dvarphi dtheta . } $ Новые переменные будут изменяться в пределах: $ { 0 le rho le R, } ;; { 0 le varphi le frac { pi } { 2 } , } ;;0 { le theta le frac { pi } { 2 } . } $ Тогда интеграл в сферических координатах равен $ { I = iiintlimits_U { xyzdxdydz } } = { iiintlimits_ { U’ } { left[ { rho cos varphi sin theta cdot rho sin varphi sin theta cdot rho cos theta cdot { rho ^2 } sin theta drho dvarphi dtheta }right] } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { cos varphi sin varphi dvarphi } intlimits_0^R { { rho ^5 } drho } intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { sin } ^3 } theta cos theta dtheta } } = \ = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { left( { frac { 1 } { 2 } sin 2varphi dvarphi }right) } intlimits_0^R { { rho ^5 } drho } intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { sin } ^3 } theta cos theta dtheta } } = \ = { frac { 1 } { 2 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { sin 2varphi dvarphi } intlimits_0^R { { rho ^5 } drho } intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { sin } ^3 } theta dleft( { sin theta }right) } } = { frac { 1 } { 2 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { sin 2varphi dvarphi } intlimits_0^R { { rho ^5 } drho } cdot left[ { left. { left( { frac { { { { sin } ^4 } theta } } { 4 } }right) }right|_ { theta = \ = 0 } ^ { theta = largefrac { pi } { 2 } normalsize } }right] } = { frac { 1 } { 8 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { sin 2varphi dvarphi } intlimits_0^R { { rho ^5 } drho } cdot left( { { { sin } ^4 } frac { pi } { 2 } — { { sin } ^4 } 0 }right) } = \ = { frac { 1 } { 8 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { sin 2varphi dvarphi } intlimits_0^R { { rho ^5 } drho } cdot 1 } = { frac { 1 } { 8 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { sin 2varphi dvarphi } cdot left[ { left. { left( { frac { { { rho ^6 } } } { 6 } }right) }right|_0^R }right] } = { frac { { { R^6 } } } { { 48 } } left[ { left. { left( { — frac { { cos 2varphi } } { 2 } }right) }right|_0^ { largefrac { pi } { 2 } normalsize } }right] } = { frac { { { R^6 } } } { { 96 } } left( { — cos pi + cos 0 }right) } = { frac { { { R^6 } } } { { 96 } } cdot 2 } = { frac { { { R^6 } } } { { 48 } } . } $

Пример 13

Найти тройной интеграл $iiintlimits_U { left( { frac { { { x^2 } } } { { { a^2 } } } + frac { { { y^2 } } } { { { b^2 } } } + frac { { { z^2 } } } { { { c^2 } } } }right)dxdydz } ,$ где область (U) ограничена эллипсоидом $ { frac { { { x^2 } } } { { { a^2 } } } + frac { { { y^2 } } } { { { b^2 } } } + frac { { { z^2 } } } { { { c^2 } } } } = 1.$

Решение:

Для вычисления интеграла перейдем к обобщенным сферическим координатам путем следующей замены переменных: $ { x = arho cos varphi sin theta , } ;; { y = brho sin varphi sin theta , } ;; { z = crho cos theta . } $ Модуль якобиана данного преобразования равен (left| I right| = abc { rho ^2 } sin theta .) Поэтому для дифференциалов справедливо соотношение $dxdydz = abc { rho ^2 } sin theta drho dvarphi dtheta .$ В новых координатах интеграл принимает вид: $ { I = iiintlimits_U { left( { frac { { { x^2 } } } { { { a^2 } } } + frac { { { y^2 } } } { { { b^2 } } } + frac { { { z^2 } } } { { { c^2 } } } }right)dxdydz } } = { iiintlimits_ { U’ } { left[ { frac { { { { left( { arho cos varphi sin theta }right) } ^2 } } } { { { a^2 } } } + frac { { { { left( { brho sin varphi sin theta }right) } ^2 } } } { { { b^2 } } } + frac { { { { left( { crho cos theta }right) } ^2 } } } { { { c^2 } } } }right]abc { rho ^2 } sin theta drho dvarphi dtheta } } = \ = { iiintlimits_ { U’ } { left[ { { rho ^2 } { { cos } ^2 } varphi , { { sin } ^2 } theta + { rho ^2 } { sin^2 } varphi , { { sin } ^2 } theta + { rho ^2 } { { cos } ^2 } theta }right]abc { rho ^2 } sin theta drho dvarphi dtheta } } = \ = { iiintlimits_ { U’ } { left[ { { rho ^2 } { { sin } ^2 } theta underbrace { left( { { { cos } ^2 } varphi + { sin^2 } varphi }right) } _1 + { rho ^2 } { { cos } ^2 } theta }right]abc { rho ^2 } sin theta drho dvarphi dtheta } } = \ = { iiintlimits_ { U’ } { { rho ^2 } underbrace { left( { { sin^2 } theta + { { cos } ^2 } theta }right) } _1abc { rho ^2 } sin theta drho dvarphi dtheta } } = { abciiintlimits_ { U’ } { { rho ^4 } sin theta drho dvarphi dtheta } . } $

Область интегрирования (U’) в сферических координатах представляет собой параллелепипед и определяется неравенствами $ { 0 le rho le 1, } ;; { 0 le varphi le 2pi , } ;; { 0 le theta le pi . } $ Тогда тройной интеграл становится равным $ { I = abciiintlimits_ { U’ } { { rho ^4 } sin theta drho dvarphi dtheta } } = { abcintlimits_0^ { 2pi } { dvarphi } intlimits_0^1 { { rho ^4 } drho } intlimits_0^pi { sin theta dtheta } } = { abcintlimits_0^ { 2pi } { dvarphi } intlimits_0^1 { { rho ^4 } drho } cdot left[ { left. { left( { — cos theta }right) }right|_0^pi }right] } = \ = { abcintlimits_0^ { 2pi } { dvarphi } intlimits_0^1 { { rho ^4 } drho } cdot left( { — cos pi + cos 0 }right) } = { 2abcintlimits_0^ { 2pi } { dvarphi } intlimits_0^1 { { rho ^4 } drho } } = { 2abcintlimits_0^ { 2pi } { dvarphi } cdot left[ { left. { left( { frac { { { rho ^5 } } } { 5 } }right) }right|_0^1 }right] } = \ = { frac { { 2abc } } { 5 } intlimits_0^ { 2pi } { dvarphi } } = { frac { { 2abc } } { 5 } cdot left[ { left. varphi right|_0^ { 2pi } }right] } = { frac { { 2abc } } { 5 } cdot 2pi = frac { { 4abcpi } } { 5 } . } $

Пример 14

Вычислить интеграл $intlimits_0^1 { dx } intlimits_0^ { sqrt { 1 — { x^2 } } } { dy } intlimits_0^ { sqrt { 1 — { x^2 } — { y^2 } } } { { { left( { { x^2 } + { y^2 } + { z^2 } }right) } ^2 } dz } ,$ используя сферические координаты.

Решение:

Область интегрирования представляет собой часть шара, расположенная в первом октанте и, следовательно, ограничена неравенствами $ { 0 le rho le 1, } ;; { 0 le varphi le frac { pi } { 2 } , } ;; { 0 le theta le frac { pi } { 2 } . } $

Учитывая, что подынтегральное выражение равно $ { { left( { { x^2 } + { y^2 } + { z^2 } }right)^2 } } = { { left[ { { { left( { rho cos varphi sin theta }right) } ^2 } + { { left( { rho sin varphi sin theta }right) } ^2 } + { { left( { rho cos theta }right) } ^2 } }right]^2 } } = \ = { { left[ { { rho ^2 } { { cos } ^2 } varphi , { { sin } ^2 } theta + { rho ^2 } { sin^2 } varphi , { { sin } ^2 } theta + { rho ^2 } { { cos } ^2 } theta }right]^2 } } = { { left[ { { rho ^2 } { { sin } ^2 } theta underbrace { left( { { { cos } ^2 } varphi + { sin^2 } varphi }right) } _1 + { rho ^2 } { { cos } ^2 } theta }right]^2 } } = { { left[ { { rho ^2 } { { sin } ^2 } theta + { rho ^2 } { { cos } ^2 } theta }right]^2 } } = \ = { { left[ { { rho ^2 } underbrace { left( { { { sin } ^2 } theta + { { cos } ^2 } theta }right) } _1 }right]^2 } } = { { rho ^4 } , } $

а дифференциалы связаны соотношениями $dxdydz = { rho ^2 } sin theta drho dvarphi dtheta ,$ получаем $ { I = intlimits_0^1 { dx } intlimits_0^ { sqrt { 1 — { x^2 } } } { dy } intlimits_0^ { sqrt { 1 — { x^2 } — { y^2 } } } { { { left( { { x^2 } + { y^2 } + { z^2 } }right) } ^2 } dz } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { dvarphi } intlimits_0^1 { left( { { rho ^4 } cdot { rho ^2 } drho }right) } intlimits_0^ { largefrac { pi } { 2 } normalsize } { sin theta dtheta } } = \ = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { dvarphi } intlimits_0^1 { { rho ^6 } drho } cdot left[ { left. { left( { — cos theta }right) }right|_0^ { largefrac { pi } { 2 } normalsize } }right] } = \ = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { dvarphi } intlimits_0^1 { { rho ^6 } drho } cdot left( { — cos frac { pi } { 2 } + cos 0 }right) } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { dvarphi } intlimits_0^1 { { rho ^6 } drho } cdot 1 } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { dvarphi } cdot left[ { left. { left( { frac { { { rho ^7 } } } { 7 } }right) }right|_0^1 }right] } = \ = { frac { 1 } { 7 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { dvarphi } } = { frac { 1 } { 7 } cdot left[ { left. varphi right|_0^ { largefrac { pi } { 2 } normalsize } }right] } = { frac { 1 } { 7 } cdot frac { pi } { 2 } } = { frac { pi } { { 14 } } . } $