Содержание:
Теорема синусов, теорема косинусов:
Теорема синусов
Вы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть
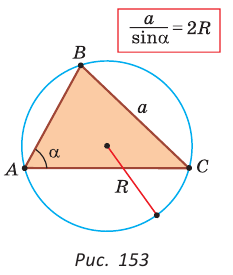
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
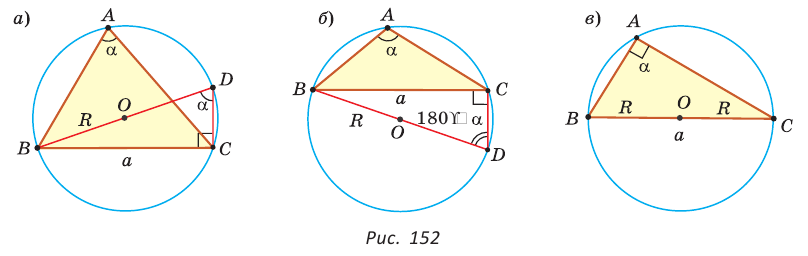
Доказательство:
Пусть дан треугольник АВС, ВС = 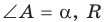
1) Угол 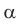
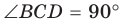
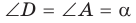
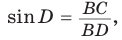
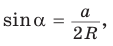
2) Угол 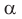
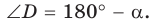
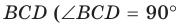
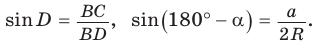
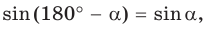
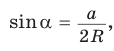
3) Для 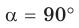
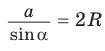
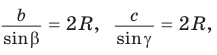
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция 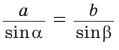
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы 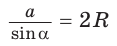
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
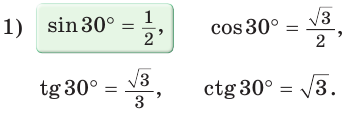
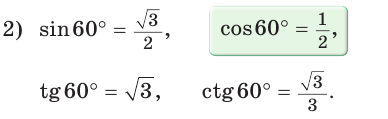
Пример:
В остроугольном треугольнике известны стороны 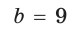
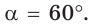
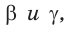
Решение:
По теореме синусов 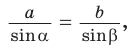
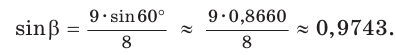
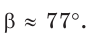
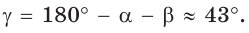
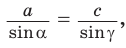
Ответ:
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом 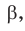
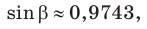
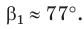
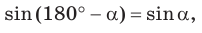
Пример:
Доказать справедливость формулы площади треугольника 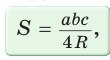
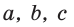
Доказательство:
Воспользуемся известной формулой площади треугольника: 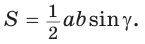
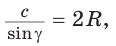
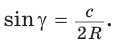
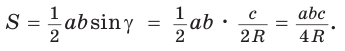
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника
Пример:
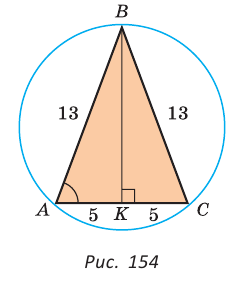
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13 (рис. 154).
Решение:
Способ 1. Из формулы 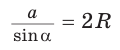
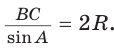
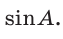
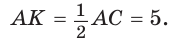
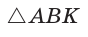
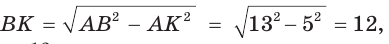
Тогда
Способ 2. Используем формулу 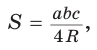
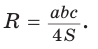
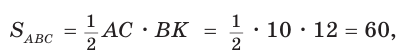
Ответ:
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников. Также мы могли использовать формулу 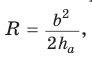
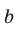
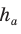
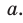
Заменив 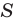
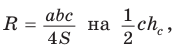
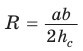

Теорема косинусов
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны 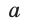
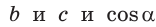
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
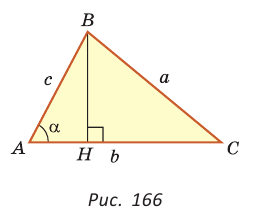
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166).
Проведем высоту ВН к стороне АС. Из 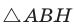
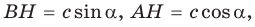
Из 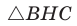
По основному тригонометрическому тождеству
Тогда
Справедливость теоремы для случаев, когда 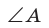
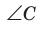
Для сторон 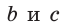
Замечание. Если 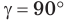
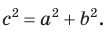
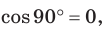
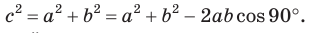
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
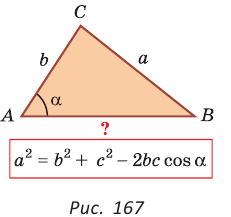
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства 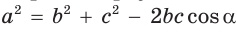
Для углов 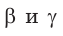
Пример:
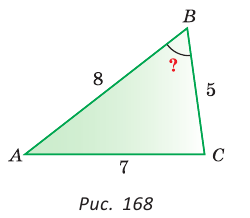
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы 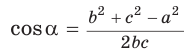
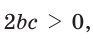
- если
то
и угол
острый;
- если
то
и угол
тупой;
- если
то
и угол
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как 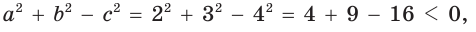
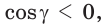
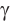
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
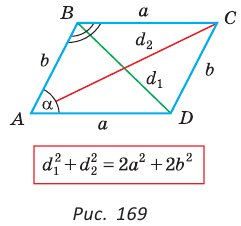
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD 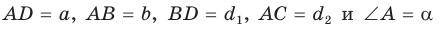
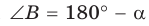
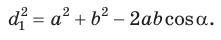
Из 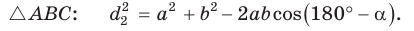
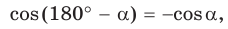
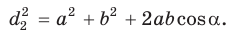
Сложив почленно равенство (1) и равенство (2), получим 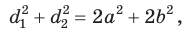
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
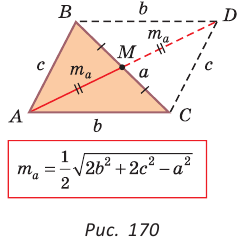
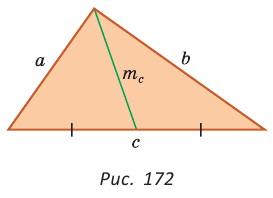
Медиану 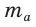
Доказательство:
Рассмотрим 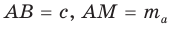
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 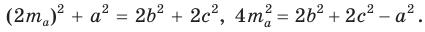
Утверждение доказано.
Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, 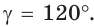
Решение:
а) По теореме косинусов
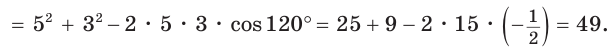
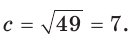
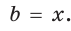
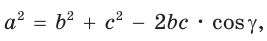
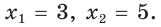
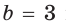
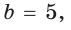
Ответ: а) 7; б) 3 или 5.
Пример:
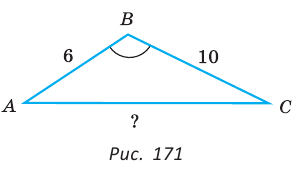
Две стороны треугольника равны 6 и 10, его площадь —
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в 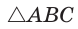
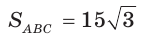
Поскольку 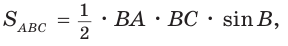
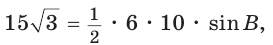
Так как 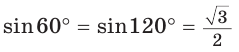
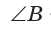

Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника 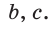
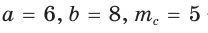
По формуле медианы 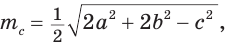
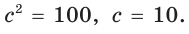
Ответ: 24.
Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: 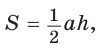
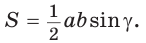
Теорема (формула Герона).
Площадь треугольника со сторонами 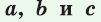
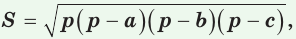
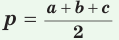
Доказательство:
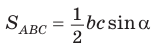
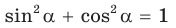
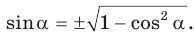
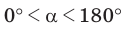
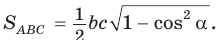
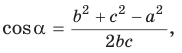
Тогда
Так как
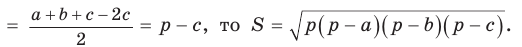
Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
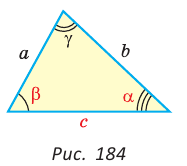
Пример №1 (решение треугольника по двум сторонам и углу между ними).
Дано: 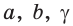
Найти :
Решение:
Рис. 184
1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол 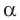
4) Угол
Замечание. Нахождение угла 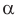
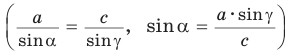
Пример №2 (решение треугольника по стороне и двум прилежащим к ней углам).
Дано: 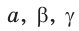
Найти:
Решение:
1) Угол
2) По теореме синусов 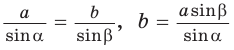
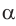
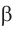
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: 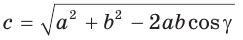
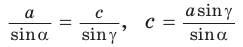
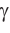
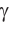
Пример №3 (решение треугольника по трем сторонам).
Дано: 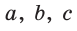
Найти: 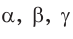
Решение:
1) По следствию из теоремы косинусов
2) Зная 
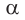
3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле 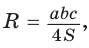
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов 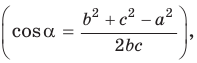
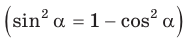
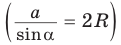
Пример №4
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:
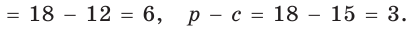
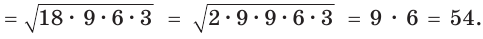
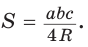
Ответ:
Способ 2. Так как 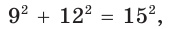
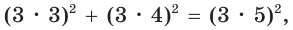
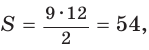
Пример №5
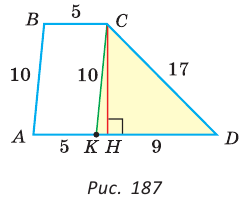
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и 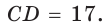
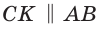
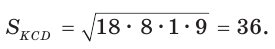
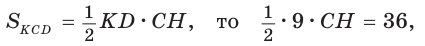
Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
Пример:
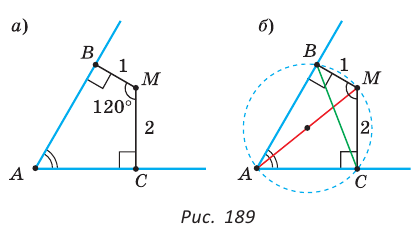
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть 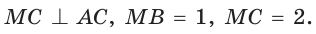
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому
Так как в четырехугольнике АВМС 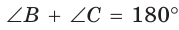
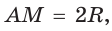
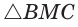
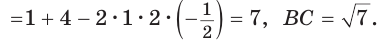
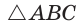
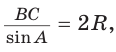
Ответ:
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
Пример №6
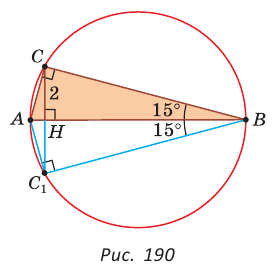
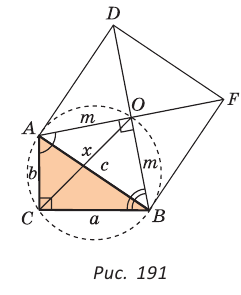
В прямоугольном треугольнике АВС известно: 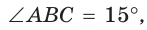
Решение:
Построим 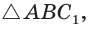
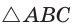
Поскольку 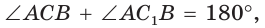
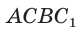
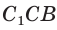
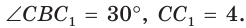
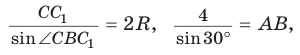
Ответ: 8.
Пример №7
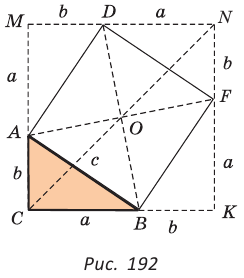
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = 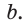
Решение:
Способ 1. Так как 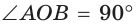
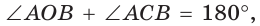
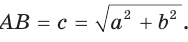
Пусть СО = х. По теореме косинусов из 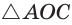
из 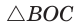
По свойству вписанного четырехугольника 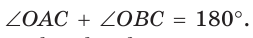
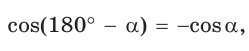
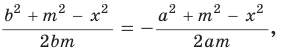
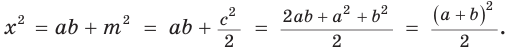
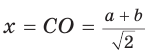
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим 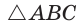
Ответ:
Пример №8
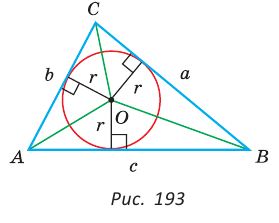
Точка О — центр окружности, вписанной в треугольник АВС, 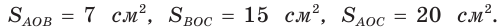
Решение:
Пусть 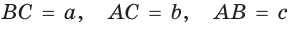
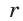
Тогда
Отсюда 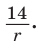
С другой стороны, 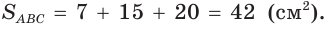
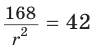
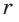
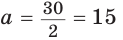
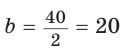
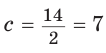
Ответ: 15 см; 20 см; 7 см.
Теорема Стюарта
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
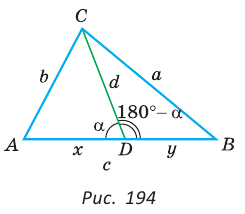
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из 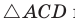
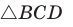
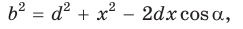
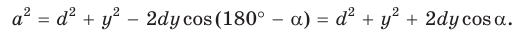
Умножим обе части равенства (1) на у, равенства (2) — на
Сложим почленно полученные равенства:
Из последнего равенства выразим
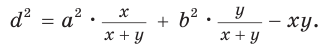
Следствие:
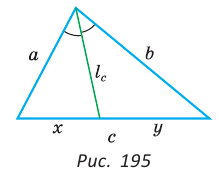
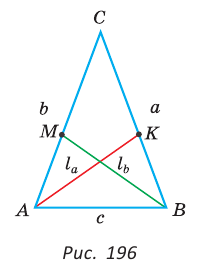
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника 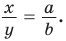
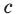
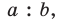
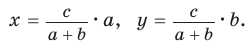
Пример №9
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, 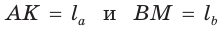
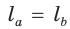
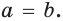
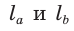
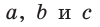
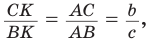
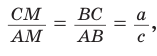
По формуле биссектрисы треугольника
Из условия 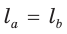
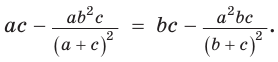
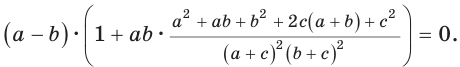
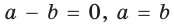
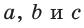
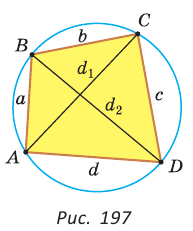
Теорема Птолемея о вписанном четырехугольнике
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е.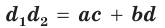
Доказательство:
Из 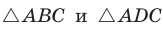
Так как 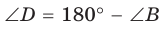
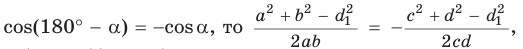
Аналогично из 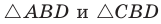
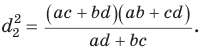
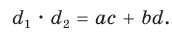
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
- Радиус описанной окружности треугольника можно найти, используя формулы:
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- Пусть
— стороны треугольника и с — большая сторона. Если
, то треугольник тупоугольный, если
то треугольник остроугольный, если
, то треугольник прямоугольный.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
- Формула Герона:
- Формула медианы:
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
Теорема косинусов отлично помогает в решении треугольников. Решение треугольника – это нахождение всех его сторон и углов. Но если нам даны только стороны треугольника, как определить углы в нем? Вот тогда и приходит на помощь теорема косинусов. Это общий случай теоремы Пифагора, подходящий для треугольника с любым углом, не только с углом 900.
Теорема и доказательство
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Доказательство теоремы косинусов
Докажем теорему. Для этого нарисуем треугольник ABC и докажем, что:
Если рассматривать стороны треугольника, как векторы, то будет справедливо равенство:
.
В теореме в квадрате, значит возведем векторное равенство в квадрат, получим:
Так как, ,
, а скалярное произведение векторов равно произведению их модулей на косинус угла между ними, то есть
.
Подставим все в формулу (2):
.
Что и требовалось доказать.
Следствие теоремы косинусов
Проведем высоты :
Обратим внимание, что . То есть
– это проекция стороны
на сторону
треугольника
. Если угол А острый, то
, если угол А тупой, то косинус угла А будет отрицательным и
. То есть из теоремы косинусов вытекает важное следствие:
квадрат стороны треугольника равен сумме квадратов двух других сторон “
” удвоенное произведение одной из них на проекцию другой на эту сторону. Знак
надо брать, если угол тупой, а знак
, если угол острый.
Задачи на теорему косинусов
Задача 1
Найдите , если дано:
,
,
.
Решение: Так как нам известен угол между сторонами и
и известна сторона
– мы сможем найти сторону
, если воспользуемся теоремой косинусов.
Из теоремы косинусов выразим сторону
.
Получим:
Обозначим
Тогда
Получаем квадратное уравнение. Подставим в него значения и решим:
Находим дискриминант:
.
Тогда .
– не может быть длиной стороны треугольника.
Ответ: 12.
Задача 2
В треугольника ABC ,
,
. Найдите
Решение: Нарисуем треугольник ABC. Это равнобедренный треугольник.
Запишем теорему косинусов для сторону так как нам дан угол между двумя другими сторонами:
.
Так как , то из формулы (1), получим:
Сделаем замену: :
,
перенесем в правую часть равенства и получим квадратное уравнение:
,
Подставим значения:
Так как , значит,
.
Ответ: 6
Задача 3
Решите треугольник ABC, если известно, что ,
,
.
Решение: Решить треугольник – это значит, найти все его стороны и все углы. Нам два угла даны, значит, зная, что сумма всех углов в треугольнике равна получим:
.
Обозначим неизвестные стороны треугольника: ,
.
Выразим сторону треугольник по теореме косинусов:
Выразим сторону треугольника по теореме косинусов:
или
Решим уравнения (1) и (2) совместно, записав их в систему уравнений:
Преобразуем второе уравнение системы:
Сложим первое и второе уравнения системы и запишем получившееся уравнение вместо второго уравнения, получим:
Из второго уравнения выразим :
Итак, мы выразили из второго уравнения системы, теперь возьмем и подставим его в первое уравнение и сделаем необходимые преобразования.
, раскрываем скобки и умножим левую и правую части уравнения на 2:
Разделим левую и правую части уравнения на 2:
.
Получили квадратное уравнение. Решим его.
Находим дискриминант:
Тогда корни уравнения:
.
Оба значения подходят – они положительны. Находим, :
– отрицательное значение нам не подходит.
.
Таким образом, получаем следующие значения ,
.
Вы можете самостоятельно сделать проверку и убедиться в том, что данные значения верны.
Ответ: ,
.
Теорема косинусов для треугольника очень помогает в решении геометрических задач, однако некоторые задачи усложняются, если не знать еще одну теорему – синусов. Например, третью задачу мы могли решить гораздо проще – используя теорему синусов, с помощью которой мы бы довольно быстро получили тот же результат для . Однако, с ней мы бы получили лишь приближенное значение
. Теорема косинусов дает нам точный результат. Однако, в дальнейшем, когда вы выучите две теоремы – рекомендуем решать задачи, используя их обе.
Теорема косинусов и теорема Пифагора. В этой статье мы рассмотрим теорему косинусов и как она используется для нахождения элементов треугольника. А так же разберём её взаимосвязь с теоремой Пифагора.
Знать эту теорему НЕОБХОДИМО. Что мы можем найти, используя её?
Если нам будут известны две стороны и угол между ними, мы без труда найдём третью сторону. Для этого нужно просто подставить в формулу известные величины. Для других сторон всё то же самое:
Можно ли использовать теорему косинусов для нахождения третьей стороны, если известны любые две стороны и угол, не лежащий между этими сторонами? Например, нам известны стороны a и b и угол альфа. Тогда из формулы
мы можем найти сторону «с». Приводим к виду:
То есть, мы получаем квадратное уравнение с переменной «с» (все остальные величины нам известны). Решив его, получим искомую сторону.
Мы можем найти любой угол, если нам известны все три стороны треугольника:
Разумеется, что учить все эти формулы не нужно, так как достаточно понимать сам смысл Теоремы косинусов. А косинус любого угла не трудно выразить используя простые алгебраические преобразования.
*Если вы вычисляете косинус тупого угла, то имейте ввиду, что должно получиться отрицательное значение, так как косинус угла от 90 до 180 градусов отрицателен. Если при решении в задачах получите положительное значение, то ищите ошибку.
Следующий вопрос: а если нам дана сторона и любые два угла, что делать? В этом случае теорема косинусов не используется, а на помощь приходит теорема синусов, её мы рассмотрим в одной из следующих статей, не пропустите!
Если вы будете в совершенстве владеть теоремами Пифагора, косинусов, синусов и свойствами подобия треугольников, то для вас не возникнет никаких сложностей с решением треугольников (в большинстве задач).
Следующий факт знают все, но всё же о взаимосвязи теоремы косинусов с теоремой Пифагора сказать стоит. Посмотрите на исходный рисунок, если угол альфа равен 90 градусов, то получим:
То есть, по сути, теорема Пифагора это как бы частный случай теоремы косинусов.
Рассмотрим прямоугольный треугольник. Покажем то же самое, но с другими обозначениями:
По теореме косинусов:
Так как угол С равен 90, то
Напомню, что зная любые две стороны в прямоугольном треугольнике, мы всегда можем найти третью. А далее без труда можем найти значение любой тригонометрической функции острого угла в нём. Можете изучить статью об этом.
Получить материал статьи в формате PDF
На этом всё. Успехов вам!!!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
Формула косинуса:
- a² = b² + c² – 2b.c.cosα
- b² = a² + c² – 2a.c.cosβ
- c² = a² + b² – 2a.b.cosγ
Например:
Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.
Решение по формуле a² = b² + c² – 2b.c.cosα:
b = 12 см
c = 8 см
cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)
a² = 12² + 8² – 2×12×8×(- 1/2)
a² = 144 + 64 – (–96)
a² = 304
a = √304
a ≈ 17,436
Длина третьей стороны — примерно 17,436 см.
Следствия
Следствие косинуса угла треугольника
При помощи теоремы косинусов можно найти косинус угла треугольника.
Формула:
Либо
Либо
Например:
сторона c = 6
сторона b = 7
сторона a = 8
Используйте теорему косинусов, чтобы найти угол β.
Решение:
Будем использовать эту версию формулы:
cos β = (6² + 8² − 7²) / 2×6×8
= (36 + 64 − 49) / 96
= 51 / 96
= 0,53125
= cos¯¹(0,53125)
≈ 57,9°
Следствие верхней части формулы cos α
Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):
- b²+c²−a²<0, значит угол α — тупой;
- b²+c²−a²=0, значит угол α — прямой;
- b²+c²−a²>0, значит угол α — острый.
Доказательство теоремы косинусов
Нужно доказать, что c² = a² + b² − 2a.b.cos C
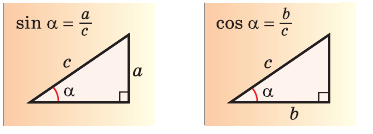
1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a <=> CD = a.cos C.
2. Вычитаем это из стороны b, так мы получим DA:
DA = b − a.cosC
3. Мы знаем из определения синуса, что в том же треугольнике BCD:
sin C = BD/a <=> BD = a.sinC.
4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²
5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²
6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C
6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC
7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC
8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C
Q.E.D.
Теорема косинусов для равнобедренного треугольника
В равнобедренном треугольнике:
- две его стороны равны;
- углы при основании равны.
Рассмотрим пример:
Используем формулу теоремы косинусов
a² = b² + c² – 2b.c.cosα
Подставляем все известные:
x² = 8² + 8² – 2×8×8×cos140º
x² = 64 + 64 – 128 × (-0,766)
x² ≈ √226,048
x ≈ 15,035.
Теорема синусов
Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:
Узнайте также, что такое Теорема Пифагора и Теорема Менелая.
При решении задач по геометрии из ЕГЭ и ОГЭ по математике довольно часто возникает необходимость, зная две стороны треугольника и угол между ними, найти третью сторону. Или же, зная все стороны треугольника, найти его углы. Для решение этих задач вам потребуется значение теоремы косинусов для треугольника. В данной статье репетитор по математике и физике рассказывает о том, как формулируется, доказывается и применяется на практике при решении задач данная теорема.
Формулировка теоремы косинусов для треугольника
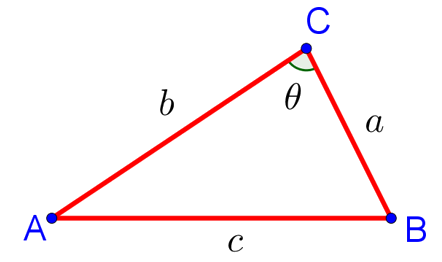
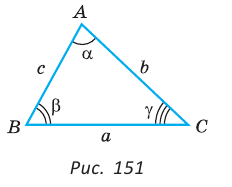
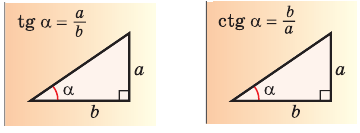
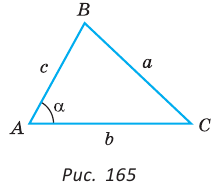
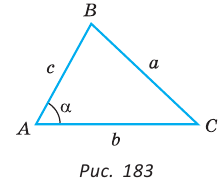
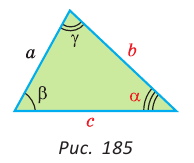
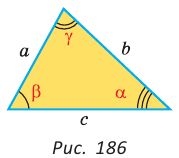
Теорема косинусов для треугольника связывает две стороны треугольника и угол между ними со стороной, лежащей против этого угла. К примеру, обозначим буквами ,
и
длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.
Тогда имеет теорема косинусов для этого треугольника может быть записана в виде:
На рисунке для удобства дальнейших рассуждений угол С обозначен углом . Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»
Понятно, что если бы вы выражали другую сторону треугольника, например, сторону , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны
и
. Выражение для квадрата стороны
получается аналогично:
Доказательство теоремы косинусов для треугольника
Доказательство теоремы косинусов для треугольника проводят обычно следующим образом. Разбивают исходный треугольник на два прямоугольных треугольника высотой, а дальше играются со сторонами полученных треугольников и теоремой Пифагора. В результате после долгих нудных преобразований получаю нужный результат. Мне лично этот подход не по душе. И не только из-за громоздких вычислений, но ещё и потому что в этом случае приходится отдельно рассматривать случай, когда треугольник является тупоугольным. Слишком много трудностей.
Я предлагаю доказать эту теорему с помощью понятия «скалярного произведения векторов». Я сознательно иду на этот риск для себя, зная, что многие школьники предпочитают обходить эту тему стороной, считая, что она какая-то мутная и с ней лучше не иметь дела. Но нежелание возиться отдельно с тупоугольным треугольником во мне всё же пересиливает. Тем более, что доказательство в результате получается удивительно простым и запоминающимся. Сейчас вы в этом убедитесь.
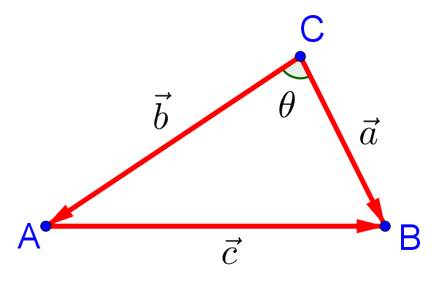
Заменим стороны нашего треугольника следующими векторами:
Согласно правилам сложения векторов имеем: . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим
в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение:
.
Теперь возьмём скалярный квадрат обеих частей полученного выражения. В результате чего получим:
Я напоминаю, что по определению скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Из этого определения также следует, что скалярный квадрат вектора равен квадрату его длины. Действительно, ведь угол между вектором и им же самим равен нулю, то есть соответствующих косинус равен 1. То есть остаётся только квадрат длины вектора. Исходя из этого мы сразу получаем выражение для теоремы косинусов:
Что и требовалось доказать. Причём данное доказательство хорошо ещё тем, что позволяет лучше запомнить саму формулу. Ведь теперь становится понятным, откуда берётся этот хвост . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол
может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.
Кстати, в случае, когда угол прямой, мы получаем
, и выражение принимает следующий вид:
. Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.
Примеры решения задач с использованием теоремы косинусов для треугольника
Надо сказать, что даже если вы не поняли приведённое выше доказательство, это не страшно, если ваша цель состоит в сдаче ЕГЭ или ОГЭ по математике. Специфика этих экзаменов состоит в том, что само доказательство теоремы косинусов у вас никто на них не спросит. Эти экзамены фактически вообще не проверяют знание теоретического материла из школьного курса математики. Важно лишь, чтобы вы знали, как эта теорема формулируется и умели применять её на практике для решения задач.
Используя теорему косинусов для треугольника, можно найти третью сторону, зная две стороны треугольника и угол между ними. Или же, зная длины всех сторон треугольника, найти величину всех его углов. Рассмотрим на примерах, как это делается.
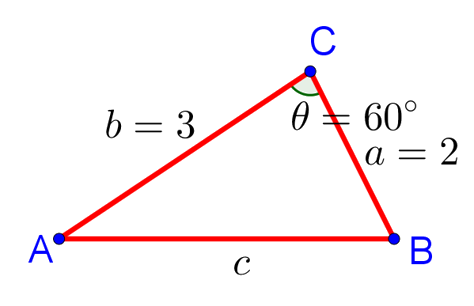
Пример 1. В треугольнике ABC сторона AC равна 3, сторона CB равна 2, а угол C равен 60°. Найдите длину стороны AB.
Используем теорему косинусов для треугольника ABC. Квадрат стороны равен сумме квадратов сторон
и
за вычетом удвоенного произведения этих сторон на косинус угла между ними:
Поскольку , то в результат получаем:
Значит, . Понятно, что отрицательное решение мы не берём, потому что длина отрезка — это число положительное.
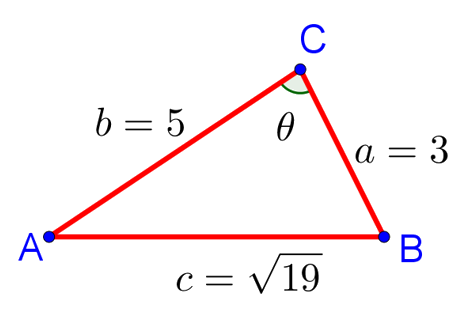
Пример 2. В треугольнике ABC сторона AB равна , сторона AC равна 5, сторона BC равна 3. Найдите угол C.
Искомый угол на рисунке обозначен . Вновь запишем теорему косинусов для треугольника ABC. Поскольку все обозначения у нас сохранились, то и формула, выражающая теорему косинусов для этого треугольника, останется прежней:
Подставим теперь в эту формулу все величины, которые даны. В результате получаем следующее выражение:
После всех вычислений и преобразований получаем следующее простое выражение:
Какой должна быть величина острого угла , чтобы его косинус был равен
Смотрим в таблицу, которую можно найти в этой статье, и получаем ответ:
.
Вот так решаются задачи по геометрии с использованием теоремы косинусов для треугольника. Если вы собираетесь сдавать ОГЭ или ЕГЭ по математике, то этот материал вам нужно освоить обязательно. Соответствующие задачи почти наверняка будут на экзамене. Потренируйтесь самостоятельно в их решении. Выполните следующие задания:
- В треугольнике ABC сторона AB равна 4 см, сторона BC равна 6 см, угол B равен 30°. Найдите сторону AC.
- В треугольнике ABC сторона AB равна 10, сторона BC равна 8, сторона AC равна 9. Найдите косинус угла A.
Свои ответы и варианты решения пишите в комментариях. Удачи вам!
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич

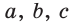
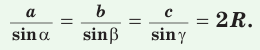
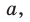
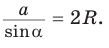
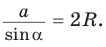
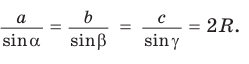
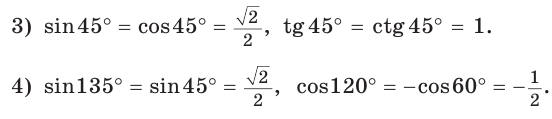
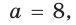
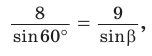
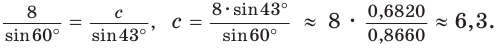


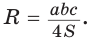
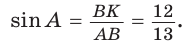
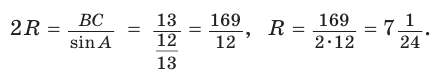
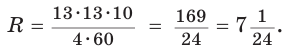
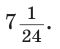
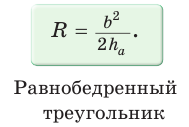
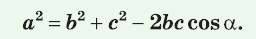
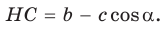
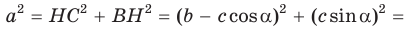
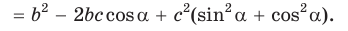
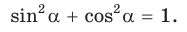
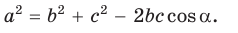
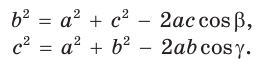
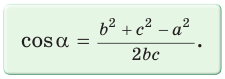
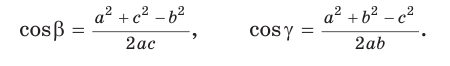

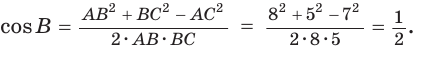
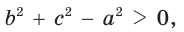 то
то 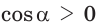 и угол
и угол 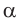 острый;
острый;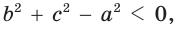 то
то 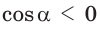 и угол
и угол 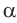 тупой;
тупой; то
то 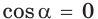 и угол
и угол 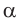 прямой.
прямой.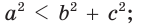
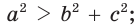
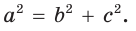
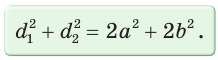
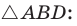
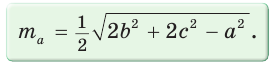
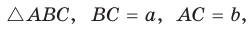
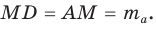
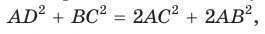
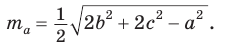
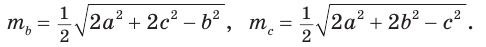
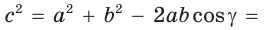
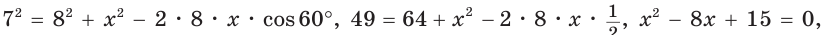
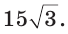
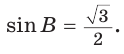
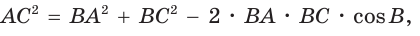
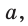
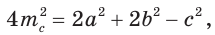
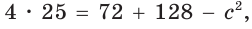
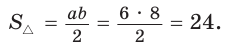
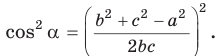
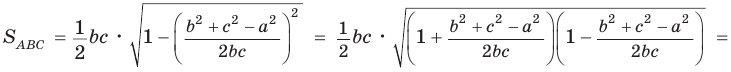
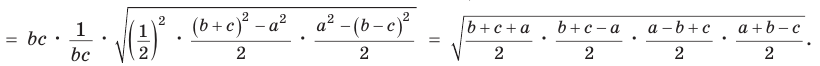
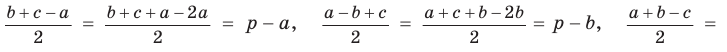
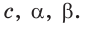
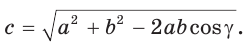
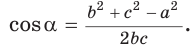
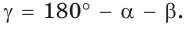
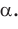
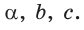
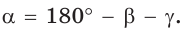
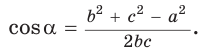
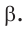
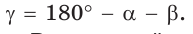
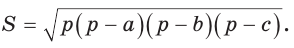
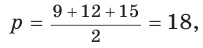
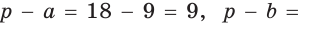
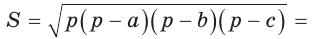
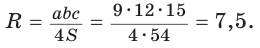
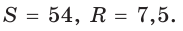
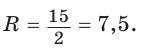
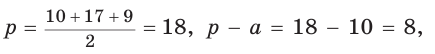
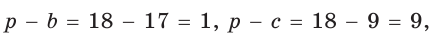
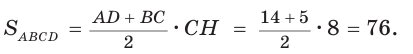
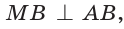
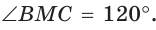
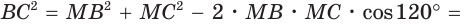
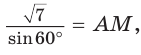
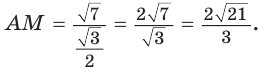
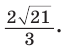
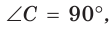
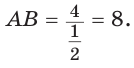
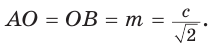
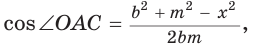
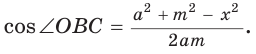
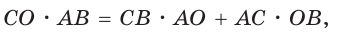
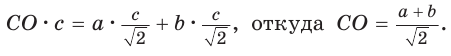
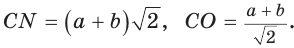
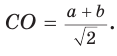
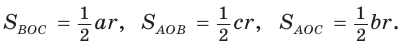
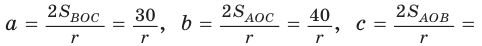
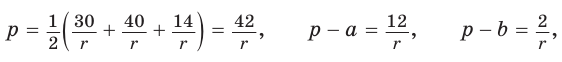
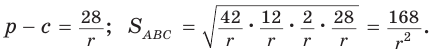
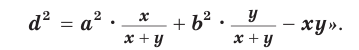
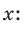
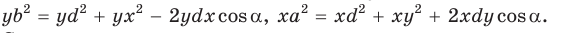
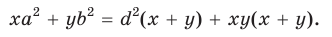
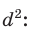
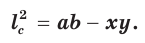
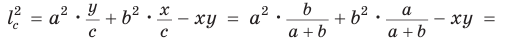
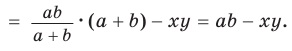
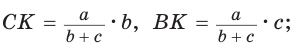
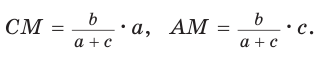
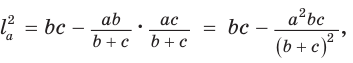
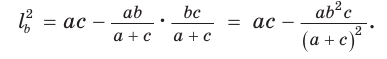
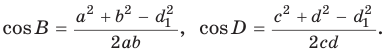
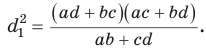
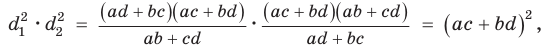
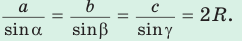
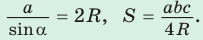
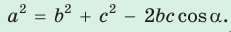
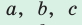 — стороны треугольника и с — большая сторона. Если
— стороны треугольника и с — большая сторона. Если 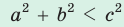 , то треугольник тупоугольный, если
, то треугольник тупоугольный, если 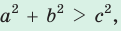 то треугольник остроугольный, если
то треугольник остроугольный, если 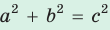 , то треугольник прямоугольный.
, то треугольник прямоугольный.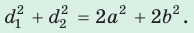
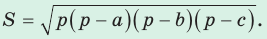
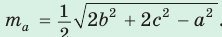





![Rendered by QuickLaTeX.com [left{ begin{aligned} AB^2={x}^2+y^2-2{xy} cdot cos {45^{circ}}\ y^2={x}^2+16-8{x}cdot cos {30^{circ}}.\ end{aligned} right.]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-30320ec6e39a25f00186bb323ebb0a4b_l3.png)
![Rendered by QuickLaTeX.com [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ y^2={x}^2+16-4{x}cdot sqrt{3}.\ end{aligned} right.]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-8678bdf8bad15043893e9bf2593a42ba_l3.png)
![Rendered by QuickLaTeX.com [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ -16={x}^2-y^2-4{x}cdot sqrt{3}.\ end{aligned} right.]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-76cf8b6954d16cd69742ca39f37aedfc_l3.png)
![Rendered by QuickLaTeX.com [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ 0=2{x}^2-xy sqrt{2}-4{x}cdot sqrt{3}.\ end{aligned} right.]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-67d0d01169f7374358518053704d8414_l3.png)