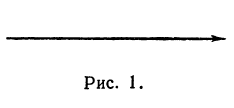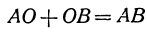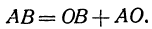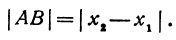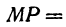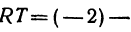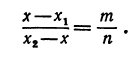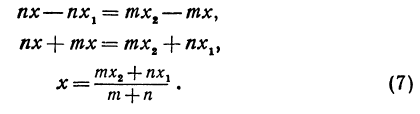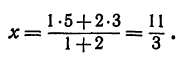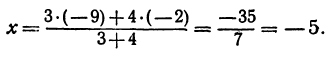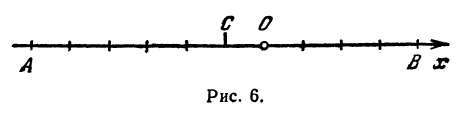У меня есть отрезок с известными координатами концов. На этом отрезке есть точка. Я знаю расстояние от начала отрезка до этой точки. Мне надо найти координаты этой точки. Как найти эти координаты?
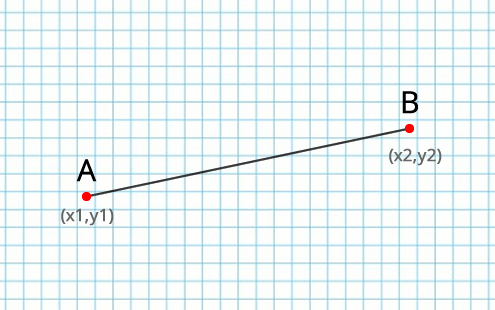
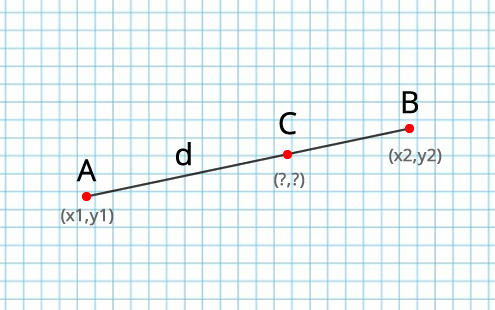
Пример: Есть 2 точки А(3,3) и В(6,4). Длина отрезка примерно 3,16. И есть точка С(?,?) на отрезке. Как найти координаты, если от А до С =1,8 ???
Dmytro
6,7011 золотой знак20 серебряных знаков55 бронзовых знаков
задан 3 мар 2016 в 20:40
4
Имеется отрезок AB с координатами A(Xa, Ya) и B(Xb, Yb).
Требуется найти координаты точки C(Xc, Yc), лежащей на отрезке AB на расстоянии Rac от точки A.
Rab = sqrt((Xb - Xa) ^ 2 + (Yb - Ya) ^ 2)
k = Rac / Rab
Xc = Xa + (Xb - Xa) * k
Yc = Ya + (Yb - Ya) * k
Обозначения:
f ^ n — возведение f в степень n, в нашем случае (первом) f будет Xb - Xa и n будет 2.
sqrt(f) — квадратный корень из f, в нашем случае f будет (Xb - Xa) ^ 2 + (Yb - Ya) ^ 2.
f / n — деление f на n, в нашем случае f будет Rac и n будет Rab.
f * n — умножение f на n, в нашем случае (первом) f будет Xb - Xa и n будет k.
ответ дан 4 мар 2016 в 6:54
Konstantin LesKonstantin Les
1,5388 серебряных знаков12 бронзовых знаков
2
Алгоритм без кода (довольно элементарный):
Имеем:
Две точки A, B; len — расстояние от точки А до требуемой точки C
full_len = |B - A| // длина вектора, соединяющего две точки == длина отрезка
C = A + (B - A) * (len / full_len)
Сложение векторов и умножение на число — очевидные операции.
ответ дан 3 мар 2016 в 20:56
int3int3
2,4579 серебряных знаков19 бронзовых знаков
8
nodet — точка конец вектора, в твоем случае точка b
nodef — точка начало вектора, в твоем случае точка a
dx = nodet.x - nodef.x
dy = nodet.y - nodef.y
dz = nodet.z - nodef.z
r = math.sqrt(dx ** 2 + dy ** 2 + dz ** 2)
xx = dx * (step/r)
yy = dy * (step /r)
zz = dz * (step /r)
newnode = node(nodef.x + xx,nodef.y + yy,nodef.z + zz)
newnode — новая точка на заданом расстоянии
ответ дан 12 ноя 2019 в 16:31
qvuer7qvuer7
113 бронзовых знака
Есть координаты двух точек, образующих отрезок, известна длина отрезка (например, 141), как найти координаты точки на этом отрезке, которая находится на определенной длине отрезка (например, 23)?
Например точки с координатами
x1 = 100, y1 = 0
x2 = 0, y2 = 100
Длина отрезка составит 141
А теперь как найти точку, которая лежит на этом отрезке, где его длина составит 23, т.е точка, которая внутри этого отрезка?
Имеем отрезок AB с координатам x1,y1 и x2, y2:
Необходимо найти координаты новой точки С, которая находится на отрезке, на определенном расстоянии от точки A.
1
PHP-функция
$x1, $y1 – координаты точки A,
$x2, $y2 – координаты точки B,
$d – расстояние от точки A до точки C.
function pointToLine($x1, $y1, $x2, $y2, $d)
{
$Rab = sqrt(pow($x2 - $x1, 2) + pow($y2 - $y1, 2));
$k = $d / $Rab;
$Xc = $x1 + ($x2 - $x1) * $k;
$Yc = $y1 + ($y2 - $y1) * $k;
return array('x' => $Xc, 'y' => $Yc);
}PHP
2
JS-функция
function pointToLine(x1, y1, x2, y2, d)
{
var Rab = Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
var k = d / Rab;
var Xc = x1 + (x2 - x1) * k;
var Yc = y1 + (y2 - y1) * k;
return {x: Xc, y: Yc};
}JS
3
Координата точки на отрезке онлайн
Координаты на прямой:
Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление—положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).
Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О. Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.
Определение: Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.
Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором— букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.
Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным: если же его направление противоположно направлению оси, то—отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:
Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.
Сложение направленных отрезков производится по следующему правилу: Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:
(рис. 2 и 3).
Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.
Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать
(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или
Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, посколькуего начало не является началом координат. Но в силу равенства (1)
поэтому можно написать
Получен следующий результат:
Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.
Это верно для любого отрезка, лежащего на координатной оси. Теперь дадим одно из самых важных определений:
Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.
Точку А, имеющую координатной число 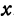
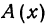
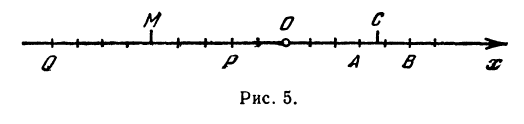
Указанные на рис. 4 точки имеют следующие координаты: 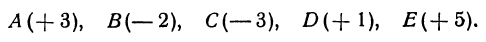
Если даны точки 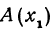
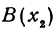
т. е. направленный отрезок равен разности координат его конца и начала. Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.
Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:
- Заказать решение задач по высшей математике
Пример:
Если даны точки 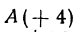
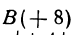
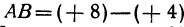
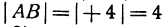
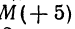
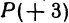
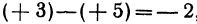
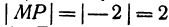
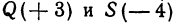
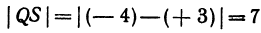
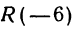
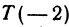
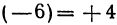
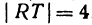
Пример:
Начало отрезка АВ находится в точке 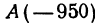
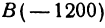
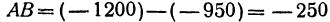
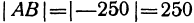
Пример:
На координатной оси даны две точки: 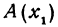
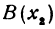
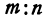
Обозначая координату искомой точки С через 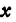
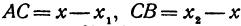
Решая последнее уравнение относительно 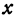
Это и есть координата искомой точки.
Пример:
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка 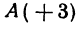
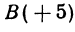
Решение:
Здесь 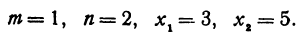
Пример:
Найти точку 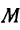
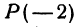
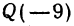
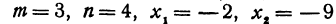
Решение:
Если 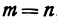
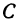
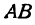
Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.
Пример:
Найдем середину отрезка, заключенного между точками 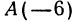
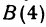
Решение:
Применяя формулу (8), получим, 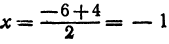
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
На чтение 4 мин Просмотров 1.2к.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 – y1)² + (x2 – x1)². В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 – 1)² + (5 – 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.
Рассчитаем длину отрезка А, для этого найдем квадратный корень:
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка (средней точки) по декартовым координатам концов отрезка. Отрезок и средняя точка отображаются на графике, также на графике показан графический способ нахождения середины отрезка.
Эта страница существует благодаря следующим персонам
Timur
- Статья : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
- Калькулятор : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка по введенным декартовым координатам двух точек – концов отрезка.
Формула вычисления расстояния между двумя точками и это формула длины гипотенузы прямоугольного треугольника . Координаты середины отрезка – среднее арифметическое координат точек .
Отрезок и средняя точка отображаются на графике. Также среднюю точку можно найти построением. Для этого на графике надо построить две дуги с центрами на концах отрезка и с радиусом равным длине отрезка. Затем надо построить прямую линию между точками пересечения дуг. Эта линия пересечет исходный отрезок в середине.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 – y1, а на ось х длина проекции равна х2 – х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.