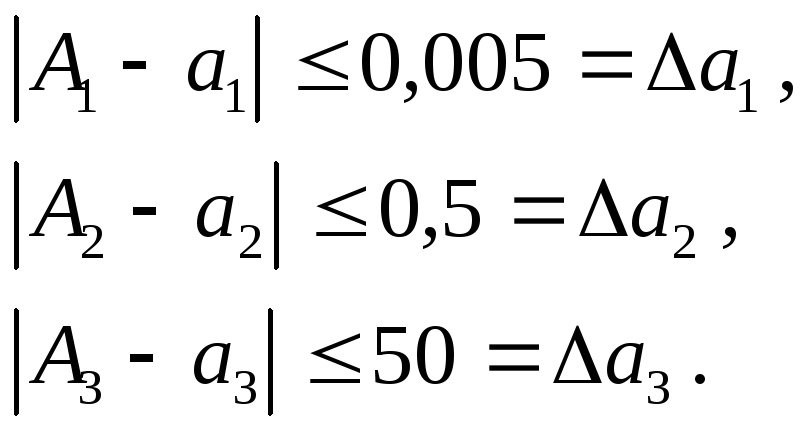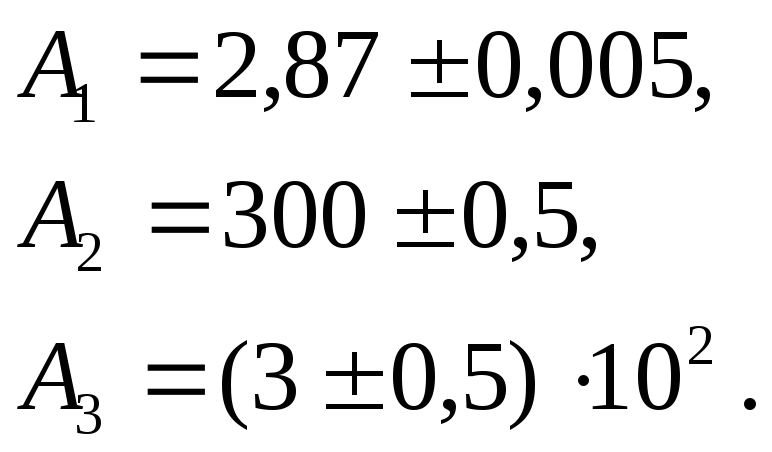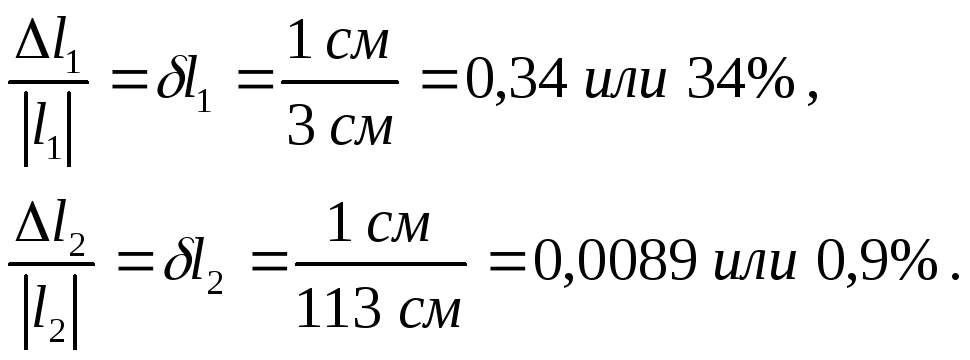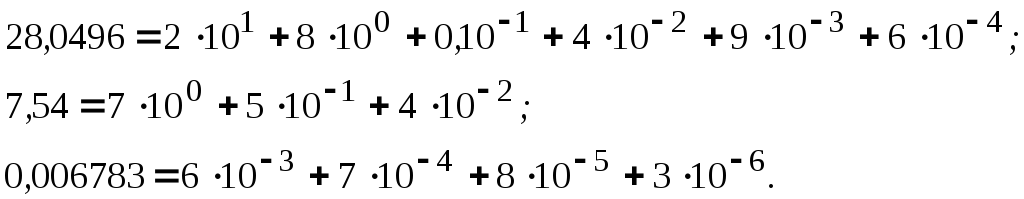Как найти точность числа - AvtoShod.ru - решение различных проблем

Содержание:

Приближённые вычисления
Абсолютная и относительная погрешности
Выполнение действий над приближёнными числами
Выполнение действий без точного учёта погрешности

Приближённые вычисления

Приближённые вычисления — вычисления, в которых данные и результат (или только результат) являются числами, приближенно представляющими истинные значения соответствующих величин. Числовые данные, полученные измерением реальных объектов, редко бывают точными значениями соответствующей величины, а обычно имеют некоторую погрешность

Абсолютная и относительная погрешности

При решении практических задач часто приходится иметь дело с приближёнными значениями разных числовых величин. К ним относятся: результаты измерения разных величин с помощью приборов; значения полученные при считывании на графиках, диаграммах, номограммах; проектные данные; результаты округления чисел; результаты действий над приближёнными числами; табличные значения некоторых величин; результаты вычислений значений функции. Приближённые значения (приближение, приближённые числа) могут значительно отличаться от точных, либо быть близкими к ним.

Для оценки отклонения приближённых чисел от точных используют такие понятия как абсолютная и относительная погрешности.

Абсолютной погрешностью приближённой называется модуль разности между точным значением величины и её приближённым значением х, то есть

Пример.

Абсолютная погрешность приближённого числа числом 0,44 составляет

Если точное число неизвестно, то найти абсолютную погрешность невозможно. На практике вводят оценку допустимой при данных измерениях или вычислениях абсолютной погрешности, которую называют пределом абсолютной погрешности и обозначают буквой h. Считают, что h. Как правило, предел абсолютной погрешности устанавливают из практических соображений, например, при измерениях пределом абсолютной погрешности считают наименьшее деление прибора.

При записи приближённых чисел часто используют понятия верной и сомнительной цифры.

Цифра называется верной, если предел абсолютной погрешности данного приближения не превышает единицы того разряда, в котором записана эта цифра. В другом случае цифра называется сомнительной.

Например: в числе две цифры верны, поскольку погрешность 0,04 не превышает единицу разряда десятых. Цифры 9 и 7 верны, поскольку а цифры 4 и 6 являются сомнительными, поскольку

В конечной записи приближённого числа сохраняют только верные цифры. Так число можно записать в виде , число в виде Если в десятичной дроби последние верные цифры — нули, то их оставляют в записи числа.

Например: если , то правильной записью числа будет 0,260.

Если в целом числе последние нули являются сомнительными, их исключают из записи числа.

Именно поэтому при работе с приближёнными числами широко используют стандартную форму записи числа.

Например: в числе верными являются три первые цифры, а два последних нуля — сомнительные цифры. Запись числа возможна только в виде:

Следовательно, в десятичной записи приближённого числа последняя цифра указывает на точность приближённости, то есть предел абсолютной погрешности не превышает единицу последнего разряда.

Например:

1. Запись означает, что , то есть предел абсолютной погрешности h=0,01.

2. Запись

3. Если

В десятичной записи числа значимыми цифрами называются все его верные цифры начиная с первой слева, отличной от нуля.

Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в числе 0,303 — три, в числе 5,200 — четыре, в числе 25_*10³— две значимых цифры.

При таком подходе к записи приближенного числа необходимо уметь округлять числа.

Правила округления чисел:

— Если первая цифра, которую отбрасываем является меньше пяти, то в основном разряде, который сохраняется цифра не меняется. Например: 879,673≈879,67.

— Если первая цифра, которую отбрасываем больше пяти, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 456,87≈456,9.

— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны от нуля, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 1246,5002≈1247.

— Если первая цифра, которая отбрасывается — пять и за ней нет больше никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 0,275≈0,28; 1,865≈1,86.

Абсолютная погрешность не полностью характеризует точность приближения. Например, будет грубой ошибкой при измерении жука, и незначительной при измерении кита. Тоже самое можно сказать и про предел абсолютной погрешности. Качество (точность) приближённости лучше характеризуется относительной погрешностью.

Относительной погрешностью (омега) приближённости х величины называется отношением абсолютной погрешности этого приближения к модулю приближённого значения х, то есть

Поскольку абсолютная погрешность обычно бывает неизвестна, то на практике оценивают модуль относительной погрешности некоторым числом, которое не меньше чем этот модуль:

Число называется пределом относительной погрешности.

Предел относительной погрешности можно вычислить по формуле:

Конечно относительная погрешность выражается в процентах.

С помощью относительной погрешности легко установить точность приближённости.

Пример 1. Найти относительную погрешность числа

Решение: Имеем

Следовательно

Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола H (см), если известно, что .

Решение:

Как видим, точность измерения высоты стола значительно выше.

Выполнение действий над приближёнными числами

Результат арифметических действий над приближёнными числами является также приближённым числом.

Необходимо уметь устанавливать погрешности результатов вычислений. Их находят с точным и без точного учёта погрешностей исходных данных. Правила нахождения погрешностей результатов действий с точным учётом погрешности приведены в таблице (обозначения — исходные данные; пределы абсолютных погрешностей относительно чисел; пределы относительных погрешностей).

Пример 3. Вычислить приближение значения выражения и найти предел погрешностей результата.

Решение: находим значение квадрата числа 5,62 и квадратного корня из числа 18,50.

Найдём границу относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ:

Пример 4. Вычислить приближение значения выражения и найти предел погрешностей результата.

Решение: находим значение квадратного корня из числа 6,24 и , имеем:

Граница относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ:

Выполнение действий без точного учёта погрешности

Точный учёт погрешности усложняет вычисление. Поэтому, если не надо учитывать погрешность промежуточных результатов, можно использовать более простые правила.

Сложение и вычитание приближённых вычислений рекомендуется выполнять так:

а) выделить слагаемое с наименьшим числом верных десятичных знаков;

б) округлить другие слагаемые так, чтобы каждое из них содержало на один десятичный знак больше чем выделенное;

в) выполнить действия, учитывая все сохранённые десятичные знаки;

г) результаты округлить и сохранить столько десятичных знаков, сколько их есть в приближённом числе с наименьшим числом десятичных знаков.

Умножение и деление приближённых вычислений рекомендуется выполнять так:

а) выделить среди данных чисел, число с наименьшим количеством верных значимых цифр;

б) округлить оставшиеся данные так, чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;

в) выполнить действия — сохранить все значимые цифры;

г) сохранять в результате столько значащих цифр, сколько их имеет выделенное число с наименьшим количеством верных значимых цифр.

При возведении в степень приближённого числа в результате сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа степени.

При извлечении корня из приближённого числа в результате сохраняют столько верных цифр, сколько имеет подкоренное число.

Лекции:

Уравнение сферы
Пределы: примеры решения
Площадь поверхности конуса
Целые рациональные выражения
Числовые ряды. Числовой ряд. Сумма ряда
Свойства логарифмов
Линейные дифференциальные уравнения первого порядка
Скрещивающиеся прямые
Скалярное призведение двух векторов
Теоремы, связанные с понятием производной

Источник

Загрузить PDF

В области математики и точных наук слова правильность и точность имеют численное выражение. Часто правильность и точность используют как синонимы, но они означают различные понятия. Правильность является мерой того, насколько измеренное значение близко к действительному. Точность — это мера разброса повторных измерений. Высокая точность означает высокую повторяемость результата. Высокая правильность означает высокую близость к действительному значению. Иногда следует затратить усилия, чтобы вычислить точность; в итоге получается наиболее ожидаемое значение и оценка погрешности. Ниже описано, как произвести подобные вычисления.

Шаги

1

Найдите подходящий объект для измерений, например, ручку.
2
Разграфите лист бумаги на две колонки и семь рядов для записи результатов измерений.
- Напишите «Испытание» в левой верхней ячейке и «Длина в сантиметрах» в правой верхней.
- Пронумеруйте ячейки испытаний от 1 до 5.
- Напишите «Среднее значение» в нижней левой ячейке.
3
Измерьте длину ручки пять раз до сотой доли сантиметра и запишите результаты измерений в таблицу.
- Полученные результаты будут слегка отличаться друг от друга. Например, первое значение будет равняться 12,54 см, второе — 12,57, третье — 12,52, четвертое — 12,53, и пятое — 12,55.
4
Вычислите среднее значение.
- Сложите результаты всех измерений и поделите полученную сумму на количество измерений, то есть на 5. В нашем примере средняя величина равна 12,54 см.
- Запишите вычисленное среднее значение в нижней правой ячейке таблицы.
5
Нарисуйте линию с числовыми метками, которая включала бы все результаты ваших измерений.
- Проведите на листке бумаги прямую горизонтальную линию. Нанесите на нее десять перпендикулярных ей меток. Отметьте каждую из них числом; начните с 12,50, затем следуют 12,51, 12,52, и так вплоть до 12,60.
6
Нанесите на линию результаты ваших измерений.
- Отметьте каждый результат точкой на линии.
- Полученное ранее среднее значение нанесите на линию точкой другого цвета или формы.
7
Определите интервал неопределенности.
- Возьмите среднее значение и вычтите из него минимальный результат измерений. В нашем примере получится 12,54 минус 12,52, что равняется 0,02. Повторите это для максимального результата измерений, но поменяйте среднее значение и результат местами. В нашем случае будет 12,57 минус 12,54, то есть 0,03.
- Сложите две полученных величины для определения диапазона неопределенности. В нашем примере получится 0,02 плюс 0,03, что равно 0,05. Интервал неопределенности составляет среднее значение плюс и минус полученный диапазон, то есть в нашем случае интервал равен 12,54 � 0,05 см.
8

Запишите полученное значение.
9

Готово.

Реклама

Советы

Если одно из измерений дало намного больший или меньший результат, чем все остальные, не исключайте его из последующих вычислений. Даже если это была ошибка, тем не менее это результат измерения, который следует учитывать в расчетах.
При измерении других объектов вы получите иные величины, нежели приведенные в нашем примере для ручки. Следуйте шагам, описанным в этой статье, но подставляйте измеренные вами величины.
Для более точных расчетов проведите более пяти измерений. Чем больше испытаний (измерений) вы сделаете, тем более точное значение получите.

Что вам понадобится

Лист бумаги
Ручка
Калькулятор
Измерительная линейка
Карандаш

Об этой статье

Эту страницу просматривали 8771 раз.

Была ли эта статья полезной?

Источник

Определение
2. Абсолютной погрешностью приближенного
числа а назовем величину
,
про которую известно, что

. (1.1)

Таким образом,
точное число заключено в границах

(1.2)

или сокращенно

. (1.3)

Пример 2.
Приближенные числа

получены округлением, точные значения
чисел неизвестны. Что можно сказать об
абсолютной погрешности данных приближенных
чисел?

Решение.
Пользуясь правилами округления чисел,
можно сказать, что абсолютные погрешности
приближенных чисел не превосходят
половины единицы последнего разряда,
т.е.

Кроме того,
можно записать:

Пример 3.
Округлить числа  =
3,14159265…и е = 2,71828182…до сотых и
определить абсолютную погрешность
полученных приближенных чисел.

Решение. В
силу правил округления имеем

а₁ = 3,14; а₂
= 2,72.

По определению
абсолютной погрешности

Замечание 1.
Абсолютную погрешность принято записывать
в виде числа, содержащего не более одной
или двух цифр, отличных от нуля (двух
значащих цифр).

Замечание 2.
В силу определения погрешности абсолютную
погрешность округляют до одной или двух
значащих цифр только в большую сторону
(не придерживаясь сформулированных
выше правил округления чисел).

В примере 3 в
качестве абсолютной погрешности чисел
а₁ и а₂ можно взять значения:

Абсолютная
погрешность отражает лишь количественную
сторону погрешности, но не качественную,
т.е. не показывает, хорошо или плохо
проведено измерение или вычисление.

Пример 4.
при измерении толщины и длины крышки
стола были получены результаты:

Определить, в
каком случае измерение было сделано
более качественно.

Решение.
Абсолютная погрешность измерения для
l₁ и l₂
одинакова и равна

Однако очевидно,
что измерение l₂
было проведено более качественно, чем
l₁ . Для того,
чтобы определить качество измерений и
вычислений, необходимо выяснить, какую
долю составляет абсолютная погрешность
от определяемой величины. В связи с этим
вводится понятие относительной
погрешности.

Определение
3. Относительной погрешностью

приближенного числа а называется
отношение абсолютной погрешности

к абсолютной величине приближенного
числа а:

(1.4)

В примере 4
относительные погрешности измерения
толщины и длины соответственно равны

Следовательно,
измерение длины l₂
было произведено намного качественнее.

Замечание 3.
Относительная погрешность представляет
собой безразмерную величину.

При вычислении
относительную погрешность округляют
в большую сторону и записывают в
виде числа, содержащего одну-две значащие
цифры.

1.4. Число верных знаков приближенного числа. Связь абсолютной и относительной погрешности с числом верных знаков. Правила подсчета числа верных знаков

Всякое
положительное десятичное число а
может быть единственным образом
представлено в виде конечной или
бесконечной десятичной дроби:

(1.5)

или

(1.6)

где

— десятичные цифры (),
причем

, т – некоторое число (старший разряд
числа а). Например, в десятичной
системе счисления:

Определение
4. Значащими цифрами числа а
называют все цифры в его записи (1.5)
начиная с первой слева, отличной от
нуля. Например, приводимые ниже числа
имеют следующее количество значащих
цифр:

5423,47 6 Значащих цифр,

0,0000605 3 Значащие цифры,

0,060500 5 Значащих цифр.

Как видно из
приведенных примеров, цифра 0 имеет
особое значение при определении числа
значащих цифр. Например, в числе 0,00710300
первые три нуля не являются значащими
цифрами и служат только для установления
старшего десятичного разряда числа.
Остальные три являются значащими
цифрами, так как первый из них находится
между значащими цифрами, а второй и
третий, как отражено в записи, указывают,
что в приближенном числе сохранены
десятичные разряда 10^-7 и 10^-8.
Если же в данном числе 0,00710300 последние
две цифры не являются значащими цифрами,
то это число лучше записать в виде
0,007103. Числа 0,00710300 и 0,007103 не равноценны,
так как первое из них имеет 6 значащих
цифр, а второе – только 4 значащих цифры.
Цифра 0, стоящая в конце числа, может
иметь двоякий смысл, как это видно из
следующих утверждений:

а) 1 кг = 1000 г;

б) население
США по одной из переписей составляло
195530000 человек

В первом случае
имеем точное соотношение, поэтому все
нули здесь – значащие цифры. Во втором
случае нули стоят вместо неизвестных
цифр, и число имеет только 5 значащих
цифр. Для того чтобы избежать недоразумения,
никогда не следует писать нули вместо
неизвестных цифр, а лучше применять
такую форму записи:

Пример 5.
Пусть в результате измерения получено
число, имеющее две значащие цифры, l
= 72 мм. Если этот результат, не измеряя
отрезок с большей точностью, выразить
в метрах, километрах или микронах и
написать, что l =0,072 м,
или l =0,000072 км, или l
=72000 мкм, то нули ни в первом, ни во втором,
ни в третьем случаях не будут значащими.
В дальнейшем условимся различать такие
числа, как 7,2; 7,20; 7,200.

Все они выражают
одно и то же числовое значение некоторой
величины, но определены с разным
количеством значащих цифр.

Точность
приближенного числа зависит не от
количества значащих цифр, а от количества
верных значащих цифр. Различают значащие
цифры верные в узком и широком смыслах.

Определение
5. Цифры

приближенного числа а называют
верными в узком смысле, если абсолютная
погрешность

приближенного числа а не превосходит
половины единицы (т-п+1) – го разряда,
которому принадлежит цифра
,
т.е. если

. (1.7)

Пример 6.
Оценить абсолютную погрешность
приближенного числа а = 4,483, если
известно, что оно имеет 3 верных знака
в узком смысле.

Решение. По
определению 5

В нашем случае
старший разряд числа равен 10⁰,
т.е. т = 0, а п = 3. Поэтому получаем

В математических
таблицах все числа определены до верных
значащих цифр в узком смысле. Так,
например, в четырехзначных таблицах
Брадиса В.М. гарантировано, что абсолютная
погрешность квадратных корней не
превосходит 0,5*10^-3 (так как там
приведены квадратные корни чисел от 1
до 100). В некоторых случаях, например при
получении числа путем измерения, удобнее
говорить о числе верных знаков в широком
смысле.

Определение
6. Цифры

приближенного числа а называют
верными в широком смысле, если абсолютная
погрешность

приближенного числа а не превосходит
единицы (т-п+1) – го разряда, которому
принадлежит цифра
,
т.е. если

. (1.8)

Например, если
число а = 4,483 имеет п = 3 верных
знака в широком смысле, то его абсолютная
погрешность не превосходит

Определения 5
и 6 можно обобщить.

Определение
7. Цифры

приближенного числа а называются верными
в смысле , если
абсолютная погрешность числа а не
превосходит величины
,
т.е.

. (1.9)

Определение
числа верных значащих цифр позволяет
решать и обратную задачу, т.е. определять,
какие знаки в приближенном числе верные,
а какие нет, если известна его абсолютная
погрешность.

Пример 7.
Определить, какие значащие цифры
приближенного числа а = 2,4483 будут
верными в узком (широком) смысле, если
его абсолютная погрешность равна
.

Решение.
Следуя определению числа верных значащих
цифр, для того чтобы

были верными значащими цифрами числа
а, необходимо потребовать выполнения
неравенства:

, где
,

которое в нашем
примере имеет вид

Решая неравенство
при
,
получим

а при 
= 1 получим

Таким образом,
у числа а = 2,4483 три верные цифры в
широком смысле и две – в узком. Остальные
цифры приближенного числа 2,4483 не верны.

Приведенный
способ определения числа верных значащих
цифр по известной абсолютной погрешности,
связанный с решением неравенства, можно
заменить более простым правилом: число
верных знаков в приближенном числе
отсчитывается, начиная с первой значащей
цифры числа до первой значащей цифры
его абсолютной погрешности.

Пример 8.
Определить количество верных значащих
цифр в узком и широком смысле для числа
а = 0,0076539, если
.

Решение.
Напишем абсолютную погрешность над
числом

Очевидно, что
все значащие цифры, стоящие слева перед
вертикальной чертой, проведенной перед
первой значащей цифрой погрешности,
будут всегда верными в широком смысле,
так как число, стоящее за вертикальной
чертой (в погрешности), всегда меньше
единицы разряда, стоящего слева от
черты, в данном случае

0,000037<0,0001

В нашем случае
значащие цифры 7 и 6, стоящие слева от
черты, будут верными и в узком смысле,
так как величина погрешности
0.000037<0.00005 -половины единицы разряда
десятитысячных, которому принадлежит
последняя цифра 6. Если же для числа а
= 0,0076539
,
то по этому же правилу

число будет
иметь две значащие цифры в широком
смысле слова и только одну в узком, так
как

На основании
обобщенного определения абсолютная
погрешность приближенного числа а
связана с числом верных знаков соотношением
(1.9)

В какой же
зависимости от числа верных значащих
цифр находится относительная погрешность?

Пусть приближенное
число а,

(1.10)

имеет п
верных значащих цифр в смысле определения
7.

Разделив обе
части неравенства (1.9) на выражение
(1.10), получим

т.е.

, (1.11)

где

— первая значащая цифра числа, п –
количество верных значащих цифр.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Точность и округление

Статья на тему «Математика за 20 уроков»

Раздел 1. Есть ли абсолютная точность? (00:00)

В жизни мы всё время округляем. Например, когда нас спрашивают: «Который час?», мы часто отвечаем приблизительно, потому что хотим дать ориентир по времени и плюс-минус 5 минут не так важны. Но если человек опаздывает на поезд, то ему такая точность не подойдёт, потому что ценность минуты для него существенно выше (Рис. 1).

Поэтому точность определяется целью измерения. Каждая задача имеет свою, потребную для этой задачи, точность. Для нее может быть достаточная или избыточная точность, а абсолютной точности не бывает.

И речь не только о математике: ни о чем нельзя сказать точно. Кажется, назовешь совершенно конкретный предмет, но оказывается, что ты сказал о нем неточно. Например, сказал: «Стол». Вроде бы точно. Но столы бывают разные – из какого материала он сделан? Скажем: «Деревянный стол». Возникнет вопрос: а какие у него закругления и т.д.

Может появиться возражение: «Как это нельзя? Вот, например, два одинаковых стула – это абсолютно точно» (Рис. 2).

Рис. 2. Два одинаковых стула

На самом деле неточность просто перешла в другое место. Они не идеально одинаковые, если присмотреться, то у одного есть трещина, а у другого нет и т.д.

Рис. 3. Различия в одинаковых стульях

Если же мы уточняем цель задачи описания стульев (например, нас интересует, сколько людей можно на них посадить), тогда нам не важны трещины и прочие отличия. Главное, что на обоих стульях можно сидеть, и для такой цели стулья будут одинаковыми. Можно поставить еще третий стул, и он для нашей цели будет таким же, как и предыдущие два (3 места для сидения), хотя будет выглядеть совершенно по-другому (Рис. 4).

Рис. 4. Три одинаковых стула – места для сидения

Повторим важный вывод: точность и округление зависят от задачи, которую мы решаем.

Раздел 2. Экономическая и достижимая точность (02:52)

Бывают случаи, когда точность действительно важна. К примеру, при изготовлении деталей для какой-то машины или прибора на заводе. Особенно, если эти детали производят на разных заводах и потом в отдельном месте собирают. В таком случае точность очень важна: если одна деталь будет плохо подходить к другой, то вся машина или прибор будут работать некачественно (или вообще не будут работать). С другой стороны, чем выше требования к точности, тем больше будет стоимость производства каждой из деталей и конечного продукта в целом.

Поэтому различают такие понятия, как достижимая точность и экономическая точность. Скажем, самолёт состоит из десятков тысяч деталей, они все делаются на разных заводах и должны быть подогнаны друг к другу. Грубо говоря, сидение должно поместиться в отверстие, которое было сделано под него.

Но если поставить задачу делать все детали с максимально достижимой (технически) точностью, то стоимость самолета может вырасти в разы. Поэтому говорят об экономической точности, то есть минимальной по стоимости точности обработки деталей, при которой будут достигаться необходимая эффективность (безопасность, надёжность).

Раздел 3. Ошибка при округлении в многозвенных структурах (04:10)

Есть и другой пример того, что точность может быть критически важна.

Предположим, есть две реки, которые впадают в водохранилище. Известно, что при определенном критическом уровне водного потока нужно перекрыть водосток, чтобы не допустить наводнения (Рис. 6).

Рис. 6. Реальная ситуация с водостоком в реках

Если каждый из операторов передаст округленное значение, и мы их сложим, то суммарный уровень воды окажется меньше критического, мы не будем опускать решетку и произойдет наводнение (Рис. 7).

Рис. 7. Ситуация с водостоком в реках, которую получает оператор водохранилища

В рассмотренном примере каждый из операторов округляет до десятых и в результате получается довольно большая погрешность. Если бы они передавали показания с точностью до сотых и округление мы бы выполнили только при суммировании, а затем принимали решение, то ошибки бы не было (Рис. 8).

Рис. 8. Какая точность информации о водостоке необходима

Получается, что человек, который находится во главе любой структуры (будь то директор предприятия, премьер-министр или президент), должен учитывать, какую погрешность допустили те, кто передавал ему данные.

В многозвенной системе суммарная ошибка при округлении может быть очень большой (хотя в каждом отдельном звене отклонение при округлении будет маленьким, но большое количество звеньев приведёт к накоплению), и, как следствие, может быть принято неправильное решение.

Проиллюстрируем это таким примером: мы собираем данные по школам, затем сводим их по районам, затем передаем эти данные в областные органы и т.д. В качестве собираемой информации возьмем относительно небольшую величину (например, количество медалистов). Округления на каждом из этапов могут исказить окончательные результаты кардинально. Мы можем получить отклонение в несколько процентов как в большую, так и в меньшую сторону. Соответственно, манипуляция статистическими данными возможна: если мы все сначала округлим до десятых, а потом сложим или все сложим, а затем округлим до десятых, то можем получить два существенно отличающихся результата (Рис. 9).

Рис. 9. Разные варианты округления данных по количеству медалистов

Аналогичным образом дело обстоит с системой голосования на выборах. Есть прямая система выборов президента (как, например, в России), а есть непрямая система (например, в США), с использованием выборщиков: страна разбита на какое-то количество штатов и голоса населения каждого штата представляют своими голосами определенное количество выборщиков. При этом все выборщики штата А голосуют за кандидата, который набрал в этом штате больше 50% голосов.

Фактически мы округляем голоса всех жителей штата в пользу кандидата, который набрал в этом штате большинство. Но ошибка округления при этом может сильно отличаться: если кандидат набрал 90% голосов штата, то после округления с помощью голосования выборщиков дополнительно он получит всего лишь 10%, а если 51% — то целых 49%. Учитывая, что население по штатам может быть распределено неравномерно, может возникать ситуация, при которой по стране большинство проголосовавших будет за кандидата A, а большинство выборщиков – за кандидата В, который и станет президентом (Рис. 10, 11). В 2016 году такая ситуация произошла на выборах президента США.

Рис. 10. Распределение проголосовавших и выборщиков в разных штатах

Рис. 11. Возможные результаты выборов при непрямой системе голосования

Раздел 4. Ошибки при округлении (08:59)

Существует еще один пример. Посчитаем √2 на обычном (не инженерном) калькуляторе, а затем умножим полученное число на себя. По идее должно получиться 2, однако на экране мы увидим 1,(9). Это связано с тем, что когда калькулятор считает √2, он выполняет округление (по количеству знаков, которые помещаются на экране), а умножаем на себя мы уже это округлённое число, поэтому и получаем почти 2, но не в точности 2 (Рис. 12).

Рис. 12. Ошибка округления при вычислении на калькуляторе

Поэтому, когда производят расчеты при решении физических задач, важно понимать, с какой точностью нужно выполнять каждый шаг вычислений. Часто учителя физики просят не делать промежуточные вычисления, а доводить задачу до получения рабочей формулы в общем виде, не подставляя числа (Рис. 13).

Рис. 13. Пример решения задачи по физике без промежуточных вычислений

Это один из способов обезопасить себя от ошибки округления. Выполняя промежуточные вычисления, мы будем округлять полученные промежуточные значения. Ошибка может накапливаться, и результат будет отличаться от правильного. Заранее не всегда можно угадать, с какой точностью нужно выполнять вычисления, чтобы ошибка не накопилась. Если ответ проверяет компьютер, то даже небольшая ошибка из-за промежуточных округлений может привести к тому, что ответ не будет засчитан как правильный.

Есть еще один хороший пример того, как небольшое отклонение может привести к большой суммарной ошибке. Возьмите большое количество одинаковых книг (например, Большую Советскую энциклопедию) и попробуйте выложить их одну на другую в стопку. Дойдя до определённого количества книг, мы увидим, что стопка обязательно разрушится. Это связано с тем, что вы не можете в точности сделать так, чтобы центр тяжести предыдущей книги совпадал с центром тяжести следующей (Рис. 14).

Рис. 14. Стопка из одинаковых книг

Также нет окружности, отношение длины которой к радиусу в точности равно π. Невозможно начертить такую окружность, потому что нет такой точной линейки (Рис. 15).

Окружность, по определению, – это все точки, находящиеся на одном расстоянии от заданной.

Но в самом определении содержится ошибка, если учесть точность измерения реальной линейкой. Само число π, как характеристика идеального математического объекта – окружности, содержит в себе бесконечную точность, но для практических вычислений всегда приходится округлить его с точностью до некоторого знака (например, эту точность может определять инженер, который соотносит её с точностью расчетов, которые ему надо провести).

Рис. 15. Идеальные и реальные объекты

Даже окружность, изображённая на экране компьютера, – это на самом деле большой правильный n-угольник (Рис. 16).

Рис. 16. Окружность на экране компьютера

Раздел 5. Округление и точность в литературе (13:46)

Округление и точность тесно связаны друг с другом. В жизни мы постоянно округляем, всё время действуем и говорим не совсем точно. Сколько бы мы ни говорили, высказать абсолютно точно свои мысли невозможно. С другой стороны, нам никогда абсолютно точно и не нужно этого делать. У нас всегда есть задача, которую мы в данный момент решаем, а для данной задачи всегда есть конкретная точность.

Об этом есть несколько стихотворений, которые полезно прочитать:

Silentium!

Молчи, скрывайся и таи
И чувства и мечты свои –
Пускай в душевной глубине
Встают и заходят оне
Безмолвно, как звезды в ночи, –
Любуйся ими – и молчи

Как сердцу высказать себя?
Другому как понять тебя?
Поймет ли он, чем ты живешь?
Мысль изреченная есть ложь.
Взрывая, возмутишь ключи,
Питайся ими – и молчи.

Лишь жить в себе самом умей –
Есть целый мир в душе твоей
Таинственно-волшебных дум;
Их оглушит наружный шум,
Дневные разгоняй лучи, –
Внимай их пенью – и молчи!..

Ф.И. Тютчев

Милый друг, иль ты не видишь,
Что все видимое нами –
Только отблеск, только тени
От незримого очами?

Милый друг, иль ты не слышишь,
Что житейский шум трескучий –
Только отклик искаженный
Торжествующих созвучий?

Милый друг, иль ты чуешь,
Что одно на целом свете –
Только то, что сердце сердцу
Говорит в немом привете?

В.С. Соловьёв

Существует поговорка: «Не ошибается тот, кто ничего не делает». Её можно интерпретировать следующим образом: как только ты начинаешь что-то делать, в любом случае где-то получится ошибка, не надо этого бояться.

Абсолютной точности не существует практически нигде.

Если точность не может быть абсолютно достижима, то нужно понимать, как правильно округлить. Для того чтобы общаться, нужно что-то сообщать, а значит, какую-то часть информации мы упускаем (всю информацию передать невозможно). Значит, точность определяется целью задачи, которую мы решаем.

Источник

Как найти точность приближенного значения

Количественного понятия «точность» в науке не существует. Это качественное понятие. При защите диссертаций говорят только о погрешности (например, измерений). И даже если прозвучало слово «точность», то следует иметь в виду весьма расплывчатую меру величины, обратной погрешности.

Инструкция

Небольшой анализ понятия «приблизительное значение». Возможно, что имеется в виду приблизительный результат вычисления. Погрешность (точность) здесь задает сам исполнитель работы. В таблицах эта погрешность указывается, например «до 10 в минус четвертой степени». Если же погрешность относительная – то в процентах или долях процента. Если вычисления велись на основе числового ряда (чаще всего Тейлора) – на основе модуля остаточного члена ряда.

О приблизительных значениях величин часто говорят как об оценочных их значениях. Результаты измерений случайны. Поэтому это те же случайные величины, обладающие своими характеристиками разброса значений, как та же дисперсия или с.к.о. (среднее квадратичное отклонение). В математической статистике вопросам оценок параметров посвящены целые разделы. При этом различают точечные и интервальные оценки. Последние здесь не рассматриваются. Точечную оценку некоторого параметра λ, подлежащего определению договоримся обозначать λ*. Оценки параметров просто вычисляются по каким-то формулам (статистикам), удовлетворяющим своим требованиям, называемыми критериями качества оценки.

Первый критерий называется несмещенность. Имеется в виду то, что среднее значение (математическое ожидание) оценки λ* равно ее истинному значению, то есть M[λ*]=λ. Об остальных критерия качества говорить пока не стоит. Ими иногда и пренебрегают, обосновывая вопрос тем, что самое главное, чтобы оценка достаточно «слабо» отличалась от истины. Поэтому берется основная характеристика разброса – дисперсия оценки и просто вычисляется. Если исследователь принимает самостоятельное решение, что она достаточно мала, то этим и ограничиваются.

Наиболее часто оценивается среднее значение (математическое ожидание). Это среднее выборочное, вычисляемое, как среднее арифметическое имеющихся результатов наблюдений mx*=(1/n)(x1+x2+ … +xn). Легко показать, что М[mx*]=mx, то есть mx* оценка несмещенная. Дисперсию оценки математического ожидания найдите следуя выкладкам, приведенным на рисунке 1а. Так как истинное значение Dх недоступно, взамен возьмите среднюю выборочную дисперсию (см. рис.1b).

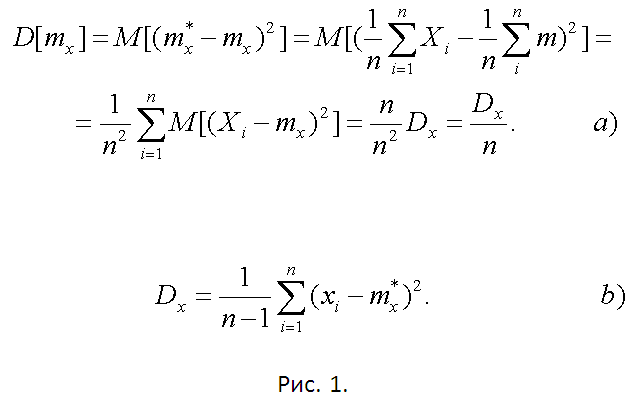
Источники:

Тихонов В.И. Статистическая радиотехника. – М.: Радио и связь, 1982. – 624 с.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Приближённые вычисления

Абсолютная и относительная погрешности

Выполнение действий над приближёнными числами

Выполнение действий без точного учёта погрешности

Шаги

Советы

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

1.4. Число верных знаков приближенного числа. Связь абсолютной и относительной погрешности с числом верных знаков. Правила подсчета числа верных знаков

5423,47 6 Значащих цифр,

0,0000605 3 Значащие цифры,

0,060500 5 Значащих цифр.

Как найти точность приближенного значения

Не пропустите также: