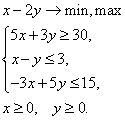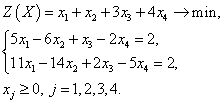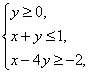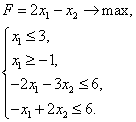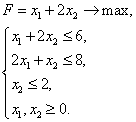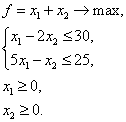Графический
метод применяется для решения задач
линейного программирования малой
размерности, когда количество искомых
переменных не более 3. На практике этот
метод применяют чаще всего для задач с
двумя переменными.
В
основе графического метода в случае
двух (трех) переменных лежат следующие
представления. Множество допустимых
планов
можно представить в виде некоторого
многогранного выпуклого множества на
плоскости (в пространстве). Оптимальное
решение, если оно существует и единственно,
лежит в угловой точке множества допустимых
решений, где пересекаются прямые
(плоскости), ограничивающие это множество.
Заметим,
что ЗЛП может не иметь решения, когда
множество допустимых планов пусто. ЗЛП
может иметь бесконечное множество
решений, в этом случае решением является
часть прямой для двумерной задачи или
часть плоскости для трехмерной.
Рассмотрим
для определенности задачу максимизации
для целевой функции, зависящей от двух
переменных:
,

Шаг
1.
Построение множества допустимых планов.
Каждое
-тое
ограничение задачи записывается как
равенство.
Геометрически полученное уравнение
определяет прямую линию, которая делит
плоскость на две полуплоскости, в одной
из которых выполняется условие
,
в другой.
Полуплоскость, для точек которой
выполняется требуемое ограничение,
назовем допустимой полуплоскостью.
Если
пересечение допустимых полуплоскостей
для всех ограничений не пусто, тогда
оно представляет собой область допустимых
решений, которая называется многоугольником
решений.
Множество точек, принадлежащих этому
многоугольнику, образует множество
допустимых планов
(1.12) исходной задачи. При условии не
отрицательности переменных многоугольник
будет лежать в первой четверти.
Шаг
2. Нахождение
оптимального плана.
Необходимо
найти точку из многоугольника решений,
в которой целевая функция принимает
максимальное значение. Если многоугольник
решений не пуст и целевая функция на
нем ограничена, такая точка всегда
найдется, причем она будет лежать в
одной из вершин построенного многоугольника
решений.
Целевая
функция может принимать одно и то же
максимальное значение в двух вершинах.
В этом случае множество оптимальных
решений представляет собой множество
точек, лежащих на прямой, соединяющей
эти точки.
Для
нахождения оптимальной точки рассмотрим
целевую функцию задачи
.
Запишем ее в виде:
,
где
.
Это
уравнение задает линии уровня целевой
функции, которые являются параллельными
прямыми линиями в пространстве переменных
.
Вектор
нормали к прямой
к линии уровня целевой функции называется
градиентом.Градиент
указывает направление возрастания
целевой функции.
Для
нахождения точки экстремума графическим
методом, необходимо сначала построить
линию уровня для некоторого произвольного
значения целевой функции. Затем
осуществить ее параллельное передвижение
в направлении градиента, если решается
задача максимизации, и в обратном
направлении, при решении задачи
минимизации. Смещение производится до
тех пор, пока не будет достигнута
«последняя» точка области допустимых
планов
.
Для задач максимизации (минимизации)
такой точке области D соответствует
наибольшее из возможных значений линии
уровня. Последнее означает, что для
нахождения точки экстремума в задаче
линейного программирования мы должны
сначала построить линию уровня для
некоторого произвольного значения
целевой функции. Затем необходимо
осуществлять ее параллельное передвижение
(так, чтобы она оставалась перпендикулярной
векторус
) до тех пор, пока не достигнем такой
точки области допустимых планов D , из
которой смещение в направлении вектора
с было бы невозможно. Такой метод
решения получил название графического
. Заметим, что решение задачи поиска
минимума линейной функции осуществляется
аналогично, с той лишь разницей, что
движение по линиям уровня должно
производиться в направлении, обратном
градиенту целевой функции, т. е. по
вектору (-с
).
Изобразим
вектор градиента на плоскости и будем
сдвигать линию уровня целевой функции
в направлении градиента. Последняя
вершина многоугольника решений, с
которой пересечется линия уровня и
будет оптимальной точкой.
Шаг
3.
Нахождение максимального значения
функции
.
Аналитически
оптимальная точка с координатами
находится как точка пересечение двух
прямых. Векторявляется оптимальным планом задачи.
Затем вычисляется значение целевой
функции в оптимальной точке.
Задача.
При производстве товаров А и В используются
три вида ресурсов: R1,
R2, R3.
Сведения о количестве ресурсов,
необходимых для производства единицы
каждого товара, запасе ресурсов и ценах,
по которым товары продаются, приведены
в табл. 1.3. Найдите оптимальный план,
максимизурующий доход.
|
Таблица |
|||
|
Товары |
|||
|
Ресурсы |
A |
B |
Запас |
|
R1 |
2 |
1 |
60 |
|
R2 |
4 |
5 |
140 |
|
R3 |
2 |
4 |
100 |
|
Цена |
3 |
5 |
1).
Искомые переменные задачи:
—объем
производства товара А (шт.);
—объем
производства товара B
(шт.);
2).
Ограничения задачи.
а)
Ограничения на ресурсы. Расход используемых
ресурсов не должен превышать их запас.
,
(ресурс R1),
,
(ресурс R2), (1.13)
,
(ресурс
R3).
b)
Ограничения на знак. Объемы производства
товаров не могут быть отрицательными:
,
.
3).
Целевая функция
максимизирует
доход компании.
Запишем
математическую постановку задачи
максимизации в стандартном виде, в
скобках указаны номера ограничений:
Шаг
1.
Построение множества допустимых планов.
Рассмотрим
первое ограничение
,
запишем его в виде уравнения,
которое задает прямую линию на плоскости.
Построим уравнение этой прямой линии
в прямоугольной системе координат.
Для этого найдем пересечение данной
прямой с осями координат.
Пусть
,
подставив это значение в уравнение
прямой найдем.
Аналогично, пусть,
подставив это значение в уравнение
прямой найдем.
Прямая проходит через две точки с
координатамиAи В
.
Проведем прямую.
Определим
допустимую полуплоскость методом
пробной точки. Возьмем точку в начале
координат
и подставим в первое ограничение, получим
верное неравенство.
Следовательно, начало координат
принадлежит допустимой полуплоскости.
В качестве пробной точки можно взять
любую точку на плоскости, не принадлежащую
данной прямой.
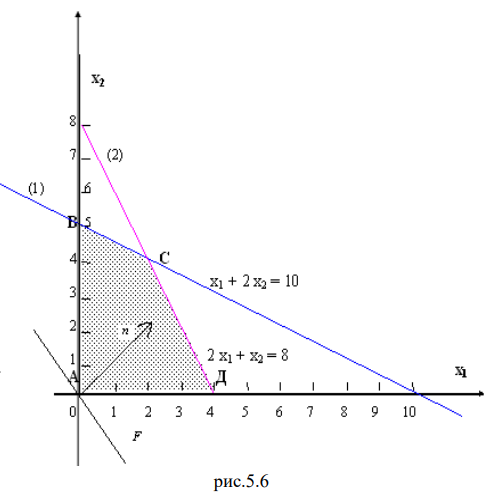
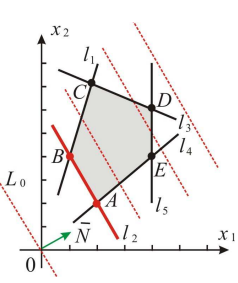
Рис.
1.1. Допустимая полуплоскость для
ограничения (1)
Аналогично
построим допустимые полуплоскости для
ограничений (2) и (3). Условия неотрицательности
переменных (4) ограничивают область
допустимых планов первой четвертью.
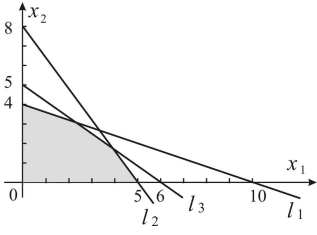
В
результате будет построена искомая
область допустимого плана
,
которая ограничена многоугольникомOACDE
(рис. 1.2). Для точек
выполняются все ограничения задачи.
Осталось
найти точку, в которой целевая функция
примет наибольшее значение.
Рис.
1.2. Область допустимого плана OACDE
Шаг
2. Нахождение
оптимального плана.
Найдем
оптимальный план, то есть точку из
многоугольника решений OACDE,
в которой целевая функция принимает
максимальное значение. Так как полученный
многоугольник решений не пуст и ограничен,
искомая точка лежит в одной из вершин
этого многоугольника.
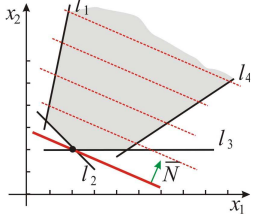
Построим
градиент целевой функции
,
он указывает направление возрастания
целевой функции. Любой вектор, коллинеарный
градиентутакже будет указывать направление
возрастания целевой функции, по этому,
при необходимости векторможно растянуть или перенести параллельно
самому себе (рис. 1.3).
Построим
линии уровня целевой функции
,
где— константа. Линии уровня представляют
собой прямые линии, перпендикулярные
градиенту. Придавая константеразличные значения, будем передвигать
их в направлении градиента. Последняя
вершина многоугольника решений, с
которой пересечется линия уровня целевой
функции и будет оптимальной точкой.
Рис.
1.3. Направление градиента указано
пунктиром
На
рис. 1.4. изображены пунктиром линии
уровня для трех значений константы
.
Видно, что оптимальному плану соответствует
точка D.
Рис.
1.4. Поиск оптимальной точки
Оптимальная
точка D
является пересечением двух прямых,
соответствующих ограничениям (2) и (3).
Поэтому координаты оптимальной точки
определяются как решения системы
линейных алгебраических уравнений
(СЛАУ):

Найдем
решение СЛАУ (1.14). Второе уравнение можно
разделить на 2, получим:
Выразим
из второго уравнения
и подставим в первое уравнение.
Решим
первое уравнение, получим
,
найдем.
Оптимальный
план
.
Оптимальное значение целевой функции
(доход) составиту.е.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Введение в графический метод
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.
Возможно эта страница вам будет полезна:
Задача линейного программирования в стандартной форме с двумя переменными имеет вид:
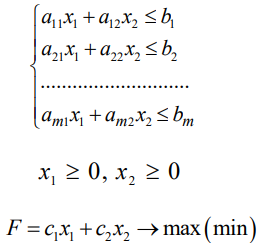
Эти задачи допускают простое геометрическое истолкование.
Рассмотрим вначале геометрическое истолкование системы ограничений задачи. Каждую совокупность значений переменных 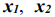


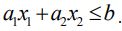
Рассмотрим прямую на плоскости с уравнением:
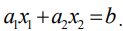
Эта прямая делит плоскость на две полуплоскости, в одной из которых справедливо наше неравенство, а в другой — противоположное. Для того чтобы проверить, какая из полуплоскостей состоит из решений нашего неравенства, следует взять точку из какой-либо полуплоскости и проверить, выполняется ли наше неравенство в этой точке. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. Для системы из нескольких таких неравенств точки, координаты которых удовлетворяют всем неравенствам одновременно, должны находиться во всех соответствующих полуплоскостях, т. е. принадлежать теоретико-множественному пересечению этих полуплоскостей. Множество точек на плоскости, удовлетворяющих системе ограничений, составляет, таким образом, некоторую выпуклую многоугольную область (область допустимых решений). Условия неотрицательности переменных 
При решении двумерных задач линейного программирования возможны следующие ситуации (ОДР — область допустимых решений):
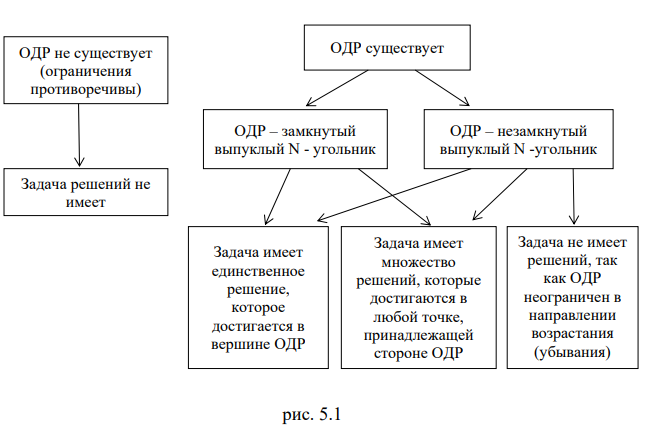
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция 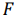
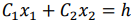
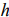
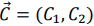
Отметим, что при нахождении решения задачи (5.1)-(5.3) могут встретиться случаи, изображенные на рис. 5.2- 5.5. Рис.5.2 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке 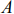
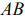
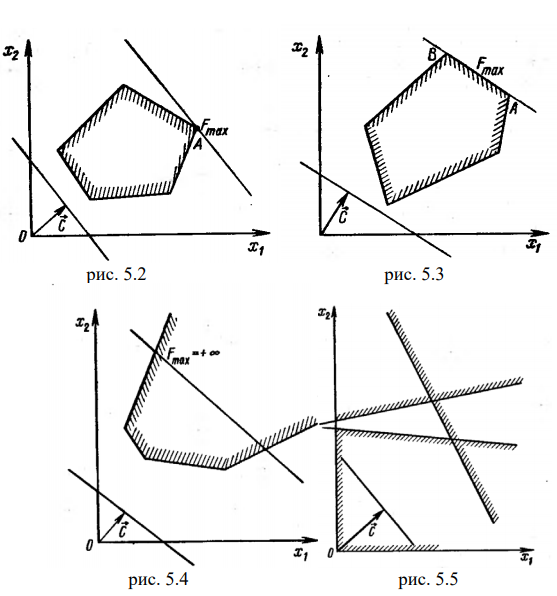
Также отметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня 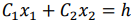
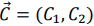
Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
Алгоритм графического метода решении задач линейного программирования
- Построить область допустимых решений.
- Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, построить нормаль линий уровня
и одну из линий уровня, имеющую общие точки с этой областью.
- Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум — в противоположном направлении.
- Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
- Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.
Пример задачи №1
Пусть имеется два станка 


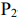
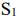
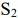

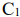
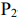
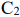

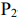
Решение:
Для наглядности сведем условие задачи в таблицу 5.1.
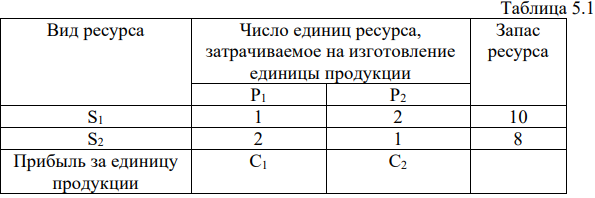
Составим математическую модель задачи. Обозначим через 


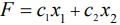


Переменные 

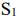
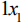
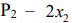
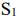


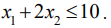
Аналогично можно получить неравенство для станка 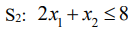


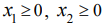
по смыслу задачи. Такие задачи кратко записываются следующим образом:
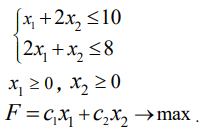
Итак, математическая модель задачи: найти такой план выпуска продукции 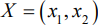
Решения, удовлетворяющие системе ограничений (5.4) и требованиям неотрицательности (5.5), являются допустимыми, а решения, удовлетворяющие одновременно и требованию (5.6) — оптимальными.
Рассмотрим геометрическое истолкование задачи:
Возьмем 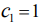
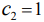
Математическая модель задачи:
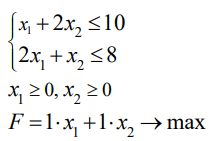
Построение области допустимых решений целевой функции 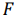
1.Построим прямоугольную систему координат. Так как, 

Рассмотрим первое ограничение:
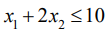
Рассмотрим второе ограничение:
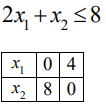
Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют данным ограничениям.
Двумерные задачи линейного программирования решаются графически.
Для случая 
В общем виде, когда в задаче участвуют 
Для решения ЗЛП любой размерности существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
Графический метод решения задач линейного программирования
Множество решений системы ограничений задачи ЛП образует область допустимых решений (ОДР).
Графический метод решения задач ЛП основывается на возможности графического изображения ОДР и нахождении среди них оптимального решения. Этот метод применяется для задач ЛП с одной, двумя или тремя переменными, для которых система ограничений стандартна (состоит из неравенств), и задач со многими переменными, для которых система ограничений содержит 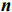
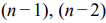
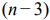
ОДР задачи строится как пересечение областей решений каждого из ограничений и представляет собой выпуклый многогранник (многоугольник, интервал). Область допустимых решений может содержать бесконечное число точек. Для того чтобы найти решение ЗЛП, нужно рассмотреть поведение целевой функции в ОДР.
I. Одномерное пространство переменных
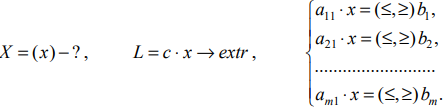
Решение системы ограничений есть пересечение лучей, что определяет интервал решений (ОДР): точку, отрезок, луч или всю числовую прямую.
Значения целевой функции в угловых точках интервала решений определяют наименьшее (наибольшее) значение исследуемой целевой функции, монотонно убывающей (если 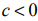
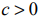
В случае неограниченности ОДР задача ЛП может и не иметь оптимума.
II. Двумерное пространство переменных
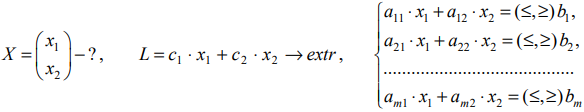
Областью решений линейного неравенства
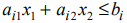
является одна из полуплоскостей, на которые прямая делит всю координатную плоскость. Для того, чтобы определить, какая из двух координатных полуплоскостей является областью допустимых решений неравенства, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку; если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.
Решение системы ограничений есть пересечение полуплоскостей с граничными прямыми
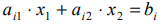
многоугольник решений (ОДР).
Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение
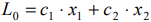
задаёт семейство линий уровня исследуемой целевой функции 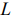
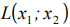
Замечание.
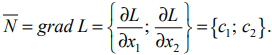
Т. о., если линию уровня 


• Прямая
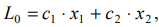
имеющая с многоугольником решений, расположенным по одну сторону от неё, хотя бы одну общую точку, называется опорной. ОДР любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
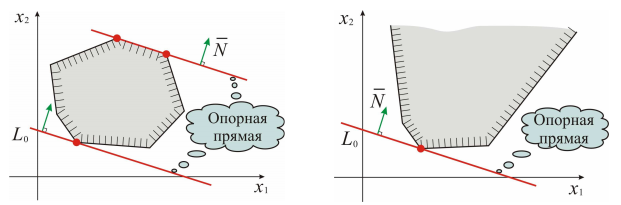
Значение 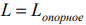
Графически опорная прямая определяет оптимум целевой функции в угловой точке многоугольника решений. Поэтому перебором значений целевой функции во всех угловых точках можно так же выбрать искомый оптимум.
Замечание. Если заданы ограничения неотрицательности переменных, то все построения проводятся в первой четверти.
Особые случаи

Алгоритм графического метода решения задач линейного программирования с двумя переменными
- Находим область допустимых решений из системы ограничений. Если ОДР является пустым множеством, то задача ЛП неразрешима (не имеет решения) в виду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, строим направляющий вектор
прямой
и параллельно ему проводим линию уровня
.
- Строим вектор нормали
перпендикулярно прямой
.
- Линию уровня
перемещаем до положения опорной прямой в направлении вектора
для задач на максимум или в направлении, противоположном
для задач на минимум. Т. е. перемещение проводится до тех пор, пока линия уровня не коснется области допустимых решений. Общая точка (точки) будет точкой экстремума (оптимума) целевой функции в ОДР.
- Находим координаты точки экстремума и значение целевой функции в ней, т. е. оптимум задачи ЛП.
Пример задачи №2
Найти 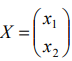
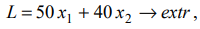
если имеются ограничения:
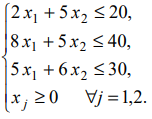
Решение:
Система ограничений определяет граничные прямые:
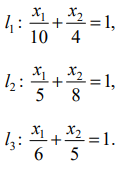
С учётом исходной системы неравенств строим ОДР.
Прямая
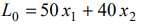
имеет вектор нормали 
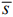
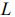
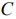
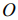
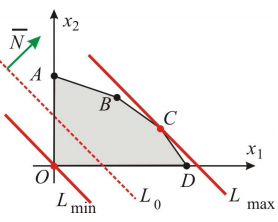
Т. о. имеем:
Тогда
Ответ:
Пример задачи №3
Найти план
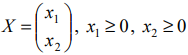
при котором:
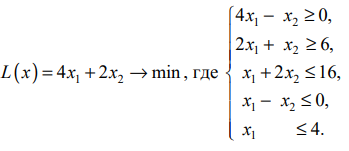
Решение:
Строим ОДР, проводим линии уровня 
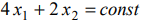
и вектор 
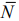
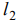
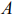
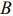
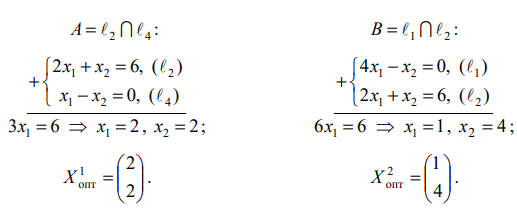
Общее решение (выпуклая линейная комбинация точек отрезка 
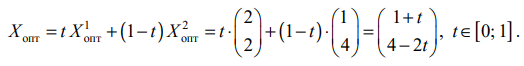
Вычисляем
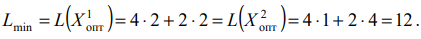
Ответ:
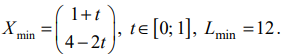
Пример задачи №4
Найти план
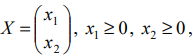
при котором
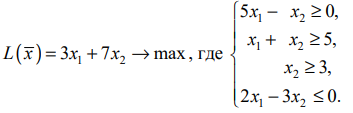
Решение:
Строим ОДР, проводим линию уровня 
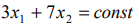
и вектор 
Таким образом, задача ЛП не имеет решения в виду неограниченности целевой функции.
Пример задачи №5
Найти план
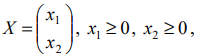
при котором
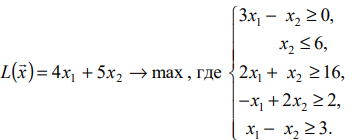
Решение:
Строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств. Область допустимых решений задачи является пустым множеством. Задача не имеет решения в виду несовместности системы ограничений.
III. Трёхмерное пространство переменных
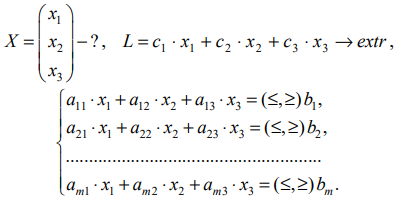
Решение системы ограничений — многогранник решений (ОДР) — пересечение полупространств с граничными плоскостями
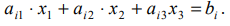
Уравнение
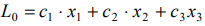
задаёт семейство поверхностей уровня функции 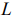
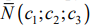
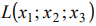
Плоскость
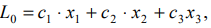
имеющая с многогранником решений, расположенным по одну сторону от нее, хотя бы одну общую точку, называется опорной. Значение 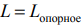
Графический метод в виду большой размерности реальных практических задач ЛП достаточно редко применяется, однако он позволяет уяснить одно из основных свойств ЛП- если в задаче ЛП существует оптимальное решение, то, по крайней мере, одна из вершин допустимой области определяет собой оптимальное решение.
IV. С помощью графического метода может быть решена основная ЗЛП, система ограничений (уравнений) которой удовлетворяет условию 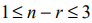
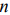
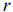
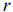
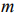
Основной случай: система ограничений содержит 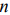
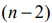
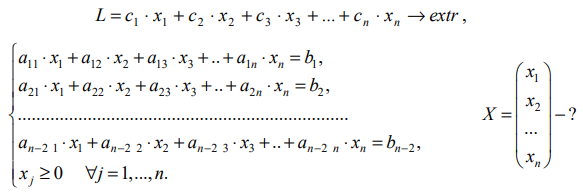
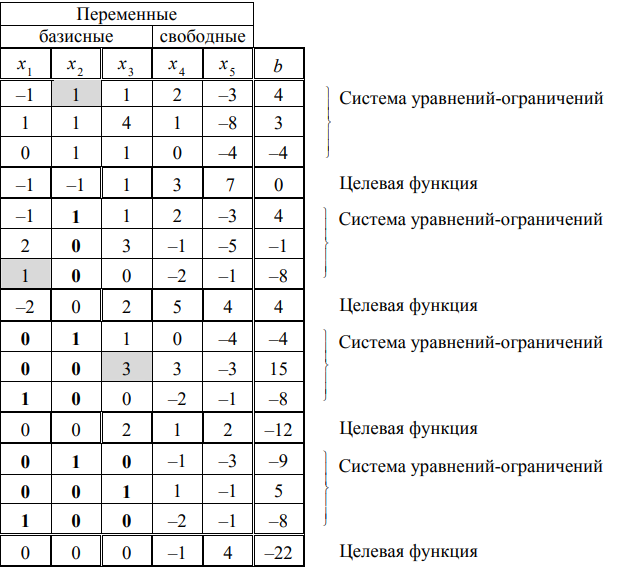
Расширенную матрицу системы с помощью элементарных преобразований строк можно привести к виду:
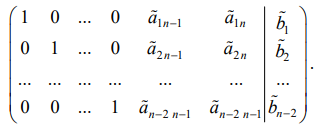
Тогда соответствующая система уравнений примет вид:
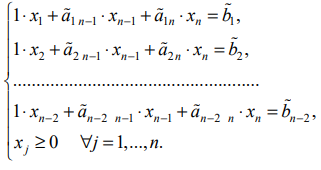
Выражая базисные неизвестные 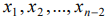
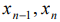
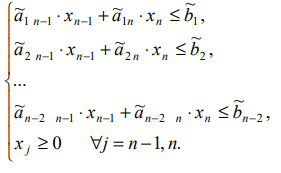
Подставляя полученные выражения для базисных неизвестных в целевую функцию, получим:
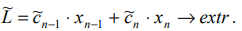
Преобразованная задача ЛП содержит только два неизвестных. Следовательно, возможен графический способ её решения на плоскости.
Найденное решение 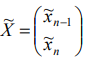
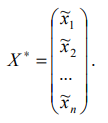
При этом оптимум:
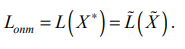
Пример. Решить задачу ЛП:
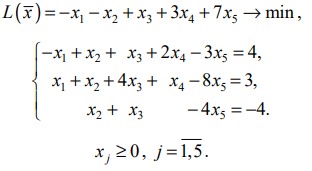
Решение. Метод применим,так как 
Используя последнюю часть табл., запишем задачу ЛП в преобразованном виде:
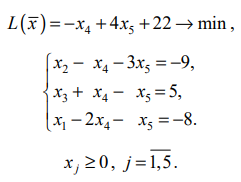
Отбросим в уравнениях-ограничениях неотрицательные базисные переменные 
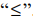
Получим вспомогательную задачу ЛП с двумя переменными:

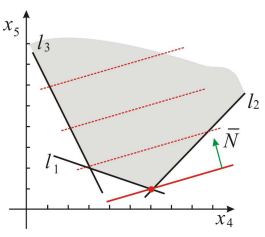
Решаем задачу графическим методом. Свободный член 22 в целевой функции не влияет на отыскание оптимального решения и учитывается только при вычислении значения целевой функции.
Находим оптимальное решение вспомогательной задачи 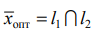
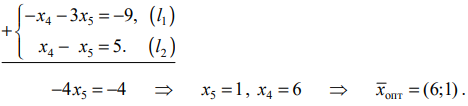
Вычисляем минимальное значение целевой функции
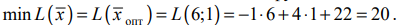
Находим оптимальное решение исходной задачи:
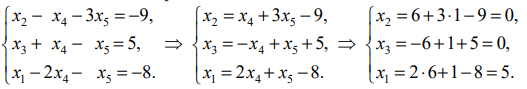
Т. о., получаем:
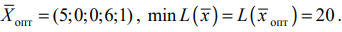
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюЛинейное программирование в ExcelКурсовая работа по линейному программированию
Управление производством предполагает постоянное принятие решений. Каждое принятое решение выбирается из определенного множества допустимых альтернатив. Задача менеджмента в данном случае состоит в том, чтобы выбрать оптимальное решение, то есть то решение, которое по определенным признакам предпочтительнее остальных. Решение будет считаться оптимальным, если оно приведет к максимально возможному положительному эффекту (например, росту прибыли предприятия).
Одним из методов, позволяющих найти оптимальное решение среди всего множества допустимых решений, является исследование операций. Исследование операций — один из разделов прикладной математики, суть которого заключается в поиске максимума (минимума) целевой функции, с учетом всех имеющихся ограничений. Суть экономики предприятия заключается в максимизации прибыли, с учетом ограниченности ресурсов, которыми располагает организация. Этим обусловлена применимость методов исследования операций в решении задач организации производственного процесса на предприятии. В экономике предприятия такие задачи называются задачами распределения ресурсов (или задачами оптимизации).
Рассмотрим пример, как можно применять методы исследования операций для решения производственных задач и как можно ускорить данный процесс путем применения встроенных возможностей MS Excel.
Предположим, автосервисное предприятие разработало для клиентов сезонные стимулирующие акции, суть которых заключается в том, что клиент, заплатив фиксированную сумму, получает целый пакет услуг по подготовке автомобиля к летнему сезону. Всего клиентам предложено два вида пакетов услуг:
1) пакет «Чистое стекло» стоимостью 3600 руб., в который входит комплекс работ по диагностике и осмотру автомобиля, очистка внутренней поверхности стекол автомобиля с применением специального спрея (плюс один флакон спрея в подарок); заливка в омывательный бачок стеклоочищающей жидкости (плюс одна бутыль стеклоочищающей жидкости в подарок);
2) пакет «Свежий воздух» стоимостью 4300 руб., в который входит комплекс работ по диагностике и осмотру автомобиля, включая работы по очистке и дезинфекции кондиционера автомобиля с применением специального средства; очистка внутренней поверхности стекол автомобиля с применением специального спрея; заливка в омывательный бачок стеклоочищающей жидкости.
В табл. 1 представлен комплекс работ по диагностике и осмотру автомобиля (количество нормо-часов).
|
Таблица 1. Комплекс работ по диагностике и осмотру автомобиля (количество нормо-часов) |
||
|
Работа |
Пакет «Чистое стекло» |
Пакет «Свежий воздух» |
|
Проверка уровня моторного масла |
0,10 |
0,10 |
|
Проверка уровня и плотности охлаждающей жидкости |
0,10 |
0,10 |
|
Проверка уровня тормозной жидкости |
0,10 |
0,10 |
|
Проверка состояния салонного фильтра |
0,10 |
0,10 |
|
Визуальный контроль герметичности агрегатов |
0,10 |
0,10 |
|
Визуальная проверка состояния тормозных дисков и колодок |
0,35 |
0,35 |
|
Проверка тормозной системы на испытательном стенде |
0,35 |
0,35 |
|
Корректировка давления в шинах |
0,25 |
0,25 |
|
Функциональная проверка стеклоочистителей и стеклоомывателей |
0,25 |
0,25 |
|
Проверка резиновых щеток стеклоочистителя на износ и наличие трещин |
0,10 |
0,10 |
|
Проверка состояния радиатора охлаждения на предмет загрязнения |
0,10 |
0,10 |
|
Проверка и корректировка фар |
0,15 |
0,15 |
|
Проверка заряда аккумуляторной батареи |
0,15 |
0,15 |
|
Короткий тест с помощью диагностической программы |
0,30 |
0,30 |
|
Очистка и дезинфекция кондиционера |
1,10 |
|
|
Итого |
2,50 |
3,60 |
Таким образом, данные два пакета услуг отличаются друг от друга тем, что в первый пакет дополнительно входит подарок в виде одного флакона спрея для внутренней очистки стекол и одной бутыли стеклоочищающей жидкости, а во второй — проведение работ по очистке и дезинфекции кондиционера с применением специального средства.
Проведение сезонных акций позволяет предприятию решить целый ряд задач:
1. Привлечение клиентов.
2. Сбыт залежавшихся сезонных товаров (автохимия).
3. Загрузка механиков.
4. Получение дополнительной прибыли.
По задумке менеджмента организации, количество пакетов ограничено:
-
во-первых, акция будет продолжаться до тех пор, пока не кончатся складские остатки участвующей в акции автохимии;
-
во-вторых, срок проведения акции органичен одним месяцем (апрелем);
-
в-третьих, на выполнение сервисных мероприятий могут быть задействованы только четыре механика.
Таким образом, ресурсы, выделяемые на проведение данной акции, ограничены. Ограничения по ресурсам на проведение сезонной акции представлены в табл. 2.
|
Таблица 2. Ограничения по ресурсам на проведение сезонной акции |
|||
|
Задействованные ресурсы |
Расход ресурсов |
Запас ресурсов |
|
|
пакет «Чистое стекло» |
пакет «Свежий воздух» |
||
|
Работа механика, ч |
2,5 |
3,6 |
616 |
|
Спрей для очистки внутренней поверхности стекла, уп. |
2 |
1 |
320 |
|
Стеклоомывающая жидкость, уп. |
2 |
1 |
260 |
|
Жидкость для очистки и дезинфекции кондиционера, уп. |
0 |
1 |
150 |
На проведение сезонной акции может быть выделено не более:
- 320 флаконов спрея для очистки внутренней поверхности стекла;
- 260 бутылей стеклоомывающей жидкости;
- 150 бутылей жидкости для очистки и дезинфекции кондиционера.
К тому же ограничено время работы механиков: в апреле 22 рабочих дня, продуктивный рабочий день механика — 7 ч в день. Следовательно, располагаемый фонд рабочего времени четырех механиков равен 616 ч (4 × 22 × 7).
Всего на один пакет «Чистое стекло» необходимо затратить:
- 2,5 ч работы механика;
- 2 флакона спрея для очистки внутренней поверхности стекла (один использовать, один — в подарок);
- 2 бутыли стеклоомывающей жидкости (одну использовать, одну — в подарок).
На пакет «Свежий воздух» необходимо затратить:
- 3,6 ч работы механика;
- 1 флакон спрея для очистки внутренней поверхности стекла;
- 1 бутыль стеклоомывающей жидкости и одну бутыль жидкости для очистки и дезинфекции кондиционера.
Ограничение по ресурсам является одним из условий задачи исследования операций. Характерной особенностью исследования операций является системный подход. В связи с этим существующие ограничения по ресурсам можно представить в виде системы уравнений. Для начала введем обозначения для переменных нашей задачи:
-
X1 — количество пакетов «Чистое стекло»;
-
Х2 — количество пакетов «Свежий воздух»;
-
A — количество часов механика;
-
B — количество флаконов спрея для внутренней очистки стекол;
-
C — количество бутылей стеклоомывающей жидкости;
-
D — количество бутылей жидкости для очистки и дезинфекции кондиционеров.
Далее нужно определиться с ограничениями, которым должны удовлетворять переменные нашей задачи:
1) во-первых, количество пакетов не может быть отрицательным: Х1, Х2 ≥ 0;
2) во-вторых, расход ресурсов не должен превышать имеющиеся запасы. Это можно выразить при помощи неравенств:
-
по ресурсу А: 2,5 × Х1 + 3,6 × Х2 ≤ 616;
-
по ресурсу В: 2 × Х1 + 1 × Х2 ≤ 320;
-
по ресурсу С: 2 × Х1 + 1 × Х2 ≤ 260;
-
по ресурсу D: 0 × Х1 + 1 × Х2 ≤ 150.
Затем следует определиться с целевой функцией (направлением для оптимизации). Логично было бы распределить квоту на оказание пакетов услуг таким образом, чтобы предприятие получило максимальную прибыль. Для этого нужно рассчитать, сколько прибыли приносит продажа одного пакета услуг, то есть сопоставить цену реализации пакета и стоимость затрачиваемых ресурсов. Как уже говорилось выше, стоимость пакета «Чистое стекло» составляет 3600 руб., а пакета «Свежий воздух» — 4300 руб. Данные суммы необходимо сопоставить с затратами на выполнение услуг:
-
тарифная часовая ставка механика составляет 350 руб. за нормо-час (включая налоги и взносы с ФОТ);
-
стоимость флакона жидкости для очистки внутренней поверхности стекла — 661 руб.;
-
стоимость бутыли стеклоочищающей жидкости — 250 руб.;
-
стоимость бутыли жидкости для очистки и дезинфекции кондиционеров — 1589 руб.
Расчет прибыли от реализации каждого из пакетов на основании имеющихся данных представлен в табл. 3.
|
Таблица 3. Прибыль от реализации пакетов услуг, руб. |
|||
|
Ресурс |
Цена ресурса |
Пакет «Чистое стекло» |
Пакет «Свежий воздух» |
|
Затраты на оплату труда механика |
350,00 |
875,00 |
1260,00 |
|
Затраты на спрей для очистки стекол |
661,00 |
1322,00 |
661,00 |
|
Затраты на стеклоомывающую жидкость |
250,00 |
500,00 |
250,00 |
|
Затраты на жидкость для очистки и дезинфекции кондиционера |
1589,00 |
0,00 |
1589,00 |
|
Итого затраты на пакет |
2697,00 |
3760,00 |
|
|
Стоимость пакета |
3600,00 |
4300,00 |
|
|
Прибыль от продажи пакета |
903,00 |
540,00 |
Итак, продажа одного пакета «Чистое стекло» принесет предприятию 903 руб. прибыли, а пакета «Свежий воздух» — 540 руб.
Целевая функция (Z) в данном случае примет вид:
Z = 903 × Х1 + 540 × Х2.
Задача — найти максимум целевой функции с учетом существующих ограничений:
-
2,5 × Х1 + 3,6 × Х2 ≤ 616;
-
2 × Х1 + 1 × Х2 ≤ 320;
-
2 × Х1 + 1 × Х2 ≤ 260;
-
1 × Х2 ≤ 150;
-
Х1, Х2 ≥ 0.
Решим эту задачу, используя симплекс-метод. Симплекс-метод представляет собой алгоритм решения оптимизационной задачи линейного программирования путем перебора вершин выпуклого многогранника в многомерном пространстве. Дело в том, что представленная система уравнений имеет бесконечное множество решений. Если представить это множество графически, то получится многогранник, в одной из вершин которого находится оптимальное решение. Симплекс-метод как раз и заключается в нахождении исходной вершины множества допустимых решений, в последовательном переходе от одной вершины к другой, ведущий к оптимизации значения целевой функции.
Для решения нашей задачи симплекс-методом ее нужно привести к так называемому стандартному виду: преобразовать неравенства нашей системы ограничений в равенства, добавив в левую часть каждого из уравнений неотрицательные числа (назовем их Х3, Х4, Х5 и Х6), которые называются балансовыми переменными (переменные Х1 и Х2 называются свободными). Получится следующая система уравнений:
-
2,5 × Х1 + 3,6 × Х2 + Х3 = 616;
-
2 × Х1 + 1 × Х2 + Х4 = 320;
-
2 × Х1 + 1 × Х2 + Х5 = 260;
-
1 × Х2 + Х6 = 150;
-
Х1, Х2, Х3, Х4, Х5, Х6 ≥ 0.
Решить поставленную задачу симплекс-методом удобнее всего с помощью симплекс-таблицы. Этапы поиска оптимального решения следующие:
построение первой симплекс-таблицы;
последовательное преобразование симплекс-таблиц по определенному алгоритму, до выполнения определенных условий.
Последовательное преобразование симплекс-таблиц и будет означать переход из одной точки множества допустимых решений в другую, до тех пор, пока не будет найдено оптимальное решение. Прежде чем составить первую симплекс-таблицу, необходимо преобразовать целевую функцию в следующий вид:
Z – 903 × Х1 – 540 × Х2 = 0.
Теперь строим первую симплекс-таблицу. Столбцами будут переменные Х1–Х6, а строками — имеющиеся ресурсы (А, В, С, D). На пересечении строки и столбца находятся коэффициенты перед переменными по каждому виду ресурса в нашей системе ограничений. Так, по строке А (время работы механиков) в столбце Х1 будет стоять коэффициент 2,5; в столбце Х2 — 3,6; в столбце Х3 — 1, а в Х4–Х6 — 0.
Также вводится дополнительный столбец (назовем его b), в котором стоят ограничения по каждому из ресурсов. После этого вводится дополнительная строка Е, в которой содержатся коэффициенты в нашей целевой функции (Z – 903 × Х1 – 540 × Х2 = 0). Получилась следующая симплекс-таблица, представленная в табл. 4.
|
Таблица 4. Первая симплекс-таблица |
|||||||
|
Ресурс |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
b |
|
A |
2,5 |
3,6 |
1 |
0 |
0 |
0 |
616 |
|
B |
2 |
1 |
0 |
1 |
0 |
0 |
320 |
|
C |
2 |
1 |
0 |
0 |
1 |
0 |
260 |
|
D |
0 |
1 |
0 |
0 |
0 |
1 |
150 |
|
Е |
–903 |
–540 |
0 |
0 |
0 |
0 |
0 |
Значение функции Z равно числу, стоящему в правом нижнем углу табл. 4. Последующее преобразование симплекс-таблицы связано с выбором разрешающей строки и разрешающего столбца.
Разрешающим столбцом является тот столбец, у которого коэффициенты в целевой функции (строка Е) являются отрицательными и наибольшими по модулю. В данной таблице это будет столбец Х1, у которого по строке Е стоит значение –903. Следует заметить, что преобразование симплекс-таблиц будет происходить до тех пор, пока в строке Е не останется отрицательных значений.
Теперь нужно найти разрешающую строку. Она определяется путем нахождения минимального отношения коэффициентов в столбце b к соответствующим коэффициентам разрешающего столбца (за исключением нулевых и отрицательных элементов, по которым соотношение не определяется).
Для нашей первой симплекс-таблицы разрешающей будет строка С, так как именно в ней наименьшее соотношение элемента столбца b и элемента разрешающего столбца Х1 (260 / 2 = 130). Элемент таблицы, который находится на пересечении разрешающего столбца и разрешающей строки, называется разрешающим элементом (в табл. 4 ячейка данного элемента выделена цветом).
После нахождения разрешающего элемента производится процедура симплекс-преобразования. Цель данной процедуры — сделать разрешающий элемент равным единице, а все остальные элементы разрешающего столбца — нулевыми.
Преобразование осуществляется определенными методами:
1) разрешающую строку можно делить и умножать на любое число;
2) к любой строке можно прибавлять или отнимать соответствующие элементы разрешающей строки, поделенные или умноженные на любое число.
Выполним предложенные преобразования. Чтобы приравнять разрешающий элемент к единице, разделим все элементы разрешающей строки на 2. Затем из элементов строки А отнимем элементы разрешающей строки С, умноженные на 2,5. Далее из элементов строки В отнимем элементы разрешающей строки С, умноженные на 2. Со строкой D никаких преобразований не производим (в разрешающем столбце итак стоит нулевое значение). К элементам строки Е прибавляем элементы разрешающей строки С, умноженные на 903. Получилась вторая симплекс-таблица, которая представлена в табл. 5.
|
Таблица 5. Вторая симплекс-таблица |
|||||||
|
Ресурс |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
b |
|
A |
0 |
2,35 |
1 |
0 |
–1,25 |
0 |
291 |
|
B |
0 |
0 |
0 |
1 |
–1 |
0 |
60 |
|
C |
1 |
0,5 |
0 |
0 |
0,5 |
0 |
130 |
|
D |
0 |
1 |
0 |
0 |
0 |
1 |
150 |
|
Е |
0 |
–88,5 |
0 |
0 |
451,5 |
0 |
117 390 |
Повторяем ту же процедуру, что и с табл. 4. Для начала находим разрешающий столбец (с наибольшим по модулю отрицательным коэффициентом перед целевой функцией). Разрешающим в данном случае будет столбец Х2. Далее находим разрешающую строку. Это будет строка А, так как для нее выполняется условие минимальности соотношения элемента столбца b к соответствующему элементу разрешающего столбца Х2 (291 / 2,35 = 123,83).
Элемент на пересечении строки А и столбца Х2 будет разрешающим. Выполняем преобразование разрешающего элемента в единицу, а остальных элементов столбца Х2 в нули. Все элементы строки А делим на 2,35. Со строкой В никаких преобразований не производим (в разрешающем столбце и так стоит нулевое значение). Из элементов строки С отнимем элементы разрешающей строки А, умноженные на 0,5 и деленные на 2,35. Из элементов строки D отнимем элементы разрешающей строки А, деленные на 2,35. К элементам строки Е прибавляем элементы разрешающей строки А, умноженные на 88,5 и деленные на 2,35. Получилась третья симплекс-таблица, которая представлена в табл. 6.
|
Таблица 6. Третья симплекс-таблица |
|||||||
|
Ресурс |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
b |
|
A |
0 |
1 |
0,426 |
0 |
–0,532 |
0 |
123,8298 |
|
B |
0 |
0 |
0 |
1 |
–1 |
0 |
60 |
|
C |
1 |
0 |
–0,213 |
0 |
0,766 |
0 |
68,0851 |
|
D |
0 |
0 |
–0,426 |
0 |
0,532 |
1 |
26,1702 |
|
Е |
0 |
0 |
37,660 |
0 |
404,426 |
0 |
128 348,94 |
В полученной симплекс-таблице в строке Е, содержащей коэффициенты целевой функции, нет отрицательных значений, следовательно вычисление завершено. Значения переменных Х1 и Х2 расположены в столбце b на тех строках, в которых в столбцах Х1 и Х2 стоят единицы. Соответственно, Х1 = 68,0851, а Х2 = 123,8298. Значение целевой функции при таких переменных будет равно:
Z = 903 × 68,0851 + 540 × 123,8298 = 128 348,94.
Полученная сумма — это максимальная прибыль предприятия от продажи пакетов. Однако следует заметить, что при решении поставленной задачи не была учтена одна существенная оговорка. Дело в том, что количество проданных сезонных пакетов может быть лишь целым числом (автосервис не может продать часть пакета услуг).
Существует ряд приемов, которые позволяют вводить в задачу оптимизации условие целочисленности переменных за счет ввода дополнительных ограничений системы. Однако современному специалисту проще решать данную задачу, используя инструмент MS Excel — «Поиск решения», который позволяет не только находить оптимальное решение задачи, но и делать его таковым, чтобы оно удовлетворяло условию целочисленности переменных.
Покажем это на наглядном примере. Для начала следует ввести все данные задачи в рабочий лист MS Excel (рис. 1).
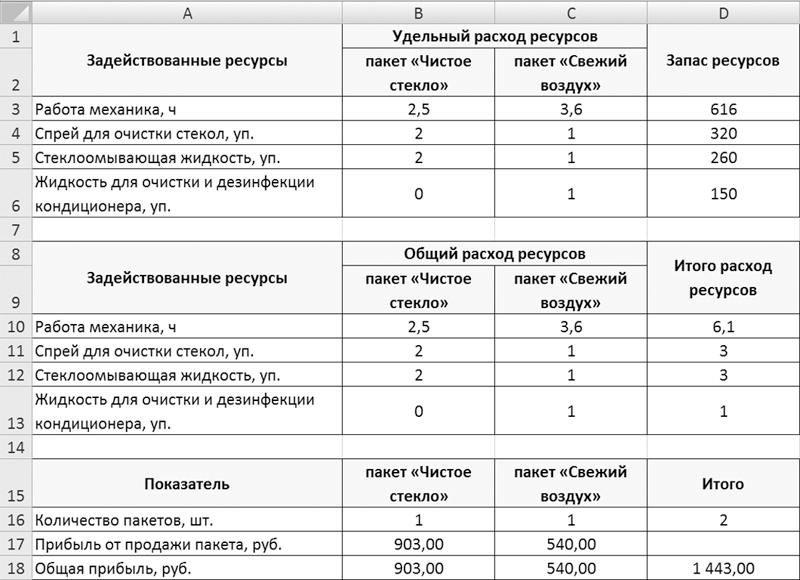
Рис. 1. Ввод данных задачи оптимизации в MS Excel
Сначала следует ввести нормативы расхода имеющихся ресурсов на каждый из пакетов:
- в ячейки B3:B6 вводятся нормативы расхода всех ресурсов на продажу одного пакета «Чистое стекло»;
- в ячейки C3:C6 вводятся нормативы расхода всех ресурсов на продажу одного пакета «Свежий воздух»;
- в ячейки D3:D6 заносят запасы (лимиты расхода) по каждому из ресурсов.
Для того чтобы посчитать общий расход ресурсов и соотнести его с запасами, необходимо ввести данные о количестве проданных пакетов (ячейки В16 и С16). Для начала проставим там единичные значения (как будто продано по одному сезонному пакету). Общий расход ресурсов рассчитывается в диапазоне ячеек A8:D13, в котором количество проданных пакетов (ячейки В16 и С16) умножается на норматив расхода (диапазоны B3:B6 и C3:C6). В диапазоне D10:D13 рассчитывается суммарный расход по каждому из ресурсов.
Так, например, расход нормо-часов механиков по пакету «Чистое стекло» производится в ячейке В10 путем умножения значений ячейки В16 (количество проданных пакетов «Чистое стекло») на ячейку В3 (норматив выполнения работ по пакету «Чистое стекло»). Расход нормо-часов механиков по пакету «Свежий воздух» производится в ячейке С10 путем умножения значений ячейки С16 (количество проданных пакетов «Свежий воздух») на ячейку С3 (норматив выполнения работ по пакету «Свежий воздух»).
Итоговое значение расхода часов механиков рассчитывается в ячейке D10 путем сложения значений ячеек В10 и С10 (сумма в ячейке D10 не должна превышать лимит, установленный в ячейке D3).
Также на рабочем листе идет расчет прибыли от продажи пакетов (ячейки В18 и С18). Для этого размер прибыли от продажи одного пакета (значения проставлены в ячейках В17 и С17) умножается на количество проданных пакетов (ячейки В16 и С16). В ячейке D18 стоит итоговое значение прибыли.
Цель — максимизировать значение, рассчитываемое в ячейке D18 при соблюдении всех ограничений задачи.
Воспользуемся инструментом «Поиск решения» (находим в меню «Данные» — «Анализ»). Диалоговое окно представлено на рис. 2.
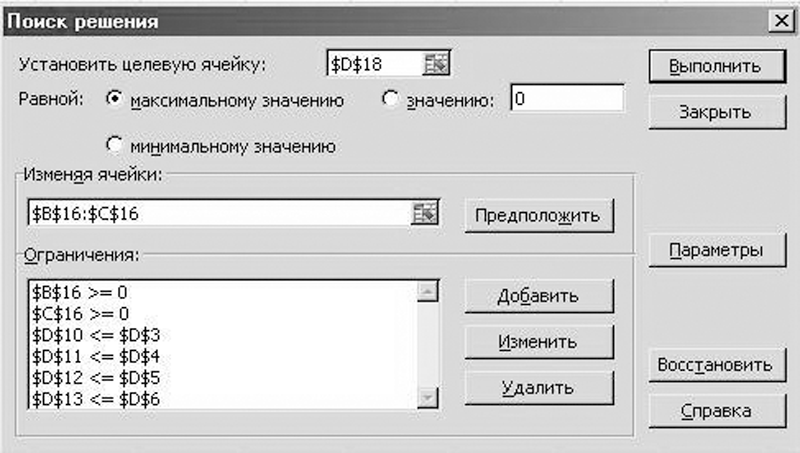
Рис. 2. Диалоговое окно инструмента «Поиск решения»
По условиям поставленной задачи необходимо установить в целевую ячейку D18 (общая прибыль от продажи пакетов) максимальное значение, изменяя ячейки В16:С16 (количество проданных пакетов «Чистое стекло» и «Свежий воздух»).
При этом должны быть прописаны все ограничения нашей задачи:
- В16 и С16 >= 0 (количество проданных пакетов неотрицательно);
- D10 <= D3 (расход нормо-часов механиков не превышает имеющийся фонд рабочего времени);
- D11 <= D4 (расход спрея для очистки стекол не превышает складских остатков);
- D12 <= D5 (расход стеклоочищающей жидкости не превышает складских остатков);
- D13 <= D6 (расход жидкости для очистки и дезинфекции кондиционеров не превышает складских остатков).
После ввода ограничений нажимаем кнопку «Выполнить». Ячейки В16 и С16 заполняются автоматически. В целевой ячейке D18 получается значение прибыли. На рис. 3 представлены результаты вычислений.
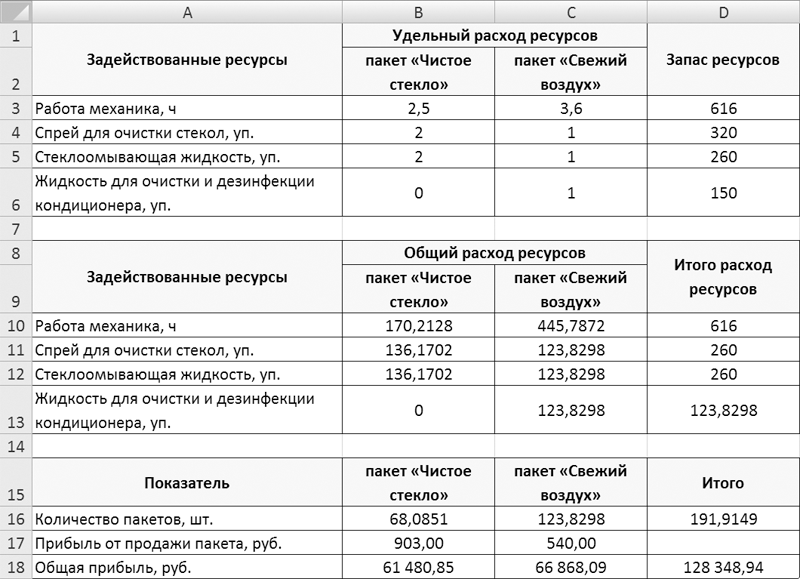
Рис. 3. Результаты вычислений
Как видно из рис. 3, результаты вычислений получились аналогичными тем, что были достигнуты при помощи симплекс-таблиц. Однако эти данные, как уже говорилось выше, не могут быть приняты по причине своей нецелочисленности. Чтобы устранить данный недостаток, необходимо в диалоговом окне инструмента «Поиск решения» прописать дополнительные условия (рис. 4).
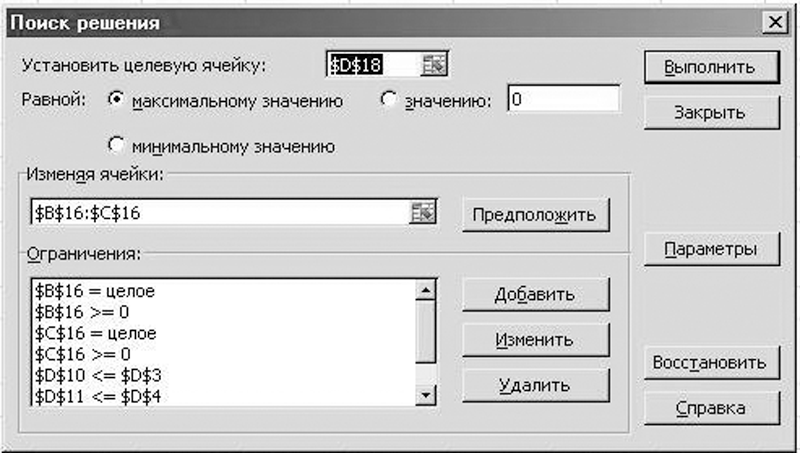
Рис. 4. Диалоговое окно инструмента «Поиск решения» с добавлением условия целочисленности
Результаты вычисления после добавления условия целочисленности показаны на рис. 5.
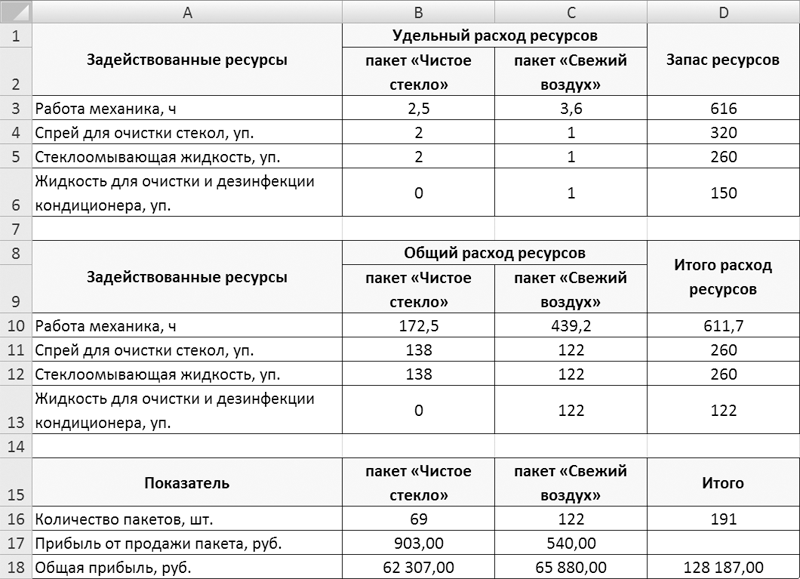
Рис. 5. Результаты вычисления после добавления условия целочисленности
Полученные данные удовлетворяют всем заданным условия. Если руководство предприятия выделит на проведение сезонной акции 69 пакетов «Чистое стекло» и 122 пакета «Свежий воздух», то за счет имеющихся в распоряжении ресурсов будет получена максимальная прибыль, которая составит 128 187 руб.
Заключение
В данной статье на простых примерах мы рассмотрели, как можно применять методы исследования операций для решения производственных задач, и выяснили, как можно ускорить данный процесс путем применения встроенных возможностей MS Excel.
Статья опубликована в журнале «Планово-экономический отдел» № 9, 2013.
Решение задач линейного программирования
графическим методом
Существуют два наиболее распространенных способа решения задач линейного программирования (ЗЛП): графический метод и симплекс-метод. Графический метод существенно нагляднее и обычно проще для понимания и решения (хотя занимает много времени, так как требует тщательного построения чертежа). Также этот метод позволяет практически одновременно найти решение на минимум и максимум, тогда как симплекс-методом придется делать «два подхода».
Основные шаги по решению ЗПЛ графическим методом следующие: построить область допустимых решений задачи (выпуклый многоугольник), который определяется как пересечение полуплоскостей, соответствующих неравенствам задачи, построить линию уровня целевой функции, и, наконец, двигать линию уровня в нужном направлении, пока не достигнем крайней точки области — оптимальной точки (или множества). При этом можно найти единственное оптимальное решение (точку), множество (отрезок) или ни одного (область пустая или не ограниченная в нужном направлении).
А за конкретикой — к примерам ниже: вы найдете там решенные графическим способом задачи линейного программирования. Примеры решений выложены бесплатно для вашего удобства — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий по методам оптимальных решений, перейдите в раздел: Решение задач ЛП на заказ (решаем для студентов очников и заочников).
Лучшее спасибо — порекомендовать эту страницу
Графический метод решения ЗЛП: примеры онлайн
Задача 1. Колхоз имеет возможность приобрести не более 19 трехтонных автомашин и не более 17 пятитонных. Отпускная цена трехтонного грузовика — 4000 руб., пятитонного — 5000 руб. Колхоз может выделить для приобретения автомашин 141 тысяч рублей. Сколько нужно приобрести автомашин, чтобы их суммарная грузоподъемность была максимальной?
Задачу решить графическими и аналитическими методами.
Задача 2. Решить задачу графическим методом на минимум и на максимум
Задача 3. Решить задачу графическим методом на минимум и на максимум
Задача 4. Среди чисел x и y, удовлетворяющих условиям
найти такие, при которых разность этих чисел y-x принимает наибольшее значение.
Задача 5. Решить графическим методом ЗЛП, заданную указанной математической моделью.
Задача 6. Решите графически следующие задачи линейного программирования
Задача 7. Решить графическим методом
Решаем задачи линейного программирования на заказ









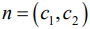 и одну из линий уровня, имеющую общие точки с этой областью.
и одну из линий уровня, имеющую общие точки с этой областью.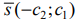 прямой
прямой 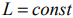 и параллельно ему проводим линию уровня
и параллельно ему проводим линию уровня 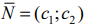 перпендикулярно прямой
перпендикулярно прямой