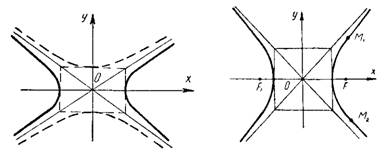
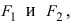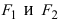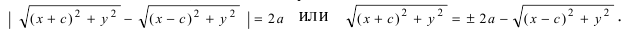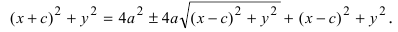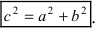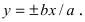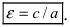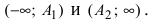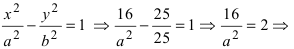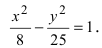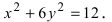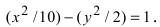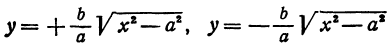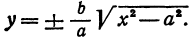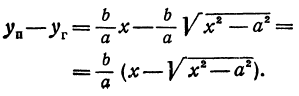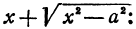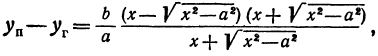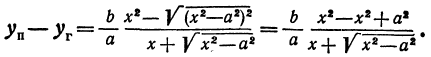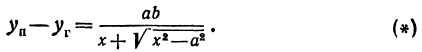Гиперболой
называется множество всех точек
плоскости, модуль разности расстояний
от каждой из которых до двух заданных
точек этой же плоскости, называемых
фокусами, есть величина постоянная,
меньшая, чем расстояние между фокусами.
К
аноническое уравнение гиперболы:
(9)
где
—
действительная полуось,
—
мнимая полуось гиперболы,
—
фокусное расстояние. Числа
,
,
связаны соотношением
.
(10)
Координаты
фокусов
,
.
Точки
и
называются
вершинами гиперболы, точка O
– центром
гиперболы.
Важными
характеристиками гиперболы являются:
—
эксцентриситет
(1<
<
)
(11)
если
~ 1, то ветви гиперболы широкие, почти
вертикальные,
если
~
,
то ветви гиперболы узкие, гипербола
приближается к оси Ox.
—
асимптоты
.
(12)
Прямоугольник
,
центр которого совпадает с точкой О,
а стороны равны и параллельны осям
гиперболы называется основным
прямоугольником гиперболы. Диагонали
основного прямоугольника лежат на
асимптотах.
—
директрисы
гиперболы
– прямые, параллельные мнимой оси
гиперболы и отстоящие от нее на расстоянии,
равном
.
Уравнения директрис:
,
.
(13)
—
фокальные
радиусы
определяются формулами:
для точек правой
ветви гиперболы:
,
;
(14)
для точек левой
ветви:
,
.
(15)

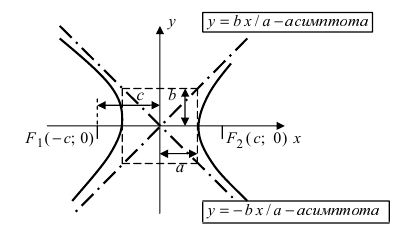
Рис. 5. Гипербола,
ее асимптоты и основной прямоугольник
Если
,
то гипербола (9) называется равносторонней
(равнобочной). Ее уравнение принимает
вид
.
(16)
Если
фокусы гиперболы лежат на оси
,
то уравнение гиперболы имеет вид:
(17)
эксцентриситет этой гиперболы равен
,
асимптоты определяются уравнениями
,
уравнения директрис
.
Гипербола (17) называется сопряженной
гиперболе (9).
Пример
3.1.
Дано
уравнение гиперболы
.
Найти:
-
длины
его полуосей; -
координаты
фокусов; -
эксцентриситет
гиперболы; -
уравнения
асимптот и директрис; -
фокальные
радиусы точки
-
на
гиперболе найти точку, для которой
расстояние от левого фокуса в 3 раза
больше, чем от правого.
Решение.
Разделив
обе части уравнения
на
,
приведем уравнение гиперболы к
каноническому виду:
Отсюда:
1)
,
,
т.е. действительная полуось
,
мнимая полуось
.
2)
Используя соотношение (10), находим
,
т.е.
.
Запишем фокусы гиперболы:
,
.
3)
По формуле (11) находим эксцентриситет
гиперболы
.
4)
Уравнения асимптот и директрис найдем
по формулам (12) и (13):
и
.
5)
точка
лежит
на правой ветви гиперболы
,
используем формулы (14):
,
.
6)
Найдем на гиперболе точку
такую, что
.
Используя формулы (14) и
,
получим:
;
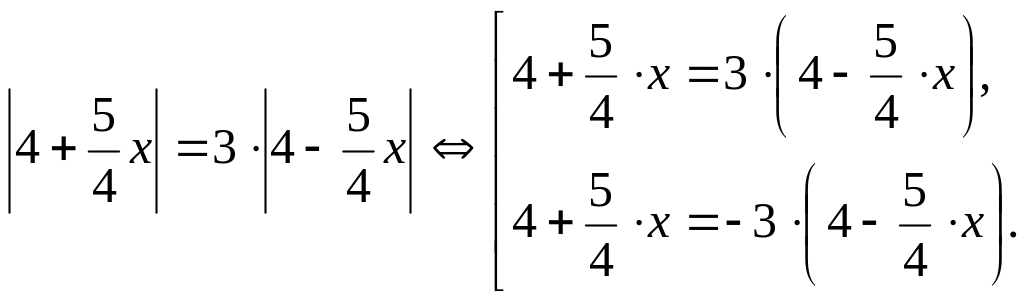
Находим
и
.
Поскольку
лежит на гиперболе
,
то ординаты соответствующих точек
найдем из этого уравнения при найденных
значениях x:
и,
если
,
то
(это число не существует в нужном нам
смысле), а если
,
то
.
Итак,
получили две точки на гиперболе,
удовлетворяющие данным условиям:
и
.
Пример
3.2.
Составить
уравнение гиперболы, симметричной
относительно координатных осей, которая
проходит через точку
и ее асимптоты имеют уравнения
.
Решение.
Подставим
координаты точки
в уравнение (9):
.
Уравнения
асимптот гиперболы
,
поэтому
,
тогда
.
Получим систему двух уравнений:
Запишем
уравнение гиперболы:
Задачи для
самостоятельного решения:
1.
Дана гипербола
.
Найти: 1) полуоси
и
;
2) фокусы;
3)
эксцентриситет; 4) уравнения асимптот;
5) уравнения директрис.
2.
Дана гипербола
.
Найти: 1) полуоси
и
;
2) фокусы;
3)
эксцентриситет; 4) уравнения асимптот;
5) уравнения директрис.
3.
Составить уравнение гиперболы, фокусы
которой расположены на оси абсцисс
симметрично относительно начала
координат, зная, кроме того, что:
1)
ее оси
и
;
2)
расстояние между фокусами
и ось
;
3)
расстояние между фокусами
и эксцентриситет
;
4)
ось
и эксцентриситет
;
5)
уравнения асимптот
и расстояние между фокусами
;
6)
расстояние между директрисами равно
и расстояние между фокусами
;
7)
расстояние между директрисами равно
и ось
;

расстояние между директрисами равно
и эксцентриситет
;
9)
уравнения асимптот
и расстояние между директрисами равно
;
10)
точки
и
гиперболы;
11)
точка
гиперболы и эксцентриситет
;
12)
точка
гиперболы и уравнения асимптот
;
13)
точка
гиперболы и уравнения директрис
;
14)
уравнения асимптот
и уравнения директрис
.
4.
Составить уравнение гиперболы, фокусы
которой расположены на оси ординат
симметрично относительно начала
координат, зная, кроме того, что:
1)
ее полуоси
и
(буквой
мы обозначаем полуось гиперболы,
расположенную на оси абсцисс);
2)
расстояние между фокусами
и эксцентриситет
;
3)
уравнения асимптот
и расстояние между вершинами равно 48;
4)
расстояние между директрисами равно
и эксцентриситет
;
5)
уравнения асимптот
и расстояние между директрисами равно
.
5.
Установить, какие линии определяются
следующими уравнениями:
1)
;
2)
;
3)
;
4)
.
Изобразить
эти линии на чертеже.
6.
Вычислить площадь треугольника,
образованного асимптотами гиперболы
и прямой
.
7.
Дана точка
на гиперболе
.
Составить уравнения прямых, на которых
лежат фокальные радиусы точки
.
8.
Убедившись, что точка
лежит на гиперболе
,
определить фокальные радиусы точки
.
9.
Эксцентриситет гиперболы
,
фокальный радиус ее точки
,
проведенный из некоторого фокуса, равен
16. Вычислить расстояние от точки
до односторонней с этим фокусом
директрисы.
10.
Эксцентриситет гиперболы
,
расстояние от точки
гиперболы до директрисы равно 4. Вычислить
расстояние от точки
до фокуса, одностороннего с этой
директрисой.
11.
Эксцентриситет
гиперболы
,
центр ее лежит в начале координат, один
из фокусов
.
Вычислить расстояние от точки
гиперболы с абсциссой, равной 13, до
директрисы, соответствующей заданному
фокусу.
12.
Эксцентриситет гиперболы
,
центр ее лежит в начале координат, одна
из директрис дана уравнением
.
Вычислить расстояние от точки
гиперболы с абсциссой, равной 10, до
фокуса, соответствующего заданной
директрисе.
13.
Определить точки гиперболы
,
расстояние от которых до правого фокуса
равно 4,5.
14.
Определить точки гиперболы
,
расстояние от которых до левого фокуса
равно 7.
15.
Составить уравнение гиперболы, если ее
эксцентриситет равен 2 и фокусы совпадают
с фокусами эллипса
.
16.
Составить уравнение гиперболы, фокусы
которой лежат в вершинах эллипса
,
а директрисы проходят через фокусы
этого эллипса.
17.
Найти уравнение гиперболы, вершины и
фокусы которой находятся в соответствующих
фокусах и вершинах эллипса
.
18.
Определить эксцентриситет равносторонней
гиперболы.
19.
Определить эксцентриситет гиперболы,
если отрезок между ее вершинами виден
из фокусов сопряженной гиперболы под
углом
.
20.
Прямая
касается гиперболы, фокусы которой
находятся в точках
и
.
Составить уравнение этой гиперболы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Математическая гипербола.
Функция заданная формулой (y=frac{k}{x}), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac{k}{x}) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.


2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$yneqcolor{red} {frac{1}{x}}+0$$
(frac{1}{x}) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
$$y=color{red} {frac{1}{x+2}}-1$$
Дробь (color{red} {frac{1}{x+2}}) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Пример №3:
$$begin{align*}
&y=frac{2+x}{1+x} \\
&y=frac{color{red} {1+1}+x}{1+x} \\
&y=frac{1}{1+x}+frac{1+x}{1+x}\\
&y=frac{1}{1+x}+1\\
&y=frac{1}{color{red} {1+x}}+1
end{align*}$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
$$y=color{red}{frac{1}{1+x}}+1$$
(color{red}{frac{1}{1+x}}) Дробь убираем.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
$$y=frac{1}{x}$$
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
$$y=frac{1}{x}$$
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.
5. Гипербола нечетная функция.
$$f(-x)=frac{1}{-x}=-frac{1}{x}=-f(x)$$
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
$$y=frac{-1}{x-1}-1$$
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
$$y=color{red} {frac{-1}{x-1}}-1$$
Дробь (color{red} {frac{-1}{x-1}}) удаляем.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.
8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама
Свойства гиперболы
1) Область определения и область значений
По аналитическому заданию функции видно, что х ≠-a, поскольку знаменатель дроби не может ровняться нулю. Таким образом получим:
D(f)=(-∞;-а) U (-a;+∞)
Область значений
Е(f)=(-∞;+∞)
2) Нули функции
Если b=0, то график функции не пересекает ось ОХ;
Если b≠0, то гипербола имеет одну точку пересечения с ОХ:*
x=-(k+ab)/b
3) Промежутки знакопостоянства
Рассмотрим только 2 простых случая, остальные случаи вы можете рассмотреть аналитически самостоятельно по алгоритму из раздела Свойства функций -> Знакопостоянство
Случай 1: a=0, b=0, k>0
f(x)>0, при x ∈ (0; +∞)
f(x)<0, при x ∈ (-∞;0)
Случай 1: a=0, b=0, k<0
f(x)<0, при x ∈ (0; +∞)
f(x)>0, при x ∈ (-∞;0)
4) Промежутки монотонности
Аналогично с промежутками знакопостоянства рассмотрим только 2 случая
Случай 1: a=0, b=0, k>0
Функция убывает при
x ∈ (-∞;0) U (0; +∞)
Функция возрастает при
x ∈ (-∞;0) U (0; +∞)
5) Четность и нечетность
Функция является нечетной при a=0, b=0, то есть если имеет вид y=k/x
Гипербола:
Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек
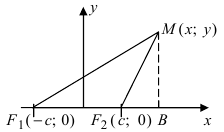
Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы
Рис. 31. Вывод уравнения гиперболы.
Расстояние между фокусами (фокусное расстояние) равно 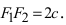
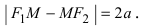
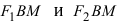
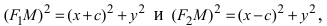
Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим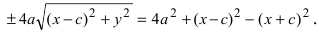
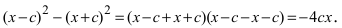
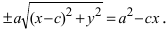
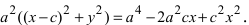
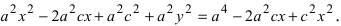
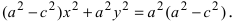
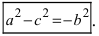
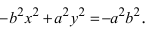
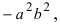
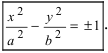
Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки 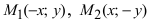
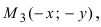
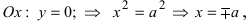
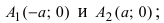
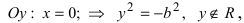
Рис. 32. Асимптоты и параметры гиперболы
Определение: Найденные точки 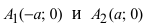
Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 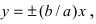
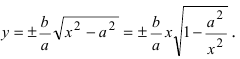
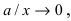
Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр а называется действительной, а параметр b — мнимой полуосями гиперболы.
Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы
Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 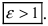
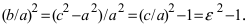
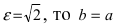
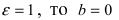
Пример:
Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).
Решение:
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:
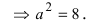
Пример:
Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах эллипса
Решение:
Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 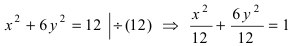
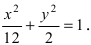
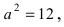
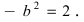
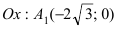
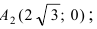
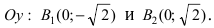
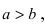
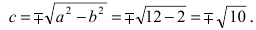
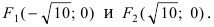
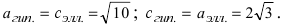
Рис. 33. Параметры эллипса и гиперболы
Вычислим длину мнимой полуоси 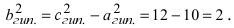
Гипербола в высшей математике
Рассмотрим уравнение
Решая его относительно 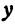
или одну двузначную функцию
Функция 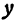

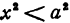
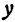
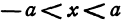
При 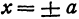
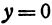
При 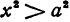
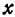
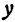
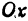
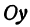
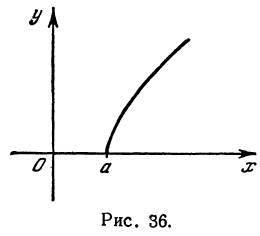
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.
Гипербола в силу симметрии имеет вид, указанный на рис. 37.
Точки пересечения гиперболы с осью 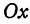
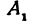
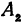
Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.
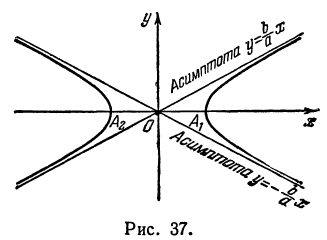
Рассмотрим прямую, заданную уравнением 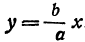
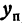
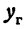
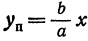
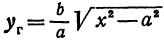
Умножим и разделим правую часть на
или
Окончательно
Будем придавать 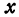
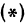

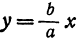
Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 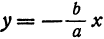
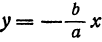
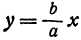
Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.
Таким образом, гипербола имеет две асимптоты, определяемые уравнениями 
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
1. Гипербола
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, равная 2а (рис.1). Каноническое уравнение гиперболы имеет вид
Координаты фокусов гиперболы: F(c;0) и F₁(-c;0). Расстояние между фокусами равно 2с.
Точки пересечения гиперболы с осью абсцисс А(а;0) и A₁(—а;0) называются действительными вершинами.
Рис.2
Отрезок АА₁ = 2а называется действительной осью гиперболы. Точки В (0;b) и В₁(0;—b) называются мнимыми вершинами гиперболы, а отрезок ВВ₁ = 2b называется мнимой осью гиперболы.
Эксцентриситет гиперболы
Расстояния r и r₁ точки М(x;у) гиперболы до ее фокусов называются фокальными радиусами этой точки и определяются формулами:
если точка М лежит на правой ветви;
если точка М лежит на левой ветви.
Две прямые PQ и P₁Q₁ параллельные мнимой оси гиперболы и
отстоящие от нее на расстоянии a/e, называются директрисами гиперболы. Их уравнения:
или
Отношение расстояний любой точки гиперболы до фокуса и соответствующей директрисы есть величина постоянная, равная эксцентриситету гиперболы
Прямые RS и R₁S₁ определяемые уравнениями
называются асимптотами гиперболы.
Уравнение гиперболы с осями, параллельными координатным осям, имеет вид:
где x₀, у₀ — координаты центра гиперболы. Две гиперболы, выраженные уравнениями
называются сопряженными (рис.3). Они имеют общие асимптоты.
Рис. 3. Рис. 4.
Если оси гиперболы равны, т. е. a = b, то гипербола называется равнобочной или равносторонней (рис.4). Ее уравнение имеет вид
ее асимптотами служат биссектрисы координатных углов. Если за оси координат принять асимптоты равносторонней гиперболы, то ее уравнение примет вид
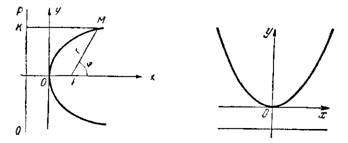
2. Парабола
Параболой называется геометрическое место точек плоскости, равноудаленных oт данной точки — фокуса и данной прямой — директрисы (рис.5).
Каноническое уравнение параболы имеет вид
где Р — есть расстояние от фокуса до директрисы. Вершина параболы находится в начале координат, осью симметрии служит ось абсцисс.
Координаты фокуса F(p/2;0). Уравнение директрисы PQ параболы имеет вид
Фокальный радиус точки М(х;у) параболы равен:
Эксцентриситет параболы считается равным единице, е=1. Если осью симметрии параболы служит ось ординат (рис.6). то уравнение параболы имеет вид:
Рис. 3. Рис. 4.
Уравнение директрисы в этом случае
Уравнение параболы с осью симметрии, параллельной одной из координатных осей, имеет вид:
или
где (x₀; y₀) — координаты вершины параболы.
3. Уравнения эллипса, гиперболы и параболы в полярных координатах
Уравнения эллипса, гиперболы и параболы в полярных координатах имеют один и тот же вид:
где е — эксцентриситет кривой.
Если е<1, то кривая, определяемая уравнением (27), есть эллипс; если е>1, то кривая — гипербола и если е=1, то кривая — парабола.
р — фокальный параметр для эллипса и гиперболы находится по формуле
Для параболы р имеет то же значение, что и в уравнении
у² = 2рх.
При этом полюс расположен для эллипса в левом фокусе, для гиперболы — в правом фокусе.