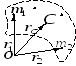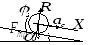Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Сущность понятия «центр масс»
Понятие «центр масс» широко используется в физике для решения задач, связанных с движением тел. Например, математический маятник удобно представить себе как подвешенное на нити тело, вся масса которого сконцентрирована в единой точке. В законе всемирного тяготения тоже речь идет о расстоянии не между телами, а между центрами тел, под каковыми подразумеваются именно центры масс, а не геометрические центры.
Определение 1
Центр масс — точка, характеризующая размещение и движение исследуемой системы как единого целого.
Признаком центра масс является то, что если тело подвесить, закрепив за эту точку, оно останется в покое, т.е. не будет раскачиваться или вращаться относительно этого центра. В простейшем случае, если речь идет о симметричном теле с равномерной плотностью, центр масс находится на пересечении осей симметрии рассматриваемого тела. Например, если взять линейку длиной 30 см, то ее центр масс будет расположен на отметке «15 см». Подложив карандаш под эту отметку, легко привести линейку в положение равновесия.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
На практике далеко не все тела, центр масс которых нужно найти, являются симметричными и однородными по плотности. Более того, многие исследуемые объекты представляют собой системы из нескольких тел с различными геометрическими и химическими характеристиками. Для расчетов их разбивают на элементарные фрагменты и производят вычисления поэтапно.
Нахождение координат центра масс
Определение 2
Центр масс двух тел с точечными массами $m_1$ и $m_2$ и координатами на координатной прямой $x_1$ и $x_2$ находится в точке, делящей расстояние между этими телами на отрезки с длинами обратно пропорциональными массам рассматриваемых тел.
Отсюда следует, что чем массивнее тело в такой элементарной системе, тем ближе оно к общему центру масс.
Расстояние между точечными телами равно:
$Delta x = x_2 — x_1$
Пропорция между массами и расстояниями, согласно определению:
$frac{l_1}{l_2} = frac{m_2}{m_1}$,
«Как найти координаты центра масс» 👇
где $l_1$, $l_2$ — расстояния от соответствующих тел до центра масс.
Выразив, длины через координаты
$l_1 = x_c — x_1; l_2 = x_2 — x_c$,
центр масс можно определить как
$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$.
где $x_c$ — координата центра тяжести.
Разложив любую сложную систему на множество элементарных тел с точечными массами, можно обобщить изложенный принцип в виде формулы (для оси абсцисс):
$x_c = frac{sumlimits^N_{i=1}{m_i cdot x_i}}{sumlimits^N_{i=1}{m_i}}$
В большинстве случаев центр масс требуется найти не на координатной прямой, а в двух- или трехмерной системе координат. Для дополнительных осей координаты центра масс ($y_c$, $z_c$) находят по аналогичному принципу.
Замечание 1
Центр тяжести системы тел представляет собой точку, подобную центру масс, но рассчитывается не для масс, а для весов (обусловленных гравитацией сил), действующих на точечные тела, входящие в систему. Центр тяжести определяется так же, как и центр масс, если размеры системы малы в сравнении с радиусом планеты Земля. Он в большинстве случаев с достаточной для практики точностью совпадает с центром масс рассматриваемой системы.
Пример 1
Найти центр масс двух линеек, изготовленных из одинакового материала, одинаковой толщины и ширины, левые концы линеек совмещены. Длины линеек — 10 и 30 см. Толщиной линеек можно пренебречь.
Поскольку толщиной можно пренебречь, найти нужно лишь координату центра масс по оси $x$.
Разобьем мысленно систему на два отрезка. Первый — где толщина линеек складывается. Его координаты — $[0, 10]$. Второй отрезок — где длинная линейка продолжается одна. Его координаты — $[10, 30]$. Примем за единицу измерения массу одного погонного сантиметра линейки. Тогда масса второго фрагмента:
$m_2 = 30 — 10 = 20$
На каждый сантиметр первого фрагмента приходится вдвое больше массы, поскольку там сложены две линейки:
$m_1 = 10 cdot 2 = 20$
Центры масс отрезков находятся на их осях симметрии, т.е. на середине длины каждого:
$x_{c1} = frac{10}{2} = 5$;
$x_{c2} = 10 + frac{20}{2} = 20$
Подставим значения в формулу:
$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$
$x_c = frac{20 cdot 5 + 20 cdot 20}{20 +20} = frac{100 + 400}{40} = 12, 5$
Ответ: центр масс находится на расстоянии 12,5 см от левого конца системы линеек.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Определение центра масс, теория и онлайн калькуляторы
Определение центра масс
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Радиус-вектор и координаты центра масс
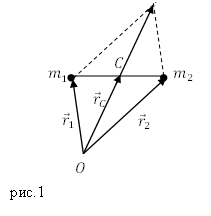
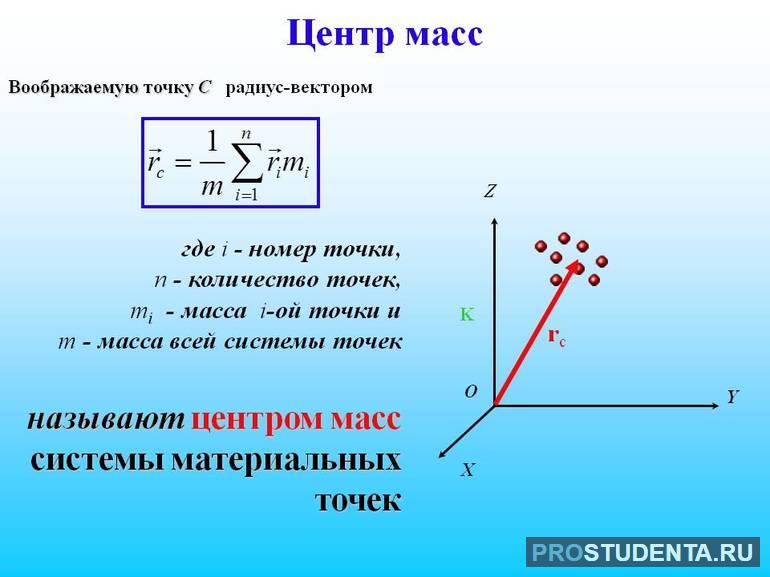
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: ${overline{r}}_1 и {overline{r}}_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором ${overline{r}}_C$ (рис.1).
Из рис.1 видно, что:
[{overline{r}}_C=frac{{overline{r}}_1+ {overline{r}}_2}{2}left(1right).]
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен ${overline{r}}_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
[{overline{r}}_C=frac{{overline{r}}_1m_1+ {overline{r}}_2m_2}{m_1+m_2}left(2right).]
Радиус -вектор ${overline{r}}_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц ${overline{r}}_1$ и ${overline{r}}_2$. Это становится очевидным, если формулу (2) представить в виде:
[{overline{r}}_C=frac{m_1}{m_1+m_2}{overline{r}}_1+frac{m_2}{m_1+m_2}{overline{r}}_2left(3right).]
Выражение (3) показывает, что радиус-вектор каждой частицы входит в ${overline{r}}_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(4right).]
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(5right).]
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Скорость центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) запишем как:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(8right),]
где $overline{P}$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач на определение центра масс
Пример 2
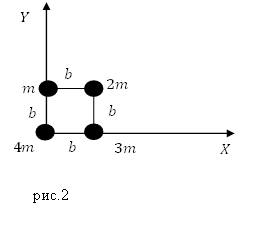
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_с=frac{sumlimits_i{Delta m_iy_i}}{m}. end{array}
right.]
Вычислим массу рассматриваемой системы точек:
[m=m+2m+3m+4m=10 m.]
Тогда абсцисса центра масс $x_{c } $равна:
[x_c=frac{0cdot 4m+3mcdot b+2mcdot b}{10m}=0,5 b.]
Ордината $y_с$:
[y_с=frac{0cdot m+mcdot b+2mcdot b}{10m}=0,3 b.]
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Пример 2
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
[frac{s_1}{s_2}=frac{m_2}{m_1}left(2.1right).]
По условию:
[s=s_1+s_2left(2.2right).]
Из уравнений (2.1) и (2.2) получаем:
[s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}.]
Ответ. $s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}$
Читать дальше: период и частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Точку, в которой происходит равное распределение величины, определяющей инерционные и гравитационные свойства, называют центром масс. Формула для определения параметра зависит от радиус-вектора частиц системы и их полной энергии. Эту характеристику тела отличают от тяжести, при этом в трудах советских учёных Ландау, Лифшица для неё используется термин «центр инерции».
Оглавление:
- Общие сведения
- Связь с центром тяжести
- Вычисление положения
- Геометрический способ определения
Общие сведения
Допустим, имеется тело, на которое действуют скомпенсированные силы. В этом случае оно будет в состоянии покоя или прямолинейного равномерного движения. Пусть тело будет неподвижным. Например, лодка на воде. К ней можно приложить воздействие F1 в районе её кормы. Под действием силы она начнёт разворачиваться. Аналогично если воздействовать на её нос F2, то она тоже будет поворачиваться, но при этом разворот будет происходить в другую сторону.
Получается, что можно подобрать такую линию, на которой действие сил приведёт её к ускоренно поступательному движению. Пусть это будет F3. На самом деле таких сил может быть несколько. При этом их можно перемещать вдоль линии их воздействия. Если все такие силы изобразить в виде линий, то они пересекутся в одной точке. Такое место и называют центром масс тела (ЦМ). То есть точку, в которой пересекаются линии действия сил, вызывающие только ускоренное поступательное механическое движение.
Эта важная точка в теле и движется она довольно просто. Перемещение любого тела можно представить, как комбинацию двух видов движения:
- центра масс;
- вращения.
Существует теорема: ЦМ тела движется так, как перемещалась бы материальная точка, в которой сосредоточена вся масса и к которой приложены все воздействия, действующие на объект. Таким образом, различные виды изменения положения точек в пространстве можно описать с помощью законов Ньютона. Согласно же теореме их можно применять и к телу, если считать, что все силы приложены к центру масс.
Рассматривая объект, можно не учитывать его размер, форму, а брать во внимание только инерцию, ускорение и принцип парного взаимодействия. Фактически в механике перемещение сколь угодно сложного вида рассматривается по принципу суперпозиции и закона сохранении энергии. При этом довольно удобно изучать изменение положения в системе отсчёта связанной с этим центром. В ней полный импульс всегда будет равным нулю, что позволяет упростить уравнение движения.
Связь с центром тяжести
Пусть имеется объект, находящийся на Земле. Говорят, что на него действует сила тяжести. Но на самом деле она воздействует не на вещество, а на каждый его атом, частичку. Если предположить, что ускорение свободного падения буде одинаковым, то на объект действует очень множество сил тяжести. Рассматривать такую систему неудобно. Поэтому все воздействия заменяют равнодействующей. И считают, что действует одна сила, которая приложена к центру тяжести твёрдого тела.
Для того чтобы найти взаимосвязь между тяжестью и массой нужно представить, что объект вдруг распался на отдельные равные кусочки. Они держатся вместе, но не прикреплены друг к другу. Если тело отпустить, то они будут падать вместе, так как ускорение свободного падения не зависит от массы. При этом движение будет поступательным. Значит, сила, приложенная к телу в целом, будет приложена к центру масс.
Получается, что центральная точка является общей как для тяжести, так и для масс. Это две точки положение которых совпадает несмотря на разный их принцип определения в физике. Но существуют условия, когда это правило не выполняется. Например, если система материальных точек неоднородна по объёму плотности в гравитационном поле, то центры не совпадут.
Для примера можно привести список однородных фигур с указанием их центральной точки:
- отрезок — середина;
- параллелограмм — место пересечения диагоналей;
- треугольник — точка пересечения медиан (центроид);
- любой правильный многоугольник — центр поворотной симметрии;
- полукруг — точка, в которой перпендикулярный радиус делится в отношении 4:3p считая от центра круга.
Чтобы найти координату центра масс объекта, который можно представить, как совокупность связанных материальных точек используют два метода: аналитический и геометрический. Но второй способ не всегда можно применить. В однородном гравитационном поле центры тяжести и масс всегда совпадают. И это часто подтверждается на практике, из-за того, что внешнее гравитационное поле в задачах, связанных с действиями на Земле, считают постоянным в пределах объёма тела.
Поэтому эти термины объединяют в геометрии, статике и так далее. То есть в тех областях, где применение определения можно назвать метафорическим и предполагается ситуация их эквивалентности.
При таком понимании оба термина синонимичны, но при этом чаще предпочитают использовать термин, связанный с тяжестью. Это происходит в силу того, что исторически он появился раньше.
Вычисление положения
Пусть тело представляет собой совокупность материальных точек, лежащих на одной прямой при этом их массы разные. Задача состоит в нахождении его центра. Для этого следует вести систему координат с осью икс, которая будет совпадать с линией расположения точек. При этом тело пусть подвешено на невесомой опоре и находится под действием Земного тяготения. Это условие даёт возможность воспользоваться тем фактом, что положения центров масс и тяжести совпадают.
На каждую из материальных точек действует своя сила: m1g, m2g… mng. Если предоставить это тело самому себе, то оно будет в состоянии свободного падения. Остановить тело — подпереть, но при этом так, чтобы оно находилось в равновесии. Это значит, что сила реакции опоры должна проходить через центр тяжести, так как равнодействующая тоже её пересекает.
Получится, что сила реакции опоры будет лежать на одной прямой с силой тяжести действующей на тело в совокупности и их моменты тоже будут проходить через неё. С помощью координатной оси точкам можно присвоить положение, x1, x2… xn, а ЦМ xц. Чтобы тело находилось в равновесии необходимо выполнение двух условий:
- векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
- сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.
Из первого условия можно найти силу реакции опоры: F = (m1 + m2 +…+mn) * g. Если вращение выбрать против часовой стрелки, тогда относительно оси все моменты силы тяжести будут отрицательными, а опоры — положительные. Тогда справедливо записать: F * хц = (m1 x 1 + m2 x 2 +…+mn xn) * g.
Из последнего равенства можно выразить координату ЦМ: xц = ((m1 x 1 + m2 x 2 +…+mn xn) * g) / F. В эту формулу можно подставить выражение для F. В результате ускорение свободного падения сократится и получится: xц = (m1 x 1 + m2 x 2 +…+mn xn) / (m1 + m2 +…+mn). Это формула выглядит громоздко, но запомнить её легко. В числителе стоят произведения масс материальных точек на их координаты, а в знаменателе — вес всего тела.
Если точки не будут лежать на одной прямой, то координата ЦМ тоже не изменится. То есть приведённая формула справедлива для любого положения тела относительно координаты y.
При этом её можно применять и для рассмотрения предметов в пространстве, так как все направления в существующем мире равноправные.
Геометрический способ определения
Для простейших симметричных фигур ЦМ можно определить геометрическим методом. Для этого используются свойства диагоналей и медиан. Пусть имеется произвольной формы четырёхугольник. Изготовлен он из однородного материала.
Идея вычисления состоит в том, что эту фигуру необходимо разбить на два треугольника. Для этого нужно провести диагональ, которая разделит фигуру на два тела. Затем провести в каждом треугольном теле три медианы. Точка их пересечения и будет ЦМ. В результате вместо четырёхугольника можно рассматривать две материальные точки.
Несмотря на то что масса у них разная ЦМ будет находиться на соединяющем их отрезке. Теперь четырёхугольник можно разбить на два других треугольника и выполнить аналогичные действия уже для них. Получится два отрезка, на которых одновременно расположен ЦМ. Значит, его положение будет определяться точкой их пересечения.
Для более сложной фигуры, например, шести или восьмиугольника можно использовать такой же подход. Сначала нужно разделить тело на прямоугольники, а затем треугольники. Найти ЦМ для полученных фигур и определить точку пересечения. Следует понимать, что ЦМ может находиться и за пределами объекта.
Но в реальных ситуациях бывают фигуры, которые имеют неправильную форму. Для них нельзя применить расчёт или геометрический метод. Поэтому выясняют, где расположен ЦМ экспериментальным путём.
Например, пусть имеется тело сложной неправильной формы. Чтобы найти ЦМ необходимо фигуру подвесить в пространстве. На неё действует две силы: тяжести и реакции оси. Первая заставляет фигуру поворачиваться с определённой скоростью до тех пор, пока момент силы тяжести относительно оси крепления не станет равным нулю. То есть точка опоры, ось и центр тяжести окажутся на одной вертикале.
Чтобы узнать, где же находится ЦМ, тело нужно подвесить, используя другую точку. При этом на самой фигуре следует отметить, как проходит вертикаль.
Повторяя такой опыт минимум три раза, можно увидеть точку пересечения осей, которая и будет искомым ЦМ. Причём чем будет больше экспериментов, тем точнее он будет определён.
В
любой системе частиц можно найти точку,
называемую центром масс
,
которая обладает рядом важных свойств.
Её положение относительно начала данной
системы отчета, определяется
радиусом-вектором
.
Центр
масс совпадает с центром тяжести для
однородного поля сил тяготения.
Найдем
скорость движения центра масс системы
;
Если
,
то система, как целое, покоится, т.е.
имеет смысл скорости движения всей
системы, как целого. Поскольку,
,
то
т.е., импульс
системы равен произведению ее массы на
скорость движения центра масс.
3.4. Уравнение движения центра масс.
Основной
закон динамики
можно записать в иной форме, зная понятие
центра масс системы:
Это
есть уравнение
движения центра масс системы,
одно из важнейших уравнений механики.
Оно утверждает, что центр
масс любой системы частиц движется так,
как если бы вся масса системы была
сосредоточена в этой точке и к ней были
бы приложены все внешние силы.
Ускорение
центра масс системы совершенно не
зависит от точек приложения внешних
сил.
Если
,
то
,
значит
и
— это случай замкнутой системы в
инерциальной системе отсчета. Таким
образом, если центр масс системы движется
равномерно и прямолинейно, это означает,
что её импульс сохраняется в процессе
движения.
Пример:
однородный цилиндр массы
и радиуса
скатывается без скольжения по наклонной
плоскости, составляющей угол
с горизонтом. Найти уравнение движения?
Совместное
решение дает значение параметров
Уравнение движения
центра масс
совпадает
с основным уравнением динамики
материальной точки и является его
обобщением на систему частиц: ускорение
системы как целого пропорционально
результирующей всех внешних сил и
обратно пропорционально массе системы.
Систему
отсчета, жестко связанную с центром
масс, которая движется поступательно
относительно ИСО называют системой
центра масс. Ее особенностью является
то, что полный импульс системы частиц
в ней всегда равен нулю, так, как
.
4.Работа и энергия
4.1 Работа
П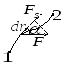
частица М под действием силы
совершает перемещение по некоторой
траектории 1-2. Сила, в общем случае, может
меняться во времени по модулю и
направлению, но на элементарном
перемещении
её можно считать
.
Действие
силы на перемещении
характеризуется физической величиной,
равной скалярному произведению
,
которая называется элементарной
работой силы
на перемещении
.
Её можно записать как
,
где
— угол между
и
— элементарный путь
проекция вектора
на вектор
,
или на направление s.
З
начит, элементарная работа
(*)
—
величина алгебраическая, она может быть
,
или
,
а также равна нулю при
.
Суммируя
элементарные работы (т.е., интегрируя )
по всем элементарным участкам пути от
1 к 2 найдем работу силы
на данном пути.
.
Геометрический
смысл этого выражения виден из рисунка,
на котором
—
площадь полоски шириной
и высотой
;
—
площадь под всей кривой. Над осью работа
силы положительна, под осью — отрицательна.
Размерность
работы
.
Найдем
для примера работу некоторых центральных
сил.
1.
Работа гравитационной или кулоновской
силы.
Пусть
в точке О находится неподвижная
материальная точка, действующая на
частицу М с силой
;
—орт радиуса- вектора
,
-постоянная, равная -jm1m2
для
гравитационной и kq1q2
для кулоновской силы. Элементарная
работа этой силы на перемещении
:
;
Скалярное произведение—
приращение модуля вектора
;
Тогда
,
а работа на всем пути:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Это некоторое положение, определяемое относительно объекта или системы объектов. Это среднее положение всех частей системы, взвешенное в соответствии с их массами.
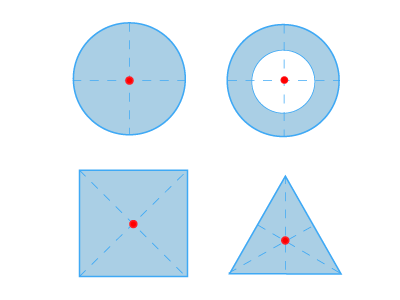
Для простых жестких объектов с равномерной плотностью центр масс находится в центре тяжести. Например, центр масс однородной формы диска будет в его центре. Иногда центр масс не находится в объекте. Например, центр масс кольца находится в его центре, где нет материала самого кольца.
Рисунок 1. Центр масс для некоторых простых геометрических фигур (обозначен красными точками).
Для более сложных фигур нужно более общее математическое определение:
Это уникальная позиция, в которой взвешенные векторы позиций всех частей системы суммируются до нуля.
Что полезного в центре масс?
Интересная вещь о центре масс объекта или системы состоит в том, что это точка, где действует любая однородная сила на объект. Это очень важно, потому что понимание этого облегчает решение механических задач, в которых мы должны описывать движение объектов разной формы и сложных систем.
Для расчетов мы можем рассматривать объект необычной формы, как если бы вся его масса была сосредоточена в крошечном объекте, расположенном в центре масс. Мы иногда называем этот воображаемый объект точечной массой.
Если мы нажимаем на твердый объект в его центре масс, то объект всегда будет двигаться, как будто это точечная масса. Он не будет вращаться вокруг любой оси, независимо от его фактической формы. Если объект подвергается неуравновешенной силе в какой-то другой точке, он начнет вращаться вокруг центра масс.
Как можно найти центр масс любого объекта или системы?
В общем, центр масс может быть найден путем сложения взвешенных векторов положения, которые указывают на центр масс каждого объекта в системе. Один из быстрых методов, который позволяет избежать использования векторной арифметики является нахождение центра масс отдельно для компонентов вдоль каждой оси. То есть:
Для положений объекта вдоль оси x:
ЦМx =m1x1+m2x2+m3x3 m1+m2+m3ЦМ_x;=frac{m_1x_1+m_2x_2+m_3x_3;}{m_1+m_2+m_3}
И аналогично для оси у:
ЦМy =m1y1+m2y2+m3y3 m1+m2+m3ЦМ_y;=frac{m_1y_1+m_2y_2+m_3y_3;}{m_1+m_2+m_3}
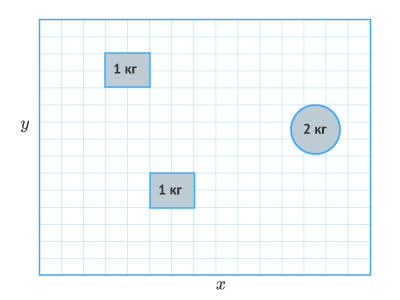
Вместе они дают полные координаты (Цмx, Цмy) центра масс системы. Например, рассмотрим систему из трех плоских объектов одинаковой плотности, показанную на рисунке 2.
Рисунок 2. Система из трех плоских объектов.
Расположение центра масс по оси х:
1⋅4+1⋅6+2⋅12 1+1+2=8,5frac{1cdot4+1cdot6+2cdot12;}{1+1+2}=8,5
и по оси y:
1⋅5+1⋅12+2⋅8,5 1+1+2=8,5frac{1cdot5+1cdot12+2cdot8,5;}{1+1+2}=8,5
Сложные объекты часто могут быть представлены в виде наборов простых форм, каждый из которых имеет одинаковую массу. Затем мы можем представить форму каждого компонента в виде точечной массы, расположенной в центре тяжести. Пустоты внутри объектов можно даже объяснить, представив их в виде фигур с отрицательной массой.
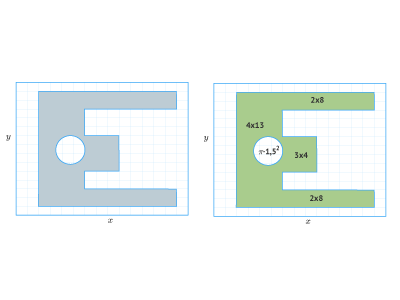
Рассмотрим плоский объект неправильной формы с равномерной плотностью, показанный на рисунке 3.
Рисунок 3. Плоский объект неправильной формы. Объект делится на простые формы.
Мы можем разбить этот сложный объект на четыре прямоугольника и один круг, как показано на рисунке справа. Здесь нас интересует только положение центра масс в относительных единицах, показанных на рисунке. Материал имеет однородную плотность, поэтому масса пропорциональна площади. Для простоты мы можем представить массу каждого сечения в единицах «квадратов», как показано на диаграмме.
По х оси, центр масс находится в:
16⋅10+52⋅4+12⋅7,5+16⋅10+(−7,1)⋅4,5 16+52+12+16−7,1=6,6frac{16cdot10+52cdot4+12cdot7,5+16cdot10+(-7,1)cdot4,5;}{16+52+12+16-7,1}=6,6
Важно, что площадь круговой пустоты π⋅1,52π·1,52 ∼7,1sim7,1 учитывается как отрицательная масса.
По y оси, центр масс находится в:
16⋅13+52⋅7,5+12⋅7,0+16⋅2+(−7,1)⋅7,5 16+52+12+16−7,1=7,4frac{16cdot13+52cdot7,5+12cdot7,0+16cdot2+(-7,1)cdot7,5;}{16+52+12+16-7,1}=7,4
Продолжение статьи читайте здесь.