Мосты
Определение
Пусть дан неориентированный граф. Мостом называется такое ребро, удаление которого делает граф несвязным (или, точнее, увеличивает число компонент связности). Требуется найти все мосты в заданном графе.
Неформально, эта задача ставится следующим образом: требуется найти на карте такие дороги, при удалении которых пропадает путь между какими-либо двумя точками.
Суть алгоритма
Идея
Мы можем заметить тот факт, что ребро между точками v и u является мостом тогда и только тогда, когда из вершины u и её потомков нельзя вернуться в вершину v или подняться выше нее. Осталось лишь понять, как нам это выяснить.
Алгоритм
Разобьём ребра на ориентированные и будем хранить их в отдельной структуре. Пусть мы будем запоминать номер вершины, в которую направлено ребро, номер данного ребра (номер ребра равен номеру обратного ребра) и ссылку на его обратное ребро.
Заведём граф ссылок на рёбра и заполним его.
Запустим обход графа в глубину (DFS).
Будем для каждой вершины v хранить два значения:
-
dp[v] — минимально возможная вершина в которую мы можем опуститься из этой вершины в процессе обхода в глубину (по умолчанию текущая глубина)
-
d[v] — глубина текущей вершины
В процессе обхода:
-
Если встречаем вершину u, в которой еще не были, то спускаемся в неё и тогда dp[v] = min(dp[v], dp[u]). Тем самым проверяем опустились ли мы из вершины u и её потомков выше v.
-
Если встречаем вершину v, в которой уже были, то dp[v] = min(dp[v], d[u]). Тем самым проверяем не встретили ли мы вершину выше по обходу графа, чем вершина v.
По завершении обхода вершины v и её потомков:
Если из вершины v нельзя опуститься выше нее самой и мы знаем проверяемое ребро (dp[v] == d[v] && p != nullptr(текущее ребро)), то ребро из этой вершины — есть мост.
Тогда:
p->is_bridge = true — вершина v
p->bck->is_bridge = true — вершина другого конца ребра
Реализация
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fast_cin() ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL)
struct Edge{
ll v,num;
bool is_bridge;
Edge* bck;
Edge(){}
Edge(ll v, ll num):v(v),num(num){}
};
vector<vector<Edge*>> gr;
vector<ll> dp,d,bridges;
vector<bool> used;
void dfs(ll v, ll depth = 0, Edge* p = nullptr){
used[v] = true;
dp[v] = d[v] = depth;
for(auto u : gr[v]){
if(!used[u->v]){
dfs(u->v,depth+1,u);
dp[v] = min(dp[v],dp[u->v]);
}
else if (p && p->num != u->num){
dp[v] = min(dp[v],d[u->v]);
}
}
if(p != nullptr && dp[v] == d[v]){
p->is_bridge = true;
p->bck->is_bridge = true;
bridges.push_back(p->num+1);
}
}
int main(){
fast_cin();
ll n,m;
cin >> n >> m;
gr.resize(n);
dp.resize(n);
d.resize(n);
used.resize(n);
ll v,u;
for(ll i = 0;i < m;i++){
cin >> v >> u;
v--;
u--;
Edge* a = new Edge(u,i);
Edge* b = new Edge(v,i);
a->bck = b;
b->bck = a;
gr[v].push_back(a);
gr[u].push_back(b);
}
for(ll i = 0;i < n;i++)
if(!used[i])
dfs(i);
sort(bridges.begin(),bridges.end());
cout << bridges.size() << endl;
for(auto i : bridges){
cout << i << " ";
}
}Задачи по теме
https://informatics.mccme.ru/mod/statements/view.php?id=31311#1
https://informatics.mccme.ru/mod/statements/view.php?id=40111&chapterid=389#
https://informatics.mccme.ru/mod/statements/view.php?id=28842#1
https://informatics.mccme.ru/mod/statements/view.php?id=28842&chapterid=3586#1
Точки сочленения
Определение
Точкой сочленения называется вершина, удаление которой делает граф несвязным.
Суть алгоритма
Идея
Мы можем заметить два факта:
-
Рассмотрим ребро между вершинами v и u. Тогда если из вершины u и ее потомков нельзя попасть в какого-либо предка вершины v и притом вершина v не является корнем дерева, то данная вершина и есть точка сочленения
-
Если вершина v — корень дерева, то она является точкой сочленения тогда и только тогда, когда эта точка имеет более одного сына в обходе графа в глубину
Алгоритм
Заведем общий счетчик времени входа timer и два массива:
-
tin[v] — время входа в вершину v
-
fup[v] — минимально достижимая вершина из вершины v
Запустим обход графа в глубину (DFS).
В процессе обхода:
-
Если встречаем уже посещенную вершину u, то fup[v] = min(fup[v], tin[u]). Проверяем не спустились ли мы выше v.
-
Если встречаем не посещенную вершину v, то спускаемся в неё. Затем fup[v] = min(fup[v], fup[u]). Тем самым проверим не спустились ли мы выше v из вершины u и ее потомков. И наконец если из вершины u нельзя спуститься ниже вершины v и вершины v — не корень дерева обхода графа (v fup[u] >= tin[v] && p != -1), то вершина v и есть искомая точка сочленения. Добавляем 1 к количеству сыновей вершины v (children++)
По завершении обхода:
Если вершина v является корнем обхода графа в глубину и имеет более одного сына, то она также является точкой сочленения (p == -1 && children > 1)
Реализация
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fast_cin() ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL)
ll timer = 0;
vector<vector<ll>> gr;
vector<ll> tin,fup;
set<ll> points_of_connectebility;
vector<bool> used;
void dfs(ll v,ll p = -1){
used[v] = true;
tin[v] = fup[v] = timer++;
ll children = 0;
for(auto u : gr[v]){
if(u == p){
continue;
}
if(used[u]){
fup[v] = min(fup[v],tin[u]);
}
else{
dfs(u,v);
fup[v] = min(fup[v],fup[u]);
if(fup[u] >= tin[v] && p != -1){
points_of_connectebility.insert(v+1);
}
children++;
}
}
if(p == -1 && children > 1){
points_of_connectebility.insert(v+1);
}
}
int main() {
fast_cin();
ll n, m;
cin >> n >> m;
gr.resize(n);
tin.resize(n);
fup.resize(n);
used.resize(n);
ll v, u;
for (ll i = 0; i < m; i++) {
cin >> v >> u;
v--;
u--;
gr[v].push_back(u);
gr[u].push_back(v);
}
for (ll i = 0; i < n; i++)
if (!used[i])
dfs(i);
cout << points_of_connectebility.size() << endl;
for(auto i : points_of_connectebility){
cout << i << " ";
}
}Задачи по теме
https://informatics.mccme.ru/mod/statements/view3.php?id=40111&chapterid=111690#1
https://informatics.mccme.ru/mod/statements/view.php?id=40111&chapterid=111795#1
https://informatics.mccme.ru/mod/statements/view.php?id=40111&chapterid=3883#1
https://informatics.mccme.ru/mod/statements/view.php?id=40111&chapterid=3586#1
Содержание
- 1 Алгоритм
- 1.1 Описание алгоритма
- 1.2 Псевдокод
- 1.3 Доказательство корректности
- 1.4 Асимптотика
- 2 См. также
- 3 Источники информации
Алгоритм
Описание алгоритма
Запустим обход в глубину из произвольной вершины графа; обозначим её через . Заметим следующий факт:
- Пусть мы находимся в обходе в глубину, просматривая сейчас все рёбра из вершины . Тогда, если текущее ребро (,) таково, что из вершины и из любого её потомка в дереве обхода в глубину нет обратного ребра в вершину или какого-либо её предка, то эта вершина является точкой сочленения. В противном случае она ей не является. (В самом деле, мы этим условием проверяем, нет ли другого пути из в , кроме как спуск по ребру (,) дерева обхода в глубину.)
Теперь осталось научиться проверять этот факт для каждой вершины эффективно. Для этого воспользуемся «временами входа в вершину», вычисляемыми алгоритмом поиска в глубину.
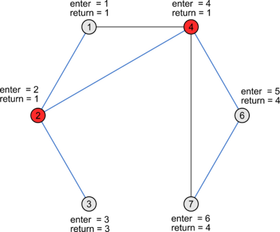
Красным цветом обозначены точки сочленения
Синим — ребра по которым идет DFS
Пусть — время входа поиска в глубину в вершину . Через обозначим минимум из времени захода в саму вершину , времен захода в каждую из вершин , являющуюся концом некоторого обратного ребра , а также из всех значений для каждой вершины , являющейся непосредственным сыном в дереве поиска.
Тогда из вершины или её потомка есть обратное ребро в её предка такой сын , что .
Таким образом, если для текущей вершины существует непосредственный сын : , то вершина является точкой сочленения, в противном случае она точкой сочленения не является.
Псевдокод
function findCutPoints(G[n]: Graph): // функция принимает граф G с количеством вершин n и выполняет поиск точек сочленения во всем графе
visited = array[n, false]
function dfs(v: int, p: int):
time = time + 1
up[v] = tin[v] = time
visited[v] = true
count = 0
for u: (v, u) in G
if u == p
continue
if visited[u]
up[v] = min(up[v], tin[u])
else
dfs(u, v)
count = count + 1
up[v] = min(up[v], up[u])
if p != -1 and up[u] >= tin[v]
v — cutpoint
if p == -1 and count >= 2
v — cutpoint
for i = 1 to n
if not visited[i]
dfs(i, -1)
Доказательство корректности
| Теорема: |
|
Пусть — дерево обхода в глубину, — корень .
|
| Доказательство: |
|
Асимптотика
Оценим время работы алгоритма. Процедура вызывается от каждой вершины не более одного раза, а внутри процедуры рассматриваются все такие ребра . Всего таких ребер для всех вершин в графе , следовательно, время работы алгоритма оценивается как . Такое же, как у обхода в глубину.
См. также
- Использование обхода в глубину для поиска мостов
- Обход в глубину, цвета вершин
- Обход в ширину
Источники информации
- Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — Лань, 2010. — 368 с. — ISBN 978-5-8114-1068-2
- MAXimal :: algo :: Поиск точек сочленения
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Обходы графов
В этой статье рассмотрены основные применения обхода в глубину: топологическая сортировка, нахождение компонент сильной связности, решение задачи 2-SAT, нахождение мостов и точек сочленения, а также построение эйлерова пути и цикла в графе.
Поиск в глубину
Поиском в глубину (англ. depth-first search, DFS) называется рекурсивный алгоритм обхода дерева или графа, начинающий в корневой вершине (в случае графа её может быть выбрана произвольная вершина) и рекурсивно обходящий весь граф, посещая каждую вершину ровно один раз.
const int maxn = 1e5;
bool used[maxn]; // тут будем отмечать посещенные вершины
void dfs(int v) {
used[v] = true;
for (int u : g[v])
if (!used[u])
dfs(v);
}Немного его модифицируем, а именно будем сохранять для каждой вершины, в какой момент мы в неё вошли и в какой вышли — соответствующие массивы будем называть (tin) и (tout).
Как их заполнить: заведем таймер, отвечающий за «время» на текущем состоянии обхода, и будем инкрементировать его каждый раз, когда заходим в новую вершину:
int tin[maxn], tout[maxn];
int t = 0;
void dfs(int v) {
tin[v] = t++;
for (int u : g[v])
if (!used[u])
dfs(u);
tout[v] = t; // иногда счетчик тут тоже увеличивают
}У этих массивов много полезных свойств:
- Вершина (u) является предком (v) (iff tin_v in [tin_u, tout_u)). Эту проверку можно делать за константу.
- Два полуинтервала — ([tin_v, tout_v)) и ([tin_u, tout_u)) — либо не пересекаются, либо один вложен в другой.
- В массиве (tin) есть все числа из промежутка от 0 до (n-1), причём у каждой вершины свой номер.
- Размер поддерева вершины (v) (включая саму вершину) равен (tout_v — tin_v).
- Если ввести нумерацию вершин, соответствующую (tin)-ам, то индексы любого поддерева всегда будут каким-то промежутком в этой нумерации.
Эти свойства часто бывают полезными в задачах на деревья.
Мосты и точки сочленения
Определение. Мостом называется ребро, при удалении которого связный неориентированный граф становится несвязным.
Определение. Точкой сочленения называется врешина, при удалении которой связный неориентированный граф становится несвязным.
Пример задачи, где их интересно искать: дана топология сети (компьютеры и физические соединения между ними) и требуется установить все единые точки отказа — узлы и связи, без которых будут существовать два узла, между которыми не будет пути.
Наивный алгоритм поочередного удаления каждого ребра ((u, v)) и проверки наличия пути (u leadsto v) потребует (O(m^2)) операций. Чтобы научиться находить мосты быстрее, сначала сформулируем несколько утверждений, связанных с обходом в глубину.
Запустим DFS из произвольной вершины. Введем новые виды рёбер:
-
Прямые рёбра — те, по которым были переходы в dfs.
-
Обратные рёбра — то, по которым не было переходов в dfs.
Заметим, что никакое обратное ребро ((u, v)) не может являться мостом: если его удалить, то всё равно будет существовать какой-то путь от (u) до (v), потому что подграф из прямых рёбер является связным деревом.
Значит, остается только проверить все прямые рёбра. Это уже немного лучше — такой алгоритм будет работать за (O(n m)).
Сооптимизировать его до линейного времени (до одного прохода dfs) поможет замечание о том, что обратные рёбра могут вести только «вверх» — к какому-то предку в дереве обхода графа, но не в другие «ветки» — иначе бы dfs увидел это ребро раньше, и оно было бы прямым, а не обратным.
Тогда, чтобы определить, является ли прямое ребро (v to u) мостом, мы можем воспользоваться следующим критерием: глубина (h_v) вершины (v) меньше, чем минимальная глубина всех вершин, соединенных обратным ребром с какой-либо вершиной из поддерева (u).
Для ясности, обозначим эту величину как (d_u), которую можно считать во время обхода по следующей формуле:
[
d_v = min begin{cases}
h_v, &\
d_u, &text{ребро } (v to u) text{ прямое} \
h_u, &text{ребро } (v to u) text{ обратное}
end{cases}
]
Если это условие ((h_v < d_u)) не выполняется, то существует какой-то путь из (u) в какого-то предка (v) или саму (v), не использующий ребро ((v, u)), а в противном случае — наоборот.
const int maxn = 1e5;
bool used[maxn];
int h[maxn], d[maxn];
void dfs(int v, int p = -1) {
used[u] = true;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
for (int u : g[v]) {
if (u != p) {
if (used[u]) // если рябро обратное
d[v] = min(d[v], h[u]);
else { // если рябро прямое
dfs(u, v);
d[v] = min(d[v], d[u]);
if (h[v] < d[v]) {
// ребро (v, u) -- мост
}
}
}
}
}Примечание. Более известен алгоритм, вместо глубин вершин использующий их (tin), но автор считает его чуть более сложным для понимания.
Точки сочленения
Задача поиска точек сочленения не сильно отличается от задачи поиска мостов.
Вершина (v) является точкой сочленения, когда из какого-то её ребёнка (u) нельзя дойти до её предка, не используя ребро ((v, u)). Для конкретного прямого ребра (v to u) этот факт можно проверить так: (h_v leq d_u) (теперь нам нам достаточно нестрогого неравенства, так как если из вершины можно добраться до нее самой, то она все равно будет точкой сочленения).
Используя этот факт, можно оставить алгоритм практически прежним — нужно проверить этот критерий для всех прямых рёбер (v to u):
void dfs(int v, int p = -1) {
used[u] = 1;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
int children = 0; // случай с корнем обработаем отдельно
for (int u : g[u]) {
if (u != p) {
if (used[u])
d[v] = min(d[v], h[u]);
else {
dfs(u, v);
d[v] = min(d[v], d[u]);
if (dp[v] >= tin[u] && p != -1) {
// u -- точка сочленения
}
children++;
}
}
}
if (p == -1 && children > 1) {
// v -- корень и точка сочленения
}
}Единственный крайний случай — это корень, так как в него мы по определению войдём раньше других вершин. Но фикс здесь очень простой — достаточно посмотреть, было ли у него более одной ветви в обходе (если корень удалить, то эти поддеревья станут несвязными между собой).
Топологическая сортировка
Задача топологической сортировки графа звучит так: дан ориентированный граф, нужно упорядочить его вершины в массиве так, чтобы все графа рёбра вели из более ранней вершины в более позднюю.
Это может быть полезно, например, при планировании выполнения связанных задач: вам нужно одеться, в правильном порядке надев шорты (1), штаны (2), ботинки (3), подвернуть штаны (4) — как хипстеры — и завязать шнурки (5).
Во-первых, сразу заметим, что граф с циклом топологически отсортировать не получится — как ни располагай цикл в массиве, все время идти вправо по ребрам цикла не получится.
Во-вторых, верно обратное. Если цикла нет, то его обязательно можно топологически отсортировать — сейчас покажем, как.
Заметим, что вершину, из которой не ведет ни одно ребро, можно всегда поставить последней, а такая вершина в ациклическом графе всегда есть (иначе можно было бы идти по обратным рёбрам бесконечно). Из этого сразу следует конструктивное доказательство: будем итеративно класть в массив вершину, из которой ничего не ведет, и убирать ее из графа. После этого процесса массив надо будет развернуть.
Этот алгоритм проще реализовать, обратив внимание на времена выхода вершин в dfs. Вершина, из которой мы выйдем первой — та, у которой нет новых исходящих ребер. Дальше мы будем выходить только из тех вершин, которые если имеют исходящие ребра, то только в те вершины, из которых мы уже вышли.
Следовательно, достаточно просто выписать вершины в порядке выхода из dfs, а затем полученный список развернуть, и мы получим какую-то из корректных топологических сортировок.
Компоненты сильной связности
Мы только что научились топологически сортировать ациклические графы. А что же делать с циклическими графами? В них тоже иногда требуется найти какую-то структуру.
Для этого можно ввести понятие сильной связности.
Определение. Две вершины ориентированного графа связаны сильно (англ. strongly connected), если существует путь из одной в другую и наоборот. Иными словами, они обе лежат в каком-то цикле.
Понятно, что такое отношение транзитивно: если (a) и (b) сильно связны, и (b) и (c) сильно связны, то (a) и (c) тоже сильно связны. Поэтому все вершины распадаются на компоненты сильной связности — такое разбиение вершин, что внутри одной компоненты все вершины сильно связаны, а между вершинами разных компонент сильной связности нет.
Самый простой пример сильно-связной компоненты — это цикл. Но это может быть и полный граф, или сложное пересечение нескольких циклов.
Часто рассматривают граф, составленный из самих компонент сильной связности, а не индивидуальных вершин. Очевидно, такой граф уже будет ациклическим, и с ним проще работать. Задачу о сжатии каждой компоненты сильной связности в одну вершину называют конденсацией графа, и её решение мы сейчас опишем.
Если мы знаем, какие вершины лежат в каждой компоненте сильной связности, то построить граф конденсации несложно: дальше нужно лишь провести некоторые манипуляции со списками смежности. Поэтому сразу сведем исходную задачу к нахождению самих компонент.
Лемма. Запустим dfs. Пусть (A) и (B) — две различные компоненты сильной связности, и пусть в графе конденсации между ними есть ребро (A to B). Тогда:
[
maxlimits_{a in A}(tout_a) > maxlimits_{bin B}(tout_b)
]
Доказательство. Рассмотрим два случая, в зависимости от того, в какую из компонент dfs зайдёт первым.
Пусть первой была достигнута компонента (A), то есть в какой-то момент времени dfs заходит в некоторую вершину (v) компоненты (A), и при этом все остальные вершины компонент (A) и (B) ещё не посещены. Но так как по условию в графе конденсаций есть ребро (A to B), то из вершины (v) будет достижима не только вся компонента (A), но и вся компонента (B). Это означает, что при запуске из вершины (v) обход в глубину пройдёт по всем вершинам компонент (A) и (B), а, значит, они станут потомками по отношению к (v) в дереве обхода, и для любой вершины (u in A cup B, u ne v) будет выполнено (tout_v] > tout_u), что и утверждалось.
Второй случай проще: из (B) по условию нельзя дойти до (A), а значит, если первой была достигнута (B), то dfs выйдет из всех её вершин ещё до того, как войти в (A).
Из этого факта следует первая часть решения. Отсортируем вершины по убыванию времени выхода (как бы сделаем топологическую сортировку, но на циклическом графе). Рассмотрим компоненту сильной связности первой вершины в сортировке. В эту компоненту точно не входят никакие рёбра из других компонент — иначе нарушилось бы условие леммы, ведь у первой вершины (tout) максимальный . Поэтому, если развернуть все рёбра в графе, то из этой вершины будет достижима своя компонента сильной связности (C^prime), и больше ничего — если в исходном графе не было рёбер из других компонент, то в транспонированном не будет ребер в другие компоненты.
После того, как мы сделали это с первой вершиной, мы можем пойти по топологически отсортированному списку дальше и делать то же самое с вершинами, для которых компоненту связности мы ещё не отметили.
vector<int> g[maxn], t[maxn];
vector<int> order;
bool used[maxn];
int component[maxn];
int cnt_components = 0;
// топологическая сортировка
void dfs1(int v) {
used[v] = true;
for (int u : g[v]) {
if (!used[u])
dfs1(u);
order.push_back(v);
}
// маркировка компонент сильной связности
void dfs2(int v) {
component[v] = cnt_components;
for (int u : t[v])
if (cnt_components[u] == 0)
dfs2(u);
}
// в содержательной части main:
// транспонируем граф
for (int v = 0; v < n; v++)
for (int u : g[v])
t[u].push_back(v);
// запускаем топологическую сортировку
for (int i = 0; i < n; i++)
if (!used[i])
dfs1(i);
// выделяем компоненты
reverse(order.begin(), order.end());
for (int v : order)
if (component[v] == 0)
dfs2(v);TL;DR:
-
Сортируем вершины в порядке убывания времени выхода.
-
Проходимся по массиву вершин в этом порядке, и для ещё непомеченных вершин запускаем dfs на транспонированном графе, помечающий все достижимые вершины номером новой компонентой связности.
После этого номера компонент связности будут топологически отсортированы.
2-SAT
Ликбез. Конъюнкция — это «правильный» термин для логического «И» (обозначается (wedge) или &). Конъюкция возвращает true тогда и только тогда, когда обе переменные true.
Ликбез. Дизъюнкция — это «правильный» термин для логического «ИЛИ» (обозначается (vee) или |). Дизъюнкция возвращает false тогда и только тогда, когда обе переменные false.
Рассмотрим конъюнкцию дизъюнктов, то есть «И» от «ИЛИ» от каких-то перемений или их отрицаний. Например, такое выражение:
(a | b) & (!c | d) & (!a | !b)Если буквами: (А ИЛИ B) И (НЕ C ИЛИ D) И (НЕ A ИЛИ НЕ B).
Можно показать, что любую логическую формулу можно представить в таком виде.
Задача satisfiability (SAT) заключается в том, чтобы найти такие значения переменных, при которых выражение становится истинным, или сказать, что такого набора значений нет. Для примера выше такими значениями являются a=1, b=0, c=0, d=1 (убедитесь, что каждая скобка стала true).
В случае произвольных формул эта задача быстро не решается. Мы же хотим решить её частный случай — когда у нас в каждой скобке ровно две переменные (2-SAT).
Казалось бы — причем тут графы? Заметим, что выражение (a , | , b) эквивалентно (!a rightarrow b ,| , !b rightarrow a). Здесь «(rightarrow)» означает импликацию («если (a) верно, то (b) тоже верно»). С помощью это подстановки приведем выражение к другому виду — импликативному.
Затем построим граф импликаций: для каждой переменной в графе будет по две вершины, (обозначим их через (x) и (!x)), а рёбра в этом графе будут соответствовать импликациям.
Заметим, что если для какой-то переменной (x) выполняется, что из (x) достижимо (!x), а из (!x) достижимо (x), то задача решения не имеет. Действительно: какое бы значение для переменной (x) мы бы ни выбрали, мы всегда придём к противоречию — что должно быть выбрано и обратное ему значение.
Оказывается, что это условие является не только достаточным, но и необходимым. Доказательством этого факта служит описанный ниже алгоритм.
Переформулируем данный критерий в терминах теории графов. Если из одной вершины достижима вторая и наоборот, то эти две вершины находятся в одной компоненте сильной связности. Тогда критерий существования решения звучит так: для того, чтобы задача 2-SAT имела решение, необходимо и достаточно, чтобы для любой переменной (x) вершины (x) и (!x) находились в разных компонентах сильной связности графа импликаций.
Пусть решение существует, и нам надо его найти. Заметим, что, несмотря на то, что решение существует, для некоторых переменных может выполняться, что из (x) достижимо (!x) или из (!x) достижимо (x) (но не одновременно). В таком случае выбор одного из значений переменной (x) будет приводить к противоречию, в то время как выбор другого — не будет. Научимся выбирать из двух значений то, которое не приводит к возникновению противоречий. Сразу заметим, что, выбрав какое-либо значение, мы должны запустить из него обход в глубину/ширину и пометить все значения, которые следуют из него, т.е. достижимы в графе импликаций. Соответственно, для уже помеченных вершин никакого выбора между (x) и (!x) делать не нужно, для них значение уже выбрано и зафиксировано. Нижеописанное правило применяется только к непомеченным ещё вершинам.
Утверждается следующее. Пусть (space{rm comp}[V]) обозначает номер компоненты сильной связности, которой принадлежит вершина (V), причём номера упорядочены в порядке топологической сортировки компонент сильной связности в графе компонентов (т.е. более ранним в порядке топологической сортировки соответствуют большие номера: если есть путь из (v) в (w), то (space{rm comp}[v] leq space{rm comp}[w])). Тогда, если (space{rm comp}[x] < space{rm comp}[!x]), то выбираем значение !x, иначе выбираем x.
Докажем, что при таком выборе значений мы не придём к противоречию. Пусть, для определённости, выбрана вершина (x) (случай, когда выбрана вершина (!x), доказывается также).
Во-первых, докажем, что из (x) не достижимо (!x). Действительно, так как номер компоненты сильной связности (space{rm comp}[x]) больше номера компоненты (space{rm comp}[!x]) , то это означает, что компонента связности, содержащая (x), расположена левее компоненты связности, содержащей (!x), и из первой никак не может быть достижима последняя.
Во-вторых, докажем, что из любой вершины (y), достижимой из (x) недостижима (!y). Докажем это от противного. Пусть из (x) достижимо (y), а из (y) достижимо (!y). Так как из (x) достижимо (y), то, по свойству графа импликаций, из (!y) будет достижимо (!x). Но, по предположению, из (y) достижимо (!y). Тогда мы получаем, что из (x) достижимо (!x), что противоречит условию, что и требовалось доказать.
Итак, мы построили алгоритм, который находит искомые значения переменных в предположении, что для любой переменной (x) вершины (x) и (!x) находятся в разных компонентах сильной связности. Выше показали корректность этого алгоритма. Следовательно, мы одновременно доказали указанный выше критерий существования решения.
Эйлеров цикл
Определение. Эйлеров путь — это путь в графе, проходящий через все его рёбра.
Определение. Эйлеров цикл — это эйлеров путь, являющийся циклом.
Для простоты в обоих случаях будем считать, что граф неориентированный.
Также существует понятие гамильтонова пути и цикла — они посещают все вершины по разу, а не рёбра. Нахождение гамильтонова цикла (задача коммивояжера, англ. travelling salesman problem) — одна из самых известных NP-полных задач, в то время как нахождение эйлерового цика решается за линейное время — и мы сейчас покажем, как.
Теорема. Эйлеров цикл существует тогда и только тогда, когда степени всех вершин чётны.
Доказательство. Необходимость показывается так: можно просто взять эйлеров цикл и ориентировать все его ребра в порядке обхода. Тогда из каждой вершины будет выходить столько же рёбер, сколько входить, а значит степень у всех вершин исходного неориентированного графа была четной.
Достаточность докажем конструктивно — предъявим алгоритм нахождения.
const int maxn = 1e5;
set<int> g[maxn];
void euler(int v) {
while (!g[v].empty()) {
u = *g[v].begin();
g[v].erase(g[v].begin());
dfs(u);
}
cout << v << " ";
}Если условие на четность степеней вершин выполняется, то этот алгоритм действительно выводит эйлеров цикл, то есть последовательность из ((m+1)) вершин, между соседними есть связи.
Следствие. Эйлеров путь существует тогда и только тогда, когда количество вершин с нечётными степенями не превосходит 2.
Кстати, аналогичная теорема есть и для ориентированного графа (можете сами попытаться сформулировать).
Доказать это можно например через лемму о рукопожатиях.
Как теперь мы будем решать задачу нахождения цикла в предположении, что он точно есть. Давайте запустимся из произвольной вершины, пройдем по любому ребру и удалим его.
void euler(int v){
stack >s;
s.push({v, -1});
while (!s.empty()) {
v = s.top().first;
int x = s.top().second;
for (int i = 0; i < g[v].size(); i++){
pair e = g[v][i];
if(!u[e.second]){
u[e.second]=1;
s.push(e);
break;
}
}
if (v == s.top().first) {
if (~x) {
p.push_back(x);
}
s.pop();
}
}
}Упражнение. Сформулируйте и докажите аналогичные утверждения для случая ориентированного графа.
Графы, DFS, MST
A. Топологическая сортировка
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 256 мегабайт
ввод: стандартный ввод
вывод: стандартный вывод
Дан ориентированный невзвешенный граф. Необходимо его топологически отсортировать.
Входные данные
В первой строке входного файла даны два натуральных числа N и M (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 100 000) — количество вершин и рёбер в графе соответственно. Далее в M строках перечислены рёбра графа. Каждое ребро задаётся парой чисел — номерами начальной и конечной вершин соответственно.
Выходные данные
Вывести любую топологическую сортировку графа в виде последовательности номеров вершин. Если граф невозможно топологически отсортировать, вывести -1.
Примеры
входные данные
6 6 1 2 3 2 4 2 2 5 6 5 4 6
выходные данные
Решение
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 256 мегабайт
ввод: стандартный ввод
вывод: стандартный вывод
Дан неориентированный граф, не обязательно связный, но не содержащий петель и кратных рёбер. Требуется найти все мосты в нём.
Входные данные
Первая строка входного файла содержит два натуральных числа n и m — количества вершин и рёбер графа соответственно (1 ≤ n ≤ 20 000, 1 ≤ m ≤ 200 000).
Следующие m строк содержат описание рёбер по одному на строке. Ребро номер i описывается двумя натуральными числами bi, ei — номерами концов ребра (1 ≤ bi, ei ≤ n).
Выходные данные
Первая строка выходного файла должна содержать одно натуральное число b — количество мостов в заданном графе. На следующей строке выведите b целых чисел — номера рёбер, которые являются мостами, в возрастающем порядке. Рёбра нумеруются с единицы в том порядке, в котором они заданы во входном файле.
Примеры
входные данные
6 7 1 2 2 3 3 4 1 3 4 5 4 6 5 6
выходные данные
Решение
C. Точки сочленения
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 256 мегабайт
ввод: стандартный ввод
вывод: стандартный вывод
Дан неориентированный граф. Требуется найти все точки сочленения в нём.
Входные данные
Первая строка входного файла содержит два натуральных числа n и m — количества вершин и рёбер графа соответственно (1 ≤ n ≤ 20 000, 1 ≤ m ≤ 200 000).
Следующие m строк содержат описание рёбер по одному на строке. Ребро номер i описывается двумя натуральными числами bi, ei — номерами концов ребра (1 ≤ bi, ei ≤ n).
Выходные данные
Первая строка выходного файла должна содержать одно натуральное число b — количество точек сочленения в заданном графе. На следующей строке выведите b целых чисел — номера вершин, которые являются точками сочленения, в возрастающем порядке.
Примеры
входные данные
6 7 1 2 2 3 2 4 2 5 4 5 1 3 3 6
выходные данные
Решение
D. Компоненты реберной двусвязности
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 64 мегабайта
ввод: стандартный ввод
вывод: стандартный вывод
Компонентой реберной двусвязности графа 〈 V,E 〉 называется подмножество вершин S ⊂ V, такое что для любых различных u и v из этого множества существует не менее двух реберно не пересекающихся путей из u в v.
Дан неориентированный граф. Требуется выделить компоненты реберной двусвязности в нем.
Входные данные
Первая строка входного файла содержит два натуральных числа n и m — количества вершин и ребер графа соответственно (1 ≤ n ≤ 20 000, 1 ≤ m ≤ 200 000).
Следующие m строк содержат описание ребер по одному на строке. Ребро номер i описывается двумя натуральными числами bi, ei — номерами концов ребра (1 ≤ bi, ei ≤ n).
Выходные данные
В первой строке выходного файла выведите целое число k — количество компонент реберной двусвязности графа. Во второй строке выведите n натуральных чисел a1, a2, …, an, не превосходящих k, где ai — номер компоненты реберной двусвязности, которой принадлежит i-я вершина.
Примеры
входные данные
6 7 1 2 2 3 3 1 1 4 4 5 4 6 5 6
выходные данные
Решение
E. Компоненты вершинной двусвязности
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 64 мегабайта
ввод: стандартный ввод
вывод: стандартный вывод
Компонентой вершинной двусвязности графа 〈 V,E 〉 называется максимальный по включению подграф (состоящий из вершин и ребер), такой что любые два ребра из него лежат на вершинно простом цикле.
Дан неориентированный граф без петель. Требуется выделить компоненты вершинной двусвязности в нем.
Входные данные
Первая строка входного файла содержит два натуральных числа n и m — количества вершин и ребер графа соответственно (1 ≤ n ≤ 20 000, 1 ≤ m ≤ 200 000).
Следующие m строк содержат описание ребер по одному на строке. Ребро номер i описывается двумя натуральными числами bi, ei — номерами концов ребра (1 ≤ bi, ei ≤ n).
Выходные данные
В первой строке выходного файла выведите целое число k — количество компонент вершинной двусвязности графа. Во второй строке выведите m натуральных чисел a1, a2, …, am, не превосходящих k, где ai — номер компоненты вершинной двусвязности, которой принадлежит i-е ребро. Ребра нумеруются с единицы в том порядке, в котором они заданы во входном файле.
Примеры
входные данные
5 6 1 2 2 3 3 1 1 4 4 5 5 1
выходные данные
Решение
F. Конденсация графа
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 256 мегабайт
ввод: стандартный ввод
вывод: стандартный вывод
Требуется найти количество ребер в конденсации ориентированного графа. Примечание: конденсация графа не содержит кратных ребер.
Входные данные
Первая строка входного файла содержит два натуральных числа n и m — количество вершин и ребер графа соответственно (n ≤ 10 000, m ≤ 100 000). Следующие m строк содержат описание ребер, по одному на строке. Ребро номер i описывается двумя натуральными числами bi, ei — началом и концом ребра соответственно (1 ≤ bi, ei ≤ n). В графе могут присутствовать кратные ребра и петли.
Выходные данные
Единственная строка выходного файла должна содержать одно число — количество ребер в конденсации графа.
Примеры
входные данные
выходные данные
Решение
G. Планирование вечеринки
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 512 мегабайт
ввод: стандартный ввод
вывод: стандартный вывод
Петя планирует вечеринку, это дело непростое. Одна из главных проблем в том, что некоторые его друзья плохо ладят друг с другом, а некоторые — наоборот. В результате у него есть множество требований, например: «Я приду только если придет Гена» или «Если там будет Марина, то меня там точно не будет».
Петя формализовал все требования в следующем виде: «[+-]name1 => [+-]name2», здесь «name1» и «name2» — имена двух друзей Пети, «+» означает, что друг придет в гости, «-» — что не придет. Например, выражение «Если Андрея не будет, то Даша не придет» записывается так: «-andrey => -dasha».
Помогите Пете составить хоть какой-нибудь список гостей, удовлетворяющий всем свойствам, или скажите, что это невозможно
Входные данные
В первой строке входного файла записаны числа n и m — число друзей Пети и число условий (1 ≤ n, m ≤ 1000). В следующих n строках записаны имена друзей. Имена друзей состоят из маленьких латинских букв и имеют длину не больше 10. В следующих m строках записаны условия.
Выходные данные
Выведите в первой строке число k — число друзей, которых нужно пригласить. В следующих k строках выведите их имена.
Примеры
входные данные
3 3 vova masha gosha -vova => -masha -masha => +gosha +gosha => +vova
выходные данные
входные данные
выходные данные
входные данные
2 4 vova masha +vova => +masha +masha => -vova -vova => -masha -masha => +vova
выходные данные
Решение
H. Авиаперелеты
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 256 мегабайт
ввод: avia.in
вывод: avia.out
Главного конструктора Петю попросили разработать новую модель самолета для компании «Air Бубундия». Оказалось, что самая сложная часть заключается в подборе оптимального размера топливного бака.
Главный картограф «Air Бубундия» Вася составил подробную карту Бубундии. На этой карте он отметил расход топлива для перелета между каждой парой городов.
Петя хочет сделать размер бака минимально возможным, для которого самолет сможет долететь от любого города в любой другой (возможно, с дозаправками в пути).
Входные данные
Первая строка входного файла содержит натуральное число n (1 ≤ n ≤ 1000) — число городов в Бубундии.
Далее идут n строк по n чисел каждая. j-ое число в i-ой строке равно расходу топлива при перелете из i-ого города в j-ый. Все числа не меньше нуля и меньше 10^9. Гарантируется, что для любого i в i-ой строчке i-ое число равно нулю.
Выходные данные
Первая строка выходного файла должна содержать одно число — оптимальный размер бака.
Примеры
входные данные
4 0 10 12 16 11 0 8 9 10 13 0 22 13 10 17 0
выходные данные
Решение
I. Остовное дерево
ограничение по времени на тест: 4 секунды
ограничение по памяти на тест: 256 мегабайт
ввод: стандартный ввод
вывод: стандартный вывод
Даны точки на плоскости, являющиеся вершинами полного графа. Вес ребра равен расстоянию между точками, соответствующими концам этого ребра. Требуется в этом графе найти остовное дерево минимального веса.
Входные данные
Первая строка входного файла содержит натуральное число n — количество вершин графа (1 ≤ n ≤ 10 000). Каждая из следующих n строк содержит два целых числа xi, yi — координаты i-й вершины ( - 10 000 ≤ xi, yi ≤ 10 000). Никакие две точки не совпадают.
Выходные данные
Первая строка выходного файла должна содержать одно вещественное число — вес минимального остовного дерева.
Примеры
входные данные
выходные данные
Решение
J. Остовное дерево 2
ограничение по времени на тест: 2 секунды
ограничение по памяти на тест: 256 мегабайт
ввод: стандартный ввод
вывод: стандартный вывод
Требуется найти в связном графе остовное дерево минимального веса.
Входные данные
Первая строка входного файла содержит два натуральных числа n и m — количество вершин и ребер графа соответственно. Следующие m строк содержат описание ребер по одному на строке. Ребро номер i описывается тремя натуральными числами bi, ei и wi — номера концов ребра и его вес соответственно (1 ≤ bi, ei ≤ n, 0 ≤ wi ≤ 100 000). n ≤ 200 000, m ≤ 200 000.
Граф является связным.
Выходные данные
Первая строка выходного файла должна содержать одно натуральное число — вес минимального остовного дерева.
Примеры
входные данные
4 4 1 2 1 2 3 2 3 4 5 4 1 4
выходные данные
Решение
K. Алгоритм двух китайцев
ограничение по времени на тест: 6 секунд
ограничение по памяти на тест: 256 мегабайт
ввод: стандартный ввод
вывод: стандартный вывод
Вам дан взвешенный ориентированный граф, содержащий n вершин и m рёбер. Найдите минимально возможную сумму весов n - 1 ребра, которые нужно оставить в графе, чтобы из вершины с номером 1 по этим ребрам можно было добраться до любой другой вершины.
Входные данные
В первой строке даны два целых числа n и m (1 ≤ n ≤ 1 000, 0 ≤ m ≤ 10 000) — количество вершин и ребер в графе.
В следующих m строках даны ребра графа. Ребро описывается тройкой чисел ai, bi и wi (1 ≤ ai, bi ≤ n; - 10^9 ≤ wi ≤ 10^9) — номер вершины, из которой исходит ребро, номер вершины, в которую входит ребро, и вес ребра.
Выходные данные
Если нельзя оставить подмножество ребер так, чтобы из вершины с номером 1 можно было добраться до любой другой, в единственной строке выведите «NO».
Иначе, в первой строке выведите «YES», а во второй строке выведите минимальную возможную сумму весов ребер, которых необходимо оставить.
Примеры
входные данные
выходные данные
входные данные
4 5 1 2 2 1 3 3 1 4 3 2 3 2 2 4 2
выходные данные
Решение
Добавил:
Вуз:
Предмет:
Файл:
Царев Р. Ю. Алгоритмы и структуры данных (CDIO) by Коллектив авторов (z-lib.org).pdf
Скачиваний:
82
Добавлен:
28.12.2020
Размер:
4.31 Mб
Скачать

Алгоритмы и структуры данных (CDIO)
выполнения алгоритма поиска в ширину порядка O(е), т. е. такое же, как и для алгоритма поиска в глубину.
Метод поиска в ширину можно использовать для обнаружения циклов в произвольном графе, причем за время O(п) (п – количество вершин графа), которое не зависит от количества ребер. Как показано в п. 7.1, граф с п вершинами и с n или большим количеством ребер обязательно имеет цикл. Однако если в графе п – 1 или меньше ребер, то цикл может быть только в том случае, когда граф состоит из двух или более связных компонент. Один из способов нахождения циклов состоит в построении остовного леса методом поиска в ширину. Тогда каждое поперечное ребро (v, w) замыкает простой цикл, состоящий из ребер дерева, ведущих к вершинам v и w от общего предка этих вершин, как показано на рис. 7.10.
Рис. 7.10. Цикл, найденный методом поиска в ширину
Методы поисков в глубину и в ширину часто используются как основа при разработке различных эффективных алгоритмов работы с графами. Например, оба этих метода можно применить для нахождения связных компонент графа, поскольку связные компоненты представимы отдельными деревьями в остовном лесу графа.
Точкой сочленения графа называется такая вершина v, когда при удалении этой вершины и всех ребер, инцидентных вершине v, связная компонента графа разбивается на две или несколько частей. Например, точками сочленения для графа из рис. 7.8, а являются вершины а и с. Если удалить вершину а, то граф, который является одной связной компонентой, разбивается на два «треугольника» {b, d, е} и {с, f, g}. Если удалить вершину с, то граф расчленяется на подграфы {а, b, d, е} и {f, g}. Но если удалить какую-либо другую вершину, то в этом случае не удастся разбить
150

7. Неориентированные графы
связную компоненту на несколько частей. Связный граф, не имеющий точек сочленения, называется двусвязным. Для нахождения двусвязных компонент графа часто используется метод поиска в глубину.
Метод нахождения точек сочленения часто применяется для решения важной проблемы, касающейся k-связности графов. Граф называется k-связным, если удаление любых k – 1 вершин не приведет к расчленению графа1. В частности, граф имеет связность 2 или выше тогда и только тогда, когда он не имеет точек сочленения, т. е. только тогда, когда он является двусвязным. Чем выше связность графа, тем больше можно удалить вершин из этого графа, не нарушая его целостности, т. е. не разбивая его на отдельные компоненты.
Опишем простой алгоритм нахождения всех точек сочленения связного графа, основанный на методе поиска в глубину. При отсутствии этих точек граф, естественно, будет двусвязным, т. е. этот алгоритм можно рассматривать так же, как тест на двусвязность неориентированного графа.
1.Выполняется обход графа методом поиска в глубину, при этом для всех вершин v вычисляются числа dfnumber[v], введенные в разделе 5.5.
Всущности, эти числа фиксируют последовательность обхода вершин в прямом порядке вершин глубинного остовного дерева.
2.Для каждой вершины v вычисляется число low[v], равное миниму-
му чисел dfnumber потомков вершины v, включая и саму вершину v, и предков w вершины v, для которых существует обратное ребро (х, w), где х – потомок вершины v. Числа low[v] для всех вершин v вычисляются при обходе остовного дерева в обратном порядке, поэтому при вычислении low[v] для вершины v уже подсчитаны числа low[x] для всех потомков х вершины v. Следовательно, low[v] вычисляется как минимум следующих чисел:
а) dfnumber[v];
б) dfnumber[z] всех вершин z, для которых существует обратное реб-
ро (v, z);
в) low[x] всех потомков х вершины v.
3. Теперь точки сочленения определяются следующим образом:
а) корень остовного дерева будет точкой сочленения тогда и только тогда, когда он имеет двух или более сыновей. Так как в остовном дереве, которое получено методом поиска в глубину, нет поперечных ребер, то удаление такого корня расчленит остовное дерево на отдельные поддеревья с корнями, являющимися сыновьями корня построенного остовного дерева;
1 Существует другое, более конструктивное определение k-связности. Граф называется k-связным, если между любой парой вершин v и w существует не менее k разных путей, таких, что, за исключением вершин v и w, ни одна из вершин, входящих в один путь, не входит ни в какой другой из этих путей.
151

Алгоритмы и структуры данных (CDIO)
б) вершина v, отличная от корня, будет точкой сочленения тогда
итолько тогда, когда имеет такого сына w, что low[w] ≥ dfnumber[v]. В этом случае удаление вершины v (и, конечно, всех инцидентных ей ребер) отделит вершину w и всех ее потомков от остальной части графа. Если же low[w] < dfnumber[v], то существует путь по ребрам дерева к потомкам вершины w и обратное ребро от какого-нибудь из этих потомков к истинному предку вершины v (именно значение dfnumber для этого предка равно low[w]). Поэтому в данном случае удаление вершины v не отделит от графа поддерево с корнем w.
Числа dfnumber и low, подсчитанные для вершин графа из рис. 7.8, а, показаны на рис. 7.11. В этом примере вычисление чисел low начато в обратном порядке с вершины е. Из этой вершины выходят обратные ребра (е, а)
и(е, b), поэтому low[e] = min(dfnumber[e], dfnumber[a], dfnumber[b]) = 1.
Затем рассматривается вершина d, для нее low[d] находится как минимум чисел dfnumber[d], low[e] и dfnumber[a]. Здесь число low[e] участвует потому, что вершина е является сыном вершины d, а число dfnumber[a] – из-за того, что существует обратное ребро (d, а).
Рис. 7.11. Числа dfnumber и low, подсчитанные для графа, изображенного на рис. 7.8, а
Для определения точек сочленения после вычисления всех чисел low просматривается каждая вершина остовного дерева. Корень а является точкой сочленения, так как имеет двух сыновей. Вершина с также является точкой сочленения – для ее сына, вершины f, выполняется неравенство low[f] ≥ dfnumber[c]. Другие вершины не являются точками сочленения.
Время выполнения описанного алгоритма на графе с n вершинами и е ребрами имеет порядок O(е). Можно легко проверить, что время, затрачиваемое на выполнение каждого этапа алгоритма, зависит или от количества посещаемых вершин, или от количества ребер, инцидентных этим вершинам, т. е. в любом случае время выполнения, с точностью до кон-
152

Рис. 7.12. Двудольный граф
7. Неориентированные графы
станты пропорциональности, является функцией как количества вершин, так и количества ребер. Поэтому общее время выполнения алгоритма имеет порядок O(n + е) или O(е), что то же самое при n ≤ е.
7.5.Паросочетания графов
Вэтом разделе будет описан алгоритм решения «задачи о паросочетании» графов. Простым примером, приводящим к такой задаче, может служить ситуация распределения преподавателей по множеству учебных курсов. Надо назначить на чтение каждого курса преподавателя определенной квалификации так, чтобы ни на какой курс не было назначено более одного преподавателя. С другой стороны, желательно использовать максимально возможное количество преподавателей из общего состава.
Описанную ситуацию можно представить
ввиде графа, показанного на рис. 7.12, где все
вершины разбиты на два множества V1 и V2 так,
что вершины из множества V1 соответствуют
преподавателям, а вершины из множества V2 – учебным курсам. Тот факт, что преподаватель v может вести курс w, отражается посредством ребра (v, w). Граф, у которого множество вершин распадается на два непересекающихся подмножества V1 и V2 таких, что каждое ребро графа имеет один конец из V1, а другой – из V2, называется двудольным. Таким образом, задача распределения преподавателей по учебным курсам сводится к задаче выбора определенных ребер в двудольном графе, имеющем множество вершин-преподавателей и множество вершин – учебных курсов.
Задачу паросочетания можно сформулировать следующим образом. Есть граф G = (V, Е). Подмножество его ребер, такое, что никакие два ребра из этого подмножества не инциденты какой-либо одной вершине из V, называется паросочетанием. Задача определения максимального подмножества таких ребер называется задачей нахождения максимального паросочетания. Ребра, выделенные толстыми линиями на рис. 7.12, составляют одно возможное максимальное паросочетание для этого графа. Полным паросочетанием называется паросочетание, в котором участвуют (в качестве концов ребер) все вершины графа. Очевидно, что любое полное паросочетание является также максимальным паросочетанием.
153

Алгоритмы и структуры данных (CDIO)
Существуют прямые способы нахождения максимальных паросочетаний. Например, можно последовательно генерировать все возможные паросочетания, а затем выбрать то, которое содержит максимальное количество ребер. Но такой подход имеет существенный недостаток – время его выполнения является экспоненциальной функцией от числа вершин.
а
б
Рис. 7.13. Паросочетание и чередующаяся цепь: а – паросочетание;
б– чередующаяся цепь
Внастоящее время разработаны более эффективные алгоритмы нахождения максимальных паросочетаний. Эти алгоритмы используют в основном метод, известный как «чередующиеся цепи». Пусть М – паросочетание в графе G. Вершину v будем называть парной, если она является концом одного из ребер паросочетания М. Путь, соединяющий две непарные вершины, в котором чередуются ребра, входящие и не входящие
вмножество М, называется чередующейся (аугментальной) цепью относительно М. Очевидно, что чередующаяся цепь должна быть нечетной длины, начинаться и заканчиваться ребрами, не входящими в множество М. Также ясно, что, имея чередующуюся цепь Р, можно увеличить паросочетание М, удалив из него те ребра, которые входят в цепь Р, и вместо удаленных ребер добавить ребра из цепи Р, которые первоначально не входили в паросочетание М. Это новое паросочетание можно определить как M
P, где обозначает симметрическую разность множеств М и Р, т. е.
вновое множество паросочетаний войдут те ребра, которые входят или
вмножество М, или в множество Р, но не в оба сразу.
154

7. Неориентированные графы
На рис. 7.13, а показаны граф и паросочетание М, состоящее из ребер (на рисунке они выделены толстыми линиями) (1, 6), (3, 7) и (4, 8). На рис. 7.13, б представлена чередующаяся цепь относительно М, состоящая из вершин 2, 6, 1, 8, 4, 9. На рис. 7.14 изображено паросочетание (1, 8), (2, 6), (3, 7), (4, 9), которое получено удалением из паросочетания М ребер, входящих в эту чередующуюся цепь, и добавлением новых ребер, также
|
входящих в эту цепь. |
|
|
Паросочетание М будет максимальным |
|
|
тогда и только тогда, когда не будет существо- |
|
|
вать чередующейся цепи относительно М. Это |
|
|
ключевое свойство максимальных паросо- |
|
|
четаний будет основой следующего алгоритма |
|
|
нахождения максимального паросочетания. |
|
|
Пусть М и N – паросочетания в графе G, |
|
|
причем |М| < |N| (здесь |М| обозначает количе- |
|
|
ство элементов множества М). Для того чтобы |
|
|
показать, что M N содержит чередующуюся |
|
|
цепь относительно М, рассмотрим граф G‘ = |
|
|
= (V‘, М N), |
где V‘ – множество концевых |
|
вершин ребер, |
входящих в М N. Нетрудно |
|
заметить, что каждая связная компонента гра- |
Рис. 7.14. Увеличенное |
|
|
фа G‘ формирует простой путь (возможно, |
||
|
паросочетание |
||
|
цикл), в котором чередуются ребра из М и N. |
||
Каждый цикл имеет равное число ребер, при-
надлежащих М и N, а каждый путь, не являющийся циклом, представляет собой чередующуюся цепь относительно или М, или N, в зависимости от того, ребер какого паросочетания больше в этой цепи. Поскольку |М| < |N|, то множество M N содержит больше ребер из паросочетания N, чем М, и, следовательно, существует хотябыодначередующаясяцепьотносительно М.
Теперь можно описать алгоритм нахождения максимального паросочетания М для графа G = (V, Е).
1.Сначала положим М = .
2.Далее ищем чередующуюся цепь Р относительно М, и множество
М заменяется на множество M P.
3. Шаг 2 повторяется до тех пор, пока существуют чередующиеся цепи относительно М. Если таких цепей больше нет, то М – максимальное паросочетание.
Теперь осталось показать способ построения чередующихся цепей относительно паросочетания М. Рассмотрим более простой случай, когда граф G является двудольным графом с множеством вершин, разбитым на два подмножества V1 и V2. Будем строить граф чередующейся цепи,
155

Алгоритмы и структуры данных (CDIO)
по уровням i = 0, 1, 2, …, используя процесс, подобный поиску в ширину. Граф чередующейся цепи уровня 0 содержит все непарные вершины из множества V1. На уровне с нечетным номером i добавляются новые вершины, смежные с вершинами уровня i – 1 и соединенные ребром, не входящим в паросочетание (это ребро тоже добавляется в строящийся граф). На уровне с четным номером i также добавляются новые вершины, смежные с вершинами уровня i – 1, но которые соединены ребром, входящим в паросочетание (это ребро тоже добавляется в граф чередующейся цепи).
Процесс построения продолжается до тех пор, пока к графу чередующейся цепи можно присоединять новые вершины. Отметим, что непарные вершины присоединяются к этому графу только на нечетном уровне. В построенном графе путь от любой вершины нечетного уровня до любой вершины уровня 0 является чередующейся цепью относительно М.
На рис. 7.15 изображен граф чередующейся цепи, построенный для графа из рис. 7.13, а относительно паросочетания, показанного на рис. 7.14. На уровне 0 имеем одну непарную вершину 5. На уровне 1 добавлено ребро (5, 6), не входящее в паросочетание. На уровне 2 добавлено ребро (6, 2), входящее в паросочетание. На уровне 3 можно добавить или ребро (2, 9), или ребро (2, 10), которые не входят в паросочетание. Поскольку вершины 9 и 10 пока в этом графе непарные, можно остановить процесс построения графа чередующейся цепи, добавив в него одну или другую вершину. Оба пути 9, 2, 6, 5 и 10, 2, 6, 5 являются чередующимися цепями относительно паросочетания из рис. 7.14.
Рис. 7.15. Увеличенное паросочетание
Пусть граф G имеет п вершин и е ребер. Если используются списки смежности для представления ребер, то на построение графа чередующейся цепи потребуется времени порядка O(е). Для нахождения максимального паросочетания надо построить не более п / 2 чередующихся цепей, поскольку каждая такая цепь увеличивает текущее паросочетание не менее чем на одно ребро. Поэтому максимальное паросочетание для двудольного графа можно найти за время порядка O(п е).
156