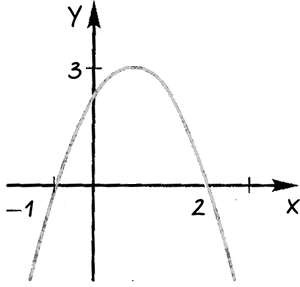Как найти точки пересечения параболы с осями - AvtoShod.ru

В предыдущем уроке мы подробно разобрали,
как построить параболу.
В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.

Как найти нули квадратичной функции

Запомните!

Чтобы найти координаты точек нулей функции, нужно
в исходную функцию подставить вместо «y» число
ноль.

Рассмотрим задачу.

Найти нули квадратичной
функции «y = x² − 3».

Подставим в исходную функцию вместо «y» ноль и решим полученное
квадратное уравнение.

0 = x² − 3
x² − 3 = 0

x_1;2 =

0 ±
√0² − 4 · 1 · (−3)

2 · 1

x_1;2 =

x_1;2 = ±√3

Ответ: нули функции «y = x² − 3» :

x₁ = √3;

x₂ = −√3 .

Как найти при каких значениях
«x» квадратичная функция принимает заданное
числовое значение

Запомните!

Чтобы найти при каких значениях «x» квадратичная функция принимает заданное числовое значение,
нужно:

вместо «y» подставить в функцию заданное числовое значение;
решить полученное квадратное уравнение относительно «x».

Рассмотрим задачу.

При каких значениях «x» функция
«y = x² − x − 3» принимает значение
«−3».

Подставим в исходную функцию
«y = x² − x − 3» вместо «y = −3» и
найдем «x».

y = x² − x − 3

−3 = x² − x − 3
x² − x − 3 = −3
x² − x − 3 + 3 = 0
x² − x = 0
x_1;2 =

1 ±
√1² − 4 · 1 · 0

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 1	x₂ = 0

Ответ: при «x = 0» и
«x = 1» функция «y = x² − x − 3»
принимает значение «y = −3».

Как найти координаты точек пересечения параболы и прямой

Запомните!

Чтобы найти точки пересечения параболы с прямой нужно:

приравнять правые части функций (те части функций, в которых содержатся «x»);
решить полученное уравнение относительно «x»;
подставить полученные числовые значения «x»
в любую из функций и найти координаты точек по оси «Оy».

Рассмотрим задачу.

Найти координаты точек пересечения параболы «y = x²»
и прямой «y = 3 − 2x».

Приравняем правые части функций и решим
полученное уравнение относительно «x».

x² = 3 − 2x
x² − 3 + 2x = 0
x² + 2x − 3 = 0

x_1;2 =

−2 ±
√2² − 4 · 1 · (−3)

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 1	x₂ = −3

Теперь подставим в любую из заданных функций (например, в
«y = 3 − 2x») полученные
числовые значения «x», чтобы найти координаты
«y» точек пересечения.

1) x = −3
y = 3 − 2x
y(−3) = 3 − 2 · (−3) = 3 − (−6) = 3 + 6 = 9
(·) A (−3; 9) — первая точка пересечения.

2) x = 1
y = 3 − 2x
y(1) = 3 − 2 · 1 = 3 − 2 = 1
(·) B (1; 1) — вторая точка пересечения.

Запишем полученные точки пересечения с их координатами в ответ.

Ответ: точки пересечения параболы
«y = x²»
и прямой «y = 3 − 2x»:
(·) A (−3; 9) и
(·) B (1; 1).

Как определить, принадлежит ли точка графику функции параболы

Запомните!

Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.

Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.

Если получится верное равенство, значит, точка принадлежит графику функции.
Если получится неверное равенство, значит, точка
не принадлежит графику функции.

Рассмотрим задачу:

Не строя графика функции «y = x²», определить, какие точки принадлежат ему:
(·) А(2; 6),
(·) B(−1; 1).

Подставим в функцию
«y = x²»

координаты точки (·) А(2; 6).

y = x²
6 = 2²
6 = 4

(неверно)

Значит, точка (·) А(2; 6)
не принадлежит графику функции
«y = x²».

Подставим в функцию
«y = x²»

координаты точки (·) B(−1; 1).

y = x²
1 = (−)1²
1 = 1

(верно)

Значит, точка (·) B(−1; 1)
принадлежит графику функции
«y = x²».

Как найти точки пересечения параболы с осями координат

Рассмотрим задачу

Найти координаты точек пересечения параболы
«y = x² −3x + 2» с осями координат.

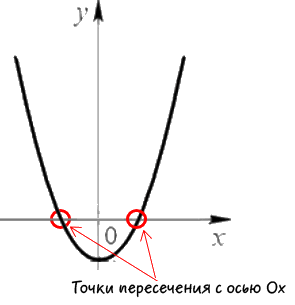
Сначала определим точки пересечения функции с осью «Ox».
На графике функции эти точки выглядят так:

Как видно на рисунке выше, координата «y» точек пересечения с осью «Ox»
равна нулю, поэтому подставим «y = 0» в
исходную функцию «y = x² −3x + 2»
и найдем их координаты по оси «Ox».

0 = x² −3x + 2
x² −3x + 2 = 0

x_1;2 =

3 ±
√3² − 4 · 1 · 2

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 2	x₂ = 1

Запишем координаты точек пересечения графика с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).

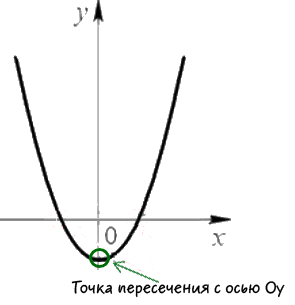
Теперь найдем координаты точки пересечения с осью «Oy».

Как видно на рисунке выше, координата «x»
точки пересечения с осью «Oy» равна нулю.

Подставим «x = 0»
в исходную функцию
«y = x² −3x + 2»
и найдем координату точки по оси
«Oy».

y(0) = 0² − 3 · 0 + 2 = 2

Выпишем координаты полученной точки: (·) C (0; 2)

Запишем в ответ все координаты точек пересечения параболы с осями.

Ответ: точки пересечения с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
С осью «Oy»: (·)C (0; 2).

Как определить при каких значениях x функция принимает
положительные или
отрицательные значения

Напоминаем, что когда в задании говорится «функция принимает
значения» — речь идет о
значениях«y».
Другими словами, необходимо ответить на вопрос: при каких значениях
«x», координата
«y» положительна или отрицательна.

Запомните!

Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:

провести прямые через точки в местах, где график пересекает ось «Ox»;
определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
записать ответ для каждого промежутка относительно «x».

Рассмотрим задачу.

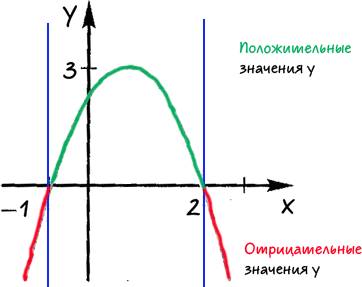
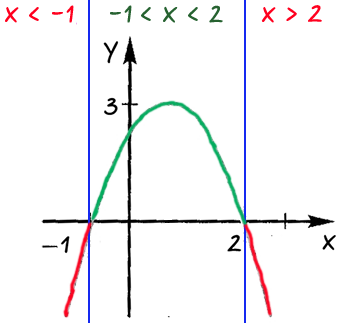
С помощью графика квадратичной функции, изображенного на рисунке, ответить:
При каких значениях «x» функция принимает 1) положительные значения; 2) отрицательные значения.

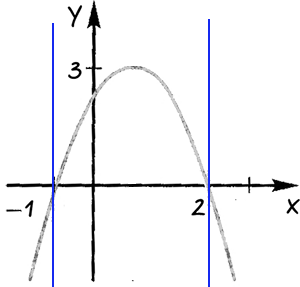
Проведем через точки, где график функции пересекает ось «Ox» прямые.

Определим области, где функция принимает отрицательные или положительные значения.

Подпишем над каждой полученной областью, какие значения принимает
«x» в каждой из выделенных областей.

Ответ: при «x < −1» и
«x > 2» функция принимает отрицательные значения;
при «−1 < x < 2» функция принимает
положительные значения.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Расположение графика квадратного трёхчлена относительно осей координат

В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:

$$ ax^2+bx+c = a(x+ frac{b}{2a})^2-frac{D}{4a}, D = b^2-4ac $$

Мы получаем:

ось симметрии $x = -frac{b}{2a}$
вершину параболы на оси симметрии $(–frac{b}{2a}; -frac{D}{4a})$
точку пересечения (0;c) с осью OY

Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c).

Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.

Если $D gt 0$, парабола имеет две точки пересечения с $x_1,2 = frac{-b pm sqrt{D}}{2a}$ на оси OX.

Если D = 0, парабола имеет одну точку пересечения $x_0 = -frac{b}{2a}$, которая лежит на оси OX и является вершиной параболы.

Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.

Точки пересечения параболы с осью OX

	$a gt 0$	$a lt 0$
$D gt 0$
$x_(1,2) = frac{-b pm sqrt{D}}{2a}$
D = 0
$x_0 = -frac{b}{2a}$
$ D lt 0 $
${ varnothing }$-нет пересечений

Точки пересечения двух парабол

На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.

Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:

$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$

В точках пересечения выполняется равенство:

$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$

$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$

Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:

$$ Ax^2+Bx+C = 0 $$

Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).

A = B = C = 0

$ a_1 = a_2, b_1 = b_2, $

$ c_1 = c_2 $

Две параболы совпадают

Бесконечное множество общих точек, $x in Bbb R$

$A = B = 0, C neq 0$

$ a_1 = a_2, b_1 = b_2, $

$ c_1 neq c_2 $

Параболы имеют вид

$y = ax^2+bx+c_1$

$ y = ax^2+bx+c_2 $

У них общая ось симметрии

$ x = -frac{b}{2a}$, одна парабола находится над другой.

Ветки сходятся только на бесконечности.

Точек пересечения нет

$A = 0, B neq 0, C = 0$

$ a_1 = a_2, b_1 neq b_2 $

$ c_1 = c_2 $

Параболы имеют вид

$y = ax^2+b_1 x+c$

$ y = ax^2+b_2 x+c $

Обе проходят через точку (0;c).

Это – единственная точка пересечения.

Одна точка пересечения

(0;c)

$A = 0, B neq 0, C neq 0$

$ a_1 = a_2, b_1 neq b_2 $

$ c_1 neq c_2 $

Параболы имеют вид

$y = ax^2+b_1 x+c_1$

$ y = ax^2+b_2 x+c_2 $

Абсцисса точки пересечения

$ x = — frac{C}{B} = -frac{c_1-c_2}{b_1-b_2}$

Одна точка пересечения (касание)

$A neq 0, B = 0, C = 0$

$ a_1 neq a_2, b_1 = b_2 $

$ c_1 = c_2 $

Параболы имеют вид

$ y = a_1 x^2+bx+c$

$ y = a_2 x^2+bx+c $

Пересекаются при x=0 (точка касания)

Одна точка пересечения (касание) (0;c)

$A neq 0, B = 0, C neq 0$

$ a_1 neq a_2, b_1 = b_2 $

$ c_1 neq c_2 $

Параболы имеют вид

$ y = a_1 x^2+bx+c_1$

$ y = a_2 x^2+bx+c_2 $

Не пересекаются, если

$- frac{c_1-c_2}{a_1-a_2} lt 0 $

Две точки пересечения

Если

$- frac{c_1-c_2}{a_1-a_2} gt 0 $

Пересекаются в двух точках

$$ x_{1,2} = pm sqrt{-frac{c_1-c_2}{a_1-a_2}} $$

Две точки пересечения

$A neq 0, B neq 0, C = 0$

$ a_1 neq a_2, b_1 neq b_2 $

$ c_1 = c_2 $

Параболы имеют вид

$$ y = a_1 x^2+b_1 x+c $$

$$ y = a_2 x^2+b_2 x+c $$

Две точки пересечения

$ x_1 = 0 $

$$x_2 = -frac{b_1-b_2}{a_1-a_2}$$

Две точки пересечения,

одна из которых (0;c)

$A neq 0, B neq 0, C neq 0$

$ a_1 neq a_2, b_1 neq b_2 $

$ c_1 neq c_2 $

Все параметры парабол разные

Ищем дискриминант:

$$ D = B^2-4AC $$

Если $D gt 0$

Две точки пересечения

$$ x_1,2 = frac{-B pm sqrt{D}}{2A} $$

Две точки пересечения

Если D = 0

Одна точка пересечения (касание)

$$ x_0 = -frac{B}{2A} $$

Одна точка пересечения

(касание)

Если $D lt 0$

Точек пересечения нет

Внимание!

Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.

Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!

Примеры

Пример 1. Найдите точки пересечения параболы с осями координат:

$а) y = 3x^2+2x-1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -1end{array} right.}$

Пересечение с осью OX:

$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$

$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{3} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ — две точки пересечения

$б) y = -4x^2-3x+1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$

Пересечение с осью OX:

$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$

$$ (4x-1)(x+1) = 0 Rightarrow$$

$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{4} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ — две точки пересечения

$в) y = 5x^2-2x+1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$

Пересечение с осью OX:

$$ 5x^2-2x+1 = 0 $$

$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$

Парабола не пересекает ось OX

$ г) y = -x^2+4x-4 $

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -4end{array} right.}$

Пересечение с осью OX:

$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$

$$ Rightarrow (x-2)^2 = 0 Rightarrow {left{ begin{array}{c} x = 2 \ y = 0 end{array} right.}$$ — одна точка пересечения

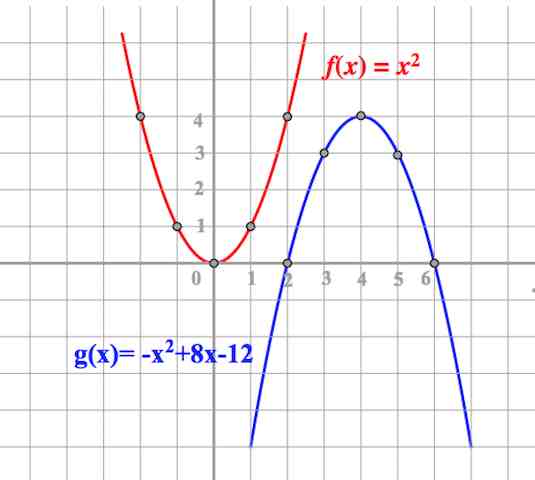
Пример 2*. Даны две параболы

$$ y = 2x^2+5x+1 и y = x^2+3x+k $$

Найдите такое значение параметра k, чтобы параболы

1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.

По условию

$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$

$$ a_1 neq a_2, b_1 neq b_2 $$

A = 2-1 = 1, B = 5-3 = 2, C = 1-k

Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.

1) Параболы имеют две точки пересечения в двух случаях:

1 случай: $c_2 = c_1$, k = 1

$$x_1 = 0, x_2 = -frac{B}{A} = -2$$

$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x+1 end{array} right.} Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x_1 = 0 \ y_1 = 1end{array} right.} \ {left{ begin{array}{c} x_2 = -2 \ y_2 = -1 end{array} right.} end{array} right.$$

2 случай: $c_2 ≠ c_1, D gt 0$

$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$

Например, k = 4

$$ D = 4k = 16 = 4^2 $$

$$ x_1,2 = frac{-B pm sqrt{D}}{2A} = frac{-2 pm 4}{2} = left[ begin{array}{cc} x_1 = -3\ x_2 = 1 end{array} right. $$

Оба случая можем объединить требованием $k gt 0$.

2) Параболы имеют одну точку пересечения, если:

$$ D = 4k = 0 Rightarrow k = 0 $$

$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x end{array} right.} $$

$$ x_0 = frac{-B}{2A} = -1 $$

3) Параболы не имеют общих точек, если:

$$ D = 4k lt 0 Rightarrow k lt 0 $$

Например, k = -1

Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$

Пример 3. Две параболы с общей вершиной

Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.

Пусть уравнения парабол:

$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$

Координаты вершин:

$$ left( -frac{b_1}{2a_1}, — frac{D_1}{4a_1} right), left(- frac{b_2}{2a_2},- frac{D_2}{4a_2} right) $$

По условию:

$$ {left{ begin{array}{c} -frac{b_1}{2a_1} = -frac{b_2}{2a_2} \ -frac{D_1}{4a_1} = -frac{D_2}{4a_2} end{array} right.} Rightarrow {left{ begin{array}{c} frac{b_1}{a_1} = frac{b_2}{2a_2} \ frac{D_1}{a_1} = frac{D_2}{a_2} end{array} right.} $$

Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.

Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac{x^2}{2}-3x+1$.

Координаты вершины:

$$ x_0 = — frac{b}{2a} = — frac{-3}{2 cdot frac{1}{2}} = 3, D = b^2-4ac = 3^2-4 cdot frac{1}{2} cdot 1 = 7 $$

$$ y_0 = — frac{D}{4a} = — frac{7}{4 cdot frac{1}{2}} = -3,5 $$

Уравнение искомой параболы: $y = ax^2+bx+c$

Пропорции для параметров (см. пример 3):

$$ {left{ begin{array}{c} frac{b}{a} = frac{-3}{1/2} = -6 \ frac{D}{a} = frac{7}{1/2} = 14 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = 14a end{array} right.} $$

Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:

$$ {left{ begin{array}{c} a = 1 \ b = -6a = -6 \ D = 14a = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ b^2-4ac = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ 36-4c = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ c = frac{36-14}{4} = 5,5 end{array} right.}$$

$$ y = x^2-6x+5,5 $$

$$ {left{ begin{array}{c} a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ c = — frac{1,44+2,8}{0,8} = -5,3 end{array} right.} $$

$$ y = -0,2x^2+1,2x-5,3 $$

Параболы

$$ y = frac{x^2}{2}-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$

имеют общую вершину (3;-3,5)

Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac{x^2}{3}-2x+5$.

Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.

Координаты вершины траектории кометы:

$$ x_0 = -frac{b}{2a} = -frac{-2}{2 cdot frac{1}{3}} = 3, D = b^2-4ac = 2^2-4 cdot frac{1}{3} cdot 5 = — frac{8}{3} $$

$$ y_0 = — frac{D}{4a} = — frac{-8/3}{4 cdot 1/3} = 2 $$

Уравнение траектории космического аппарата: $y = ax^2+bx+c$.

Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.

Пропорции для параметров (см. пример 3) с учетом c = 0:

$$ {left{ begin{array}{c} frac{b}{a} = frac{-2}{1/3} = -6 \ frac{D}{a} = frac{-frac{8}{3}}{frac{1}{3}} = -8 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = b^2-4a underbrace{c}_{text{= 0 }} = b^2 = -8a end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ b^2 = -8a end{array} right.} Rightarrow $$

$$ {left{ begin{array}{c} b = frac{-8a}{-6a} = frac{4}{3} \ a = -frac{b}{6} = -frac{2}{9} end{array} right.} $$

Уравнение траектории космического аппарата с «перехватом» кометы в вершине:

$$ y = -frac{2}{9} x^2+ frac{4}{3} x $$

Источник

Функция вида

y=ax2+bx+c

, где (a), (b), (c) — реальные числа, (a)

≠

(0), называется квадратичной функцией.

Графиком квадратичной функции является парабола.

Область определения функции (D(f)) — все действительные числа.

Рассмотрим для примера две квадратичные функции.

Пример 1.

y=x2−2x−1

(рис. (1)).

Пример 2.

y=−2×2+4x

(рис. (2)).

Область значений функции (E(f)) считывается с графика, она зависит от координаты (y), вершины параболы и направления ветвей параболы.
(1) пример —

E(f)=[−2;+∞)

;
(2) пример —

E(f)=(−∞;2]

Параметр (a) определяет направление ветвей параболы:
если (a > 0), то ветви направлены вверх (см. пример (1));
если (a < 0), то ветви направлены вниз (см. пример (2)).

Параметр (c) указывает, в какой точке парабола пересекает ось (Oy).

Чтобы построить график квадратичной функции, необходимо:

1) вычислить координаты вершины параболы:

x0=−b2aиy0

— которую находят, подставив значение

в формулу функции;

2) отметить вершину параболы на координатной плоскости, провести ось симметрии параболы;

3) определить направление ветвей параболы;

4) отметить точку пересечения параболы с осью (Oy);

5) составить таблицу значений, выбрав необходимые значения аргумента (x).

Решив квадратное уравнение

ax2+bx+c=0

, получаем точки пересечения параболы с осью (Ox), или корни функции (если дискриминант (D > 0));

если (D < 0), то точек пересечения параболы с осью (Ox) не существует;

если (D = 0), то вершина параболы находится на оси (Ox).

Но не всегда точки пересечения с осью (Ox) являются рациональными числами; если невозможно точно вычислить корень из (D), то такие точки не используют для построения графика.

1. Построй график функции

y=x2−2x−1

x0=−b2a=22=1;y0=12−2⋅1−1=−2.

Ветви параболы направлены вверх, т. к.

(a = 1 > 0).

Парабола пересекает ось (Oy) в точке ((0; -1)).

(x)	(2)	(3)	(4)
(y)	(-1)	(2)	(7)

Симметрично строим левую сторону параболы

Рис. (1). График функции

y=x2−2x−1

2. Построй график функции

y=−2×2+4x

В данном случае легко вычислить корни:

−2×2+4x=0;x(−2x+4)=0;x=0,или−2x+4=0;x=2;x1=0;x2=2.

Координаты вершины параболы:

x0=−42⋅−2=1;y0=−2⋅12+4⋅1=2.

В таблице достаточно одного значения:

если (x = 3), то

Симметрично, если (x = -1),

то (y = -6)

Рис. (2). График функции

y=−2×2+4x

Источник

Функция вида , где называется квадратичной функцией.

График квадратичной функции – парабола.

Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА

, то есть , ,

Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай , , , то есть , то мы получим параболу, симметричную относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:

II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать , , ? Как изменится поведение параболы? При парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях ордината каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при парабола «станет шире» параболы :

Давайте подитожим:

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»

Теперь давайте введем в игру (то есть рассматриваем случай, когда ), будем рассматривать параболы вида . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы вдоль оси вверх или вниз в зависимости от знака :

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда перестанет быть равным .

Здесь для построения параболы нам понадобится формула для вычисления вершины: $x_o=frac{-b}{2a}$ , .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы :

$x_o=frac{4}{2}=2$ , . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы , ведь в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку . Действительно, подставив в формулу x=0, получим, что . То есть ордината точки пересечения параболы с осью (оу), это . В нашем примере (выше), парабола пересекает ось ординат в точке , так как .

2) осью симметрии параболы является прямая $x=frac{-b}{2a}$ , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая к , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение . В зависимости от дискриминанта, будем получать одну (, $x=-frac{b}{2a}$ ), две (, $x_{1,2}=frac{-bpmsqrt{b^2-4ac}}{2a}$ ) или нИсколько () точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана в виде

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины параболы по формуле $x_o=frac{-b}{2a}$ , .

3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если , то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение

Пример 1

Пример 2

Замечание 1. Если же парабола изначально нам задана в виде , где – некоторые числа (например, ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины . Почему?

Возьмем квадратный трехчлен и выделим в нем полный квадрат: $ax^2+bx+c=a(x^2+frac{b}{a}x+frac{c}{a})=a((x^2+2frac{b}{2a}x+frac{b^2}{4a^2})-frac{b^2}{4a^2}+frac{c}{a})=a(x+frac{b}{2a})^2-frac{b^2}{4a}+c.$ Посмотрите, вот мы и получили, что $m=frac{-b}{2a}$ , $n=-frac{b^2}{4a}+c=y(frac{-b}{2a})$ . Мы с вами ранее называли вершину параболы , то есть теперь , .

Например, $y=-frac{1}{3}{(x+2)}^2+6$ . Отмечаем на плоскости вершину параболы , понимаем, что ветви направлены вниз, парабола расширена (относительно ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

Источник

В уравнении квадратичной функции:

a – старший коэффициент

b – второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции y=x^2 имеет вид:

Точки, обозначенные зелеными кружками – это, так
называемые «базовые точки». Чтобы найти координаты этих точек для
функции y=x^2 , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент a=1 , то график квадратичной функции имеет ровно такую же форму, как график функции y=x^2 при любых значениях остальных коэффициентов.

График функции y=-x^2 имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции y=-x^2 симметричен графику функции y=x^2 относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

В процессе решения квадратного уравнения находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если D<0 ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

2. Если D=0 ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

$x_1={-b+sqrt{D}}/{2a}$ , $x_2={-b-sqrt{D}}/{2a}$

Если ,то график функции выглядит примерно так:

Следующий важный параметр графика квадратичной функции – координаты вершины параболы:

$x_0=-{b/{2a}}$

$y_0=-{D/{4a}}=y(x_0)$

Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы.

И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c .