Как найти точки пересечения функций в excel

Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.

Строим графики с точками пересечений

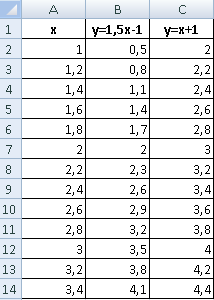
Имеются две функции, по которым нужно построить графики:

Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:

1. Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
2. Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.

Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.



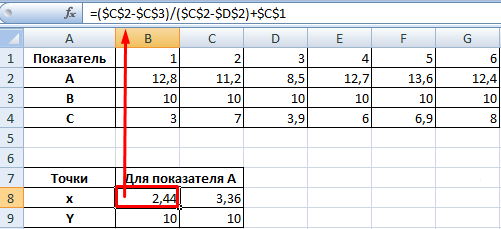
Находим точку пересечения графиков в Excel

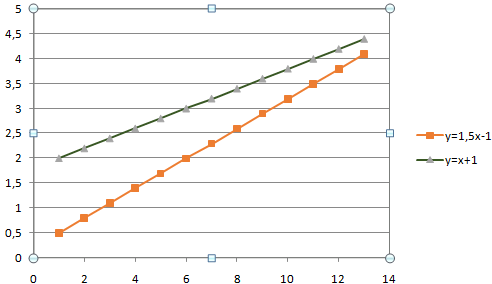
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.

Первый способ. Найти общие значения в рядах данных для указанных функций.

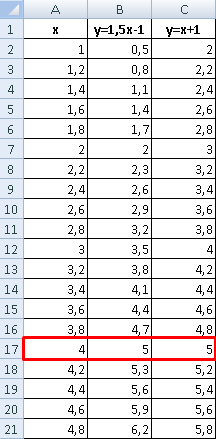
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.

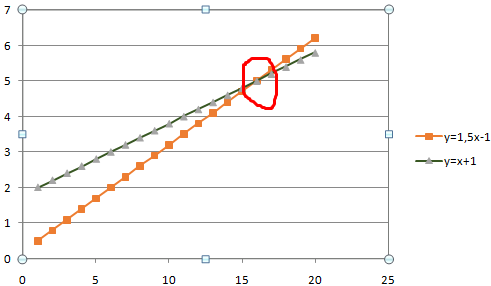
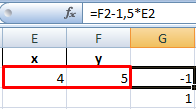
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.

Изменим график, добавив новые данные. Получим две пересекающиеся линии.

Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».

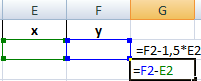
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.

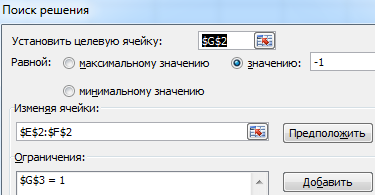
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.

Нажимаем «Выполнить» — инструмент предлагает решение уравнений.

Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.

Точки пересечения для трех показателей

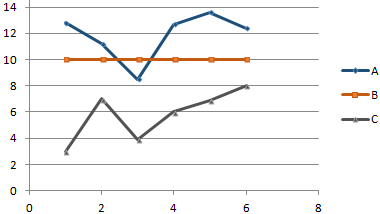
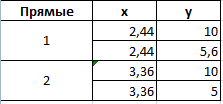
Существует три показателя, которые измерялись во времени.

По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).

Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.

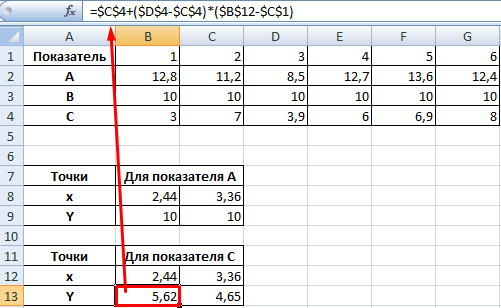
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:

На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.

Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:

На основе новых данных построим точечные диаграммы на том же поле (где наши графики).

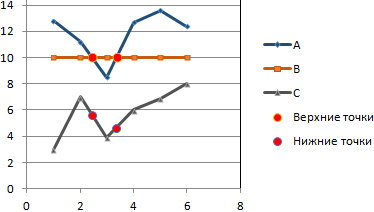
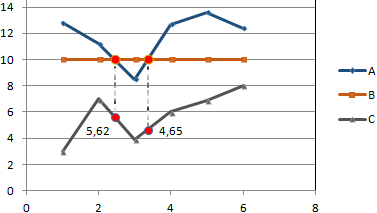
Получается такой рисунок:

Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:

Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.

Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.

The intersection of the two curves is the point where the two curves meet, and their coordinates are the same. In this article, we will learn about how to find the intersection point of the two curves in excel. Finding the intersection point of two curves can be very useful in data analysis. Let’s learn the steps for the same,

Intersection Point of two curves in Excel

Consider two sales curves of different regions Vs the year, and if they intersect at some point, then we would have insight at what time interval the sales of two different regions are matching or how close or how apart they are. For example, “Arushi” is a data analyst, and she notices that sales pattern 1 follows the curvey = x² and sales pattern 2 follows the curvey = 2.7^x. Her task is to find the intersection point of the two sales curves. Given a data set with x, y1, and y2 values, the formula used to calculate y1 values is by sales pattern 1, and the formula used to calculate y2 values is by sales pattern 2. A chart is also created.

Following are the steps,

Step 1: Create a new table range with headings x, y1, y2, and differences. Write any random value of x in cell D14. For example, 4.

Step 2: Write the same formula used in y1, as above, i.e.,y = x². For example, =D14*D14. Press Enter.

Step 3: The value appears in cell E14. For example, 16.

Step 4: Write the same formula used in y2, as above, i.e.,Y = 2.7^x. For example, =2.7^D14. Press Enter.

Step 5: The value appears in cell F14. For example, 53.1441.

Step 6: In the difference column, we are storing the difference between y1 and y2. This is done because we know that, at the intersection, the value y of both curves will be equal. This will be helpful in the later stages. Write =E14 – F14 is the cell G14. Press Enter.

Step 7: The value appears in cell G14. For example, -37.1441.

Step 8: Your active cell should be G14. Go to the Data tab, under the Forecast section, and click on the What-if Analysis. Click on the ribbon, and a drop-down appears. Select Goal Seek.

Step 9: Goal Seek dialogue box appears. In the set cell, select the cell G14, i.e., the difference column cell.

Step 10: We know that at the point of intersection, the difference between the y coordinates of the 2 curves is the same. So, it states that we need to put our difference value to zero(0).

Step 11: As all the formulas are dependent on the x value, we need to calculate the difference of 0 by changing the x value. So, select D14 in by changing Cell. Click Ok.

Step 12: The intersection point appears. The value of x is -0.70468, y1 is 0.49658, and y2 is 0.49662. The difference is 10^-5, which tends to be 0.

Step 13: By graph also, we can observe that our values are correct.

Last Updated :
24 Jul, 2022

Like Article

Save Article

' Апроксимация полиномом для всего массива исходных данных
' В подпрограмму передаются все заданные точки и апроксимация ведётся по всем точкам!
' Данные из листа Excel

Public Function polinomEx_all(xVal As Range, yVal As Range, X As Single, stepen As Integer) As Variant
Dim I As Integer
' Проверка требования "число элементов массива на 1 больше чем степень полинома"
If xVal.Count < stepen + 1 Then
    stepen = xVal.Count - 1
End If
polinomEx_all = 0#

Select Case stepen
    Case 1 ' Уравнение а·х+b
        For I = 1 To stepen + 1
            polinomEx_all = polinomEx_all + (X ^ (stepen + 1 - I)) * Application.Index(WorksheetFunction.LinEst(yVal, xVal, True, True), 1, I)
        Next I
    Case 2 ' Уравнение а·х^2+b·x+c
        For I = 1 To stepen + 1
            polinomEx_all = polinomEx_all + _
            (X ^ (stepen + 1 - I)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2)), True, True), 1, I)
        Next I
    Case 3 ' Уравнение а·х^3+b·x^2+c·x+d
        For I = 1 To stepen + 1
            polinomEx_all = polinomEx_all + _
            (X ^ (stepen + 1 - I)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3)), True, True), 1, I)
        Next I
    Case 4 ' Уравнение а·х^4+b·x^3+c·x^2+d·x+e
        For I = 1 To stepen + 1
            polinomEx_all = polinomEx_all + _
            (X ^ (stepen + 1 - I)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4)), True, True), 1, I)
        Next I
    Case 5 ' Уравнение а·х^5+b·x^4+c·x^3+d·x^2+e·x+f
        For I = 1 To stepen + 1
            polinomEx_all = polinomEx_all + _
            (X ^ (stepen + 1 - I)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5)), True, True), 1, I)
        Next I
    Case 6 ' Уравнение а·х^6+b·x^5+c·x^4+d·x^3+e·x^2+f·x+g
         For I = 1 To stepen + 1
            polinomEx_all = polinomEx_all + _
            (X ^ (stepen + 1 - I)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5, 6)), True, True), 1, I)
        Next I
    Case 7 ' Уравнение а·х^7+b·x^6+c·x^5+d·x^4+e·x^3+f·x^2+g·x+h
        For I = 1 To stepen + 1
            polinomEx_all = polinomEx_all + _
            (X ^ (stepen + 1 - I)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5, 6, 7)), True, True), 1, I)
        Next I
    Case Else

End Select
End Function

Хороший вопрос…

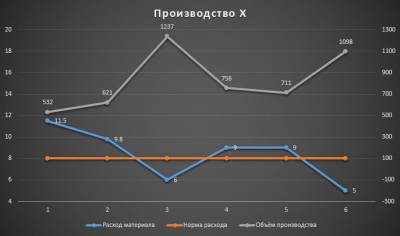
Задали мне тут недавно вопрос. Есть график, на котором имеем 3 показателя работы производства: удельный расход материала, норматив расхода и объём производства, а по горизонтальной оси временной период (недели, например).

Исходные данные выглядят так:

Удельный расход материала зависит от объёма производства. Он то выше, то ниже норматива по итогам периода и возникает естественный вопрос показать на диаграмме те моменты времени и те объёмы производства, когда линия расхода пересекает линию норматива. Может быть эта проблема и лишена какого-то великого смысла, но тем не менее вопрос был задан, значит потребность такая у людей есть.

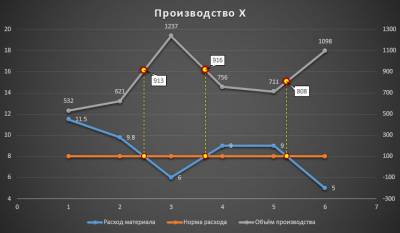
А это наша конечная цель:

Скачать пример

ChartsIntersection.xlsx

Решение

Шаг 1

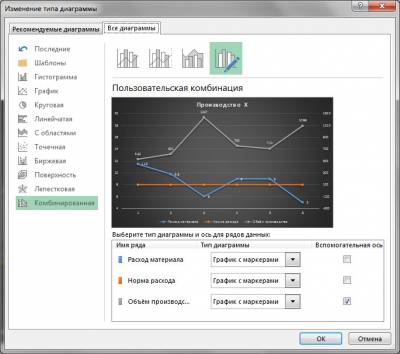
Для начала обратим внимание, что исходный тип диаграммы — График с маркерами.

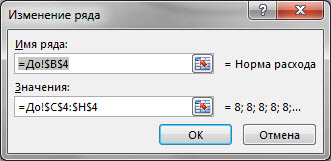
Ряды этого типа описываются так:

Заметьте, что тут нет значений координат по оси X, а есть только координаты по условной оси Y. Этим подразумевается, что условная ось X — общая для всех рядов, а также, что при их построении не используются значения, отличные от заранее фиксированного ряда оси X. Вот есть у нас периоды: 1, 2, 3 и т.д., нанесенные на ось Х, и использовать можно только их. Периода, где X=3.5 не существует для данного типа диаграммы.

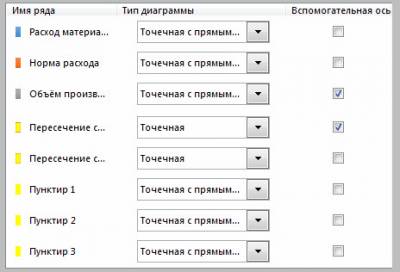
Однако, нам для решения этой задачи необходимо, чтобы мы могли задавать любое значение X, в том числе промежуточные, так как наши линии как раз пересекаются где-то «между периодами». Поэтому тип диаграммы мы меняем для всех рядов с «графика с маркерами» на «точечную с прямыми отрезками и маркерами«.

Следует упомянуть, что наш случай осложняется наличием двух вертикальных осей: основной и вспомогательной, так как значения расхода материала и объёма производства сильно друг от друга отличаются.

Шаг 2

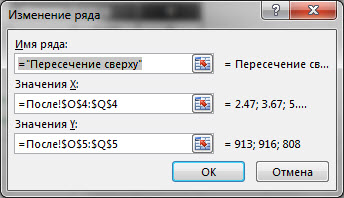
Теперь нам необходимо нанести на диаграмму дополнительные ряды данных:

1. Точки пересечения линий расхода материала с нормами расхода. Таких точек у нас будет 3, исходя из условий примера. Эти точки нам необходимо будет расчитать, вспомнив школьный курс геометрии (см. лист Треугольники). В файле учебного примера на листе После в таблице N3:Q5 мы получили координаты нужных точек путем нехитрых формул. Тип диаграммы Точечная в отличие от рядов с показателями работы производства.

2. Точки пересечения найденных значений по оси X с объемом производства. Расчитывается в таблице N8:Q10 по близким формулам. Тип диаграммы Точечная.

3. Пунктирные линии, которые мы рисуем из эстетических соображений. Таблица с их координатами находится в N12:P18.

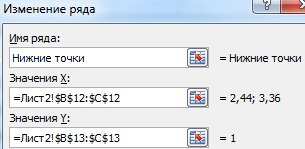
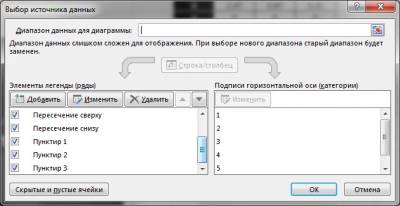
Добавляем ряды данных в соответствии с теми точками, которые мы расчитали. Щёлкните ПКМ по диаграмме и выберите «Выбрать данные…«, далее воспользуйтесь кнопкой «Добавить«.

Пример одного из рядов:

Шаг 3

Отформатируйте линии и маркеры новых рядов данных, так как вам необходимо. Готово!

Пример 1

Дана функция:

Нужно построить ее график на промежутке [-5;5] с шагом равным 1.

Создание таблицы

Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.

Вычисление значений функции

Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).

Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры.               Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).

Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.

Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.

Построение графика

Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).

Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.

Пример 2

Даны функции:

и y=50x+2. Нужно построить графики этих функций в одной системе координат.

Создание таблицы и вычисление значений функций

Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.

Мы получили таблицу значений переменной х и обеих функций в этих точках.

Построение графиков

Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.

Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.

Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.