|
Как найти тангенс угла, если известен косинус? Как найти котангенс угла, если известен косинус? Итак, читаем внимательно условие вопроса, и вспоминаем, чему нас учили в школе, у нас есть косинус угла, и этого окажется вполне достаточным для того, чтобы мы выполнили задание автора вопроса и нашли тангенс и котангенс данного угла. Вспоминаем, что мы можем найти, зная косинус, конечно-же, мы сразу можем найти синус, это очень легко, и в этом нам поможет вот это волшебное тождество и то, что из него следует, — формула для нахождения синуса: Теперь, зная чему равен синус угла, через косинус, проще простого решать дальше по известным формулам для нахождения тангенса и котангенса, просто подставляя в них эти формулы для синуса, которые я разместила выше: система выбрала этот ответ лучшим Ксарфакс 5 лет назад Для того, чтобы найти тангенс и котангенс через косинус, достаточно вспомнить тригонометрические формулы: tgα = sinα / cosα. ctgα = cosα / sinα. Так как косинус известен, то синус можно найти из основного тригонометрического тождества: sin²α + cos²α = 1. sinα = √(1 — cos²α), если угол α находится в 1 и 2 четверти. sinα = — √(1 — cos²α), если угол α находится в 3 и 4 четверти. Таким образом: tgα = ± √(1 — cos²α) / cosα. ctgα = ± cosα / √(1 — cos²α). Так как произведение тангенса и котангенса = 1, то ctgα также можно найти из формулы: ctgα = 1 / tgα. Пример Косинус угла α равен 0,94, при этом α находится в 1 четверти (0 < α < 90). Нужно найти тангенс и котангенс. Воспользуемся формулой: tgα = √(1 — cos²α) / cosα. В первой четверти синус и косинус больше 0, поэтому тангенс и котангенс также будут положительными. tgα ≈ 0,34 / 0,94 ≈ 0,36. Соответственно ctgα ≈ 1 / 0,36 ≈ 2,78. Лара Изюминка 6 месяцев назад В школе изучают следующую тригонометрическую формулу: Косинус в квадрате альфа равно единица разделить на сумму единицы и тангенса в квадрате альфа. Из этой формулы легко выразить тангенс в квадрате альфа. Он очевидно равен 1 деленная на косинус в квадрате альфа и из этой дроби нужно вычесть один, а можно еще преобразовать как на картинке. Ну, а для того чтобы выразить котангенс, нужно вспомнить , что произведение тангенса и котангенса равно единице, тогда просто меняем числитель и знаменатель местами и получается формула для нахождения котангенса через косинус. Ну, а знак тангенса и котангенса определяем по той четверти, в которой находится угол. Если это первая и третья четверти, то плюс, иначе минус. bezdelnik 5 лет назад tg а = Sin a/Cos a. Чтобы выразить тангенс через косинус осталось выразить синус через косинус. Для этого воспользуемся основной тригонометрической формулой (Sin a)^2 +/(Cos a)^2 = 1. Тогда (Sin a)^2 = 1 — (Cos a)^2, Sin a = √(1 — (Cos a)^2), а tg = √(1 — (Cos a)^2)/Cos a. Например, при а= 60 градусов Cos 60° = 0,5, tg = √(1 — 0,25)/0,5 = √(0,75)/0,5 = √(3*0,25)/0,5 = (0,5*√3)/0,5 = √3 = 1,732… . ctg a = Cos a/Sin a, то-есть величина обратная tg а, и при а = 60° ctg 60° = 1/√3 = √3/3 = 0,57735… . 127771 3 года назад Первым делом стоит вспомнить определение тангенса и котангенса, а именно: То есть получаются следующие формулы: tg(x) = sin(x) / cos(x) ctg(x) = cos(x) / sin(x) Из условия задачи нам известен косинус, значит нам нужно будет найти синус. Для этого есть такая формула: sin^2(x) + cos^2(x) = 1 Значит: sin^2(x) = 1 — cos^2(x) sin(x) = √(1 — (Cos a)^2) Теперь у нас есть значения синуса и косинуса, которые можно будет подставить в следующие формулы: Rafail 5 лет назад Наверное все помнят основное тождество тригонометрии: sin^2(x)+cos^2(x)=1. Почему-то также чётко я запомнил следующие простые формулы: tg^2(x)+1=sec^2(x) и ctg^2(x)+1=cosec^2(x). Ну и три определения: sec(x)=1/cos(x), cosec(x)=1/sin(x) и ctg(x)=1/tg(x). Теперь осталось выбрать нужные и применить. Допустим, cos(x)=(√3)/2, тогда sec(x)=2/√3, sec^2(x)=4/3, tg^2(x)=1/3, tg(x)=1/√3, ctg(x)=√3. Зайцевана 5 лет назад Пусть cosa = 1/2, тогда tga^2 = 1/(cosa)^2-1, (tga)^2 =1/0,25 — 1 = 3, tga =корень квадратный из 3, (со знаком + или — в зависимости в какой четверти находится а). ctga = 1/корень из 3. Синус, косинус, тангенс и котангенс угла — это тригонометрические функции. Можно сказать, что все они связаны между собой. Часто для нахождения одной из этих функций при условии, что известна другая, приходится вспоминать основные тригонометрические равенства или тождества, а также определение самих этих понятий. Зная все перечисленное выше, несложно выразить одну функцию через другую. Тангенс угла — это отношение синуса этого угла к его косинусу. Котангенс угла — это отношение косинуса угла к его синусу. Нам известен косинус, из основного тригонометрического тождества ( sin²α + cos²α = 1 ) выразим синус: sinα = √(1 — cos²α) для α из 1 и 2 четвертей, sinα = -√(1 — cos²α) для α из 3 и 4 четвертей. Подставив формулу для синуса угла в формулу тангенса и котангенса, получим формулы для вычисления значений этих функций: tgα = ± √(1 — cos²α) / cosα, ctgα = ± cosα / √(1 — cos²α). Котангенс, впрочем, можно вычислить путем попроще, вспомнив, что тангенс и котангенс — функции обратные, то есть ctgα = 1 / tgα. Подставляем в формулу значение тангенса и вычисляем котангенс. Если вам требуется найти тангенс и котангенс при помощи косинуса, то вам предстоит воспользоваться определенной тригонометрической формулой: при которой вы сможете отыскать синус из данной формулы, при том, что мы имеем известный косинус. Получившаяся формула выглядит таким образом: Теперь, нам следует подставить значение синуса в формулу вычисления тангенса, а именно речь идет о : Теперь подставим аналогичную формулу через косинус для котангенса: TheSun 3 года назад Для нахождения тангенса и котангенса через косинус необходимо воспользоваться приведенной ниже тригонометрической формулой: Находим синус из формулы указанной выше (при условии, что косинус нам известен), получается: Подставляем в формулу вычисления тангенса значение синуса: tg? = sin? / cos? = ± ?(1 — cos??) / cos?. Теперь аналогично для котангенса через косинус. ctg? = cos? / sin? = ± cos? / ?(1 — cos??). Все функции мы знаем из курса тригонометрии, и в это же время проходят и алгоритм нахождения тангенса/котангенса через косинус. Ну как следует из вопроса косинус нам известен. Если нет, то находим по формулам — Имея на руках значения двух вводных — синуса и косинуса, далее еще проще действовать по формулам нахождения тангенса и котангенса. Знаете ответ? |
Все формулы по тригонометрии
Основные тригонометрические тождества
$$sin^2x+cos^2x=1$$
$$tgx= frac{sinx}{cosx}$$
$$ctgx= frac{cosx}{sinx}$$
$$tgxctgx=1$$
$$tg^2x+1= frac{1}{cos^2x}$$
$$ctg^2x+1= frac{1}{sin^2x}$$
Формулы двойного аргумента (угла)
$$sin2x=2cosxsinx$$
begin{align}
sin2x &=frac{2tgx}{1+tg^2x}\
&= frac{2ctgx}{1+ctg^2x}\
&= frac{2}{tgx+ctgx}
end{align}
begin{align}
cos2x & = cos^2x-sin^2x\
&= 2cos^2x-1\
&= 1-2sin^2x
end{align}
begin{align}
cos2x & = frac{1-tg^2x}{1+tg^2x}\
&= frac{ctg^2x-1}{ctg^2x+1}\
&= frac{ctgx-tgx}{ctgx+tgx}
end{align}
begin{align}
tg2x & = frac{2tgx}{1-tg^2x}\
&= frac{2ctgx}{ctg^2x-1}\
&= frac{2}{ctgx-tgx}
end{align}
begin{align}
ctg2x & = frac{ctg^2x-1}{2ctgx}\
&= frac{2ctgx}{ctg^2x-1}\
&= frac{ctgx-tgx}{2}
end{align}
Формулы тройного аргумента (угла)
$$sin3x=3sinx-4sin^3x$$
$$cos3x=4cos^3x-3cosx$$
$$tg3x= frac{3tgx-tg^3x}{1-3tg^2x}$$
$$ctg3x= frac{ctg^3x-3ctgx}{3ctg^2x-1}$$
Формулы половинного аргумента (угла)
$$sin^2 frac{x}{2}= frac{1-cosx}{2}$$
$$cos^2 frac{x}{2}= frac{1+cosx}{2}$$
$$tg^2 frac{x}{2}= frac{1-cosx}{1+cosx}$$
$$ctg^2 frac{x}{2}= frac{1+cosx}{1-cosx}$$
begin{align}
tg frac{x}{2} & = frac{1-cosx}{sinx}\
&= frac{sinx}{1+cosx}
end{align}
begin{align}
ctg frac{x}{2} & = frac{1+cosx}{sinx}\
&= frac{sinx}{1-cosx}
end{align}
Формулы квадратов тригонометрических функций
$$sin^2x= frac{1-cos2x}{2}$$
$$cos^2x= frac{1+cos2x}{2}$$
$$tg^2x= frac{1-cos2x}{1+cos2x}$$
$$ctg^2x= frac{1+cos2x}{1-cos2x}$$
$$sin^2 frac{x}{2}= frac{1-cosx}{2}$$
$$cos^2 frac{x}{2}= frac{1+cosx}{2}$$
$$tg^2 frac{x}{2}= frac{1-cosx}{1+cosx}$$
$$ctg^2 frac{x}{2}= frac{1+cosx}{1-cosx}$$
Формулы кубов тригонометрических функций
$$sin^3x= frac{3sinx-sin3x}{4}$$
$$cos^3x= frac{3cosx+cos3x}{4}$$
$$tg^3x= frac{3sinx-sin3x}{3cosx+cos3x}$$
$$ctg^3x= frac{3cosx+cos3x}{3sinx-sin3x}$$
Формулы тригонометрических функций в четвертой степени
$$sin^4x= frac{3-4cos2x+cos4x}{8}$$
$$cos^4x= frac{3+4cos2x+cos4x}{8}$$
Формулы сложения аргументов
$$sin(alpha + beta) = sin alpha cos beta + cos alpha sin beta$$
$$cos(alpha + beta) = cos alpha cos beta — sin alpha sin beta$$
$$tg(alpha + beta)= frac{tg alpha + tg beta}{1 — tg alpha tg beta}$$
$$ctg(alpha + beta)= frac{ctg alpha ctg beta -1}{ctg alpha + ctg beta}$$
$$sin(alpha — beta) = sin alpha cos beta — cos alpha sin beta$$
$$cos(alpha — beta) = cos alpha cos beta + sin alpha sin beta$$
$$tg(alpha — beta)= frac{tg alpha — tg beta}{1 + tg alpha tg beta}$$
$$ctg(alpha — beta)= frac{ctg alpha ctg beta +1}{ctg alpha — ctg beta}$$
Формулы суммы тригонометрических функций
$$sinalpha + sinbeta = 2sin frac{alpha + beta }{2} cdot cos frac{alpha — beta }{2}$$
$$cosalpha + cosbeta = 2cos frac{alpha + beta }{2} cdot cos frac{alpha — beta }{2}$$
$$tgalpha + tgbeta = frac{sin(alpha + beta) }{cos alpha cos beta}$$
$$ctgalpha + ctgbeta = frac{sin(alpha + beta) }{cos alpha cos beta}$$
$$(sinalpha + cosalpha)^2= 1+sin2alpha$$
Формулы разности тригонометрических функций
$$sinalpha — sinbeta = 2sin frac{alpha — beta }{2} cdot cos frac{alpha + beta }{2}$$
$$cosalpha — cosbeta = -2sin frac{alpha + beta }{2} cdot sin frac{alpha — beta }{2}$$
$$tgalpha — tgbeta = frac{sin(alpha — beta) }{cos alpha cos beta}$$
$$ctgalpha — ctgbeta = — frac{sin(alpha — beta) }{sin alpha sin beta}$$
$$(sinalpha + cosalpha)^2= 1-sin2alpha$$
Формулы произведения тригонометрических функций
$$sinalpha cdot sinbeta = frac{cos(alpha — beta)-cos(alpha + beta)}{2}$$
$$sinalpha cdot cosbeta = frac{sin(alpha — beta)+sin(alpha + beta)}{2}$$
$$cosalpha cdot cosbeta = frac{cos(alpha — beta)+cos(alpha + beta)}{2}$$
begin{align}
tgalpha cdot tgbeta & = frac{cos(alpha — beta)-cos(alpha + beta)}{cos(alpha — beta)+cos(alpha + beta)}\
&= frac{tgalpha + tgbeta}{ctgalpha + ctgbeta}
end{align}
begin{align}
ctgalpha cdot ctgbeta & = frac{cos(alpha — beta)+cos(alpha + beta)}{cos(alpha — beta)-cos(alpha + beta)}\
&= frac{ctgalpha + ctgbeta}{tgalpha + tgbeta}
end{align}
$$tgalpha cdot ctgbeta = frac{sin(alpha — beta)+sin(alpha + beta)}{sin(alpha + beta)-sin(alpha — beta)}$$
Как найти тангенс, если известен косинус
Понятие тангенса является одним из основных в тригонометрии. Оно обозначает некую тригонометрическую функцию, которая является периодической, но не непрерывной в области определения, как синус и косинус. И имеет разрывы в точках (+,-)Пи*n+Пи/2, где n — это период функции. В России он обозначается как tg(x). Его можно представить через любую тригонометрическую функцию, так как все они тесно взаимосвязаны между собой.

Вам понадобится
- Учебник по тригонометрии.
Инструкция
Для того, чтобы выразить тангенс угла через синус, нужно вспомнить геометрическое определение тангенса. Итак, тангенсом острого угла в прямоугольном треугольнике, называют отношение противолежащего катета к прилежащему.
С другой стороны, рассмотрите декартову систему координат, на которой начерчена единичная окружность с радиусом R=1, и центром О в начале координат. Примите поворот против часовой стрелки, как положительный, а в обратную сторону отрицательный.
Отметьте некую точку M на окружности. Из нее опустите перпендикуляр на ось Ох, назовите ее точкой N. Получился треугольник OMN, у которого угол ONM является прямым.
Теперь рассмотрите острый угол MON, по определению синуса и косинуса острого угла в прямоугольном треугольнике
sin(MON) = MN/OM, cos(MON) = ON/OM. Тогда MN= sin(MON)*OM, а ON = cos(MON)*OM.
Вернувшись к геометрическому определению тангенса (tg(MON) = MN/ON), подставьте полученные выше выражения. Тогда:
tg(MON) = sin(MON)*OM/cos(MON)*OM, сократите OM, тогда tg(MON) = sin(MON)/cos(MON).
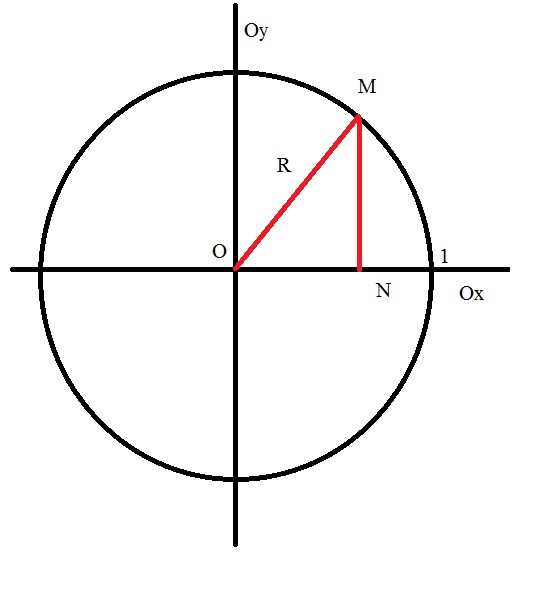
Из основного тригонометрического тождества (sin^2(x)+cos^2(x)=1) выразите косинус, через синус: cos(x)=(1-sin^2(x))^0,5 Подставьте это выражение в полученное на шаге 5. Тогда tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
Иногда существует потребность в вычисление тангенса двойного и половинчатого угла. Тут тоже выведены соотношения:tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
Также возможно выразить квадрат тангенса через двойной угол косинуса, либо синус. tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).
Обратите внимание
Обратите внимание на области допустимых значений при решение уравнений и неравенств.
Полезный совет
Знание наизусть основных тождеств, поможет быстро переходить от одних тригонометрических функций к другим.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi
Как найти тангенс фи, если известен косинус фи формула:
- tg φ = (√(1-cos²φ))/cos φ
Калькулятор онлайн — косинус в тангенс
cos φ:
tg φ:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор — онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Формулы двойного аргумента (двойного угла)
Выражения sin 2x, cos 2x, tg 2x можно выразить через sin x, cos x, tg x. Эти преобразующие формулы называются формулами двойного аргумента (или двойного угла).
Логику преобразования можно понять на примере выражения sin 2x.
Представим это выражение в виде sin (x + x).
Тогда мы легко можем применить формулу синуса суммы аргументов:
sin (x + x) = sin x cos x + cos x sin x = 2 sin x cos x.
Мы получили первую из формул двойного аргумента. А вот все формулы:
sin 2x = 2 sin x cos x
cos 2x = cos2 x – sin2 x
2 tg x
tg 2x = ————
1 – tg2 x
В первых строках мы показали, как была получена первая формула из таблицы. Вычислим остальные три.
2) cos 2x = cos2 x – sin2 x.
Здесь так же представляем 2х в виде х + х и применяем формулу косинуса сложения аргументов:
cos 2x = cos (x + x) = cos x cos x – sin x sin x = cos2 x – sin2 x.
3) cos 2x = 1 – 2 sin2 x.
Здесь мы просто продолжим преобразовывать предыдущую формулу.
Используем для этого основное тригонометрическое тождество cos2x + sin2x = 1.
Из этого тождества следует, что cos2x = 1 – sin2x. Итак, выпишем предыдущую формулу, вставим значение cos2x, сведем подобные члены и получим результат:
cos 2x = cos2 x – sin2 x = 1 – sin2 x – sin2 x = 1 – 2sin2 x.
2 tg x
4) tg 2x = ————
1 – tg2 x
Способов, как прийти к такому тождеству, два.
Первый способ. Здесь нам поможет формула тангенса сложения аргументов. Для этого представим tg 2x в виде tg (x + х). Итак:
tg х + tg х 2 tg х
tg 2x = tg (x + х) = —————— = —————
1 – tg х tg х 1 – tg2 х
Второй способ. Он сложнее. Сначала применяем формулы синуса и косинуса сложения аргументов:
sin (x + х) sin x cos х + cos x sin х
tg 2x = tg (x + х) = —————— = ———————————
cos (x + х) cos x cos х – sin x sin х
Теперь, чтобы упростить выражение, делим все его части на cos x cos х, сокращаем подобные члены и приходим к решению:
sin x cos х cos x sin х 2 sin х
————— + ————— —————
cos x cos х cos x cos х 2 cos х 2 tg x
———————————— = ——————— = —————
cos x cos x sin x sin х sin2 x 1 – tg2 x
————— – ————— 1 – ————
cos x cos x cos x cos х cos2 x
ПРИМЕЧАНИЕ:
При решении конкретных задач важно помнить, что задача имеет смысл лишь в том случае, если в процессе решения знаменатели нигде не оказываются равны нулю.
Теперь для наглядности решим несколько примеров по теме.
Пример 1. Упростить выражение:
sin 2α
———
sin α
Решение:
sin 2α 2 sin α cos α
——— = —————— = 2 cos α
sin α sin α
Пример 2. Пусть tg α = 3/4 и 180º < α < 270º.
Найти sin 2α.
Решение.
В первую очередь, отмечаем, что угол находится в третьей четверти. Значит, синус будет со знаком минус.
1
1) Значение синуса мы могли бы найти через формулу 1 + ctg2 α = ———.
sin2 α
Значит, нам надо сначала вычислить значение котангенса. Мы знаем, что tg α · ctg α = 1. Следовательно:
1 1 4
ctg α = —— = —— = ——
tg α 3/4 3
2) Теперь находим значение синуса:
1 1 1 1 9
sin2 α = ————— = ————— = ———— = —— = ——
1 + ctg2 α 1 + (4/3)2 1 + 16/9 25/9 25
3
sin α = – ——
5
3) Мы знаем, что sin 2α = 2 sin α cos α. Значит, находим еще косинус (по формуле cos2 α + sin2 α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак:
9 16
cos2 α = 1 – sin2 α = 1 – —— = ——
25 25
4
cos α = – ——
5
4) Осталось применить формулу двойного угла:
3 4 2 · 3 · 4 24
sin 2α = 2 · (– ——) · (– ——) = ———— = —— = 0,96.
5 5 5 · 5 25
Пример решен.
Пример 3: Вычислить
π π
cos2 — – sin2 —
8 8
Решение.
Это выражение соответствует правой части формулы косинуса двойного
аргумента (cos 2x = cos2 x – sin2 x). Значит, просто приравняем его к левой части. Для этого замечаем, что
π
х = —
8
Остается ввести в формулу это значение х и решить уравнение:
π π π 2π π √2
cos2 —— – sin2 —— = cos 2 ∙ —— = cos —— = cos —— = —— .
8 8 8 8 4 2
Пример решен.













