Как найти тепловой потенциал

Использование тепловых потенциалов для анализа территорий

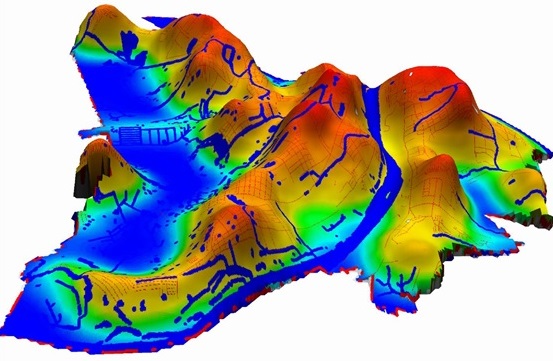
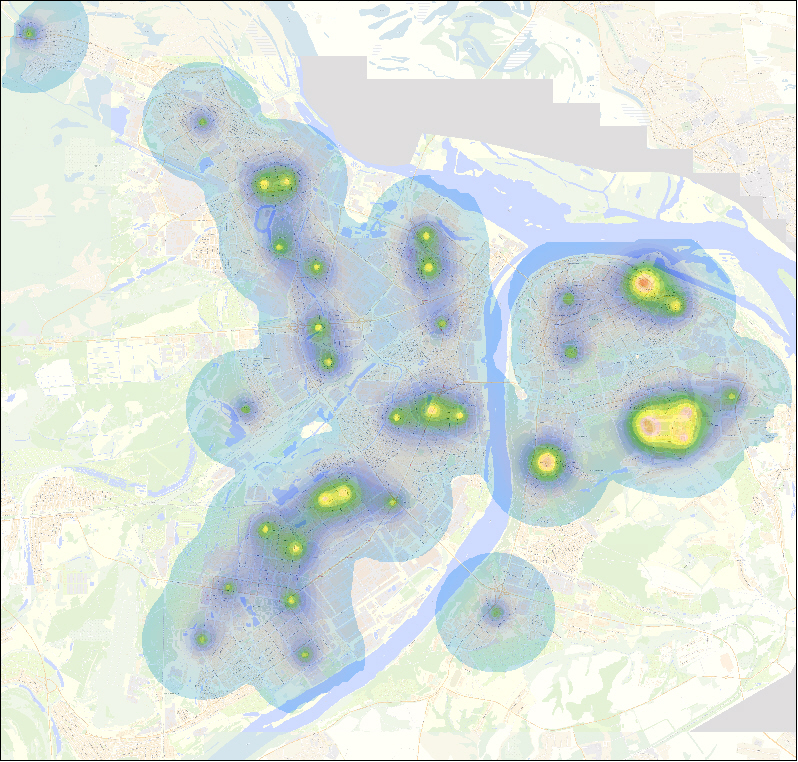
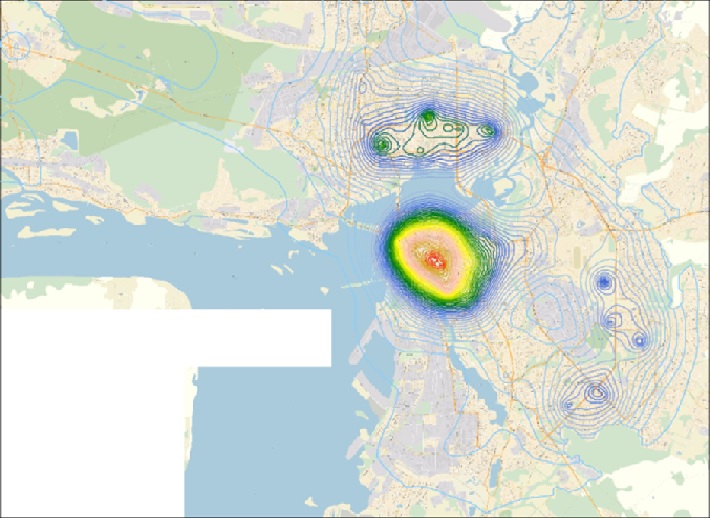
Пример расчета теплового потенциала для уличной сети г. Нижнего Новгорода

Территория города – сложная, неоднородная система, находящаяся в постоянном изменении. Описать территорию и провести оценку городской среды можно с помощью пространственных объектов (факторов). Факторы, описывающие территорию, различны по характеру влияния (положительное, отрицательное) и геометрической конфигурации (точки, линии, полигоны).

Зачастую определить степень влияния каждого отдельного объекта на уровень развития территории в целом или какой-то отдельный ее аспект довольно сложно. На сегодня проблема определения и описания таких понятий как «культура», «социальная сфера», «социальная напряженность», «хорошая жизнь», «экономическое развитие», «здоровье населения» становится все более актуальной. Неоднозначность этих понятий увеличивается, если мы хотим применить их относительно разных социальных групп, населения разного возраста и пола.

Также, следует отметить, что границы города в современном понятии достаточно условны. Суточная миграция населения, транспортная доступность удаленных районов «размывают границу» города еще больше. Широко используемое сейчас понятие агломерации в целом отражает границы города, но в тоже время делает само понятие границы города еще более расплывчатой.

Несмотря на описанные выше проблемы, анализ и оценка территорий на сегодня являются одними из перспективных и интересных направлений, позволяющих решать множество актуальных задач городской среды.

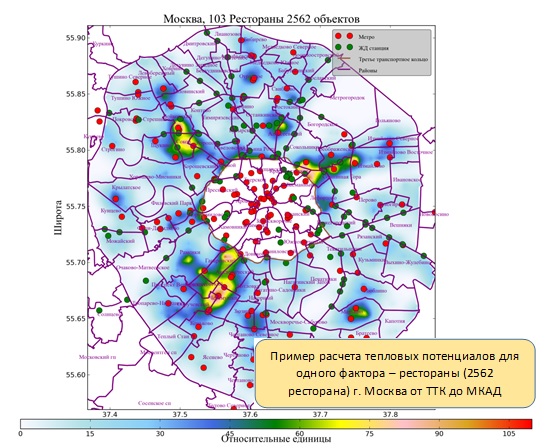
В статье предлагается к рассмотрению метод анализа территории с использованием «тепловой» модели. В основе данного метода лежит исследование потенциалов, создаваемых объектами (факторами) различной природы (точечные, линейные и площадные). Анализ территории с помощью этого метода дает возможность перейти от набора пространственных данных (факторов), описывающих территорию, к точной числовой (бальной) оценке в каждой точке территории.

Исследуемые в рамках проведения анализа территории потенциалы, имеют физическую интерпретацию – распространение тепла в средах разной размерности (2D, 3D). Это явление можно представить в виде «тепловых» изображений («тепловых» карт территории), дающих представление о степени развития территории в зависимости от интенсивности цвета изображения.

Факторы территории

Анализ территории подразумевает поиск и обработку информации о факторах влияния на территорию и об их индикаторах. Факторами влияния выступают объекты, влияющие на окружающую территорию, обладающие набором характеристик и пространственными координатами. Примерами факторов влияния могут служить магазины, промышленные объекты, дороги, леса, водные объекты.

Индикаторами влияния выступают объекты, отражающие влияние объектов и также обладающие набором характеристик и пространственными координатами. Примеры индикаторов влияния: банкоматы, рекламные щиты, памятники.

В дальнейшем изложении будем использоваться понятием факторы влияния, объединяющим в себе оба термина – факторы и индикаторы влияния.

Ниже приведен пример пространственных данных, которые выступают факторами влияния.

Одним из важных этапов проведения работ по анализу территорий является этап сбора и обработки исходной информации. На сегодня информации о факторах влияния на территорию разной степени подробности достаточно много.

Информация может быть получена из открытых источников или источников ограниченного доступа. Во многих случаях открытой информации достаточно для анализа, хотя, как правило, она нуждается в достаточно трудоемкой обработке.

Среди открытых источников лидером, по нашему мнению, является ресурс — ОpenStreetMap (OSM). Информация, получаемая из этого источника, обновляется ежедневно по всему миру.

Информация ресурса ОpenStreetMap (OSM) представлена в следующих форматах:

— OSM формат. Основной формат c расширением «.osm» используется для описания графических образов XML– узлы, пути, отношения.

— «Польский формат». Текстовый формат с расширением «.mp» используется для работы с графикой.

— PBF формат. Формат хранения данных с расширением «.osm.pbf».

В качестве источников информации также можно использовать:

— 2ГИС
Ресурс содержит качественную, ежемесячно обрабатываемую информацию, с прекрасным 3х-уровневым классификатором по предприятиям и организациям.

— KML (Keyhole Markup Language) файлы
KML (Keyhole Markup Language) файлы — это формат файлов, который используется для отображения географических данных в программах Google Планета Земля, Карты Google и Карты Google для мобильных устройств.

С помощью файлов KML можно:
— устанавливать различные значки и делать подписи для обозначения мест на поверхности Земли
— создавать различные ракурсы для выбранных объектов, изменяя положение камеры
— использовать различные накладываемые изображения
— определять стили для настройки отображения объекта, применять код HTML для создания гиперссылок и встроенных изображений
— использовать папки для иерархической группировки элементов
— динамически получать и обновлять файлы KML из удаленных или локальных узлов сети
— получать данные KML в соответствии с изменениями в средстве трехмерного просмотра

— Федеральная служба государственной регистрации, кадастра и картографии «Росреестр»
Информация на портале Росреестра ценна своим содержанием и актуальностью, но, к сожалению, не дает возможности получать графику по объектам капитального строительства и земельным участкам на безвозмездной основе. Портал Росреестра также содержит большой объем информации ограниченного доступа.

— Органы статистики
Статистические данные – легитимный источник информации о территории, однако по состоянию на сегодня данные органов статистики доступны только по некоторому числу показателей, в основном в отчетах органов статистики и докладах региональной власти.

— Информационные системы органов власти
Качественная информация содержится в информационных системах органах власти, однако лишь небольшая их часть публикуется в открытом доступе и доступна для анализа.

Проведение анализа территорий не накладывает каких-либо определенных требований к составу информации, по сути можно пользоваться всем, что удалось найти, информация из источников открытого типа как правили взаимозаменяемая. Однако, следует отметить, что даже одной только информации полученной с ресурса OSM достаточно, чтобы сделать анализ незнакомой территории.

Анализ территории с использованием «тепловой» модели. Физическая интерпретация потенциалов

Как уже было сказано ранее, анализ территории на сегодня является актуальной темой и мощным инструментом для аргументированного привлечения инвестиций в развитие инфраструктуры различных городских сред.

Разнообразие задач, решаемых с помощью проведения анализа территорий, можно объединить в несколько крупных направлений:

— Получение максимально интерпретируемой и детализированной оценки территории в каждой ее точке.
Решая поставленную задачу можно получить набор балльных оценок в каждой точке территории, дающий представление об уровне развития территории в общем, а также в некоторой предметной области. Такой предметной областью может быть, например, культура, промышленность, торговля и т.д.

— Определение наиболее выгодных мест для размещения инвестиционных объектов определенного типа (например, банков, профильных магазинов, торгово-развлекательных центров и др.) на выбранной территории.

— Анализ наиболее эффективного использования территории.
Данное направление позволяет проводить подробное исследование характеристик территории, рыночной ситуации, сложившейся на исследуемой территории, идентификацию востребованных вариантов.

— Определения вклада одного фактора в модель стоимости, на примере появления новых дорог и новых маршрутов.

— Анализ разных аспектов одной территории и анализ разных территорий (сравнение территорий).

Оригинальность предлагаемого в статье метода анализа территории с применением «тепловой» модели состоит в использовании показателей развития территории — потенциалов, представленных в числовом выражении и отражающих степень влияния объекта (фактора влияния) на территорию.

Для понимания сути исследования следует сказать несколько слов о самом тепловом потенциале, дать его физическую интерпретацию.

В физике существуют такие понятия как силовое поле и силовая функция. Силовое поле имеет размерность энергии, силовая функция – размерность силы.

Для закона всемирного тяготения силовое поле определено формулой:

, где
k – константа;
r – расстояние между взаимодействующими объектами.

Силовая функция ϕ определяется выражением:

, где
ϕ — потенциал силового поля;
dϕ, dr – дифференциалы;
r — расстояние между взаимодействующими объектами,

следовательно

.

Физический смысл потенциала силового поля ϕ – это работа Е, совершаемая силовым полем при прохождении некоторого пути. В случае закона всемирного тяготения при изменении расстояния до объекта от r2 до r1 силовая функция определяется по формуле

, где
Е – работа, совершаемая силовым полем при прохождении некоторого пути;
r1, r2 – начальное и конечное положение объекта.

Для задачи анализа территории влияние объектов (факторов) на территорию можно рассматривать как силу (силовая функцию), а уровень развития территории, как суммарный тепловой потенциал (силовое поле) от всех объектов (факторов). В задачах физики тепловой потенциал является температурой, а в задачах анализа территорий с использованием «тепловой» модели потенциал представляет собой суммарное воздействие всех факторов влияния на точку территории.

Пространственные данные представляют собой точки, линии, полигоны. Для расчета потенциалов протяженные пространственные данные разбиваются на мелкие фрагменты. Для каждого фрагмента рассчитывается потенциал от точки со множителем равным размеру фрагмента объекта (фактора).

Данные разбиваются на смысловые группы по принципу близкого сходства. Например, объекты торговли объединены по товарам. Есть группы лесных объектов, водных объектов, населенных пунктов, остановок транспорта и т.д. Объединенные по смыслу группы представляют собой фактор. Пройдя по всем объектам (факторам), получаем набор тепловых потенциалов, пригодных к дальнейшей обработке.

Использование потенциалов («тепловых карт») позволяет перейти от пространственных данных к «тепловым» изображениям объектов (факторов) влияния на территории (визуализация потенциалов). Такой переход дает возможность определить степень присутствия фактора в каждой точке территории и проводить дальнейший анализ, т.е. отобразить разные направления развития города в цвете. Таким образом, получим свечение различной интенсивности для каждой точки территории.

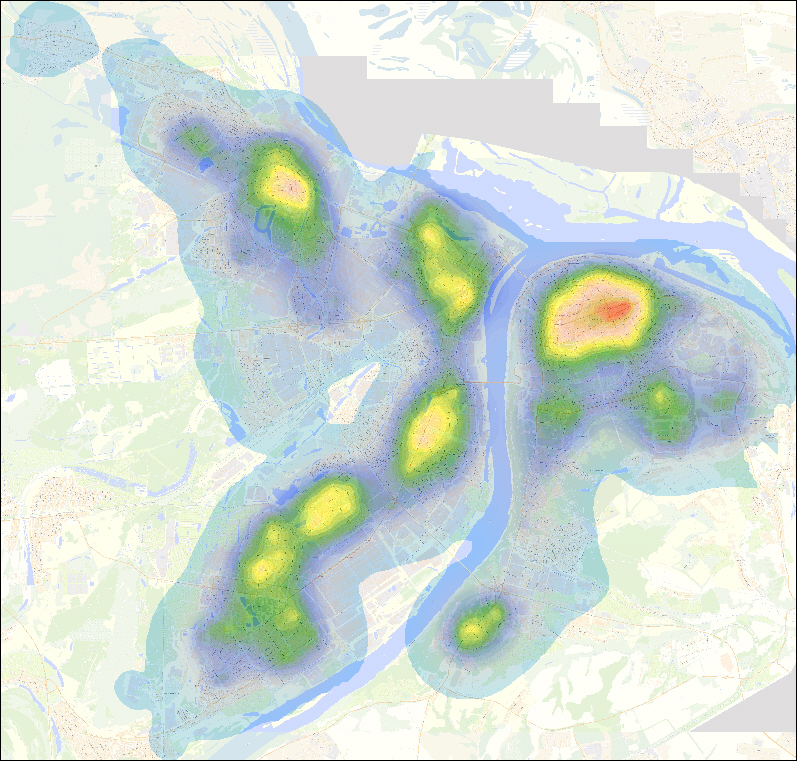
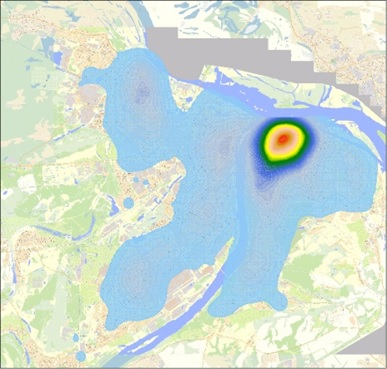
Примеры «тепловых» изображений территории г. Нижнего Новгорода в разрезе нескольких факторов, представлены ниже.

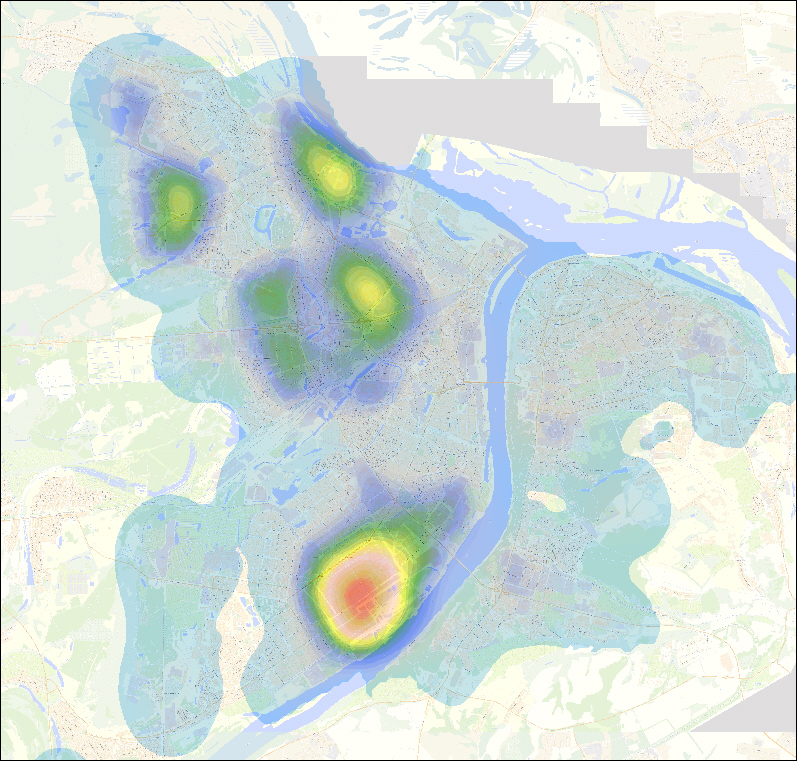
«Тепловая» карта г. Н. Новгорода, отражающая фактор «Аптечная сеть»

«Тепловая» карта г. Н. Новгорода, отражающая фактор «Поликлиники для взрослых»

«Тепловая» карта г. Н. Новгорода, отражающая фактор «Детские поликлиники»

«Тепловая» карта г. Н. Новгорода, отражающая фактор «Промышленные зоны»

«Тепловые» изображения территории позволяют определить концентрацию потенциалов от различных объектов влияния. Далее необходимо объединить полученные потенциалы в интегральную характеристику, позволяющую провести оценку территории по большому количеству факторов. Для этого необходим метод, позволяющий анализировать большой объем информации, распознавать объекты, а также уменьшить размерность данных, потеряв наименьшее количество информации. Одним из таких методов является метод главных компонент (Рrincipal component analysis, PCA). Более подробно о данном методе можно прочитать в Википедии.

Суть метода – нахождение линейной комбинации исходных параметров, наиболее сильно меняющейся в области анализа. Для пространственных данных – наиболее сильно меняющейся по территории.

Метод главных компонент выделяет объекты (факторы), наиболее сильно изменяющиеся по территории. В результате работы метода появляются новые переменные – главные компоненты, являющиеся более информативными по сравнению с исходными данными, с помощью которых легче анализировать, описывать и визуализировать территорию, по которым проще строить модели.

Главные компоненты представляет собой аналитические выражения — сумму потенциалов исходных факторов с некоторыми коэффициентами. Однако если какой-либо фактор оказывает существенное влияние на территорию, но не меняется по анализируемой территории, метод главных компонент не включит этот фактор в состав главных компонент.

Главные компоненты упорядочиваются по убыванию информации – т.е. распространению по территории. Первые главные компоненты несут в себе существенно большую информацию, чем отдельные факторы, и хорошо описывают территорию. Как правило, при использовании около сотни факторов, первая главная компонента несет в себе около 50% всей информации (дисперсии) по территории. Главные компоненты не коррелируют между собой и могут использоваться для моделей в качестве характеристик территории в каждой точке.

Главная компонента, как некоторый абстрактно вычисленный показатель территории, не имеет четкого названия и классификации. Однако, совокупность, сильно коррелирующих с главной компонентой, факторов позволяют интерпретировать главные компоненты. Как правило, с главными компонентами коррелируют следующие факторы:

— уровень развития инфраструктуры;
— транспортная составляющая территории;
— климатические зоны;
— уровень развития сельского хозяйства;
— экономический потенциал территории.

Дальнейший анализ, в том числе кластеризация идет с несколькими первыми значимыми главными компонентами.

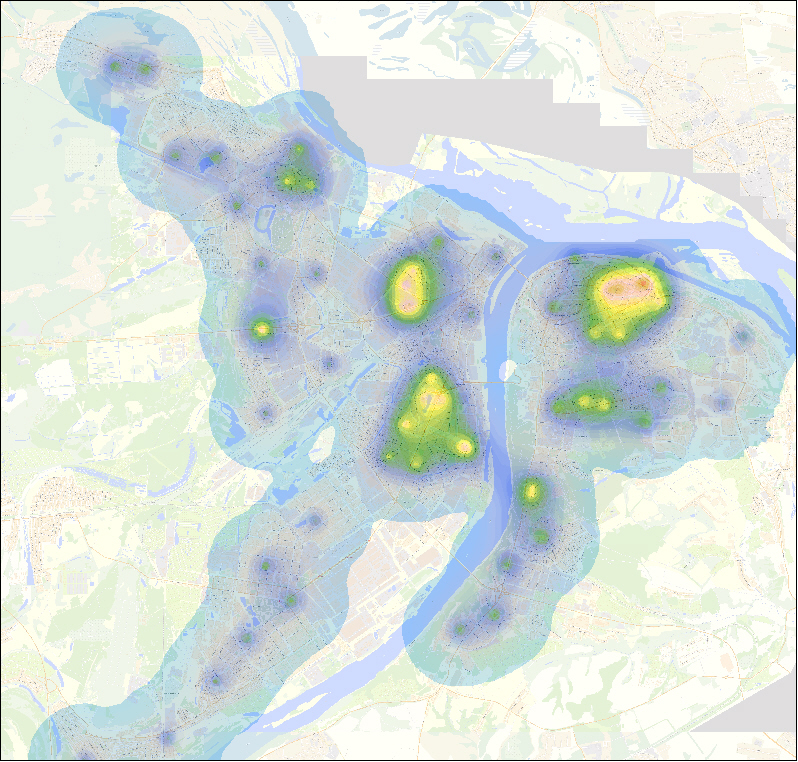
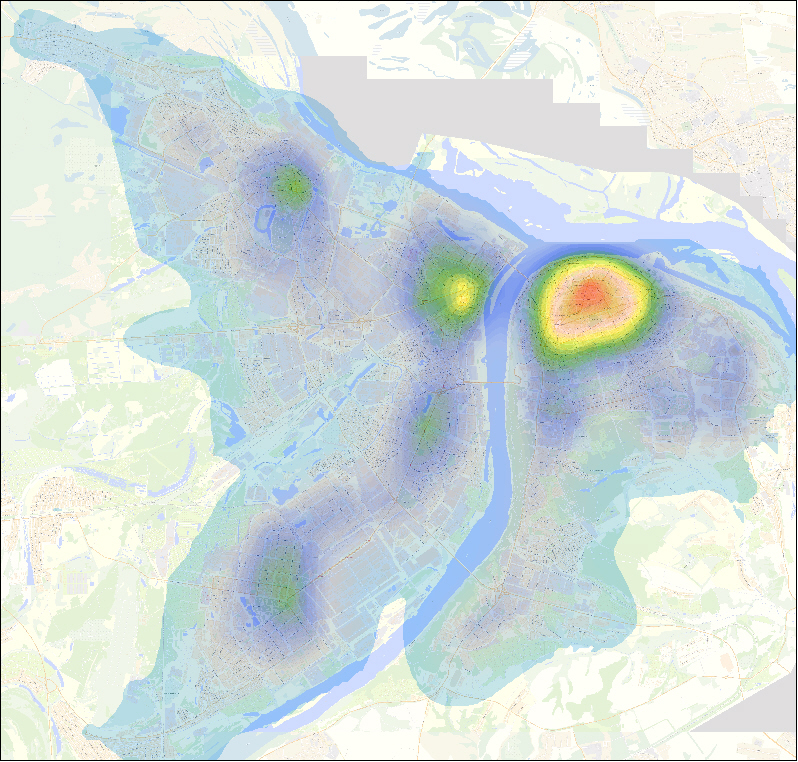
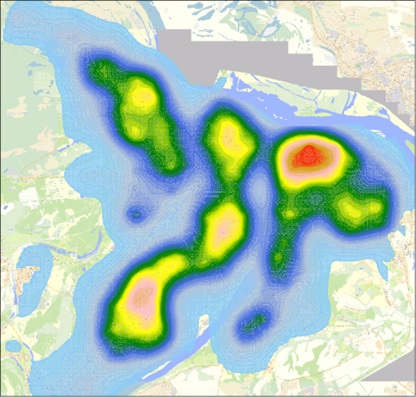
На рисунках можно видеть графическое отображение первых главных компонент на территории нескольких городов Российской Федерации.

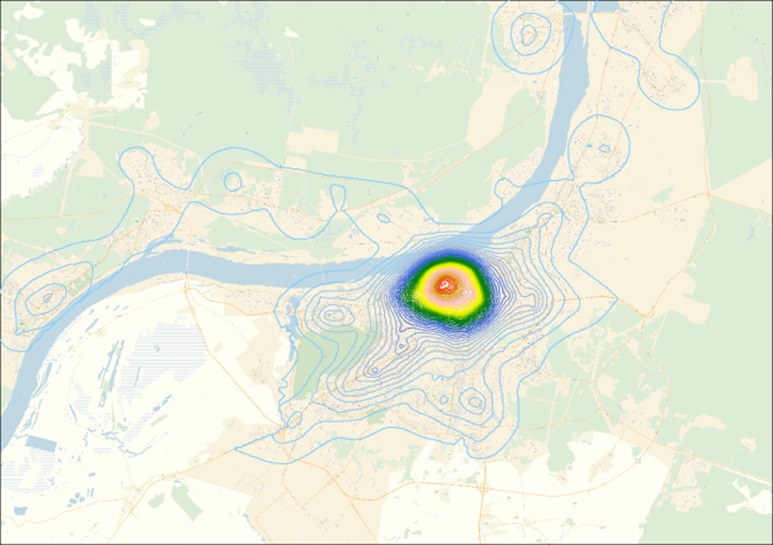
Первая главная компонента, характеризующая уровень развития городской инфраструктуры г. Н. Новгорода

Первая главная компонента, характеризующая уровень развития городской инфраструктуры г. Екатеринбурга

Первая главная компонента, характеризующая уровень развития городской инфраструктуры г. Казани

Первая главная компонента, характеризующая уровень развития городской инфраструктуры г. Перми

Первая главная компонента, характеризующая уровень развития городской инфраструктуры г. Самары

Первая главная компонента, характеризующая уровень развития городской инфраструктуры г. Хабаровска

Интегральные характеристики: кластеризация

Дальнейший этап работ по анализу территорий представляет собой поиск зон городской среды, однородных по качеству. Этот поиск основывается на анализе значений главных компонент в каждой точке территории. Задача поиска указанных однородных зон может быть решена с помощью кластеризации – процесса группировки территорий по принципу близости совокупности характеристик.

Кластеризация территории преследует две цели:

— создание лучше воспринимаемой визуализации территории;
— выделение областей для составления отдельных моделей.

Территории кластеризуются в соответствии с отобранными факторами для анализа. Эти факторы могут быть факторами, влияющими на ценообразование или факторами, описывающими какую-то сторону развития территории, например, социальную сферу.

Существует два распространенных классических метода кластеризации: метод K-means и метод дендрограмм. При работе с территориями хорошо себя зарекомендовал метод K-means, особенностью которого является «выращивание» кластера, путем присоединения к точкам роста новых объектов. Преимущества метода K-means заключается в похожести его работы на естественный процесс формирования территорий: интеграция похожих, а не разделение непохожих.

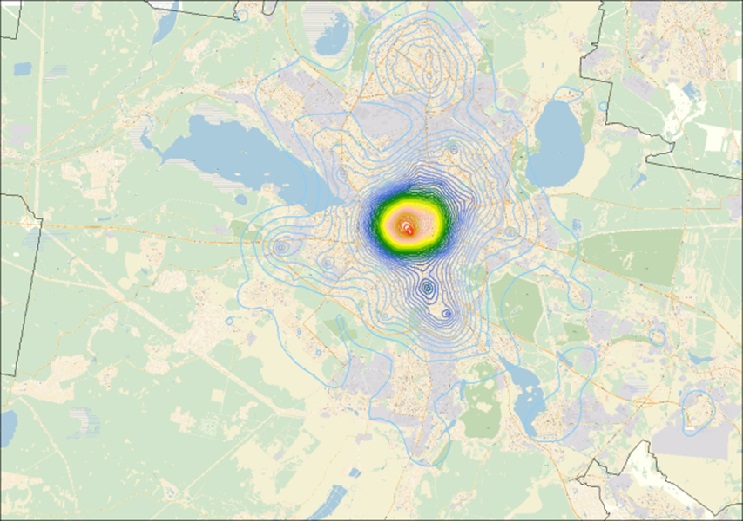
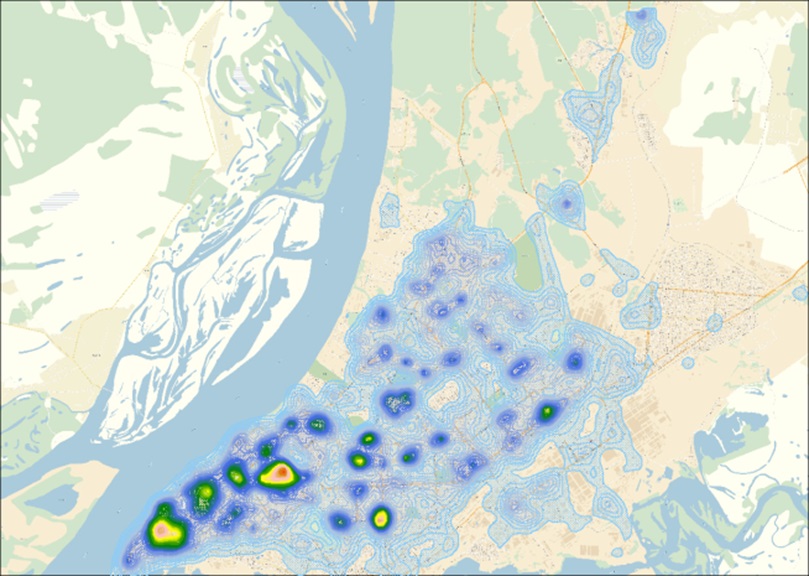
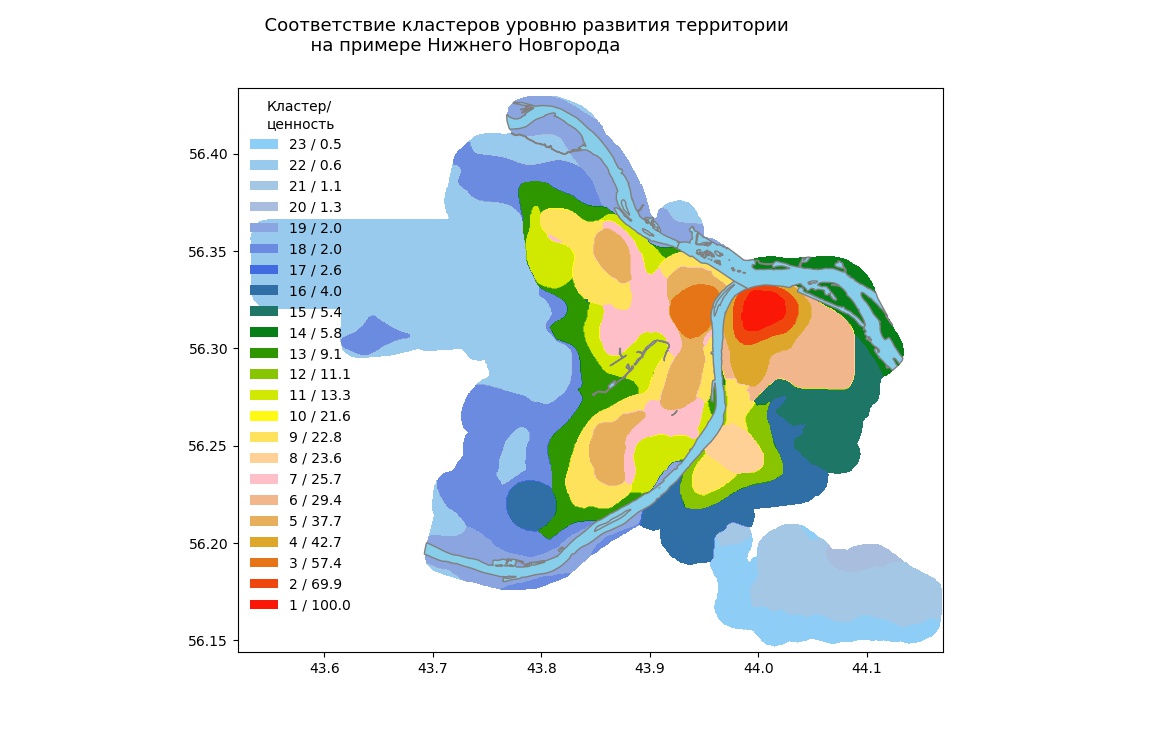
Методом K-means был произведен расчет по Нижнему Новгороду (рисунок ниже).

Соответствие кластеров уровню развития территории на примере г. Н.Новгорода

При предложенном подходе можно получить представление о территории по различным темам. Интересующими нас темами могут быть, например, уровень развития городской инфраструктуры, уровень «элитности» территории, уровень развития культуры, социальная составляющая развития территории. Эти темы являются плохо определенными интегральными понятиями, и состоят из множества взаимосвязанных факторов.

При некотором алгоритме отбора параметров для анализа (в том числе с привлечением экспертов), мы получим тематические карты, дающие представление об одном аспекте развития территории.

Под интегральными характеристиками понимаются первые главные компоненты, прежде всего самая информативная первая главная компонента, и кластеризация территория по отобранным параметрам.

Тематические карты первых главных компонент по различным аспектам развития представлены на рисунках ниже.

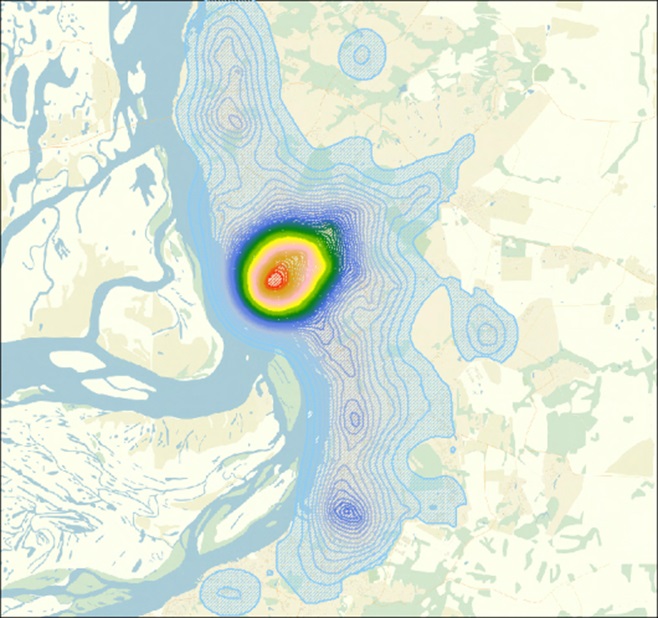
Тематическая карта «Объекты культуры» на примере г. Н.Новгорода

Тематическая карта «Социальная сфера» на примере г. Н.Новгорода

Интегральные характеристики дают возможность понять особенности территории, оперируя множеством факторов с минимальными потерями информации.

В заключении стоит еще раз отметить, что на сегодня анализ территорий является крайне важным этапом при решении задач развития городской среды, выбора мест для инвестирования в строительство, поиска наиболее выгодного месторасположения новых объектов и других задач.

Предложенный в статье метод анализа территории с использованием «тепловой» модели от факторов разной природы не является критичным к набору факторов, т.е не накладывает ограничения и требования к исходной информации.

Многообразие и избыточность исходной информации, а также возможность пользоваться открытыми данными предоставляет неограниченные перспективы для анализа любых территорий мира.

В следующих публикациях, посвященных задачам анализа территорий мы планируем раскрыть особенности составление моделей с использованием главных компонент и методы их реализации для таких задач как:

— выбор наилучшего места при размещении нового объекта;
— построение ценовой поверхности для определенной категории объектов с использованием рыночной стоимости;
-оценка доходности определенного вида деятельности в зависимости от местоположения объектов.

Также в планах представить методы обратного перехода от главных компонент к факторам, что в свою очередь позволяет получить модель от факторов для данной территории.

Тема 9.Теплопроводность

9.1. Температурное поле. Уравнение теплопроводности

Будем рассматривать только однородные и изотропные тела, т.е. такие тела, которые обладают одинаковыми физическими свойствами по всем направлениям. При передачи теплоты в твердом теле, температура тела будет изменяться по всему объему тела и во времени. Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:

где:t –температура тела;

x,y,z -координаты точки;

Такое температурное поле называется нестационарным ∂t/∂ i ¹ 0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности

Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным:

t = f(x,y,z) , ∂t/∂ i = 0 (9.2)

Уравнение двухмерного температурного поля:

для нестационарного режима:

t = f(x,y,τ) ; ∂t/∂z = 0 (9.3)

для стационарного режима:

t = f(x,y) , ∂t/∂z = 0; ∂t/∂ i = 0 (9.4)

Уравнение одномерного температурного поля:

для нестационарного режима:

t = f(x,τ) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂ i ¹ 0 (9.5)

для стационарного режима:

t = f(x) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂ i = 0 (9.6)

Изотермической поверхностью называется поверхность тела с одинаковыми температурой.

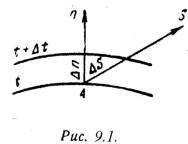
Рассмотрим две изотермические поверхности (Рис.9.1) с температурами t и t + ∆t. Градиентом температуры называют предел отношения изменения температуры∆t к расстоянию между изотермами по нормали ∆n, когда стремится к нулю:

Температурный градиент-это вектор, направленной по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры t по нормалиn:

Количество теплоты, проходящее через изотермическую поверхность F в единицу времени называется тепловым потоком – Q, [Вт=Дж/с].

Тепловой поток, проходящий через единицу площади называют плотностью теплового потока – q = Q / F, [Вт/м 2 ]

Для твердого тела уравнение теплопроводности подчиняется закону Фурье:

Тепловой поток, передаваемая теплопроводностью, пропорциональна градиенту температуры и площади сечения, перпендикулярного направлению теплового потока.

q = -λ ∙ ∂t/∂n ∙n_o = -λ∙gradt , (9.9)

где: q – вектор плотности теплового потока;

Численное значение вектора плотности теплового потока равна:

q = -λ∙ ∂t/∂n = -λ∙|gradt| , (9.10)

Коэффициент теплопроводности является физическим параметром вещества, характеризующим способность тела проводит теплоту, Она зависит от рода вещества, давления и температуры. Также на её величину влияет влажность вещества. Для большинства веществ коэффициент теплопроводности определяются опытным путем и для технических расчетов берут из справочной литературы.

Теплопроводность через сферическую оболочку

Теплопроводность через сферическую оболочку

Теплопроводность через сферическую оболочку

Объектом исследования является сферическая оболочка заданной толщины с переменным коэффициентом теплопроводности и с заданными значениями температуры на внутренней и внешней поверхностях оболочки.

Цель проекта — определить распределение температуры внутри оболочки.

В процессе работы выведено дифференциальное уравнение теплопроводности применительно к данным конкретным условиям задачи и получено решение этого уравнения в виде функции T(r), где T — температура в произвольной точке оболочки а r — расстояние между этой точкой и геометрическим центром оболочки. Разработана программа TSO, рассчитывающая функцию T(r) и строящая её график для различных задаваемых пользователем параметров задачи.

Результатом исследования является аналитическое решение уравнения теплопроводности T(r) и графическая иллюстрация этого решения, изображаемая на экране компьютера программой TSO.

Полученная в проекте функция T(r) и разработанная программа TSO могут быть полезными для разработчиков химических и ядерных реакторов, котлов тепловых станций и различных сосудов в области промышленной и бытовой техники.

Курсовой проект выполнен в текстовом редакторе Microsoft WORD 7.0.

В учении о теплообмене рассматриваются процессы распространения теплоты в твердых, жидких и газообразных телах. Эти процессы по своей физико-механической природе весьма многообразны, отличаются большой сложностью и обычно развиваются в виде целого комплекса разнородных явлений.

Перенос теплоты может осуществляться тремя способами: теплопроводностью, конвекцией и излучением, или радиацией. Эти формы глубоко различны по своей природе и характеризуются различными законами.

Процесс переноса теплоты теплопроводностью происходит между непосредственно соприкасающимися телами или частицами тел с различной температурой. Учение о теплопроводности однородных и изотропных тел опирается на весьма прочный теоретический фундамент. Оно основано на простых количественных законах и располагает хорошо разработанным математическим аппаратом. Теплопроводность представляет собой, согласно взглядам современной физики, молекулярный процесс передачи теплоты.

Известно, что при нагревании тела кинетическая энергия его молекул возрастает. Частицы более нагретой части тела, сталкиваясь при своем беспорядочном движении с соседними частицами, сообщают им часть своей кинетической энергии. Этот процесс постепенно распространяется по всему телу. Перенос теплоты теплопроводностью зависит от физических свойств тела, от его геометрических размерах, а также от разности температур между различными частями тела. При определении переноса теплоты теплопроводностью в реальных телах встречаются известные трудности, которые на практике до сих пор удовлетворительно не решены. Эти трудности состоят в том, что тепловые процессы развиваются в неоднородной среде, свойства которой зависят от температуры и изменяются по объему; кроме того, трудности возникают с увеличением сложности конфигурации системы.

Целью данного курсового проекта является нахождение закона распределения температуры в веществе, которым заполнено пространство между двумя сферами.

2 Основные положения теплопроводности

2.1 Температурное поле

Теплопроводность представляет собой процесс распространения энергии между частицами тела, находящимися друг с другом в соприкосновении и имеющими различные температуры.

Рассмотрим нагрев какого-либо однородного и изотропного тела. Изотропным называют тело, обладающее одинаковыми физическими свойствами по всем направлениям. При нагреве такого тела температура его в различных точках изменяется во времени и теплота распространяется от точек с более высокой температурой к точкам с более низкой. Из этого следует, что в общем случае процесс передачи теплоты теплопроводностью в твердом теле сопровождается изменением температуры Tкак в пространстве, так и во времени:

,———(2.1)

где — координаты точки;

Эта функция определяет температурное поле в рассматриваемом теле. В математической физике температурным полем называют совокупность значений температуры в данный момент времени для всех точек изучаемого пространства, в котором протекает процесс.

Если температура тела есть функция координат и времени, то температурное поле называют нестационарным, т. е. зависящим от времени:

.———(2.2)

Такое поле отвечает неустановившемуся тепловому режиму теплопроводности.

Если температура тела есть функция только координат и не изменяется с течением времени, то температурное поле тела называют стационарным:

.———(2.3)

Уравнения двухмерного температурного поля для режима стационарного:

;———(2.4)

.———(2.5)

На практике встречаются задачи, когда температура тела является функцией одной координаты, тогда уравнения одномерного температурного поля для режима стационарного:

;—-(2.6)

.—-(2.7)

Одномерной, например, является задача о переносе теплоты в стенке, у которой длину и ширину можно считать бесконечно большой по сравнению с толщиной.

2.2 Градиент температуры

Если соединить точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Изотермические поверхности между собой никогда не пересекаются. Они либо замыкаются на себя, либо кончаются на границах тела.

Рассмотрим две близкие изотермические поверхности с температурами T и T + Δ T(рисунок 2.1).

Перемещаясь из какой либо точки А, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. Если перемещаться по изотермической поверхности, то изменения температуры не обнаружим. Если же перемещаться вдоль какого-либо направления P, то наблюдаем изменение температуры. Наибольшая разность температур на единицу длины будет в направлении нормали к изотермической поверхности. Предел отношения изменения температуры к расстоянию между изотермами по нормали , когда стремится к нулю, называют градиентом температуры.

———(2.8)

Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный частной производной от температуры по этому направлению. За положительное направление градиента принимается направление возрастания температур.

2.3 Основной закон теплопроводности

Для распространения теплоты в любом теле или пространстве необходимо наличие разности температур в различных точках тела. Это условие относится и к передаче теплоты теплопроводностью, при которой градиент температуры в различных точках тела не должен быть равен нулю.

Связь между количеством теплоты , проходящим за промежуток времени через элементарную площадку dS, расположенную на изотермической поверхности, и градиентом температуры устанавливается гипотезой Фурье, согласно которой

.—-(2.9)

Минус в правой части показывает, что в направлении теплового потока температура убывает и grad T является величиной отрицательной. Коэффициент пропорциональности называется коэффициентом теплопроводности или более кратко — теплопроводностью. Справедливость гипотезы Фурье подтверждено многочисленными опытными данными, поэтому эта гипотеза в настоящее время носит название основного уравнения теплопроводности или закона Фурье.

Отношение количества теплоты, проходящего через заданную поверхность, ко времени называют тепловым потоком. Тепловой поток обозначают q и выражают в ваттах (Вт):

.———(2.10)

Отношение теплового потока dq через малый элемент изотермической поверхности к площади dS этой поверхности называют поверхностной плотностью теплового потока (или вектором плотности теплового потока), обозначают j и выражают в ваттах на квадратный метр (Вт/м2):

.————(2.11)

Вектор плотности теплового потока направлен по нормали к изотермической поверхности в сторону убывания температуры. Векторы j и grad T лежат на одной прямой, но направлены в противоположные стороны.

Тепловой поток q, прошедший сквозь произвольную поверхность S, находят из выражения

.———(2.12)

Количество теплоты, прошедшее через эту поверхность в течение времени t, определяется интегралом

.———(2.13)

Таким образом, для определения количества теплоты, проходящего через какую-либо произвольную поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу аналитической теории теплопроводности.

2.4 Дифференциальное уравнение теплопроводности

Изучение любого физического процесса связано с установлением зависимости между величинами, характеризующими данный процесс. Для сложных процессов, к которым относится передача теплоты теплопроводностью, при установлении зависимостей между величинами удобно воспользоваться методами математической физики, которая рассматривает протекание процесса не во всем изучаемом пространстве, а в элементарном объеме вещества в течение бесконечно малого отрезка времени. Связь между величинами, участвующими в передаче теплоты теплопроводностью, устанавливается дифференциальным уравнением теплопроводности. В пределах выбранного элементарного объема и бесконечно малого отрезка времени становится возможным пренебречь изменением некоторых величин, характеризующих процесс.

При выводе дифференциального уравнения теплопроводности принимаются следующие допущения:

внутренние источники теплоты отсутствуют;

среда, в которой распространяется тепло, однородна и изотропна;

используется закон сохранения энергии, который для данного случая формулируется так: разность между количеством теплоты, вошедшей вследствие теплопроводности в элементарный параллелепипед за время dt и вышедшей из него за тоже время, расходуется на изменение внутренней энергии рассматриваемого элементарного объема.

Выделим в среде элементарный параллелепипед с ребрами (рисунок 2.2). Температуры граней различны, поэтому через параллелепипед проходит теплота в направлении осей . Через площадку за время dt, согласно уравнению Фурье, проходит количество теплоты:

———(2.14)

(grad T взят в виде частной производной, т. к. предполагается зависимость температуры не только от x, но и от других координат и времени).

Через противоположную грань на расстоянии dz отводится количество теплоты, определяемое из выражения:

,———(2.15)

где — температура второй грани, а величина определяет изменение температуры в направлении z.

Последнее уравнение можно представить в другом виде:

.—-(2.16)

Итак, приращение внутренней энергии в параллелепипеде за счёт потока тепла в направлении оси z равно:

.———(2.17)

Приращение внутренней энергии в параллелепипеде за счёт потока тепла в направлении оси y выразится аналогичным уравнением:

,———(2.18)

а в направлении оси x:

.———(2.19)

Полное приращение внутренней энергии в параллелепипеде:

.—-(2.20)

С другой стороны, согласно закону сохранения энергии:

,———(2.21)

где — объем параллелепипеда;

— масса параллелепипеда;

c — удельная теплоемкость среды;

— плотность среды;

— изменение температуры в данной точке среды за время dt.

Левые части уравнения (2.20) и (2.21) равны, поэтому:

,—-(2.22)

.———(2.23)

Величину называют оператором Лапласа и обычно обозначают сокращенно ; величину называют температуропроводностью и обозначают буквой a. При указанных обозначениях дифференциальное уравнение теплопроводности принимает вид:

.———(2.24)

Уравнение (2.24) называется дифференциальным уравнением теплопроводности (или дифференциальным уравнением Фурье) для трехмерного нестационарного температурного поля при отсутствии внутренних источников теплоты. Оно является основным при изучении вопросов нагревания и охлаждения тел в процессе передачи теплоты теплопроводностью и устанавливает связь между временным и пространственным изменениям температуры в любой точке поля.

Температуропроводность является физическим параметром вещества и имеет единицу м2/c. В нестационарных тепловых процессах a характеризует скорость изменения температуры.

Из уравнения (2.24) следует, что изменение температуры во времени для любой точки тела пропорционально величине a. Поэтому при одинаковых условиях быстрее увеличивается температура у того тела, которое имеет большую температуропроводность.

Дифференциальное уравнение теплопроводности с источником теплоты внутри тела имеет вид:

,———(2.25)

гдеqV — удельная мощность источника, то есть количество выделяемой теплоты в единице объёма вещества в единицу времени.

Это уравнение записано в декартовых координатах. В других координатах оператор Лапласа имеет иной вид, поэтому меняется и вид уравнения. Например, в цилиндрических координатах дифференциальное уравнение теплопроводности с внутренним источником теплоты таково:

,—-(2.26)

гдеr — радиус-вектор в цилиндрической системе координат;

— полярный угол.

2.5 Краевые условия

Полученное дифференциальное уравнение Фурье описывает явления передачи теплоты теплопроводностью в самом общем виде. Для того чтобы применить его к конкретному случаю, необходимо знать распределение температур в теле или начальные условия. Кроме того, должны быть известны:

геометрическая форма и размеры тела,

физические параметры среды и тела,

граничные условия, характеризующие распределение температур на поверхности тела, или взаимодействие изучаемого тела с окружающей средой.

Все эти частные особенности совместно с дифференциальным уравнением дают полное описание конкретного процесса теплопроводности и называются условиями однозначности или краевыми условиями.

Обычно начальные условия распределения температуры задаются для момента времени t = 0.

Граничные условия могут быть заданы тремя способами.

Граничное условие первого рода задается распределением температуры на поверхности тела для любого момента времени.

Граничное условие второго рода задается поверхностной плотностью теплового потока в каждой точке поверхности тела для любого момента времени.

Граничное условие третьего рода задается температурой среды, окружающей тело, и законом теплоотдачи между поверхность тела и окружающей средой.

Решение дифференциального уравнения теплопроводности при заданных условиях однозначности позволяет определить температурное поле во всем объеме тела для любого момента времени или найти функцию .

2.6 Теплопроводность через шаровую стенку

С учётом описанной в разделах 2.1 — 2.5 терминологии задачу данной курсовой работы можно сформулировать так. Постоянный тепловой поток направлен через шаровую стенку, причем источником теплоты является внутренняя сфера радиусом R1. Мощность источника P постоянна. Среда между граничными сферами изотропна, поэтому её теплопроводность χ является функцией одной переменной — расстояния от центра сфер (радиуса) r. По условию задачи . Вследствие этого температура среды тоже является в данном случае функцией одной переменной — радиуса r: T = T(r), а изотермические поверхности это концентрические сферы. Таким образом искомое температурное поле — стационарное и одномерное, а граничные условия являются условиями первого рода: T(R1) = T1, T(R2) = T2.

Из одномерности температурного поля следует, что плотность теплового потока j так же, как теплопроводность и температура, являются в данном случае функциями одной переменной — радиуса r. Неизвестные функции j(r) и T(r) можно определить одним из двух способов: или решать дифференциальное уравнение Фурье (2.25), или использовать закон Фурье (2.11). В данной работе избран второй способ. Закон Фурье для исследуемого одномерного сферически симметричного температурного поля имеет вид:

.————(2.27)

В этом уравнении учтено, что вектор нормали к изотермической поверхности n параллелен радиус-вектору r. Поэтому производная может быть записана как.

Определим зависимость плотности теплового потока j от r. Для этого сначала вычислим тепловой поток q через сферу произвольного радиуса r > R.

.————(2.28)

В частности, тепловой поток q1 через внутреннюю сферу радиусом R1 и тепловой поток q2 через наружную сферу радиусом R2 равны

———(2.29)

Все эти три потока создаются одним и тем же источником мощностью P. Поэтому все они равны P и поэтому равны между собой.

.————(2.30)

С учётом (2.28) и (2.29) это равенство можно записать в виде:

.———(2.31)

,———

получаем искомую зависимость плотности теплового потока j от радиуса r:

,————(2.32)

где C1 — это константа, определяемая формулой

.———(2.33)

Физический смысл полученного результата достаточно ясен: это известный закон обратных квадратов, характерный для задач со сферической симметрией.

Теперь, так как функция j(r) известна, можно рассматривать уравнение (2.27) как дифференциальное уравнение относительно функции T(r). Решение этого уравнение и даст искомое распределение температур. Подставив в (2.27) выражение (2.32) и заданную функцию , получим следующее дифференциальное уравнение:

.————(2.34)

Данное уравнение решается методом разделения переменных:

.————

Интегрирование этого выражения даёт:

———

Итак, функция T(r) имеет вид:

.———(2.35)

Константы C1 и C2 можно определить из граничных условий T(R1) = T1,
T(R2) = T2. Подстановка этих условий в (2.35) даёт линейную систему двух уравнений с двумя неизвестными C1 и C2:

.———(2.36)

Вычитая из первого уравнения второе, получим уравнение относительно C1:

,———

.———(2.37)

С учётом этого выражение (2.35) можно записать в виде:

.———(2.38)

Теперь первое граничное условие T(R1) = T1 даёт:

,———(2.39)

откуда следует выражение для константы C2:

.———(2.40)

Подстановка (2.40) в (2.39) даёт окончательное выражение для искомой функцииT(r):

.———(2.41)

Зная функцию T(r), можно из закона Фурье

————

определить и окончательное выражение для плотности теплового потока j как функции от радиуса r:

. ———(2.42)

Интересно отметить, что распределение температур не зависит от коэффициента b, но зато плотность потока пропорциональна b.

В результате проделанной работы выведено дифференциальное уравнение теплопроводности применительно к данным конкретным условиям задачи и получено решение этого уравнения в виде функции T(r). Разработана программа TSO, рассчитывающая функцию T(r) и строящая её график для различных задаваемых пользователем параметров задачи.

Поверхностный тепловой потенциал.

Тепловой потенциал с плотностью называется поверхностным тепловым потенциалом (простого слоя с плотностью ),

Если — ограниченная функция в , то поверхностный тепловой потенциал существует в , принадлежит классу , представляется интегралом Пуассона:

(2.30)

Постановка задачи Коши для уравнения теплопроводности.

(2.31)

(2.32)

Считаем и . Предположим, что существует классическое решение этой задачи. Это значит, что , удовлетворяет уравнение (2.31) при и начальное условие (2.32) при .

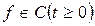
Продолжая функции и нулём при , заключаем, что продолженные функции и удовлетворяют в уравнению теплопроводности:

(2.33)

Равенство (2.33) показывает, что начальное возмущение для функции играет роль мгновенно действующего источника (типа простого слоя на плоскости ) и классические решения задачи Коши (2.31) — (2.32) содержатся среди тех решений уравнения (2.33), которые обращаются в нуль при . Это даёт основание ввести следующее обобщение задачи Коши для уравнения теплопроводности.

Обобщённой задачей Кошидля уравнения теплопроводности с источником назовём задачу о нахождении обобщённой функции , обращающейся в нуль при и удовлетворяющей уравнению теплопроводности

(2.34)

Уравнение (2.34) эквивалентно следующему:

Для любой справедливо равенство:

(2.35)

Из уравнения (2.34) следует, что необходимым условием разрешимости обобщенной задачи Коши является обращение в нуль при .

Решение задачи Коши.

Пусть , где и — ограниченная функция в . Тогда решение соответствующей обобщённой задачи Коши существует и единственно в классе и представляется формулой Пуассона:

(2.36)

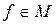
Таким образом, общее решение распределения интересующего нас потока по координате и времени в аналитическом диффузионном приближении может быть представлено в виде двух функций, одна из которых характеризует форму потока в начале координат, вторая характеризует изменения потока во времени, f(x, t)и θ(t) определяются из общей постановки задачи и индивидуальны для каждого потока.

Во многих случаях, решение можно представить в виде сумы конечного ряда:

, (2.37)

где Ф(x, t) – интеграл ошибок.

В более сложных случаях решение может быть выражено в виде бесконечных рядов, полиномов Лежандра, функции Бесселя, Ханкеля или других специализированных функций. Однако такое представление выходит за рамки нашего курса.

Численное решение уравнений переноса в диффузионном приближении.

В тех случаях, когда среду нельзя представить в виде уравнений с постоянными коэффициентами, или граничные условия нельзя представить в виде среды с бесконечно распространяющимися потоками, используют более сложную форму.

, (2.38)

где — удельная емкость исследуемого потока (теплоёмкость),

— удельная проводимость исследуемого потока (теплопроводность),

— источник потока,

— коэффициент связывающей скорость прохождения потока в веществах, имеющих различные свойства (коэффициент теплопроводности),

— скорость переноса потока.

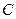
Во многих случаях, применим набор граничных условий, который позволяет, не выясняя, что происходит на удаленных границах, ставить задачу, которая описывает процесс с качеством, достаточным для наших целей. Такая постановка особенно важна в случае моделирования процессов проходящих при высоких температурах, давлении или в средах, имеющих высокую степень агрессивности, где затруднено непосредственное измерение параметров.

В этих случаях можно предположить, что:

1. Потоки на невзаимодействующих границах просто отражаются от стенки. Такое приближение называется «зеркально отражающая граница». В этом случае предполагается, что мы можем поставить следующие граничные условия:

, (2.39)

где U гр _+- — соответствует интенсивности прямого и отраженного потока на удаленной границе;

t_гр – время за которое поток достигает границы.

2. Все потоки на удаленной границе равны нулю – абсолютное поглощение.

=0 (2.40)

В этом случае уравнение решается численно с помощью достаточно простых сеточных методов. Однако граничные условия на взаимодействующей границе лучше выбирать, используя решение в аналитическом приближении в узкой области у границы раздела. Определение величины этой области выбирается следующим методом.

Определяется, для каких x и t нашей задачи справедливо выражение:

В этом случае аналитическое решение изменяется вместе с изменением входных параметров и применимо как граничное условие для более точного решения.

Тепловой потенциал

Cтраница 1

Тепловые потенциалы для трех — Черт.
 [1]

Следовательно, тепловым потенциалом является температура. Легко видеть, что температура удовлетворяет правилу знаков, сформулированному выше.
 [2]

К недостаткам метода тепловых потенциалов следует отнести его некоторую сложность и громоздкость, а также невозможность его непосредственного применения в случае неоднородных начальных условий ( которые вначале должны быть сведены к однородным); в последнем случае нетрудно обойти указанное затруднение с помощью использования интеграла Пуассона.
 [3]

Для создания разности тепловых потенциалов в машине затрачивается работа L. Эта работа вместе с отведенной теплотой Q9 передается в окружающую среду.
 [5]

Более рациональное использование теплового потенциала процесса путем получения большого количества воды и газа с температурой, значительно превышающей 100 С.
 [6]

Газы эти обладают высоким тепловым потенциалом.
 [8]

Величину kTle называют тепловым потенциалом микрочастицы.
 [9]

В системах геотермального теплоснабжения тепловой потенциал, не использованный потребителем, теряется безвозвратно.
 [11]

В этой главе приводятся различные тепловые потенциалы, связанные с оператором Бесселя, и некоторые их свойства. Доказываются оценки их норм через нормы плотности в различных пространствах функций. Приводятся обобщенные операторы Абеля, которые на самом деле являются предельными значениями тепловых потенциалов или их нормальных производных на боковой поверхности. Для этих операторов устанавливаются оценки как в гельдеровских — пространствах, так и в Wp. Даются формулы суперпозиции операторов Абеля, которые, как видно из гл.
 [12]

В первой схеме используют тепловой потенциал выхлопных газов для нагрева технологических продуктов.
 [13]

Одним из достоинств метода тепловых потенциалов является то, что он позволяет сводить решение дифференциального уравнения параболического типа к интегральному уравнению, которое более удобно для проведения числовых расчетов.
 [14]

Страницы:  

   1

   2

   3

   4

Дифференциальное уравнение для безразмерного потенциала тепло-переноса Ть найдем следующим образом из уравнения (4-2-2) определим 0ь, его вторую производную 0″ь и подставим полученные выражения в уравнение (4-2-3), После упрощений получим  [c.117]

Как говорит само название, термотрансформатор представляет собой устройство, служащее для изменения потенциала тепла. Таким образом, в термотрансформаторе происходит преобразование одного количества тепла данного потенциала в другое количество тепла иного потенциала.  [c.185]

Для создания устойчивого режима работы теплообменного аппарата с промежуточным жидким теплоносителем необходимо непрерывно восстанавливать двухфазную среду газ — жидкость, осуществляя подачу выделяющегося из потока промежуточного жидкого теплоносителя, улавливаемого поверхностью нагрева или сепарационным устройством, устанавливаемым за теплообменником, к месту распыла (к форсунке, барбо-тажной тарелке и т. п.). Для уменьшения падения температуры при распылении в газе промежуточного жидкого теплоносителя и улучшения использования потенциала тепла теплообменник с промежуточным жидким теплоносителем целесообразно разделять на несколько секций, в каждой из которых осуществляется свой замкнутый цикл циркуляции промежуточного теплоносителя.  [c.185]

Третья причина состоит в том, что предложенные в первой половине текущего века и зачастую используемые сейчас методы анализа не делают никакой разницы между качеством тепла, отбираемого для потребителя перед турбиной, и качеством тепла, отдаваемого потребителю из отборов паровой турбины. Вместе с тем второй принцип термодинамики как раз и учитывает потенциал тепла при любых тепловых процессах как тех, в которых совершается переход тепла в работу, так и тех, где такого перехода нет. Этой стороне второго закона термодинамики будет уделено значительное внимание в настоящей книге.  [c.8]

Тепловыми насосами называются установки, служащие для повышения потенциала тепла. Они применяются на промышленных предприятиях в тех случаях, когда располагаемые параметры пара из отборов турбин, отработавшего пара машин-орудий или теплообменных устройств недостаточны для удовлетворения потребителей.  [c.218]

Тепловыми насосами называются установки, служащие для повышения потенциала тепла.  [c.235]

Тепловые насосы, повышающие потенциал тепла от уровня, лежащего ниже тем-  [c.235]

Трансформаторы тепла бывают механическими, Б которых для повышения потенциала тепла используется механическая (электрическая) энергия, и тепловыми, в которых для повышения потенциала тепла используется тепловая энергия.  [c.236]

По оценке Ленинградского горного института прогнозный энергетический потенциал тепла, которое можно использовать для создания ПЦС, при температурах 100 — 150°С может составить величину порядка сотен млрд. т у.т. (СНГ).  [c.82]

Понятие химического потенциала введем следующим образом. Если бы система была закрытой, то для нее можно было бы записать (предполагая для простоты рассуждения, что система с окружающей средой обменивается энергией только в виде тепла и работы изменения объема)  [c.23]

Фазовые переходы, сопровождающиеся поглощением или выделением тепла, называются фазовыми переходами первого рода. Фазовые переходы первого рода характеризуются скачкообразным изменением ряда свойств вещества. Скачком изменяются при переходе через кривую фазового равновесия объем и энтропия и, как следствие этого, внутренняя энергия, энтальпия и теплоемкость некоторые из свойств, например изобарный потенциал, при фазовом переходе первого рода скачка не испытывают. К фазовым переходам первого рода относятся испарение и конденсация, плавление и кристаллизация, многие переходы из одной кристаллической модификации в другую.  [c.137]

Примером обратимой реакции при постоянных Тир является реакция, происходящая в гальваническом элементе между электролитом и веществом положительного электрода при малой силе тока В замкнутой цепи, когда джоулевым теплом можно пренебречь. По ве- личине максимальной э. д. с. элемента можно определить максимальную работу, а следовательно, и убыль изобарного потенциала в данной реакции.  [c.319]

Эффективность эжекторной установки, затрачивающей для охлаждающего действия энергию не в виде работы, а в виде тепла высокого потенциала, оценивают коэффициентом использования тепла  [c.485]

С теплопроводностью мы познакомились в первой части курса. Диф ференциальное уравнение теплопроводности = 0 описывает бесчисленное множество конкретных процессов, принадлежащих к одному и тому же классу. Общность этих процессов определяется одинаковым механизмом процесса распространения тепла. Однако известны и другие дифференциальные уравнения, аналогичные по форме записи уравнению теплопроводности, например уравнение электрического потенциала ( ii. 3-12). Если для температуры и электрического потенциала ввести одинаковые обозначения, то оба уравнения по своему внешнему виду не будут отличаться друг от друга. Однако, хотя по форме записи оба уравнения совпадают, физическое содержание входящих в эти уравнения величин различно. Те явления природы, которые описываются одинаковыми по форме записи дифференциальными уравнениями, но различны по своему физическому содержанию, называются аналогичными.  [c.157]

Однако на достаточно длительном отрезке времени доля ядерного горючего в общем расходе энергетических ресурсов будет расти относительно медленно и вряд ли превысит 25—30% к концу первой четверти XXI в. Определяется это, в частности, тем, что темпы развития атомной энергетики, особенно в развитых капиталистических странах, существенно сдерживаются противодействием общественности (за период 1977—1980 гг. прогнозируемый МАГАТЭ и МИРЭК на 2000 г. уровень развития атомной энергетики в мире снизился в 3—3,5 раза). Необходимо также учитывать, что объективно роль ядерного горючего в мировом энергетическом балансе в значительной мере зависит от уровня его использования для централизованного теплоснабжения и получения тепла высокого потенциала. Это происходит потому, что на производство электроэнергии и в промышленно развитых странах расходуется лишь около 1/3 используемых энергетических ресурсов. Так что если атомные электростанции будут производить даже 3/4 всей электроэнергии, то и тогда доля ядерного горючего в общем энергетическом балансе не превысит 1/4 (углубление уровня электрификации может несколько повысить эту величину). Существенное развитие централизованное теплоснабжение и теплофикация в настоящее время получили лишь в СССР и частично европейских странах — членах СЭВ.  [c.115]

Иначе обстоит дело с энергией упругих микроискажений кристаллической решетки, вызванных пластической деформацией тела. Накопленная в результате пластической деформации кристалла энергия упругих искажений решетки превращается в тепло при нагреве выше температуры рекристаллизации и оценивается калориметрическим методом [16]. Количество отведенной теплоты равно изменению энтальпии, так как процесс протекает в изобарных условиях. Поскольку химические реакции обычно идут также в изобарных условиях, термодинамической функцией (мерой максимальной полезной работы химической реакции) здесь является свободная энтальпия — изобарно-изотермический потенциал (термодинамический потенциал). Так как энтропийный член в данном случае пренебрежимо мал, деформационный сдвиг равновесного потенциала может быть вычислен по величине изменения энтальпии, запасенной вследствие пластической деформации тела.  [c.24]

Печь для сушки древесины, снабженная тепловым насосом. Традиционный способ сушки древесины заключается в ее нагреве с последующим выпуском влажного воздуха в атмосферу. Энергетическая эффективность такой системы низка, и имеется возмож.ность заменить топливо электроэнергией, если вторичные тепловые энергоресурсы, содержащиеся в струе выходящего воздуха, будут утилизированы. Для этого необходимо повысить энергетический потенциал отводимого из камеры воздуха — сперва осушить его, а затем поднять его температуру до такого уровня, который требуется при повторной подаче воздуха в сушильную камеру. Если пропускать струю удаляемого из камеры влажного воздуха над испарителем теплового насоса, влага будет осаждаться на испарителе и воздух станет сухим после этого он опять нагреется, проходя над конденсатором теплового насоса. Таким образом, тепловой насос (осушитель) повышает температуру воздуха, сохранившего остаточное тепло, и утилизирует скрытую теплоту, содержащуюся в удаленной из древесины влаге.  [c.196]

В процессе коррозии, протекающей с образованием твердых продуктов, например в водопроводной воде, потенциал сдвигается в сторону более положительных значений в результате экранирования анодных участков. Существенное смещение потенциала цинка к положительным значениям наблюдается при эксплуатации цинковых и оцинкованных изделий в теплой воде. В этих условиях потенциал цинка может достигать более положительных значений, чем потенциал железа. Такие изменения связаны с образованием гидроокисных продуктов коррозии, которые под действием высокой температуры превращаются в устойчивую окись цинка.  [c.112]

Термин энергетический потенциал означает наличие в перечисленных продуктах определенного запаса энергии (химически связанного тепла, физического тепла, потенциальной энергии избыточного давления).  [c.6]

При водяном охлаждении повышение температуры охлаждающей воды во избежание образования накипи на охлаждаемых элементах допускается не более чем на 15—20°С. При этом не используется огромное количество тепла, отводимого от охлаждаемых элементов металлургических печей, ввиду его низкого потенциала. Перевод элементов доменных печей (холодильников, воздушных фурм, клапанов горячего дутья) на испарительное охлаждение дает большие технологические преимущества, так как увеличивается срок службы охлаждаемых элементов, сокращается расход охлаждающей воды и, следовательно, расход электроэнергии на ее перекачку.  [c.41]

Для защиты футеровки пирометаллургических агрегатов цветной металлургии применяется искусственное охлаждение. В производственной практике основным теплоносителем для охлаждения элементов печей является вода. Однако это требует ее большого расхода. Кроме того, тепло нагретой воды трудно использовать из-за его низкого потенциала (50°С). В последнее время получают распространение установки испарительного охлаждения. Они предназначены для охлаждения конструктивных  [c.54]

Водоаммиачные установки широкого распространения в нашей стране не получили, так как для осуществления их рабочего процесса необходим подвод тепла высокого потенциала, а их рабочий агент — аммиак весьма токсичен.  [c.205]

Известны следующие группы абсорбционных машин первого типа одноступенчатые, применяемые при наличии источника тепла с температурой 100—150°С для температур кипения в интервале -Ь5°Ч—45° С двухступенчатые, применяемые при наличии источника тепла низкого потенциала или для  [c.609]

Топки паровых котлов также являются рекуперативными теплообменниками, служащими, однако, не только для целей теплообмена, но и для получения тепла высокого потенциала.  [c.123]

Из предыдущего параграфа следует, что метод коэффициентов полезного действия учитывает потери, обусловленные лишь внутренней необратимостью цикла, но никак не учитывает потерь, обусловленных конечной разностью температур источника тепла и рабочего тела. Тем не менее метод коэффициентов полезного действия широко распространен в практике теплотехнических расчетов. Объясняется это тем, что внешняя необратимость не влияет на количественные результаты анализа — если внутренняя необратимость цикла приводит к тому, что часть тепла, сообш енного рабочему телу, уходит из цикла в виде теплопотерь, то внешняя необратимость не приводит к потерям тепла одно и то же количество тепла будет передано от горячего источника к рабочему телу вне зависимости от того, какова разность температур между ними. Внешняя необратимость приводит к потере работоспособности (т. е. недоиспользованию температурного потенциала тепла, который в случае термодинамически более совершенной организации процесса подвода тепла позволил бы получить большую работу).  [c.310]

Анализ величин потерь работоспособности по отдельным элементам установки показывает, что наибольшие потери работоспособности (1593 кДж/кг=380,6 ккал/кг) имеют место в котлоагрегате, где необратимость наиболее велика вследствие большой разности температур тоночных газов и рабочего тела потери работоспособности, обусловленные только этой разностью, т. е. недоиспользованием температурного потенциала тепла, полученного при сжигании топлива, составляют AL =1305 кДж/кг (311,7 ккал/кг).  [c.383]

Баланс тепла. Практика составления ба- развернутой приходной части баланса тепла, лансов тепла в ряде европейских социалисти- охватывающей все источники генерирования ческих стран показала, что еще недостаточно тепла среднего и низкого потенциала (тепло-полно и четко определены как собственно по- электроцентрали, котельные, утилизационные нятие баланса тепла, так и содержание его установки, отопительные печи и т. п.). основных разделов, в частности структура В ряде таблиц 3-2 структура и содержа-основных групп потребителей, а также гене- ние позиций приходной части балансов со-рирующих установок. ставлены исходя из принятого выше опреде-  [c.17]

При работе по понысительной схеме в установке осуществляется повышение потенциала тепла, подводимого на низком температурном уровне 7j,, до более высокого температурного уровня 7″с- Для выполнения работы используется внешний источник энергии в форме тепла, подводимого к установке на высоком температурном уровне Гв-  [c.424]

Образование двухфазной среды газ—жидкость может осуществляться различными способами в барботажных и распылительных системах, оросительных устройствах и т. д. Для устойчивой работы такого аппарата необходимо восстанавливать двухфазную среду газ—жидкость, осуществляя непрерывное улавливание промежуточного теплоносителя (воды) и подачу его к форсункам или барботажным тарелкам. Для уменьшения падения температуры при распылива-нии в газе воды или иной жидкости и улучшения использования потенциала тепла такой теплообменник целесообразно разделить на несколько секций, в каждой из которых осуществляется замкнутый цикл в определенной температурной зоне и для различных зон возможно применение различных теплоносителей, отвечающих заданному температурному уровню. Проблема тепло- и массопереноса в дисперсном газожидкостном потоке относится к сопряженным задачам. Процесс определяется системой уравнений гидромеханики и энергии для газовой и жидкой фаз (капель, пленок), уравнениями конвективной диффузии, условиями сопряжения на поверхности раздела фаз и условиями однозначности.  [c.61]

Коэффициенты Z., в этом линейном законе называются феноменологическими, или кинетическими, коэффициентами. Причем диагональные коэффициенты La определяют прямые явления переноса, а недиагональные коэффициенты Lik, непрерывно связанные с прямыми, — перекрестные или сопряженные процессы. Так, по закону теплопроводности Фурье (1.20) градиент температуры вызывает поток тепла (L,i = L = x) по закону Фика градиент концентрации вызывает диффузию /=—Dgrad , L=D по закону Ома градиент потенциала вызывает ток / = —а grad ф, L = o и т. д. Наряду с этими прямыми процессами переноса возникают и сопряженные с ними процессы. Например, при существовании градиента температуры кроме переноса тепла может происходить и перенос массы (термодиффузия). Такие перекрестные процессы характеризуются недиагональными коэффициентами Lik- Так, плотность потока массы 1 при наличии градиента концентрации и градиента температуры равна  [c.14]

Существенной положительной особенностью термоэмиссионных генераторов (ТЭмГ) является то, что различие теплот испарения и конденсации электронов не зависит от температур этих процессов, как в парожидкостных ПЭ, а определяется работами выхода катода срк и анода фа и падением потенциала внутри ПЭ — AeY. Поэтому преимуществом электронного газа, как рабочего тела принято считать возможность испарять его при очень высоких температурах. Однако, как показано выше при анализе КПД цикла Карно, это преимущество малоэффективно, особенно с учетом быстро возрастающих с повышением температуры потерь тепла и разрушений материалов.  [c.75]

Магний имеет самый отрицательный стационарный потенциал из всех металлов, используемых в технике. Ввиду этого свойства и высокой теоретической токоотдачи он особенно подходит для применения в качестве протекторов. Гидроксид Mg (ОН) 2 разъедается уже слабыми кислотами и не проявляет склонности к образованию изолирующих поверхностных слоев даже в теплой пресной воде. Однако магний подвергается значительной собственной коррозии, скорость которой возрастает по мере увеличения содержания солей в среде [18]. Практическая токоотдача чистого магния во всех случаях заметно меньше тео-  [c.185]

Накопленная в результате пластической деформации кристалла энергия упругих искажений решетки превращается в тепло при нагреве выше температуры рекристаллизации и оценивается калориметрическим методом [14]. Количество отведенной теплоты равно изменению энтальпии, так как процесс протекает в изобарных условиях. Поскольку химические реакции обычно идут также в изобарных условиях, термодинамической функцией (мерой максимальной полезной работы химической реакции) здесь является свободная энтальпия — изобарно-изотермический потенциал (термодинамический потенциал). Так как энтропийный член в данном случае пренебрежимо малТ дёфбрмационный» сдвиг  [c.26]

Геотермальная энергия. Геотермальная энергия существует в следующих четырех формах сухой пар из недр, горячая вода из недр, геоапрессованные растворы, тепло горячих пород И магмы. Энергетический потенциал ресурсов сухого пара в США ограничен. Однако в настоящее время — это единственная форма геотермальной энергии, которая в США используется. В Долине Гейзеров в Калифорнии общая мощность геотермальных электростанций составляет немногим более 500 МВт.  [c.87]

Тепловой насос. Нередко бывает так, что температурный потенциал теплоты, выделяемый в ходе одного процесса, слушком низок для того, чтобы он мог быть использован в другом процессе. Для повышения этой температуры можно применить тепловой насос. Он работает по тому же принципу, что и холодильный агрегат в испарителе образуется холод, а в конденсаторе — тепло. Большинство тепловых насосов снабжено электродвигателем, приводящим в действие компрессорн ю систему. На 1 кВт-ч электроэнергии, потребляемой компрессором, приходятся, как правило, 2-—3 кВт-ч выработанной теплоты, причем температурный -потенциал ее выше, чем у источника. Тепловые насосы выгоднее всего применять в тех случаях, когда одновременно существует необходимость в охлаждении и  [c.192]

Физические аналогии с адиабатическим движением представляют нагретые тела, при изменении состояния которых тепло и не подводится к ним и не отнимается у них (отсюда термин адиабатический также и в применении к аналогичным движениям механических циклов), электрические цепи при постоянных электродвижущих силах, движущиеся проводники, статически заряженные постоянными количествами электричества. Соответствующие физические процессы делаются аналогичными изоциклическим движениям, если температура нагретых тел, сила электрического тока в цепях, потенциал электростатически заряженного проводника поддерживаются постоянными. При вращении твердого тела движение делается изоциклическим, если тело путем ременной или зубчатой передачи соединено с вращающимся маховиком бесконечной массы или с твердым телом, угловая скорость которого поддерживается строго постоянной физические аналогии дает нагретое тело, соединенное посредством хорощего проводника тепла с бесконечным запасом тепла, электрический проводник, на концах которого поддерживается постоянная разность потенциалов (соединен клеммами с источником питания), в электростатике — заземленное тело, что Гельмгольц обозначает как соединение с землей, с запасом тепла и т. д.  [c.488]

Температура уходящих газов воздухонагревателей доменных печей изменяется за цикл от 150 до 600°С. Воздухонагреватели работают со сдвигом во времени, а уходящие газы из всех воздухонагревателей доменной печи направляются в общий боров, поэтому их температура усредняется. На различных заводах средняя температура уходящих газов кауперов изменяется в широких пределах (от 250 до 500°С). Хотя тепловой потенциал этих газов довольно значительный, в настоящее время он еще не используется. Тем не менее, в связи с тенденцией повышения температуры доменного дутья температура уходящих газов воздухонагревателей постоянно увеличивается. Поэтому в ближайшем будущем утилизация тепла уходящих газов может оказаться экономически выгодной. Это тепло может быть использовано для выработки пара, горячей воды или в системе ГУБТ для подогрева очищенного доменного газа. В настоящее время ведутся разработки по использованию этого тепла.  [c.42]

После рекуператоров уходящие газы имеют температуру примерно 300°С и содержат еще значительный тепловой потенциал. Физическое тепло уходящих газов после рекуператора в принципе может использоваться для подогрева воды или щихты перед загрузкой в печь, однако практически использование этого тепла не решено.  [c.49]

В связи с трудностями использования теплового потенциала этих видов ВЭР в незначительной степени утилизируется тепло уходящих газов отражательных печей, печей кипящего слоя и прочих металлургических печей, а также тепло охлаждения шахтных печей. Тепло уходящих газов конвертеров и прокалочпых печей анод-  [c.78]

Например, в химической промышленности значительную долю выхода ВЭР составляют низкотемпературные жидкости с температурой 90°С и ниже и дымовые газы с температурой 250°С и ниже. Эти ВЭР почти не используются, так как их носителями, как правило, являются загрязненные коррозионно-активные жидкости и газы, охлаждение которых с помощью стандартных теплообменных аппаратов невозможно. Кроме того, тепло столь низкого потенциала не находит потребителей в пределах основных технологических линий. Такое положение характерно для содовой промышленности, где 90% всех ВЭР — низкотемпературные. Основные потери тепла здесь — это потери с дистиллерной жидкостью, которая сбрасывается в специальные накопители с температурой 95°С. Тепло дистиллерной жидкости может быть использовано в аппаратах мгновенного вскипания, для подогрева питательной воды ТЭЦ, для теплофика-  [c.197]

Одним из способов использования отбросного тепла низкого потенциала является применение термокомпрессии и тепловых насосов. Для этих целей могут применяться паровые эжекторы и инжекторы, повышающие давление низкопотенциального пара. Такой метод может быть применен для использования тепла загрязненных жидкостей в результате их самоиспарения под вакуумом когда охлаждение их в поверхностных теплообменника невозможно. По такому способу может быть использова но значительное количество тепла дистиллерной жидко сти в производстве кальцинированной соды, где в на стоящее время это тепло еще не используетсЯ  [c.200]

Ведутся также разработки специального отойМтёЛЬ-но-вентиляционного оборудования, использующего отбросное тепло уходящих газов с температурой 150— 200°С и тепло охлаждающей воды с температурой 40— 50°С для целей отопления, вентиляции и кондиционирования воздуха. Разработка и освоение такого оборудования позволят эффективно использовать значительное количество отбросного тепла низкого потенциала.  [c.201]

Выше говорилось о том, что не вся работа неупругого деформирования переходит в тепло, и что часть работы идет на повышение потенциала тела в связи со всевозможными остаточными искажениями внутренней структуры тела. При отжиге тела удается обнаружить долю (до 20%) работы внешних сил, идущей на деформацию тела, которая (эта доля) остается в теле в виде скрытой энергии. Отмеченная энергия связана с дислокациями, искажениями решетки и т. п. Обнаружить при отжиге долю скрытой энергии, обусловленную трещинами, не удается, поскольку отжиг залечивает трещины в очень малой мере. Так как в конечном итоге все дефекты теми или иными путями приводят к образованию трещин, правильно полагать всю скрытую энергию, аккому-лированную в теле, как энергию, связанную с подготовкой к разрушению тела.  [c.593]

Принцип работы термоэмиссионного преобразователя. Рассмотрим действие простейшего ТЭП [142, 150, 151, 159] (рис. 2.1). На катод, изготавливаемый обычно из тугоплавкого материала (например, молибдена), от источника тепла поступает тепловая энергия Q, достаточная для возникновения термоэмиссии электронов с поверхности этого металла. Электроны, увеличив свою кинетическую энергию, преодолевают межэлектродное пространство и попадают на поверхность металлического анода. При этом электроны отдают ему часть своей кинетической энергии и нагревают его, а с другой стороны, создают избыток отрицательных зарядов па поверхности этого металла, увеличивая его отрицательный потенциал. Избыток зарядов стекает по внешней электрической цепи, проходя по сопротивлению нагрузки в виде полезного тока, и вновь попадает на катод. Если в этой модели обеспечить непрерывное подведение тепла Q, достаточное для термоэмиссии — испарения электронов, то во внешней цепи по сопротивлению нагрузки будет протекать непрерывный электрический ток.  [c.18]