Как найти тепловое равновесие двух жидкостей

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.

Что такое теплообмен и при каких условиях он происходит

Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

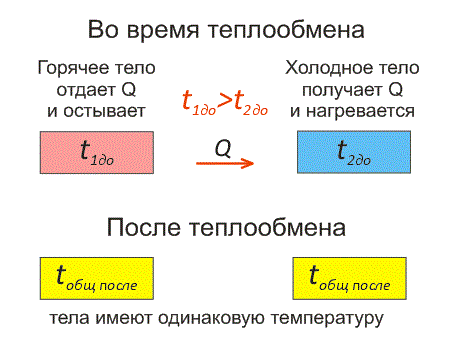
Рассмотрим два тела, имеющие различные температуры (рис. 1).

Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Уравнение теплового баланса и сохранение тепловой энергии

Когда тело остывает, оно отдает тепловую энергию (теплоту).  Утерянное количество теплоты Q имеет знак «минус».

А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».

Эти факты отражены на рисунке 2.

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.

Уравнение теплового баланса

Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]

(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.

(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.

В некоторых учебниках применяют сокращения:

[large Q_{1} + Q_{2} = 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

• равными по модулю и
• имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:

[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]

При этом:

• Q для каждого нагреваемого тела будет обладать знаком «+»,
• Q для каждого охлаждаемого тела — знаком «-».

Пример расчетов для теплообмена между холодным и горячим телом

К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.

Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

 Решение:

В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.

Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]

2). Теперь запишем формулу для каждого количества теплоты:

[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]

[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]

Примечания:

1. (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
2. Массу воды переводим в килограммы;
3. Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
4. Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]

Проведем упрощение:

[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

[large t_{text{общ}} = 58,33 ]

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.

Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:

• (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
• (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
• (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.

Выводы

1. Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
2. Когда тела будут иметь равную температуру, теплообмен прекратится;
3. Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
4. А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
5. Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
6. Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
7. В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
8. В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.

Тепловое равновесие и уравнение теплового баланса

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.

Что такое теплообмен и при каких условиях он происходит

Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

Рассмотрим два тела, имеющие различные температуры (рис. 1).

Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Уравнение теплового баланса и сохранение тепловой энергии

Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».

А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».

Эти факты отражены на рисунке 2.

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.

Уравнение теплового баланса

Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

(large Q_<text<остывания горяч>> left( text <Дж>right) ) – это количество теплоты горячее тело теряет.

(large Q_<text<нагревания холод>> left( text <Дж>right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.

В некоторых учебниках применяют сокращения:

[large Q_ <1>+ Q_ <2>= 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

• равными по модулю и
• имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:

[large boxed < Q_<1>+ Q_ <2>+ Q_ <3>+ ldots + Q_ = 0 > ]

• Q для каждого нагреваемого тела будет обладать знаком «+»,
• Q для каждого охлаждаемого тела — знаком «-».

Пример расчетов для теплообмена между холодным и горячим телом

К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.

Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

Решение:

В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.

Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

2). Теперь запишем формулу для каждого количества теплоты:

Примечания:

1. (large c_<text<воды>> ) – удельную теплоемкость воды находим в справочнике;
2. Массу воды переводим в килограммы;
3. Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_<text<общ>> — t_<text<горяч>> ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
4. Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_<text<общ>> — t_<text<холодн>> ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_<text<общ>> — 80 ) + 4200 cdot 0,1 cdot (t_<text<общ>> — 15 ) = 0 ]

[large 840 cdot (t_<text<общ>> — 80 ) + 420 cdot (t_<text<общ>> — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.

Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:

• (large Q_ <1>) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
• (large Q_ <2>) – охлаждение керосина от температуры +80 градусов до конечной температуры;
• (large Q_ <3>) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.

Решение задач на теплообмен с использованием уравнения теплового баланса (методические рекомендации)

Разделы: Физика

Пособие рекомендовано учащимся, желающим получить практические навыки в решении задач на теплообмен, и может быть полезным для учителей и абитуриентов.

При соприкосновении тел, имеющих разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической теории, это объясняется так: молекулы более нагретого тела имеют большую кинетическую энергию, чем молекулы тела, менее нагретого. При “столкновениях” молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии, при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного тела возрастает, поэтому температура этого тела будет увеличиваться. В конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры тел станут одинаковыми. На этом теплообмен прекращается.

Энергию, которую тело получает или отдаёт в процессе теплообмена, называют количеством теплоты (Q).

Количество теплоты, как и все другие виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж. (Здесь и в дальнейшем единицы измеряются в системе СИ.)

Нагревание или охлаждение

При нагревании или охлаждении тела количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:

(t₂ – t₁) – разность температур тела,° С (или К);

с – удельная теплоёмкость вещества, из которого состоит тело,

Удельная теплоёмкость вещества – это количество теплоты, которое нужно сообщить одному килограмму данного вещества, чтобы увеличить его температуру на 1° С (или это количество теплоты, которое выделяет один килограмм данного вещества, остывая на 1° С).

Значения удельных теплоемкостей других веществ можно найти в справочниках, а также в школьном учебнике или задачнике.

При нагревании тела его внутренняя энергия увеличивается. Это требует притока энергии к телу от других тел. Значит, оно поглощает некоторое количество теплоты, принимая его от других тел, участвующих в теплообмене.

При охлаждении тела его внутренняя энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое количество теплоты.

Обычно конечную температуру, установившуюся в результате теплообмена, обозначают греческой буквой (тэта).

В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью тела и обозначают С:

Размерность теплоемкости: Теплоемкость тела показывает, сколько энергии нужно подвести к данному телу, чтобы нагреть его на 1° С (или сколько энергии выделяет это тело, остывая на 1° С).

Теплообмен между телами, имеющими одинаковые температуры, не происходит, даже если контактируют вещества, находящиеся в разных агрегатных состояниях. Например, при температуре плавления (0° С) лёд и вода могут находиться бесконечно долго, при этом количество льда и количество воды останутся неизменными. Аналогично ведут себя пар и жидкость, находящиеся при температуре кипения. Теплообмен между ними не происходит.

Плавление или кристаллизация

Если при нагревании тела его температура достигнет температуры плавления, то начинает происходить процесс перехода этого вещества из твердого состояния в жидкое. При этом идут изменения в расположении и характере взаимодействия молекул. Температура при плавлении не изменяется. Это означает, что средние кинетические энергии молекул жидкости и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия тела при плавлении возрастает за счет увеличения энергии взаимодействия молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по формуле

(3)

где m – масса тела, кг;

– удельная теплота плавления,

При кристаллизации, наоборот, внутренняя энергия тела уменьшается на величину и эта теплота данным телом выделяется. Она поглощается другими телами, участвующими в теплообмене.

Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного вещества, взятого при температуре плавления, чтобы полностью превратить его при этой температуре в жидкость (или сколько энергии выделяет 1 кг жидкости, взятой при температуре кристаллизации, если вся она при этой температуре полностью превратится в твёрдое тело).

Удельную теплоту плавления любого вещества можно найти в справочниках. Для льда же

Температура плавления у каждого вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что температура плавления вещества равна температуре кристаллизации этого же вещества. У льда t_пл = 0° С.

Кипение или конденсация

При достижении жидкостью температуры кипения начинает происходить другой фазовый переход – кипение, при котором расстояния между молекулами значительно увеличиваются, а силы взаимодействия молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей между молекулами. При конденсации пара в жидкость, наоборот, расстояния между молекулами значительно сокращаются, а силы взаимодействия молекул увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при конденсации пара энергия выделяется. Количество теплоты, поглощаемое при кипении или выделяемое при конденсации, рассчитывается по формуле:

где m – масса тела, кг; L – удельная теплота парообразования,

Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости, взятой при температуре кипения, чтобы при этой температуре полностью превратить её в пар (для конденсации: сколько энергии выделяет один килограмм пара, взятого при температуре конденсации, полностью превращаясь в жидкость).

При одинаковом давлении температура кипения и температура конденсации одного и того же вещества одинаковы.

Температуры кипения и удельные теплоты парообразования также можно найти в справочниках. Для воды же они соответственно равны: рис. 9 (при нормальном атмосферном давлении).

Уравнение теплового баланса

Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её; теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами.

Это утверждение описывает частный случай закона сохранения и превращения энергии в применении к процессу теплообмена. А формула (5) является одним из видов уравнения теплового баланса.

При решении задач с помощью данного вида уравнения теплового баланса в формуле (1) в качестве t₂ следует брать большую температуру, а в качестве t₁ – меньшую. Тогда разность (t₂ – t₁) будет положительна и всё произведение cm(t₂–t₁) также будет положительным. Все теплоты, отданные и полученные, будут положительными.

Уравнение теплового баланса можно записать и в таком виде:

где n – количество тел системы.

Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю.

Q₁, Q₂, …, Q_n – это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что в этом случае какие-то теплоты должны быть положительны, а какие-то – отрицательны. При записи уравнения теплового баланса в виде (6) всегда t₂ – конечная температура, а t₁ – начальная.

Если тело нагревается, то разность (t₂ – t₁) положительна и все произведение cm(t₂ – t₁) положительно. То есть Q > 0 тогда, когда теплота к данному телу подводится.

А если t₂ 0; если тело выделяет энергию (кристаллизация, конденсация), то Q

	Проведём анализ: Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t1 = t2 = 20° С. При опускании в воду с температурой 20° С свинцового тела с температурой 90° С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться.
	Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ). Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q3.
Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают.
Решим задачу с использованием уравнения теплового баланса в виде (5):

Решим задачу с использованием уравнения теплового баланса в виде (6):

Ответ: Вода нагреется до 24° С.

Предлагаю читателю самостоятельно сделать проверку размерности.

Уравнение теплового баланса. Пособие Самарина

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Лицей естественных наук г. Кирова

Решение задач на теплообмен

с использованием уравнения теплового баланса

Печатается по решению редакционно-издательского совета Лицея естественных наук г. Кирова

Рецензент: К.А. Коханов, кандидат педагогических наук, старший преподаватель кафедры дидактики физики Вятского государственного гуманитарного университета, заместитель заведующего кафедрой дидактики физики.

С 17 Самарин Г.Г. Решение задач на теплообмен с использованием уравнения теплового баланса: Методические рекомендации. – Киров: Издательство Лицея естественных наук, 2002. – 35 с.

Пособие рекомендовано учащимся, желающим получить практические навыки в решении задач на теплообмен, и может быть полезным для учителей и абитуриентов.

© Лицей естественных наук, 2002

© Г.Г. Самарин, 2002

При соприкосновении тел, имеющих разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической теории, это объясняется так: молекулы более нагретого тела имеют большую кинетическую энергию, чем молекулы тела, менее нагретого. При «столкновениях» молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии, при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного тела возрастает, поэтому температура этого тела будет увеличиваться. В конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры тел станут одинаковыми. На этом теплообмен прекращается.

Энергию, которую тело получает или отдаёт в процессе теплообмена, называют количеством теплоты ( Q ).

Количество теплоты, как и все другие виды энергии, измеряется в системе СИ в Джоулях: [ Q ] = Дж. 

Нагревание или охлаждение

При нагревании или охлаждении тела количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:

где m – масса тела, кг;

с – удельная теплоёмкость вещества, из которого состоит тело,

или .

Удельная теплоёмкость вещества – это количество теплоты, которое нужно сообщить одному килограмму данного вещества, чтобы увеличить его температуру на 1  С (или это количество теплоты, которое выделяет один килограмм данного вещества, остывая на 1  С).

Например, С_воды = 4200, С_{льда, водяного пара} = 2100, С_свинца = 140, С_меди = 380, С_{железа, стали} = 460, С_{алюминия} = 920.

Значения удельных теплоемкостей других веществ можно найти в справочниках, а также в школьном учебнике или задачнике.

При нагревании тела его внутренняя энергия увеличивается. Это требует притока энергии к телу от других тел. Значит, оно поглощает некоторое количество теплоты, принимая его от других тел, участвующих в теплообмене.

При охлаждении тела его внутренняя энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое количество теплоты.

Обычно конечную температуру, установившуюся в результате теплообмена, обозначают греческой буквой  (тэта).

В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью тела и обозначают С:

Размерность теплоемкости: [С] = . Теплоемкость тела показывает, сколько энергии нужно подвести к данному телу, чтобы нагреть его на 1  С (или сколько энергии выделяет это тело, остывая на 1  С).

Теплообмен между телами, имеющими одинаковые температуры, не происходит, даже если контактируют вещества, находящиеся в разных агрегатных состояниях. Например, при температуре плавления (0  С) лёд и вода могут находиться бесконечно долго, при этом количество льда и количество воды останутся неизменными. Аналогично ведут себя пар и жидкость, находящиеся при температуре кипения. Теплообмен между ними не происходит.

Плавление или кристаллизация

Если при нагревании тела его температура достигнет температуры плавления, то начинает происходить процесс перехода этого вещества из твердого состояния в жидкое. При этом идут изменения в расположении и характере взаимодействия молекул. Температура при плавлении не изменяется. Это означает, что средние кинетические энергии молекул жидкости и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия тела при плавлении возрастает за счет увеличения энергии взаимодействия молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по формуле

где m – масса тела, кг;

 – удельная теплота плавления, .

При кристаллизации, наоборот, внутренняя энергия тела уменьшается на величину Q =  m , и эта теплота данным телом выделяется. Она поглощается другими телами, участвующими в теплообмене.

Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного вещества, взятого при температуре плавления, чтобы полностью превратить его при этой температуре в жидкость (или сколько энергии выделяет 1 кг жидкости, взятой при температуре кристаллизации, если вся она при этой температуре полностью превратится в твёрдое тело).

Удельную теплоту плавления любого вещества можно найти в справочниках. Для льда же  = 3,4  10 5 .

Температура плавления у каждого вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что температура плавления вещества равна температуре кристаллизации этого же вещества. У льда t _пл = 0  С.

Кипение или конденсация

При достижении жидкостью температуры кипения начинает происходить другой фазовый переход – кипение, при котором расстояния между молекулами значительно увеличиваются, а силы взаимодействия молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей между молекулами. При конденсации пара в жидкость, наоборот, расстояния между молекулами значительно сокращаются, а силы взаимодействия молекул увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при конденсации пара энергия выделяется. Количество теплоты, поглощаемое при кипении или выделяемое при конденсации, рассчитывается по формуле:

где m – масса тела, кг;

L – удельная теплота парообразования, .

Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости, взятой при температуре кипения, чтобы при этой температуре полностью превратить её в пар (для конденсации: сколько энергии выделяет один килограмм пара, взятого при температуре конденсации, полностью превращаясь в жидкость).

При одинаковом давлении температура кипения и температура конденсации одного и того же вещества одинаковы.

Температуры кипения и удельные теплоты парообразования также можно найти в справочниках. Для воды же они соответственно равны: t _кип = 100  С, L = 2,3  10 6 (при нормальном атмосферном давлении).

Уравнение теплового баланса

Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её; теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами.

Это утверждение описывает частный случай закона сохранения и превращения энергии в применении к процессу теплообмена. А формула (5) является одним из видов уравнения теплового баланса.

При решении задач с помощью данного вида уравнения теплового баланса в формуле (1) в качестве t ₂ следует брать большую температуру, а в качестве t ₁ – меньшую. Тогда разность ( t ₂ – t ₁) будет положительна и всё произведение cm ( t ₂– t ₁) также будет положительным. Все теплоты, отданные и полученные, будут положительными.

Уравнение теплового баланса можно записать и в таком виде:

Где n – количество тел системы.

Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю.

Q ₁, Q ₂, …, Q _n – это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что в этом случае какие-то теплоты должны быть положительны, а какие-то – отрицательны. При записи уравнения теплового баланса в виде (6) всегда t ₂ – конечная температура, а t ₁ – начальная.

Если тело нагревается, то разность ( t ₂ – t ₁) положительна и все произведение cm ( t ₂ – t ₁) положительно. То есть Q > 0 тогда, когда теплота к данному телу подводится.

А если t ₂ t ₁ (тело остывает), то разность ( t ₂ – t ₁) отрицательна, то есть Q Q > 0; если тело выделяет энергию (кристаллизация, конденсация), то Q  С. В воду опускают свинцовую деталь массой 2 кг, имеющую температуру 90  С. До какой температуры нагреется вода? Потерями теплоты пренебречь. 

m ₁ = 0,1 кг

с ₁ = 380 Дж/(кг  0 С)

с ₂ =4200 Дж/(кг  0 С)

с ₃ = 140 Дж/(кг  0 С)

 – ?

Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t ₁ = t ₂ = 20  С.

При опускании в воду с температурой 20  С свинцового тела с температурой 90  С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться.

Изменение температур тел с течением времени удобно изображать на графике зависимости t (  ).

Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q ₃.

Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q ₁ и Q ₂, которую они поглощают.

Решим задачу с использованием уравнения теплового баланса в виде (5):

 =

Решим задачу с использованием уравнения теплового баланса в виде (6):

 = = 24 (  С)

Ответ: Вода нагреется до 24  С.

Предлагаю читателю самостоятельно сделать проверку размерности.

Задача 2

Т
ри пластины: медную, имеющую массу m ₁ = 1 кг и температуру t ₁ = 100  С, железную ( m ₂ = 1,2 кг, t ₂ = 150  С) и алюминиевую ( m ₃ = 0,8 кг, t ₃ = 80  С) сложили вплотную (см рис). Какую температуру будут иметь пластины, когда теплообмен прекратится? Потерями теплоты в окружающую среду пренебречь.

с ₁ = 380 Дж/(кг  0 С)

с ₂ = 460 Дж/(кг  0 С)

с ₃ = 920 Дж/(кг  0 С)

Решение

Решим задачу с помощью уравнения теплового баланса в виде (5).

1. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная  нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая – нагреваться.

Мысленно соединим сначала эти две пластины и найдём температуру t , которой они при этом достигнут:

t =

t =

2. Теперь медная пластина вступает в теплообмен с железной и алюминиевой. Медная будет нагреваться от температуры t ₁ до температуры  , а железная и алюминиевая – остывать от температуры t до температуры  . Тогда:

Q ₁ = Q ₂‘+ Q ₃‘_,

 =

3. Решим задачу, применив уравнение теплового баланса в виде (6):

 = = 108 (  С)

Ответ: Пластины будут иметь температуру 108  С.

Как видим, второй способ оказался и в данном случае более рациональным. Однако, первый способ зачастую оказывается более понятным, особенно при наличии фазовых переходов. Поэтому в дальнейшем автор будет придерживаться первого способа решения задач. Желательно, чтобы читатель пробовал решать их и вторым способом.

Задача 3

В железном ведре массой 1,2 кг находится 5 кг воды при температуре 20  С. Сколько льда температурой –10  С надо положить в ведро, чтобы температура воды понизилась до 12  С? Теплообменом с окружающей средой пренебречь.

с ₁ =460 Дж/(кг  0 С)

с ₂ =4200 Дж/(кг  0 С)

с ₃ =2100 Дж/(кг  0 С)

t ₄ = 0 о С

Известна конечная температура, Значит, анализ ситуации довольно прост: вода и ведро будут остывать, не испытывая фазовых переходов, отдавая теплоты Q ₁ и Q ₂, а лёд сначала будет нагреваться до температуры плавления t ₄, поглощая теплоту Q ₃, затем плавиться,

поглощая теплоту Q ₄, а затем вода, образовавшаяся из льда, будет нагреваться до конечной температуры  , поглощая теплоту Q ₅.

Так как иных участников теплообмена нет, то можно так записать уравнение теплового баланса:

Ответ: Потребуется 0,4 кг льда.

Задача 4

В алюминиевую кастрюлю массой 200 г, содержащую 3 кг воды при 20  С, поместили стальную деталь массой 0,5 кг, нагретую до 500  С. При этом часть воды выкипела, а оставшаяся вода нагрелась до 22  С. Сколько воды выкипело?

m ₁ = 3 кг

L = 2,3  10 6 Дж/кг

Стальная деталь, не претерпевая фазовых переходов, остыла от 500  С до 22  С, выделив при этом количество теплоты

2. Часть воды массой m ₀ нагрелась до температуры кипения (100 о С) и выкипела. При этом была поглощена теплота

3. Оставшаяся в кастрюле вода массой ( m ₁  m ₀ ) и сама кастрюля массой m ₂ нагрелись от 20 0 С до 22  С. При этом была поглощена теплота

4. Так как потерь тепла нет, то записываем уравнение теплового баланса:

5. Решая это уравнение, находим m ₀:

m ₀ = ,

m ₀ =

Ответ: Выкипело 32 г воды.

Задача 5

Комок мокрого снега массой 400 г опустили в медный таз массой 500 г, содержащий 2 кг воды при температуре 20  С. После установления теплового равновесия температура воды в тазу стала 10  С. Сколько воды было в комке снега?

m ₃ = 0,4 кг

с₁ = 380 Дж/(кг  0 С)

1. Медный таз и вода находятся в тепловом равновесии. Поэтому 20  С – их общая температура. При остывании от 20  С до 10  С ни медь, ни вода фазовых превращений не испытывают. При этом они отдают суммарную теплоту:

2. Мокрый снег – это снег, содержащий воду. Значит, снег и вода находятся в тепловом равновесии. Это возможно только при температуре фазового перехода, то есть при 0  С.

Итак, начальная температура мокрого снега 0  С.

3. На пути к температуре 10  С снег массой m ₃ — m _в будет сначала таять. Для этого требуется теплота Q ₃ =  ( m ₃  m _в ). А затем вся вода массой m ₃ будет нагреваться от 0  С до 10  С. Для этого ей надо получить количество теплоты Q ₄ = c ₂ m ₃ (   t ₃ ).

4. Так как нет потерь тепла, то можно написать уравнение теплового баланса:

5. Решая это уравнение, находим m _в:

m _в =

m _в =

Ответ: В комке мокрого снега было 0,2 кг воды.

Задача 6

В холодную воду массой 2 кг, имеющую температуру 10  С, находящуюся в кастрюле, влили 3 кг горячей воды при температуре 80  С. До какой температуры нагреется холодная вода, если известно, что 25% теплоты, отданной горячей водой, пошло на нагревание кастрюли? Какова теплоемкость кастрюли?

Так как 25% теплоты отданы кастрюле, то 75% теплоты пошло на нагревание холодной воды. Значит, можно говорить о КПД процесса нагревания холодной воды:

 ₂ = (  ₂ = 0,75)

Здесь Q _полез — теплота, идущая на нагревание холодной воды: Q _полез = c ₁ m ₁ (   t ₁ );

Q _затр — теплота, отданная горячей водой: Q _затр = c ₂ m ₂ (t ₂   ).

Удельные теплоты с₁ холодной и с₂ горячей воды равны.

 ₂ =   ₂ m ₂ (t ₂   ) = m ₁ (   t ₂ ),

 =

 =

Так как 25% теплоты, отданной горячей водой, пошло на нагревание кастрюли, то можно говорить и о КПД процесса нагревания кастрюли:

,

откуда:

Ответ: Холодная вода нагреется до температуры 47  С. Теплоемкость кастрюли 2809 Дж/ 0 С.

Задача 7

Сколько керосина нужно сжечь, чтобы превратить в пар 1 кг льда, взятого при температуре  40  С? КПД нагревательного устройства равен 60%, удельная теплота сгорания керосина 46 МДж/кг.

m ₁ = 1 кг

L = 2,3  10 6 Дж/кг

 = 0,6 (60%)
q = 46  10 6 Дж/кг

1. Изобразим на графике t (  ) процессы: нагревание льда, плавление льда, нагревание получившейся из льда воды, кипение этой воды. Для осуществления каждого из этих процессов необходим подвод теплоты. Теплоту выделяет керосин в процессе сгорания (на графике не показано).

2. Применим формулу КПД нагревателя:

 = .

Получаем:  = ,

откуда: m ₂ = .

m _{2 =}

Ответ: Нужно сжечь 114 г керосина.

Сколько водяного пара, имеющего температуру 120  С, надо впустить в калориметр, содержащий 800 г льда при температуре  20  С, чтобы температура образовавшейся воды оказалась 20  С? Теплоёмкостью калориметра пренебречь.

m ₁ = 0,8 кг

Решение

1. Так как теплоемкостью калориметра можно пренебречь, то систему лед — пар можно считать теплоизолированной: теплообмен происходит только между паром и льдом.

2. Получают теплоту тела:

лёд, нагреваясь от –20 0 С до температуры плавления: Q ₁ = c ₁ m ₁(0  t ₁);

лёд, превращаясь в воду при температуре плавления: Q ₂ =  m ₁;

вода, образовавшаяся из льда, нагреваясь от 0  С до 20  С: Q ₃ = с₃ m ₁(   0).

3. Отдают теплоту тела:

пар, остывая от 120  С до температуры конденсации: Q ₄ = c ₂ m ₂( t ₂  100);

пар, превращаясь в воду при 100  С: Q ₅ = Lm ₂;

вода, образовавшаяся из пара, остывая от 100  С до 20  С: Q ₆ = c ₃ m ₂(100   ).

4. Других участников теплообмена нет, поэтому записываем уравнение теплового баланса:

Ответ: Потребуется 140 г водяного пара.

Часто при решении задач можно встретиться со следующей проблемой. В теплообмене участвуют вещества, находящиеся в различных агрегатных состояниях, и конечная температура теплообмена не известна. Тогда уравнение теплового баланса сразу написать не удастся, так как его вид зависит от того, в каких агрегатных состояниях будут находиться конечные продукты. В этом случае последовательность решения задачи немного изменяется. Сначала нужно сделать предварительные расчеты: сколько теплоты выделит или поглотит каждое вещество в предполагаемом процессе, сравнить эти теплоты и сделать вывод о том, в каких агрегатных состояниях будут находиться продукты теплообмена. И только после этого можно записывать уравнение теплового баланса. Такие задачи значительно сложнее задач, в которых конечная температура известна. Рассмотрим ряд таких задач.

Задача 9

В калориметр, содержащий воду массой 0,5 кг при температуре 25  С, впускают водяной пар массой 50 г при температуре 120  С. Какая температура установится в калориметре, если его теплоёмкость 1200 Дж/ о С?

с ₁ =4200 Дж/(кг  0 С)

c ₂ =2100 Дж/(кг  0 С)

L = 2,3  10 6 Дж/кг

1. Если в конечном итоге весь пар остынет от 120  С до 100  С, затем сконденсируется в воду, затем образовавшаяся из

пара вода остынет от 100  С до  , то в калориметре будет находиться вода при температуре  , а уравнение теплового баланса примет вид:

.

2. Если пар остынет от 120  С до 100  С, а сконденсируется не весь, то в калориметре будет находиться смесь воды и пара при температуре 100  С, а уравнение теплового баланса будет таким:

_{Здесь m}  _{— масса сконденсировавшегося пара.}

3. Пар может остыть от 120  С до 100  С, а вода и калориметр уже нагреются до 100  С, и при этом часть воды даже выкипит. В калориметре будет смесь пара и воды при температуре 100  С.

Уравнение теплового баланса будет иметь вид:

, где m  — масса превратившейся в пар воды.

Каким из трёх уравнений пользоваться?

C делаем предварительные расчёты. Вычислим:

а) сколько теплоты нужно для того, чтобы нагреть воду и калориметр от 25  С до 100  С:

Q ₁ = c ₁ m ₁ (100  t ₁ ) + C(100  t ₁ ) = 4200  0,5  75+1200  75 = 247500 ( Дж ).

б) сколько теплоты выделится, если весь пар остынет от 120  С до 100  С: Q ₂ = c ₂ m ₂( t ₂  100) =2100  0,05  20 = 2100 (Дж).

в) сколько теплоты выделится, если весь пар сконденсируется в воду при температуре 100  С:

Q ₃ = Lm ₂ = 2300000  0,05 = 115000 ( Дж ).

Выделяющаяся теплота Q ₂ + Q ₃ = 2100 Дж + 115000 Дж = 117100 Дж при охлаждении пара и его конденсации меньше теплоты, которая требуется для нагревания «холодной» воды и калориметра. Значит, чтобы вода вместе с калориметром смогла нагреться до 100  С, ей нужно больше энергии, чем может отдать пар, остывая и конденсируясь. Поэтому 117100 Дж пар отдаст, став при этом «горячей» водой при 100  С, а «холодная» вода при этом до 100  С ещё не нагреется. Тогда в калориметре будут одновременно находиться сконденсировавшаяся из пара вода при 100  С и подогретая «холодная» вода. В результате дальнейшего теплообмена «горячая» вода остынет, а «холодная» нагреется. И в итоге в калориметре будет вода, температура которой ниже 100 0 С, но выше 25 0 С.

Уравнение теплового баланса будет иметь вид (1):

Ответ: В калориметре установится температура 63  С.

В калориметре находится вода массой 0,8 кг при температуре 20  С. В воду опустили 2 кг льда при температуре  30  С. Что будет в калориметре после того, как теплообмен прекратится? Теплоёмкостью калориметра пренебречь.

m ₁ = 0,8 кг

с ₁ =4200 Дж/(кг  0 С)

c ₂ =2100 Дж/(кг  0 С)

Рассмотрим варианты решения:

1. Вода остынет от 20  С до 0  С, затем эта вода замёрзнет и станет льдом при температуре 0  С, затем лёд, образовавшийся из воды, остынет до температуры  (см. график).

А опущенный в воду лёд только нагреется от температуры  30  С до температуры  . В калориметре будет находиться лёд при температуре  .

Уравнение теплового баланса запишется так:

 , m _в , m _л – ?

2. Вода остынет от 20  С до 0  С, часть её замёрзнет и станет льдом при 0  С, остальная – останется водой при 0  С. Лёд при этом нагреется от  30  С до 0  С (см. график). И тогда в калориметре будет находиться смесь воды со льдом при температуре 0  С. Уравнение теплового баланса запишется так:

c ₁ m ₁( t ₁  0) +  m  = c ₂ m ₂(   t ₂), где m   масса превратившейся в лед воды.

3. Вода остынет от 20  С до 0  С. Лёд при этом нагреется от  30  С до 0  С, затем частично или полностью расплавится и станет водой при 0  С. В калориметре будет смесь воды и льда при температуре 0  С. Уравнение теплового баланса запишется так:

c ₁ m ₁( t ₁  0) = c ₂ m ₂(0  t ₂) +  m  , где m   масса превратившегося в воду льда.

4. Лёд нагреется от  30  С до 0  С, расплавится, и образовавшаяся из льда вода нагреется от 0  С до температуры  . А вода массой m ₁ при этом остынет от 20  С до температуры  . Тогда в калориметре будет находиться вода при температуре  . Уравнение теплового баланса запишется так:

Проведем численный анализ ситуации. Сколько теплоты:

а) выделит вода при остывании от 20  С до 0  С:

Q ₁ = c ₁ m ₁ (t ₁  0) = 4200  0,8  20 = 67200 ( Дж );

б) выделит вода при превращении в лед при 0  С:

Q ₂ =  m ₁ = 340000  0,8 = 272000 (Дж);

в) нужно получить льду, чтобы нагреться от  30  С до 0  С:

Q ₃ = c ₂ m ₂ (0  t ₂ ) = 2100  2  30 = 126000 ( Дж );

г) нужно получить льду, чтобы полностью расплавиться при температуре 0  С:

Q ₄ =  m ₂ = 340000  2 = 680000 (Дж).

Получаем: чтобы весь лёд нагрелся от  30  С до 0  С, ему нужно передать 126000 Дж теплоты, а вода при этом, остывая от 20  С до 0  С, может дать только 67200 Дж. Значит, лёд эти 67200 Дж у воды «возьмет», но ему ещё не будет хватать Q  = 126000 Дж  67200 Дж = 58800 Дж, чтобы нагреться до 0  С. Он их «возьмёт» у превращающейся в лед воды (если бы вода полностью превратилась в лед, то она бы выделила 272000 Дж, а это больше, чем «нужно» льду):

Q  =  m   m  = Q  /  = 58800/340000  0,2 (кг), где

m   это масса воды, обратившейся в лёд при температуре 0  С.

Как только лёд нагреется до 0  С, теплообмен между льдом и водой прекратится, так как они будут иметь одинаковые температуры.

Итак, получили: вода остынет до 0  С, часть её (а именно m  = 0,2 кг) замёрзнет и станет льдом при 0  С, а лёд нагреется до 0  С. И в результате в калориметре будет находиться смесь воды и льда при 0  С. При этом масса воды будет равна:

m _в = m ₁  m  = 0,8 кг  0,2 кг = 0,6 кг,

а масса льда равна: m _л = m ₂ + m  = 2 кг + 0,2 кг = 2,2 кг.

Ответ: В калориметре при 0  С находится смесь воды (0,6 кг) и льда (2,2 кг).

В калориметр, содержащий 1 кг льда при  20  С, впускают 200 г водяного пара при 120  С. Что будет в калориметре, когда теплообмен прекратится? Теплоёмкостью калориметра пренебречь.

L = 2,3  10 6 Дж/кг

1. Вычислим, сколько теплоты нужно получить льду, чтобы нагреться от  20  С до 0  С:

Q ₁  = c ₁ m ₁ (0  t ₁ ) = 2100  1  20 = 42000 ( Дж );

2. Вычислим, сколько теплоты нужно получить льду, чтобы при 0  С растаять:

Q ₁  =  m ₁ = 340000  1 = 340000 (Дж);

3. Вычислим, сколько теплоты нужно получить воде, образующейся из льда, чтобы нагреться от 0  С до 100  С:

Q ₁  = c ₃ m ₁(100  0) = 4200  1  100 = 420000 (Дж);

4. Найдем, сколько теплоты выделит пар, остывая от 120  С до 100  С:

Q ₂  = c ₂ m ₂ (t ₂  100) = 2100  0,2  20 = 8400 ( Дж );

5. Найдем, сколько теплоты выделит пар, конденсируясь в воду при 100  С:

Q ₂  = Lm ₂ = 2300000  0,2 = 460000 ( Дж );

6. Рассчитаем, сколько теплоты может выделить вода, образовавшаяся из пара, остывая от 100  С до 0  С:

Q ₂  = c ₃ m ₃(100  0) = 4200  0,2  100 = 84000 (Дж).

Проведем анализ ситуации:

а) льду надо получить 42000 Дж, чтобы нагреться от  20  С до 0  С, а пар, остывая от 120  С до 100  С, может отдать только 8400 Дж. Значит, лёд «возьмёт» у пара 8400 Дж, но ещё не нагреется до 0  С. Льду не достает еще 42000 Дж – 8400 Дж = 33600 Дж, чтобы нагреться до 0  С;

б) недостающая энергия может быть получена от конденсации пара. Пар будет конденсироваться при 100  С и выделит при этом 460000 Дж. Лёд за счёт этого сначала нагреется до 0  С, а затем будет плавиться. Для этого ему нужна энергия: 33600 Дж + 340000 Дж = 373600 Дж. Это меньше, чем выделит пар, превращаясь в воду;

в) значит, лед растает и станет водой при 0  С. А у пара еще «останется» 460000 Дж – 373600 Дж = 86400 (Дж). Но этого не хватит, чтобы вода, образующаяся из льда, нагрелась до 100  С. Но на сколько-то она все же нагреется. Поэтому можно сделать вывод: в калориметре будет находиться только вода. Она будет состоять из воды, образованной из льда, и воды, образованной из пара. Её масса: m _в = m ₁ + m ₂ = 1,2 кг.

Конечную температуру воды  будем искать из уравнения теплового баланса:

Используем результаты сделанных ранее вычислений:

 = .

Ответ: В калориметре будет находиться 1,2 кг воды при температуре 17  С.

Иногда в задачах говорится о веществах, находящихся при указанных температурах в таких агрегатных состояниях, которые не соответствуют указанной температуре. Например, перегретая жидкость – жидкость, находящаяся при температуре выше температуры кипения (при обычном давлении); переохлаждённая жидкость – жидкость, находящаяся при температуре ниже температуры замерзания, но остающаяся ещё жидкостью. Такое возможно в условиях, когда нет центров парообразования или центров кристаллизации. При малейшем возмущении эти вещества самопроизвольно и очень быстро переходят в то агрегатное состояние, которое соответствует указанной температуре. В таких веществах энергия, необходимая для того или иного процесса, заключена в самом веществе. При решении подобных задач строить графики нет необходимости.

Колбу , содержащую 120 г перегретой воды при температуре 118  С и нормальном атмосферном давлении, слегка встряхивают, отчего происходит бурное вскипание воды. Сколько воды останется в колбе? Теплоёмкостью колбы и теплообменом с окружающей средой пренебречь.

с = 4200 Дж/(кг  0 С)

L = 2,3  10 6 Дж/кг

Обозначим: m ₁ – масса выкипевшей воды.

Q ₁ = Lm ₁ – энергия, необходимая для превращения в пар воды массой m ₁. Этот переход обычно происходит при 100  С. а вся вода находится при температуре 118  С.

Значит, вся вода остывает до 100  С, выделяя при этом теплоту Q ₂ = cm ( t ₁  t ₂). Эта теплота и поглощается выкипающей водой.

Уравнение теплового баланса: Q ₁ = Q ₂

Lm ₁ = cm(t ₁  t ₂ )  m ₁ = m

m – m ₁ = m – m = m(1 – ) =

= 0,12(1  ) = 0,116 (кг) = 116 (г)

Ответ: В колбе останется 116 г воды.

Пробирку, содержащую 100 г воды, переохлаждённой до температуры  10  С, слегка встряхивают, отчего вода превращается в лёд с температурой 0  С. Какова масса образовавшегося льда? Теплоёмкость пробирки мала.

с =4200 Дж/(кг  0 С)

Вся вода нагревается от  10  С до 0  С, получая энергию Q за счёт того, что часть воды при этом превращается в лёд с температурой 0  С и выделяет при этом энергию Q₁.

Получается, что вся вода нагревается за счет теплоты, выделяющейся при кристаллизации своей части. Поэтому:

m ₁ = ;

m ₁ = .

Ответ: Масса образовавшегося льда равна 12 г.

Задачи для самостоятельного решения

Для приготовления ванны ёмкостью 100 л смешали холодную воду, имеющую температуру 12  С, и горячую, имеющую температуру 72  С. Сколько той и другой воды надо взять, чтобы температура воды в ванне была 36  С? 

Когда в 2 кг воды, находящейся в калориметре при 20  С, опустили алюминиевое тело массой 0,8 кг, имеющее температуру 100  С, температура воды поднялась до 25  С. Определить теплоёмкость калориметра.

В 2 кг воды, имеющей температуру 20  С, опустили сначала медное тело массой 2 кг, имеющее температуру 80  С. После того, как температура перестала меняться, в воду опустили железное тело массой 3 кг, имеющее температуру  20  С. Какой после этого стала температура воды? Теплоёмкостью сосуда пренебречь.

После опускания в воду, имеющую температуру 100  С, тела с температурой 20  С, установилась общая температура 80  С. Какой станет температура воды, если, не вынимая первого тела, в нее опустить ещё два таких же тела, имеющих температуру 20  С?

В чайник налили воду при температуре 20 0 С и поставили на электроплитку. Через 13 минут вода закипела. Через какое время половина воды выкипит?

Для того, чтобы на спиртовом нагревателе, с КПД 70%, нагреть до кипения 1,4 кг воды и половину ее превратить в пар, израсходовали 100 г спирта. Какова начальная температура воды? Удельная теплота сгорания спирта 29  10 6 Дж/кг.

В калориметре находится лёд массой 500 г при температуре 0  С. В калориметр впускают водяной пар температурой 100  С. Сколько воды окажется в калориметре, когда весь лёд растает, а температура образовавшейся воды будет равна 0  С?

В калориметр, содержащий 400 г воды и 200 г льда при 0  С, впустили водяной пар с температурой 100  С. Сколько пара было впущено в калориметр, если в калориметре установилась температура 20  С? Теплоёмкость калориметра 1000 Дж/ 0 С.

В сосуд теплоёмкостью 1000 Дж/ 0 С, содержащий 5 кг воды при температуре 20  С, положили лёд, имеющий температуру  40  С. Температура образовавшейся смеси оказалась равна  2  С. Сколько льда было положено в сосуд?

В алюминиевом калориметре массой 200 г находится кусок льда с температурой  20  С. В калориметр впустили водяной пар, имеющий температуру 100  С. Когда температура калориметра стала равна 20  С, измерили массу его содержимого. Она оказалась равной 400 г. Найти массу льда, находящегося в калориметре, и массу сконденсировавшегося пара.

В калориметр, содержащий 3 кг воды при температуре 20  С, опустили 2 кг льда, имеющего температуру  10  С. Что будет в калориметре, когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.

В калориметр, содержащий 1 кг льда и 800 г воды при 0  С впускают 100 г водяного пара при 100  С. Что будет в калориметре, когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.

В калориметре находится вода массой 600 г при температуре 5  С. К ней долили ещё 300 г воды с температурой 10  С и положили 600 г льда с температурой  60  С. Что будет в калориметре после того, как теплообмен прекратится? Теплоемкостью калориметра пренебречь.

В теплоизолированном медном сосуде массой 400 г находятся 2 кг льда при температуре  10  С. В сосуд помещают 400 г водяного пара при температуре 110  С. Что будет в сосуде после того, как теплообмен прекратится?

В колбе находятся 200 г воды при температуре 0  С. Откачиванием паров всю воду в колбе заморозили. Сколько получилось льда?

Ответы и решения

60 л холодной и 40 л горячей воды.

t ₁ = 12  С

Q ₁ = cm ₁(   t ₁) – теплота, которую получит холодная вода, нагреваясь от 12  С до 36  С;

Q ₂ = c ( m  m ₁)( t ₂   ) – теплота, которую отдаст горячая вода, остывая от 72  С до 36  С,

V ₁ = V  ;

V ₁ = 100  = 60 (л),

V ₂ = V  V ₁ = 100 – 60 = 40 (л).

2. 2640 .

m ₁ = 2 кг

с ₁ =4200 Дж/(кг  0 С)

с ₂ = 920 Дж/(кг  0 С)

Q ₂ – теплота, отданная алюминиевым телом;

Q ₁ – теплота, полученная водой,

Q  теплота, полученная калориметром.

C _к = .

C _к = = 2640 (Дж/ 0 С)

c ₁ =4200 Дж/(кг  0 С)

c ₂ = 380 Дж/(кг  0 С)

c ₃ = 460 Дж/(кг  0 С)

Здесь удобнее пользоваться уравнением теплового баланса в виде (6), так как при решении этим способом последовательность опускания в воду тел не важна:

 = .

С₁– теплоёмкость воды;

С₂– теплоёмкость тела;

При опускании в воду с температурой t ₁ первого тела:

При опускании в воду с температурой t ₂ сразу трех тел:

Делим уравнение (1) на уравнение (2) и получаем:

,

Решая это уравнение, находим, что : t ₄  53  С.

Тепловое равновесие и уравнение теплового баланса

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.

Что такое теплообмен и при каких условиях он происходит

Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

Рассмотрим два тела, имеющие различные температуры (рис. 1).

Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Уравнение теплового баланса и сохранение тепловой энергии

Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».

А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».

Эти факты отражены на рисунке 2.

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.

Уравнение теплового баланса

Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

(large Q_<text<остывания горяч>> left( text <Дж>right) ) – это количество теплоты горячее тело теряет.

(large Q_<text<нагревания холод>> left( text <Дж>right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.

В некоторых учебниках применяют сокращения:

[large Q_ <1>+ Q_ <2>= 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

• равными по модулю и
• имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:

[large boxed < Q_<1>+ Q_ <2>+ Q_ <3>+ ldots + Q_ = 0 > ]

• Q для каждого нагреваемого тела будет обладать знаком «+»,
• Q для каждого охлаждаемого тела — знаком «-».

Пример расчетов для теплообмена между холодным и горячим телом

К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.

Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

Решение:

В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.

Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

2). Теперь запишем формулу для каждого количества теплоты:

Примечания:

1. (large c_<text<воды>> ) – удельную теплоемкость воды находим в справочнике;
2. Массу воды переводим в килограммы;
3. Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_<text<общ>> — t_<text<горяч>> ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
4. Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_<text<общ>> — t_<text<холодн>> ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_<text<общ>> — 80 ) + 4200 cdot 0,1 cdot (t_<text<общ>> — 15 ) = 0 ]

[large 840 cdot (t_<text<общ>> — 80 ) + 420 cdot (t_<text<общ>> — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.

Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:

• (large Q_ <1>) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
• (large Q_ <2>) – охлаждение керосина от температуры +80 градусов до конечной температуры;
• (large Q_ <3>) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.

Источник

Вода лед находятся тепловом равновесии

В калориметре находятся в тепловом равновесии вода и лёд. После опускания в калориметр болта, имеющего массу 165 г и температуру –40 °С, 20% воды превратилось в лёд. Удельная теплоёмкость материала болта равна 500 Дж/(кг · К). Какая масса воды первоначально находилась в калориметре? Теплоёмкостью калориметра пренебречь.

Так как вода и лёд находятся в тепловом равновесии, то и до опускания болта, и после его нагревания температура в сосуде t₀ = 0 °С. Согласно уравнению теплового баланса количество теплоты, выделившееся при замерзании воды, было затрачено на нагревание болта: где m — масса воды в сосуде, m₁ — масса болта, с — удельная теплоёмкость болта, r — удельная теплота плавления льда, t — начальная температура болта. Получим:

Ответ: m = 0,05 кг.

Критерии оценивания выполнения задания	Баллы
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом: (в данном случае: условие теплового равновесия воды и льда, формулы для расчёта количества теплоты при нагревании и кристаллизации, уравнение теплового баланса); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный	2
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены преобразования, направленные на решение задачи. Но имеются один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты. В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. Источник Вода лед находятся тепловом равновесии В калориметр, удельная теплоёмкость которого пренебрежимо мала, налили 200 г воды при температуре +5 °С и положили туда 100 г льда при температуре −5 °С. Что будет находиться в калориметре после установления в нём теплового равновесия? 1) вода при температуре выше 0 °С 2) вода при температуре 0 °С 3) лёд при температуре 0 °С 4) смесь воды и льда при температуре 0 °С Определим, сколько тепла выделится при охлаждении 200 г воды от +5 °С до 0 °С: Вычислим теперь, сколько тепла необходимо для нагрева 100 г льда от -5 °С до 0 °С: следовательно, когда весь лед нагреется до 0 °С, вода будет находится еще при ненулевой температуре. Таким образом, лед начнет превращаться в воду (все тепло, поступающее от охлаждения воды будет идти на плавление льда). Рассчитаем, сколько тепла необходимо, чтобы расплавить весь лед: Это величина сильно больше, чем может дать охлаждающаяся вода. Отсюда заключаем, что после установления теплового равновесия в калориметре будет находиться смесь воды и льда при температуре 0 °С (при этом, воды будет больше, чем 200 г). Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) представлены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены преобразования, направленные на решение задачи, но имеется один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты. В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. Источник Вода лед находятся тепловом равновесии В калориметре находится 5 кг льда при температуре –20 °С. Затем в калориметр наливают 0,5 кг воды, температура которой равна +10 °С. Теплообменом с окружающей средой можно пренебречь. Выберите из предложенного перечня два верных утверждения. Укажите их номера. (Удельная теплоёмкость льда 2100 Дж/(кг·°C), удельная теплоёмкость воды 4200 Дж/(кг·°C), удельная теплота плавления льда 3,3·10 5 Дж/кг). 1) В состоянии теплового равновесия всё вещество в калориметре будет находиться в жидком состоянии. 2) При достижении теплового равновесия температура воды уменьшится на 5 °С. 3) В состоянии теплового равновесия всё вещество в калориметре будет находиться в твёрдом состоянии. 4) При достижении теплового равновесия в калориметре будет смесь воды со льдом. 5) В состоянии теплового равновесия температуры изначально твёрдого и изначально жидкого веществ сравняются. Более тёплая вода будет отдавать теплоту, для повышения температуры льда, затем, если теплоты будет достаточно, то весь лёд превратится в жидкость, если же нет, то возможны два состояния: когда в калориметре после установления теплового равновесия находится только лёд, либо находится смесь льда и воды. Сравним теплоту, которую может отдать вода, находясь в жидком состоянии, с теплотой, необходимой для расплавления всего льда: Где — начальные массы льда и воды соотвественно, — начальные температуры льда и воды соответственно, — удельные теплоёмкости льда и воды соответственно, — температура плавления льда, равная 0 °C. Видим, что то есть весь лёд расплавить не удастся. Теперь, предположим, что наоборот, вся вода перешла в твёрдое состояние: Теплота больше теплоты соответственно вся вода превратится в лёд, при этом весь лёд останется в твёрдом состоянии. Температура воды уменьшится больше, чем на 5° C. В состоянии теплового равновесия температуры веществ с изначально различной температурой уравниваются. Источник Adblock detector Критерии оценивания выполнения задания Баллы 2

Лицей естественных
наук г. Кирова

Г.Г. Самарин

 

Решение
задач на теплообмен

с использованием уравнения
теплового баланса

(методические рекомендации)

Киров

2002

ББК
74.204.2

С
17

Печатается
по решению редакционно-издательского совета Лицея естественных наук г. Кирова

Рецензент:  К.А. Коханов, кандидат
педагогических наук, старший преподаватель кафедры дидактики физики Вятского
государственного гуманитарного университета, заместитель заведующего кафедрой
дидактики физики.

С 17  Самарин Г.Г.   Решение задач на теплообмен с использованием уравнения теплового
баланса:  Методические рекомендации. – Киров: Издательство Лицея естественных
наук, 2002. – 35 с.

Пособие рекомендовано учащимся,
желающим получить практические навыки в решении задач на теплообмен, и может
быть полезным для учителей и абитуриентов.

©
Лицей естественных наук, 2002

©
Г.Г. Самарин, 2002

При соприкосновении тел, имеющих
разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической
теории, это объясняется так: молекулы более нагретого тела имеют большую
кинетическую энергию, чем молекулы тела, менее нагретого. При «столкновениях»
молекул соприкасающихся тел  происходит процесс выравнивания их средних кинетических
энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии,
при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного
тела  возрастает, поэтому температура этого тела будет увеличиваться.  В
конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры
тел станут одинаковыми. На этом теплообмен прекращается.

Энергию, которую тело получает
или отдаёт в процессе теплообмена, называют количеством теплоты (Q).

Количество теплоты, как и все другие
виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж. *

Нагревание или охлаждение

 При нагревании или охлаждении тела
количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:

Q = сm(t₂ – t₁), ⁽¹⁾

 где m – масса тела, кг;

(t₂ – t₁) – разность 
температур тела,°С (или К);

с – удельная теплоёмкость вещества, из
которого состоит тело,

 или .

Удельная теплоёмкость вещества – это количество теплоты, которое нужно
сообщить одному килограмму данного вещества, чтобы увеличить его температуру на
1°С (или
это количество теплоты, которое выделяет один килограмм данного вещества,
остывая на 1°С).

Например, С_воды = 4200,     С_{льда, водяного пара} =
2100,     С_свинца = 140, С_меди = 380, С_{железа, стали} = 460, С_{алюминия} = 920.

Значения удельных теплоемкостей других
веществ можно найти в справочниках, а также в школьном учебнике или задачнике.

При нагревании тела его внутренняя
энергия увеличивается. Это требует притока энергии к телу от других тел.
Значит, оно поглощает некоторое количество теплоты, принимая его от других тел,
участвующих в теплообмене.

При охлаждении тела его внутренняя
энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое
количество теплоты.

 Обычно конечную температуру,
установившуюся в результате теплообмена, обозначают греческой буквой q (тэта).

В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью
тела и обозначают С:

C
= c×m.⁽²⁾

 Размерность теплоемкости: [С] = .  Теплоемкость
тела показывает, сколько энергии нужно подвести к данному телу, чтобы нагреть
его на 1°С
(или сколько энергии выделяет это тело, остывая на 1°С).

Теплообмен между телами, имеющими
одинаковые температуры, не происходит, даже если контактируют вещества,
находящиеся  в разных агрегатных состояниях. Например, при температуре
плавления (0°С) лёд и вода могут находиться бесконечно долго, при этом количество
льда и количество воды останутся неизменными. Аналогично ведут себя пар и
жидкость, находящиеся при температуре кипения. Теплообмен между ними не
происходит.

Плавление или кристаллизация

 Если при нагревании тела его
температура достигнет температуры плавления, то начинает происходить процесс
перехода этого вещества из твердого состояния в жидкое. При этом идут изменения
в расположении и характере взаимодействия молекул.    Температура при плавлении
не изменяется. Это означает, что средние кинетические энергии молекул жидкости
и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия
тела при плавлении возрастает за счет увеличения энергии взаимодействия
молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по
формуле

 Q = l×m⁽³⁾,

где m
– масса тела, кг;

      l – удельная
теплота плавления, .

При кристаллизации, наоборот,
внутренняя энергия тела уменьшается на величину Q = l×m, и
эта теплота данным телом выделяется. Она поглощается другими телами,
участвующими в теплообмене.

Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного
вещества, взятого при температуре плавления, чтобы полностью превратить его при
этой температуре в жидкость (или сколько энергии выделяет 1
кг жидкости, взятой при температуре кристаллизации, если вся она при этой
температуре полностью превратится в твёрдое тело).

Удельную теплоту плавления любого
вещества можно найти в справочниках.  Для льда же l = 3,4×10⁵ .

Температура плавления у каждого
вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что
температура плавления вещества равна температуре кристаллизации этого же
вещества. У льда  t_пл = 0°С.

Кипение или конденсация

При достижении жидкостью температуры
кипения начинает происходить другой фазовый переход – кипение, при котором
расстояния между молекулами значительно увеличиваются, а силы взаимодействия
молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей
между молекулами. При конденсации пара в жидкость, наоборот, расстояния между
молекулами значительно сокращаются, а силы взаимодействия молекул
увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при
конденсации пара энергия выделяется. Количество теплоты, поглощаемое при
кипении или выделяемое при конденсации, рассчитывается по формуле:

Q = L×m ⁽⁴⁾,

 где m – масса тела, кг;

       L – удельная теплота парообразования, .

Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости,
взятой при температуре кипения, чтобы при этой температуре полностью превратить
её в пар (для конденсации: сколько энергии выделяет один килограмм пара,
взятого при температуре конденсации, полностью превращаясь в жидкость).

При одинаковом давлении температура
кипения и температура конденсации  одного и того же вещества одинаковы.

Температуры кипения и удельные теплоты
парообразования также можно найти в справочниках. Для воды же они
соответственно равны: t_кип = 100°С,  L = 2,3×10⁶  (при нормальном атмосферном
давлении).

Уравнение теплового баланса

Тела, участвующие в теплообмене,
представляют собой термодинамическую систему. Термодинамическая система
называется теплоизолированной, если она не получает энергию извне и не
отдаёт её; теплообмен происходит только между телами, входящими в эту систему. 
Для любой теплоизолированной системы тел справедливо следующее утверждение: количество
теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими
телами.

Q_отд. = Q_получ.⁽⁵⁾

Это утверждение описывает частный
случай закона сохранения и превращения энергии в применении к процессу
теплообмена. А формула (5) является одним из видов уравнения теплового баланса.

При решении задач с помощью данного
вида уравнения теплового баланса в формуле (1) в качестве t₂ следует брать большую температуру, а в
качестве t₁ – меньшую.
Тогда разность (t₂ – t₁) будет положительна и всё произведение cm(t₂–t₁) также будет положительным. Все теплоты,
отданные и полученные, будут положительными.

Уравнение теплового баланса можно
записать и в таком виде:

Q₁+ Q₂+…+ Q_n=
0,⁽⁶⁾

Где n –
количество тел системы.

Алгебраическая сумма  всех
количеств теплоты  (поглощенных и выделенных) в теплоизолированной системе
равна нулю.

Q₁, Q₂, …, Q_n –
это  теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что
в этом случае какие-то теплоты должны быть положительны, а какие-то –
отрицательны. При записи уравнения теплового баланса в виде (6) всегда t₂ – конечная температура, а t₁ – начальная.

 Если тело нагревается, то разность (t₂ –  t₁) положительна и все произведение cm(t₂ – t₁) положительно. То есть Q > 0 тогда, когда
теплота к данному телу подводится.

 А если t₂ < t₁ (тело
остывает), то разность (t₂
– t₁) отрицательна, то
есть Q < 0. В этом случае тело энергию выделяет.

Если при фазовом переходе энергия к
телу подводится (плавление, кипение), то Q > 0; если
тело выделяет энергию (кристаллизация, конденсация), то Q
< 0.

В принципе уравнения (5) и (6)
равносильны. Результат решения задачи не зависит от того, каким видом уравнения
пользуемся. Выбор способа решения – за читателем.

Применим уравнение теплового баланса
для решения ряда задач.

Задача 1

В медном калориметре массой 100
г находится 1 кг воды при температуре 20°С. В воду опускают свинцовую
деталь массой 2 кг, имеющую температуру 90°С. До какой температуры
нагреется вода? Потерями теплоты пренебречь.*

Решение

m1 = 0,1 кг с1= 380 Дж/(кг×0С) t2 = 20°С m2 = 1 кг с2=4200 Дж/(кг×0С) m3 = 2 кг с3= 140 Дж/(кг×0С) t3 = 90°С     q  – ?	Проведём анализ: Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t1 =  t2 = 20°С. При опускании в воду с температурой 20°С свинцового тела с температурой 90°С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе  участвует  и калориметр, который, как и вода, будет тоже нагреваться.
	Изменение температур  тел с течением времени  удобно изображать на графике зависимости t(t). Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q3.
	Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают.
	Решим задачу с использованием уравнения теплового баланса в виде (5): Q1 + Q2 = Q3, c1m1(q — t1) + c2m2(q — t2) = c3m3(t3 — q). Выражаем температуру q: q =

 Решим
задачу с использованием уравнения теплового баланса в виде (6):

Q₁ + Q₂ + Q₃ = 0,

c₁m₁(q — t₁) + c₂m₂(q — t₂) + c₃m₃(q — t₃) = 0.

q =  = 24 (°С)

Ответ: Вода нагреется до 24 °С.

  Предлагаю читателю
самостоятельно сделать проверку размерности.

Задача
2

Три пластины: медную, имеющую массу m₁ = 1
кг и температуру t₁ = 100°С,
железную (m₂ = 1,2 кг, t₂ = 150°С)
и алюминиевую (m₃ = 0,8 кг, t₃ = 80°С)
сложили вплотную (см рис). Какую температуру будут иметь пластины, когда
теплообмен прекратится? Потерями теплоты в окружающую среду  пренебречь.

m1 = 1 кг с1= 380 Дж/(кг×0С) t1 = 100°С m2 = 1,2 кг с2= 460 Дж/(кг×0С) t2 = 150°С m3 = 0,8 кг с3= 920 Дж/(кг×0С) t3 = 80°С

Решение Решим задачу с помощью уравнения теплового баланса в виде (5). 1. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная — нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая – нагреваться. Мысленно соединим сначала эти две пластины и найдём температуру t, которой они при этом достигнут: Q2 = Q3  Þ  c2m2(t2 — t) =  c3m3(t — t3)      t =

q — ?

t =

2. Теперь медная пластина вступает в
теплообмен с железной и алюминиевой. Медная будет нагреваться от температуры t₁ до температуры q, а железная и алюминиевая –
остывать от температуры t до температуры q. Тогда:

Q₁
= Q₂‘+ Q₃‘_,

c₁m₁(q — t₁) = (c₂m₂
+ c₃m₃)(t —
q),

c₁m₁q – c₁m₁t₁ = (c₂m₂
+ c₃m₃)t – (c₂m₂ + c₃m₃)q

q
=

3. Решим
задачу, применив уравнение теплового баланса в виде (6):

Q₁ + Q₂ + Q₃ = 0,

c₁m₁(q — t₁) + c₂m₂(q – t₂) + c₃m₃(q — t₃)
= 0,

q =  = 108 (°С)

Ответ: Пластины будут иметь температуру 108 °С.

  Как видим,
второй способ оказался и в данном случае более рациональным. Однако, первый
способ зачастую оказывается более  понятным, особенно при наличии фазовых
переходов. Поэтому в дальнейшем автор будет придерживаться первого способа
решения задач. Желательно, чтобы читатель пробовал решать их и  вторым
способом.

Задача
3

В
железном ведре массой 1,2 кг находится 5
кг воды при температуре 20°С. Сколько льда температурой –10°С надо положить в
ведро, чтобы температура воды понизилась до 12°С? Теплообменом с окружающей
средой пренебречь.

m1 = 1,2 кг с1=460 Дж/(кг×0С) m2 = 5 кг с2=4200 Дж/(кг×0С) t1 = t2 = 20°С t3 = —10°С с3=2100 Дж/(кг×0С) t4 = 0оС   q = 12°С

Решение Известна конечная температура, Значит, анализ ситуации довольно прост: вода и ведро будут остывать, не испытывая фазовых переходов, отдавая теплоты Q1 и Q2, а лёд сначала будет нагреваться до температуры плавления t4, поглощая теплоту Q3, затем плавиться, поглощая теплоту Q4, а затем вода, образовавшаяся из льда, будет нагреваться до конечной температуры q, поглощая теплоту Q5. Так как иных участников теплообмена нет, то можно так  записать уравнение теплового баланса:  Q1 + Q2 = Q3 + Q4 + Q5. (c1m1 + c2m2)(t1 — q) = = c3m3(t4 — t3) + lm3 + c2m3(q — t4)

m3 – ?

Ответ:  Потребуется 0,4
кг льда.

Задача
4

В алюминиевую кастрюлю массой 200
г, содержащую 3 кг воды при  20°С,
поместили стальную деталь массой 0,5 кг, нагретую до 500°С. При этом часть воды выкипела, а оставшаяся
вода нагрелась до 22°С.
Сколько воды выкипело?

m1 = 3 кг с1=4200Дж/(кг°С) m2 = 0,2 кг с2 =920 Дж/(кг°С) t1 = t2 = 20°С q = 22°С m3 = 0,5 кг с3 = 460 Дж/(кг0С) t3 = 500°С L = 2,3×106 Дж/кг	Решение 1.     Стальная деталь, не претерпевая фазовых переходов, остыла от 500°С до 22°С, выделив при этом количество теплоты        Q3 = c3m3(t3 — q). 2. Часть воды массой  m0 нагрелась до температуры кипения (100оС) и выкипела. При  этом была поглощена теплота               Q1  = c1m0(100 — t1) + Lm0. 3. Оставшаяся в кастрюле вода массой (m1 — m0) и сама кастрюля массой m2 нагрелись от 200С до 22°С. При этом была поглощена теплота Q2 = c1(m1 — m0)(q — t1) + c2m2(q — t1).
m0 – ?
4. Так как потерь тепла нет, то записываем уравнение теплового баланса: Q1 + Q2 = Q3, c1m0(100 — t1) + Lm0 + c1(m1 — m0)(q — t1) + + c2m2(q — t2) = c3m3(t3 — q). 5. Решая это уравнение, находим m0: m0 = , m0 =

Ответ: Выкипело 32
г воды.

Задача
5

Комок мокрого снега массой 400
г опустили в медный таз массой 500 г, содержащий 2
кг воды при температуре 20°С. После установления теплового равновесия температура воды в тазу
стала 10°С. Сколько воды было в комке снега?

m3 = 0,4 кг l = 3,4×105 Дж/кг t1 = t2 = 20°С t3 = 0°С m1 = 0,5 кг с1 = 380 Дж/(кг×0С) m2 = 2 кг с2=4200Дж/(кг×0С) q = 10°С	Решение 1. Медный таз и вода находятся в тепловом равновесии. Поэтому 20°С – их общая температура. При остывании от 20°С до 10°С ни медь, ни вода фазовых превращений не испытывают. При этом они отдают суммарную теплоту: Q1 + Q2  =  c1m1(t1 — q) + c2m2(t2 — q). 2. Мокрый снег – это снег, содержащий воду. Значит, снег и вода находятся в тепловом равновесии. Это возможно только при температуре фазового перехода, то есть при 0°С.
mв – ?
Итак, начальная температура мокрого снега 0°С. 3. На пути к температуре 10°С снег массой m3—mв будет сначала таять. Для этого требуется теплота Q3 = l(m3 — mв). А затем вся вода массой m3 будет нагреваться от 0°С до 10°С. Для этого ей надо получить количество теплоты Q4 = c2m3(q — t3). 4. Так как нет потерь тепла, то можно написать уравнение теплового баланса: Q1 + Q2 = Q3 + Q4, с1m1(t1 — q) + c2m2(t2 — q) = l(m3 — mв) + c2m2(q — t3). 5. Решая это уравнение, находим mв: mв = mв = Ответ: В комке мокрого снега было 0,2 кг воды.

Задача
6

В холодную воду массой 2
кг, имеющую температуру 10°С, находящуюся в кастрюле, влили 3
кг горячей воды при температуре 80°С. До какой температуры нагреется холодная вода,
если известно, что 25% теплоты, отданной горячей водой, пошло на нагревание
кастрюли? Какова теплоемкость кастрюли?

M1 = 2 кг t1 = 10°С m2  = 3 кг t2 = 80°С h1=0,25 (25%)

Решение Так как 25% теплоты отданы кастрюле, то 75% теплоты пошло на нагревание холодной воды.   Значит, можно говорить о КПД  процесса нагревания холодной воды: h2 =     (h2 = 0,75) Здесь  Qполез —  теплота, идущая на нагревание холодной воды: Qполез = c1m1(q — t1);             Qзатр —  теплота, отданная горячей водой: Qзатр = c2m2(t2 — q). Удельные теплоты с1 холодной и с2 горячей воды равны. h2 =  Þ h2m2(t2 — q) = m1(q — t2), h2m2t2 — h2m2q = m1q — m1t1,

q — ? С — ?

q =

q =

Так как 25% теплоты, отданной горячей водой, пошло на
нагревание кастрюли, то можно говорить и о КПД процесса нагревания кастрюли:

  ,

откуда:

Ответ: Холодная вода нагреется до температуры 47°С. Теплоемкость кастрюли 2809 Дж/⁰С.

Задача
7

Сколько керосина нужно сжечь, чтобы превратить
в пар 1 кг льда, взятого при температуре —40°С?
КПД нагревательного устройства равен 60%, удельная теплота сгорания керосина
46      МДж/кг.

m1 = 1 кг t1 = —40°С с1 =2100Дж/(кг×0С) l = 3,4×105 Дж/кг с2 =4200Дж/(кг×0С) L = 2,3×106 Дж/кг h = 0,6 (60%) q = 46×106 Дж/кг

Решение 1.  Изобразим на графике t(t) процессы: нагревание льда, плавление льда, нагревание получившейся из льда воды, кипение этой воды. Для осуществления каждого из этих процессов необходим подвод теплоты. Теплоту выделяет керосин в процессе сгорания (на графике не показано).  2.  Применим формулу КПД нагревателя: h = . Здесь Qполез = Q1 + Q2 + Q3 + Q4 = = m1[c1(0 — t1) + l + c2(100 — 0) + L], а Qзатр = qm2. Получаем: h = , откуда: m2 = .  m2 = = 114 г

m2 — ?

Ответ: Нужно сжечь 114
г керосина.

Задача 8

Сколько
водяного пара, имеющего температуру 120°С, надо впустить в калориметр,
содержащий 800 г льда при температуре —20°С, чтобы температура
образовавшейся воды оказалась 20°С? Теплоёмкостью калориметра пренебречь.

m1 = 0,8 кг t1 = —20°С с1 = с2 = 2100 Дж/(кг×0С) t2 = 120°С с3 =4200Дж/(кг×0С) q = 20°С

Решение 1. Так как теплоемкостью калориметра можно пренебречь, то  систему лед — пар можно считать теплоизолированной: теплообмен происходит только между паром и льдом. 2.  Получают теплоту тела: —           лёд, нагреваясь от –200С до температуры плавления: Q1 = c1m1(0 — t1); —           лёд, превращаясь в воду при температуре плавления: Q2 = lm1; —           вода, образовавшаяся из льда, нагреваясь от 0°С до 20°С: Q3 = с3m1(q — 0). 3. Отдают теплоту тела: —           пар, остывая от 120°С до температуры конденсации: Q4 = c2m2(t2 — 100); —           пар, превращаясь в воду при 100°С: Q5 = Lm2; —           вода, образовавшаяся из пара, остывая от 100°С до 20°С: Q6 = c3m2(100 — q). 4. Других участников теплообмена нет, поэтому записываем уравнение теплового баланса: Q1 + Q2 + Q3 =  Q4 + Q5 + Q6, c1m1(0 – t1) + lm1 + c3m1(q — 0) = c2m2(t2 — 100) + + Lm2 + c3m2(100 — q),

m2-?

Ответ: Потребуется 140 г водяного пара.

  Часто при
решении задач можно встретиться со следующей проблемой. В теплообмене участвуют
вещества, находящиеся в различных агрегатных состояниях, и конечная температура
теплообмена не известна. Тогда уравнение теплового баланса сразу написать не
удастся, так как его вид зависит от того, в каких агрегатных состояниях будут
находиться конечные продукты. В этом случае последовательность решения задачи
немного изменяется. Сначала нужно сделать предварительные расчеты: сколько
теплоты выделит или поглотит каждое вещество в предполагаемом процессе,
сравнить эти теплоты и сделать вывод о том, в каких агрегатных состояниях будут
находиться продукты теплообмена. И только после этого можно записывать
уравнение теплового баланса. Такие задачи значительно сложнее задач, в которых
конечная температура известна. Рассмотрим ряд таких задач.

Задача
9

В калориметр, содержащий воду массой 0,5
кг при температуре 25°С, впускают водяной пар массой 50
г при температуре 120°С. Какая температура установится в калориметре, если его теплоёмкость
1200 Дж/^оС?

m1 = 0,5 кг с1 =4200 Дж/(кг×0С) t1 = 25°С m2 = 0,05 кг t2 = 120°С c2=2100 Дж/(кг×0С) С = 1200 Дж/0С L = 2,3×106 Дж/кг	Решение 1. Если в конечном итоге весь пар остынет от 120°С до 100°С, затем сконденсируется в воду, затем образовавшаяся из пара  вода  остынет  от 100°С до q, то в калориметре будет находиться вода при температуре q, а уравнение теплового баланса примет вид:  .
q-?
	2. Если  пар остынет от 120°С до 100°С, а сконденсируется не весь, то в калориметре будет находиться смесь воды и пара при температуре 100°С, а уравнение теплового баланса будет таким: Здесь m¢ — масса сконденсировавшегося пара.
	3. Пар может остыть от 120°С до 100°С, а вода и калориметр уже нагреются до 100°С, и при этом часть воды даже выкипит. В калориметре будет смесь пара и воды при температуре 100°С. Уравнение теплового баланса будет иметь вид: , где m¢¢— масса превратившейся в пар воды.
Каким из трёх уравнений пользоваться? Cделаем предварительные расчёты. Вычислим: а) сколько теплоты нужно для того, чтобы нагреть воду и калориметр от 25°С до 100°С: Q1 = c1m1(100 — t1) + C(100 — t1) = 4200×0,5×75+1200×75 = 247500 (Дж). б) сколько теплоты выделится, если весь пар остынет от 120°С до 100°С: Q2 = c2m2(t2 — 100) =2100×0,05×20 = 2100 (Дж). в) сколько теплоты выделится, если весь пар сконденсируется в воду  при температуре 100°С: Q3 = Lm2 = 2300000×0,05 = 115000 (Дж).

 Выделяющаяся
теплота Q₂ + Q₃ = 2100 Дж + 115000 Дж = 117100 Дж при
охлаждении пара и его конденсации меньше теплоты, которая требуется для
нагревания «холодной» воды и калориметра. Значит, чтобы вода вместе с
калориметром смогла нагреться до 100°С, ей нужно больше энергии, чем может отдать пар,
остывая и конденсируясь. Поэтому 117100 Дж пар отдаст, став при этом «горячей»
водой при 100°С, а «холодная» вода при этом до 100°С ещё не нагреется. Тогда в
калориметре будут одновременно находиться сконденсировавшаяся из пара вода при
100°С и
подогретая «холодная» вода. В результате дальнейшего теплообмена «горячая» 
вода остынет, а «холодная» нагреется. И в итоге в калориметре будет вода,
температура которой ниже 100⁰С, но выше 25⁰С.

Уравнение
теплового баланса будет иметь вид (1):

c₁m₁(q — t₁) + C(q — t₁) = c₂m₂(t₂ — 100) + Lm₂ + c₁m₂(100 — q), откуда

c₁m₁q — c₁m₁t₁ + Сq
— Сt₁ = 117100 + c₁m₂×100
— c₁m₂q.

Ответ: В
калориметре установится температура 63°С.

Задача 10

В калориметре
находится вода массой 0,8 кг при температуре 20°С. В воду опустили 2
кг льда при температуре —30°С. Что будет в калориметре после того, как теплообмен прекратится?
Теплоёмкостью калориметра пренебречь.

1)   Весь лёд нагреется до температуры 0°С, весь расплавится и
образуется из льда вода, которая нагреется с 0°С до температуры q:

Уравнение
теплового баланса:

c₁m₁(t₁—q)=c₂m₂(0-t₂)+lm₂+c₁m²¢(q-0)

Тогда в
калориметре будет вода при температуре q.

m1 = 0,8 кг с1=4200 Дж/(кг×0С) t1 = 20°С m2 = 2 кг t2 = —30°С c2=2100 Дж/(кг×0С) l = 3,4×105 Дж/кг

Решение Рассмотрим варианты решения: 1. Вода остынет от 20°С до 0°С, затем эта вода замёрзнет и станет льдом при температуре 0°С, затем лёд, образовавшийся из воды, остынет до температуры q (см. график). А опущенный в воду лёд только нагреется от температуры —30°С до температуры q. В калориметре будет находиться лёд при температуре q. Уравнение теплового баланса запишется так: c1m1(t1 — 0) + lm1 + c2m1(0 — q) = c2m2(q — t2).

q, mв, mл – ?

2. Вода остынет от 20°С до 0°С, часть её замёрзнет и станет льдом при 0°С, остальная –
останется водой при 0°С.
Лёд при этом нагреется от —30°С до 0°С (см. график). И тогда в калориметре будет
находиться смесь воды со льдом при температуре 0°С. Уравнение
теплового баланса запишется так:

c₁m₁(t₁ — 0) + lm¢ = c₂m₂(q — t₂), где m¢ — масса превратившейся
в лед воды.

3. Вода
остынет от 20°С до 0°С. Лёд при этом нагреется от —30°С до 0°С, затем частично или полностью расплавится и станет водой при 0°С. В калориметре
будет смесь воды и льда при температуре 0°С. Уравнение теплового
баланса запишется так:

c₁m₁(t₁ — 0) = c₂m₂(0 — t₂) + lm², где m² — масса
превратившегося в воду льда.

4. Лёд нагреется от —30°С  до 0°С,  расплавится, и образовавшаяся из льда вода нагреется от 0°С до температуры q. А вода массой m₁ при этом остынет от 20°С до температуры q. Тогда в калориметре
будет находиться вода при температуре q. Уравнение теплового баланса запишется так:

c₁m₁(t₁ — q) = c₂m₂(0 — t₂) + lm₂ + c₁m₂(q —
0).

Проведем численный анализ ситуации. Сколько теплоты:

а) выделит вода при остывании от 20°С до 0°С:

Q₁ = c₁m₁(t₁
— 0) = 4200×0,8×20
= 67200 (Дж);

б) выделит вода при превращении в лед при 0°С:

Q₂ = lm₁ = 340000×0,8 = 272000 (Дж);

в) нужно получить льду, чтобы нагреться от —30°С до 0°С:

Q₃ = c₂m₂(0
— t₂) = 2100×2×30
= 126000 (Дж);

г) нужно получить льду, чтобы полностью
расплавиться при температуре 0°С:

Q₄ = lm₂ = 340000×2 = 680000 (Дж).

  Получаем: чтобы весь лёд нагрелся от —30°С  до 0°С, ему нужно передать
126000 Дж теплоты, а вода при этом, остывая от 20°С до 0°С, может дать только 67200
Дж. Значит, лёд эти 67200 Дж у воды «возьмет», но ему ещё не будет хватать Q¢ = 126000 Дж — 67200 Дж = 58800 Дж,
чтобы нагреться до 0°С. Он их «возьмёт» у превращающейся в лед  воды (если бы вода
полностью превратилась в лед, то она бы выделила 272000 Дж, а это больше, чем
«нужно» льду):

 Q¢ = lm¢ Þ  m¢ = Q¢/l = 58800/340000 » 0,2 (кг), где

m¢ — это масса воды, обратившейся в лёд при температуре 0°С.

 Как только лёд
нагреется до 0°С, теплообмен между льдом и водой прекратится, так как они будут иметь
одинаковые температуры.

 Итак, получили:
вода остынет до 0°С, часть её (а именно m¢ = 0,2 кг) замёрзнет и станет льдом при 0°С, а лёд нагреется до 0°С. И в результате в
калориметре будет находиться смесь воды и льда при 0°С.    При этом масса воды
будет равна:

m_в = m₁ — m¢= 0,8
кг — 0,2
кг  = 0,6 кг,

 а масса льда
равна: m_л = m₂ + m¢ = 2 кг + 0,2 кг = 2,2 кг.

Ответ: В калориметре
при 0°С 
находится смесь воды (0,6 кг) и льда (2,2
кг).

Задача 11

В калориметр,
содержащий 1 кг льда при —20°С, впускают 200 г водяного пара при 120°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоёмкостью калориметра пренебречь.

m1 = 1 кг с1 = c2 = 2100 Дж/(кг×0С) t1 = —20°С m2 = 0,2 кг t2 = 120°С L = 2,3×106 Дж/кг l = 3,4×105 Дж/кг с3 =4200Дж/(кг×0С)	Решение 1. Вычислим, сколько теплоты нужно получить льду, чтобы нагреться от —20°С до 0°С: Q1¢ = c1m1(0 — t1) = 2100×1×20 = 42000 (Дж); 2. Вычислим, сколько теплоты нужно получить льду, чтобы при 0°С растаять: Q1² = lm1 = 340000×1 = 340000 (Дж); 3. Вычислим, сколько теплоты нужно получить  воде, образующейся из льда, чтобы нагреться от 0°С до 100°С: Q1²¢ = c3m1(100 — 0) = 4200×1×100 = 420000 (Дж); 4. Найдем, сколько теплоты выделит пар, остывая от 120°С до 100°С: Q2¢ = c2m2(t2 — 100) = 2100×0,2×20 = 8400 (Дж); 5. Найдем, сколько теплоты выделит пар, конденсируясь в воду  при 100°С: Q2² = Lm2 = 2300000×0,2 = 460000 (Дж); 6. Рассчитаем, сколько теплоты может выделить вода, образовавшаяся из пара, остывая от 100°С  до 0°С: Q2²¢ = c3m3(100 — 0) = 4200×0,2×100 = 84000 (Дж).
q – ? mв – ? mл – ?

Проведем анализ ситуации:

а) льду надо
получить 42000 Дж, чтобы нагреться от —20°С до 0°С, а пар, остывая от 120°С до 100°С, может отдать только 8400 Дж. Значит, лёд «возьмёт» у пара 8400 Дж,
но ещё не нагреется до 0°С. Льду не достает еще 42000 Дж – 8400 Дж = 33600 Дж, чтобы нагреться
до 0°С;

б)
недостающая энергия может быть получена от конденсации пара. Пар будет
конденсироваться при 100°С и выделит при этом 460000 Дж. Лёд за счёт этого сначала нагреется до
0°С, а
затем  будет плавиться. Для этого ему нужна энергия: 33600 Дж + 340000  Дж =
373600 Дж. Это меньше, чем выделит пар, превращаясь в воду;

в) значит,
лед растает и станет водой при 0°С. А у пара еще «останется» 460000 Дж – 373600 Дж = 86400 (Дж). Но
этого не хватит, чтобы вода, образующаяся из льда, нагрелась до 100°С. Но на сколько-то
она все же  нагреется. Поэтому можно сделать вывод: в калориметре будет
находиться только вода. Она будет состоять из воды, образованной из льда, и
воды, образованной из пара. Её масса: m_в = m₁ + m₂ = 1,2
кг.

Конечную
температуру воды q будем искать из уравнения теплового баланса:

c₁m₁(0 —
t₁) + lm₁ + c₃m₁(q —
0) =c₂m₂(t₂ — 100) + Lm₂ + c₃m₃(100 — q).

Используем результаты сделанных ранее вычислений:

c₃m₁(q — 0) — c₃m₂(100 — q) = 86400,

c₃m₁q —  c₃m₂100 + c₃m₂q = 86400,

q = .

Ответ: В калориметре будет находиться  1,2
кг воды при температуре 17°С.

Иногда в задачах говорится о
веществах, находящихся при указанных температурах в таких агрегатных
состояниях, которые не соответствуют указанной температуре. Например,
перегретая жидкость – жидкость, находящаяся при температуре выше температуры
кипения (при обычном давлении); переохлаждённая жидкость – жидкость,
находящаяся при температуре ниже температуры замерзания, но остающаяся ещё
жидкостью. Такое возможно в условиях, когда нет центров парообразования или
центров кристаллизации. При малейшем возмущении эти вещества самопроизвольно и
очень быстро переходят в то агрегатное состояние, которое соответствует
указанной температуре. В таких веществах энергия, необходимая для того или
иного процесса, заключена в самом веществе. При решении подобных задач строить
графики нет необходимости.

Задача 12

Колбу , содержащую 120
г перегретой воды при температуре 118°С и нормальном атмосферном
давлении, слегка встряхивают, отчего происходит бурное вскипание воды. Сколько
воды останется в колбе? Теплоёмкостью колбы и теплообменом с окружающей средой
пренебречь.

m = 0,12 кг t1 = 118°С t2 = 100°С с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг

Решение Обозначим: m1 – масса выкипевшей воды. Q1 = Lm1 – энергия, необходимая для превращения в пар воды массой m1. Этот переход обычно происходит при 100°С. а вся вода находится при температуре 118°С. Значит, вся вода остывает до 100°С, выделяя при этом теплоту Q2 = cm(t1 — t2). Эта теплота и поглощается выкипающей водой. Уравнение теплового баланса: Q1 = Q2 Lm1 = cm(t1 — t2)  Þ  m1 = m m – m1 = m – m = m(1 – ) = = 0,12(1 — ) = 0,116 (кг) = 116 (г)

(m – m1) — ?

Ответ:  В колбе останется 116
г воды.

Задача 13

Пробирку, содержащую 100
г воды, переохлаждённой до температуры —10°С, слегка
встряхивают, отчего вода превращается в лёд с температурой 0°С. Какова масса
образовавшегося льда? Теплоёмкость пробирки мала.

m = 0,1 кг с =4200 Дж/(кг×0С) l = 3,4×105  Дж/кг t1 = —10°С t2 = 0°С	Решение  Вся вода нагревается от —10°С до 0°С, получая энергию Q за счёт того, что часть воды при этом превращается в лёд с температурой 0°С и выделяет при этом энергию Q1.
m1 – ?

Получается, что вся вода нагревается за счет теплоты,
выделяющейся при кристаллизации своей части. Поэтому:

Q = Q₁,

cm(t₂ — t₁)
= lm₁,

m₁ = ;

m₁ = .

Ответ:  Масса образовавшегося льда равна 12
г.

Задачи для самостоятельного
решения

1.          
Для приготовления ванны ёмкостью 100
л смешали холодную воду, имеющую температуру 12°С, и горячую, имеющую
температуру 72°С. Сколько той и другой воды надо взять, чтобы температура воды в ванне
была 36°С?^*

2.          
Когда в 2
кг воды, находящейся в калориметре при 20°С, опустили алюминиевое тело
массой 0,8 кг, имеющее температуру 100°С, температура воды поднялась до 25°С. Определить
теплоёмкость калориметра.

3.          
В 2 кг воды, имеющей температуру 20°С, опустили сначала
медное тело массой 2 кг, имеющее температуру 80°С. После того, как
температура перестала меняться, в воду опустили железное тело массой 3
кг, имеющее температуру —20°С. Какой после этого стала температура воды? Теплоёмкостью сосуда 
пренебречь.

4.          
После опускания в воду, имеющую температуру 100°С, тела с
температурой 20°С, установилась общая температура 80°С. Какой станет температура
воды, если, не вынимая первого тела, в нее опустить ещё два таких же тела,
имеющих температуру 20°С?

5.          
В чайник налили воду при температуре 20⁰С
и поставили на электроплитку. Через 13 минут вода закипела. Через какое время
половина воды выкипит?

6.          
Для того, чтобы на спиртовом нагревателе, с КПД 
70%, нагреть до кипения 1,4 кг воды и половину ее превратить в пар,  израсходовали
100 г спирта. Какова начальная температура воды? Удельная теплота сгорания
спирта 29×10⁶ Дж/кг.

7.          
В калориметре находится лёд массой 500
г  при температуре 0°С. В калориметр впускают  водяной пар температурой 100°С. Сколько воды
окажется в калориметре, когда весь лёд растает, а температура образовавшейся
воды будет равна 0°С?

8.          
В калориметр, содержащий 400
г воды и 200 г льда при 0°С, впустили водяной пар с температурой 100°С. Сколько пара было впущено
в калориметр, если в калориметре установилась температура 20°С? Теплоёмкость
калориметра 1000 Дж/⁰С.

 

9.          
В сосуд теплоёмкостью 1000 Дж/⁰С,
содержащий 5 кг воды при температуре 20°С, положили лёд, имеющий температуру —40°С. Температура
образовавшейся смеси оказалась равна —2°С. Сколько льда было положено в сосуд?

 

10.     
В алюминиевом калориметре массой 200
г находится кусок льда с температурой —20°С. В калориметр впустили водяной пар, имеющий температуру 100°С. Когда температура 
калориметра стала равна 20°С, измерили массу его содержимого. Она оказалась равной 400
г. Найти массу льда, находящегося в калориметре, и массу сконденсировавшегося
пара.

 

11.     
В калориметр, содержащий 3
кг воды при температуре 20°С, опустили 2 кг льда, имеющего температуру —10°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.

 

12.     
В калориметр, содержащий 1
кг льда и 800 г воды при 0°С впускают 100 г водяного пара при 100°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.

 

13.     
В калориметре находится вода массой 600
г при температуре 5°С. К ней долили ещё 300 г воды с температурой 10°С и положили 600
г льда с температурой —60°С. Что будет в калориметре после того, как теплообмен прекратится?
Теплоемкостью калориметра пренебречь.

14.     
В теплоизолированном медном сосуде массой 400
г находятся 2 кг льда при температуре —10°С. В сосуд помещают 400 г водяного пара при температуре 110°С. Что будет в сосуде
после того, как теплообмен прекратится?

 

15.     
В колбе находятся 200
г воды при температуре 0°С. Откачиванием паров всю воду в колбе заморозили. Сколько получилось
льда?

Ответы и решения

1.    60 л холодной и 40
л горячей воды.

t1 = 12°С t2 = 72°С q = 36°С V = 100 л	Решение Q1 = cm1(q — t1) – теплота, которую получит холодная вода, нагреваясь от 12°С до 36°С; Q2 = c(m — m1)(t2 — q) – теплота, которую отдаст горячая вода, остывая от 72°С до 36°С,
V1 — ?  V2 — ?

Q₁ = Q₂,

cm₁(q — t₁) = c(m — m₁)(t₂ — q),

m₁(q — t₁) + m₁(t₂ — q) = m(t₂ — q),

rV₁(q —
t₁ + t₂ — q) = rV (t₂ — q),

V₁ = V×;

V₁ = 100× = 60 (л),

V₂  = V — V₁ = 100 – 60 = 40 (л).

2. 2640 .

m1 = 2 кг t1 = 20°С с1=4200 Дж/(кг×0С) m2 = 0,8 кг t2 = 100°С с2 = 920 Дж/(кг×0С) q = 25°С_______ Ск — ?

Решение Q2  = Q + Q1, где Q2 – теплота, отданная алюминиевым телом; Q1 – теплота, полученная водой, Q — теплота, полученная калориметром. c2m2(t2 — q) = (Cк + c1m1)(q — t1), Cк = . Cк =   = 2640 (Дж/0С)

3. 19⁰С.

m1 = 2 кг c1=4200 Дж/(кг×0С) t1 = 20°С m2 = 2 кг c2 = 380 Дж/(кг×0С) t2 = 80°С m3 = 3 кг c3 = 460 Дж/(кг×0С) t3 = —20°С	Решение Здесь удобнее пользоваться уравнением теплового баланса в виде (6), так как при решении этим способом последовательность опускания в воду тел не важна: Q1 + Q2 + Q3 = 0, c1m1(q — t1) + c2m2(q — t2) + c3m3(q — t3) = 0, q = .
q – ?

4. 53°С

С1– теплоёмкость воды; t1 = 100°С С2– теплоёмкость тела; t2 = 20°С t3 = 80°С	Решение 1.    При опускании в воду с температурой t1 первого тела: С1(t1 — t3) = С2(t3 — t2). (1) 2.    При опускании в воду с температурой t2 сразу трех тел: С1(t1 — t4) = 3С2(t4 — t2). (2) 3.    Делим уравнение (1) на уравнение (2) и получаем: , Решая это уравнение, находим, что :  t4 » 53 °С.
t4 — ?

5.    44,5 мин.

t1 = 13 мин t1 = 20°С t2 = 100°С m2 = m1/2 с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг

t2 – ?

Решение

Мощность электроплитки подразумеваем 
постоянной. Поэтому:

,

,

откуда:,

6. 29°С

m1 = 1,4 кг с1=4200 Дж/(кг×0С) t2 = 100°С h = 0,7 m2 = 0,1 кг q = 29×106 Дж/кг	Решение h = , где Qполез = Q1 + Q2 = = cm1(t2 — t1) + L, а Qзатр = qm2. Тогда h =
t1-?

Выражаем t₁:   t₁ = t₂ –

t₁ =
100 —  100 – 71 = 29 (°С).

7.  563
г.

m1 = 0,5кг l = 3,4×105   Дж/кг t1 = 0°С с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг t2 = 100°С	Решение Q1 = Q2 + Q3, lm1 = Lm2 + cm2(t2 — t1), m2 = , m2 =
m – ?

                                                                              
= 0,063 (кг) = 63
г

       В итоге:   m = m₁ + m₂ = 500 +63 = 563 (г).

8.    65 г

m1 = 0,4 кг m2 = 0,2 кг l = 3,4×105 Дж/кг t1 = 0°С c =4200Дж/(кг×0С) t2 = 100°С L = 2,3×106 Дж/кг q = 20°С C = 1000 Дж/0С	Решение Q1 + Q2 + Q3 = Q4 + Q5, lm2 + c(m1 + m2)(0 — t1) + + C(q — t1) = = Lm3 + cm3(t2 — q),             m3 =  0,065 (кг).
m3 – ?

9.    27,1 кг.

C = 1000 Дж/0С m1 = 5 кг c1=4200 Дж/(кг×0С) t1 = 20°С t2 = —40°С c2=2100 Дж/(кг×0С) l = 3,4×105 Дж/кг q = —2°С	Решение Q1 + Q2 + Q3 + Q4 + Q5 = Q6, Q2  + Q4 = C(t1 — q) – теплота, отданная калориметром; Q1 + Q3 + Q5 = c1m1(t1 — 0) + lm1 + c2m1(0 — q) – теплота, отданная водой; Q6  = c2m2(q — t2) – теплота, принятая льдом.
m2 – ?

Тогда m₂
= .

m₂  =
 27,1 (кг).

10. 340
г льда и 60 г пара.

с1 = 920Дж/(кг×0С) m1 = 0,2 кг t1 = t2 = —20°С c2=2100 Дж/(кг×0С) t3 = 100°С L = 2,3×106 Дж/кг l = 3,4×105 Дж/кг c3=4200 Дж/(кг×0С) q = 20°С m =  0,4 кг	Решение Q1 + Q2 + Q3 + Q4 + Q5 = = Q6 + Q7. Q2, Q3, Q4 – теплоты, полученные льдом;      Q1, Q5 – теплоты, полученные калориметром; Q6, Q7 – теплоты, отданные паром. c1m1(q — t1) + c2m2(0 — t2) + lm2 +  c3m2(q — 0) = = L(m — m2) + c3(m — m2)(100 — q), Масса льда:
m2 – ?  m3 – ?

m₂ =

     m₂ =
 0,34 (кг)

     Масса пара: m₃ = m – m₂ = 0,4 кг – 0,34 кг = 0,06 кг.

11. Смесь, состоящая из 1,4 кг льда и 3,6
кг воды при температуре 0⁰С.

m1 = 3 кг t1 = 20°С c1= 4200 Дж/(кг×0С) m2 = 2 кг t2 = —10°С c2= 2100 Дж/(кг×0С) l = 3,4×105 Дж/кг	Решение 1. Q1 = c1m1(t1 — 0) = 4200×3×20 = 252000 (Дж) – может отдать вода, остывая от 20°С  до 0°С. 2. Q2 = c2m2(0 — t2) = 2100×2×10 = 42000 (Дж) – нужно льду, чтобы нагреться от –10°С до 0°С. 3. Q3 = lm2 = 340000×2 = 680000 (Дж) – нужно льду, чтобы полностью расплавиться. 4. Q1 — Q2 < Q3 – значит, у воды не хватит      энергии, чтобы расплавить весь лёд.
m¢1 – ? m¢2 – ? q – ?

    Вывод: лёд растает не весь, и
в калориметре будет находиться смесь воды со льдом при температуре 0°С.

   Сколько растает льда?

lm¢ = Q₁
— Q₂ Þ m¢ =  (кг)

 Тогда останется  льда: m¢₂ = m₂ — m¢ = 2 кг – 0,6
кг = 1,4 кг.

Масса воды: m¢₁ = m₁
+ m¢ = 3
кг + 0,6 кг  =
3,6 кг

12. 0,2
кг льда и 1,7 кг воды при температуре 0⁰С.

m1 = 1 кг m2 = 0,8 кг t1 = t2 = 0°С l = 3,4×105 Дж/кг c = 4200 Дж/(кг×0С) m3 = 0,1 кг t3 = 100°С L = 2,3×106 Дж/кг

Решение 1. Q1 = lm1 = 340000×1 = 340000 (Дж) – нужно льду, чтобы полностью растаять при 00С. 2. Q2 = Lm3 = 2300000×0,1 = 230000 (Дж) – может отдать пар, конденсируясь при 1000С  в воду. 3. Q3 = cm3(t3 — t1) = 4200×0,1×100 = 42000 (Дж) – может отдать пар, остывая от 1000С до 00С.         4.  Q2 + Q3 = 230000 + 42000 = 272000 (Дж) < Q1.  Поэтому лёд растает не весь, пар весь сконденсируется, а образовавшаяся из него вода остынет до 0°С.

q – ? m¢1 ­– ? m¢2 – ?

  Сколько льда растает?

lm¢ = Q₂ + Q₃ Þ m¢ =  (кг).

В калориметре останется льда: m¢₁
= m₁
— m¢ = 1 кг – 0,8
кг = 0,2 кг .

Масса воды: m¢₂ =
m₂
+ m¢ +  m₃ = (0,8 + 0,8 + 0,1) кг  = 1,7 (кг)

Полученная смесь находится при температуре 0°С.

13. Смесь воды (750
г) и льда (750 г) при 0⁰С.

m1 = 0,6 кг c1= 4200 Дж/(кг×0С) t1 = 5°С m2 = 0,3 кг t2 = 10°С m3 = 0,6 кг t3 = —600С с2= 2100 Дж/(кг×0С) l = 3,4×105 Дж/кг

Решение 1. Q1 = c1m1(t1 — 0) = 4200×0,6×5 = 12600 (Дж) – выделят 600 г воды, остывая от 5°С до 0°С. 2. Q2 = c1m2(t2 — 0) = 4200×0,3×10 = 12600 (Дж) – выделят 300 г воды, остывая от 10°С до 0°С. Q1 + Q2 = 25200 Дж. 3. Q3 = c2m3(0 — t3) = 2100×0,6×60 = 75600 (Дж) – нужно льду, чтобы нагреться от -60°С до 0°С. Q3 > Q1 + Q2 Þ вся вода остынет до 0°С, а лёд ещё при этом не нагреется до 0°С. DQ = Q3 — (Q1 + Q2) = 75600 – 25200 = 50400 (Дж). Нагреваясь до 0°С, лед «приморозит» к себе часть воды m¢:

q – ? mводы – ? mльда – ?

lm¢ = DQ Þ
m¢ =  =  (кг).

Итак, в калориметре будет находиться
смесь воды со льдом при температуре 0°С:

m_воды = m₁ + m₂ — m¢ = 0,6 + 0,3 — 0,15 = 0,75 (кг),

m_льда = m₃ + m¢ =
0,6 + 0,15 = 0,75 (кг)

14. 2,4
кг воды при температуре 36⁰С.

m1 = 0,4 кг c1 = 380 Дж/(кг×0С) m2 = 2 кг c2= 2100 Дж/(кг×0С) t1 = t2 =  —10°С l = 3,4×105 Дж/кг m3 = 0,4 кг t3 = 110°С с3= 2100 Дж/(кг×0С) L = 2,3×106 Дж/кг c4= 4200 Дж/(кг×0С)	Решение 1. Q1 = c1m1(0 — t1) = 380×0,4×10 = 1520 (Дж) – нужно получить медному сосуду, чтобы нагреться от -10°С до 0°С. 2. Q2 = c2m2(0 — t1) = 2100×2×10 = 42000 (Дж) – нужно получить льду, чтобы он нагрелся от      —10°С до 0°С. 3. Q3 = lm2 = 340000×2 = 680000 (Дж) – нужно получить льду, чтобы растаять и стать водой при 0°С. Q1 + Q2 + Q3 = 723520 (Дж) – нужно получить сосуду и льду, чтобы в сосуде при 0°С была вода. 4. Q4 = c3m3(t3 — 100) = 2100×0,4×10 = 8400 (Дж) – может отдать пар, остывая от 110°С до 100°С. 5. Q5  = Lm3 = 2300000×0,4 = 920000 (Дж) – может отдать пар, конденсируясь в воду при 1000С.
q – ? m – ?

Q₄ + Q₅ = 8400 + 920000 = 928400 (Дж) – может отдать пар, превращаясь в пар с
температурой 100°С;

DQ = (Q₄ + Q₅) — (Q₁ + Q₂ + Q₃) = 928400 – 723520 = 204880 (Дж) –
столько энергии останется у пара, когда он станет водой при 100⁰С, 
(лед при этом превратится в воду при 0°С).

Проверим, хватит ли этой энергии,
чтобы вода, образовавшаяся из льда, нагрелась вместе с сосудом от 0°С до 100°С?

Q₆ =
(c₁m₁ + c₂m₂)(100 — 0) = (380×0,4 + 4200×2)×100 =  855200 (Дж).

Это больше, чем 204880 Дж. Значит,
вода, образовавшаяся из льда, нагреется не до 100°С. Найдем, до какой 
температуры нагреются вода и сосуд:

Q₁ + Q₂ + Q₃ + (c₁m₁
+ c₄m₂)(q — 0) = Q₄ + Q₅ + c₄m₃(100
— q),

c₁m₁q + c₄m₂q + c₄m₃q = c₄m₃×100 + 204880,

q =  36(°С).

15. 174
г.

m = 0,2 кг l = 3,4×105 Дж/кг L = 2,3×106 Дж/кг	Решение
m1  — ?

Q₁ = lm₁ – энергия,
которая выделяется при замерзании воды массой m₁.

       Q₂ = L(m – m₁) – энергия, которая необходима для превращения оставшейся воды в пар.

Q₁ = Q₂,

lm₁
= L(m — m₁)

                                                                  
m₁ = m×, откуда

m₁ =  (кг) = 0,174 кг = 174 г.

Учебное издание

Самарин Григорий Геннадьевич

Решение задач на теплообмен с использованием уравнения теплового
баланса

(методические рекомендации)

Редактор
– Г. Д. Попырина

Компьютерная
верстка – К. В. Маренин

Подписано
в печать:

Бумага
типографская

Условных
печатных листов – 2,25

Тираж
– 100 экз.

Заказ
–

Цена
договорная.

Лицей естественных наук

610006, г. Киров, ул. Возрождения, 6