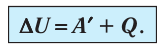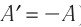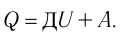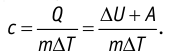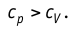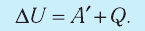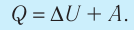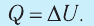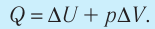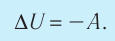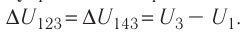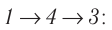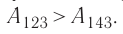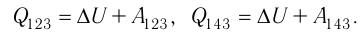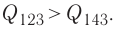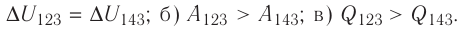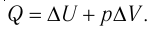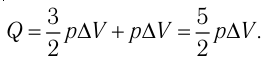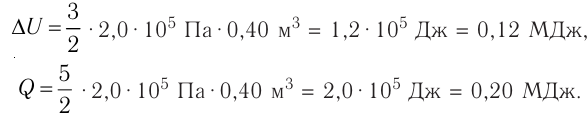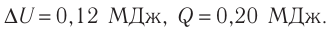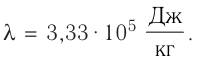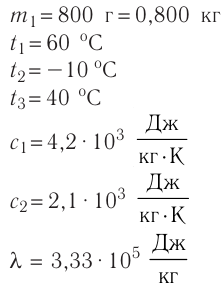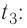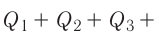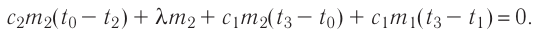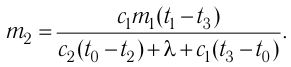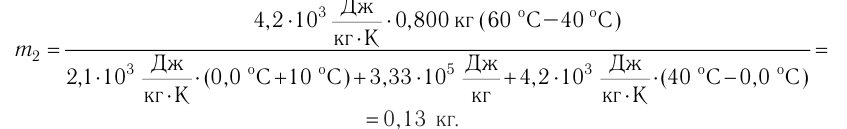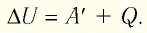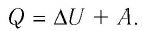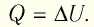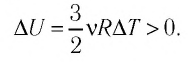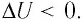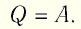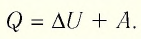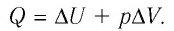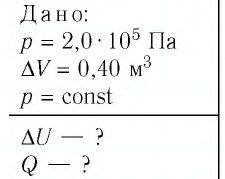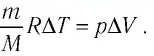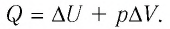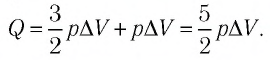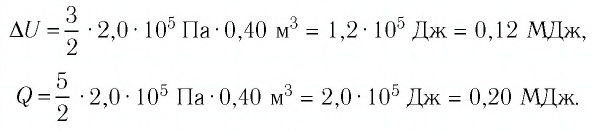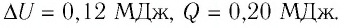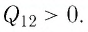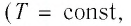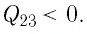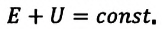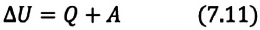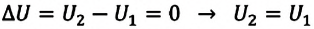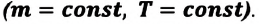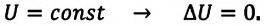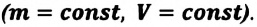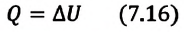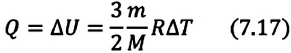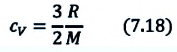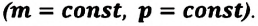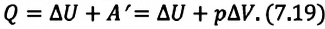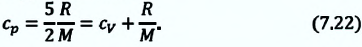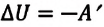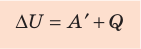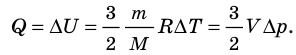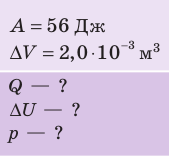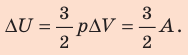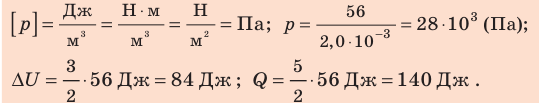Идеальный одноатомный газ
Определение идеального одноатомного газа
Количество атомов в молекуле оказывает влияние на то, как распределяется энергия по степеням свободы. Так для одноатомного газа молекула имеет три степени свободы (). Формулу для расчета внутренней энергии идеального одноатомного газа очень просто получить.
Внутренняя энергия одноатомного идеального газа
Учтем, что молекулы идеального газа представлены как материальные точки, которые не взаимодействуют на расстоянии. Отсутствие сил взаимодействия между молекулами обозначает, что потенциальная энергия взаимодействия молекул постоянна. Суммарная энергия покоя самих молекул также неизменна, так как молекулы при тепловых процессах не изменяются. Следовательно, внутренняя энергия идеального одноатомного газа является суммой кинетических энергий поступательного движения молекул и еще некоторая постоянная.
Обозначим внутреннюю энергию газа как U, тогда сказанное выше запишем как:
где – сумма кинетических энергий поступательного движения молекул; N – число молекул в газе. Примем во внимание то, что средняя кинетическая энергия молекулы (
) равна:
По закону о равномерном распределении энергии по степеням свободы имеем:
для одноатомного газа:
– постоянная Больцмана; T – температура по шкале Кельвина.
Внутреннюю энергию одноатомного идеального газа можно записать как:
Обычно постоянную величину в выражении (5) опускают, так как в расчётах она роли не играет.
Выражение (5) говорит о том, что внутренняя энергия идеального газа определена его температурой. Она является функцией состояния и не зависит от процесса который провели для того чтобы газ пришел в состояние с этой температурой. При этом изменение внутренней энергии идеального газа определено только его начальным и конечным состояниями, и не связано с характером процесса.
Выражение (5) часто используют в виде:
где m – масса газа; – молярная масса газа;
– универсальная газовая постоянная;
– количество вещества.
Теплоемкость одноатомного идеального газа
Для изохорного процесса, проводимого в идеальном газе работа равна нулю (A), поэтому первое начало термодинамики:
запишем как:
где – теплоемкость газа при постоянном объеме. Используя выражения (8) и (6) получим:
Используя формулу (10) можно вычислить молярную теплоемкость любого одноатомного газа при постоянном объеме:
Молярная теплоемкость одноатомного газа при изобарном процессе () связана с
соотношением Майера:
Примеры решения задач
Как
показывают результаты экспериментов,
во многих случаях приращение температуры
тела прямо пропорционально количеству
теплоты, сообщенного ему. Для количественного
описания этого соотношения вводится
коэффициент
пропорциональности между
количеством теплоты, сообщаемого телу,
и изменением его температуры, называемым
теплоёмкостью:
|
|
(2.55) |
Этот
коэффициент позволяет определить
количество теплоты
,
которое необходимо сообщить телу для
повышения его температуры на величину.
В
самом общем случае для произвольного
тела его теплоемкость может зависеть
от параметров состояния этого тела,
например, от его температуры или объема.
Очевидно, что теплоемкость термодинамической
системы изменяется при изменении
количества вещества в ней. Для систем,
находящихся в состоянии термодинамического
равновесия, их теплоемкость пропорциональна
количеству вещества. Это позволяет
ввести для описания свойств тела удельную
теплоемкость:
|
|
(2.56) |
и,
соответственно, молярную
теплоемкость:
|
|
(2.57) |
где:
—
масса тела,—
количество вещества в нем. Эти теплоемкости
связаны между собой через молярную
массуследующим
соотношением:
|
|
(2.58) |
Теплоемкость,
так же как и количество переданной телу
теплоты, зависит от того, каким образом,
а точнее при осуществлении какого
процесса, теплота передавалась этому
телу.
Если
в процессе изменения состояния идеального
газа теплоёмкость его не изменяется,
то такой процесс называется политропическим.
Частными случаями политропического
процесса являются рассмотренные ранее
изопроцессы, протекающие при постоянных
значениях температуры, давления или
объема.
Проведем
определение теплоёмкости идеального
газа в процессе, при котором его объём
остаётся неизменным. При таком процессе
работа не совершается:
,
так как нет изменения объема газа (см.
формулу(1.12)).
Поэтому, в соответствии с первым началом
термодинамики (1.5),
имеем равенство подведенной к телу
теплоты
и
изменения его внутренней энергии:
|
|
(2.59) |
Считая,
что внутренняя энергия идеального газа
пропорциональна количеству вещества:
|
|
(2.60) |
его
теплоемкость в изохорическом процессе
можно определить с помощью формулы:
|
|
(2.61) |
Здесь:
—
внутренняя энергия одного моля газа, амолярная
теплоемкость при постоянном объемравна:
|
|
(2.62) |
или,
как обычно принято записывать в
термодинамике
|
|
(2.63) |
Символ
после
закрывающей скобки указывает на то, что
дифференцирование происходит при
неизменном значении объема.
В
соответствии с формулой (2.27)
кинетическая, а, следовательно, и
внутренняя энергия идеального газа,
линейно зависят от его температуры. Из
этого следует, что молярная
теплоемкость идеального газа в
изохорическом процессе постоянна:,
и не зависит от температуры идеального
газа. Тогда выражение для его внутренней
энергии с точностью до произвольной
постоянной, которую обычно принимают
равной нулю, можно записать в следующем
виде:
|
|
(2.64) |
Из
этого выражения следует, что внутренняя
энергия идеального газа зависит только
от его температуры и не зависит от других
параметров его состояния, в частности
от его объема.
Отсутствие
зависимости внутренней энергии идеального
газа от его объема было экспериментально
подтверждёно в опытах Гей-Люссака и
Джоуля, схема которых показана на рис.
2.6.
|
|
|
Рис. 1 — отделения сосуда, разделенные |
В
опытах Гей-Люссака адиабатически
изолированный жёсткий сосуд имел
несколько отделений 1, разделённых
перегородками 2, которые можно было
медленно извлекать, причём трение в
системе практически отсутствовало. В
одном из отделений первоначально
находился газ, который, по мере открывания
перегородок постепенно заполнял другие
отделения сосуда, причём каждый раз
после открытия перегородки система
приходила в состояние термодинамического
равновесия. При этом процессе, так как
сосуд был адиабатически изолированным,
внутренняя энергия газа не изменялась.
Опыты показали, что температура газа
при этом также не изменяется. Это
подтверждало независимость внутренней
энергии идеального газа при постоянстве
температуры от его объёма.
Опыты
Джоуля являлись усовершенствованным
продолжением опытов Гей-Люссака. Джоуль
поместил сосуд в калориметр 3, и тем
самым избавил себя от необходимости
использовать адиабатически изолированный
сосуд. Это дало возможность более
тщательно добиваться установления
термодинамического равновесия и повысить
точность эксперимента. Температуру
газа в сосудах Джоуль контролировал
посредством измерения температуры воды
в калориметре. Опыты Джоуля подтвердили,
что внутренняя энергия идеального газа
не зависит от занимаемого им объёма.
Однако дальнейшие более точные опыты
Джоуля, проведённые им совместно с
Томсоном (лордом Кельвином) показали,
что если газ не является идеальным, его
внутренняя энергия зависит от объёма,
занимаемого им (эффект Джоуля-Томпсона).
В
параграфе
2.2
нами была рассмотрена молекулярно-кинетическую
модель идеального газа и получена
зависимость (2.41)
кинетической энергии молекул газа от
его температуры. Так как внутренняя
энергия идеального газа с точностью до
произвольной постоянной равна кинетической
энергии теплового движения его молекул,
то сравнение выражений (2.41)
и (2.64)
позволяет записать формулу для молярной
теплоемкости такого газа:
|
|
(2.65) |
где
число степеней свободы
зависит
от физико-химической структуры молекулы
газа.
Из
формулы (2.65)
следует, что для одноатомного газа
молярная теплоемкость
,
а для газа, молекулы которого состоят
из двух жестко связанных атомов.
Соответственно для газов из жестких,
многоатомных молекул.
При
использовании выражения (2.65)
для практических расчетов реальных
газов необходимо помнить, что оно
является приближенным. Как указывалось
в параграфе
2.2
при обсуждении выражения (2.42)
для кинетической энергии многоатомного
газа, существует зависимость количества
учитываемых при расчете степеней свободы
от температуры. Это приводит к тому, что
при значительных изменениях температуры
теплоемкость газа может существенно
изменяться. Например, для молекул
водорода, при температуре порядка 50 К
вращательные степени свободы как бы
«вымерзают» и его молярная
теплоёмкость
становится
близкой к.
А при температурах порядка 300 — 400 К
вращательные степени свободы «включаются»
и его теплоёмкостьприобретает
значение.
При дальнейшем, значительном по сравнению
с комнатной, повышении температуры
начинают проявляться колебательные
степени свободы. Для двухатомного газа,
например водорода, это приводит к
увеличению энергии его молекулы на
величину,
и соответственно к возрастанию молярной
теплоемкости на.
Поэтому при очень высоких температурах
молярная теплоёмкость водорода стремится
к значению.
Теплоемкость
идеального газа в процессе, происходящем
с изменением объема, отличается от
полученного выше выражения (2.65).
Это связано с тем, что при изменении
объема газа им совершается работа и, в
соответствии с первым началом термодинамики
(1.5),
подведенная теплота и изменение
внутренней энергии становятся не равными
друг другу. При расширении газа часть
подведенной теплоты затрачивается на
совершение им работы.
Поэтому
для произвольного политропического
процесса при определении молярной
теплоемкости необходимо вместо выражения
(2.62)
использовать формулу:
|
|
(2.66) |
где:
—
объем одного моля газа. Последнее
слагаемое в числителе этой формулы
описывает работу, совершенную одним
молем газа в рассматриваемом процессе
(см. формулу(1.12)).
Если
процесс происходит при постоянном
давлении, то с учетом выражения (2.62)
имеем
|
|
(2.67) |
Использование
уравнения Клапейрона-Менделеева (2.2),
записанного для одного моля газа
|
|
(2.68) |
дает:
|
|
(2.69) |
Тогда
из выражения (2.67)
следует формула для нахождения молярной
теплоемкости при постоянном давлении:
|
|
(2.70) |
которая
называется соотношением
Майера,
в честь Юлиуса
Роберта Майера
(1814 — 1878). Из этой формулы с учетом выражения
(2.65)
имеем:
|
|
(2.71) |
Анализ
выражения (2.70)
показывает, что теплоемкость при
постоянном давлении больше теплоемкости
при постоянном объеме. Это связано с
тем, что при изобарическом процессе, в
отличие от изохорического, совершается
работа, на выполнение которой затрачивается
часть подведенной теплоты.
Таким
образом, молярная теплоёмкость идеального
газа зависит от вида процесса, в котором
он участвует, и от внешних условий,
обеспечивающих протекание этого
процесса. Например, в соответствии с
определением теплоёмкости (2.55),
для адиабатического процесса, когда
теплообмен с окружающей средой отсутствует
и
,
она равна нулю, а для изотермического
при—
бесконечности.
Сформулированный
в параграфе
2.2
закон равнораспределения энергии по
степеням свободы позволяет определять
теплоемкость не только газов, но и
твёрдых тел. В 1819 г. Пьер
Луи Дюлонг
(1785 — 1838) и Алексис
Терез Пти
(1791 — 1820) установили, что произведение
удельной (на единицу массы вещества)
теплоёмкости на атомную массу элемента,
из которого состоит твёрдое тело, есть
величина почти постоянная.
Закон
Дюлонга и Пти был установлен ими
эмпирически путём проведения большого
количества опытов. В этих опытах
измерялась скорость охлаждения различных
веществ, находящихся при одинаковых
внешних условиях, при которых передача
теплоты определялась только разностью
температуры вещества и окружающей
среды. Если для различных веществ
разности температур одинаковы, то
отношение их теплоёмкостей будет равно
обратному отношению скоростей изменения
температуры.
В
то время, когда Дюлонг и Пти проводили
свои эксперименты, атомные массы многих
элементов ещё не были установлены.
Сейчас, с учетом того факта, что молярная
масса пропорциональна атомной массе
элемента (см. формулы (2.7)
и (2.8)),
закон Дюлонга и Пти может быть сформулирован
как закон
постоянства молярной теплоёмкости (при
постоянном объёме) для большинства
твёрдых тел, состоящих из простых
соединений.
Величина этой теплоемкости равна 24,9
Дж/моль*К.
Закон
постоянства молярной теплоёмкости
может быть объяснён равнораспределением
энергии по степеням свободы. Считая
твёрдое тело состоящим из атомов, каждый
из которых представляет собой гармонический
осциллятор с тремя степенями свободы,
имеем на каждую степень свободы атома
среднюю кинетическую энергию
и
такую же среднюю потенциальную энергию.
Тогда внутренняя энергия одного моля
вещества может быть определена с помощью
формулы:
|
|
(2.72) |
а,
соответственно, его молярная теплоемкость
примет вид:
|
|
(2.73) |
что
хорошо согласуется с указанным выше
значением.
Закон
Дюлонга и Пти удовлетворительно
выполняется при комнатных и более
высоких температурах. Однако при низких
температурах происходит «вымерзание»
колебательных степеней свободы, и
молярная теплоёмкость твердых тел
уменьшается. Существуют вещества,
например алмаз, бериллий, а также сложные
кристаллические соединения, для которых
закон Дюлонга и Пти не выполняется.
Задача
2.1. Пусть
молей
идеального газа, молекулы которого
имеют
степеней
свободы, находятся в вертикальном
цилиндрическом сосуде, закрытом сверху
поршнем, массой
.
Поршень закреплен к дну сосуда с помощью
пружины, с жесткостью
.
В нейтральном положении расстояние от
дна сосуда до поршня считаем равным
.
Считая трение в системе и внешнее
атмосферное давление отсутствующими,
определить её теплоемкость.
Решение:
При подъеме поршня на величину
объем
газа в сосуде станет равным
,
где:
—
площадь поршня.
Давление
газа в сосуде будет уравновешиваться
весом поршня и силой упругости пружины:
или
.
Уравнение
Клапейрона-Менделеева (2.2)
позволяет записать следующее выражение:
,
подстановка
в которое формул для объема
и
давления
дает:
или
.
Умножение
этого выражения на площадь
дает:

При
сообщении рассматриваемой системе
теплоты
,
происходит нагревание газа в сосуде на
,
приводящее к его расширению и подъему
поршня на величину
.
В соответствии с первым началом
термодинамики (1.5)
имеем:
или
с учетом полученных выражений и формулы
(2.65)
имеем:

Тогда
теплоемкость системы в соответствии с
формулой (2.55)
будет равна:

Таким
образом, для рассматриваемой системы
её теплоемкость зависит не только от
количества газа
,
но и от величины смещения поршня
,
а также от параметров системы: массы
поршня
,
жесткости пружины
и
первоначальной высоты сосуда
.
Очевидно, что рассматриваемый процесс
не является политропическим.
Если
цилиндрический сосуд расположить
горизонтально, то на газ перестанет
воздействовать сила веса поршня и
выражение для теплоемкости несколько
упростится:
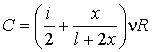
При
учете действия внешнего атмосферного
давления
в
выражении для теплоемкости необходимо
к весу поршня
добавлять
еще силу
,
действующую на него со стороны атмосферы.
В этом случае теплоемкость можно
вычислить по формуле:

Таким
образом, в этом случае теплоемкость
системы будет зависеть еще и от величины
атмосферного давления
и
площади поршня
.
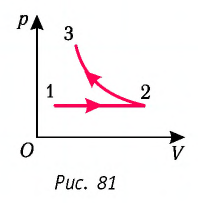
Определить количество теплоты, необходимое для перевода одного моля одноатомного идеального газа из состояния 1 в состояние 3. В состоянии 1 температура газа T1 = 300 К.
Спрятать решение
Решение.
При изобарном процессе Изменение внутренней энергии одноатомного газа
По первому закону термодинамики
При изохорном процессе Изменение внутренней энергии
Количество теплоты равно
Тогда при переходе получено количество теплоты
Из уравнения Клапейрона-Менделеева откуда количество теплоты, полученное газом, равно
Ответ: 13,7 кДж.
Источник: Кирик Л. А. Самостоятельные и контрольные работы для 10 класса, Х.: «Гимназия», 2002 (№ 1 (высок.) стр. 44)
Два
моля идеального одноатомного газа сначала расширяются изобарно, а затем
изохорно переходят в состояние с начальной температурой 300 K. Определите количество теплоты, переданной газу, если объем в
этом процессе увеличился в 6 раз.
Решение.
Согласно
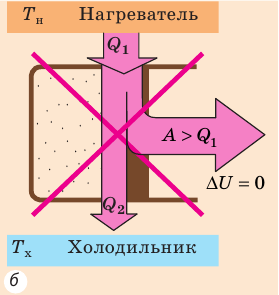
первому началу термодинамики количество теплоты, сообщенное системе,
расходуется на увеличение ее внутренней энергии и на работу, совершаемую
системой против внешних сил: Q = DU + A. В частности, при изобарном расширении газа Q1 = DU1 + A1 , где изменение внутренней
энергии газа DU1.
T – температура газа
после завершения этого процесса. При изохорном процессе Q2 = DU2 + A2 = DU2.
Тогда
полное количество переданной газу теплоты Q
= Q2 + Q2 = A1 = (n-1)vRT1 = 5•2,0•8,31•300 = 25
кДж.
Ответ:
Q = 25 кДж.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Содержание:
Первый закон термодинамики:
При изучении физики в 9 классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия? Если бутылку, заполненную до половины водой при комнатной температуре, встряхивать в течение нескольких минут, то окажется, что вода нагрелась на 1—2 °С. Каким образом нагрелась вода?
В середине XIX века известный английский физик Дж. Джоуль (1818— 1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX века Г. Гельмгольца (1821 —1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы. Согласно этому закону при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.
Для термодинамических систем (в термодинамике обычно рассматривают макроскопически неподвижные системы) закон сохранения и превращения энергии называют первым законом термодинамики. Согласно первому закону термодинамики, приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:
Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком (
Если система представляет собой действующее устройство, периодически возвращающееся в исходное состояние, то при этом AU-0 и A-Q. Механизм, который мог бы совершать работу без изменения состояния составляющих его тел и без теплопередачи от внешних тел, называют «вечным двигателем первого рода». Поэтому первый закон термодинамики можно сформулировать и следующим образом: невозможен вечный двигатель первого рода, т. е. такой двигатель, который при неизменном значении собственной внутренней энергии совершал бы работу большую, чем энергия, получаемая им извне.
Применим первый закон термодинамики к различным изопроцессам, происходящим с идеальным одноатомным газом.
Изохорный процесс
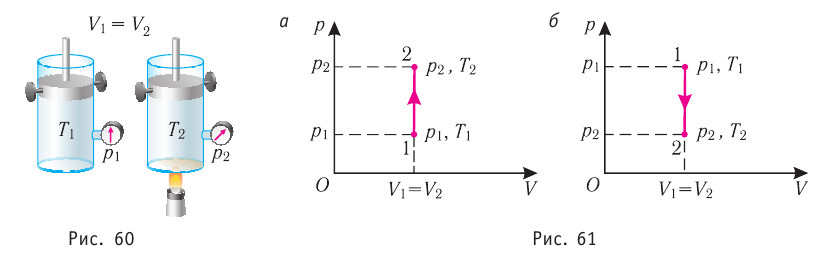
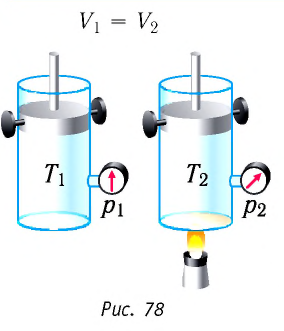
Пусть идеальный одноатомный газ находится в цилиндрическом сосуде, закрытом неподвижным поршнем (V = const). Нагреем сосуд с газом. Объём газа остаётся практически постоянным (тепловым расширением сосуда пренебрегаем) (рис. 60), следовательно, работа силы давления газа А= 0. Тогда первый закон термодинамики примет вид
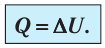
Это означает, что всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии. При этом приращение внутренней энергии газа 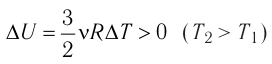
процессе отдаёт количество теплоты, то его внутренняя энергия убывает:
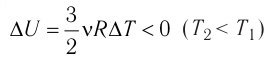
Изотермический процесс
Пусть цилиндрический сосуд с газом под поршнем находится в термостате — устройстве, в котором поддерживается постоянная температура. В этом случае внутренняя энергия идеального одноатомного газа 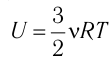
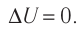
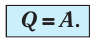
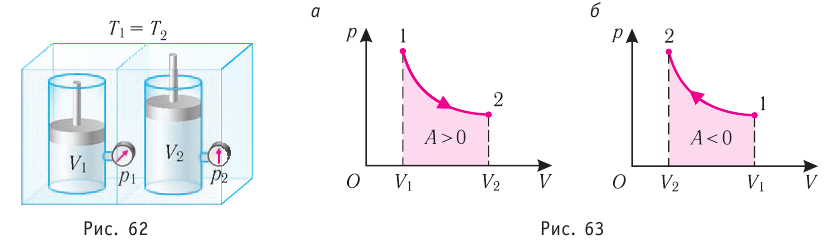
Какие выводы следуют из этого? Если с помощью внешнего устройства медленно перемещать поршень в сосуде так, чтобы объём газа увеличивался (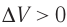
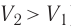
Если же внешнее устройство обеспечивает медленное уменьшение объёма газа в сосуде (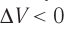
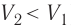
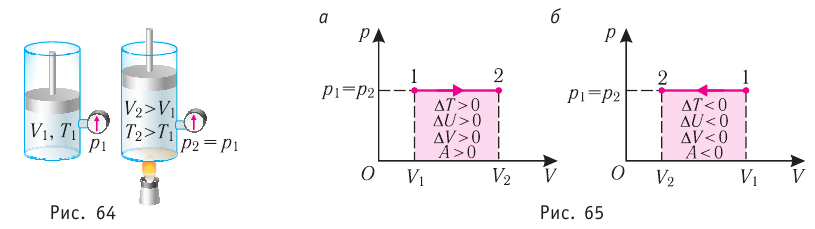
Изобарный процесс
Пусть газ находится в цилиндрическом сосуде, закрытом поршнем, который может свободно или под постоянной нагрузкой перемещаться (рис. 64). Нагреем газ, передав ему некоторое количество теплоты (Q > 0). Согласно первому закону термодинамики (11.2) переданное газу количество теплоты частично расходуется на увеличение внутренней энергии 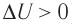
При изобарном процессе работа расширения (сжатия) газа 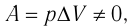
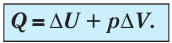
При изобарном сжатии газа внешние силы совершают работу А’ > 0. Чтобы давление газа при этом оставалось постоянным, газ необходимо охлаждать, т. е. он должен отдавать в окружающую среду некоторое количество теплоты (Q < 0). Понижение температуры газа при изобарном сжатии приводит к уменьшению его внутренней энергии (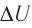
Удельная теплоёмкость вещества зависит не только от его свойств, но и от характера осуществления процесса теплопередачи. Действительно, из формулы (10.4) следует, что удельная теплоемкость
Тогда согласно первому закону термодинамики при изохорном процессе (11.3)
удельная теплоёмкость идеального газа 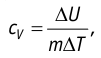
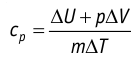
Это объясняется тем, что при постоянном давлении часть подводимой энергии расходуется на совершение силой давления газа работы при расширении.
Расширение жидких и твёрдых тел при нагревании при постоянном давлении значительно меньше, чем газов, поэтому для них 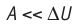
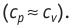
Адиабатный процесс
Адиабатным называют процесс, в ходе которого термодинамическая система не получает и не отдаёт энергию путём теплопередачи. Таким образом, при адиабатном процессе
Q = 0.
Применяя к этому процессу первый закон термодинамики, получим:
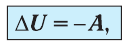
или
При адиабатном процессе изменение внутренней энергии системы происходит только за счёт совершения работы. Если внешние силы совершают работу по сжатию газа (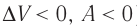
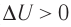
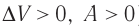
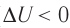
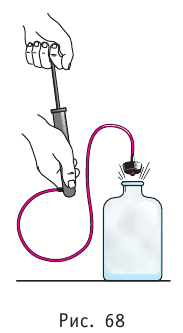
Если процесс протекает очень быстро, то теплопередача практически не сказывается. Очень нагляден опыт, иллюстрирующий уменьшение температуры газа при его адиабатном расширении. Используя насос, через отверстие в пробке будем накачивать в стеклянный сосуд воздух (рис. 68). Через некоторый промежуток времени накачивания сжатый воздух совершит работу по преодолению силы трения, с которой сосуд действует на пробку, и силы атмосферного давления. Теплопередача между сосудом и окружающими телами не успевает проявиться за тот малый промежуток времени, пока пробка вылетает из сосуда. Уменьшение внутренней энергии воздуха в сосуде выражается в понижении его температуры, что приводит к конденсации водяных паров, т. е. к образованию тумана.
В качестве примера адиабатного процесса можно привести охлаждение воздуха в атмосфере. Нагретый возле поверхности Земли воздух при быстром подъёме в верхние слои атмосферы расширяется почти адиабатно и при этом резко охлаждается. Водяной пар в нём конденсируется в маленькие капли воды и кристаллики льда, образуя облака. Близкий к адиабатному процесс используют в двигателях внутреннего сгорания.
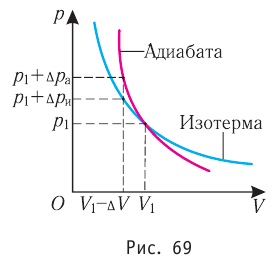
Обратимый адиабатный процесс относят к изопроцессам, так как он характеризуется постоянством функции состояния, называемой энтропией. В отличие от остальных изопроцессов при обратимом адиабатном процессе происходят изменения давления, объёма и температуры. График адиабатного процесса в координатах (р, V) похож на график изотермического процесса (рис. 69). Однако одному и тому же изменению объёма 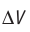
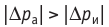
Это объясняется тем, что в случае адиабатного расширения давление 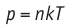
1. Приращение внутренней энергии термодинамической системы при
переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:
2. Количество теплоты, полученное или отданное термодинамической системой при взаимодействии с внешними телами при её переходе из одного состояния в другое, идёт на приращение внутренней энергии системы и на работу, которую система совершает при расширении:
3. При изохорном процессе всё передаваемое системе количество теплоты идёт на увеличение её внутренней энергии:
4. При изотермическом процессе работа расширения или сжатия идеального газа сопровождается теплопередачей между газом и термостатом:
A=Q.
5. При изобарном процессе переданное идеальному газу количество теплоты частично расходуется на увеличение внутренней энергии газа и частично идёт на совершение работы газом при его расширении:
6. При адиабатном процессе приращение внутренней энергии газа равно работе, которую совершает сила давления газа, взятой с противоположным знаком:
Пример №1
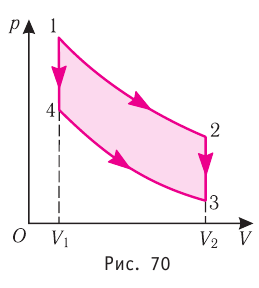
Идеальный газ, масса которого постоянна, переводят из состояния / в состояние 3 двумя различными способами: 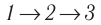
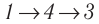
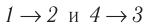
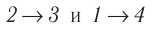
Решение, а) Так как начальное и конечное состояния для обоих переходов одинаковы, то будут одинаковы и приращения внутренней энергии:
б) Из рисунка 70 видно, что площадь фигуры, ограниченной осью OV, изотермой и изохорами, проходящими через точки 3 и 4, меньше площади фигуры, ограниченной осью ОV, изотермой и изохорами, проходящими через точки 1 и 2. Следовательно, в процессе перехода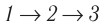
в) Из первого закона термодинамики следует:
Поскольку приращения внутренней энергии в обоих случаях одинаковы, а совершённая силой давления газа работа больше при переходе 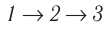
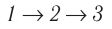
Ответ: а)
Пример №2
Идеальный одноатомный газ, давление которого 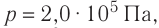
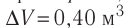
Дано:
р = 2,0 • 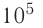
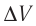
р =const
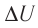
Решение. Приращение внутренней энергии идеального одноатомного газа 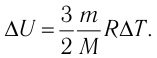
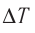
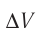
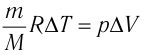
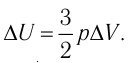
Отсюда
Ответ:
Пример №3
В сосуд налита вода массой 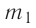
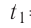
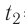
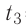
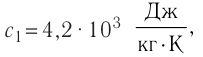
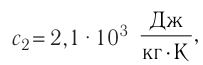
Дано
Решение. Если пренебречь потерями энергии в окружающую среду, то термодинамическая система «сосуд—вода—лёд» является изолированной. Поэтому учитываем только обмен энергией между входящими в систему телами при теплопередаче. Рассмотрим тепловые процессы, происходящие в системе: 1) нагревание льда от температуры 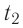
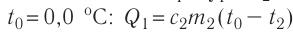
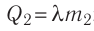
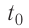
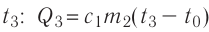
массой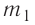
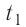
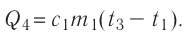
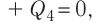
Отсюда масса льда
Ответ: 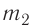
Первый закон термодинамики
В 9-м классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия?
Закон сохранения энергии
В середине XIX в. известный английский физик Дж. Джоуль (1818—1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX в. Г. Гельмгольца (1821 — 1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы.
Закон сохранения и превращения энергии: при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.
Закон сохранения и превращения энергии является всеобщим законом природы и связывает воедино все физические явления. Этот закон выполняется абсолютно точно, на нём базируется всё современное естествознание.
Первый закон термодинамики:
В предыдущих параграфах мы рассматривали процессы, в которых внутренняя энергия системы изменялась или при совершении работы, или в результате теплообмена. Однако чаще всего при переходе системы из одного состояния в другое внутренняя энергия изменяется как за счёт совершения работы, так и за счёт теплообмена с окружающими телами.
Для термодинамических систем закон сохранения и превращения энергии называют первым законом термодинамики.
Первый закон термодинамики: приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного (или отданного) системой при взаимодействии с внешними телами.
Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком 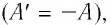
Количество теплоты, полученное (или отданное) термодинамической системой при взаимодействии с внешними телами при её переходе из одного состояния в другое, идёт на приращение внутренней энергии системы и на работу, которую она совершает против внешних сил:
Применим первый закон термодинамики к различным изопроцессам изменения состояния идеального одноатомного газа.
Рассмотрим в качестве термодинамической системы идеальный одноатомный газ, находящийся в цилиндрическом сосуде, закрытом поршнем.
Изохорный процесс:
Если сосуд закрыт неподвижным поршнем, то при нагревании объём газа остаётся постоянным 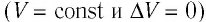
При изохорном процессе всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии:
Если газ при изохорном процессе отдаёт количество теплоты, то его внутренняя энергия убывает:
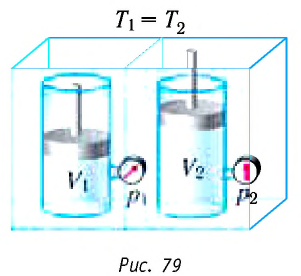
Изотермический процесс:
Поместим сосуд с газом, находящимся под подвижным поршнем, в термостат — устройство, в котором поддерживается постоянная температура (рис. 79). С помощью внешнего устройства медленно переместим поршень в сосуде так, чтобы объём газа увеличился (или уменьшился). Значения температуры газа в начальном и конечном состояниях одинаковы. В этом случае внутренняя энергия идеального одноатомного газа 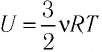
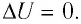
При изотермическом процессе переданное газу количество теплоты расходуется на совершение газом работы.
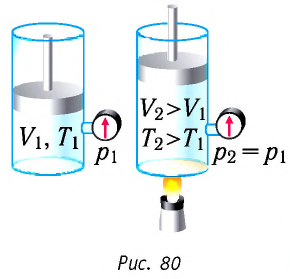
Изобарный процесс:
Если сосуд закрыт подвижным поршнем, то при нагревании увеличится как температура газа, так и его объём (рис. 80). Тогда первый закон термодинамики имеет вид:
При изобарном процессе переданное газу количество теплоты частично расходуется на увеличение внутренней энергии системы и частично идёт на совершение работы силой давления газа при его расширении.
С учётом того, что при изобарном процессе работа расширения (сжатия) газа 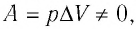
Пример №4
Идеальный одноатомный газ, давление которого 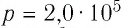
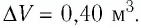
Решение. 11риращение внутренней энергии идеального одноатомного газа 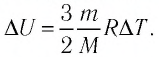
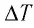
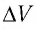
Тогда 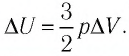
Следовательно,
Ответ:
Пример №5
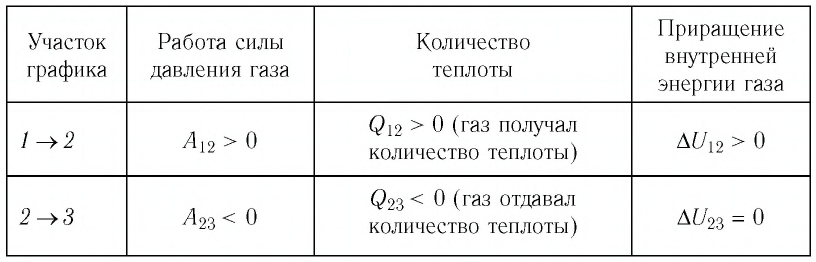
На рисунке 81 представлен график процесса изменения состояния некоторой массы идеального газа (участок 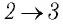
Решение. Участок 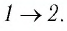
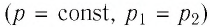
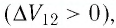
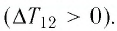
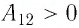
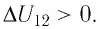
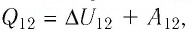
Участок 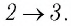
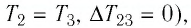
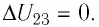
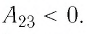
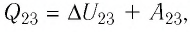
Ответ:
Определение первого закона термодинамики
Невозможно представить себе повседневную жизнь без разноцелевой техники, облегчающей нашу жизнь. При помощи этой техники люди вспахивают землю, добывают нефть, газ, руду и другие полезные ископаемые, «сокращают» большие расстояния и т.д. Главное свойство всей техники — способность совершения ими работы.
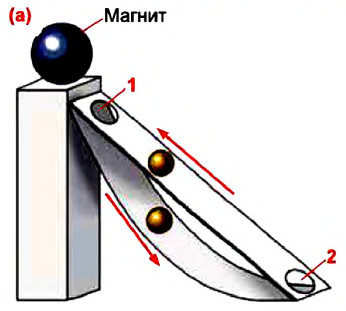
По этой причине еще с древних времен люди пытались создать способный работать вечно perpetuum mobile, то есть вечный двигатель. Как одну из интересных работ в этом направлении можно показать оригинальный проект, предложенный английским священником Джоном Уилкенсином в XVII веке, основанный на действии магнитного поля. По идее проекта, вечный двигатель должен работать так: шарообразный магнит помещен на высокую опору, к которой прикрепляются две наклонные плоскости, верхняя плоскость прямолинейная, а нижняя изогнутая (а).
В результате притяжения магнитом шарик, помещенный в нижней части прямой плоскости, начинает подниматься вверх и проваливается на нижнюю плоскость через отверстие 1 в верхней части плоскости. Затем, скатываясь вниз по изогнутой плоскости, снова попадает на прямую плоскость через отверстие 2, и всё повторяется снова.
Первый закон термодинамики:
Согласно одному из фундаментальных законов природы — закону сохранения энергии, полная энергия (механическая и внутренняя энергия) замкнутой системы остается постоянной при всех процессах, происходящих внутри этой системы:
Закон сохранения энергии, применяемый к тепловым процессам, называют первым законом термодинамики:
Изменение внутренней энергии термодинамической системы равно количеству теплоты, переданному этой системе, и работе внешних сил, совершенной над системой:
Над замкнутой и изолированной системой внешние силы не совершают работу 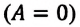
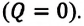
Так как работа, совершаемая системой над внешними силами, равна работе, совершаемой внешними силами над системой с противоположным знаком: 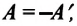
Количество теплоты, сообщенное термодинамической системе, затрачивается на изменение ее внутренней энергии и работу, которую система совершает против внешних сил:
После открытия закона сохранения энергии стала очевидной невозможность создания вечного двигателя первого рода:
Вечный двигатель первого рода (perpetuum mobile I) — это двигатель, который будучи однажды приведен в действие и не получая энергию извне, совершает работу вечно.
Согласно выражению (7.11), для совершения работы система или должна получать энергию извне, или использовать свою внутреннюю энергию:
В противном случае, то есть если 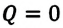
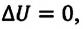
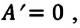
Применение первого закона термодинамики к разным процессам
1. Изотермический процесс
Так как в этом процессе температура системы остается постоянной, то и ее внутренняя энергия остается постоянной, изменение же внутренней энергии равно нулю:
Из выражений первого закона термодинамики (7.11) и (7.12) получаем:
• При изотермическом процессе все количество теплоты, переданное системе, затрачивается на совершение работы.
2. Изохорный процесс
Так как в этом процессе объем системы остается постоянным, то из выражения (7.10) следует, что работа не совершается 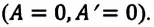
Для одноатомного идеального газа:
• При изохорном процессе количество теплоты, переданное системе, целиком затрачивается на изменение внутренней энергии.
Удельная теплоемкость одноатомного идеального газа, при постоянном объеме
Если в выражении (7.17) учесть выражения внутренней энергии одноатомного идеального газа (7.7) и количества теплоты (7.4), то получим формулу для удельной теплоемкости при постоянном объеме:
3. Изобарный процесс
В этом процессе давление системы остается постоянным, а температура и объем изменяются. Для этого процесса первый закон термодинамики записывается, так:
• При изобарном процессе (расширении) переданное системе количество теплоты затрачивается на увеличение его внутренней энергии и на совершение газом работы против внешних сил.
Удельная теплоемкость одноатомного идеального газа при постоянном давлении
Приняв в (7.19) во внимание выражения для одноатомного идеального газа:
получим:
С учетом этих выражений можно определить удельную теплоемкость одноатомного идеального газа при постоянном давлении как:
Из сравнения выражений (7.20) и (7.21) видно, что при изобарном процессе для одноатомного идеального газа существуют следующие соотношения между переданным количеством теплоты, изменением внутренней энергии и совершенной работой:
4. Адиабатный процесс
Адиабатный процесс — это процесс, происходящий без теплообмена системы с окружающей средой.
Так как в этом процессе отсутствует теплообмен системы со сторонними телами, то первый закон термодинамики можно записать так:
или
При адиабатном расширении газа его температура и внутренняя энергия уменьшаются, то есть газ охлаждается, а при адиабатном же сжатии, наоборот, его температура и внутренняя энергия увеличиваются, то есть газ нагревается.
История первого закона термодинамики
Один из фундаментальных законов природы — закон сохранения и превращения энергии. Первым этот закон сформулировал немецкий врач и физик Юлиус Роберт фон Майер (1814–1878). интересно, что к открытию ученого подтолкнули наблюдения над цветом крови у людей. Майер заметил, что венозная кровь у жителей тропиков светлее, чем у жителей его страны, и по цвету напоминает артериальную. он сделал вывод, что разница в цвете обусловлена количеством потребления кислорода, или «силой процесса сгорания», происходящего в организме. независимо от Майера и совсем иначе к открытию закона сохранения энергии пришли английский промышленник и ученый Джеймс Прескотт Джоуль (1818–1889) и немецкий физик, физиолог и психолог Герман Людвиг Фердинанд фон Гельмгольц (1821–1894). закон сохранения и превращения энергии управляет всеми явлениями природы, неизвестно ни одного случая, когда бы этот закон не выполнялся.
В термодинамике рассматривают системы, механическая энергия которых при переходе из одного термодинамического состояния в другое не изменяется. Тогда, если внешние силы совершили работу A′ и одновременно системе передано определенное количество теплоты Q, вся энергия идет на изменение внутренней энергии системы (∆U) . Закон сохранения и превращения энергии в таком случае называют первым законом (началом) термодинамики:
Изменение внутренней энергии системы ( ∆U) при переходе из одного термодинамического состояния в другое равно сумме работы A′ внешних сил и количества теплоты Q, сообщенного системе или переданного системой окружающим телам в процессе теплообмена:
Рис. 38.1. согласно третьему закону ньютона сила 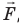
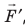
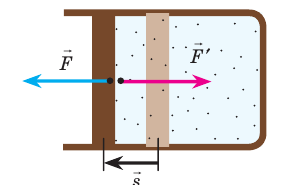
Обратите внимание! Если система получает некоторое количество теплоты, то в приведенной формуле Q берется со знаком «+», если отдает, то со знаком «–». На практике чаще рассматривают не работу A′ внешних сил, а работу A совершаемую данной системой против внешних сил. Учитывая, что A = −A ′ (рис. 38.1), первый закон (начало) термодинамики можно сформулировать так:
Количество теплоты Q, переданное системе, идет на изменение внутренней энергии системы (∆U) и на совершение системой работы A против внешних сил:
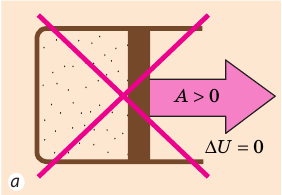
Согласно первому закону термодинамики невозможно создать вечный двигатель первого рода — циклическое устройство, которое совершало бы механическую работу без потребления энергии извне (рис. 38.2, а) или совершало бы работу большую, чем потребляемая им энергия (рис. 38.2, б).
Рис. 38.2. Циклические процессы, которые невозможны с точки зрения первого закона термодинамики
Какой вид имеет первый закон термодинамики для изопроцессов
Рассмотрим, какой вид принимает первый закон термодинамики в случаях, когда идеальному газу неизменной массы передают некоторое количество теплоты таким образом, что один из макроскопических параметров газа (V, p или T) остается неизменным.
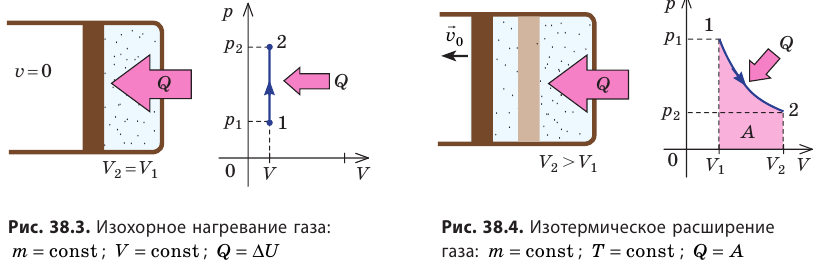
- Изохорный процесс (рис. 38.3). В ходе изохорного процесса объем газа не изменяется (∆V=0) и газ работу не совершает (A = 0), поэтому уравнение первого закона термодинамики имеет вид: Q=∆U . При изохорном процессе все переданное газу количество теплоты расходуется на увеличение внутренней энергии газа. Если идеальный газ одноатомный, то количество теплоты, переданное газу, равно:
- Изотермический процесс (рис. 38.4). В ходе изотермического процесса температура, а значит, и внутренняя энергия газа не изменяются (∆U=0), поэтому уравнение первого закона термодинамики имеет вид: Q=A.
При изотермическом процессе все переданное газу количество теплоты идет на совершение механической работы.
Каковы особенности адиабатного процесса
Адиабатный процесс — это процесс, который происходит без теплообмена с окружающей средой. При адиабатном процессе количество теплоты Q, переданное системе, равно нулю, поэтому первый закон термодинамики имеет вид: Q=∆U + A, или A = −∆U.
При адиабатном расширении газ совершает положительную работу за счет уменьшения внутренней энергии; температура газа уменьшается.
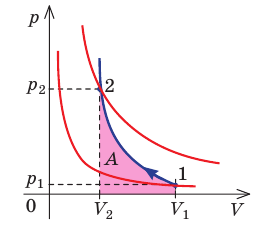
Поскольку p =nkT, при адиабатном сжатии давление газа возрастает намного быстрее, чем при изотермическом, ведь одновременно с увеличением концентрации молекул газа увеличивается и его температура (рис. 38.6).
Рис. 38.6. изменение давления газа в ходе адиабатного сжатия. синим цветом показана адиабата, красным — изотермы
Аналогично при адиабатном расширении давление падает быстрее, чем при изотермическом, ведь одновременно уменьшаются и концентрация, и температура газа.
В реальных условиях процесс, близкий к адиабатному, можно осуществить, если газ будет находиться в оболочке с очень хорошими термоизоляционными свойствами. Адиабатными можно считать и процессы, которые происходят очень быстро: в таком случае газ не успевает обменяться теплотой с окружающей средой (например, расширение и сжатие воздуха при распространении звуковых волн, расширение газа при взрыве).
Увеличение температуры при резком сжатии воздуха используется в дизельном двигателе, в котором нет системы зажигания горючей смеси.
Пример №6
При изобарном расширении неон совершил работу 56 Дж. Какое количество теплоты передано газу? Каково изменение его внутренней энергии? При каком давлении происходил процесс, если объем газа увеличился на 2,0 л?
Решение:
Для изобарного процесса работа газа равна: A=p∆V. Отсюда 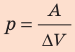
Согласно первому закону термодинамики: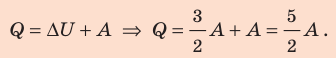
Ответ: Q = 140 Дж; ∆U = 84 Дж; p = 28 кПа.
Выводы:
- Закон сохранения энергии, записанный для тепловых процессов, называют первым законом (началом) термодинамики: количество теплоты, переданное системе, идет на изменение внутренней энергии системы и на совершение системой работы против внешних сил: Q=∆U + A.
- При изохорном процессе газ не выполняет работу (A = 0 ) , поэтому вся теплота, переданная газу, идет на увеличение его внутренней энергии: Q=∆U.
- При изотермическом процессе внутренняя энергия газа не изменяется (∆U=0), поэтому вся теплота, переданная газу, идет на совершение газом работы: Q=A.
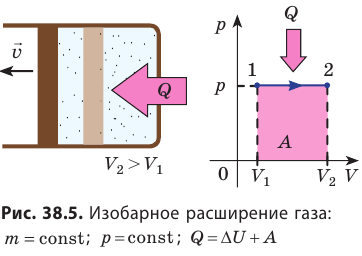
- При изобарном процессе теплота, переданная газу, идет как на увеличение внутренней энергии газа, так и на совершение газом работы: Q=∆U + A.
- При адиабатном процессе газ не получает теплоты (Q = 0) , поэтому увеличение его внутренней энергии происходит за счет совершения над газом работы (адиабатное сжатие): ∆U=A′. Если газ сам совершает работу (адиабатное расширение), его внутренняя энергия уменьшается: A = −∆U.
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Изменение агрегатного состояния вещества
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория
- Работа в термодинамике

 ,
, .
. ,
, .
. .
.
 .
. .
.