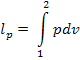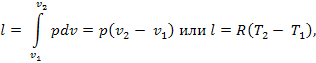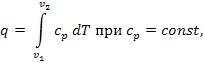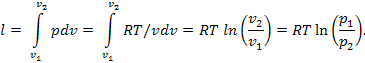Изохорный (изохорический) процесс относится к основным процессам термодинамики и возможен исключительно при постоянном объеме. При этом два других параметра, а именно, давление и температура, изменяются.
В термодинамике давление, объем и температуру называют макроскопическим параметрами. В каждом из трех изопроцессов один из макроскопических параметров остается неизменным.
Изопроцессами, в свою очередь, называют изменение термодинамических систем макроскопических тел.
Как уже отмечалось, в изохорном процессе неизменен объем, в изотермическом постоянной остается температура, в изобарическом – давление.
Наиболее удобно рассматривать термодинамические процессы на примере идеальных газов.
Условие осуществления изохорного процесса в идеальном газе
Необходимым и достаточным условием для протекания изопроцесса в идеальном газе или жидкости является постепенное изменение – увеличение или уменьшение – температуры вещества, в котором происходит процесс. Первоначальный объем вещества должен оставаться неизменным, для чего вещество помещается в замкнутое пространство, т. е. в закрытый сосуд.
Зависимость температуры и давления идеального газа в изохорном процессе
В изохорном процессе давление идеального газа всегда прямо пропорционально его температуре. В реальных газах эта зависимость не выполняется.
На графиках такое физическое явление как изохорный нагрев (охлаждение) отображает изохора. Это линия, связывающая три физических параметра:
- температуру рабочего тела (вещества) – T;
- объем рабочего тела (вещества) – V;
- внутренне давление – Р.
Для идеальных газов изохоры всегда являются прямыми линиями.
Возникновение и развитие теории изохорного процесса
В 1702 году французский физик-механик, член Французской Академии наук, Гийом Амонтон опубликовал свою работу «Парижские мемуары». В ней ученый подробно описал свои наблюдения за поведением фиксированного объема идеального газа в «стабильном воздушном термометре», в котором жидкость, под влиянием энергии газа в резервуаре и атмосферного давления, находилась в равновесии. При постепенном нагревании давление газа увеличивалось пропорционально температуре, и жидкость вытеснялась, заполняя следующий выступающий столб.
Дальнейшее развитие изучение изохорного процесса газа получило благодаря экспериментам английского физика Джона Дальтона. В своих экспериментах ученый определил, что при совпадающих начальных и конечных показателях, а также при постоянном давлении, все газы и пары при изменении температуры сжимаются или расширяются одинаково. Результаты исследований Джон Дальтон опубликовал в 1801 году.
Через некоторое время полученные Дальтоном результаты смог подтвердить и член Французской Академии наук, физик Жозеф Луи Гей-Люссак. Ученый провел свои независимые опыты и также выявил одинаковое распределение различных газов с практически тем же коэффициентом, что и Дальтон. Свои исследования Гей-Люссак объединил с законом Бойля-Мариотта, благодаря чему впоследствии удалось более подробно описать изохорный процесс. А закон пропорциональной зависимости объема газа от температуры в изохорическом процессе получил название закона Гей-Люсака.
Первый закон термодинамики для изохорного процесса
Формула
Формула первого закона термодинамики имеет следующий вид:
[boldsymbol{Q=Delta U+A}]
Где Q – количество теплоты, [boldsymbol{Delta U}] – сумма изменения внутренней энергии, A – работа системы.
Закон подразумевает, что для каких-либо изменений внутри системы необходимо приложить внешние усилия. Таким образом, можно предложить следующую простейшую формулировку первого закона термодинамики: для изменения внутренней энергии некоторой системы требуется внешнее воздействие. Именно этот закон доказывает невозможность изобретения вечного двигателя, над которым так долго бились ведущие ученые разных стран.
Изохорный процесс:
- Процесс, происходящий с газом неизменной массы при постоянном объеме называется изохорным.
- Закон Шарля: при изохорном нагревании газа относительное изменение его давления пропорционально конечной температуре.
[frac{p V}{T}=text { const }\frac{p_{1}}{T_{1}}=frac{p_{2}}{T_{2}}]
Как уже отмечалось, изохорным процессом в термодинамике считается физическое явление, протекающее при постоянном объеме. То есть при изменении температуры некоторого газа, находящегося внутри сосуда, его объем не изменится. Следовательно, работа, совершаемая газом при [V=c o n s t], равна нулю, т.е. A=0.
Формула
Таким образом, первый закон термодинамики для изохорного процесса выражается следующей формулой:
[boldsymbol{Q=Delta U=Uleft(T_{2}right)-Uleft(T_{1}right)}]
Где [boldsymbol{Uleft(T_{1}right)}] – внутренняя энергия идеального газа при начальной температуре, [boldsymbol{Uleft(T_{2}right)}] – внутренняя энергия идеального газа при конечной температуре.
При изохорном нагреве внутренняя энергия газа возрастает за счет поглощения тепла [(Q>0)], а при охлаждении газ отдает тепло и его внутренняя энергия уменьшается [(Q<0)].
Изучения термодинамических изменений подразумевает под собой определение следующих параметров: работы, которая была совершена в данном процессе, изменения внутренней энергии и количества теплоты. Также определяется взаимосвязь некоторых величие, характеризующих состояние газа.
Исследование изохорических процессов проводится по следующему методу:
- устанавливается взаимосвязь показателями рабочего тела на начальный и конечный момент, то есть выводится физическое уравнение;
- определяется работа, совершаемая газом, при изменении объема;
- определяется количество подводимой/отводимой теплоты;
- вычисляется изменение внутренней энергии и энтропии (функции состояния исследуемой системы).
Нет времени решать самому?
Наши эксперты помогут!
Эффект изохорного процесса и его применение
Свойства изохорного процесса, так же как и свойства изобарного и изотермического процессов, широко применяются в современных изобретениях.
Главный эффект изохорного процесса заключается в том, что при неизменном объеме теплоемкость значительно ниже, чем при постоянном давлении. Теплоемкость – величина, показывающая, какое количество теплоты необходимо для нагрева тела на один градус.
В изохорном процессе при изменении температуры система не совершает никакой работы, и, следовательно, вся подведенная теплота расходуется на изменение тепловой энергии: [d U=D q].
Согласно закону Шарля, в идеальном газе при изохорном процессе изменение давления прямо пропорционально изменению температуры. Однако для неидеальных газов закон Шарля не применим. Так как в этом случае некоторая часть теплоты, сообщаемой газу, расходуется на увеличение энергетического потенциала взаимодействия элементарных частиц.
В бензиновом двигателе внутреннего сгорания, в работе которого в максимальном приближении внедрен идеальный цикл Отто, такты 2-3 и 4-1 являются изохорными процессами. 2-3 – изохорный подвод тепла, 4-1 – изохорный отвод тепла. Работа, которая совершается на выходе мотора, равна разности основных работ. То есть разности между работой, совершаемой газом во время рабочего хода (над поршнем во время третьего такта), и работой, затрачиваемой поршнем на сжатие газа во втором такте. Принудительное сжигание смеси, используемое в таких двигателях, позволяет увеличить степень сжатия газа в 7-12 раз.
Изохорные такты также присутствуют в двигателях с циклом Стирлинга. В таких двигателях установлен регенератор, обеспечивающий выполнение изохорного процесса в двух тактах. Проходя через наполнитель в одну сторону, газ передает регенератору тепловую энергию рабочего тела. Двигаясь в обратном направлении, газ снова возвращает энергию рабочей системе. КПД и обратимость идеального цикла Стирлинга равны показателям цикла Карно.
Также изохорный подвод тепла используется в циклах ГТУ – газотурбинных установок.
Теплоемкостью
тела называется
величина, равная количеству теплоты,
которое нужно сообщить телу, чтобы
повысить его температуру на 1
К.
Удельная
теплоемкость вещества
– величина, равная количеству теплоты,
необходимому для нагревания 1
кг
вещества на 1
К:
.
Молярная
теплоемкость вещества –
величина, равная количеству теплоты,
необходимому для нагревания 1
моля
вещества на 1
К:
, откуда
.
Различают
теплоемкости газа при изохорном и
изобарном процессах.
1. Молярная
теплоемкость газа при изохорном процессе
.
Для изохорного
процесса первое начало термодинамики:
.
Следовательно
,
откуда.
2. Молярная
теплоемкость газа при изобарном процессе
.
Для изобарного
процесса первое начало термодинамики:
.
Так как для
изобарного процесса
,
то
,
откуда
.
Уравнение Майера.
Сравнение между
собой Ср
и СV
приводит к уравнению
Майера:
.
Это уравнение
показывает, что Ср
больше, чем СV
на величину универсальной газовой
постоянной R.
Это объясняется тем, что при изобарном
нагревании газа, в отличие от изохорного
нагревания, требуется дополнительное
количество теплоты на совершение работы
расширения газа.
Таким образом,
молярная теплоемкость газа определяется
лишь числом степеней свободы и не зависит
от температуры. Это утверждение
справедливо в довольно широком интервале
температур лишь для одноатомных газов.
Уже у
двухатомных газов число степеней
свободы, проявляющееся в теплоемкости,
зависит от температуры.
Тема 9. Адиабатический процесс.
Адиабатическим
называется процесс, при котором
отсутствует теплообмен между системой
и окружающей средой. При адиабатическом
процессе изменяются все термодинамические
параметры (р,
V,
Т)
в соответствии с уравнением
Пуассона:
,
где
–коэффициент
Пуассона,
равный отношению молярных теплоемкостей
.
Полученное выражение
есть уравнение
адиабатического процесса
в переменных р
и V
.
Для перехода от
переменных р
и V
к переменным V,
Т
или p,
Т
при описании адиабатического процесса
используется уравнение Клапейрона —
Менделеева:
.
В результате
соответствующие уравнения адиабатического
процесса:
в переменных
V
и Т
,
в переменных
р
и
Т .
Работа газа при
адиабатическом процессе.
Из первого начала
термодинамики ()
для адиабатического процесса ()
следует, что.
Если газ адиабатически
расширяется от объема V1
до объема V2
, то его
температура уменьшается от T1
до T2
и работа расширения идеального газа:
.
Используя уравнение
адиабатического процесса в переменных
V
и Т
, то
есть
полученное выражение для работыА
при адиабатическом расширении газа
можно преобразовать к иному виду,
отражающему адиабатическое изменение
объема газа от величины V1
до величины
V2
:

Тема 10. Обратимый и необратимый процессы. Круговой процесс. Тепловая машина и цикл Карно.
Термодинамический
процесс называется обратимым,
если он может проходить как в прямом,
так и в обратном направлении, причем
если такой процесс проходит сначала в
прямом, а затем в обратном направлении,
и система возвращается в исходное
состояние, то в окружающей среде и в
этой системе не происходит никаких
изменений. Всякий процесс, не удовлетворяющий
этим условиям, является необратимым.
Круговым процессом
(или циклом)
называется процесс, при котором система,
пройдя через ряд состояний, возвращается
в исходное состояние.
Тепловая машина
– это устройство для преобразования
теплоты в работу.
Принцип действия
тепловой машины приведен на рис. 5. От
термостата с более высокой температурой
Т1
,
называемого нагревателем,
за цикл отнимается количество теплоты
Q1
,
а термостату с более низкой температурой
Т2
,
называемому холодильником,
за цикл передается количество теплоты
Q2
,
при этом совершается работа: А
= Q1
– Q2.
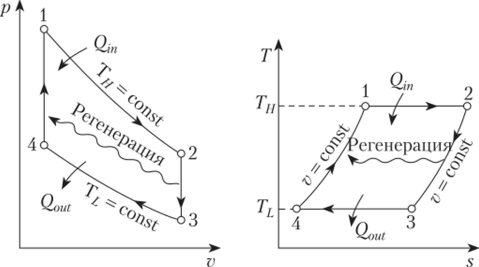
Французский физик
Карно рассмотрел обратимый циклический
процесс, состоящий из чередования двух
изотермических и двух адиабатических
процессов (рис. 6). В цикле Карно в качестве
рабочего тела используется идеальный
газ, находящийся в цилиндре с подвижным
поршнем.
Рис. 5
Рис. 6
График цикла Карно
в координатах р
и V
изображен на рис. 6, где изотермическим
расширению и сжатию соответствуют
кривые 1–2
и 3–4,
а адиабатическим расширению и сжатию
– кривые 2–3
и 4–1.
При изотермическом процессе U=const,
поэтому количество теплоты Q1,
полученное газом от нагревателя, равно
работе расширения А12,
совершаемой газом при переходе из
состояния 1
в состояние
2:
.
При адиабатическом
расширении 2–3
работа А23
совершается за счет изменения внутренней
энергии:
.
Количество
теплоты Q2
,
отданное газом холодильнику при
изотермическом сжатии, равно работе
сжатия А34
:
.
Работа адиабатического
сжатия:
.
Работа, совершаемая
в результате кругового процесса:
,
Термический
коэффициент полезного действия цикла
Карно можно определить по формуле:
или
,
то есть
к.п.д. тепловой
машины, работающей по циклу Карно,
определяется только температурами
нагревателя
Т1
и холодильника
Т2
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Таблицы DPVA.ru — Инженерный Справочник
Адрес этой страницы (вложенность) в справочнике dpva.ru: 
Изобарный (изобарический) и изохорный процессы. Энтропия, работа, количество теплоты.
|
|||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Как правильно рассчитать количество теплоты, необходимое для нагревания газообразного вещества при изохорном процессе
Задача 32.
Определить количество теплоты, необходимое для нагревания 10 г азота от 20 до 25°С, если объем газа не изменяется.
Решение:
М(N2) = 28 г/моль.
Количество теплоты, получаемое системой при изохорном процессе, может быть вычислено по уравнению:
Qp = nCv(T2 — T1) = m/MCv(T2 — T1)
Молярная теплоемкость идеального газа при постоянном объеме для двухатомных молекул:
Cv = 5/2R . Следовательно,
Qp = 10/28 . 5/2 . 8,314 . (25 — 20) = 37,116 Дж.
Ответ: Qp = 37,116 Дж.
Задача 33.
Определите количество теплоты, которое нужно затратить для нагревания 10 г водорода от 30 до 100 °С при постоянном объеме.
Решение:
М(Н2) = 2 г/моль.
Количество теплоты, получаемое системой при изохорном процессе, может быть вычислено по уравнению:
Qp = nCv(T2 — T1) = m/MCv(T2 — T1)
Молярная теплоемкость идеального газа при постоянном объеме для двухатомных молекул:
Cv = 5/2R. Следовательно,
Qp = 10/2 . 5/2 . 8,314 . (100 — 30) = 7274,75 Дж.
Ответ: 7274,75 Дж.
Задача 34.
Определите количество теплоты, которое нужно затратить для нагревания 8,5 г аммиака от 25 до 40 °С при постоянном объеме.
Решение:
М(NH3) = 17 г/моль.
Количество теплоты, получаемое системой при изохорном процессе, может быть вычислено по уравнению:
Qp = nCv(T2 — T1) = m/MCv(T2 — T1)
Молекула аммиака имеет форму треугольной пирамиды. Молярная теплоемкость идеального газа при постоянном объеме без учета энергии колебательного движения, то есть при сравнительно невысоких температурах для нелинейных трехатомных и многоатомных молекул:
Сv = 3R. Следовательно,
Qp = 8,5/17 . 3 . 8,314 . (40 — 25) = 187 Дж.
Ответ: 187 Дж.
Характеристики основных видов термодинамических процессов идеальных газов при изменениях таких параметров, как температура, объем, давление и производимая газом работа.
Виды процессов. Основными процессами в технической термодинамике, весьма важными и в теоретическом, и в прикладном отношениях, являются:
изохорный – протекающий при постоянном объеме;
изобарный – протекающий при постоянном давлении;
изотермический – протекающий при постоянной температуре;
адиабатный – при котором отсутствует теплообмен с окружающей средой;
политропный – удовлетворяющий уравнению pvn = const.
Первые четыре процесса являются частными случаями политропного процесса.
При исследовании этих процессов определяют уравнение процесса в координатах p, v и T, s,связь между параметрами состояния газа, измерение внутренней энергии, величину внешней работы и количество отведенной теплоты.
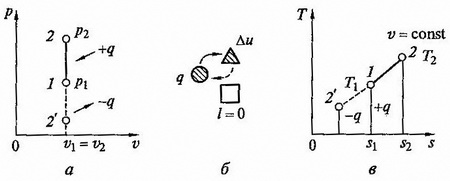
Изохорный процесс. При изохорном процессе выполняется условие dv = 0 или v = const.Из уравнения идеального газа следует, что
p/T = R/v = const
т.е. давление газа прямо пропорционально его абсолютной температуре:
p2/p1 = T2/T1.
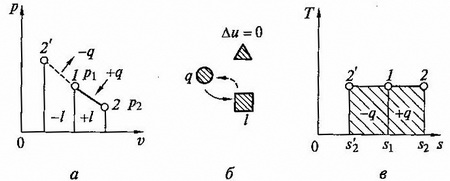
рис. 2.4 Изохорный процесс на p — v и T — s диаграммах (а, в) и схема энергобаланса (б)
Графики процесса на p – v и T – s – диаграммах, а также схема энергобаланса представлены на рисунке. Работа расширения в этом процессе равна нулю, так как dv = 0. Количество теплоты, подведенной к рабочему телу в процессе 1 – 2 при cv = const, определяется из соотношения
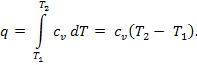
Так как l = 0, то в соответствии с первым законом термодинамики
Δu = q и Δu = cv(T2 – T1) при p = const.
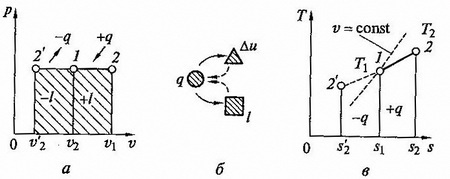
Изобарный процесс. Изобарным называется процесс, происходящий при постоянном давлении. Из уравнения состояния идеального газа при p = const находим
v/T = R/p = const
или
v2/v1 = T2/T1
т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака). Графики процесса на p — v и T – s – диаграммах, а ттакже схема знергобалланса изображены на рис. 2.5.
рис.2.5. Изобарный процесс на p — v и T — s — диаграммах (а,в) и схема энергобаланса (б)
Из выражения
следует, что
так как pv1 = RT1 и pv2 = RT2.
Количество теплоты сообщаемое газу при нагревании (или отдаваемое им при охлаждении), находим из уравнения
Или
q = cp(T2 = T1).
Изотермический процесс. При изотермическом процессе температура постоянная, следовательно, pv = RT = const или p2/p1 = v1/v2, т.е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – падает (закон Бойля – Мариотта).
Графиком изотермического процесса в координатах p, v (рис.2.6,а) является равнобокая гипербола, для которой координатные оси служат асимптомами.
Работа процесса
Так как энергия не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (Δu = 0) и вся подводимая к газу теплота полностью превращается в работу расширения q = l.
рис. 2.6. Изотермический процесс на p — v и T — s — диаграммах (а,в) и схема энергобаланса (б)
При изотермическом сжатии от газа отводится теплота в количестве, равным затраченной на сжатие работе. Схема энергобаланса и и график изобарного процесса на T – s – диаграмме приведены на рис. 2.6, б,в.
Адиабатный процесс. Адиабатным называется процесс изменения состояния газа, который происходит без теплообмена с окружающей средой. Такой процесс соответствует случаю, когда сосуд или оболочка, вмещающие в себе газ, изолированы в тепловом отношении от окружающей среды. Для данного случая уравнение первого закона термодинамики, поскольку в нем по условию dq = 0, принимает вид
du + pdv = 0
или
Δu + l = 0
Откуда
Δu = —l.
Это означает, что в адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа и что при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.
Обозначим теплоемкость в адиабатном процессе через сад и выразим условие du= 0 следующим образом:
du= садdT = 0
Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю, т.е. сад = 0. Известно, что
Cp/Cv = k
Уравнение кривой адиабатного процесса (адиабаты) в координатах p, v (рис.2.7 а) имеет вид
pvk = const,
где k – называется показателем адиабаты (эту величину называют также коэффициентом Пуассона).
Из выражений l = -Δu = cv(T1 – T2) и i1 – i2 = cp(T1 – T2) следует, что
i1 – i2 = lтехн,
т.е. техническая работа адиабатного процесса расширения равна разности энтальпий начала и конца процесса.
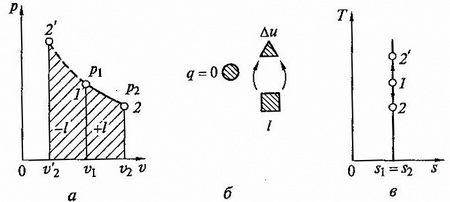
Рис.2.7 Адиабптный процесс на p — v и T — s lиаграммах (а, в) и схема энергобаланса (б)
Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. На T – s диаграмме (рис.2.7, в) он изображается вертикальной прямой.
Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате которого всегда выделяется теплота, которая тут же сообщается самому рабочему телу. В этом случае ds > 0, процесс называется реальным адиабатным процессом.
Политропный процесс и его обобщающее значение. Политропным называется процесс, который происходит при постоянной теплоемкости и описывается уравнением
pvn = const.
Показатель политропы n может принимать любое численное значение в пределах от -∞ до +∞, но для данного процесса он является величиной постоянной.
Из уравнения (2.13) и уравнения Клайперона нетрудно получить выражения, устанавливающие связь между p v и T в любых двух точках на политропе:
Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

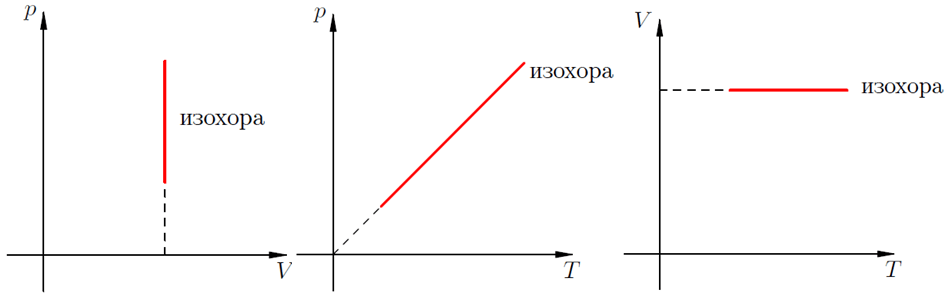

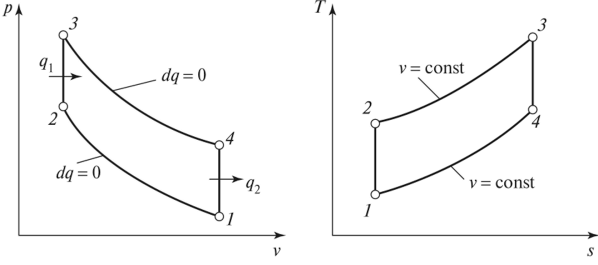


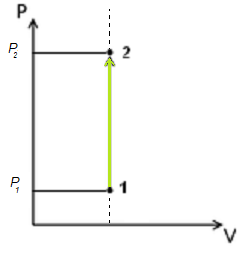 Изохорный процесс происходит при постоянном объёме, при этом давление идеального газа прямо пропорционально его температуре
Изохорный процесс происходит при постоянном объёме, при этом давление идеального газа прямо пропорционально его температуре