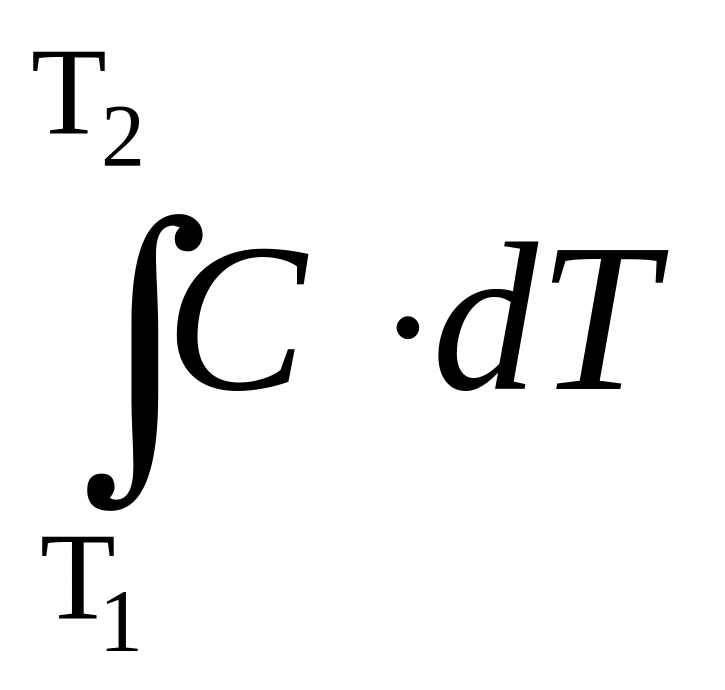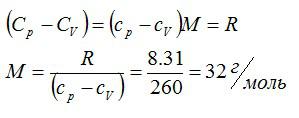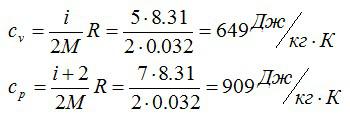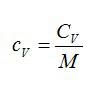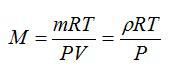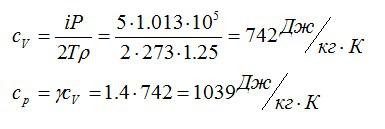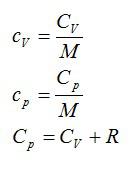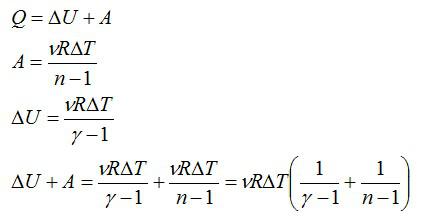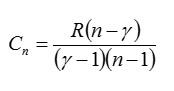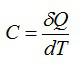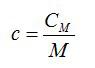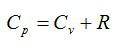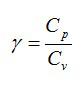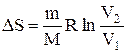Как найти теплоемкость газа с показателем адиабаты - AvtoShod.ru

Теплоёмкость
характеризует одно из свойств, какого–либо
рабочего тела и, как известно, представляет
собой количество подводимой или отводимой
теплоты соответственно при нагреве или
охлаждении рабочего тела на 1 Кельвин.
При данных исходных параметрах состояния
(Т,
р
или Т)
теплоемкость 1 кг рабочего
тела определяется в бесконечно малом
интервале температур dT

C
= lim

, Дж/(кг·К). (2.20)

Эта
теплоёмкость, в основном применяемая
при расчётах, является удельной
массовой, которую для краткости будем
называть просто теплоёмкостью
(заметим, что существуют и другие удельные
теплоёмкости – единицы объёма
или одного моля, но они используются
редко).

Теплоёмкость
зависит от трех основных факторов.
Прежде всего, от природы
вещества. Газ, жидкость, твёрдое тело
естественно имеют своё определённое и
конкретное значение теплоёмкости,
характерное только данному веществу.
Например, теплоёмкость
воды в 4 раза больше, чем теплоёмкость
воздуха, теплоёмкость водорода в 14,5 раз
больше,
чем теплоёмкость воздуха и в 3,5 раза
больше, чем теплоёмкость воды и т.д.

Второй
фактор – это исходные параметры
состояния, при которых теплоёмкость
определяется. Для газов (рабочих тел
ГТД и ДВС) теплоёмкость зависит практически
только от температуры С
= f
(T).
Заметим, что у идеальных газов теплоёмкость
от температуры не зависит. Но у рабочих
тел
ГТД и ДВС, хотя и близких к идеальным
газам, влияние температуры все, же
заметно. Так, в характерных для ГТД
диапазонах изменения температуры
воздуха
от ~ 250 до 800 К и продуктов сгорания от
700 до 1 600 К теплоёмкости
возрастают
соответственно примерно на 10 % и на 15 %.
Условие С
= const
принимают
лишь при весьма приближённых расчётах.
Поэтому будет учитываться
зависимость от температуры и теплоёмкости
и также других, связанных с
ней и рассматриваемых ниже параметров.
Но влияние давления и удельного объёма
при не очень высоких давлениях до ~
(70·10⁵…100·10⁵
Па) ничтожно мало.

С
учётом зависимости “С”
от Т
конечное количество теплоты Q
подводимой к единице массы рабочего
тела при его нагреве (или отводимой при
охлаждении)
в конечном интервале температур
Т,
определяется из уравнения (2.20)

Q_1-2=

= C_c_р·(T₂
– T₁),
(2.21)

где индексами 1 и
2 обозначены начальное и конечное
состояние рабочего тела;
С_ср
–
среднее значение теплоемкости в интервале
температур Т₁…Т₂.

С
достаточной
точностью (хотя и приближённо) С_ср
может
быть определена как среднее
арифметическое теплоёмкостей (иногда
их называют истинными в отличие
от средней) при температурах Т₁
и Т₂.

C_cp
= 0,5·[C
(T₁)
+ C
(T₂)]
(2.22)

Значение
С
= С
(Т)
приводятся
в справочниках в виде таблиц или графиков.

Третий
фактор, влияющий на теплоёмкость,
относится к сжимаемым рабочим телам –
газам. Рассмотрим, в чем проявляется
влияние этого фактора.

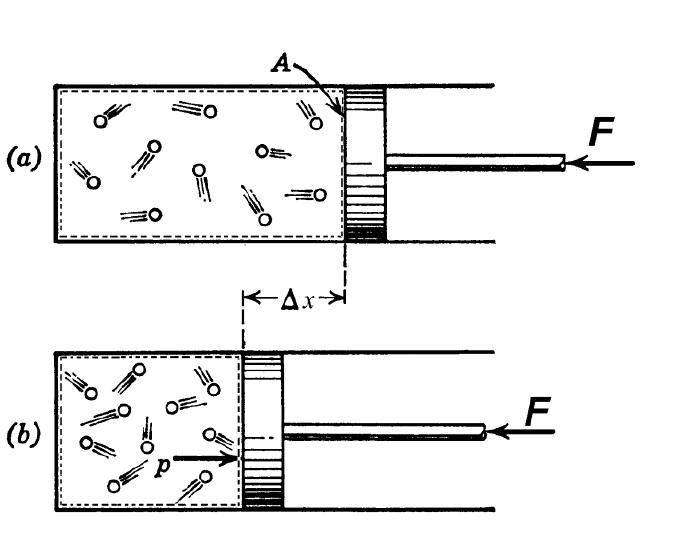
П
редположим,
что имеется жёсткая закрытая
термодинамическая система неизменного
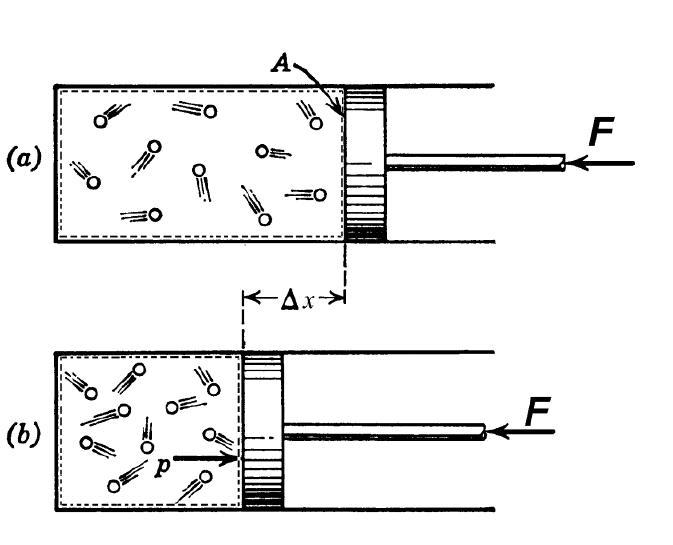
объёма, приведённая на рис. 2.6., а в виде
цилиндра, закрытого неподвижным поршнем.
В цилиндре содержится 1 кг рабочего
тела. Поэтому не изменяется так же
удельный объём , но давление
изменяется, например, при подводе теплоты
возрастает.

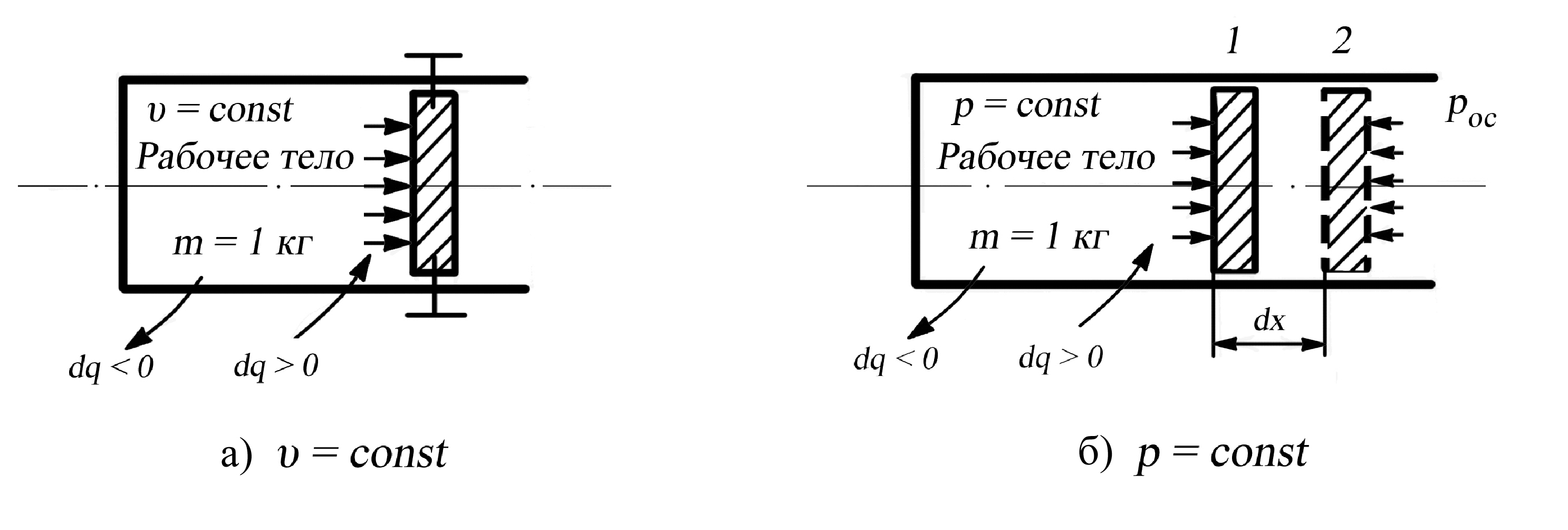
Рис. 2.6. К определению
теплоёмкости рабочего тела

при
υ
= const (a), p
= const (б)

Таким
образом, осуществляется только один
вид энергообмена – теплообмен.
Истинная теплоёмкость при постоянном
объёме определяется уравнением (2.20), в
котором для данного случая соответствующие
величины снабжены индексом υ

С
_υ
=

(2.23)

Сохраняются
и уравнения (2.21) и (2.22) также с индексами
υ
т.е. q_υ_1-2
и
C_υ_ср.

Теперь,
пусть система на рис. 2.4,б оставаясь
закрытой, станет нежёсткой – поршень
в цилиндре может свободно перемещаться
в обе стороны. Тогда, например, при
подводе теплоты (dq
> 0) и нагреве рабочего тела давление
остается постоянным,
но газ расширяется, и его удельный объём
возрастет на величину dυ
=
F·dx,
где
F
– площадь поршня. Осуществляются оба
вида энергообмена – теплообмен
и работа изменения объёма, определяемая
уравнением (2.14) при бесконечно
малом перемещении поршня и (2.15)
при
конечном перемещении, причем
при р
= const
L_υ
=
р·(υ₂
– υ₁).

В
результате подводимая к термодинамической
системе теплота затрачивается и на
нагрев газа и на работу термодинамической
системы над окружающей
средой (при отводе теплоты все описанные
явления происходят в обратном
направлении также при р
= const).
Обозначим бесконечно малую теплоту,
отводимую
термодинамической системе в процессе
р
= const
с индексом р,
dq_р.По
аналогии с уравнением (2.23)
истинная
теплоёмкость при постоянном давлении
равна

С_р
=

.
(2.24)

Поскольку
dq_p
> dq_υ
из–за
наличия работ изменения объёма dL_υ
,
то
С_р
> C_υ.
В
уравнениях (2.21) и (2.22) соответствующие
величины также снабжаются индексом р
т.е. q_p_1-2
и C_p_cp.

При
теплообмене параметры состояния газа
р
и
υ
по-разному изменяются в
жёсткой и нежёсткой термодинамических
системах, соответственно υ
= const,
р
= var
и р
= const,
υ
= var.
Но на количество поглощаемой непосредственно
только
газом теплоты (или отводимой от газа)
это не влияет, поскольку, как отмечалось
ранее, теплоёмкость газов практически
не зависит от параметров состояния
р
и υ,
а только от температуры Т.
Поэтому в жёсткой (υ
= const)
и нежёсткой
(р
= const)
термодинамических системах при одинаковых
изменениях,
температуры в данном случае бесконечно
малых dT
газ поглощает (или отдает) одинаковое
количество теплоты dq_υ.
С учётом уравнения (2.14) количество
теплоты, подводимой к нежёсткой
термодинамической системе (а не только)
определяется суммой

dq_p
= dq_υ
+ p·dυ.

(2.25)

Продифференцируем
уравнение состояния (1.11)

d(pυ)
= υ·dp
+ p·dυ
= R·dT
.
(2.26)

В данном частном
случае для системы р
= const
это уравнение упрощается, т.к. dp
= 0, поэтому имеем:

p·dυ
= R·dT
. (2.26′)

Используя полученное
уравнение (2.26′), а так же уравнения
(2.23) и (2.24) из уравнения (2.25) получим

C_p
= C_υ
+ R
или С_р
– C_υ
= R.
(2.27)

Это уравнение,
связывающее С_р
, C_υи R
называются уравнением Майера. Приведем
порядок величин, входящих в это уравнение,
например, для воздуха при стандартной
температуре 288 К (15 °С): С_р
= 1005 Дж/(кг·К), C_υ
= 718
Дж/(кг·К), R
= 287 Дж/(кг·К). Теплоёмкости С_р
и C_υ
зависятот
температуры, а их разность численно
равная значению газовой постоянной R
от температуры не зависит. В этом и
состоит физический
смысл газовой постоянной R,
которая численно равна величине работы,
совершенной газом массой в 1 кг при
изменении температуры в 1 К при постоянном
давлении.

В термодинамике
и при термодинамических расчетах ГТД
и ДВС широко используется отношение
теплоёмкостей

^,
(2.28)

которое называется
показанием адиабаты. Сущность этого
термина выяснится из дальнейшего
изложения, хотя, казалось бы, что С_р
и C_υникакого
отношения к адиабатной системе не имеют.

Показатель адиабаты,
как и теплоёмкости, зависит от вида газа
и от температуры. Поскольку с ростом
температуры обе теплоёмкости С_р
и C_υ возрастают,
то зависимость “k”
от температуры получается довольно
слабой, причём убывающей по Т.
Например, для воздуха при Т
= 288 К показатель адиабаты
k
= 1,401, а при Т
= 800 К (527 °С) – k
= 1,353; для продуктов сгорания при Т
= 700 К (427°С)
– k
= 1,350, а при Т
= 1 500 К (1 227°С) – k
= 1,295. В приближённых расчётах обычно
принимают: для воздуха k
= 1,4, для продуктов сгорания k
= 1,33.

Из уравнений (2.27)
и (2.28) получаются следующие соотношения,
которые часто используются при расчётах.

С_р
=
·R
(2.29)

С_υ
=
·R
(2.30)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Решение задач дело полезное, но не всегда интересное. Чтобы вы справлялись с решением задач по теме «Теплоемкость идеального газа» быстрее, приведем здесь несколько примеров и вопросов с объяснениями.

Подписывайтесь на наш телеграм-канал, чтобы получать полезную и интересную рассылку.

Задачи по теме «Теплоемкость идеального газа» с решениями

Повторение и практика – залог успеха в любом деле. И решение задач не исключение. Поэтому не забываем держать под рукой памятку по задачам и полезные формулы

Задача №1. Определить удельную теплоемкость идеального газа

Условие

Определить молярную массу M двухатомного газа и его удельные теплоемкости, если известно, что разность cр — cv удельных теплоемкостей этого газа равна 260 Дж/(кг*К)

Решение

По определению:

Значит, газ из задачи – кислород. Если кто не понял, как это определяется, учитесь пользоваться таблицей Менделеева.

Считаем удельные теплоемкости:

Ответ: 32 г/моль; 649 Дж/кг*К; 909 Дж/кг*К.

Задача №2. Удельная теплоемкость

Условие

Плотность некоторого газа при нормальных условиях ρ = 1,25 кг/м3. Отношение удельных теплоемкостей γ = 1,4. Определить удельные теплоемкости cv и сp этого газа.

Решение

Исходя из отношения удельных теплоемкостей, можно сделать вывод, что газ – двухатомный, i=5. При постоянном объеме удельная теплоемкость равна:

Молярную массу можно найти из уравнения Клапейрона-Менделеева:

Отсюда:

Ответ: 742 Дж/кг*К; 1039 Дж/кг*К.

Задача №3. Молярная теплоемкость

Условие

Вычислить молярные теплоемкости газа, зная, что его молярная масса М = 4∙10 3 кг/моль и отношение удельных теплоемкостей ср/сv = 1,67.

Решение

Удельные теплоемкости равны:

Можно найти:

Ответ: 12,4 Дж/моль*К; 20,71 Дж/моль*К

Задача №4. Теплоемкость при изопроцессах

Условие

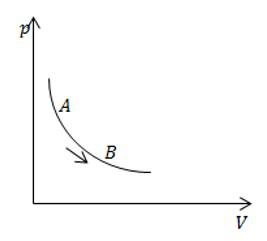
На рисунке изображен изотермический процесс с газом постоянной массы. Сравните теплоемкость в процессе АВ с теплоемкостью этой же массы газа в изохорном процессе.

Решение

Теплоемкость при изохорном процессе является постоянной величиной. При изотермическом процесса она равна бесконечности. Значит, теплоемкость в процессе АВ больше.

Ответ: Теплоемкость в процессе АВ больше.

Задача №5. Теплоемкость при политропическом процессе

Условие

Найдите молярную теплоемкость идеального газа при политропическом процессе pVn = const, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?

Решение

Запишем первое начало термодинамики, выражения для работы и изменения внутренней энергии в политропическом процессе соответственно:

Если количество вещества и изменение температуры принять равными единице, это выражение будет равно молярной теплоемкости (по определению теплоемкости):

Ответ: см. выражение выше.

Вопросы по теме «Теплоемкость идеального газа»

Вопрос 1. Что такое теплоемкость идеального газа?

Ответ. Когда газу сообщается определенное количество теплоты, меняется его температура.

Отношение количества теплоты, сообщенного газу, к изменению его температуры, называется теплоемкостью идеального газа.

Вопрос 2. Что такое молярная и удельная теплоемкость идеального газа?

Ответ. Молярная и удельная теплоемкости активно используются в термодинамике. Молярная теплоемкость – это теплоемкость одного моля вещества.

Удельная теплоемкость – теплоемкость единичной массы вещества.

Вопрос 3. Как определяется теплоемкость газа при изопроцессах?

Ответ.

При изотермическом процессе T=const. Теплоемкость равна плюс/минус бесконечности.
При адиабатном процессе нет теплообмена с окружающей средой, теплоемкость равна нулю.
При изохорном процессе газ не совершает работы, а теплоемкость равна:

Здесь i – количество степеней свободы молекул газа. Для одноатомных газов i=3, для двухатомных i=5.

При изобарном процессе теплоемкость определяется соотношением Мейера:

Вопрос 4. Как еще связаны теплоемкости при постоянном давлении и постоянном объеме?

Ответ. Отношение теплоемкостей при постоянном давлении и постоянном объеме обозначается греческой буквой «гамма» и называется показателем адиабаты.

Вопрос 5. Как называются процессы, в которых теплоемкость газа остается неизменной?

Ответ. Такие процессы называются политропными. Адиабатный процесс – частный случай политропного процесса.

Теплоемкость реального газа не равна теплоемкости идеального газа и может сильно отличаться.

Нужна помощь в решении задач и выполнении других заданий? Специальный студенческий сервис готов оказать ее!

Источник

Роберт Майер является одним из основоположников первого начала термодинамики и механической теории теплоты. В 1842 году он вычислил механический эквивалент теплоты, показывающий соотношение между теплотой и работой или механической энергией.

Уравнение Майера — какие процессы описывает

Уравнение Майера описывает соотношение теплоемкостей 1 моля идеального газа при его постоянном давлении (C_p) и неизменном объеме (C_V:)

(C_p-C_v=R,) где

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(C_p)— постоянное давление газа;

(C_V) — постоянный объем газа;

R — универсальная газовая постоянная, равная:

R = 8,314 (Дж/(моль*Л).)

Идеальный газ состоит из молекул, взаимодействие между которыми пренебрежимо мало.

Моль — величина, описывающая количество вещества, которое содержит в себе количество частиц, равное постоянной Авогадро (Na):

(Na = 6,022cdot10^{23};моль^{-1})

Понятие теплоемкости

Теплоемкость С — количество тепла, которое нужно передать телу, чтобы повысить его температуру на 1 градус:

(С=d’Q/dT), где

С — удельная теплоемкость;

d’Q — теплота;

dT — температура, [К].

Величина С зависит от процесса, и без него данная формула не имеет смысла. То есть она является функцией.

Теплоемкость называется удельной, когда в системе используется тело с массой в 1 кг.

В зависимости от количественной единицы вещества теплоемкость делится на три вида:

Мольная — (C_mu), [Дж/кмоль·К].
Массовая — С, [Дж/кг·К].
Объемная — С´, [Дж/м3·К].

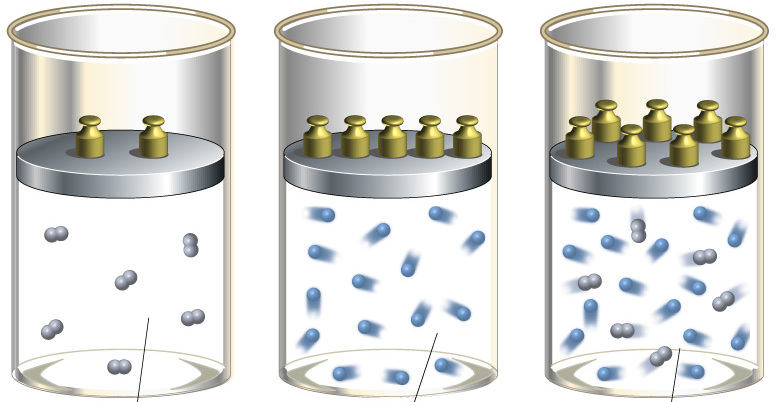
Величина С зависит от температуры линейно и нелинейно.

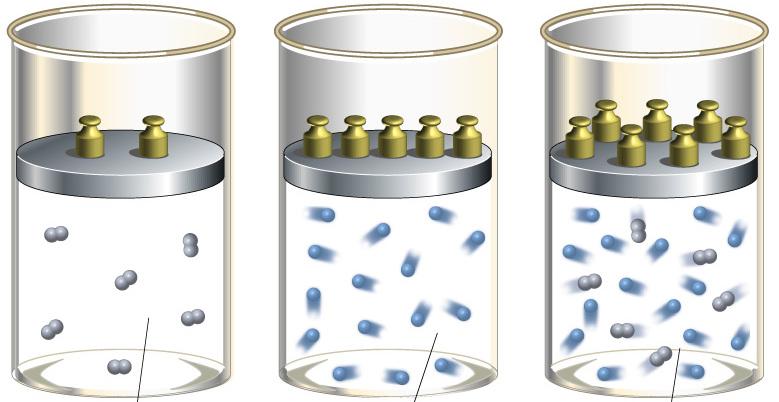
В простейших инженерных расчетах может приниматься либо постоянная зависимость теплоемкости от температуры, либо принимают, что теплоемкость не меняется с ее изменением. Тогда ее не учитывают, но расчет получается приблизительным.

В варианте с линейной зависимостью с возрастанием температуры возрастает и величина С.

С возрастанием температуры необходимо больше подводить теплоты к газу, чтобы повысить температуру и теплоемкость на равный интервал. Теплота (q_2) будет больше, чем теплота (q_1.)

В данном интервале температур (t_1-t_2, t_3-t_4,t_n-t_{n+1}) рассчитывают среднюю теплоемкость:

(overline C=frac{q_1}{t_2-t_1}=frac{q_2}{t_4-t_3}), где

(overline C) — средняя теплоемкость, рассчитанная для интервала температур.

Формула для расчета линейной зависимости теплоемкости от температуры:

C=a+b·t,

где a, b — постоянные коэффициенты для конкретного газа,

t — данная температура для газа. Разным температурам соответствуют свои коэффициенты.

Для высчитывания средней теплоемкости при изменении температур от (t_1) до (t_2) (например, от 100⁰С до 160⁰С), пользуются соотношением:

( overline C=a+bfrac{t_1+t_2}2.)

Постоянные коэффициенты для конкретных газов в известных условиях приведены в справочных таблицах.

При нелинейной зависимости теплоемкость и температура могут возрастать различными интервалами. Для расчета нелинейной зависимости С от t применяют формулу:

( overline{C_{t_1}^{t_2}}=frac{C_0^{t_2}cdot t_2-C_0^{t_1}cdot t_1}{t_2-t_1})

( C_0) — начальные теплоемкости при некой температуре. Их можно найти в справочных таблицах «Средняя объемная теплоемкость газов при постоянном давлении».

Формула Майера для теплоемкостей, вывод из первого закона термодинамики

Формула Майера для теплоемкостей

Теплоемкости при постоянном давлении и при постоянном объеме обозначают следующим образом:

(C_p) и (C_v) — массовые;
(C’_p) и (C’_v) — объемные;
(C_{pmu}) и (C_{vmu}) — мольные.

Уравнение Майера для массовых теплоемкостей имеет вид:

( C_p-C_v=R.)

Формулы для расчета этих теплоемкостей следующие:

(C_v=frac R{k-1}; C_p=frac{Rcdot k}{k-1}.)

Для выведения газовой постоянной (R_mu) и формулы Майера для мольных теплоемкостей необходимо все части уравнения умножить на молярную массу:

( mucdot C_p-mucdot C_v=R_mu.)

Для расчета теплоемкости не отдельных газов, а их смеси, применяют формулу для определения массовой теплоемкости газовой смеси, которая рассчитывается как сумма произведений массовых долей компонента, умноженная на массовую теплоемкость данного компонента:

(C_{см}=sum_{i=1}^nleft(g_icdot C_iright))

Мольная теплоемкость смеси рассчитывается как сумма произведений объемных долей, умноженная на (C_mu) этого компонента:

(C_{mucdot см}=sum_{i=1}^nleft(r_icdot C_{mucdot i}right).)

Понятие термодинамики, вывод формулы Майера из первого закона термодинамики

Термодинамика — общая теория теплоты. Она является постулатной наукой, то есть не рассматривает строение системы или вещества и физическую природу теплоты, но использует понятия и физические величины, относящиеся к системе в целом.

Термодинамика изучает макросистемы, состояние которых характеризуют термодинамические параметры: давление, объем, температура и т.д.

Формулировка первого закона термодинамики: при переходе из начального состояния 1 в конечное состояние 2 внутренняя энергия макросистемы складывается из работы, совершенной над системой внешними макроскопическими силами, и из тепла, переданного системе:

( U_2-U_1=Q+A’.)

Как правило, для расчетов используют ту работу А, которую совершила сама система над внешними телами, а не работу, проведенную по отношению к системе.

Вывод уравнения первого начала термодинамики производится с учетом того, что (A’=-A:)

(Q=triangle U+A), где

( triangle U=U_2-U_1.)

Первое начало термодинамики выражается этим правилом: количество теплоты Q, подведенное к макросистеме, идет на совершение системой работы A и изменение ее внутренней энергии (triangle U.)

Для вывода уравнения Майера из первого закона термодинамики учитывают уравнения:

(left(frac{partial U}{partial V_t}right)=0; {left(frac{partial V}{partial t}right)}_p=frac RP.)

Тогда уравнение Майера и количественное выражение первого закона термодинамики будет следующим:

(delta Q=C_vdt+PdV.)

Данное уравнение справедливо для газа, у которого (C_p) и (C_v = const)., и для газа, у которого (C_p=C_p(t)) и (C_p=C_v(t).)

Как записывается соотношение для молярных и массовых теплоемкостей

Опираясь на формулу теплоемкости (C=frac{delta Q}{dT}) и учитывая, что количество вещества Z (количество молей), содержащееся в теле, влияет на его теплоемкость, запишем соотношение для молярных теплоемкостей:

(C_m=frac CZ.)

Задачи на определение теплоемкостей

При расчете удельных теплоемкостей необходимо учитывать отличия между реальными и идеальными газами:

На теплоемкость идеальных газов влияет не только температура, но и количество в них атомов, и характер процесса. То есть она будет разной, в зависимости от того, сколько атомов имеет тот или иной идеальный газ.
На теплоемкость реальных газов влияют не только температура, давление и характер процесса, но и их природные свойства.

Теплоемкость принимают в большей степени для идеальных газов, поскольку в основном расчет и ориентация идут на них.

Примеры задач и их решение

Задача 1

Условия:

Один моль идеального газа нагрели. Давление стало пропорционально его объему:

(p=alpha V,)

где α — постоянная.

Найти теплоемкость газа.

Решение:

Помня о том, что газ при разных способах нагревания совершает разную работу, делаем вывод, что теплоемкость будет различной и при разных температурах.

Используя первое начало термодинамики для теплоемкости идеального газа:

( triangle Q=triangle U+triangle A), (1)

получим:

(C=C_v+frac{triangle A}{triangle T}.) (2)

Чтобы найти теплоемкость С необходимо определить работу ∆А, которую совершает газ в рассматриваемом процессе при нагревании его на ∆T.

Совершаемая газом работа ∆А при расширении в условиях постоянного давления вычисляется по формуле:

(triangle A=ptriangle V.) (3)

В условиях, когда давление не остается постоянным, для вычисления работы ∆A необходимо ∆V выбрать настолько малым, чтобы изменением давления газа при расширении можно было бы им пренебречь.

Для этого применим уравнение состояния:

(pV=RT.) (4)

Пусть при изменении температуры газа на ∆T его объем изменился на ∆V, а давление — на ∆p.

Уравнение (left(p+triangle pright)(V+triangle V)=R(T+triangle T)) (5) связывает эти изменения.

Вычитаем выражения (4) и (5) и пренебрегаем (triangle ptriangle V), получаем:

( ptriangle V=Vtriangle p=Rtriangle T) (6).

Возьмем во внимание формулу (1) и учтем, что в данном процессе давление газа пропорционально его объему. Получим:

( Vtriangle p=alpha Vtriangle V=ptriangle V) (7).

Подставляем V∆p из выражения (6) и (7), найдем

( triangle A=ptriangle V=frac12Rtriangle T).

С помощью формулы (2) найдем теплоемкость газа в этом процессе:

( C=C_v+frac R2.)

Поскольку (C_v) и (C_p) связаны, представим теплоемкость и получим ответ:

(C=frac12left(C_v+C_pright).)

Задача 2

Условия:

Имеется цилиндр, у которого стенки AC, BD, крышка CD и поршень MN не проводят тепло. Дно AB проводит тепло. Поршень движется в цилиндре без трения. Сверху и снизу поршня присутствует по одному молю идеального газа с показателем адиабаты γ. Молярная теплоемкость газа Cv постоянна по объему. При квазистатическом изменении температуры первого газа поршень начинает перемещение.

Выразите теплоемкость первого газа (C_1) при таком процессе через объемы газов (V_1) и (V_2). Чему равна теплоемкость второго газа (C_2?)

Решение:

Элементарное количество тепла, получаемое первым газом:

(delta Q=C_vdT_1+P_1dV_1=C_vdT_1+RT_1dV_1/V_1.)

А вторым газом — (delta Q_2=0.)

Поэтому (C_2=0) и (C_vdT_2+RT_2dV_2/V_2=0.)

Из равенства давлений (P_1) и (P_2) следует:

(V_1/V_2=T_1/T_2,)

откуда (dV_1/V_1+dV_2/V_1=dT_1/T_1-dT_2/T_2.)

Так как объем системы не изменяется, то

(dV_1+dV_2=0.)

Исключая (dV_2) и (dT_2), получим:(left(frac1{v_1}+frac1{v_2}+frac R{C_v}frac1{v_2}right)dV_1=frac{dT_1}{T_1}. ) Используя также уравнение Майера (C_p-C_v=R), найдем

(delta Q_1=left(C_v+Rfrac{V_2}{V_2+gamma V_1}right)dT_1.)

Следовательно:

(C_1=C_v+frac{V_2}{V_2+gamma V_1}R=frac{V_1+V_2}{V_2+gamma V_1}gamma Cv..)

При (V_1=V_2)

(C_1=2gamma C_v/left(gamma+1right).)

Задача 3

Условия:

Определите удельную теплоемкость кислорода при постоянном объеме. Газ нагрет до очень высокой температуры, приблизительно до нескольких килоэлектрон-вольт.

Решение:

(C_v=frac{27}{32}R=1,68;кал/(гcdot К)approx7,0;Дж/(гcdot К).)

Задача 4

Условие:

Посчитайте по классической теории удельной теплоемкости при постоянном давлении газа следующего молярного состава:

He — 20 %, H2 — 30 %, CH4 — 50 %.

Молярный состав — количество молей данного газа по отношению к общему числу молей газовой смеси.

Решение:

( C_p=frac{71}{188}Rapprox0,75;кал/(гcdot К)approx3,14;Дж/(гcdot К))

Задача 5

Условие:

Найдите полярную теплоемкость водорода (C_v). Коэффициент диссоциации α = 0,25. Молярная теплоемкость атомарного водорода (C_{v1} = 2,94) (кал/(моль·⁰С)). (C_{v2})молекулярного водорода (= 4,9) (кал/(моль·⁰С).)

Решение:

( C_v=(2C_{v1}-C_{v2})alpha+C_{v2}=5,15;кал/(мольcdot К)approx21,5;Дж/(мольcdot К).)

Источник

Показатели адиабаты: определение и процесс

При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.

Адиабатический процесс

Вам будет интересно: Задачи социологии: предметы, основные методы, цели и развитие

Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:

теплопроводность между внешней средой и системой по той или иной причине является низкой;
скорость процесса велика, поэтому обмен теплом не успевает происходить.

В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.

Уравнение Пуассона для адиабаты идеального газа

Вам будет интересно: Что такое плиз? Молодежный сленг

Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.

Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:

Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.

В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:

Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.

Что такое показатель адиабаты?

Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом CP изобарную теплоемкость, а символом CV — изохорную. Тогда для γ справедливо равенство:

Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.

Теплоемкости CP и CV

Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:

CP*dT = CV*dT + P*dV.

Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:

Откуда можно определить значение изохорной теплоемкости CV:

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

Из последних двух равенств следует значение показателя адиабаты:

Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.

Зависимость γ от числа степеней свободы

Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:

Тогда значение γ будет равно:

Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.

Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:

Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

Где γi — это величина γ для i-го компонента.

Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.

Чему равен показатель адиабаты. Уравнение пуассона

Описывает адиабатный процесс, протекающий в . Адиабатным называют такой процесс, при котором отсутствует теплообмен между рассматриваемой системой и окружающей средой: .

Уравнение Пуассона имеет вид:

Здесь – объем, занимаемый газом, – его , а величина называется показателем адиабаты.

Показатель адиабаты в уравнении Пуассона

В практических расчётах удобно помнить, что для идеального газа показатель адиабаты равен , для двухатомного – , а для трёхатомного – .

Как же быть с реальными газами, когда важную роль начинают играть силы взаимодействия между молекулами? В этом случае показатель адиабаты для каждого исследуемого газа можно получить экспериментально. Один из таких методов был предложен в 1819 году Клеманом и Дезормом. Мы наполняем баллон холодным газом, пока давление в нём не достигнет . Затем открываем кран, газ начинает адиабатически расширяться, а давление в баллоне падает до атмосферного . После того, как газ изохорно прогреется до температуры окружающей среды, давление в баллоне повысится до . Тогда показатель адиабаты можно рассчитать за формулой:

Показатель адиабаты всегда больше 1, поэтому при адиабатическом сжатии газа – как идеального, так и реального – до меньшего объема температура газа всегда возрастает, а при расширении газ охлаждается. Это свойство адиабатического процесса, называемое пневматическим огнивом, применяется в дизельных двигателях, где горючая смесь сжимается в цилиндре и воспламеняется от высокой температуры. Вспомним первый закон термодинамики: , где — , а А – выполняемая над ней работа. Поскольку то работа, осуществляемая газом, идёт только на изменение его внутренней энергии – а значит, температуры. Из уравнения Пуассона можно получить формулу для расчёта работы газа в адиабатном процессе:

Здесь n – количество газа в молях, R – универсальная газовая постоянная, Т – абсолютная температура газа.

Уравнение Пуассона для адиабатического процесса применяется не только при расчётах двигателей внутреннего сгорания, но и в проектировании холодильных машин.

Стоит помнить, что уравнение Пуассона точно описывает только равновесный адиабатный процесс, состоящий из непрерывно сменяющих друг друга состояний равновесия. Если же мы в реальности откроем кран в баллоне, чтобы газ адиабатически расширился, возникнет нестационарный переходной процесс с завихрениями газа, которые затухнут из-за макроскопического трения.

Примеры решения задач

Задание

Одноатомный идеальный газ адиабатически сжали так, что его объем увеличился в 2 раза. Как изменится давление газа?

Решение

Показатель адиабаты для одноатомного газа равен . Однако его можно рассчитать и по формуле:

где R – универсальная газовая постоянная, а і – степень свободы молекулы газа. Для одноатомного газа степень свободы равен 3: это значит, что центр молекулы может совершать поступательные движения по трём координатным осям.

Поэтому показатель адиабаты:

Представим состояния газа в начале и конце адиабатного процесса через уравнение Пуассона:

Ответ

Давление уменьшится в 3,175 раза.

Задание	100 молей двухатомного идеального газа адиабатически сжали при температуре 300 К. При этом давление газа увеличилось в 3 раза. Как изменилась работа газа?
Решение	Степень свободы двухатомной молекулы , так как молекула может двигаться поступательно по трём координатным осям, и вращаться вокруг двух осей.

Министерство образования РФ

Камский государственный политехнический институт

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ

Методические указания к лабораторной

работе по дисциплине “Теплотехника” для очной формы обучения.

г. Набережные Челны

УДК 621.1:536 (076)

Печатается по решению научно-методического совета Камского государственного политехнического института от ___________________2003 г.

Определение показателя адиабаты: Методические указания к лабораторной работе./ Составили: В.М. Гуреев, И.М. Безбородова, А.Т. Галиакбаров – Набережные Челны: КамПИ, 2003 г., 14 с.

Методические указания к лабораторной работе составлены для студентов машиностроительных специальностей.

Ил.2, список лит. 3 назв.

Рецензент к.т.н. доцент. Тазмеев Х. К.

Камский государственный политехнический институт, 2003

Цель работы : Экспериментальное определение величины отношения изобарной теплоемкости воздуха и его изохорной теплоемкости.

Теоретические основы работы

Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме, обозначаемое буквой К, часто используется в различных термодинамических расчетах. Показатель К называют показателе адиабаты.

Значение К можно выразить через отношения массовых, объемных или мольных теплоемкостей:

(1)

В молекулярно-кинетической теории газов для определения показателя адиабаты приводится следующая формула:

(2)

гдеп – число степеней свободы движения молекулы газа.

Для одноатомного газап = 3,К = 1,667, для двухатомных газовп = 5,К = 1,4 и для трехатомных газовп = 6,К = 1,33.

Теплоемкости С р и зависят от температуры, следовательно, и показатель адиабаты“К” должен зависеть от температуры. Установим эту зависимость следующим образцом:

Используя уравнение Майера,

. (3)

Запишем выражение, (1) в виде

. (4)

Для 1 моля газа получается

. (5)

Обычно зависимость показателя адиабаты от температуры выражается формулой вида:

, (6)

гдеК 0 –значение показателя “К ”при 0 0 С;

— коэффициент.

Для двухатомныхгазов при температурах до 2000 0 С эмпирически получена следующая зависимость:

Изменение состояния термодинамической системы, происходящее без теплообмена с окружающей средой(
) называется адиабатным процессом. Обратимый адиабатныйпроцесс (
и
) называется изоэнтропным процессом, т.е. процессом, в котором
,
— диссилативные потери.

Из первого начала термодинамики следует, что для1 кг закрытой термохимической гомогенной (однородной) системы, совершающей обратимый процесс, внешняя теплота.

или используя известные выражения:

;
;

(9),

Но так как для атмосферного воздуха допустимы равенства

,
;
,

совершенно точные лишь для идеального газа, то

Так как в обратимых адиабатных термодинамических процессах

и
, то:

(11)

где
— введенный ранее показатель адиабаты.

Разделив переменные и исключив P и V , при помощи равенства ,являющегося дифференциальной формой уравнения Клайперона,получим три уравнения адиабаты:

;

(12)

В интегральной форме при (
) они принимают вид:

;
;

Следовательно, показатель адиабатного процесса может быть выражен также и равенствами

;
(13)

В идеальном изотермическом процессе
,

и
или
(14)

Поэтому, если через определенную точку с параметрами
в
и
— осях (рис.1) процессы
и
, то в состоянииI отношении
или
, входящее в уравнение(13) и (14), будет одно и то же.

Т
аким образом, для определения истинного показателя адиабаты необходимы аналитически или экспериментально установленные значения калорических (,)или же термических параметров (P , V , T ) , а также их частных дифференциалов и производных.

Но если в уравнение (15) подставить малые конечные приращения, то при средний показатель адиабаты

а при Р = Рб, т.е. равном барометрическому давлению.

При уменьшении избыточного давления Р и1 средний показатель адиабаты
будет приближаться к истинному К, присущему атмосферному воздуху.

Определив средний показатель адиабаты и используя равенство:

(17)

можно вычислить,
и
, а затем известныхи
найти
,
,
и
, т.е. определить средние изохорные и изобарные весовые, мольные и объемные теплоемкости воздуха.

Описание экспериментальной установки

Лаборатория-установка (рис.2) имеет металлический бак 5, водяной U — образный манометр 1, 2, 3, компрессор 6, зажим 7, манометр 4.

Бак термически не изолирован, поэтому воздух, который находится в этом баке, вследствие теплообмена с окружающей средой принимает ее температуру. Большое проходное сечение крана позволяет очень быстро выпускать часть воздуха из бака. При этом процесс расширения воздуха, остающегося внутри бака, происходит настолько быстро, что его можно считать адиабатным.

Порядок проведения опытов

1. Определить давлениеР б и температуру t воздуха в лаборатории Полученные результаты внести в таблицу 1.

Опустить зажим и при закрытом кране, вращая маховик компрессора, накачать немного воздуха в бак. Начальное давление должно быть возможно меньшим.

Создав небольшое избыточное давление в системе, закрыть зажим.

После установления термического равновесия между воздухом в баке и окружающей средой, что будет видно по стационарному показанию манометра, записать значение.

Открыть и немедленно закрыть кран, т.е. выпустив часть газа из бака, снизить давление в нем до атмосферного. В результате адиабатного расширения воздуха, находящегося внутри бака, температура там понизится. Вследствие этого начнется изохорной процесс нагрева воздуха, оставшегося в баке, за счет подвода тепла от окружающей среды. В баке вновь возникает избыточное давление, которое растет до Р.

Опыт повторяется п -раз.

Обработка результатов измерений.

1. Определить вероятное значение показателя адиабаты воздуха.

2. Вычислить изохорные и изобарные весовые (С V , С р ) мольные (
,
) и объемные
теплоемкости воздуха, используя выражение (17) и вытекающие из него равенства:

(19)

(20)

(21)

(22)

(23)

(24)

где
— объем одного кмоля, т.е. и
) атмосферного воздуха при нормальных условиях.

3. Все полученные результаты сравнить с табличными значениями и найти допущенную абсолютную ошибку
и относительную.

4.
, где
— табличное значение показателя адиабаты.

5. Для каждого опыта вычислить значения
воздуха в точке 1, 2, 3 (рис.1). При этом использовать уравнения
,Клайперона иМайера
и равенства

;

;
,
, а при нормальных условиях
. Тогда:

По конечным результатам построить в масштабе
и
— диаграммы процессов 1-2, 2-3, 3-1.

Указания по охране труда

Запрещается стоять рядом со студентом, вращающим ручку поршневого компрессора.

Требование к отчету по работе.

Отчет по лабораторной работе должен содержать материалы:

Наименование и цель работы.

Схема установки и ее описание.

Методика проведения экспериментов и обработки результатов экспериментов.

Таблицы результатов измерений и расчетов.

Процессы, изображенные в Р-V, Т-S координатах.

Выводы о работе, содержащие сведения о величинах показателя адиабаты, полученные в результате эксперимента, и их сравнение с табличными значениями.

Контроль ные вопросы.

Ввести понятия показателя адиабаты.

Записать уравнение адиабатного термодинамического процесса в интегральной форме.

Записать уравнения Клайперона и Майера.

Записать 1-й и 2-й законы термодинамики.

Сб. под ред. Н. К. Арсланова. Практикум по технической термодинамике. – Казань, 1973.

Н. М. Беляев. Термодинамика. – Киев: Вища школа, 1987.

А. П. Баскаков. Теплотехника. – М.: Энергоиздат, 1982.

Статья является частью одноименной серии.

Уравнение состояния

Идеальный газ

Термодинамические величины

Термодинамические потенциалы

Термодинамические циклы

Фазовые переходы

См. также «Физический портал»

Показатель адиабаты (иногда называемый коэффициентом Пуассона ) — отношение теплоёмкости при постоянном давлении ( C P <displaystyle C_

> ) к теплоёмкости при постоянном объёме ( C V <displaystyle C_> ). Иногда его ещё называют фактором изоэнтропийного расширения . Обозначается греческой буквой ( гамма) или κ <displaystyle kappa >( каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинская буква k <displaystyle k>.

γ = C P C V = c P c V , <displaystyle gamma =<frac >>>=<frac >>>,> C <displaystyle C>- теплоёмкость газа, c <displaystyle c>- удельная теплоёмкость (отношение теплоёмкости к единице массы) газа, индексы P <displaystyle _

> и V <displaystyle _> обозначают условие постоянства давления или постоянства объёма, соответственно.

Для показателя адиабаты справедлива теорема Реша (1854) :

где χ t <displaystyle chi _> и χ s <displaystyle chi _~~> — изотермический и адиабатический (изоэнтропический) коэффициенты всестороннего сжатия .~~

показатели адиабаты для различных температур и газов
темп.	газ	темп.	газ	темп.	газ
−181 °C

Для понимания этого соотношения можно рассмотреть следующий эксперимент. Закрытый цилиндр с закреплённым неподвижно поршнем содержит воздух. Давление внутри равно давлению снаружи. Этот цилиндр нагревается до определённой, требуемой температуры. До тех пор, пока поршень закреплён в неподвижном состоянии, объём воздуха в цилиндре остаётся неизменным, в то время как температура и давление возрастают. Когда требуемая температура будет достигнута, нагревание прекращается. В этот момент поршень «освобождается» и, благодаря этому, начинает перемещаться под давлением воздуха в цилиндре без теплообмена с окружающей средой (воздух расширяется адиабатически). Совершая работу , воздух внутри цилиндра охлаждается ниже достигнутой ранее температуры. Чтобы вернуть воздух к состоянию, когда его температура опять достигнет упомянутого выше требуемого значения (при всё ещё «освобождённом» поршне) воздух необходимо нагреть. Для этого нагревания извне необходимо подвести примерно на 40 % (для двухатомного газа — воздуха) большее количество теплоты, чем было подведено при предыдущем нагревании (с закреплённым поршнем). В этом примере количество теплоты, подведённое к цилиндру при закреплённом поршне, пропорционально C V <displaystyle C_> , тогда как общее количество подведённой теплоты пропорционально C P <displaystyle C_

> . Таким образом, показатель адиабаты в этом примере равен 1,4 .

Другой путь для понимания разницы между C P <displaystyle C_

> и C V <displaystyle C_> состоит в том, что C P <displaystyle C_

> применяется тогда, когда работа совершается над системой, которую принуждают к изменению своего объёма (то есть путём движения поршня, который сжимает содержимое цилиндра), или если работа совершается системой с изменением её температуры (то есть нагреванием газа в цилиндре, что вынуждает поршень двигаться). C V <displaystyle C_> применяется только если P d V <displaystyle PdV>- а это выражение обозначает совершённую газом работу — равно нулю. Рассмотрим разницу между подведением тепла при закреплённом поршне и подведением тепла при освобождённом поршне. Во втором случае давление газа в цилиндре остаётся постоянным, и газ будет как расширяться, совершая работу над атмосферой, так и увеличивать свою внутреннюю энергию (с увеличением температуры); теплота, которая подводится извне, лишь частично идёт на изменение внутренней энергии газа, в то время как остальное тепло идёт на совершение газом работы.

показатели адиабаты для различных температур и газов

темп. газ темп. газ темп. газ

−181 °C

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА

Определить показатель адиабаты воздуха методом Клемана-Дезорма.

Сравнить полученное значение показателя адиабаты с его теоретическим значением и сделать вывод о точности проведенных измерений и достоверности использованного метода.

Приборы и принадлежности

Установка для определения показателя адиабаты воздуха с манометром и насосом.

Адиабатическим называется процесс, совершаемый термодинамической системой, при котором отсутствует теплообмен между этой системой и внешней средой.

Уравнение, описывающее состояние системы в адиабатическом процессе, имеет вид:

где и– давление и объем газа;– показатель адиабаты.

Показатель адиабаты – это коэффициент, численно равный отношению теплоемкостей газа при постоянном давлении и при постоянном объеме:

Физический смысл его заключается в том, что он показывает, во сколько раз количество теплоты, необходимой для нагревания газа на 1 К в изобарическом процессе (), больше количества теплоты, необходимой для той же цели в изохорическом процессе ().

Для идеального газа показатель адиабаты определяется по формуле:

где i – число степеней свободы молекул газа.

Совершение газом адиабатического процесса требует его идеальной термоизоляции, что в реальных условиях не вполне достижимо. Тем не менее будем считать, что в данной работе экспериментальная установка позволяет осуществить адиабатический процесс.

Установка (рис. 1) для определения показателя адиабаты воздуха состоит из стеклянного сосуда 1, жидкостного манометра 2 и насоса 3, соединенных резиновыми и стеклянными трубками. Горловина сосуда закрыта пробкой с краном 4 для сообщения сосуда с атмосферой. Насос позволяет изменять давление в сосуде при закрытом кране, а манометр — измерять это изменение.

Все изменения состояния воздуха в процессе эксперимента качественно представлены на рис. 2.

Суть эксперимента заключается в переводе воздуха в разные состояния различными процессами и анализе качественных изменений этих состояний (точнее — изменений давления воздуха в сосуде). Исходное состояние (точка 0) воздуха в сосуде (кран 4 открыт) характеризуется давлением p 0 , равным атмосферному, объемом V 0 и температурой T 0 , равной температуре окружающей среды.

Закрыв кран, создают насосом в сосуде избыточное давление: при этом воздух, испытывая адиабатическое сжатие, переходит в первое состояние (точка 1). Это состояние характеризуется параметрами ,и, при этоми(адиабатическое сжатие газа сопровождается его нагреванием).

После прекращения работы насоса вследствие теплообмена через стенки сосуда температура газа снижается до первоначальной температуры , что вызывает некоторое снижение его давления. В результате в сосуде устанавливается давление, превышающее атмосферное давление на некоторое значение. Это второе состояние газа (точка 2) характеризуется параметрами , и .

Если кран кратковременно открыть и закрыть, то газ в сосуде адиабатически расширится (так как теплообмен произойти не успеет), и его давление практически мгновенно выровняется с атмосферным давлением. Это третье состояние газа (точка 3) характеризуется параметрами , и, при этом (адиабатическое сжатие газа сопровождается его охлаждением).

Сразу после закрытия крана в сосуде начинается изохорический процесс нагревания воздуха путем теплообмена с внешней средой, сопровождающийся некоторым повышением его давления. В результате в сосуде устанавливается давление, повышенное по сравнению с атмосферным давлением на некоторое значение . Это четвертое состояние газа (точка 4) характеризуется параметрами , и .

Показатель адиабаты полностью определяется значениями избыточных давлений и.

Для состояний 2 и 3 выполняется соотношение, получающееся при выводе уравнения состояния газа в адиабатическом процессе:

. (4)

Для состояний 3 и 4 с помощью уравнения Клапейрона–Менделеева можно получить соотношение (закон Шарля):

С учетом того, что ,,, подставляя выражение (4) в (3), получим:

. (6)

Логарифмируя последнее выражение, получим:

. (7)

Известно, что при. С учетом этого можно записать, что

, (8)

откуда следует, что

. (9)

Избыточное давление в сосуде, измеряемое манометром, пропорционально разности уровней h жидкости в обоих коленах трубки манометра (см. рис. 2). С учетом этого обстоятельства выражение (9) примет окончательный вид:

Отсчет уровней производится с учетом кривизны поверхности жидкости в трубке. Для отсчета берется деление шкалы, совпадающее с касательной к поверхности жидкости.

Порядок выполнения работы

1. При закрытом кране насосом создать избыточное давление в сосуде (необходимо избегать резких движений, так как жидкость может быть легко вытолкнута из трубки манометра).

2. Выждать, пока уровни жидкости в манометре перестанут изменять свое положение, и произвести отсчет их разности h 1 .

3. Открыть кран для выпуска воздуха и быстро его закрыть в момент первого пересечения уровнями жидкости исходного их положения (до накачки насосом).

4. Выждать, пока уровни жидкости в манометре перестанут изменять свое положение, и произвести отсчет их разности h 2 .

Эксперимент необходимо повторить не менее 5 раз, и полученные результаты занести в таблицу 1.

6. По формуле (10) вычислить оценку показателя адиабаты, использовав средние значения ()разностей уровней жидкости в манометре.

8. Сравнить полученный доверительный интервал значений показателя адиабаты с его теоретическим значением и сделать вывод о точности проведенных измерений и достоверности использованного метода.

1. В этой работе велика роль случайных погрешностей, поэтому приборными погрешностями, ввиду их относительной малости, следует пренебречь.

Случайные погрешности рассчитываются по методу Стьюдента.

2. Полная относительная погрешность измерения показателя адиабаты:

.

3. Полная абсолютная погрешность измерения показателя адиабаты:

Полученный результат округляется и записывается в виде:

Правильность проведенных измерений и вычислений должна подтверждаться «перекрытием» полученного доверительного интервала для значения показателя адиабаты воздуха и его теоретического значения.

1. Дайте определения изохорическому, изобарическому и изотермическому процессам. Изобразите эти процессы графически в координатных осях p-V . Запишите уравнение состояния идеального газа в этих процессах и поясните смысл входящих в них физических величин.

2. Дайте определение адиабатическому процессу. Изобразите этот процесс графически в координатных осях p-V. Запишите уравнение состояния газа в этом процессе (уравнение Пуассона) и поясните смысл входящих в него физических величин.

3. Что такое показатель адиабаты? Как определить его теоретическое значение?

4. Опишите состав экспериментальной установки и порядок действий при определении показателя адиабаты воздуха.

5. Сформулируйте первый закон термодинамики.

6. Что такое внутренняя энергия вещества? Чему равна внутренняя энергия идеального газа в различных изопроцессах?

7. Дайте определение теплоемкости вещества. Что такое удельная и молярная теплоемкости вещества? Чему равна молярная теплоемкость идеального газа в различных изопроцессах?

8. Как вычислить работу, совершаемую идеальным газом, в изохорическом, изотермическом, изобарическом и адиабатическом процессах?

9. Как вычислить изменение внутренней энергии идеального газа при совершении им изохорического (изобарического, изотермического, адиабатического) процессов?

10. Как определить количество теплоты, получаемой (или отдаваемой) идеальным газом при совершении им изохорического (изобарического, изотермического, адиабатического) процессов?

Расчет давления во фронте воздушной ударной волны при разрушении емкости проводится по формулам (3.12), (3.45), в последней из которых величина aMQ v н заменяется на Е, значение коэффициента b 1 = 0,3.

Серьезную опасность представляет разлет осколков, образующихся при разрушении емкости. Движение осколка с известной начальной скоростью можно описать системой уравнений вида

sup15(x» = -f((0C1S1 b (x» -f((0C2S2 b (x»2 + y»2 (3.45)

где m — масса осколка, кг;C 1 ,C 2 — коэффициенты лобового сопротивления и подъемной силы осколка соответственно;S 1 ,S 2 — площадь лобовой и боковой поверхности осколка, м 2 ;r 0 — плотность воздуха, кг/м 3 ;a — угол вылета осколка;x, y — координатные оси.

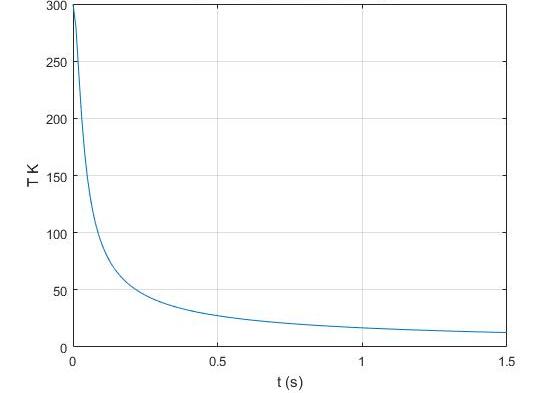
Решение этой системы уравнений приведено на рис. 3.7.

В приближенных расчетах для оценки дальности разлета осколков допускается использовать соотношение

где L m — максимальная дальность разлета осколков, м;V 0 — начальная скорость полета осколков,м/с;g = 9,81 м/с 2 — ускорение свободного падения.

Соотношение (3.46) получено для случая полета осколков в безвоздушном пространстве. При больших величинах V 0 оно дает завышение значения L m . Дальность L m , определенную таким образом, следует ограничить сверху величиной L *

L m £ L * = 238 3.47,

где Е — энергия рассматриваемого взрыва, Дж;Q v тр — теплота взрыва тротила (табл.2), Дж/кг.Значения L * получены при взрывах тротиловых зарядов в металлической оболочке (бомб, снарядов).

При взрыве емкости со сжатым горючим газом энергия взрыва Е, Дж, находится по соотношению

E = + MQ v п 3.48,

где M = awM 0 — масса газа, участвующего во взрыве, кг;Q v п — теплота взрыва горючего газа, Дж/кг;a, w — коэффициенты, определяемые согласно (3.32), (3.45);

Масса газа в емкости до взрыва M 0 = Vr 0 , где величины P 0 , P г, V имеют то же значение, что и в формуле (3.46), а величина r 0 — плотность газа при атмосферном давлении.

Как отмечалось в разделе 3.4, показатель адиабаты продуктов взрыва ГВС g » 1,25. Более точные значения показателя адиабаты некоторых газов, используемые для расчета последствий взрыва, приведены в табл.3.8.

В рассматриваемом случае также имеет место соотношение Е »E ув + Е оск + Е т, где Е — энергия взрыва, Е ув = b 1 Е — энергия, расходуемая на формирование воздушной ударной волны, Е оск = b 2 Е — кинетическая энергия осколков, Е т = b 0 Е — энергия, идущая на тепловое излучение. Согласно данным здесь коэффициенты b 1 = 0,2, b 2 = 0,5, b 3 = 0,3.

Расчет давления во фронте воздушной ударной волны и дальности разлета осколков при известных значениях энергии взрыва Е и коэффициентов b 1 , b 2 , b 3 приводится по аналогии с рассмотренным случаем взрыва емкости с инертным газом.

Необходимо отметить различие событий, происходящих при разгерметизации сосудов, содержащих газ под давлением, и сосудов, содержащих сжиженные газы. Если в первом случае основным поражающим фактором являются осколки оболочки, то во втором — осколки могут не образоваться, так как при нарушении герметичности баллонов с сжиженными газами их внутреннее давление практически одновременно с разгерметизацией становится равным внешнему и далее вступают в действие процессы истечения сжиженного газа из разрушенного баллона в окружающую среду и его испарения. При этом в случае взрыва основными поражающими факторами являются ударная волна и тепловое излучение.

Адиабатический процесс. Политропный процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстро протекающие процессы. Например, адиабатическим процессом можно считать процесс в двигателях внутреннего сгорания(расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т.д.

Из первого начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что

dА=-dU, (2.6.1)
т.е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражение для произвольной массы газа перепишем уравнение в виде

. (2.6.2)

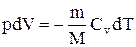
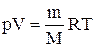
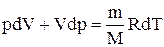
Продифференцировав уравнение состояния для идеального газа , получим

. (2.6.3)
Исключим из (2.6.2) и (2.6.3) температуру Т:

.
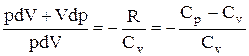
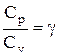
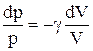
Разделив переменные и учитывая, что найдем

.

Интегрируя это уравнение в пределах от p₁ до р₂ и соответственно от V₁ до V₂, а затем потенцируя, придем к выражению

.

.

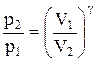
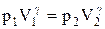
Так как состояния 1 и 2 выбраны произвольно, то можно записать

PV g =const. (2.6.4)
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из (2.6.4) с помощью уравнения Клапейрона-Менделеева:

,

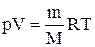
соответственно давление или объем:

(2.6.5)

. (2.6.6)

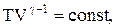
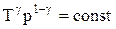
Эти выражения представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина

(2.6.7)
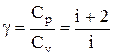
называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, g =1,67. Для двухатомных газов (Н₂, N₂, О₂ и др.) i=5, g =1,4. Значения вычисленные по формуле (2.6.7), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабат а) в координатах р, V изображается гиперболой (рис. 2.6.1).

Вычислим работу, совершаемую газом в адиабатическом процессе.
Запишем уравнение в виде

.

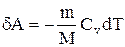
Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшается от T₁ до Т₂ и работа расширения идеального газа

. (2.6.8)

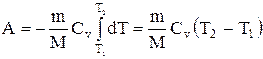
Применяя те же приемы, выражение (2.6.8) для работы при адиабатическом расширении можно преобразовать к виду

.

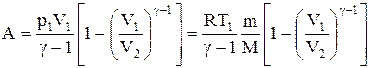
Работа, совершаемая газом при адиабатическом расширении 1-2 (определяется заштрихованной площадью, выполненной на рис. 61), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С_v и С_p, в изотермическом процессе (dT=0) теплоемкость равна ±¥, в адиабатическом (dQ=0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const), можно вывести уравнение политропы:

pV n =const, (2.6.9)
где 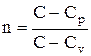— показатель политропы. Очевидно, что при С=0, n=gполучается уравнение адиабаты; при С=¥, n=l — уравнение изотермы; при С=С_p, n=0 — уравнение изобары, при С=С_v , n=±¥ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.

2.7 Круговой процесс (цикл).
Обратимые и необратимые процессы.

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой кривой (рис. 2.7.1).

Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1-2) и сжатия (2-1) газа. Работа расширения (определяется площадью фигуры 1а2V₂V₁) положительна (dV > 0), работа сжатия (определяется площадью фигуры 2blV₁V₂2) отрицательна (dV 0 (цикл протекает по часовой стрелке), то он называется прямым (рис. 2.7.1,а), если за цикл совершается отрицательная работа 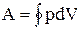0. (2.8.4)

Выражения (2.8.3) и (2.8.4) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (2.8.3) и (2.8.4) можно представить в виде неравенства Клаузиуса

DS 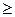0, (2.8.5)

т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (2.8.2), изменение энтропии

, (2.8.6)
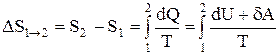
где подынтегральное выражение и пределы интегрирования надо выразить через величины, характеризующие исследуемый процесс. Формула (2.8.6) определяет энтропию лишь с точностью до аддитивной постоянной.

Физический смысл имеет не сама энтропия, а разность энтропии.

Исходя из выражения (2.8.6), найдем изменение энтропии в процессах идеального газа. Так как

,

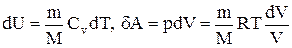
то ,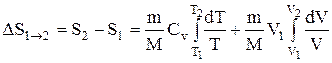

или 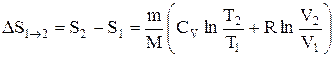, (2.8.7)

т.е. изменение энтропии 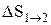идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1®2.

Так как для адиабатического процесса dQ=0, то DS=0 и, следовательно, S=const, т.е. адиабатический обратимый процесс протекает при постоянной энтропии. Из формулы (2.8.7) следует, что при изотермическом процессе (T₁=T₂)

при изохорном процессе (V₁ =V₂)

.

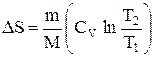
Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропии тел, входящих в систему.

Более глубокий смысл энтропии вскрывается в статистической физике, энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние.

Согласно Больцману, энтропия S системы и термодинамическая вероятность связаны между собой следующим образом:

S=kInW, (2.8.8)
где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия.
Так как реальные процессы необратимы, то можно утверждать, что все
процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных к более вероятным.

Сопоставляя выражения (2.8.5) и (2.8.8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов).

Отметим, однако, что эти утверждения имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для «малых» систем могут наблюдаться флуктуации, т.е. энтропия и термодинамическая вероятность состояний замкнутой системы на определенном отрезке времени могут убывать, а не возрастать, или оставаться постоянными.

источники:

http://my-creditor.ru/mirovoe-soglashenie/chemu-raven-pokazatel-adiabaty-uravnenie-puassona.html

http://helpiks.org/3-66116.html

Источник

Адиабатический процесс

теплопроводность между внешней средой и системой по той или иной причине является низкой;
скорость процесса велика, поэтому обмен теплом не успевает происходить.

Уравнение Пуассона для адиабаты идеального газа

dU = -P*dV.

P*V^γ = const.

Что такое показатель адиабаты?

Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом C_P изобарную теплоемкость, а символом C_V — изохорную. Тогда для γ справедливо равенство:

γ = C_P/C_V.

Теплоемкости CP и CV

Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин C_Pи C_V. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

dU = C_V*dT.

Величина C_V определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

C_P*dT = C_V*dT + P*dV.

Отсюда видно, что C_P>C_V, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

C_P = C_V + R.

Откуда можно определить значение изохорной теплоемкости C_V:

γ = C_P/C_V;

C_V = R/(γ-1).

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

C_V = 3/2*R.

Из последних двух равенств следует значение показателя адиабаты:

3/2*R = R/(γ-1) =>

γ = 5/3 ≈ 1,67.

Зависимость γ от числа степеней свободы

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для C_V приобретает вид:

C_V = 5/2*R.

Тогда значение γ будет равно:

γ = 7/5 = 1,4.

γ = 4/3 ≈ 1,33.

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна a_i. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

γ = ∑_i=1^N(a_i*γ_i).

Где γ_i — это величина γ для i-го компонента.

Источник

Задачи по теме «Теплоемкость идеального газа» с решениями

Задача №1. Определить удельную теплоемкость идеального газа

Задача №2. Удельная теплоемкость

Задача №3. Молярная теплоемкость

Задача №4. Теплоемкость при изопроцессах

Задача №5. Теплоемкость при политропическом процессе

Вопросы по теме «Теплоемкость идеального газа»

Уравнение Майера — какие процессы описывает

Формула Майера для теплоемкостей, вывод из первого закона термодинамики

Формула Майера для теплоемкостей

Понятие термодинамики, вывод формулы Майера из первого закона термодинамики

Как записывается соотношение для молярных и массовых теплоемкостей

Задачи на определение теплоемкостей

Примеры задач и их решение

Задача 1

Задача 2

Задача 3

Задача 4

Задача 5

Показатели адиабаты: определение и процесс

Адиабатический процесс

Уравнение Пуассона для адиабаты идеального газа

Что такое показатель адиабаты?

Теплоемкости CP и CV

Величина γ для газа идеального одноатомного

Зависимость γ от числа степеней свободы

Показатель адиабаты для смеси газов

Чему равен показатель адиабаты. Уравнение пуассона

Показатель адиабаты в уравнении Пуассона

Примеры решения задач

Указания по охране труда

Адиабатический процесс. Политропный процесс.

Адиабатический процесс

Уравнение Пуассона для адиабаты идеального газа

Что такое показатель адиабаты?

Теплоемкости CP и CV

Величина γ для газа идеального одноатомного

Зависимость γ от числа степеней свободы

Показатель адиабаты для смеси газов

Не пропустите также: