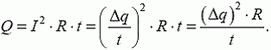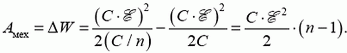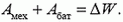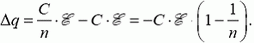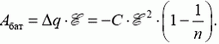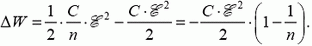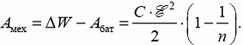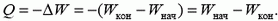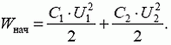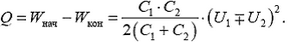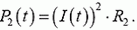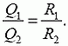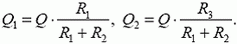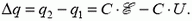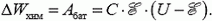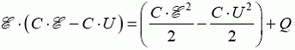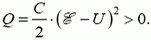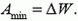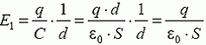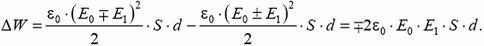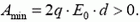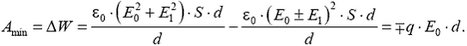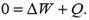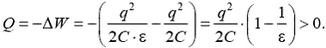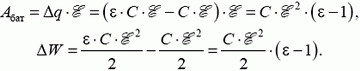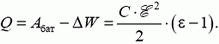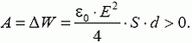Разряд конденсатора с выделением тепла
Переходные процессы — сложная тема, сложная даже для студентов, тем более — для школьников. Помните: постоянный ток не протекает через конденсатор. Напряжение на конденсаторе определяется его подключением: если параллельно резистору — то напряжение такое же, как на резисторе, если последовательно с источником — то конденсатор зарядится до ЭДС источника, после чего ток исчезнет. Если дать конденсатору возможность разрядиться — то энергия, запасенная в нем, превратится в тепло на резисторе.
Задача 1.
Источник постоянного тока с ЭДС В и внутренним сопротивлением
Ом подсоединен к параллельно соединенным резисторам
Ом,
Ом и конденсатору. Определите емкость конденсатора С, если энергия электрического поля конденсатора равна
мкДж.
К задаче 1
Определить емкость легко из энергии конденсатора, только надо знать напряжение:
Объединим резисторы в один:
Ток в неразветвленной части цепи равен
Напряжение на внутреннем сопротивлении тогда равно
Тогда на резисторах и конденсаторе напряжение
Емкость равна
Ответ: мкФ.
Задача 2.
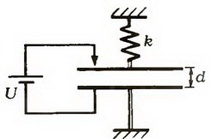
Источник постоянного напряжения с ЭДС 100 В подключен через резистор к конденсатору переменной емкости, расстояние между пластинами которого можно изменять (см. рис.). Пластины медленно раздвинули. Какая работа была совершена против сил притяжения пластин, если за время движения пластин на резисторе выделилось количество теплоты 10 мкДж и заряд конденсатора изменился на 1 мкКл?
К задаче 2
У конденсатора была энергия до того, как пластины раздвинули – пусть . И после тоже была – пусть
. В процессе раздвижения пластин совершили работу (которую надо найти), и, так как заряд уменьшился (а он именно уменьшился, так как напряжение осталось тем же), то источник тоже совершил работу. Поэтому закон сохранения энергии запишется так:
Заряд на конденсаторе сначала: , потом —
. Тогда изменение заряда равно
Работа источника
Тогда наш закон сохранения можно переписать:
Ответ: 60 мкДж
Задача 3.
Заряженный конденсатор мкФ включен в последовательную цепь из резистора
Ом, незаряженного конденсатора
мкФ и разомкнутого ключа К (см. рис.). После замыкания ключа в цепи выделяется количество теплоты
мДж. Чему равно первоначальное напряжение на конденсаторе
?
К задаче 3
Первоначально на конденсаторе есть заряд:
После замыкания ключа заряд разделится:
Но напряжение на конденсаторах одно и то же:
Тогда
Откуда:
Энергия до замыкания, запасенная в конденсаторе , сохраняется:
Ответ:
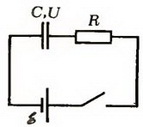
Задача 4.
В электрической схеме, показанной на рисунке, ключ К замкнут. ЭДС батарейки В, сопротивление резистора
Ом, заряд конденсатора 2 мкКл. После размыкания ключа К в результате разряда конденсатора на резисторе выделяется количество теплоты 20 мкДж. Найдите внутреннее сопротивление батарейки
.
К задаче 4
Сначала на конденсаторе напряжение такое же, как на резисторе (потому что они включены параллельно):
Определим ток. Он замыкается в контуре , потому что постоянный ток не течет через конденсатор:
Тогда напряжение на резисторе и конденсаторе:
С другой стороны, когда ключ разомкнется, вся энергия, запасенная в конденсаторе, рассеется в виде тепла через резистор:
То есть
Приравняем:
А внутреннее сопротивление равно
Ответ:
Закон сохранения энергии определяет в самом общем виде энергетический баланс при всевозможных изменениях в любой системе. Запишем его следующим образом:
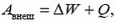
где Aвнеш — работа, совершенная над рассматриваемой системой внешними силами, ΔW — изменение энергии системы, Q — количество теплоты, выделяемое в системе. Договоримся, что если Aвнеш > 0, то над системой совершают положительную работу, а если Aвнеш < 0, положительную работу совершает система; если ΔW > 0, то энергия системы увеличивается, а если ΔW < 0, энергия уменьшается; наконец, если Q > 0, то в системе выделяется тепло, а если Q < 0, тепло системой поглощается.
В этой статье мы рассмотрим, как закон сохранения энергии «работает» в электростатике. В общем случае электростатическая система содержит взаимодействующие между собой заряды, находящиеся в электрическом поле.
Рассмотрим каждое слагаемое в уравнении (1) по отдельности.
Начнем с энергии. Энергия взаимодействия зарядов выражается через характеристики электрического поля этой системы зарядов. Так, например, энергия заряженного конденсатора емкостью C задается известным выражением
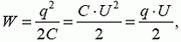
где q — заряд обкладок, U — напряжение между ними. Напомним, что конденсатор — это система двух проводников (обкладок, пластин), обладающая следующим свойством: если с одной обкладки на другую перенести заряд q (т. е. одну обкладку зарядить зарядом +q, а другую –q), то все силовые линии созданного таким образом поля будут начинаться на одной (положительно заряженной) обкладке и заканчиваться на другой. Поле конденсатора существует только внутри него.
Энергию заряженного конденсатора можно представить также как энергию поля, локализованного в пространстве между пластинами с плотностью энергии 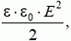
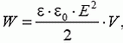
где V — объем конденсатора. Последней формулой легко пользоваться, конечно, только в случае однородного поля, но представление энергии в такой форме очень наглядно, а потому удобно.
Конечно, кроме энергии взаимодействия зарядов (энергии электрического поля) в энергию системы может входить и кинетическая энергия заряженных тел, и их потенциальная энергия в поле тяжести, и энергия пружин, прикрепленных к телам, и т. п.
Теперь о работе внешних сил. Помимо обычной механической работы Aмех (например, по раздвиганию пластин конденсатора), для электрической системы можно говорить о работе внешнего электрического поля. Например, о работе батареи, заряжающей или перезаряжающей конденсатор. Задача батареи — создать фиксированную, присущую данному источнику разность потенциалов между теми телами, к которым она присоединена. Делает она это единственно возможным способом — забирает заряд от одного тела и передает его другому. Источник никогда не создает заряды, а только перемещает их. Общий заряд системы при этом сохраняется — это один из краеугольных законов природы.
В источниках разных конструкций электрическое поле, необходимое для перемещения зарядов, создают различные «механизмы». В батареях и аккумуляторах — это электрохимические реакции, в динамомашинах — электромагнитная индукция. Существенно, что для выбранной системы зарядов (заряженных тел) это поле — внешнее, стороннее. Когда через источник с ЭДС от отрицательного полюса к положительному протекает заряд Δq, сторонние силы совершают работу
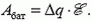
При этом если Δq > 0, то Aбат > 0 — батарея разряжается; если же Δq < 0, то Aбат < 0 — батарея заряжается и в ней накапливается химическая (или магнитная) энергия.
Наконец, о выделении тепла. Заметим только, что это джоулево тепло, т.е. тепло, связанное с протеканием тока через сопротивление.
Теперь обсудим несколько конкретных задач.
Задача 1. Два одинаковых плоских конденсатора емкостью C каждый присоединены к двум одинаковым батареям с ЭДС . В какой-то момент один конденсатор отключают от батареи, а другой оставляют присоединенным. Затем медленно разводят пластины обоих конденсаторов, уменьшая емкость каждого в n раз. Какая механическая работа совершается в каждом случае?
Если процесс изменения заряда на конденсаторе осуществляется все время медленно, тепло выделяться не будет. Действительно, если через резистор сопротивлением R протек заряд Δq за время t, то на резисторе за это время выделится количество теплоты
При достаточно больших t количество теплоты Q может оказаться сколь угодно малым.
В первом случае фиксирован заряд на пластинах (батарея отключена), равный Механическая работа определяется изменением энергии конденсатора:
Во втором случае фиксирована разность потенциалов на конденсаторе и работает батарея, поэтому
Через батарею протекает заряд
Этот заряд меньше нуля, значит, батарея заряжается и ее работа
Энергия поля в конденсаторе уменьшается:
Таким образом,
Зарядка батареи происходит за счет работы по раздвиганию пластин и за счет энергии конденсатора.
Заметим, что слова про раздвигание пластин существенной роли не играют. Такой же результат будет при любых других изменениях, приводящих к уменьшению емкости в n раз.
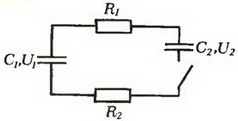
Задача 2. В схеме, изображенной на рисунке, найдите количество теплоты, выделившееся в каждом резисторе после замыкания ключа. Конденсатор емкостью C1 заряжен до напряжения U1, а конденсатор емкостью C2 — до напряжения U2. Сопротивления резисторов R1 и R2.
Рис. 1
Закон сохранения энергии (1) для данной системы имеет вид
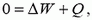
Начальная энергия конденсаторов равна
Для определения энергии в конечном состоянии воспользуемся тем, что суммарный заряд конденсаторов не может измениться. Он равен 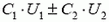
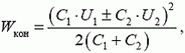
Как и должно быть, в обоих случаях выделяется тепло — есть джоулевы потери. Замечательно, что выделившееся количество теплоты не зависит от сопротивления цепи — при малых сопротивлениях текут большие токи и наоборот.
Теперь найдем, как количество теплоты Q распределяется между резисторами. Через сопротивления R1 и R2 в каждый момент процесса перезарядки текут одинаковые токи, значит, в каждый момент мощности, выделяемые на сопротивлениях, равны
Следовательно,
Кроме того, 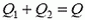
Задача 3. В схеме на рисунке 2 конденсатор емкостью C заряжен до напряжения U. Какое количество химической энергии запасется в аккумуляторе с ЭДС после замыкания ключа? Какое количество теплоты выделится в резисторе?
Рис. 2
Первоначальный заряд на конденсаторе 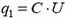
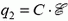
В противном случае 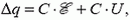
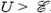
Теперь запишем закон сохранения энергии (1) –
– и найдем выделившееся количество теплоты:
Задача 4. Плоский конденсатор находится во внешнем однородном поле с напряженностью 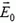
Работа будет минимальной, когда процесс проводится очень медленно — при этом не выделяется тепло. Тогда, согласно закону сохранения энергии,
Чтобы найти ΔW, воспользуемся формулой (3). Поле между пластинами представляет собой суперпозицию поля 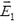
– и внешнего поля 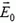
При перемене пластин местами поле 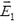
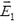
Если направления векторов 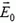
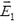
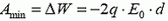
Когда пластины конденсатора расположены параллельно полю 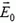
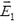
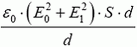
Когда конденсатор вынули из поля, в том месте, где он был, поле стало 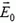
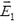
Задача 5. Конденсатор емкостью С без диэлектрика заряжен зарядом q. Какое количество теплоты выделится в конденсаторе, если его заполнить веществом с диэлектрической проницаемостью ε? То же, но конденсатор присоединен к батарее с ЭДС .
При заливании диэлектрика емкость конденсатора увеличилась в ε раз.
В первом случае фиксирован заряд на пластинах, внешних сил нет, и закон сохранения энергии (1) имеет вид
Отсюда
Тепло выделяется за счет уменьшения энергии взаимодействия зарядов.
Во втором случае есть работа батареи и фиксировано напряжение на конденсаторе:
Тогда из уравнения (1) следует
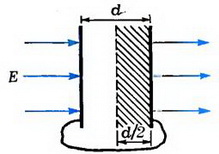
Задача 6. Две соединенные проводником пластины площадью S каждая находятся на расстоянии d друг от друга (это расстояние мало по сравнению с размерами пластин) во внешнем однородном поле с напряженностью , перпендикулярной пластинам (рис. 3). Какую работу надо совершить, чтобы сблизить их до расстояния d/2?
Рис. 3
Пластины эквипотенциальны, и между ними поля нет. Результатом работы по сближению является создание поля с напряженностью Е в объеме 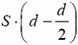
Упражнения
1. Два одинаковых плоских конденсатора емкостью С каждый соединены параллельно и заряжены до напряжения U. Пластины одного из конденсаторов медленно разводят на большое расстояние. Какая при этом совершается работа?
2. Два конденсатора, каждый емкостью С, заряжены до напряжения U и соединены через резистор (рис. 4). Пластины одного из конденсаторов быстро раздвигают, так что расстояние между ними увеличивается вдвое, а заряд на пластинах за время их перемещения не изменяется. Какое количество теплоты выделится в резисторе?
Рис. 4
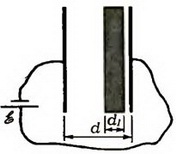
3. Плоский воздушный конденсатор присоединен к батарее с ЭДС . Площадь пластин S, расстояние между ними d. В конденсаторе находится металлическая плита толщиной d1, параллельная пластинам (рис. 5). Какую минимальную работу нужно затратить, чтобы удалить плиту из конденсатора?
Рис. 5
4. Большая тонкая проводящая пластина площадью S и толщиной d помещена в однородное электрическое поле с напряженностью , перпендикулярной поверхности пластины. Какое количество теплоты выделится в пластине, если поле мгновенно выключить? Какую минимальную работу надо совершить, чтобы удалить пластину из поля?
5. Одна из пластин плоского конденсатора подвешена на пружине (рис. 6). Площадь каждой пластины S, расстояние между ними в начальный момент d. Конденсатор на короткое время подключили к батарее, и он зарядился до напряжения U. Какой должна быть минимальная жесткость пружины, чтобы не произошло касание пластин? Смещением пластин за время зарядки пренебречь.
Рис. 6
Ответы.
1. 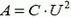
2. 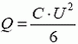
3. 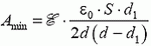
4. 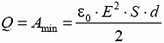
5. 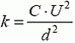
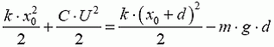
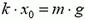
Условие задачи:
Какое количество теплоты выделяется при замыкании пластин конденсатора электроемкостью 5 мФ, заряженного до потенциала 300 В?
Задача №6.4.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(C=5) мФ, (U=300) В, (Q-?)
Решение задачи:
По закону сохранения энергии искомое количество теплоты (Q) равно разности начальной (W_1) и конечной (W_2) энергии конденсатора:
[Q = {W_1} – {W_2};;;;(1)]
Начальную энергию конденсатора (W_1) (т.е. когда он был заряжен до потенциала (U)) можно найти по формуле:
[{W_1} = frac{{C{U^2}}}{2};;;;(2)]
Когда соединят обкладки конденсатора, заряд пластин станет равным нулю, а значит и разность потенциалов между пластинами также станет равна нулю, поэтому значение конечной энергии конденсатора (W_2) равно нулю.
[{W_2} = 0;;;;(3)]
Учитывая (2) и (3), формула (1) примет такой вид:
[Q = frac{{C{U^2}}}{2}]
Задача решена, давайте найдем численный ответ к задаче:
[Q = frac{{5 cdot {{10}^{ – 3}} cdot {{300}^2}}}{2} = 225;Дж]
Ответ: 225 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.44 Батарея из четырех одинаковых конденсаторов включена один раз по схеме A, другой раз по схеме B
6.4.46 Какое количество теплоты выделяется при заземлении заряженного до потенциала 3000 В
6.4.47 Шар радиусом 25 см заряжен до потенциала 600 В. Какое количество тепла выделится
Парь
хладагента конденсируются внутри труб
конденсатора при соприкосновении с их
стенками, температура которьх ниже
темпе-ратурь насьщения пара, соответствующей
давлению в аппарате. Интенсивность
теплопередачи зависит от характера
образования конденсата, скорости и
направления движения хладагента, от
со-стояния поверхности труб, содержания
воздуха в парах, конструктивного
исполнения теплообменного аппарата и
скорости движе-ния внешней охлаждающей
средь.
Различают
два вида конденсации —
пленочную
и капельную. В первом случае жидкость
осаждается на холодной стенке трубь в
виде сплошной пленки, во втором — в
виде отдельньх капель. Пос-леднее
явление наблюдается, когда конденсат
не смачивает поверх-ность охлаждения
или когда она загрязнена маслом или
различнь-ми отложениями. Большинство
теплообменников работает со сме-шанной
конденсацией, когда в одной части
аппарата возникает ка-пельная конденсация,
а в другой — пленочная. Образующийся
жид-кий хладагент необходимо бьстро
удалять с теплопередающей по-верхности.
От
состояния внутренней поверхности
зависит толщина пленки конденсата. Она
увеличивается при шероховатой
поверхности, и зто сопровождается
снижением козффициента теплоотдачи.
Резко зависит зтот козффициент и от
наличия отложений на внутренней и
внешней сторонах труб (масло, накипь,
ржавчина, пьль, краска).
Присутствие
воздуха в парах хладагента заметно
снижает козф-фициент теплоотдачи. От
конструкции аппарата зависит характер
и скорость движения конденсата в нем,
и внешней охлаждающей средь через
аппарат. С увеличением скорости
возрастают козффи-циент теплоотдачи
и затрать мощности на перемещение
охлажда-ющего воздуха или водь. С
возрастанием скорости движения жид-кого
хладагента в трубе ламинарньй (спокойньй)
режим движения жидкости переходит в
турбулентньй (с завихрениями), при
кото-ром процессь теплопередачи
интенсифицируются.
Тепловой
расчет конденсатора предусматривает
определение либо проверку площади
теплопередающей поверхности,
обеспечи-вающей снятие тепловой нагрузки
конденсатора,
где
бпер,
бконд,
(}ож
—
соответственно теплота охлаждения
пе-регретьх паров хладагента, его
конденсации и переохлаждения жид-кости
перед дроссельньм вентилем.
Площадь
теплопередающей поверхности можно
найти по урав-нению теплопередачи:
^к
= , (2.3)
где
6 — средний температурньй напор
конденсатора, К; |/ — козффициент (индекс
противоточности), учитьвающий схему
дви-жения теплоносителей (при противотоке,
прямотоке или постоян-ной температуре
одного из теплоносителей |/ =1); К —
козффициент теплопередачи, Вт/(м2-К).
При
проектировании холодильной машинь на
заданнье усло-вия работь по найденному
значению Рк
подбирают соответству-ющий тип
конденсатора. В поверочньх расчетах
площадь Рк
со-гласовьвают с параметрами, определяющими
температурньй на-пор конденсатора, для
наиболее тяжельх условий работь маши-нь
в летнее время.
Теплопередающую
поверхность конденсатора условно
можно разделить на злементьі,
соответствующие снятию отдельньїх
составляющих тепловой нагрузки: £пер,
2конд,
Єож,
(2.4)
Схема
изменения температур хладагента 1к
и охлаждающей сре-дьі (воздуха) /в
на поверхности конденсатора приведена
на рис. 2.27.
Средний
температурньй напор конденсатора
Є
Аіб-Аім
(і2
—і»)-(і3
-і’в)
Іп
(Аі
б / ) 1п[( і2
— і3 —
і
і)]
(2.5)
где
Аґб>
Аім
—
большая и меньшая разности температур
тепло-носителей для входа в конденсатор
и вьхода из него.
Козффициент
теплопередачи для тонкостенной трубки
теплопе-редающей поверхности с наружньм
оребрением при движении хла-дагента
внутри трубь может бьть определен в
виде
К
1
1/
а к
+
Х &і
+І
а
в
пр Ф
н
(2.6)
где
ак
— козффициент теплоотдачи от хладагента
к стенке тру-
тер-
би,
Вт/(м2-К);
Кі
= 5)
мическое
сопротивление тепло-проводности
материала стенки трубь и отложений на
ее поверх-ности, (ма-К)/Вт;
5і — толщина стенки или слоя отложения,
м; — козффициент теплопроводно-сти
материала стенки или слоя отложения,
Вт/(м-К); ав
пр
—
при-веденньй козффициент теплоот-дачи
от оребренной наружной поверхности
трубь к охлаждаю
щей
среде (воздуху), Вт/(м2-К);
фн
— степень оребрения наружной поверхности
трубьі.
Определить
величину ак
в целом по конденсатору достаточно
сложно. Обьічно зто вьшолняют раздельно
для основних процес-сов, составляющих
теплоотдачу от хладагента к стенке
труби: теп-лоотдачи без изменения
агрегатного состояния и пленочной
кон-денсации.
Теплоотдача
без изменения агрегатного состояния
хладагента
при
его турбулентном движении внутри канала
(трубь )
а
к
в™0,8
в а-к0в2,
(2.7)
где
В
—
козффициент, зависящий от физических
свойств хладагента (табл. 2.4); ц
—
скорость течения хладагента (для пара
5—20 м/с, для жидкости 0,5-1,5 м/с); 8
—
поправочний козффициент, учитивающий
изменение козффициента теплоотдачи
по длине канала; ^-кв—
зквива-лентний диаметр канала (для
труби — внутренний диаметр 0вн,
м).
Таблица
2.4
|
Хладагент |
Температура |
||||
|
-10 |
0 |
10 |
20 |
30 |
|
|
К12 |
660 |
665 |
666 |
666 |
664 |
|
Я22 |
764 |
750 |
734 |
716 |
695 |
Формула
отвечает значениям числа Рейнольдса,
характеризую-
щего
режим течения,
Кє
V
—
зкв
>
104
(V
кинематическая
вяз-
кость
хладагента, м2/с).
Козффициент
8
определяют
по формуле
в
=
0,6
(
1
1
кє
а-кв
ч-1/7
(
1
+ 2,5-
1
(2.8)
где
І
—
длина канала (труби), м.
Для
течения хладагента внутри труби формула
справедлива при швн<
0,1Кє.
Пленочная
конденсация на внутренней поверхности
канала (формула Нуссельта)
а
к
0,724
грі3
д
Vе
а
а-кв
(2.9)
где
г
—
теплота парообразования хладагента,
Дж/кг; р — плот-
ность
жидкости, кг/м3;
X —козффициент теплопроводности
жидко-сти, Вт/(м-К); д
—
ускорение свободного падения, м/с2;
V — кинема-тическая вязкость жидкости,
м2/с;
6а
— разность температур конденсации
хладагента и стенки, К; ^зкв
— зквивалентний диаметр канала (для
труби — внутренний диаметр ^вн),
м.
Физические
параметри хладагента, входящие в
формулу, при-нимают по температуре
конденсации їк.
Интенсивность
теплообмена при пленочной конденсации,
име-
ющей место в конденсаторах парових
холодильних машин, в ос-
новном зависит
от плотности передаваемого теплового
потока
#к
= Общее виражение для козффициента
теплоотдачи при
конденсации
хладагента в горизонтальних трубах в
зтом случае имеет вид:
а
к
= X
я0,5
а
0,25г
0,35
вн 1
(2.10)
где
X — козффициент, значения которого
приведени в табл. 2.5.
Средние
значения козффициента теплоотдачи от
хладагента к стен-ке канала в конденсаторах
парових холодильних машин при кон-денсации
чистого хладагента составляют для КЛ2
= 1100 2300, для К22 = 1500 2800 и аммиака 7000 — 10 000
Вт/(м2-К).
Наличие в хлада-генте неконденсируемих
примесей, в частности воздуха, ухудшает
процесс теплоотдачи в особенности при
малой плотности теплового потока. Так,
для Як
= 4650 Вт/м2
при концентрации воздуха 5 % по обьему
козффициент теплоотдачи аммиака
снижается почти в 5 раз, для КЛ2 концентрация
воздуха порядка 10 % снижает козффициент
теплоотдачи на 20 %.
Термическое
сопротивление теплопроводности в
конденсаторах холодильних машин с
тонкостенной трубной теплопередаю-щей
поверхностью в основном определяется
сопротивлением слоя загрязняющих
отложений. Значения козффициентов
теплопровод-ности для металлов,
используемих при изготовлении труб
конденсатора, а также характерних
загрязнений теплопередающей по-
верхности,
Вт/(м-К):
Сталь
углеродистая 45
Алюминий 200-230
Медь 300-385
Латунь 86-106
Цинк 113
Смазочное
масло
Слой
краски
Слой
пили Слой накипи
0,14
0,23 0,80
1,75—1,80
Козффициент
теплоотдачи от наружной поверхности
трубок конденсатора к охлаждающему
воздуху ав
при поперечном обтека-нии пучков гладких
или оребренних труб (поперечние круглие
ребра) можно определить по уравнению
связи критериев Нуссельта и
Рейнольдса
для такого вида теплообмена:
N
и
а
в Іусл
сс
2
с 8
фн
тКє
п
где
С,
С2,
С8
—
козффициенти критериального уравнения;
фн=
^ор/^0
—
степень оребрения наружной поверхности
труби; Г
—
общая
площадь наружной поверхности на 1 м
длини труби (пло-
щадь
ребер и межреберной поверхности труби),
м2;
Г0
—
площадь наружной поверхности труби
при отсутствии ребер, м2;
Іусл—
характерний линейний размер, м.
Значення
козффициента С и показателя степени
т, учитьівающие расположение труб в
пучке, приведень в табл. 2.6.
Таблица
2.6
|
Расположение |
С |
т |
|
Коридорное |
0,18 |
0,7 |
|
Шахматное |
0,32 |
0,5 |
Значения
козффициента С2,
определяющего
влияние числа рядов труб в пучке по
потоку охлаждающего воздуха, собраньї
в табл. 2.7.
Таблица
2.7
|
Расположение |
ке-ш3 |
Число |
|||
|
1 |
2 |
3 |
4 |
||
|
12 |
1.4 |
1,3 |
1,0 |
1,0 |
|
|
Коридорное |
30 |
1,2 |
1.2 |
1,0 |
1,0 |
|
50 |
1.0 |
1.0 |
1,0 |
1,0 |
|
|
Шахматное |
12 |
0,82 |
0,90 |
0,97 |
1,0 |
Показатель
степени для критерия Рейнольдса п =
0,6фн0,07;
фи-зические
параметрьі воздуха отнесеньї к средней
температуре пото-ка/ скорость — к
минимальному проходному сечению пучка;
в ка-честве характерного линейного
размера трубного пучка в вьраже-ниях
критериев Ке
и
N11
принята
величина
і
усл
= (а
н
/
ф н)
+
(1
-1/ф
н)
р
‘0,785(£>р
— ар),
(2.11)
где
сІн
—
наружньїй
диаметр трубьі, м; Л
—
наружньїй
диаметр ребра, м; фн‘
— условная
степень оребрения наружной поверхности
трубьі; фн‘
= ^ор/^мр;
^мр
—
площадь
наружной поверхности в меж-
реберньх
пространствах на 1
м
длинь трубь ,
м2.
Вьгражения
для козффициента С8,
где
8Ь
82,
—
соответственно
поперечншй, продольньїй и диагональншй
шаг трубного пучка, а также граничньїе
условия применения формульї собранш
в табл. 2.8.
Для
гладкотрубньгх пучков ф
н
=
1,
а
/усл=^н.
Приведенньй
козффициент теплоотдачи от оребренной
наружной поверхности труб конденсатора
к охлаждающему воздуху на-ходят в виде
ґ
а
впр
— а
в
——
Е
р
ш
+ —-
(2.12)
V
)
где
Ер
—
площадь поверхности ребер на 1 м длиньї
трубь, м2;
Ер
—
козффиЦиент
зффективности ребра; у — козффициент
неравномер-ности теплоотдачи по вьсоте
ребра (для поперечньх ребер на круг-льгх
трубах у = 0,85).
Козффициент
зффективности ребра, зависящий от его
условной вьісотьі п и параметра т,
определяют по формуле Ер
=
ік
(тпИ)Ітк.
При
зтом условная вьсота круглого ребра
составляет
к
=
0ДО -сі
)[1+0,8051§(£>
Іі )];
параметр
т
—
д/2а
в
/(X з5
з
) , где Хр,
5р
— козффициентьі теп-
лопроводности
материала ребра и его толщина
соответственно. Оребрение труб
конденсаторов воздушного охлаждения,
использу-емьх в транспортньх холодильньх
установках, вьполняют с козф-фициентом
зффективности 0,95—1,0.
Средние
значения козффициента теплоотдачи от
наружной труб-ной поверхности конденсатора
к охлаждающему воздуху при его
принудительном движении со скоростью
3—8 м/с составляют в конденсаторах
транспортних холодильних установок
20—100 ВтІ(м2-К).
При
зтом средние значения козффициента
теплопередачи для конденсаторов
трубного типа с воздушним охлаждением
находятся в пределах 15—50
Вт/(м2-К).
Особенность
теплового расчета конденсатора состоит
в том, что условия теплоотдачи при
конденсации зависят от неизвестной
раз-ности температур хладагента и
стенки теплопередающей поверх-ности.
Позтому при машинном способе счета
тепловой расчет ве-дут методом
последовательних приближений, задаваясь
рядом значений 6а;
при
ручном способе используют графоаналитический
метод расчета в координатах разность
температур конденсации и стен-ки —
плотность
теплового потока.
Гидромеханический
расчет
конденсатора включает определение
потерь давления (сопротивлений),
возникающих при движении хладагента
и охлаждающей среди (воздух, вода), а
также мощно-сти вентилятора или насоса,
обеспечивающего движение охлаж-дающей
среди.
Потери
давления по хладагенту при его движении
в трубах
2 2
ДРХ
=ДРтр
+АРм
=
2
4
^ +
£ (2.13)
где
Д^тр,
Д^м
—
соответственно потери давления от
трения и местних сопротивлений при
изменении направления движения потока
или скорости, Па; £
и
£,
— козффициенти трения и мест-них
сопротивлений, которие определяются
по справочникам; Ь
и
^зкв
—
длина и зквивалентний диаметр канала,
по которому течет хладагент, м.
Потери
давления пр охлаждающему воздуху при
поперечном смивании трубних пучков с
круглими или спиральними ребрами,
Па,
ДРв
=
СС:С8СІС1
(р»)п. (2.14)
Значения
козффициентов С,
С$,
С1,
Сі
и
показателя степени п, учитивающие
расположение труб в пучке, приведени
в табл. 2.9
(і
—
температура воздуха, °С); значение
козффициента С
,
завися
щего
от числа рядов труб в пучке по потоку
охлаждающего воздуха 2,
приведено
в табл. 2.10 (при 2
>
6
козффициент С2
=
2);
гра-ничньїе
условия применения формульї даньї в
табл 2.9.
Таблица
2.9
|
Расположение |
С |
сі |
С |
п |
|
|
Коридорное |
0,26 |
[(52 |
10,22 й0,3 |
0,326+0,001275/ |
1.92 |
|
Шахматное |
2,70 |
1 |
10,05 й0,3 кв |
0,0505+0,00023/ |
1,75 |
й
зкв =
Зквивалентньїй
диаметр минимального проходного сечения
2[
5 р
(51
— й
н)
— 25 р
Нр
]/(2Ар
+ 5 р),
соответственно
вьісота и толщина ребра, м; 5р
шаг
рє6Єр,
м.
(2.15)
При
использовании формули для гладкотрубньїх
пучков
/
=
й
а
=
2(5,
—
а).
усл
н’ зкв 4
1 н/
1
н )
Мощность
вентилятора, обеспечивающего движение
охлажда-ющего воздуха в конденсаторе,
N
в
—
(2.16)
(Ар
в
+АРс),
Р
в
П
в
где
Єв
—
расход охлаждающего воздуха, кгІс; рв
—
плотность воздуха, кгІм3;
Г|в
—
КПД вентилятора; АРс
—
потери давления во
внешней
воздушной сети, Па.
Вьбирают
вентилятор по расходу охлаждающего
воздуха и сум-марньм потерям его давления
в системе охлаждения конденсатора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
21.02.2016563.2 Кб1441.doc
- #
21.02.201676.29 Кб121.doc
- #
- #
- #
- #
- #
- #

- Подробности
- Категория: Подстанции
Страница 20 из 26
УРАВНЕНИЯ ТЕПЛООБМЕНА В СИЛОВОМ КОНДЕНСАТОРЕ
Тепловой расчет является важной составной частью общего расчета силового конденсатора. При этом могут решаться две задачи. Одна, прямая, состоит в нахождении распределения температуры и точки максимального перегрева диэлектрика при заданной конструкции и свойствах материалов, другая, обратная и более сложная, состоит в том, чтобы, исходя из заданных режимов, условий эксплуатации и свойств активных материалов, определить оптимальную с точки зрения тепловых характеристик конструкцию конденсатора, обеспечивающую для данных конкретных условий экономически целесообразный ресурс при минимуме затрат. Обе задачи решаются с помощью уравнений теплообмена с граничными условиями применительно к конкретным конструкциям конденсаторов.
Подавляющее большинство конденсаторов имеют форму прямоугольного параллелепипеда (рис. 14.1, а, б), большую долю внутреннего объема которого занимает пакет. В первом приближении будем рассматривать активную часть пакета Ох с границей Г1 как сплошную среду (рис. 14.1, в), пренебрегая наличием прокладок и холостых витков, поскольку доля их незначительна. По активному объему практически равномерно распределены внутренние источники тепла. Коэффициенты теплопроводности объема Хх, Ху и Хх вдоль осей х, у и г постоянны и различны. Снаружи активный объем окружен слоем тепловой изоляции О2 с границей Гг.

Рнс. 14.1. К тепловому расчету силового конденсатора
Теплообмен с окружающей средой осуществляется через границу Гг. У конденсаторов с водяным охлаждением практически все образующееся в активном объеме тепло движется в направлении охлаждающей системы и отбирается сю. Особенности конструкции и расчета этих конденсаторов будут рассмотрены ниже. Здесь рассматривается тепловой расчет конденсаторов с воздушным охлаждением.
Пакет от корпуса обычно изолируется пропитанной кабельной бумагой. Схема изоляции показана на рис. 14.1, г. На рисунке обозначено: Дм—толщина стенки корпуса; — коэффициент теплопроводности материала корпуса; Д5—суммарная толщина пропитанной кабельной бумаги; Хб—коэффициент теплопроводности пропитанной кабельной бумаги; Дж—суммарная толщина прослойки пропитывающей жидкости, Хж — коэффициент теплопроводности пропитывающей жидкости. При расчетах весь этот комплекс удобнее характеризовать одним эквивалентным коэффициентом теплопроводности
(14.1)
где Дн—суммарная толщина эквивалентного слоя, равная полуразности внешних размеров корпуса и пакета.
Предполагается, что толщина изоляции одинакова во всех точках.