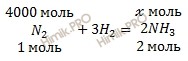Как найти теоретическое возможное

Теоретическая вероятность: определение + примеры

         
  ЗАДАЧИ НА « ТЕОРЕТИЧЕСКИ-ВОЗМОЖНЫЙ ВЫХОД»

Данный тип задач является наиболее трудным для
учащихся. Они путают массовую долю вещества и массовую долю выхода. Раньше и 
обозначения этих понятий были одинаковыми. При решении задач подобного типа
надо ученикам предложить запомнить обозначения  выхода при следующих понятиях:
1. Если вещество в массе-формула выхода   

                    2.Если вещество в
объеме-формула выхода —

                    3.Если вещество в моль-формула
выхода-

  Соответственно, и три формулы по которым решаются задачи.

1.         
2. m(прак)=       
3. m(теор)= 

*Данные формулы могут принимать другой вид при
изменении вещества.

Задача №1.» Определение выхода».Формула №1 Из 200 г. пирита  получили 100 г серной
кислоты. Определить массовую долю выхода кислоты.

Дано:                                             
Решение.     1 способ.

m (FeS₂)=200 г.                   200 г.     Х( тео

m ( H₂SO₄)=100г.      1).        
FeS₂         2)  =30, 7
%         

                                              
120г.        198 г.

  ( Н₂SO₄)-?                                Х=32,6 г.(
теор)   2 способ.

1.)  =1,66 м    2)n(H₂SO₄)==1,02 м.

                                      3) FeS₂ 2H₂SO₄ соотношение 1:2=2моль H₂SO₄

                                        4)=
30, 7%.  Ответ: Выход кислоты 30, 7 %.

Задача №2 Определение массы или объема, если
известен процент практического выхода. Формула №2

При сгорании 16 г. серы получили  газ SO₂, что составило 90% его практического выхода.
Какой объем газа выделился?

Дано:                                     
  Решение                                             1 способ

 M(S)=16                          16г.                 
Xтеор)

          1).
S  +  O₂  SO₂   
x=11 2    2)V( прак ) ==10, 08л.

   VSO2)                           32г.               
22,4л.

                                                                                             
2 способ

1)  
 n(S)==0,5 моль.   2)  
S  +  O ₂ SO₂
1nS=1nSO₂ = 0 5 моль  SO₂(теор)

     3)V(прак)==0,
45 моль.  4)V= Vm х n = 22,4 л/м х 0,45
м=10,08 л.

                       Ответ — выделится 10,08
л. газа при его практическом выходе90%.

Задача №3 Определение массы, объема или
количество вещества,если продукт реакции  составляет определенный процент
практического выхода.(используется формула №3)

Сколько было взято  цинка, если при реакции
его с сульфатной кислотой было получено 10 л. газа( н.у.), что составило 90 %
его практического выхода.

Дано:                                    Решение                        
1 способ                

 V(H₂)= 10л.

           
  1) V(теор)==11,11
л H₂.

m (Zn)- ?                                       x                                    
11, 11

  2.  Zn + H₂SO₄ZnSO₄
+ H₂                  
x=32,24 л. Н₂

        65г.                                
22,4л.

Решение                              2 способ

1.)n(H2)==0,446
л.     2)n(теор)===0,495
моль.

3)   Zn + H₂SO₄ ZnSO₄ + H₂Соотношение
1:1 Zn=0,495 моль.

4)     m(Zn)= n x M= 0,495
моль х 65 г/моль=32,24 г.

     Ответ: было взято 32, 24 г. цинка.

Задача №4. На сколько процентов теоретический
выход больше практического. Задача копия первого типа- находится массовая доля
выхода и от 100 % отнимается процент  выхода вещества.

Из 120 г. пропанола получили 10 л. пропилена. На
сколько % теоретический выход меньше практического?

Дано:                                                        

m(C₃H₇OH)=120             1)  n=  2) n(C₃H₆)==0,45 м(пр)

М( С₃Н₆)= 10

(теор)
  (прак)       
3) С₃Н₇ОН С₃Н₆ 
+Н₂О Соотношение: 2:1.Число

                                                  моль
С₃Н₆ 2 моль( теор)

                                              ==22,
5 %.

    4). 100%- 22,5% =77, 5%. Ответ : на 77,5 %
теоретический выход больше.

Прежде всего отмечу, что задача сформулирована совершенно неграмотно.

Во-первых, этен и водород при обычных условиях — газы. В задачах, связанных с газами, для того, чтобы можно было что-то рассчитывать, нужно указать условия (давление, температуру). Возможно они и указаны в оригинале задачи в виде скромного незаметного «при нормальных условиях», или даже просто при «н.у», но при переписывании Вы не придали этому значения и для «экономии», решили пропустить эту фразу. Но без этого получается «на деревню, дедушке».

Во-вторых, если с этеном более или менее понятно, то совершенно неясно, сколько было взято водорода, хватило ли его для для того, чтобы весь этен мог прореагировать?. Обычно в таких ситуациях пишут «с избытком».

Грамотная формулировка задачи должна быть примерно такая: «При взаимодействии 20 л этена, взятого (измеренного) при нормальных условиях, с избытком водорода, образовалось 22 г продукта».

Вот тогда можно вычислять.

В такого рода задачах считается, что газы идеальные. А при нормальных условиях (температура 0°С, давление 760 мм рт.ст.) 1 моль любого идеального газа занимает объём 22, л. Значит этена было взято 20/22,4=0,8929 моль. При взаимодействии этена с водородом может образоваться только этан, по реакции: С2Н4 + Н2 ——> С2Н6. Молярная масса этана 30 г. Значит образовалось 22/30=0,7333 моль этана, а теоретически могло образоваться 20/22,4 моль. Вход этана от теоретически возможного составляет (22/30)/(20/22,4)=0,­7333/0,8929=0,8213 или 82,13 %.

Избыточные вычисления производить необязательно, т.е. можно было просто вычислить (22/30)/(20/22,4)=0,­8213. Вычисление количества молей обоих веществ я произвёл исключительно с методической целью, чтобы было понятнее, что выход продукта от теоретически возможного определяется как отношение количества реально полученных молей к количеству молей которое могло получиться.

❓ Что такое теория вероятностей?

Теория вероятностей использует случайные величины и распределения вероятностей для математической оценки неопределенных ситуаций. Понятие вероятности используется для присвоения числового описания вероятности наступления события. Вероятность можно определить как число благоприятных исходов, деленное на общее число возможных исходов события.

Определение теории вероятностей

Теория вероятностей – это область математики и статистики, которая занимается определением вероятностей, связанных со случайными событиями. Существует два основных подхода к изучению теории вероятностей: теоретический и экспериментальный. Теоретическая вероятность определяется на основе логических рассуждений без проведения экспериментов. В отличие от нее, экспериментальная вероятность определяется на основе исторических данных путем проведения повторных экспериментов.

Пример теории вероятностей

Предположим, нам необходимо определить вероятность выпадения числа 4 при бросании игральной кости. Число благоприятных исходов равно 1. Возможные исходы игральной кости – {1, 2, 3, 4, 5, 6}. Из этого следует, что всего существует 6 исходов. Таким образом, вероятность выпадения 4 при бросании игральной кости, используя теорию вероятности, можно вычислить как 1 / 6 ≈ 0,167.

🎲 Основы теории вероятностей

Мы можем понять эту область математики с помощью нескольких основных терминов, напрямую связанных с теорией вероятностей.

Случайный эксперимент

Случайный эксперимент в теории вероятностей – это испытание, которое повторяется несколько раз для получения четко определенного набора возможных результатов. Подбрасывание монеты является примером случайного эксперимента.

Пространство выборки

Пространство выборки можно определить как множество всех возможных исходов, полученных в результате проведения случайного эксперимента. Например, пространство выборки при подбрасывании симметричной монеты (fair coin), стороны которой – это орел и решка.

Событие

Теория вероятностей определяет событие как набор исходов эксперимента, который образует подмножество пространства выборки.

Примеры событий:

1. Независимые – те, на которые не влияют другие события, являются независимыми.
2. Зависимые – те, на которые влияют другие события.
3. Взаимоисключающие – события, которые не могут произойти в одно и то же время.
4. Равновероятные – два или более события, которые имеют одинаковые шансы произойти.
5. Исчерпывающие – это события, которые равны выборочному пространству эксперимента.

Случайная величина

В теории вероятностей случайную переменную можно определить как величину, которая принимает значение при всех возможных исходах эксперимента.

Существует два типа случайных величин:

1. Дискретная случайная величина – принимает точные значения, такие как 0, 1, 2…. Описывается кумулятивной функцией распределения и функцией массы вероятности.
2. Непрерывная случайная величина – переменная, которая может принимать бесконечное число значений. Для определения характеристик этой переменной используются кумулятивная функция распределения и функция плотности вероятности.

Вероятность

Вероятность мы можем определить как численную вероятность наступления события. Вероятность того, что событие произойдет, всегда лежит между 0 и 1. Это связано с тем, что число желаемых исходов никогда не может превысить общее число исходов события. Теоретическая вероятность и эмпирическая вероятность используются в теории вероятностей для измерения шанса наступления события.

Условная вероятность

Ситуация, когда необходимо определить вероятность наступления события, притом что другое событие уже произошло.

Обозначается как P(A | B).

Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», на котором ты:

• Усвоишь специальную терминологию и сможешь читать статьи по Data Science без постоянных обращений к поисковику.
• Подготовишься к успешной сдачи вступительных экзаменов в Школу анализа данных Яндекс.
• Овладеешь математическим аппаратом, который необходим, чтобы стать специалистом в Data Science.

Ожидание

Ожидание случайной величины X можно определить как среднее значение результатов эксперимента, проводимого многократно. Ожидание обозначается как E[X]. Также известно как среднее значение случайной величины.

Дисперсия

Дисперсия – это мера, которая показывает, как распределение случайной величины изменяется относительно среднего значения. Дисперсия определяется как среднее квадратичное отклонение от среднего значения случайной величины. Обозначается как Var[X].

Функция распределения теории вероятностей

Распределение вероятностей или кумулятивная функция распределения – это функция, которая моделирует все возможные значения эксперимента, используя случайную переменную. Распределение Бернулли и биномиальное распределение – это примеры дискретных распределений вероятностей. Например, нормальное распределение представляет собой пример непрерывного распределения.

Массовая функция вероятности

Массовая функция вероятности определяется как вероятность того, что дискретная случайная величина будет в точности равна определенному значению.

Функция плотности вероятности

Функция плотности вероятности – это вероятность того, что непрерывная случайная величина принимает множество возможных значений.

Формулы теории вероятностей

В теории вероятностей существует множество формул, которые помогают рассчитать различные вероятности, связанные с событиями.

Наиболее важные формулы:

1. Теоретическая вероятность: Число благоприятных исходов / Число возможных исходов.
2. Эмпирическая вероятность: Число случаев, когда событие происходит / Общее число испытаний.
3. Правило сложения: P(A ∪ B) = P(A) + P(B) – P(A∩B), где A и B – события.
4. Правило комплементарности: P(A’) = 1 – P(A). P(A’) означает вероятность того, что событие не произойдет.
5. Независимые события: P(A∩B) = P(A) ⋅ P(B).
6. Условная вероятность: P(A | B) = P(A∩B) / P(B).
7. Теорема Байеса: P(A | B) = P(B | A) ⋅ P(A) / P(B).
8. Массовая функция вероятности: f(x) = P(X = x).
9. Функция плотности вероятности: p(x) = p(x) = dF(x) / dx, где F(x) – кумулятивная функция распределения.
10. Ожидание непрерывной случайной величины: ∫xf(x)dx, где f(x) является МФВ (Массовой функцией вероятности).
11. Ожидание дискретной случайной величины: ∑xp(x), где p(x) – это ФПВ (Функцией плотности вероятности).
12. Дисперсия: Var(X) = E[X2] – (E[X])2.

Применение теории вероятностей

Теория вероятностей используется во многих областях и помогает оценить риски, которые связаны с теми или иными решениями. Некоторые из направлений, где применяют теорию вероятностей:

• В финансовой отрасли теория вероятностей используется для создания математических моделей фондового рынка с целью прогнозирования будущих тенденций. Это помогает инвесторам вкладывать средства в наименее рискованные активы, которые дают наилучший доход.

• В потребительской индустрии теория вероятностей используется для снижения вероятности неудачи при разработке продукта.

• Казино использует теорию вероятностей для разработки азартных игр с максимизацией своей прибыли.

🏋️ Практические задания

Задача 1: При бросании двух игральных костей, какова вероятность того, что выпадет комбинация, сумма которой будет равна 8?

Задача 2: Какова вероятность вытащить карту королеву из колоды?

Задача 3: Из 10 человек 3 купили карандаши, 5 купили тетради, а 2 купили и карандаши, и тетради. Если покупатель купил тетрадь, какова вероятность того, что он также купил карандаш?

В заключение

Подведем итоги:

• Теория вероятностей – это раздел математики, в котором рассматриваются вероятности случайных событий.
• Понятие вероятности объясняет возможность наступления того или иного события.
• Значение вероятности всегда лежит между 0 и 1.
• В теории вероятностей все возможные исходы случайного эксперимента составляют пространство выборки.
• Теория вероятностей использует такие важные понятия, как случайные величины и кумулятивные функции распределения для моделирования случайного события. Сюда же относится определение различных вероятностей, связанных с этим.

Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», который включает в себя:

• 47 видеолекций и 150 практических заданий.
• Консультации с преподавателями курса.