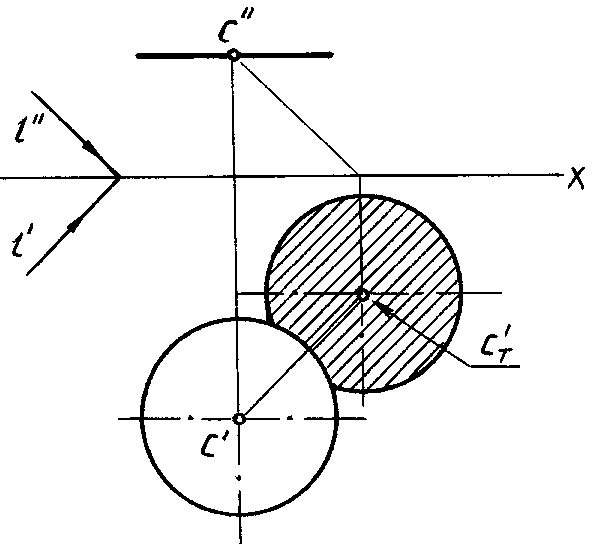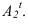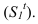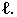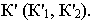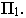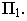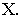-
Построение теней
План:
7.1. Основы теории теней
7.2. Тени от точки, линии и плоской фигуры
7.3. Тень, падающая от одной фигуры на
другую
7.4. Тени геометрических тел
7.5. Тени пересекающихся многогранников
(от здания)
7.6. Тени на фасадах зданий
-
Основы теории теней
Нанесением теней
пользуются для придания проекционным
чертежам большей наглядности. Особенно
широко используются тени при оформлении
архитектурных проектов, а также для
решения ряда практических задач
(например, для выявления освещенности
наружных или внутренних частей сооружения
при определенных условиях, для определения
размеров сооружения по отбрасываемой
им тени и т.п.).
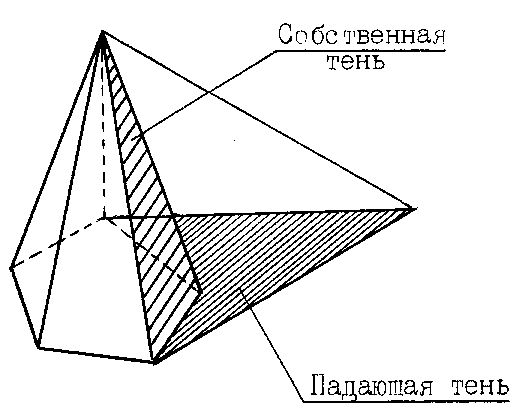
Различают
собственные и падающие тени.
СОБСТВЕННОЙ
называется тень, которая получается
на неосвещенной поверхности предмета
(или объекта) при освещении его каким-либо
источником света (рис. 72).
Рис.
72
ПАДАЮЩЕЙ
называется тень, отбрасываемая
предметом на плоскости проекций, или
возникающая на поверхности предмета
из-за того, что на пути лучей света
расположен другой предмет.
Если предмет
освещается источником света, находящимся
на конечном расстоянии от него (факелом,
лампой, свечой), то совокупность световых
лучей, падающих на предмет, образует
конус или пирамиду. Такая тень называется
ФАКЕЛЬНОЙ.
Если же источник
света находится в бесконечности, то
совокупность световых лучей образует
цилиндр или призму. Тень при этих
условиях называется СОЛНЕЧНОЙ.
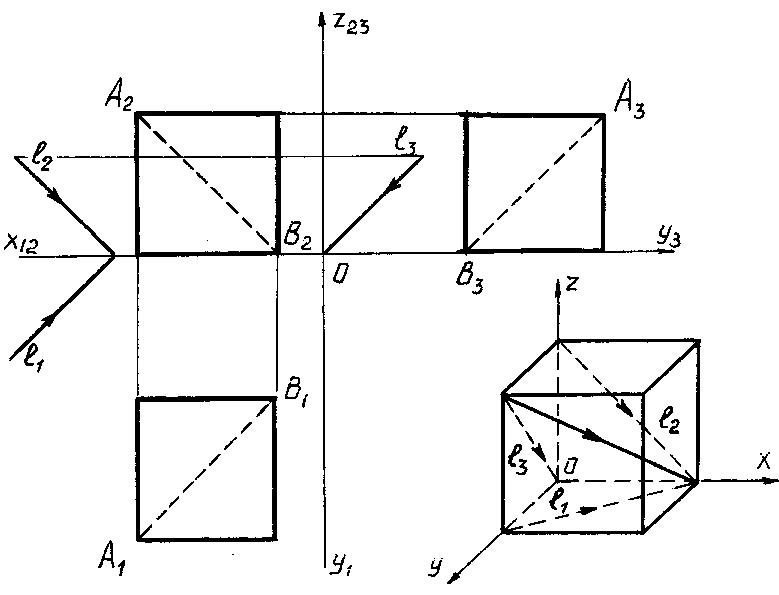
НАПРАВЛЕНИЕ
СВЕТОВЫХ ЛУЧЕЙ. При построении теней
в ортогональных проекциях, направление
lлучей света обычно принимают
параллельным диагонали куба, грани
которого параллельны плоскостям
проекций (рис. 73).
Рис.
73
Диагональ куба
АВобразует с плоскостями проекций
углы, равные 35о16′, а проекции ее
наклонены к плоскостям H, V, и W под углом
45o.
При построении
теней в аксонометрии, направление лучей
света, параллельное диагонали куба, не
всегда дает удачное расположение
светотеней; в таких случаях следует
выбрать другое направление, обеспечивающее
выразительность чертежа.
-
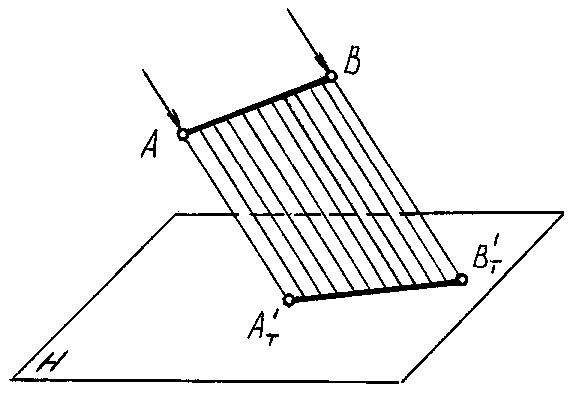
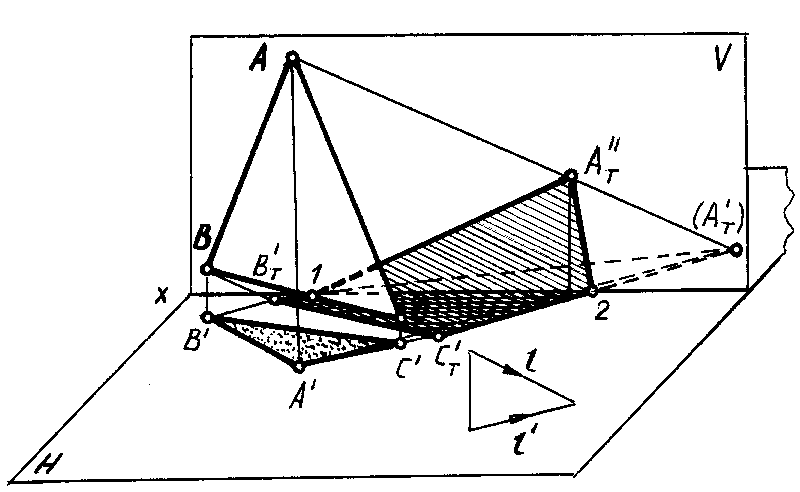
Тени от точки, линии и плоской фигуры
ПАДАЮЩАЯ ТЕНЬ ОТ
ТОЧКИ
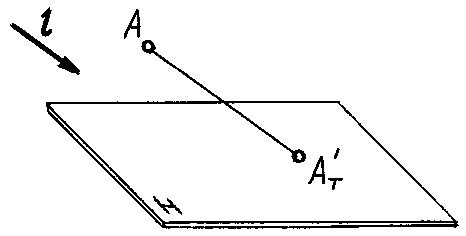
Представим себе
материальную точку А(рис. 74),
расположенную в пространстве над
плоскостью Н, которая освещается
световыми лучами, идущими из бесконечности
параллельно заданному направлениюl.
ТочкаАзадержит один из них и
отбросит теневой луч, который пересечет
плоскость Н в точкеАТ‘. Эта
точка и будет являться тенью точкиА.
Иными словами,
тень точки является следом теневого
луча.
Итак, чтобы
построить тень, падающую от точки на
какую-либо плоскость или поверхность,
необходимо через данную точку провести
прямую, параллельную направлению лучей
света, и определить точку пересечения
этой прямой с плоскостью или поверхностью,
на которую падает тень.
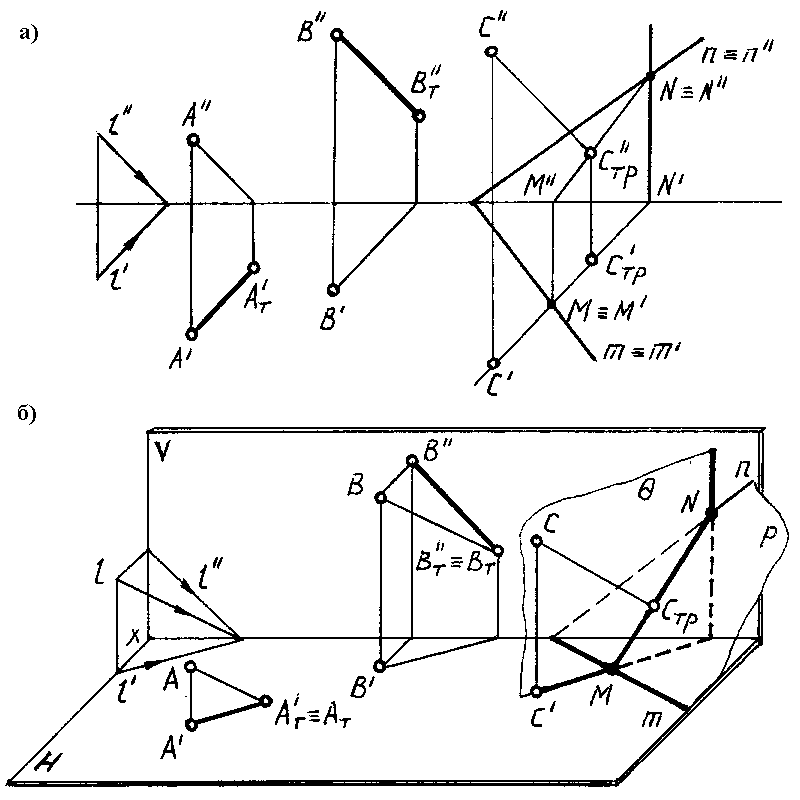
На рис. 75а в
ортогональных проекциях и на рис. 75б
в аксонометрии построены тени, падающие
на плоскости Н, V и P(nm) от точекА,ВиС.
Рис.
74
Рис.
75
Тень от точки
Ападает на плоскость Н в точкеАТ‘ (эта точка является
горизонтальным следом лучаААТ).
Тень от точки Впадает на плоскость V в точкеBТ»
(эта точка является фронтальным
следом лучаАВТ).
Тень от точки в
аксонометрииопределяется в результате
пересечения луча с его вторичной
проекцией.
Тень ВT»
(в аксонометрии) можно построить как
точку пересечения лучаВВТ с
его фронтальной проекциейВ»BT»или при помощи горизонтальной проекции
луча.
Тень от точки
Спадает на плоскость P (nm) в точкеСTP (СTP‘, СTP”),
которая определяется в результате
пересечения лучаССT с заданной
плоскостью Р при помощи
горизонтально-проецирующей плоскости.
ПАДАЮЩАЯ ТЕНЬ ОТ
ПРЯМОЙ ЛИНИИ
Тень, падающая от
прямой линии, состоит из падающих теней
от всех ее точек. Лучи, проходящие через
все точки прямой, образуют лучевую
плоскость, а тень от прямой линии есть
линия пересечения лучевой плоскости
с плоскостью или поверхностью, на
которую падает тень (то есть след лучевой
плоскости).
Тенью, падающей
от прямой на плоскость, является прямая
линия, поэтому для ее построения
достаточно построить тени от двух
точек, принадлежащих этой прямой
(рис. 76).
Рис.
76
На рис. 77
построена тень на плоскости проекций
от отрезка АВ на комплексном чертеже.
Рис.
77
Тени от точек А
и B
в этом
примере падают на одну плоскость
проекций V, поэтому для построения тени
отрезкаАВдостаточно соединить
между собой полученные точкиАT»
иВT» прямой линией.
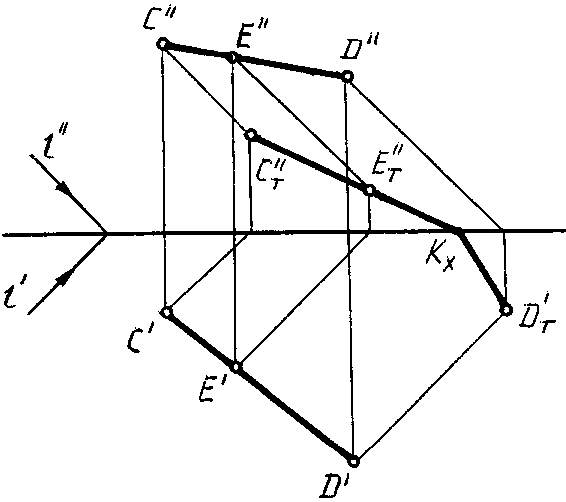
ПРИМЕР.
Построить падающую тень на H и V от
отрезка прямойСD(рис. 78, 79).

Рис. 78 Рис.
79
Решение. Тень от
отрезка СDпадает на две плоскости
проекций и представляет собой ломаную
линиюCT»KXDT‘.
Точку переломаКX можно
определить двумя способами:
1) при помощи
мнимой тени(рис. 78, 79).
Для этого строят
тень отрезка на одну из плоскостей
проекций, предполагая, что второй не
существует. На рисунке сначала построена
тень отрезка на плоскость Н (СT‘DT‘).
Построенная тень пересекает осьОХв точкеКX, в этой точке тень
переломится и с одной плоскости перейдет
на другую (в точкуСT»).
2) при помощи
тени от промежуточной точки(рис.
80).
Рис.
80
На чертеже точка
перелома КX определяется при
помощи тени от произвольной промежуточной
точкиЕ (ЕT»).
Тени от прямых,
находящихся в частных положениях
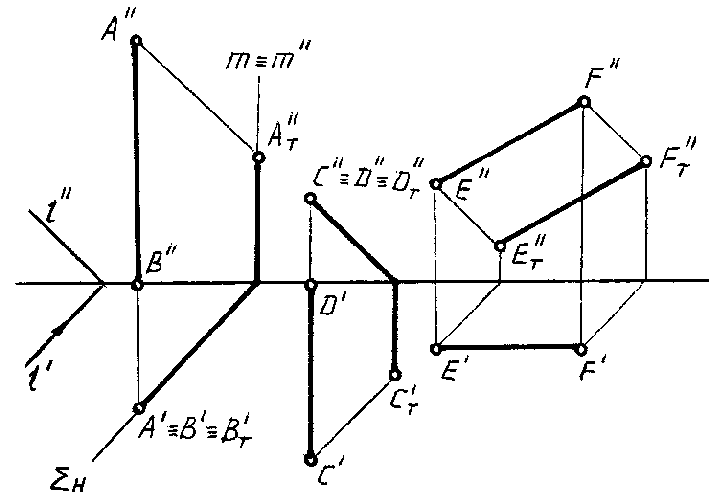
ПРИМЕР. В
ортогональных проекциях заданы отрезки
частного положенияАВ,СDиEF.
Построить тени, падающие от этих отрезков
на плоскости проекций H и V (рис. 81).
Рис.
81
Решение.
1. Отрезок АВ
занимает вертикальное положение,
поэтому лучи, проходящие через все его
точки, образуют вертикальную
(горизонтально-проецирующую) лучевую
плоскость , которая
пересечет плоскость Н по линииH,
а плоскость V — по вертикальной
прямойm=m». Следовательно,
тень от вертикальной прямой линии на
горизонтальной плоскости совпадает с
горизонтальной проекцией (следом)
лучевой плоскости.
Но, так как
горизонтальная проекция лучевой
плоскости параллельна горизонтальной
проекции луча света, то для построения
тени на горизонтальной плоскости
проекций (от вертикальной прямой)
достаточно через горизонтальную
проекцию прямой (точку) провести
горизонтальную проекцию луча света.
2. Отрезок CDперпендикулярен плоскости V, поэтому
проходящая через него лучевая плоскость
является фронтально-проецирующей
плоскостью.
В ортогональных
проекциях тень от прямой СDна
плоскости V совпадает с проекцией
лучевой плоскости.
3. Отрезок EFпараллелен плоскости V. Его теньET»FT»
параллельна и равна данному отрезку.
В ЫВОДЫ:
1. Тень от
прямой, перпендикулярной к плоскости,
совпадает с ортогональной проекцией
светового луча на эту плоскость.
2. Тень, падающая
на плоскость от отрезка прямой,
параллельной этой плоскости, параллельна
и равна отрезку прямой. На комплексном
чертеже проекция тени равна и параллельна
проекции отрезка.
ТЕНЬ ОТ ПЛОСКОЙ
ФИГУРЫ
(непрозрачной
пластинки)
Чтобы построить
падающую тень от плоской фигуры,
ограниченной многоугольником, достаточно
построить тени, падающие от всех сторон
многоугольника.
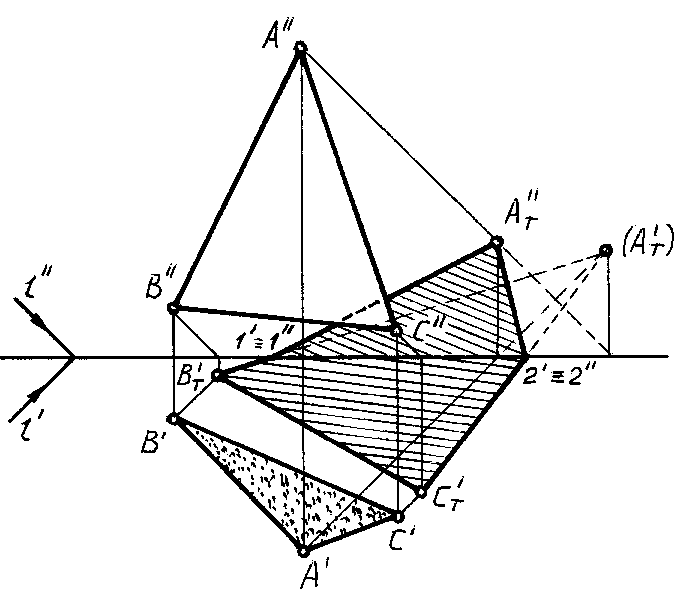
На рисунке 82
построена тень, падающая от треугольника
АВСна плоскости проекций H и V.
Тень от вершиныАпадает на плоскость
V, а от вершиныВи вершиныС— на
плоскость Н. Следовательно, тень от
стороныВСпадает на одну плоскость
Н и представляет прямую линию, а тени
от сторонАВиАСпадают на две
плоскости и представляют ломаные линии.
Рис.
82
Падающие тени от
сторон АВиАСможно построить
при помощи промежуточных точек (как на
чертеже 81) или при помощи мнимой тени
(АT‘), падающей от точкиАна заднюю полуплоскость Н. Получив
треугольникАTHВTHСTH,
определяем на осиОХточки перелома
1 и 2 падающей тени и соединяем их
с действительной теньюАTV от
точкиАна плоскости V. Сторона
плоской фигуры, обращенная к теневому
столбу, находится в тени, то есть у
плоских фигур следует различать
освещенную и неосвещенную стороны.
Иначе говоря, плоская фигура всегда
имеет собственную тень.
Для выяснения
освещенности сторон плоскости
треугольника применяем следующий
прием: обходя на исследуемой проекции
периметр треугольника по часовой
стрелке, замечаем порядок букв,
обозначающих вершины, и сопоставляем
с порядком букв, который получается
при обходе по часовой стрелке контура
падающей тени. Совпадение порядка букв
обозначает, что на данной проекции
видима освещенная сторона треугольника,
несовпадение — что видима
неосвещенная сторона плоскости.
На рисунке контур
падающей тени при его обходе по часовой
стрелке дает порядок букв АT»СT»ВT».
Такой же порядок (А»С»В»)
получается на фронтальной проекции.
Следовательно, на V видима освещенная
сторона. Горизонтальная проекция имеет
обратный порядок букв (А‘‘ё).
Это значит, что на горизонтальной
проекции к нам обращена неосвещенная
сторона плоскости треугольника (сторона,
находящаяся в собственной тени).
Этим же приемом
можно пользоваться в аксонометрии
(рис. 83).
Рис.
83
ТЕНЬ ОТ ДИСКА
(окружности)
Если плоская
фигура, бросающая тень, ограничена
кривой линией, то лучи, проходящие через
точки этой кривой, образуют цилиндрическую
лучевую поверхность. В пересечении с
плоскостью, на которую падает тень, эта
поверхность дает контур падающей тени
данной фигуры.
Если плоскость
фигуры параллельна плоскости, на которую
падает тень, то тень равна самой фигуре
(так как равны параллельные между собой
основания цилиндра).
На рис. 84 показано
построение тени от круга, параллельного
плоскости H, на плоскость H. Контуром
тени является окружность тог же радиуса.
Для построения тени достаточно найти
тень от центра С.
Рис.
84
Для построения
тени, падающей от кривой линии на
произвольно расположенную плоскость,
можно применить один из двух способов.
1. На кривой
линии намечается достаточно большое
число точек, от которых строится падающая
тень. Полученные точки (падающей тени)
соединяются между собой плавной кривой
линией.
2. Около кривой
линии описывается многоугольник,
строится падающая тень от многоугольника
и в нее вписывается тень кривой линии.
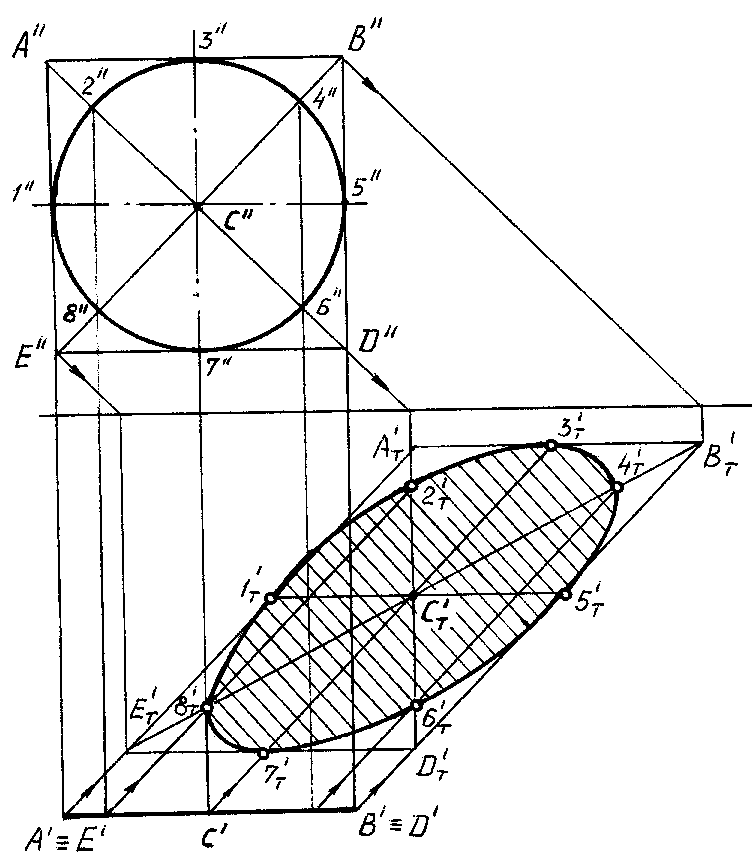
На рис. 85 для
построения падающей тени от круга,
параллельного плоскости V, на плоскость
Н использован описанный около него
квадрат АBCD. Сначала строится
падающая тень от сторон квадрата, его
диагоналей и линий, проходящих через
центрСпараллельно сторонам
квадрата, а затем вписывается в полученный
параллелограмм кривая (эллипс). На
рисунке эллипс проходит через восемь
точек, принадлежащих одновременно
падающим теням от окружности, сторон
и диагоналей квадрата.
Если тень от кривой
линии падает на две пересекающиеся
плоскости, то она будет иметь излом на
линии пересечения плоскостей.
Рис.
85
Содержание:
Проекционные чертежи архитектурных объектов выполненные в одних линиях, не дают достаточно полного представления о запроектированном объекте.
Для придания объемности и наглядности ортогональным чертежам зданий и сооружений выполняется построение теней.
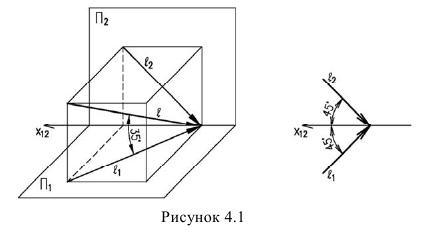
Тени строятся от естественного освещения, т.е. солнца. Так как солнце практически бесконечно удаленная точка, то лучи принимаются параллельными. За направление лучей принимается диагональ куба грани которого совпадают с плоскостями проекций, а её проекции являются диагоналями граней куба, т.е. квадратов (см. рисунок 4.1). Истинный угол наклона будет равен 35°, а проекции лучей располагаются под углом 45° к оси (см. рисунок 4.1).
Тень точки — способ следа луча, способ выноса
Тенью точки на плоскости является точка пересечения светового луча, проведенного через данную точку, с плоскостью. Если тень точки падает на плоскость проекций, то для её построения используется способ следа луча. Т.е. через проекции точки проводим проекции лучей и строим след. На рисунке 4.2 след луча фронтальный, следовательно тень падает на фронтальную плоскость —
Кроме этого может быть использован метод выноса. Особенно важен этот метод при построении теней на фасадах зданий.
Вынос — это расстояние от точки до фронтальной плоскости или плоскости фасада, если тень строится на фасаде. На рисунке 4.3 у — эго вынос.
Тень примой общего положении
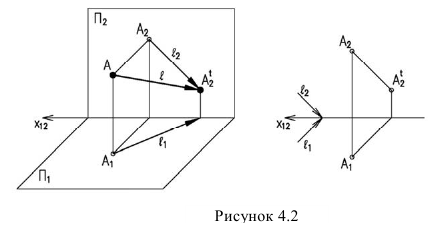
Тенью прямой на плоскость является линия пересечения лучевой плоскости, проведенной через прямую с заданной плоскостью. Т.е. тенью прямой на плоскость является прямая линия. Поэтому для построения тени прямой на плоскость, достаточно построить тени двух ее точек.
Если же тень от прямой падает на две плоскости, то она имеет точку излома, лежащую на линии пересечения плоскостей. В данном случае точка излома лежит на оси (рисунок 4.4). Для ее нахождения, необходимо строить мнимую тень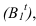
Тени прямых частного положении
Тени прямых частного положения на плоскостях проекций располагаются всегда определенно и часто служат «опорными» при построении теней различных деталей, включающих такие прямые. Рассмотрим эти случаи.
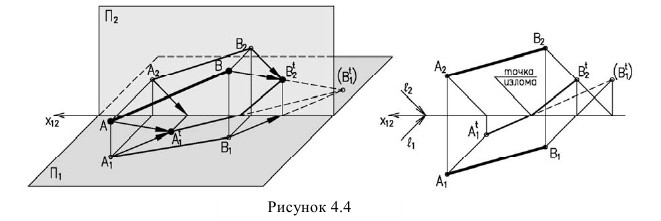
Тень от прямой, на плоскость ей параллельную, располагается параллельно прямой, т.е. параллельно проекции прямой на эту плоскость и равна ей по величине (рисунок 4.5).
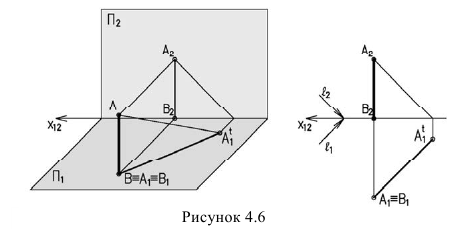
Тень от прямой на плоскость, ей перпендикулярную, располагается по проекции луча, т.е. под углом 45° (рисунок 4.6).
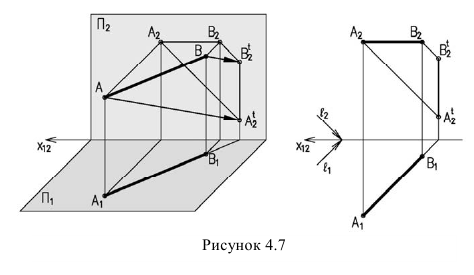
Если точка лежит на плоскости, то тень совпадает с самой точкой и такая точка называется сама себе тень. В нашем случае это точка В. Тень на фронтальной плоскости от горизонтальной прямой, расположенной под углом 45° к ней, вертикальна (рисунок 4.7)
Тени плоских фигур
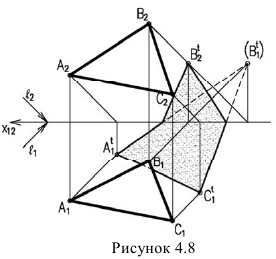
Чтобы построить тень от плоской фигуры, например треугольника, падающую на плоскости проекций достаточно построить тени от вершин (рисунок 4.8). Т.к. тень падает на две плоскости необходимо определять линию излома тени, а, следовательно, построить мнимую тень от вершины В.
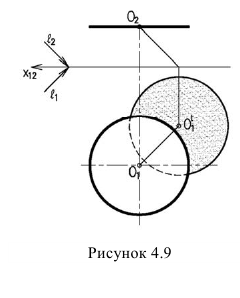
Тень от плоской фигуры, на плоскость ей параллельную, изображается фигурой равной ей по величине. Поэтому достаточно построить тень от одной точки и вычертить тень в виде той же фигуры. Так, для построения тени от окружности (рисунок 4.9) достаточно определить тень от центра и вычертить тень в виде такой же окружности.
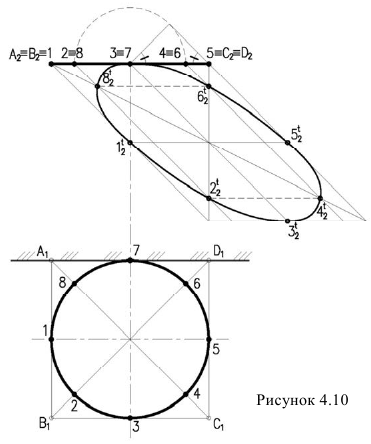
Тень окружности
Тень окружности обычно строится по восьми точкам. Из них четыре -точки касания окружности к сторонам описанного около окружности квадрата, и четыре — точки пересечения окружности с диагоналями этого квадрата (рисунок 4.10).
Тень от квадрата — параллелограмм, диагональ которого BD вертикальна. Точки 1,3,5,7 точки касания к параллелограмму. Точки, лежащие на диагоналях, делят радиус в отношении 0,707. Они могут быть получены без горизонтальной проекции. Для этого на
радиусе строим равнобедренный треугольник с углами при основании 45° и дугой окружности определяем положение точек 2,8 и 4,6. Проведем из них лучи до пересечения с диагоналями. Полученные восемь точек соединяем плавной линией, которая будет эллипсом. Практически тень окружности по восьми точкам строят без горизонтальной проекции, которая здесь приведена только для пояснения.
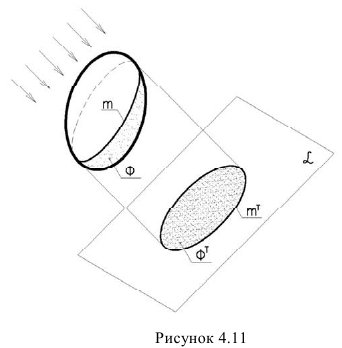
Тени поверхностей. Понятие собственной и падающей тени
Для поверхностей характерны следующие понятия: Собственная тень (ф) — неосвещенна часть поверхности (предмета) рисунок 4.11.
Контур собственной тени (ш)-граница между освещенной и неосвещенной частью поверхности (предмета).
Падающая тень
Контур падающей тени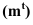
Фактически контур падающей тени -это тень от контура собственной тени. Поэтому, обычно, сначала определяют контур собственной тени, а затем уже строят падающую.
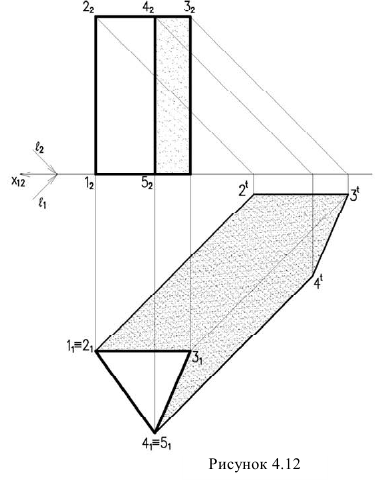
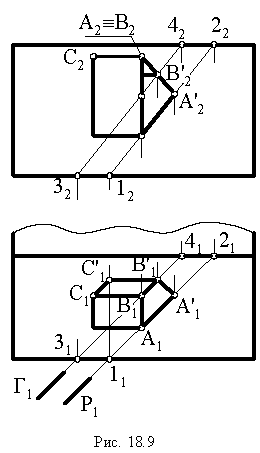
Рассмотрим примеры построения теней трехгранной призмы (рисунок 4.12) и прямого кругового конуса (рисунок 4.13).
Проведя лучи на горизонтальной проекции касательные к крайним ребрам призмы, определяем контур собственной тени. Она является пространственной ломаной 1,2,3,4,5. Т.к. точки 1 и 5 лежат на плоскости 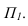
Поэтому для построения контура падающей тени, достаточно построить тени точек 2,3,4.
Проанализировав построенную тень, мы видим, что тени от ребер 1,2 и 5,4 совпадают с направлением лучей, т.к. они перпендикулярны к плоскости 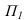
Учитывая это, построение контуров падающих теней многогранников может быть значительно упрощено.
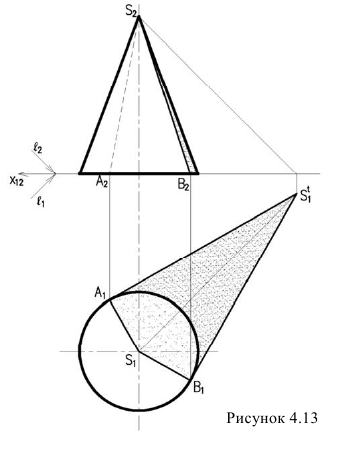
Для конуса логично сначала построить падающую тень, а затем собственную (рисунок 4.13). Для построения падающей тени, строим тень от вершины конуса
Из полученной точки проводим касательные к окружности основания. Эти касательные образуют, контур падающей тени (она является тенями от образующих конуса). Поэтому, соединив точки А и В с вершиной конуса S получим границы собственной тени конуса. А затем уже строим фронтальную проекцию контура собственной тени. Аналогично строятся тени пирамидальных поверхностей.
Тени в ортогональных проекциях. Метод лучевых сечений, метод обратных лучей. Тени фрагментов зданий
Тень точки и прямой на плоскость общего положения (способ лучевых сечений, способ обратных лучей).
Тени схематизированного здания, состоящего из призматических форм.
Тени фрагментов зданий.
Тень точки на плоскость общего положения. Способ лучевых сечений
Для построения тени точки М на плоскость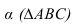
Через луч проводим горизонтально-проецирующую лучевую плоскость о. Строим линию пересечения 1-2 плоскости а и заданной плоскости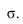
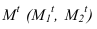
Способ обратного луча
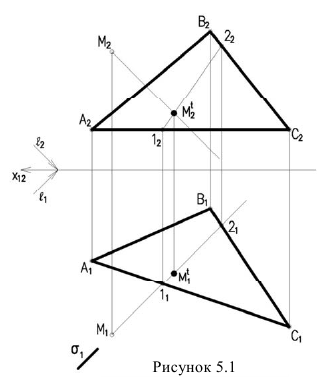
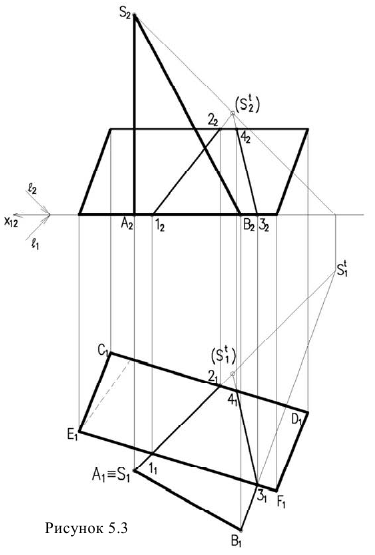
Рассмотрим построение тени от двух прямых SF и SB на непрозрачную пластинку ECDF. (рисунок 5.2).
Тень от проецирующей прямой SA строится, аналогично предыдущему примеру (рисунок 5.1), методом лучевых сечений. На горизонтальной проекции тень совпадает с направлением луча, на фронтальной — идет по лучевому сечению. Тень от точки S на пластину ESDF не надает. Для построения тени от наклонной прямой SB на пластину ESDF, необходимо построить сначала тень падающую на плоскость 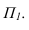
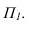
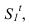
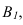
Далее строим тень от пластины ESDF на плоскость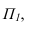
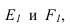
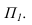
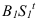
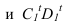
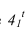
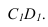
Необходимо отметить что данную задачу можно решить используя построение мнимой тени от точки S на пластину ESDF (рисунок 5.3).
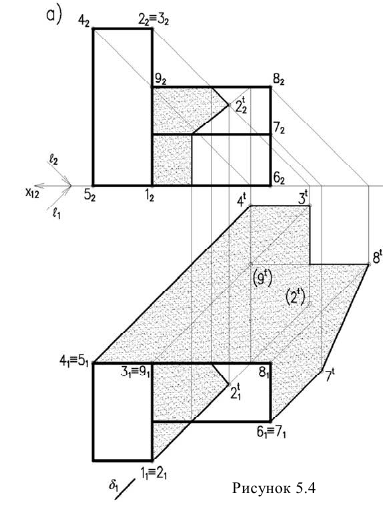
Тени схематизированною здании, состоящею из призматических форм
Здание состоит из двух призматических форм (рисунок 5.4). Обычно сначала строятся тени от двух этих форм падающие на плоскость 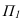
Дли построении падающих теней определяем контур собственной тени каждой из призм (рисунок 5.46). Высотная часть здания представляет прямую призму, контур собственной тени которой 1,2,3,4,5, причем точки 1 и 5 лежат на плоскости, поэтому тени строим от трех точек 2,3,4. Контур собственной тени второй призмы — 6,7,8,9. Точка 6 лежит на 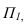
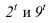
Для построения тени падающей от высотной части здания на пристройку используем метод лучевых сечений. Заключаем луч, проведенный через точку 2 в плоскость 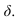
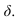
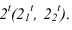
При построении теней зданий очень важно помнить положение теней прямых частного положения, это значительно упрощает процесс построения.
Тени фрагментов зданий
К фрагментам зданий относятся ниши, козырьки, трубы, лестницы и т.п. Рассмотрим построение теней некоторых из них.
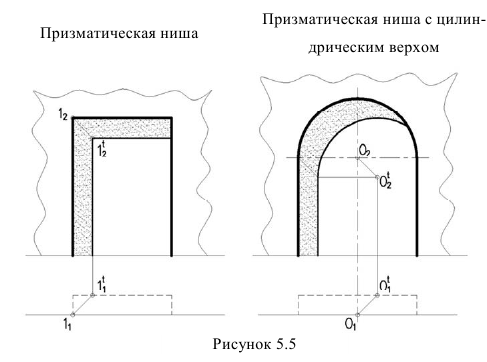
Тени в нишах
Две изображенные ниши относятся к нишам с плоским днищем, т.е. контур ниши отбрасывает тень на плоскость днища ниши параллельной контуру. Поэтому тени в нишах с — плоским днищем повторяют контур ниши. Для построения таких теней достаточно построить тень одной точки, как показано на примере (рисунок 5.5). Если дан лишь фасад здания, необходимо знать глубину ниши и тень построить методом выноса.
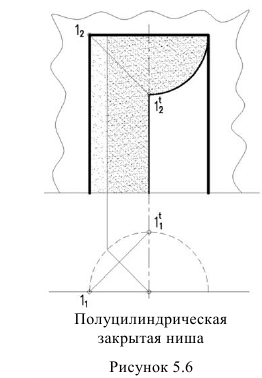
В цилиндрической нише (рисунок 5.6) сначала определяем собственную тень. Для чего удобнее провести нормаль (т.е. радиус под углом 45°). Получим контурную образующую собственной тени.
Падающую тень будет отбрасывать две прямые кромки ниши — вертикальная и продольная. Тень от вертикальной прямой надает на ось ниши. Тень от продольной прямой будет представлять четверть окружности.
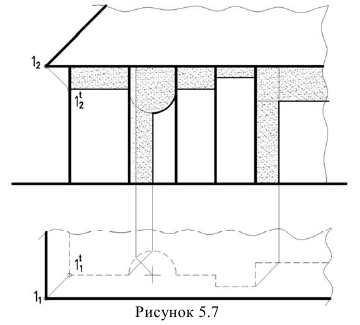
Из этого чертежа можно сделать вывод: тень от продольной прямой на фасаде с вертикальными образующими зеркально повторяется план. Этот вывод позволяет построить тень на фасаде от свеса крыши, построив тень одной точки (тень точки 1 на рисунке 5.7). Остальной контур тени зеркально повторяет план.
Тень падающая от трубы на крышу
На рисунке 5.8 дана труба призматической формы.
Тень строится методом лучевых сечений. Если отсутствует план здания, то нужно иметь ввиду, что тени от вертикальных прямых на фасаде имеют угол наклона равный углу наклона ската крыши
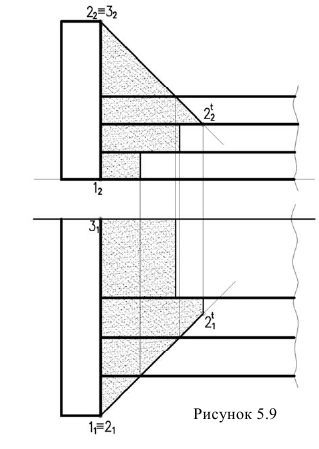
Тень от барьера на ступенях лестницы
Контур собственной тени барьера (рисунок 5.9), отбрасывающий тень на ступени представляет собой две прямые — горизонтально-проецирующую 1,2 и фронтально-проецирующую 2,3. Из точек 1 и 3 начинается тень. Следовательно, необходимо построить тень точки 2. Для построения падающей тени используется метод лучевых секущих плоскостей.
Тени в ортогональных проекциях
Строительство зданий и сооружений ведется по чертежам, выполненным в ортогональных проекциях. Представление о внешнем виде здания, в основном, создается по изображению фасада. Это изображение имеет существенный недостаток — в нем отсутствует объемность. Тени, построенные на ортогональных чертежах, дают возможность представить по чертежу расположение отдельных элементов, их освещенность, а также помогают находить наилучшие пропорции проектируемых зданий и сооружений.
При освещении лучами света каких-либо объектов на них образуются тени. Для образования тени необходим источник света и плоскость, на которую падает тень.
Освещение может быть центральным (факельным) или параллельным (солнечным). Освещение называется центральным в случае, когда световые лучи идут из одной точки (лампа, свеча); параллельным, если источник света (солнце) удален в бесконечность, и световые лучи практически будут параллельны между собой.
Основной геометрической задачей построения теней является определение контуров собственных и падающих теней (рис. 17.1).
Неосвещенная часть поверхности тела 
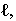
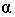
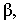
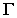
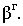
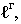
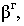
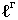
Для построения падающей тени необходимо знать направление лучей света. Направление световых лучей 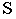
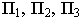
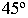
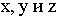
Тень от точки на плоскость проекций
Тенью от точки 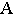
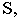
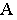
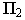
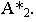
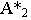
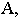
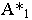
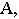
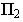
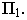
Тень от точки на плоскую фигуру
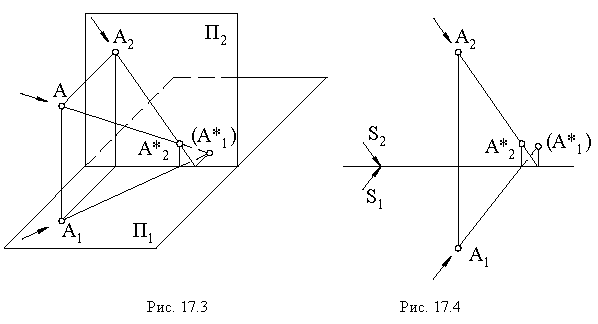
Чтобы построить тень от точки на плоскость общего положения (рис. 17.5), необходимо найти точку пересечения луча света, проходящего через заданную точку 
- Заказать чертежи
Тень от прямой линии
Построение тени от отрезка прямой линии сводится к определению тени двух или нескольких его точек. Тень от прямой можно рассматривать как след лучевой плоскости, проходящей через данную прямую. В зависимости от положения прямой, лучевая плоскость может быть общего и частного положения. Линия пересечения её с плоскостями или поверхностями определит форму тени от отрезка прямой.
Тени на плоскости проекций от прямые частного положения
Построение тени от отрезка прямой 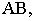
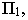
Тень 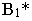
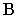
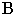
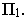
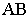
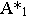
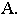
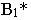
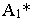
Вывод. Тень от прямой, перпендикулярной плоскости проекций, совпадает с проекцией светового луча на эту плоскость.
На рис. 17.7 показано построение тени от отрезка прямой 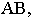
Вывод. Тень от отрезка прямой, параллельной плоскости проекций, на этой плоскости равна и параллельна самому отрезку.
Тени на плоскости проекций от прямых общего положения
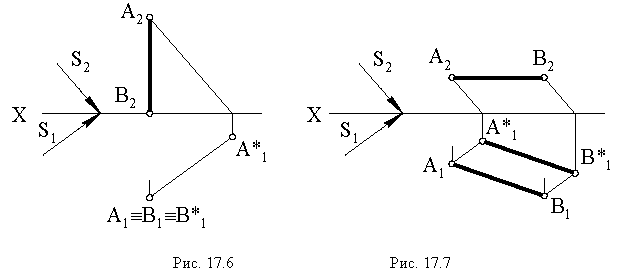
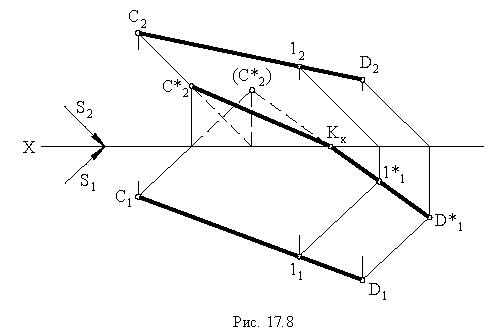
На рис. 17.8 показано построение тени от отрезка прямой 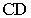
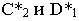
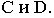
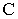
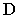
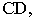
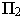
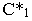
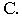
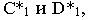
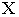
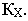
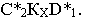
Тень от прямой на произвольную плоскость
Для построения тени от прямой на плоскость общего положения достаточно определить тени на эту плоскость от двух любых точек прямой (см. построение тени от точки на плоскую фигуру, рис. 17.5).
Тень от плоской фигуры
Падающая тень от плоской фигуры на плоскости проекций может быть построена как совокупность теней от её вершин и сторон. Таким образом, построение тени от плоской фигуры на плоскость проекций может быть сведено к известному определению теней от точек и прямых.
На рис. 17.9 показано построение тени от треугольника 
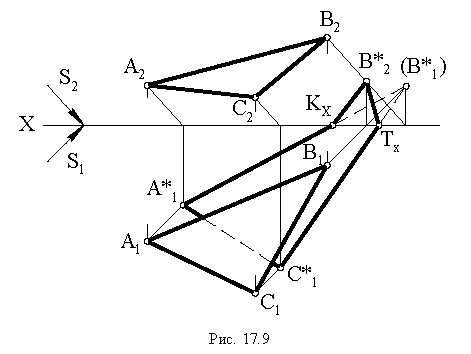
На рис. 17.10 построена тень от круглой пластины, перпендикулярной плоскости проекций 
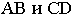
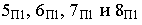
Соединив полученные точки, получим контур падающей тени круглой пластины, перпендикулярной плоскости
Метод обратных лучей
Метод обратных лучей применяется при построении теней, падающих от одного предмета на другой. Суть метода заключается в том, что строят тени заданных геометрических фигур на одну из плоскостей проекций и определяют точки пересечения теней. Через отмеченные точки проводят луч, направление которого противоположно световым лучам. Каждый из обратных лучей, пересекая данные геометрические фигуры, определяет нужные для построения тени точки.
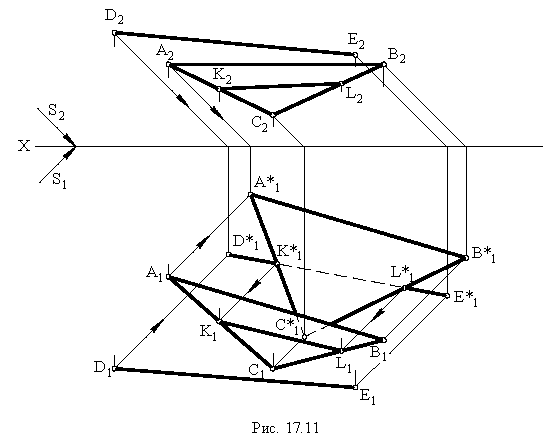
На рис. 17.11 показано применение этого метода на примере построения тени прямой на плоскость треугольника. Построены падающие тени треугольника 
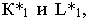
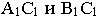
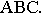
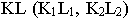
Вывод. Если падающие тени двух геометрических образов пересекаются, то тень от одного из них будет падать на другой
Тени геометрических тел
При построении теней геометрических тел вначале определяют контур собственной тени, затем находят контур падающей тени путем построения падающих теней от вершин и сторон ломаной линии (или точек кривой линии), являющейся контуром собственной падающей тени
В отдельных случаях бывает целесообразно определять контур собственной тени по уже построенной падающей тени.
Рассмотрим процесс построения теней от основных геометрических тел.
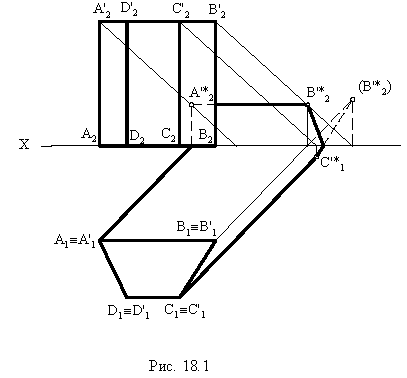
Тени призмы
Контур тени от призмы определяется тенями от рёбер (рис. 18.1). Освещенность призмы легко определить по горизонтальной проекции, где видно, что обращенными к свету являются две грани 
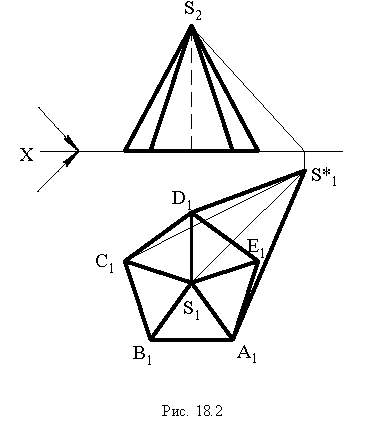
Тени пирамиды
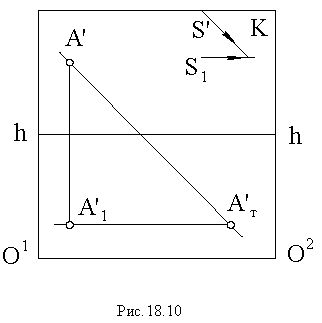
Построим тени пятиугольной пирамиды (рис. 18.2). Строим падающую тень 
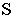
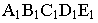
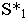
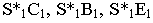
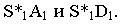
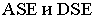
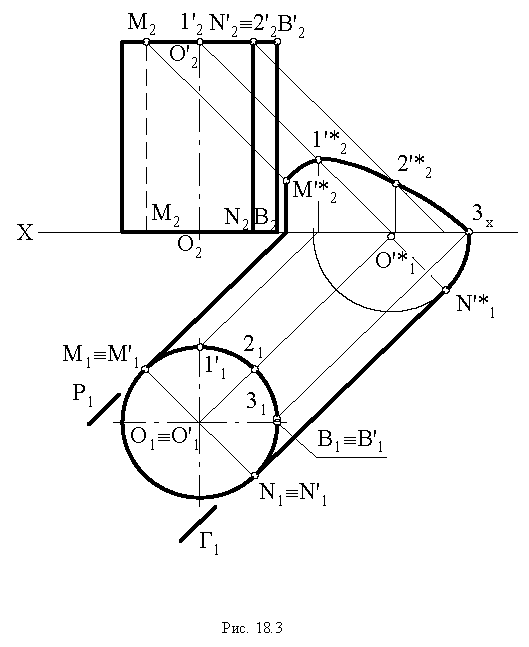
Тени цилиндра
Для определения контура собственной тени прямого кругового цилиндра необходимо провести две горизонтально-проецирующие лучевые плоскости 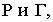
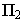
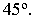
Тени конуса
На рнс. 18.4 показано построение собственной и падающей теней прямого кругового конуса. Вначале определяем мнимую тень от вершины конуса 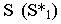
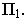
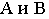
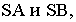
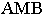
Тени элементов зданий
При построении проекций теней на фасадах зданий используются те же приемы, что и при построении теней геометрических тел.
Рассмотрим примеры построения теней некоторых частей здания
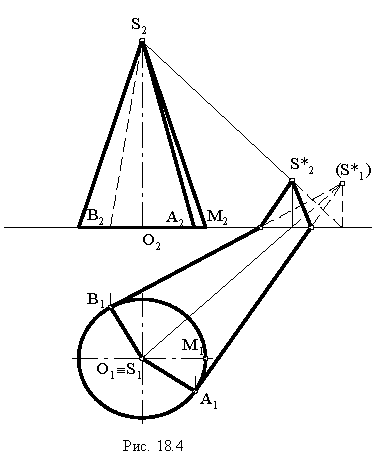
На рис. 18.5 показан пример построения теней в плоской нише. Определение границы падающей тени заключается в построении тени от ломаной линии 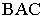
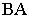
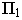
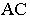
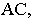
На рис. 18.6 приведен пример построения тени в прямоугольной нише с цилиндрической аркой В этом примере надо найти тень от точки 
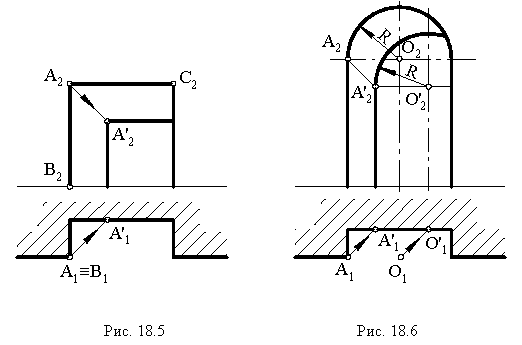
На рис. 18.7 построена тень от козырька (или балкона) здания Построения понятны из чертежа.
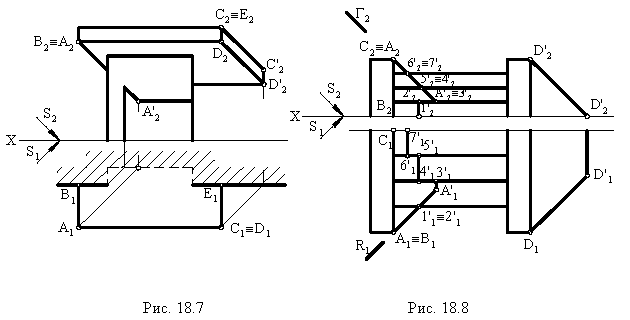
На рис. 18.8 показано построение теней на лестнице (крыльце). В собственной тени находятся правые грани вертикальных стенок. Падающая тень от правой стенки лестницы на плоскость стены здания и на землю строится как тень от плоской фигуры на плоскости проекций 
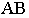
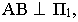
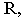
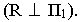
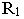
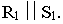
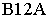
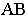
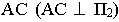
На рис. 1S.9 показано построение контура падающей тени от трубы на скат крыши здания Задача сводится к определению теней от точек и прямых на произвольно расположенную плоскость (скат крыши). Построения выполнены способом вспомогательных секущих лучевых плоскостей 
Тени в перспективе
При построении теней в перспективе в качестве источника света рассматривается естественный источник — солнце. Правила построения теней в перспективе точно такие же, как и в ортогональных проекциях.
Для упрощения построения считают, что световые лучи параллельны плоскости картины, тогда на картине перспективы оснований лучей будут параллельны основанию картины
Если на картине задана перспектива 
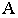
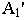
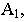
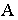
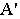
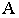
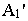
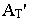
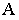
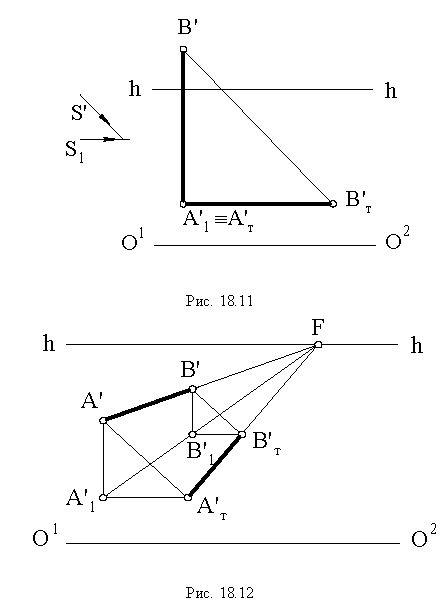
Построение тени от прямой сводится к построению тени от двух ее точек. При этом, если прямая перпендикулярна предметной плоскости (рис. 18.11), то тень от нее на этой плоскости совпадает с основанием луча, проведенного через основание прямой.
Тень от вертикальной прямой на вертикальной плоскости вертикальна.
Если прямая параллельна предметной плоскости (горизонтальная прямая), то тень от нее на этой плоскости будет параллельна данной прямой (рис. 18.12) и направлена в точку схода.
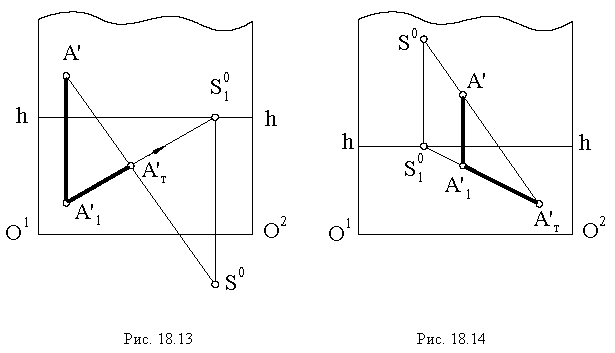
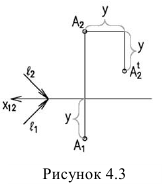
Тени в перспективе могут быть построены с различных точек расположения источника света. Направление лучей света может быть выбрано в зависимости от характера объекта и от желания показать его освещенным с той или другой стороны. Так, например, если источник света будет находиться позади предмета (рис. 18.13) или перед зрителем, но позади предмета (рис. 18.14), то для построения перспективы тени 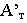
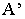
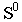
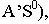
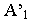
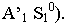
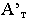
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Пересечения поверхностей с прямой и плоскостью
- Взаимное пересечение поверхностей
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ
КАЗАХСТАН
МЕЖДУНАРОДНАЯ
ОБРАЗОВАТЕЛЬНАЯ КОРПОРАЦИЯ
Жумартова
К.Г.
Шапрова
Г.Г.
ПЕРСПЕКТИВА
И ТЕНИ В КУРСЕ ИНЖЕНЕРНОЙ ГРАФИКИ
Учебное
пособие для студентов
архитектурных
специальностей
ВВЕДЕНИЕ
В целях придания архитектурным чертежам
большей наглядности часто прибегают к построению теней.
Изображение на чертежах теней, в полной
мере соответствующих реальной действительности, т.е. с учетом рассеивания
световых лучей в воздушной среде, с учетом рефлексов и т.д., является сложной
задачей. Поэтому в практике проектирования, с целью упрощения построения теней,
принимается ряд условных положений, а именно:
1)
освещенные тела сами не являются
источниками света;
2)
пределом распространения светового луча
является первая, встретившаяся на его пути материальная точка;
3)
воздействие воздушной среды не
учитывается.
При этих условиях все задачи на
построение теней решаются с помощью способов начертательной геометрии.
На архитектурно-строительных чертежах
могут быть построены тени изображаемого объекта как при искусственном (лампа,
свеча и т.п.), так и при естественном (солнце) его освещении.
В первом случае (при искусственном
освещении) источник света принимается за светящуюся точку. Если на пути
световых лучей, распространяющихся из светящейся точки S
прямолинейно по всем направлениям, встретится какое-либо непрозрачное тело,
например сфера (рис.1, а), то поверхность SABCD,
обращенная к источнику света S, будет освещена. Поверхность сферы
с другой стороны линии касания указанной конической поверхности будет
находиться в тени.
Пространство за сферой, ограниченное
касательной конической поверхностью, представляет собой пространственную тень
от сферы. Любая поверхность, попадающая в это теневое пространство, будет
находиться в тени.
Находящаяся в пределах теневой части
конуса часть плоскости π, ограниченная линией пресечения A0B0C0D0
поверхности этого конуса с плоскостью π, будет в тени и
представляет собой падающую тень от
сферы на эту плоскость.
Линия ABCD
на сфере носит наименование контура
собственной тени, а линия A0B0C0D0 на плоскости π
– падающей тени.
При естественном, т.е. при солнечном
освещении световые лучи принимаются параллельно друг другу. В этом случае на
сфере (рис.1, б) контур ABCD
собственной
тени определяется как линия касания обертывающей цилиндрической поверхности, а
контур A0B0C0D0 падающей тени – как
линия пересечения этой поверхности с
плоскостью π.
Основной
вопрос построения теней в обоих рассмотренных случаях сводится к определению
контуров собственных и падающих теней. Контуры собственных и падающих теней
получаются в виде замкнутых ломаных или кривых линий.
Контур падающей тени, как видно из чертежа, определяется как тень от контура собственной тени.
На архитектурных чертежах построение теней выполняется в
основном при параллельном направлении световых лучей, что соответствует
условиям естественного освещения.
Рис.
1.
Раздел
I.
ПОСТРОЕНИЕ ТЕНЕЙ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ
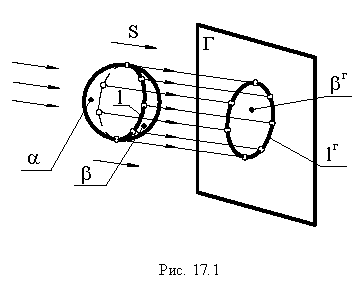
При построении теней в
ортогональных проекциях направление световых лучей принимается
параллельно диагонали куба (рис.2, а).
Рис.
2.
При таком направлении световых лучей
упрощается построение теней и имеется возможность в большинстве случаев судить
о глубине рельефа элементов тех или иных сооружений, по ширине падающих от них
тени.
При направлении светового луча по
диагонали куба горизонтальная s,
фронтальная s1 и
профильная s2 проекции светового луча составляет с
соответствующими осями проекций угол 450 (рис.2, б). Сам же луч
наклонен к плоскости π2 под углом 350 .
Для построения теней используются
различные способы, рассматриваемые ниже.
1. Способ следа луча
1.1. Тени от точки
Для
построения падающей тени от точки через эту точку следует провести луч
параллельно принятому направлению световых лучей и определить точку его
пересечения с ближайшей встретившейся на его пути плоскостью или поверхностью.
Найденная точка и будет являться падающей тенью от данной точки.
Для построения тени от точки на
ортогональном чертеже через проекции точки следует провести проекции светового
луча. На рис. 3 построены тени от точек A (A/, A//) и B (B/ , B//) на плоскостях
проекций. Тень от точки на плоскости проекций определяется как след светового
луча, проведенного через данную точку, поэтому данный способ построения теней
называется способом следа луча.
Рис.3.
Луч, проведенный через
точку A, встречается с плоскостью π2 в точке A// (A//
— её горизонтальная проекция), а с плоскостью π1 – в точке A/
(точка
A/
—
её фронтальная проекция). В дальнейшем в целях упрощения изложения проекции
теней будем называть тенями. Если плоскости проекций считать непрозрачными, то
точка A//
будет видимой, реальной тенью точки А; точка A/,
находящаяся ниже горизонтальной плоскости проекций, будет невидимой, ложной, или мнимой тенью точки A.
Реальная тень от точки B
находится на фронтальной плоскости проекций (точка B/).
Ложная тень от точки B расположена в горизонтальной
плоскости проекций (точка B/).
На
ортогональном чертеже при принятом направлении световых лучей реальная или
ложная тени точки на плоскостях π1 и π2 расположены
всегда на одной прямой, параллельной оси x.
Ложные тени в ряде
случаев используются для упрощения построения реальных теней. Из чертежа видно,
что при наличии ложной тени реальная тень может быть найдена элементарными
построениями.
1.2.
Тени от прямой линии
Тень от прямой линии,
падающей на какую-либо плоскость, представляет собой также прямую линию, за
исключением, конечно, того случая, когда прямая параллельна световым лучам.
Ниже
приведены примеры построения падающих
теней от прямых линий частного положения.
а) Прямая, перпендикулярная к горизонтальной плоскости
проекций (рис.4). Определив тени от точек A и B и
соединив их между собой прямой линией, получим падающую тень A//B//
от данной прямой. Как видно из чертежа,
тень от прямой AB падает на горизонтальную плоскость
проекций и совпадает с горизонтальной проекцией светового луча.
Рис.4
б) Прямая, перпендикулярная к фронтальной плоскости
проекций (рис.5). Тень от прямой падает на фронтальную плоскость проекций и
совпадает с фронтальной проекцией светового луча. Тень A/
совпадает
с фронтальной проекцией A1 точки А,
так как точка А прямой АВ расположена непосредственно в плоскости
π1.
Рис.5
Из
рассмотренного следует, что если прямая
перпендикулярна к плоскости, то тень, падающая от неё на эту плоскость,
совпадает с проекцией светового луча на этой плоскости.
в) Если
прямая параллельна какой-либо плоскости, то тень, падающая от прямой на эту
плоскость, параллельна самой прямой (рис.6).
Рис.6
г) Тень
от прямой частного положения, горизонтальная и фронтальная проекции которой
наклонены к оси х под углом 450. Тень от такой прямой на плоскости π2
или π1 изобразится в
виде прямой параллельной оси х (рис.7).
Рис. 7
На рис.8 показано построение теней от
отрезка прямой общего положения на две плоскости проекций. Построения
осуществляют в следующей последовательности:
—
строят тень на одну из плоскостей проекций (в данном случае на плоскостью π2),
предполагая, что второй не существует;
— если построенная тень пересекает ось
проекций х, отмечают точку
преломления (точка Кх);
— определяют, какая из построенных теней
мнимая (в данном случае точка В») и
строят действительную тень от этой точки на вторую плоскость проекций π1
(точку В’);
— соединяют действительные тени крайних
точек отрезка прямой через точку преломления, т.е. А»КхВ’.
Следовательно, тень от прямой
линий, падающая на пересекающиеся плоскости, есть ломанная прямая, имеющая
точку излома, лежащую на линии пересечения этих плоскостей.
Рис.
8
1.3. Тени плоских фигур
При одностороннем освещении плоской
фигуры одна из её сторон окажется освещенной, а вторая будет находиться в тени.
Таким образом, контуром собственной тени будет являться контур плоской фигуры.
Для построения контура падающей тени от
какой-либо плоской фигуры следует построить падающие тени от характерных точек
контура этой фигуры и соединить их между собой соответствующим образом.
Для построения
на плоскостях проекций π1 и π2 падающей тени от треугольника АВС (рис.9) следует найти вначале
тени от его вершин. Тени от вершин А
и В падают на горизонтальную
плоскость, а тень от вершины С на
фронтальную плоскость проекций. Тени от сторон АС и ВС треугольника
падают как на фронтальную, так и на горизонтальную плоскости проекций. Для
определения направления теней от этих сторон на фронтальной плоскости проекций,
а также точек перегиба этих теней использована ложная тень от точки С на плоскости π1.
В зависимости от положения плоской фигуры по отношению к
направлению световых лучей и по отношению к плоскостям проекций, на ту или иную
плоскость может проецироваться освещенная или теневая сторона плоской фигуры.
Чтобы определить, какая сторона плоской фигуры, т.е. освещенная или теневая,
проецируется на данную плоскость проекций, следует срвнить порядок расположения
проекций отдельных точек контура плоской фигуры с порядком расположения их
теней.
Рис.9
На рис.9 на
фронтальную плоскость π1 проецируется не освещенная сторона
треугольника АВС, так как
последовательность расположения обозначений точек на контуре фронтальной
проекции треугольника и на контуре его тени при чтении их, например по «часовой
стрелке», не одинакова. На горизонтальной плоскости проекций проецируется
освещенная сторона треугольника, так как на контуре горизонтальной проекции
треугольника имеет место одинаковая последовательность расстановки обозначений
точек по сравнению с расстановкой их на контуре тени.
В случае, если плоская фигура параллельна какой-либо
плоскости, то тень, падающая от фигуры на эту плоскость, равна самой плоской
фигуре и расположена подобно ей.
Как видно из чертежа (рис.10 а), для построения контура
падающей тени на плоскости π2 от квадрата достаточно построить тень на
плоскости от одной из его вершин.
Для построения
тени на горизонтальной плоскости проекций от
круга, расположенного параллельно этой плоскости (рис.10 б), достаточно
построить тень от центра круга и из полученной точки (О//)
как из центра описать окружность с радиусом, равным радиусу данного круга.
Рис.10
1.4. Тени
геометрических тел
При построении теней геометрических тел в первую очередь определяется
обычно контур собственной тени, т.е. линия раздела освещенных и находящихся в
тени частей поверхности тела. По контуру собственной тени строится затем контур
падающей тени.
На рис.11 при принятом направлении светового луча
правая, задняя и нижняя грани куба находятся в собственной тени. Остальные грани
освещены. Контуром собственной тени является замкнутая линия 1-2-3-4-5-6-1, от
которой строится контур падающей тени 1π’-2π’- ….-1π‘.
Рис. 11
На рис.12 а, б приведено построение падающих теней от призмы, основание которой
расположено в горизонтальной плоскости проекций. В первом случае (рис.12, а) от
призмы тень падает только на горизонтальную плоскость проекций, во втором
случае (рис.12, б) тень падает частично и на фронтальную плоскость проекций.
Рис.12
На рис.13 контуры собственных теней цилиндров определяются
двумя образующими AB и CD
и
заключенной между ними дугой окружности верхнего основания цилиндра.
В связи с тем, что в первом случае (рис.13,
а) вся тень от цилиндра падает на горизонтальную плоскость проекций, контур
падающей тени можно определить, построив тень от верхнего основания цилиндра и
проведя к ней и к основанию цилиндра две касательные. Во втором случае (рис.13,
б) тень от цилиндра частично падает на фронтальную плоскость проекций. Для её
построения следует определить тени A‘
и C‘ от точек A
и C,
а также тени от ряда промежуточных точек
верхнего основания цилиндра. На рис.13,б показано построение тени от точки E
.
Рис.13
Построения собственных и падающих теней
пирамиды и конуса не имеют существенных отличий. При построении теней
указанных тел в первую очередь строятся падающие тени, при помощи которых затем
определяются контуры собственных теней (рис.14).
Для построения
падающей тени от конуса (рис.14,а) сначала
строят падающую тень от вершины конуса на плоскость его основания. На чертеже
такой тенью является ложная тень (S‘). Касательные, проведенные из
этой точки к основанию конуса, определяют основания образующих AS и
BS,
которые и являются контурными линиями собственной тени. Реальная тень от
вершины конуса падает в данном случае на фронтальную плоскость проекций.
Рис.14
2. Способ обратных
лучей
Способ обратных лучей заключается в том,
что вначале строят тень, падающую от предмета на той или иной плоскости, а
затем по ней с помощью обратных лучей определяют собственную тень или тень,
падающую от предмета на другую плоскость или поверхность.
Способ обратных лучей может быть
использован, в частности, для построения контура собственной тени тела
вращения. В этом случае падающую тень от
тела вращения строят на плоскости, перпендикулярной к оси тела вращения.
Для построения падающей тени от тела
вращения строят тени от ряда сечений тела плоскостями, параллельными плоскости,
на которой строится тень. Тени от этих сечений равны самим сечениям. Контур
падающей тени тела вращения представляет собой кривую линию, огибающую тени от
отдельных сечений данного тела и касающуюся их.
На рис.15 падающая тень построена на
горизонтальной плоскости проекций, так как ось тела вращения перпендикулярна к
этой плоскости. Тени от сечений тела, лежащих в горизонтальных плоскостях Q1, Q2,
Q3,
представляют собой круги соответствующих радиусов r1, r2 и r3 . Кривая, огибающая
их, является контуром падающей тени тела
вращения.
Точки контура собственной тени
определяются по точкам контура падающей тени. Например, если контур падающей
тени тела вращения касается контура тени сечения, лежащего в плоскости Q2,
в точках ah bh , то с помощью
построений, указанных на чертеже стрелками (с помощью обратных лучей), на
фронтальной проекции этого сечения будут найдены точки a/ и
b/,, а на
горизонтальной проекции этого сечения — точки a
и b.
Способ обратных лучей находит
применение не только при построении теней поверхности тел вращения, но и в ряде
других случаев, которые будут рассмотрены в дальнейшем.
Рис.15
3. Построение теней
архитектурных деталей
3.1.
Тени в нишах
В зданиях и сооружениях часто
встречаются ниши различной конфигурации.
На рис.16 построены тени:
а) в прямоугольной плоской нише;
б) в плоской полуциркульной нише;
в)
в цилиндрической нише с плоским верхом;
г)
в цилиндрической нише со сферическим верхом;
Рис.16
В прямоугольной
плоской нише контуром собственной тени являются ребра AB и BC,
от которых и строится контур падающей тени. Так как ребра AB
и BC параллельны фронтальной стенке ниши, то на ней
падающие тени от ребер AB и BC
будут параллельны этим ребрам. Поэтому для построения тени достаточно
определить лишь тень bv
от точки B. Следует отметить, что участок AM ребра
AB бросает тень на горизонтальную плоскость ниши, а участок NC
ребра BC — на правую боковую стенку ниши.
Как видно из чертежа, ширина
падающей тени в нише равна глубине ниши,
поэтому, зная глубину ниши, падающую тень можно построить без использования
плана.
Контуром собственной тени плоской
полуциркульной ниши являются ребро AB и полуциркульная кривая между
точками B и
N
.
Точка N
(n/) определяется
проведением касательной под углом 450 к фронтальной проекции дуги ниши. От
указанного контура и строится падающая тень.
Для построения тени полуциркульного
ребра ниши следует построить тень c/v от центра дуги
окружности на фронтальную плоскость ниши и из полученной точки как из центра
провести дугу окружности того же радиуса до точки b/v
.
Тень от вертикального ребра в цилиндрической полуциркульной нише с плоским
верхом проходит по средней образующей цилиндрической поверхности ниши. Тень
от горизонтального ребра на цилиндрической поверхности изобразится в виде дуги
окружности с центром в точке c/
и с радиусом R,
равным радиусу цилиндрической поверхности ниши.
Тень от вертикального ребра AB
в цилиндрической нише со сферическим
верхом так же, как и в предыдущем случае, падает на среднюю образующую
цилиндрической поверхности до точки b/v.
Тень от полуциркульной кривой участка BN падает частично на цилиндрическую и частично
на сферическую поверхности. Эта тень с достаточной для
практики точностью может быть изображена в виде плавной кривой, проведенной
через три точки n/, m/, b/v
. Точка m/ находится на
перпендикуляре к o/ n/
на расстоянии от точки o/
, равном одной трети отрезка o/
n/
.
3.2. Тени столбов, перекрытых плитами
На рис. 17,а даны проекции столба квадратного сечения, перекрытого
квадратной плитой. Тень от столба падает как на плоскость π2,
так и на плоскость π1,
причем тень от столба на плоскости π1 перекрывается тенью от плиты.
Тень от плиты падает частично и на грани столба.
При построении тени в первую очередь
следует построить тень от ребра AB
плиты,
падающую на переднюю грань столба. Так как свесы плиты одинаковы со всех сторон, то тень от точки A
плиты упадет на левое переднее ребро столба
(точка A/1
),
а участок AN
ребра
AB плиты даст
падающую тень A/1N/1 на передней грани столба. Участок NB этого
же ребра бросит тень N/B/ на плоскость π 1.
Падающая тень от плиты на плоскости π1
может быть построена без использования горизонтальной проекции. Построив
контур падающей тени от столба, засекаем на этом контуре фронтальной проекцией
светового луча, проведенного из точки N1,
точку N/.
Затем строим точку B/,
а также точки C/,D/,E/,F/
и M/, представляющие
собой характерные точки контура падающей тени плиты. Отрезки, обозначенные на чертеже буквой l,
будут равны между собой. Следует заметить, что отрезок F/M/
контура падающей тени представляет собой тень от участка FM ребра FA плиты. Участок AM этого же ребра
плиты бросает тень на левую боковую грань столба.
а)
б)
Рис.17
На рис.17, б изображен столб
трапецеидального сечения, примкнутый к фронтальной плоскости и перекрытый
плитой аналогичной формы.
Тень от ребер плиты, падающая на грани столба,
представляет собой ломаную линию. Для определения контура указанной тени следует
построить тени от точек A,B и C. Горизонтальные проекции точек A
и B
,
бросающих тень на ребра столба, определены с помощью проекций обратных лучей
(необходимые построения показаны на чертеже стрелками).
Участок CB нижнего левого ребра плиты бросает тень C0/ B/0
на переднюю грань столба, участок BE этого
ребра — на левую грань столба (тень параллельна самому ребру) и участок ED — на фронтальную плоскость.
Построение тени на фронтальной плоскости ясно из чертежа.
На
рис. 18, а даны проекции цилиндрического
столба, перекрытого квадратной плитой. Контур собственной тени столба
строится, как на обычном цилиндре. Падающая тень от ребра AF на цилиндрической поверхности
столба представляет собой часть эллипса, который на фронтальной плоскости
проекций изобразится в виде прямой линии, т.к. световые лучи, проведенные через любые точки данного ребра,
лежат в одной фронтально-проецирующей плоскости
φ.
а)
б)
Рис.
18
Падающая тень от ребра AB представляет собой
также эллипс, который изобразится на фронтальной плоскости проекций в виде
окружности с радиусом, равном радиусу сечения столба.
Для построения указанных теней проводим
через точку A1
фронтальную проекцию светового луча до пересечения его в точке O/
с фронтальной проекцией оси столба. Из
точки O/
как из центра
проводим окружность с радиусом, равным радиусу сечения столба. Часть дуги этой
окружности между точками A/ и N/ определяет собой падающую тень от участка AN
ребра AB плиты.
Тень от участка AM
ребра AF изобразится на фронтальной
проекции в виде прямой линии, совпадающей с направлением проекции светового
луча, проведенной через точку A1.
На рис.18,б приведен пример построения тени на цилиндрическом столбе, перекрытом
круглой плитой.
Построив собственные тени на
поверхности столба и плиты, строим на поверхности столба падающую тень от
нижнего ребра плиты. Характерными точками контура падающей тени являются точки A/ и B/
, расположенные соответственно на контурной образующей цилиндра и на его
теневой образующей. Горизонтальные проекции точек А и В, бросающих тень на
указанные образующие, могут быть определены проведением проекций световых лучей
обратного направления. На чертеже построена также тень от промежуточной точки
С, произвольно взятой на нижнем ребре плиты. Контур падающей тени представляет
собой плавную кривую линию, проходящую через точки A/ , C/
и B/
.
3.3.
Тень лестницы
При наличии у лестницы
боковых стенок тень на лестнице строится от ребер АВ и ВС левой боковой стенки
(рис.19). Вертикальное ребро АВ и горизонтальное ВС бросают тень как на
проступи (горизонтальные плоскости ступеней), так и на подступенки
(вертикальные плоскости ступеней).
Рис.19
Тень от вертикального ребра АВ идет до
нижней ступени по горизонтальной плоскости и совпадает с проекцией светового
луча. Дойдя до нижней ступени, тень пойдет по подступенку параллельно самому
ребру. Дальше, перейдя на проступь ступени, тень опять совпадает с проекцией
светового луча и т.д. Таким образом, горизонтальная проекция тени от
вертикального ребра АВ выявится в виде прямой линии сорокапятиградусного
направления, а фронтальная проекция этой тени будет представлять собой ломаную
линию, вертикальные участки которой отстоят друг от друга на расстоянии m, равном ширине ступени.
По аналогии с предыдущим тень от
горизонтального ребра ВС на фронтальной проекции совпадает с фронтальной
проекцией светового луча, а на горизонтальной проекции изобразится в виде
ломаной линии, у которой участки на проступях ступеней отстоят друг от друга на
расстоянии, равном высоте ступени.
Тень от точки В определяется в
пересечении теней, падающих на лестницу от вертикального и горизонтального
ребер боковой стенки, и в зависимости от
соотношения размеров ступени лестницы может упасть как на проступь (рис.19а),
так и на подступенок (рис.19,б).
3.4.
Тень карниза
На
рис. 20 приведен пример построения теней карниза здания.
Рис.20
На верхней криволинейной части карниза –
«гуське» — падающая тень от горизонтального ребра проходит через точку 1/
, а собственная тень «гуська» проходит через точку b/ —
точку касания фронтальной проекции светового луча к профилю «гуська».
От контура собственной тени «гуська»
строится падающая тень на свешивающейся части карниза.
Проходящее через точку С (с/)
горизонтальное ребро свешивающейся части карниза будет бросать тень на
плоскость стены. Эта тень будет параллельна самому ребру и пройдет через точку
5/ . Это же ребро бросает тень и на торцы сухариков (кронштейнов).
Она проходит параллельно самому ребру через точку 3/ . На плоскости
построены также тени от соответствующих участков ребер сухариков.
На рис.21 приведен пример построения
тени, падающей от карниза на фронтально расположенную стену, без использования
горизонтальной проекции.
Рис.21
Для построения тени проводим
вертикальную прямую Z1Z2 на расстоянии l, равном удалению вертикального
ребра стены от плоскости, на которую падает тень. Прямая Z1Z2 дает
возможность рассматривать фронтальную проекцию карниза одновременно и как
профильную его проекцию. Для построения падающей тени от
какой-либо точки карниза, например от точки А, из точки а// проводим профильную проекцию светового луча до
встречи с ее с прямой Z1Z2 в точке a0. Проведя из последней горизонтальную линию до пересечения с
фронтальной проекцией светового луча, проведенного через точку а/ ,
получим искомую тень а/v от точки
А. Аналогично могут быть найдены тени и от остальных точек карниза.
3.5.
Тени фронтона
На рис.22 показано построение тени на
фронтоне здания. Тени на левой части фронтона (до оси фронтона) построены по
аналогии с построением теней на карнизе.
Для определения теней на правой части
фронтона построен профиль m/
n/
q/ фронтона, полученный в результате пересечения
фронтона с горизонтально-проецирующей плоскостью P, проведенной под углом
450 к фронтальной
плоскости. Проведя фронтальные проекции световых лучей через соответствующие
точки этого профиля, получим в пересечении с ним точки 5/ и 6/
, через которые пройдут контуры теней в правой части фронтона.
Рис.22
Переход контура падающей тени от точки
7/ к точке 8/
представляет собой плавную кривую линию. Для определения промежуточной точки
этой кривой — точки 10/1 (см.рис. 22, внизу слева) проводим через точку
9/ , взятую произвольно на профиле между точками а/ и 1/, прямую 9/ — 10/
и в пересечении с прямой 10/ —
10/1 даст искомую точку 10/1 .
Раздел
II. ТЕНИ В АКСОНОМЕТРИИ
При построении теней в аксонометрических
проекциях направление световых лучей может быть принято любым и задается
первичной и одной из вторичных проекций светового луча.
Направление световых лучей выбирается с
учетом получения светотеневого рисунка, выявляющего наилучшим образом объемный
рельеф и конфигурацию здания или сооружения.
Основные положения, рассмотренные при
построении теней в ортогональных проекциях, остаются в силе и при построении
теней в аксонометрии.
1.Тени от точки
На рис.23 точка А задана первичной и
горизонтальной проекциями. Направление световых лучей также задано первичной
проекцией S
и
горизонтальной проекцией S‘2
.
Для построения падающей тени от точки А
проводим через эту точку световой луч принятого направления (через первичную
проекцию точки проводим первичную проекцию светового луча, а через
горизонтальную проекцию — горизонтальную проекцию светового луча). Точка
пересечения светового луча с плоскостью или поверхностью, встретившейся на его
пути, и будет являться тенью от данной точки. На чертеже тень от точки А падает
на горизонтальную плоскость проекций, а тень от точки В — на профильную
плоскость проекций (в дальнейшем
горизонтальная, фронтальная и профильная плоскости проекций будут обозначаться
соответственно h, v, w).
Рис.23
2.Тени геометрических тел
При построении теней геометрических тел приходится
определять контуры как собственных, так и падающих теней. Так как контур
падающей тени строится от контура собственной тени, то в первую очередь следует
определить, в общем случае, контур собственной тени. Контур собственной тени призмы (рис.24) при заданном направлении световых лучей
представляет собой замкнутую ломаную линию ABCDEF, участками
которой являются ребра призмы. От комнаты собственной тени строится контур Av, Bv, Cv, Dv, Ev, Fv, Av
падающей тени с точками перегиба M
и N на оси x.
Рис.24
На рис.25 построены тени
цилиндра, стоящего своим основанием на горизонтальной плоскости. Горизонтальные
проекции световых лучей, проведенные касательно к основанию цилиндра,
определяют точки А и В — основания образующих цилиндра, которые являются
линиями раздела света и тени боковой поверхности цилиндра. К контуру
собственной тени относится также дуга CED верхнего основания цилиндра. От
указанного контура строится контур падающей тени, для чего достаточно
определить падающие тени Cw и Dw от точек C
и D,
а также тени от ряда промежуточных точек дуги CED верхнего основания цилиндра.
Рис.25
При построении теней конуса (рис.26) в
первую очередь строится тень Ch
от вершины конуса на плоскость его основания. Проведенные из точки Ch
прямые, касательные к основанию конуса, а
также точки А и В, через которые проходят образующие АС и ВС, являющиеся контуром собственной тени
конуса.
Тень конуса в данном случае падает
частично и на профильную плоскость проекций, на которой контур тени
определяется точками перегиба M и
N и реальной тенью Сw от вершины конуса.
На этом же чертеже показано построение
падающей тени Kh на поверхности конуса
от точки K.
Для определения указанной тени находим вначале ложную тень Kh
от точки K на
горизонтальной плоскости, через которую из точки Ch проводим прямую, и в пересечении ее с
основанием конуса отмечаем точку Е.
Прямая ЕCh
является тенью от образующей конуса, на
которой должна находиться падающая тень Kh
от точки K . Проводим из точки Е образующую
ЕС. В пересечении ее с первичной
проекцией светового луча, проведенной
через первичную проекцию точки К, находим искомую тень от точки К на
поверхности конуса.
Рис.26
3. Примеры построения теней
архитектурных деталей
На рис.27 построены собственные и
падающие тени на столбах прямоугольного и круглого сечения, перекрытых
прямоугольными плитами.
На
столбе квадратного сечения падающая
тень А0 от точки А определена
в пересечении первичной проекции светового луча S, проведенного через точку А, с
линией 1А0 , которая представляет собой линию пересечения
вертикальной плоскости, проведенной через луч S, с боковой гранью столба.
От точки А0 вправо пойдет
тень от бокового нижнего ребра плиты. Для получения направления этой тени продолжаем плоскость грани столба
до пересечения с указанным ребром плиты в точке 2. Точка 2 в этом случае
является началом тени от данного ребра на продолженной плоскости этой грани
столба. Поэтому, соединив точку 2 с точкой А0 прямой линией, получим
в пределах грани столба падающую тень от бокового ребра плиты.
Рис.
27
На столбе
круглого сечения образующая,
определяющая контур собственной тени столба, проходит через точку 3, полученную
с помощью касательной к верхнему основанию цилиндра, проведенной параллельно
горизонтальной проекции светового луча. Эта же касательная в пересечении с
ребром АВ плиты определит точку 4, тень от которой будет находиться на
указанной образующей. Тень А0 от точки А найдена по аналогии с предыдущим
чертежом.
Так как падающие тени от горизонтальных
ребер плиты на поверхности столба будут представлять собой кривые линии, то для
их построения следует взять на ребрах плиты несколько дополнительных точек и
построить от них падающие тени на поверхности столба.
На рис.28 построены собственные и
падающие тени лестницы.
Как и при построении тени лестницы в
ортогональных проекциях, тень, падающая на ступени лестницы, строится от ребер
АВ и ВС боковой стенки. От вертикального
ребра АВ тень на проступях ступеней совпадает с горизонтальной проекцией
светового луча, а на подступенках идет параллельно самому ребру. Тень от
горизонтального ребра ВС на проступях ступеней будет параллельна ребру ВС, а на
подступенках будет совпадать с направлением проекций световых лучей на
плоскости подступенков.
При заданном направлении световых лучей
тень от точки В находится на проступи второй ступени в точке В0.
Направление падающей тени на подступенке от ребра ВС определяет линия 1-2, где
точка 2 является точкой встречи ребра ВС с продолженной плоскостью подступенка.
Рис. 28
На рис.29 показано построение теней группы геометрических тел, которая может условно рассматриваться как
здание с пристройкой.
Здесь следует обратить внимание на
построение падающих теней от ребер ВС и CD. Тень от ребра ВС падает частично на
вертикальную и частично на наклонную плоскости. Тень от ребра ВС на
вертикальной плоскости пристройки от точки В0 до точки 1 будет
параллельна ребру ВС. Чтобы определить направление тени от ребра ВС на
наклонной плоскости пристройки, продолжаем ребро ВС до пересечения его с
продолженной наклонной плоскостью пристройки. Точка пересечения 2 определяется
в пересечении ребер ВС и EF. Прямая, соединяющая точки 2 и 1, определяет искомое направление.
Аналогично для определения направления
тени от ребра CD на наклонной плоскости пристройки продолжаем эту плоскость до
пересечения с ребром CD в точке 3. Прямая 3С0 определяет искомое направление тени от
ребра CD.
Рис.29
На рисунке показано также, как найти
проекции световых лучей, если задаться точкой
С0 — падающей тенью на
скате крыши от точки С. Направление первичных проекций световых лучей будет
параллельно прямой, соединяющей точки С и С0 и соединив их между собой, получим
направление горизонтальных проекций световых лучей.
Раздел
III. ТЕНИ В ПЕРСПЕКТИВЕ
1.Тени
от точки, прямой и геометрических тел
Построение теней в перспективе
принципиально ничем не отличается от построения теней в аксонометрических
проекциях, за исключением того, что в перспективе в общем случае проекции
световых лучей направлены в соответствующие точки схода.
Рассмотрим построение падающей тени от вертикальной прямой при различных положениях источника света по
отношению к прямой (рис.30).
Рис.30
а) Источник света расположен перед
прямой, слева от неё (рис.30,а).
В этом случае точка s — точка схода перспектив
горизонтальных проекций световых лучей — будет находиться на линии горизонта
справа от перспективы прямой, а точка S — тока схода перспектив самих световых лучей
— будет находиться ниже линии горизонта и на одном перпендикуляре с точкой s.
Так как прямая, от которой строится тень, перпендикулярна к предметной
плоскости, то тень, падающая от нее на эту плоскость, совпадает с проекцией
светового луча на этой плоскости. Для
построения падающей тени от прямой достаточно найти тень от точки В1,
так как тень А0 от точки А1 совпадает с точкой А1.
Чтобы построить тень от точки В1, проводим из ее основания перспективу горизонтальной проекции светового
луча, а из точки В1 перспективу
самого луча. В пересечении проведенных прямых определяется точка В0
— тень от точки В1 .
Как направление тени от прямой, так и
ее длина зависят от выбора положения
точки s
на линии горизонта и от расстояния между точками s и S.
б) При расположении источника света за
прямой и слева от нее (рис.30, б) точки s и S будут находиться слева от
перспективы прямой, причем точка S
расположена над линией горизонта.
в) В некоторых случаях для упрощения
построения теней в перспективе направление световых лучей принимается
параллельным плоскости картины. Тогда
перспективы горизонтальных проекций световых лучей будут параллельны линии
горизонта, а перспективы самих световых лучей будут параллельны между собой.
Угол α — угол наклона световых лучей — выбирается в зависимости от желания
получить ту или иную длину тени.
На
рис. 30,в проекции световых лучей
имеют направление слева направо. Вполне очевидно, что при положении источника
света справа проекции световых лучей будут направлены справа налево.
На рис.31 построены собственные и падающие тени призмы (направление световых лучей
задано точками s
и S). Контуром собственной тени
является контур a1
A1
B1
C1
c1
, от которого и строится контур падающей тени.
Рис.31
Тени а1А0 и с1С0 от вертикальных
ребер имеют направление в точку схода перспектив горизонтальных проекций
световых лучей — точку s.
Тени от горизонтальных ребер призмы
будут параллельны этим ребрам, а следовательно, их перспективы А0В0 и
В0С0 будут иметь направление соответственно в
точки F2 F1 — точки
схода перспектив этих ребер.
На рис. 32 перспективы а1А1 и b1B1 образующих
цилиндра, определяющих линию раздела света и тени цилиндра, проходят
через точки a1 и b1. определяемые путем проведения касательных из
точки s
к проекции нижнего основания
цилиндра. От этих образующих построены падающие тени a1 A0 и
b1 B0 .
Тень между точками A0 и B0
будет кривой линией и может быть построена
по отдельным точкам по аналогии с тенью C0 от
точки C1 .
Рис.32
На рис. 33 построена собственная тень
конуса, а также падающая тень на предметную плоскость и наклонную плоскость
Р. Для построения тени на плоскости Р
вначале определена на ней тень Ср от вершины конуса. Линии контура
тени на плоскости Р пойдут из точек пересечения контура падающей тени на
предметной плоскости со следом Рh в
точку Сp
.
Рис.33
2.
Примеры построения теней архитектурных деталей
На рис. 34 приведен пример построения собственных и
падающих теней лестницы. Тени
падающие от вертикального ребра А1В1 на проступи ступеней
лестницы имеют направление в точку схода s. Тени, падающие от горизонтального
ребра В1С1 на проступи ступеней, идут в точку F2,
а тени, падающие на подступенки, будут иметь общую точку схода s‘, расположенную на линии схода
перспектив плоскостей подступенков (точка s‘ находится на перпендикуляре,
восставленном из точки F1
к
линии горизонта).
Рис.34
На
рис.35 построена тень, падающая от горизонтальной плиты на столб квадратного
сечения. Из чертежа видно, что при принятом направлении световых лучей тень
А0 от точки А1
падает на левую грань столба. Она может быть получена в пересечении перспективы
светового луча, проведенного из точки А1 в точку S, с линией А01 является
линией пересечения горизонтально проецирующей плоскости, проведенной через луч,
проходящей через точку А1, с левой гранью столба. Тень от ребра А1С1
пойдет из точки А0 в точку схода F1.
На эту же грань падает тень от участка А1D1 горизонтального
ребра А1В1 плиты. Для определения направления тени A0D0 продолжаем плоскость
грани столба до пересечения в точке D1 с ребром А1В1.
Соединив точки D1
и
A0,
получим искомое направление тени. Тень от ребра А1В1 пойдет
из точки D0
в точку схода F2/
Рис.35
Раздел
IV.
ПЕРСПЕКТИВНЫЕ ПРОЕКЦИИ
Перспективное
изображение (перспектива) представляет собой центральную проекцию, построенную
при положении центра проецирования, отвечающем определенным условиям.
Перспективные проекции являются более наглядным
изображением, чем аксонометрические. Это объясняется тем, что аппарат зрения в
геометрическом отношении аналогичен аппарату центрального проецирования (за
центр проецирования при построении перспективных изображений принимается как бы
глаз зрителя).
Перспективные проекции могут быть
построены как на плоскости, так и на той или иной поверхности. Чаще всего
перспективные проекции строятся на плоскости, и в этом случае перспектива носит
наименование линейной перспективы.
Перспектива, построенная на цилиндрической поверхности, называется панорамной перспективой.
Купольной
перспективой называется перспектива, построенная на сферической
поверхности.
В архитектурном проектировании главным
образом применяется линейная перспектива.
1.Основные понятия и
определения. Перспектива точки
В линейной перспективе
вертикальная плоскость проекций К (рис.36) называется картинной плоскостью,
картиной или плоскостью картины. Горизонтальная плоскость H
называется предметной плоскостью.
Предметная
плоскость фиксирует расположение
проецируемого объекта в пространстве в вертикальном направлении. Обычно
проецируемый объект своим основанием располагается на предметной плоскости.
Рис.36
Линия kk1 — линия пересечения картинной плоскости с
предметной — называется основанием
картинной плоскости;
Z — точка зрения (центр проецирования);
z —
основание точки зрения (ортогональная проекция точки зрения на предметной плоскости);
Zz — высота точки зрения;
hh1 —
линия горизонта (линия пересечения с картинной плоскостью горизонтальной
плоскости, проведенной через точку зрения;
F0
— главная точка картины (точка пересечения с картинной плоскостью луча,
проведенного из точки зрения перпендикулярно к плоскости картины);
f0 — основание главной точки картины;
ZF0 — главное расстояние (расстояние от точки зрения до плоскости
картины);
А —
проецируемая точка;
а
— основание точки А (ортогональная
проекция точки А на плоскость H).
Для построения на
плоскости картины К перспективного
изображения точки А проводим через неё в точку зрения проецирующий луч AZ. Точка встречи луча с картинной
плоскостью определяет точку А1 — перспективу точки А.
Чтобы
найти на картине положение точки А1, через луч AZ проводим горизонтально-проецирующую
плоскость, горизонтальный след которой совпадает с горизонтальной проекцией az
(основанием) луча AZ.
Линия пересечения проведенной плоскости с плоскостью картины пройдет
вертикально через точку ak
и в пересечении с лучом AZ определит искомую
перспективу А1 точки А.
Аналогичным
образом может быть найдена точка a1
— перспектива основания точки А1.
Из
чертежа видно, что перспектива точки
пространства (точка А1) и перспектива ее основания (точка а1) лежат на одном перпендикуляре к линии горизонта и к основанию плоскости
картины.
Необходимо
отметить, что по одной перспективе точки нельзя судить о положении самой точки
в пространстве. Действительно, если на луче
AZ
или на его продолжении зададим какую-либо точку, например точку В, то перспектива
В1 точки В совпадает с перспективой А1 точки А.
Для определения положения точки в
пространстве по ее перспективе кроме перспективы самой точки необходимо иметь еще и
перспективу ее основания.
По
положению перспектив точек А и В можно
судить и о взаиморасположении самих точек. У более удаленной точки А перспектива ее основания а1
расположена выше над основанием картины, чем у точки В, расположенной ближе к
зрителю (к точке зрения).
На рис. 37
плоскость картины с перспективами точек А и В и перспективами их
оснований совмещена с плоскостью чертежа. Здесь же, вне зависимости от черт.37,
изображены перспективы точек С и D
и перспективы c1 и
d1
их оснований. Так как перспектива С1 расположена ниже перспективы с1 основания точки С, то это означает, что точка С расположена в
пространстве под предметной плоскостью. Перспектива D1 точки D совпадает с перспективой d1 своего основания. Это означает,
что точка D расположена
в предметной плоскости.
Следует
отметить, что если перспектива точки в зависимости от положения ее в
пространстве может быть на картинной плоскости как выше, так и ниже линии
горизонта, то перспектива основания любой точки пространства всегда располагается, ниже линии горизонта.
Рис.37
2.Перспектива прямой линии
На
рис. 38 изображен прямолинейный отрезок АВ и его основание ab.
Так как плоскость, проведенная через
любую проецируемую прямую, не совпадающую по направлению с проецирующим лучом,
и точку зрения, пересечет плоскость картины К по прямой линии, то,
следовательно, перспективой прямой линии будет также прямая линия. Поэтому для
построения перспективы отрезка АВ достаточно найти перспективы А1 и
В1 концов отрезка, соединив которые прямой линией, получим
перспективу А1 В1 отрезка АВ.
Если отрезок АВ продолжить до пересечения
с плоскостью картины в точке D1, то и перспектива А1В1
в своем продолжении пройдет через ту же точку D, так как последняя, находясь
непосредственно в картинной плоскости, является одновременно и
перспективой D1 и точки D.
Если отрезок АВ продолжить от картинной
плоскости и задаться на нем какой-либо точкой С, то ее перспектива С1
определится в точке пересечения проецирующего луча CZ
с продолженной перспективой А1 В1.
Если на заданной прямой взять бесконечно
удаленную точку, то луч, проецирующий эту точку на
картину, окажется параллельным данной прямой. Поэтому проведя из точки зрения Z луч
параллельно данной прямой АВ до его пересечения с продолженной перспективой А1
В1, получим точку F,
являясь перспективой бесконечно удаленной точки прямой АВ, будет являться также
и перспективой бесконечно удаленной точки прямой MN, а отрезок N1F — перспективой этой
прямой.
Рис
.38
Отсюда следует, что точка F является перспективой бесконечно
удаленных точек всех прямых, параллельных прямым АВ и MN, и перспективы всех прямых,
параллельных им, будут сходиться в той же точке F.
Точка
F
называется точкой схода перспектив прямых данного направления. По аналогии
точка f является точкой схода перспектив всех прямых,
параллельных основанию ab.
Таким образом, перспективы параллельных прямых каждого направления имеют свою точку
схода, которая определяется в пересечении с картинной плоскостью луча,
проведенного из точки зрения параллельно прямым данного направления.
На рис. 39 плоскость картины совмещена
с плоскостью чертежа. Прямые AB и MN — восходящие: направленные от картинной плоскости вверх. У
восходящих прямых точки схода их перспектив всегда будут находиться выше линии
горизонта. Точки схода перспектив всегда
будут находиться выше линии горизонта. Точки
схода перспектив нисходящих
прямых (направленных от картинной
плоскости вниз) расположены всегда ниже
линии горизонта.
Рис.39
На рис.40, а даны перспективы A1B1 и C1D1 двух
параллельных нисходящих прямых и перспективы
a1b1
и c1d1 их оснований. Так как перспективы A1 и a1, а также С1 и
с1 совпадают, то это
означает, что прямые AB и CD пересекают предметную плоскость
соответственно в точках А и С.
Точки
схода перспектив горизонтальных прямых любого направления всегда расположены на
линии горизонта. В этом случае точка схода F перспектив прямых и точка
схода f перспектив их оснований совпадают друг с другом (см. рис. 40, б).
Рис. 40
Когда прямые перпендикулярны к
плоскости картины, точка схода перспектив таких прямых находится в главной
точке картины — точке F0
.
Если прямые параллельны картинной
плоскости, то перспективы таких прямых не имеют точек схода и будут параллельны
как самим прямым, так и между собой.
На рис.40, в, г, д изображены перспективы
А1В1 и С1D1
двух параллельных прямых АВ и СD и перспективы a1 b1 и c1
d1 их оснований. Во всех
трех случаях прямые параллельны
картинной плоскости. В первом
случае прямые наклонены к предметной плоскости под углом α . Во втором случае
прямые AB и
CD
— горизонтальные. На последнем чертеже изображены перспективы двух вертикальных
прямых.
3.
Способы построения перспективных проекций
Существует ряд способов построения
перспективных проекций. До построения перспективы необходимо выбрать, в
зависимости от характера изображаемого объекта, наиболее рациональный для
данного случая способ построения, наметить положения точки зрения и картинной
плоскости. Выбор положения картинной плоскости и точки зрения будет рассмотрен
ниже.
При построении перспективы любым
способом всегда следует построить вначале перспективы основных (общих) объемов
здания или сооружения, после чего для построения перспектив отдельных деталей
необходимо использовать различные графические приемы, рассмотренные ниже.
Только при такой последовательности построения перспективы можно добиться
точного и быстрого ее выполнения. При
рассмотрении примеров построения перспектив различными способами будем считать
положения картины и точки зрения наперед заданными.
3.1.
Способ координат (способ масштабов)
Сущность данного способа показана на
примере построения перспективы точки.
На рис. 41 слева даны ортогональные
проекции точки А точки зрения Z.
Картинная плоскость задана следом kk1.
На ортогональном чертеже намечаем
оси x, y и z прямоугольной системы координат.
Начало координат О выбираем на основании картины, а ось x совмещаем с
основанием картины. В этом случае ось y
окажется перпендикулярной к основанию картины kk1, а ось z будет находиться в картинной плоскости.
Затем на плоскости картины, совмещенной с плоскостью чертежа (черт.41 справа), строим
перспективы координатных осей. Для этого наметив на основании картины основание
главной точки f0,
определяем в соответствии с ортогональным чертежом перспективу О1 начала координат. Так как оси x и z
расположены в картинной плоскости, то их перспективы x1 и
z1
будут взаимно перпендикулярны и будут проходить через точку О1.
Любые отрезки, измеряемые по осям x
и z
должны
откладываться на осях x1
и z1 без искажения. Ось y, перпендикулярная к
картинной плоскости, изобразится на картине в виде прямой y1 , проходящей через
точку О1 и точку F0 — точку схода перспектив прямых,
перпендикулярных к картинной плоскости.
Рис.41
При выбранной системе прямоугольных
координат координаты x,
y
и z
точки А будут равны на ортогональном чертеже соответственно отрезкам оаx, oay, o‘az .
Отрезки оаx, и o‘az
откладываются на картине по осям x1 и z1 без искажения (Oax
= оаx; O1az = o‘az).
Чтобы определить на картине на оси y1
точку а1, поступаем следующим образом. На ортогональном чертеже
через точку ay
проводим прямую под углом 450 к основанию картины и определяем в пересечении с ним точку ad. Точка ad будет отстоять от точки о на расстоянии,
равном координате точки А по оси y (oad = oay). Затем из точки z проводим прямую, параллельную
прямой aday
,
до пересечения ее с основанием картины в точке fd. Точка fd является основанием
точки схода Fd
перспектив прямых, параллельных прямой aday
.
Из чертежа видно, что точка fd
отстоит от точки fo на расстоянии, равном zf0,
т.е. находится на расстоянии, равном удалению (дистанционному расстоянию) точки
зрения от плоскости картины. На линии горизонта находим в соответствии с
ортогональным чертежом точку Fd.
От точки О1 на основании
картины откладываем отрезок O1ad, равный координате
точки А по оси y
(O1ad = oay
= oad). Из точки ad проводим прямую в
точку схода Fd
и в пересечении с перспективой y1
оси y
получаем искомую точку ay1.
Таким образом, в перспективе отложены
координаты точки А по всем осям.
Так как основание точки А — ее
горизонтальная проекция — расположена на пересечении перпендикуляров,
восставленных к осям x и y
в точках ax
и ay, то перспектива a1
основания точки А определится в пересечении перспектив указанных
перпендикуляров. Перспектива перпендикуляра axa
как прямой,
перпендикулярной к плоскости картины, пойдет из точки ax1
в точку F0,
а перспектива перпендикуляра aya
как прямой, параллельной плоскости картины, пойдет через точку ay1
параллельно основанию картины.
Координата, отложенная по оси z1
, определяет превышение точки А над предметной плоскостью. Но так как точка А
удалена от плоскости картины на расстоянии, равном отрезку oay , то для построения
перспективы А1 точки А
поступаем следующим образом. Из точки az
проводим прямую в точку
F0. Эта прямая является перспективой прямой,
перпендикулярной плоскости картины. Превышение перспективы А1 точки
А над перспективой ее основания будет рано отрезку ay1a1»,
поэтому, определив точку a»1
в пересечении прямых azF0
и ay1a1»
(прямая перпендикулярна к линии
горизонта), находим в пересечении прямых a1»
A1
и a1
A1 перспективу А1.
На рис. 41 показано также, как построить
перспективу B1b1 вертикального отрезка, равного по высоте превышению точки А над предметной
плоскостью, если перспектива b1
его основания задана. Построения ясны из чертежа.
В тех случаях, когда точка схода Fd находится за пределами
чертежа или когда отрезки, откладываемые на оси x1
для определения перспективных координат по оcи y, велики, прибегают к использованию
вместо точки так называемых «дробных» точек. Например, та же точка ay1
на оси y1
может быть определена на картине в пересечении с осью y1
прямой, проходящей через точки ad/2 и Fd/2. Точка ad/2 расположена от точки О1 на расстоянии, равном половине координаты по
оси y,
а точка Fd/2
находится от точки F0
на расстоянии, равном половине расстояния от точки зрения до плоскости картины.
Изображения на картине прямоугольных
координатных осей принято называть:
ось х1 — масштабом широт;
ось y1 — масштабом глубин;
ось z1 —
масштабом
высот.
На рис.42 с помощью указанных масштабов
построена перспектива куба, передняя грань которого расположена в плоскости
картины. Оси x1,
y1
и z1,
а также линия горизонта и точки схода F0 и Fd предполагаются
заданными.
Все построения перспективы куба
основаны на построениях, разобранных на рис.41. Так как основание куба
представляет собой квадрат, то, отложив по оси
x1
отрезок e1a1,
равный величине ребра куба, проводим из точки a1
прямую в точку схода Fd
и определяем в пересечении этой прямой с осью y1
точку c1. Прямая a1c1 является перспективой диагонали нижнего
основания куба.
Перспективы всех горизонтальных ребер
куба, перпендикулярных к плоскости картины, имеют общую точку схода F0.
Следует обратить внимание, что перспектива A1
C1
диагонали верхнего основания куба имеет общую точку схода F с перспективой a1c1
диагонали нижнего основания куба.
Рис.42
3.2.
Способ сеток
Масштабы широт, глубин и высот (см. способ координат)
с успехом используются при построении перспективных изображений по так
называемому способу сеток.
Для построения перспективы способом сеток на ортогональном чертеже (рис.43)
намечают расположение координатных осей x1,
y1
и z1
точки зрения. Ось x
совмещают с основанием картины kk1,
а ось y
проводят перпендикулярно к ней через точку О, которая может быть намечена в
любой точке оси. Тогда ось z
пройдет через точку О вертикально и будет расположена непосредственно в
плоскости картины.
Затем в горизонтальной плоскости
наносится сетка квадратов со сторонами, параллельными осям x и
y
. Размер стороны квадрата выбирается с учетом желания получить ту или иную
точность построения перспективы.
Прежде чем приступить к построению
перспективы на картине (рис.43 справа), задаются главной точкой F0,
наносят перспективы x1,
y1
и z1
координатных осей, отмечают точку схода Fd
,
отстоящую от точки F0 на расстоянии, равном расстоянию от точки
зрения до плоскости картины (F0Fd = ZF0)
и строят перспективу сетки квадратов.
Для построения перспективы сетки на
оси отмечаем точки 1x1,
2x1,
3x1 и другие в соответствии с ортогональным
чертежом (отрезки по осям x1 и y1
перспективы увеличены в полтора раза по сравнению с отрезками по осям x и z ортогонального чертежа), и
проводим из этих точек в точку F0
прямые линии, которые и являются перспективами
линий сетки, перпендикулярных к плоскости картины.
Для построения перспектив линий сетки,
параллельных основанию картины, из какой-либо точки, например точки 6х1,
проводим прямую в точку схода Fd. Прямая 6x1Fd является перспективой диагонали ряда квадратов
сетки, поэтому перспективы линий сетки, параллельных основанию картины, пройдут
параллельно основанию картины, через точки пересечения прямой 6x1Fd с перспективами сторон
сетки другого направления. Перспектива этой сетки используется для построения
перспективы основания объекта.
Для построения перспективы основания
какой-либо точки, расположенной в предметной плоскости, определяется на глаз
положение этой точки в том или другом квадрате сетки, в соответствии с чем на
картине и намечается ее перспектива. Так, перспектива a1 изобразится
в соответствии с ортогональным чертежом в перспективе квадрата, ограниченного
прямыми сетки, проведенными через точки 4x , 5x , и 1y , 2y .
Рис.43
Для построения перспектив точек,
расположенных вне предметной плоскости, на оси z1 отмечаем точки 1z1,
2z1
и др. в соответствии с точками, намеченными на оси z ортогонального чертежа. Из этих
точек проводим прямые линии в точку F0. Проведенные прямые
являются перспективами параллельных горизонтальных прямых, расположенных в
вертикальной плоскости, проходящей через оси y z. Перспективы этих прямых и
вертикальные прямые, проходящие через точки 1y1,
2y1
и др., образуют перспективу сетки квадратов, расположенных в указанной
вертикальной плоскости. Эта сетка дает возможность определить высоту
перспективы точки над ее основанием.
Перспектива А1 точки А
строится по перспективе а1 ее
основания с использованием масштаба высот (ход построения показан стрелками).
Положение точки a»1 на перспективе вертикальной сетки определяется
между линиями 2z1 и 3z1
на глаз с учетом расположения точки на ортогональном чертеже.
Способ сеток используется главным
образом в тех случаях, когда не требуется особой точности построения
перспективы и при построении объектов со сложными криволинейными очертаниями в
плане, перспектив застройки городских кварталов, перспектив топографических
поверхностей и т.д. Вполне очевидно, что точность построения перспективы будет
зависеть от принятых размеров квадратов сетки.
3.3.
Способ архитекторов
В практике построения перспектив способ
архитекторов имеет широкое применение.
При построении перспективы способом
архитекторов используются точки схода перспектив прямых основных направлений
изображаемого объекта. Использование указанных точек схода ускоряет построение
перспективы и повышает точность построения.
При построении перспективы в первую
очередь строится обычно перспектива основания объекта.
На рис.45 построена в соответствии с
ортогональным чертежом (рис.44) перспектива квадрата, расположенного в горизонтальной
плоскости, и перспектива его основания. Для определения точек схода перспектив
сторон основания квадрата, при заданном положении картины и точки зрения z (рис.44) проводим прямые,
параллельные сторонам основания квадрата, до пересечения их в точках f1
и f2
с основанием картины. Точки f1
и f2
являются основаниями точек схода перспектив прямых, параллельных
соответствующим сторонам квадрата.
Рис. 44
Для построения перспективы на рис.45
намечаем основание картины kk1,
линию горизонта, соответствующую высоте точки зрения, и главную точку картины F0,
а также точки схода F1
и F2
на линии горизонта, отстоящие от точки F0
на расстояниях F0F1
и F0F2 , равных отрезкам с
ортогонального чертежа.
При построении перспективы (рис.45)
размеры, переносимые на картину с
ортогонального чертежа (рис.44), увеличены. Так как любая вершина основания
квадрата определяется в пересечении его сторон, то проведя через стороны
основания квадрата прямые до пересечения их с основанием картины в точках af2,
bf2,
bf1 и cf1 (рис.44) и поcтроив перспективы этих прямых, в
пересечении последних определяют перспективы вершин основания квадрата, а,
следовательно, и перспективу основания квадрата.
Для построения перспективы точки af2, bf2,
bf1
и cf1
переносим с ортогонального чертежа на картину
(рис. 45) и, проведя из точек af2 и bf2 прямые в точку схода F2
и из точек bf1
и cf1
— в точку схода F1,
получим перспективы прямых, проведенных через стороны основания квадрата, и в
их пересечении — перспективы a1,
b1,
c1
и d1
вершин
основания квадрата. Точки af2
, bf2
, bf1 и cf1 являются
началом перспектив проведенных прямых.
Перспективы a1,
b1,
c1
и
d1
вершин основания квадрата могут быть определены также и в пересечении
вертикальных прямых, проведенных через точки ak , bk , ck и dk с прямыми af2F2
и bf2F2
или с прямыми bf1F1и
cf1F1.
Это дает возможность строить перспективу, используя лишь одну из точек схода F1
или F2,
ближайшую к точке , что обычно и имеет место в практике построения перспектив.
Рис.45
Точки ak, bk
,
ck
и dk переносятся на картину с ортогонального
чертежа (рис.44), где они определяются как точки пересечения с основанием
картины прямых, проведенных через горизонтальные проекции вершин основания
квадрата и горизонтальную проекцию точки зрения. Эти прямые представляют собой
горизонтальные следы горизонтально проецирующих плоскостей, проведенных через
проецирующие лучи и пересекающих плоскость картины по вертикальным прямым
(см.черт.39), проходящим через точки ak,
bk
,
ck и dk .
Перспективы A1,
B1,
C1
и D1
вершин квадрата (рис.45) могут быть определены по аналогии с перспективами
вершин основания квадрата в пересечении вертикальных прямых, проведенных через
точки ak, bk
,
ck и dk с прямыми Af2F2
и Bf2F2
или с прямыми Bf1F1
и Cf1F1.
Точки Af2 ,
Bf2
,
Bf1
,Cf1
расположены на вертикальных прямых, проведенных соответственно через точки af2 , bf2
, bf1
и cf1,
на расстоянии от основания картины, равном превышению H плоскости квадрата над предметной
плоскостью.
Как видно из чертежа, перспективы b1d1 и B1D1
диагоналей основания квадрата и самого квадрата имеют одну общую точку схода F45
, которую удобно использовать при построении перспектив.
Точка F45
определяется на картине по ортогональному чертежу (рис.44). Для определения ее
на ортогональном чертеже из основания z
точки зрения проводится прямая, параллельная диагонали bd квадрата, до пересечения с
основанием картинной плоскости в точке f45.
Точка f45
является основанием искомой точки схода F45.
На рис.47 построена перспектива по
ортогональным проекциям, приведенным на рис.46. Положение картины и точки
зрения будем считать заданными.
Рис. 46
Как видно из ортогонального чертежа,
горизонтальные линии объекта имеют в данном случае два направления, а именно
направления, параллельные прямым линиям AB и
BC.
Рис.47
Для определения точки схода перспектив
прямых первого направления проводим на ортогональном чертеже из основания точки
зрения прямую параллельную ab,
до пересечения ее с основанием картины в точке f1
и для определения точки схода второго направления — прямую, параллельную bc, до пересечения ее с основанием
картины в точке f2.
Для построения перспективы на рис.47
проводим основание картины kk1,
линию горизонта hh1,
отмечаем главную точку картины F0
и ее основание f0,
а также в соответствии с ортогональным чертежом точки F1 F2
— точки схода перспектив горизонтальных прямых указанных выше направлений (F0F1
= f0f1;
F0F2
= f0
f2
).
Чтобы построить перспективу B1
точки B
и перспективу b1
ее основания, а, следовательно, и перспективу B1b1
вертикального ребра, проводим через точку b (черт.48) в точку z
прямую bz
и отмечаем в пересечении этой прямой с основанием картины kk1
точку bk.
Кроме того, через ту же точку b
следует провести прямую bbf1,
параллельную zf1
или прямую bf2,
параллельную zf2.
Произведя указанные построения, наносим
на картину (рис.47) точки bk
bf1
или bf2.
Из точки bk
восставляем к основанию картины перпендикуляр, на котором и будут находиться
перспективы B1
и b1
точки B
и ее основания.
Для определения положения перспективы
точки B
из точки bf1
восставляем к основанию картины перпендикуляр, на котором откладываем от точки bf1
превышение точки B
над предметной плоскостью (Bf1
bf1 = b’bx).
Из точек Bf1
и bf1
проводим в точку F1
прямые, которые в пересечении с перпендикуляром, восставленным ранее из точки bk, определяют искомые
перспективы B1
и b1.
Перспективы B1
и b1
могли бы быть также определены на перпендикуляре, восставленном из той же точки
bk,
в пересечении его с прямыми Bf2F2
и bf2
F2,
причем Bf2bf2
= b‘bx .
Перспективы c1
и C1
определятся в пересечении прямых b1F2
и B1f2
с перпендикуляром, восставленным из
точки ck
к основанию картины.
Так как перспектива b1a1
горизонтального ребра пройдет через найденную перспективу b1
в точку схода F1,
то перспектива a1
основания точки A
определится на прямой b1F1
в пересечении ее с перпендикуляром, восставленным из точки ak к основанию картины.
На этом же перпендикуляре будет
находиться и перспектива A1,
которая может быть получена по аналогии с перспективой точки B. Для этого откладываем на прямой bf1 Bf1
от точки bf1
превышение точки над предметной плоскостью (bf1Af1
= a‘ax) и проводим из точки Af1
в точку схода F1
прямую, которая в пересечении с вертикальной прямой, проведенной ранее из точки
ak,
и определит перспективу A1.
Наличие на картине двух точек схода F1 F2
перспектив горизонтальных линий основных направлений объекта упрощает
построение его перспективного изображения, что можно видеть на примере
построения точек C1,
c1,
D1
В
практике построения перспектив, особенно больших размеров, часто приходится
ограничиваться использованием лишь одной точкой схода перспектив прямых
основных направлений объекта (ближайшей к главной точке картины), вследствие
того, что для построения перспективы по двум точкам схода требуется больше места
на чертеже.
На рис.48 построена перспектива того же
объекта с использованием одной точки схода F2,
ближайшей к главной точке картины. Здесь перспективы b1 и B1 определены в
пересечении вертикальной прямой, проведенной из точки bk, с прямыми, проведенными
соответственно из точек bf1
и Bf2
в точку схода F2.
По аналогии с этим определены
перспективы a1,
A1,
D1
и E1,
которые засечены на вертикальных прямых, проведенных из точек ak и dk, лучами, направленными
соответственно из точек af2,
Af2,
Df2
и Ef2
в точку схода F2.
Точки af2
и df2
перенесены на рис.47 с ортогонального чертежа. Отрезки af2Af2,
df2Df2
и df2Ef2
равны соответственно превышению точек и над предметной плоскостью.
Перспективы C1 и
c1 найдены так же, как и на предыдущем чертеже.
При построении перспективы с
использованием лишь одной точки схода перспектив линий одного из основных
направлений объекта, например точки F2 , в некоторых случаях
целесообразно использовать также и точки
схода перспектив линий иных направлений, не имеющих места в проектируемом
объекте. Так на рис.48 показано, что перспективы A1
и a1
могут
быть определены на вертикальной прямой, проведенной из точки ak, также в пересечении
ее соответственно с прямыми Af0
F0
и af0
F0.
Последние являются перспективами горизонтальных прямых, проведенных
перпендикулярно к картине через точки A
и a.
Точкой схода перспектив таких прямых является главная точка картины F0. Точка af0
перенесена с ортогонального чертежа, где она получена в пересечении
перпендикуляра, проведенного к kk1
из точки a,
с основанием картины kk1.
Отрезок на картине равен превышению точки A над предметной плоскостью.
Из
чертежа видно, что для построения перспектив A1
и a1
точек A и a
с использованием точки схода F0
требуется меньше места на листе бумаги, чем при построении перспектив указанных
точек с использованием точки схода F2.
Рис.
48
4.
Выбор положения картинной плоскости и точки зрения
Характер перспективного изображения
зависит от положения картинной плоскости и точки зрения.
При одном и том же положении точки
зрения и различных положениях плоскости картины, как и при одном и том же
положении плоскости картины и различных положениях точки зрения, перспективные
изображения одного и того же объекта будут отличными друг от друга.
Ниже даются некоторые рекомендации в
отношении выбора картины и точки зрения при построении перспективных
изображений.
4.1
Выбор положения картинной плоскости
На рис.49 вверху даны ортогональные
проекции четырехгранной призмы с основанием в виде квадрата. Картинная
плоскость, заданная ее горизонтальным следом kk1,
проходит в данном случае через переднее вертикальное ребро призмы и составляет
с двумя смежными вертикальными гранями призмы углы α и β .
Рис.49
На рис.50 внизу (верхний ряд
изображений) показано, как будут изменяться перспективные изображения призмы в
зависимости от изменения углов α и β.
Рис.50
Так, если угол α равен углу β
(изображение а), то при направлении основания главного луча в центральную точку
плана перспективы боковых граней призмы будут иметь равную ширину (l = l1),
а углы наклона перспектив горизонтальных ребер, отмеченные на чертеже
соответственно одной или двумя дугами, будут равны между собой.
Перспектива, выполненная при таком
положении плоскости картины, является маловыразительной, и поэтому такое
расположение картинной плоскости не может быть рекомендовано.
На этом же чертеже изображены
перспективы той же призмы при α ‹ β (изображение б) и при α › β
(изображение в). В первом случае на перспективном изображении в большей
степени выявляется грань AC,
а грань BC
имеет более сильное перспективное сокращение (l › l1).
Во втором случае при α › β, наоборот,
более сильное перспективное сокращение будет у грани AC (l ‹ l1).
Это обстоятельство следует учитывать при выборе расположения плоскости картины.
Следует отметить также, что при
выбранных углах и картинная плоскость может быть расположена различно по
отношению к самому объекту, а именно: пересекать объект — плоскость К1
(рис.51) , проходить через одно ребро объекта (плоскость К2), или
через несколько ребер, быть расположенной перед объектом (плоскость К3)
или находиться сзади него (плоскость К4).
Рис.51
При
указанных положениях плоскости картины получаемые на ней перспективные
изображения будут подобны друг другу. Однако предпочтение следует отдать
плоскости К1, пересекающей объект, так как в этом случае элементы,
через которые проходит плоскость картины, изображаются на последней без
искажения, т.е. в истинную величину, что облегчает построение перспективы.
На чертеже справа построена перспектива
на плоскости К1. В связи с тем, что высоты, взятые с ортогонального
чертежа, отложены на перпендикулярах, восставленных к основанию картины из
точек 1k,
2k, 3k и 4k без искажения, данную перспективу можно
построить с использованием лишь одной точки схода.
Само собой разумеется, что при желании
получить в перспективе изображение левой боковой грани объекта картинную
плоскость следует расположить соответствующим образом (плоскость К5).
В частных случаях картинная плоскость
может быть расположена фронтально.
4.2
Выбор положения точки зрения
При выборе положения точки зрения
необходимо учитывать возможное положение зрителя по отношению к
рассматриваемому объекту.
Основание главного луча зрения следует
направлять примерно в центральную часть плана объекта.
Расстояние от точки зрения до плоскости
картины рекомендуется принимать в 1,5–3 раза больше наибольшего из размеров перспективного изображения,
измеряемых по его ширине и высоте, что
соответствует углу между крайними проецирующими лучами в пределах от 190 до 370.
При более близком положении точки зрения могут получиться изображения с
неестественными, непривычными для глаза искажениями. При большем удалении точки зрения от предмета
перспективные изображения получаются маловыразительными.
Учитывая вышесказанное, чтобы
определить положение основания точки зрения в плане, удобно пользоваться
следующим приемом (см. рис.50). На
ортогональном чертеже на основании картины, в любом месте, задаемся
произвольным отрезком mn,
из середины которого восставляем к основанию картины перпендикуляр lq, равный, в зависимости от принимаемого удаления
точки зрения, 1,5-3 отрезкам mn.
Проведя лучи az и bz, охватывающие план объекта и
параллельные соответственно сторонам mq и nq
треугольника mnq,
получим в пересечении этих лучей положение основания точки зрения. Отрезок на
основании картины между лучами az
и bz
определяет ширину перспективного изображения.
В случае, если высота объекта
значительно больше размеров плана объекта, положение точки зрения следует
выбирать с учетом рекомендуемых углов (190 — 370) между
крайними проецирующими лучами, расположенными в вертикальной плоскости.
Высота точки зрения Z над предметной плоскостью
принимается обычно равной высоте человеческого роста или высоте, не превышающей
одной трети высоты сооружения.
Иногда точку зрения принимают
расположенной в предметной плоскости (изображение
д). Построение перспективы при таком положении точки зрения
несколько упрощается.
Располагать точку зрения выше 1/3
высоты здания, то есть в пределах верхних 2/3 его высоты, не рекомендуется
(изображение г).
Иногда высота точки зрения принимается
больше высоты объекта (изображение е). Это имеет место при построении
перспектив застройки кварталов, заводских территорий и т.д. Такое положение
точки зрения позволяет лучше показать взаимное расположение отдельных зданий.
5.
Приемы, применяемые при построении перспективных изображений
Способы построения перспективных
изображений, рассмотренные ранее, применяются в основном для построения перспектив
общих объемов зданий и сооружений.
Построение перспектив отдельных деталей
общих объемов производится уже непосредственно на самом перспективном
изображении, для чего используются различные геометрические приемы.
5.1
Деление в перспективе отрезков на равные и пропорциональные части
Деление отрезков
вертикальных прямых
Чтобы разделить перспективу A1a1
вертикального отрезка на равные части (рис.52 слева), из точки a1
проводим под произвольным углом прямую, на
которой откладываем от точки равные или заданные пропорциональные
отрезки. Соединив прямой линией конечную точку A0
с точкой A1
перспективы отрезка, получим направление A0 A1,
параллельно которому из точек 10, 20, 30
проводим прямые. Эти прямые и разделят перспективу в требуемом отношении.
Аналогичным образом производится деление
перспектив любых прямых, параллельных плоскости картины.
Рис.
52
Деление
отрезков горизонтальных прямых, не параллельных
плоскости картины
Для деления перспективы A1B1
отрезка горизонтальной прямой (рис.53 слева) из точки A1
проводим параллельно линии горизонта прямую
A1B0, на которой от точки A1
откладываем последовательно отрезки заданных размеров. Соединив конечную точку B0
с перспективой B1
прямой линией, в пересечении последней с линией горизонта найдем точку схода F1,
Линии, проведенные из точек 10, 20 в ту же точку схода F1,
поделят перспективу A1B1
в нужном отношении.
Эти построения возможны потому, что
здесь все прямые расположены в горизонтальной плоскости и, следовательно,
прямые B0B1,
2021 и 1011, являясь перспективами
параллельных прямых, имеют общую точку
схода F1,
расположенную на линии горизонта.
Рис.53
Деление
отрезков прямых общего положения
Для того, чтобы разделить перспективу M1N1 отрезка прямой общего положения (рис.53
справа), следует сначала разделить в нужном отношении перспективу ее основания
как перспективу m1
n1
горизонтальной прямой. Тогда вертикальные линии, проведенные из точек 11
и 21, полученных на перспективе основания прямой, разделят
перспективу самой прямой в том же отношении.
5.2
Перспектива окружности
Окружность, расположенная в плоскости,
параллельной картине, изобразится в перспективе также в виде окружности. Во
всех остальных случаях, за исключением некоторых частных положений окружности,
которые редко встречаются в практике проектирования, перспективой окружности
является эллипс.
На рис.54 показано построение
перспективы окружности, расположенной в горизонтальной плоскости, и перспективы
окружности, расположенной в вертикальной плоскости, перпендикулярной к плоскости
картины. Способ построения аналогичен способу построения эллипса,
представляющего проекцию окружности, вписанной в квадрат, и строится по восьми
точкам. Перспективы квадратов, в которые следует вписать эллипсы, могут быть
построены способом, рассмотренный выше (метод сетки).
Рис.
54
Эллипс как перспектива окружности,
расположенной в горизонтальной плоскости, пройдет через точки О2 ,
1, 2, 3, являющиеся перспективами середин сторон квадрата, и через четыре
точки, расположенные на перспективах диагоналей квадрата. Для получения этих
точек из точек O2
и a 1 проводим прямые под
углом 450 к прямой O2a1
до их взаимного пересечения в точке m. Затем из точки O2
как из центра проводим дугу окружности с радиусом O2 m до пересечения ее с
прямой a1
O1
в точках m1
и m2.
Прямые, проведенные из этих точек в точку схода F0,
в пересечении с перспективами диагоналей квадрата определят искомые точки
эллипса.
Аналогично построена перспектива
окружности, расположенной в вертикальной плоскости.
На рис.55 рассмотренный выше способ
применен для построения перспектив полуциркульных арок.
Рис.55
На рис.56 показан еще один из возможных
способов построения перспективы окружности, расположенной в вертикальной или
горизонтальной плоскости. На чертеже приведено построение перспективы лишь
половины окружности.
Рис.56
Построив перспективы A1,
B1 и C1 точек окружности, проводим из точек A1 и B1
через точку C1 прямые линии. Для получения других точек,
принадлежащих эллипсу, являющемуся изображением окружности, расположенной в
вертикальной плоскости, в пределах между точками A1
и B1 проводим какую-либо вертикальную прямую,
параллельную C1O1,
и отмечаем точки 1 и 2 — точки пересечения ее с ранее проведенными прямыми A1C1
и B1C1 .
Точка m , принадлежащая эллипсу, определится в пересечении прямых, проведенных
из точек A1
и
B1 соответственно через
точки 1 и 2. Аналогичным образом могут быть определены и другие точки,
принадлежащие эллипсу.
Построения, связанные с определением
точек m и n эллипса — перспективы окружности, расположенной в горизонтальной
плоскости, отличаются от построения аналогичных точек эллипса, когда окружность
расположена в вертикальной плоскости, тем, что если прямые 1-2, 3-4 в первом
случае параллельны прямой C1
O1
, то во втором случае эти прямые должны быть направлены в точку схода F , определяемую прямой C1O1
на линии горизонта. Этот способ
построения эллипсов основан на том, что в точке 2 (см.ортогональную проекцию)
пересекаются высоты треугольника A1B. Следовательно, угол BMA является прямым,
и точка M
будет принадлежать окружности.
Преимущество последнего способа
заключается в том, что он дает возможность построить любое количество точек
эллипса, что очень важно при построении перспектив окружностей больших
радиусов.
5.3 Опущенный план
При построении перспективных
изображений с низкорасположенной линией горизонта иногда приходится прибегать к
так называемому опущенному плану.
Этот метод используется в тех случаях,
когда план проектируемого сооружения имеет сложную конфигурацию, и точно
построить перспективу его при низком горизонте, затруднительно. Опущенный
план дает возможность также более точно в перспективе тени.
Если четырехугольник A1 B1
C
1D1 представляет собой перспективу основания
призмы, расположенной в предметной
плоскости, пересекающей картинную плоскость по прямой kk1 (рис.57), то четырехугольник A‘1B‘1C‘1D‘1 является перспективой опущенного плана
(опущенная предметная плоскость пересекает плоскость картины по линии kk1).
Перспектива опущенного плана может быть построена как и перспектива основания
призмы.
Рис.57
Все точки перспективы основания и
опущенного плана находятся в определенной взаимосвязи, поэтому по перспективе
основания может быть построена перспектива опущенного плана, и наоборот. Соответственные
точки опущенного плана и перспективы основания связаны между собой
перпендикулярами к линии горизонта. Точки схода перспектив линий основания и
опущенного плана являются общими.
При наличии перспективы основания
призмы, точки перспективы опущенного плана определяются следующим образом. Так
как точка A1
расположена на основании картины kk1,
то точка A‘1
перспективы опущенного плана будет расположена на основании kk1
картинной плоскости. Проведя из точки A1 прямую в точку схода F2,
получаем на ней в пересечении с перпендикуляром, проведенным к линии горизонта
из токи B1,
в точку B‘1.
Точка B‘1
может быть получена на том же перпендикуляре и в пересечении его с прямой b‘k F1.
Точка b‘k найдена на основании k‘k1
картины по точке bk,
которая определилась как точка пересечения с основанием kk1
прямой, проходящей через точки F1
и B1.
При отсутствии в пределах чертежа точек
схода F1
и F2
для определения положения точек перспективы опущенного плана может быть
использована любая точка линии
горизонта. Так, точка B‘1
могла бы быть получена и с использованием точки F3,
взятой произвольно на линии горизонта.
Основание k‘k‘1 картины на чертеже
может быть выбрано на любом расстоянии от основания kk1.
ЛИТЕРАТУРА
1. Н.В.Белов, А.А.Виксель. Начертательная геометрия. — Л.,
Стройиздат, 2000.
2. Ю.И.Короев. Строительное черчение и
рисование: Учебник для строительных специальностей вузов. – М., Высшая школа,
1999г.
СОДЕРЖАНИЕ
|
Введение |
3 |
||
|
Раздел |
5 |
||
|
1 |
Способ |
5 |
|
|
1.1 |
Тени |
5 |
|
|
1.2 |
Тени |
7 |
|
|
1.3 |
Тени |
10 |
|
|
1.4 |
Тени геометрических тел |
12 |
|
|
2 |
Способ |
16 |
|
|
3 |
Построение |
17 |
|
|
3.1 |
Тени |
17 |
|
|
3.2 |
Тени |
19 |
|
|
3.3 |
Тень |
22 |
|
|
3.4 |
Тень |
23 |
|
|
3.5 |
Тени |
25 |
|
|
Раздел |
26 |
||
|
1 |
Тени |
26 |
|
|
2 |
Тени |
27 |
|
|
3 |
Примеры |
29 |
|
|
Раздел |
32 |
||
|
1 |
Тени |
32 |
|
|
2 |
Примеры |
35 |
|
|
Раздел |
36 |
||
|
1 |
Основные |
36 |
|
|
2 |
Перспектива |
39 |
|
|
3 |
Способы |
42 |
|
|
3.1 |
Способ |
42 |
|
|
3.2 |
Способ |
46 |
|
|
3.3 |
Способ |
48 |
|
|
4 |
Выбор |
54 |
|
|
4.1 |
Выбор |
54 |
|
|
4.2 |
Выбор |
57 |
|
|
5 |
Приемы, |
58 |
|
|
5.1 |
Деление |
58 |
|
|
5.2 |
Перспектива |
60 |
|
|
5.3 |
Опущенный |
63 |
|
|
Литература |
65 |