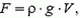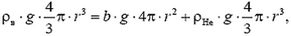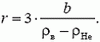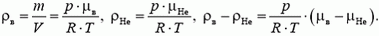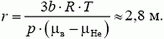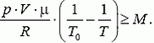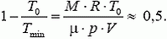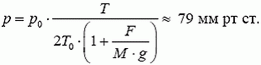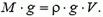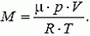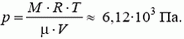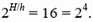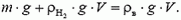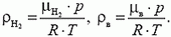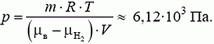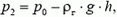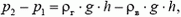Баканина Л.П. Задачи о воздушных шарах // Квант. — 1975. — № 1. — С. 60-63.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В наш век самолетов и ракет, для которых доступны любые высоты над поверхностью Земли, воздушные шары, громоздкие, ненадежные и неуправляемые, уже отошли в прошлое, хотя когда-то именно они дали человеку возможность подняться в воздух. Впрочем, в некоторых случаях воздушные шары очень удобны, они используются и сейчас. Например, с аэростата удобно обучать прыжкам с. парашютом, а метеорологи исследуют давление, температуру и воздушные потоки в атмосфере с помощью шаров-зондов.
Задачи о воздушных шарах даются иногда на вступительных экзаменах. Обычно их можно разделить на два типа:
1) задачи, в которых нужно найти связь между габаритами и наполнением шара и подъемной силой, действующей на шар у поверхности Земли;
2) задачи, в которых нужно определить максимальную высоту подъема шара; при этом задается какая-нибудь модель атмосферы, то есть закон изменения давления и температуры с высотой.
По существу, задачи обоих типов – это задачи на статику. Для их решения нужно уметь применять уравнение состояния газов и найти условие равновесия шара, на который действует сила притяжения Земли и выталкивающая сила со стороны окружающего шар воздуха. Если выталкивающая сила больше силы притяжения (разность этих сил называют подъемной силой), шар поднимается вверх. Но по мере подъема уменьшается плотность окружающего воздуха, а, следовательно, уменьшается и выталкивающая сила, по закону Архимеда равная
где ρ — плотность воздуха, а V — объем шара. На некоторой высоте выталкивающая сила окажется равной силе притяжения – это и будет максимальной высотой подъема шара.
Разберем теперь несколько конкретных задач, которые в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт.
Задача 1. Сферическая оболочка воздушного шара сделана из материала, квадратный метр которого имеет массу b = 1 кг/м2. Шар наполнен гелием при нормальном атмосферном давлении. При каком минимальном радиусе шар поднимает сам себя? Температура гелия и температура окружающего воздуха одинаковы и равны 0 ºС. Молекулярная масса воздуха 29 кг/кмоль, молекулярная масса гелия 4 кг/кмоль.
При увеличении радиуса шара выталкивающая сила растет пропорционально кубу радиуса, а вес оболочки – пропорционально квадрату радиуса. Следовательно, выталкивающая сила растет быстрее и, начиная с какого-то значения радиуса, станет больше, чем вес оболочки. Тогда шар начнет подниматься. Обозначим этот радиус оболочки через r. При этом
откуда
Плотности воздуха ρв и гелия ρНе при данных условиях найдем с помощью закона Менделеева–Клапейрона 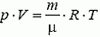
Окончательно получаем
Задача 2. Объем воздушного шара равен V = 230 м3, масса оболочки М = 145 кг. Шар наполнен горячим воздухом при нормальном атмосферном давлении. Какую температуру должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Температура наружного воздуха t0 = 0 оС.
При нагревании воздуха его плотность уменьшается, так как 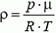
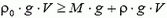
Отсюда
значит,
Tmin » 2T0 = 546 ºK = 273 ºC.
Задача 3. Для удержания на поверхности Земли метеорологического шара-зонда с массой М = 20 кг необходимо приложить силу F = 1000 Н. Шар поднимается до такой высоты, где его объем увеличивается в два раза. Температура воздуха, измеренная на этой высоте с помощью зонда, оказалась равной t = –43 ºС. Вычислить давление воздуха на этой высоте, если на поверхности Земли давление р0 = 754 мм рт. ст., а температура t0= +17 °С.
Условие равновесия шара у поверхности Земли записывается так:
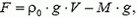
где V — объем шара у поверхности Земли, а 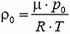
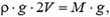
где 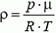
Задача 4. Шар-зонд, наполненный водородом, имеет герметичную оболочку постоянного объема V = 50 м3. Масса шара вместе с водородом М = 5 кг. Определить, на какую максимальную высоту он сможет подняться, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура в стратосфере t = –60 ºС. Молекулярная масса воздуха 29 кг/кмоль. Давление у поверхности Земли р0 = 1 атм.
На максимальной высоте выталкивающая сила равна весу шара- зонда:
Выразив плотность окружающего воздуха через давление и температуру, получим
Таким образом, давление воздуха на этой высоте равно
Посмотрим теперь, во сколько раз давление р меньше давления у поверхности Земли р0: 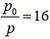
Из условия известно, что давление падает в два раза через каждые 5 км подъема, то есть 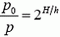
Отсюда
H = 4h = 20 км.
Задача 5. Нерастяжимая оболочка шара-зонда объема V = 75 м3 имеет в нижней части небольшое отверстие. Масса оболочки t = 7 кг. Шар наполнен водородом. Определить, на какую максимальную высоту сможет подняться этот шар-зонд, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура воздуха в стратосфере t = –60 °С, температура водорода равна температуре окружающего воздуха. Давление у поверхности Земли р0 = 1 атм.
Эта задача отличается от предыдущей тем, что оболочка шара не герметична, а имеет отверстие. Следовательно, давление внутри шара все время равно давлению в атмосфере, и по мере увеличения высоты подъема шара водород вытекает из отверстия. Будем, считать, что подъем происходит достаточно быстро и можно пренебречь диффузией воздуха внутрь оболочки, тогда условие равновесия шара на максимальной высоте
Плотности водорода и воздуха можно найти из уравнения Менделеева-Клапейрона:
Таким образом, давление на максимальной высоте
Отношение 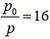
Высота подъема в задаче 5 получилась такая же, как для герметичного шара в задаче 4, но не следует забывать, что мы рассматривали разные шары, с разными объемами и массами. А если оба шара совершенно одинаковы и отличаются только тем, что у одного оболочка герметичная, а у другого имеет отверстие, — какой из шаров поднимется выше в этом случае?
Выталкивающая сила будет одинакова для обоих шаров, так как их объемы равны. Если начальные массы шаров были одинаковы, то после подъема шар с отверстием окажется легче, так как часть наполняющего его газа вытечет при подъёме. Следовательно, шар с отверстием сможет подняться на большую высоту.
Обычно человеку, впервые задумавшемуся над этим вопросом, такой результат кажется странным. Часто задают вопрос: «Как вообще в шаре с отверстием возникает подъемная сила? Ведь снизу, там, где отверстие, воздух и газ внутри шара находятся в равновесии».
Давайте рассмотрим верхнюю точку шара. Если в нижней точке шара давление воздуха и газа равно р0, в верхней точке давление воздуха 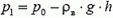
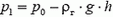
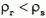
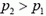
то, так как h мало — всего несколько метров, 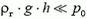
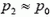
то здесь оба члена одинаковы по порядку величины, и учитывать их надо оба. Кстати сказать, то, что мы считаем ρв и ρг постоянными, — тоже приближение, на самом деле они уменьшаются с высотой по мере уменьшения давления. Но учет этого обстоятельства дал бы значительно меньшую поправку к выталкивающей силе, этой поправкой можно пренебречь.
Упражнения
1. Определить подъемную силу воздушного шара, в котором находится t г водорода. Оболочка шара герметичная и сделана из легкого неупругого материала, который может свободно растягиваться.
2. На сколько градусов надо нагреть воздух внутри сообщающегося с атмосферой воздушного шара, сферическая оболочка которого имеет диаметр 10 м и весит 10 кг, для того чтобы шар взлетел? Атмосферное давление 735 мм. рт. ст., температура окружающего воздуха +27 °С.
3. Воздушный шар представляет собой баллон постоянного объема, наполненный гелием. Через отверстие в нижней части шар сообщается с атмосферой. Как изменится максимальная высота подъема шара, если гелий нагреть до температуры t1? Температуру атмосферы считать постоянной и равной t0, а давление изменяющимся по закону 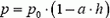
Ответы.
1. 13,5m·g.
2. Не менее чем на 5º.
3. 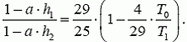
Спрятать решение
Решение.
На шар действуют сила Архимеда, направленная вверх, сила тяжести оболочки, груза и воздуха внутри шара, направленные вниз. При минимальной разности температур выполняется условие
Сила Архимеда равняется Из уравнения Клапейрона-Менделеева
масса
получаем плотность окружающего воздуха
Из уравнения Клапейрона-Менделеева для воздуха внутри шара Объединяя уравнения, выразим температуру воздуха внутри шара
Следовательно, минимальная разность температур равна или 144 °С.
Ответ: 144 °С.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
|
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) представлены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ |
3 |
|
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеется один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты. И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт IV, или в нём допущена ошибка |
2 |
|
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи |
1 |
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла |
0 |
| Максимальный балл | 3 |
Рассмотрим
охлаждение шара в среде с постоянной
температурой tcp
и постоянным коэффициентом теплоотдачи
α. В начальный момент времени при τ = 0
все точки шара с радиусом r0
имеют одинаковую температуру t0.
Теплофизические параметры λ, Ср,
ρ не зависят от температуры и считаются
известными. При заданных условиях
температура для любой точки шара будет
функцией только времени и безразмерной
координаты R
= r/r0.
Также требуется
найти распределение температуры внутри
шара, т.е. уравнение температурного
поля.
Если обозначить
текущую избыточную температуру для
любой точки шара J
= t
— tср,
то дифференциальное уравнение
теплопроводности шара в сферических
координатах запишется:
(12.35)
Геометрические и
физические условия заданы.
Начальные условия:
при τ = 0; J1
= t
— tср
для всех точек шара.
Граничные условия:
На поверхности
шара при r
= r0;
.
Из условия симметрии
задачи в центре шара при r
= 0:
.
Решая уравнение
(12.35) методом разделения переменных и,
подчиняя полученное решение начальным
и граничным условиям, после ряда
преобразований для Fo
≥ 0,3 получим:
(12.36)
Т.к. μ в уравнении
(12.36) зависит только от числа Bi,
то уравнение температурного поля в
общем виде:
Θ = f
(Fo,
Bi,
R).
Для центра шара:
ΘR=0
= f1
(Fo,
Bi)
(12.37)
Для поверхности
шара: ΘR=1
= f2
(Fo,
Bi)
(12.38)
Функции, определяемые
выражениями (12.37) и (12.38) для различных
значений Fo
и Bi
представлены в виде номограмм.
Аналогично, как
для пластины и цилиндра начальная
избыточная внутренняя энергия шара:
(12.39)
Количество теплоты,
которое отдается или воспринимается
шаром за промежуток времени от τ = 0 до
τ1,
также можно определить по номограмме,
которая построена по функции вида: Q/Q0
= f
(Bi,
Fo)/
12.8 Охлаждение (нагревание) тел конечных размеров
12.8.1 Охлаждение параллелепипеда
Р
Z
ассмотрим охлаждение параллелепипеда
в среде с постоянной температурой (tср)
и с постоянным коэффициентом теплоотдачи
на всех его гранях. В начальный момент
времени (=0)
все точки параллелепипеда имеют
одинаковую температуру (t0).
Y
X
— X
0
2y
— Z
— Y
2x
Рисунок 12.7 К
охлаждению параллелепипеда
Параллелепипед c
размерами 2dx
2dу
´
2dz
является однородным и изотропным.
Требуется найти
распределение температуры в параллелепипеде
для любого момента времени, а также
среднюю температуру, необходимую для
определения количества отведенной
(подведенной) теплоты.
Поместим начало
координат в центре параллелепипеда.
При этом дифференциальное уравнение
запишется следующим образом:
(12.40)
Нахождение
аналитического решения этого уравнения,
дополненного условиями однозначности,
представляет собой довольно сложную
задачу.
Параллелепипед
конечных размеров можно рассматривать
как тело, образованное пересечением
соответственно трех взаимно перпендикулярных
неограниченных пластин конечной толщины.
Доказано, что
решение таких задач представляется
произведением безразмерных температур
для тел неограниченных размеров, в
результате пересечения которых
образовалось рассматриваемое тело.
Параллелепипед
образован в результате пересечения
трех взаимно перпендикулярных
неограниченных пластин конечными
толщинами 2dx,
2dу,
2dz.
Следовательно, для него и решение можно
представить как произведение безразмерных
температур для трех безграничных
пластин:
= x
y
z
(12.41)
Множители в
уравнении (12.41) могут быть рассчитаны
по уравнению (12.20) или определены по
номограммам.
Этот метод известен
в теории теплопроводности под названием
теоремы о перемножении решений.
Полученное решение
справедливо и для нахождения средней
температуры:
(12.42)
Множители в
уравнении (12.42) находятся по формуле
(12.27).
12.8.2 Охлаждение
(нагревание) длинного прямоугольного
стержня
Поперечное сечение
стержня представляет собой прямоугольник
с размерами 2δх
× 2δу.
Такое тело можно рассматривать как
результат взаимного пересечения двух
неограниченных пластин толщиной 2δх
и 2δу,
условия однозначности для которых такие
же, как и для образовавшегося стержня.
Безразмерное температурное поле для
поставленной задачи:
Q
= Qx
×
Qy
(12.43)
Множители в
уравнении (12.43) также могут быть рассчитаны
по уравнению (12.20) или определены по
номограммам.
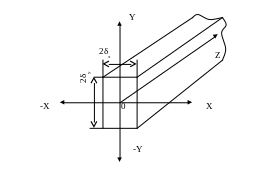
Рисунок 12.8 К
охлаждению полуограниченного
прямоугольного стержня
12.8.3 Охлаждение
цилиндра конечной длины
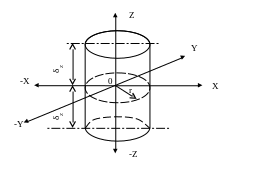
Рисунок 12.9 К
охлаждению цилиндра конечной длины
Цилиндр конечной
длины можно рассматривать как результат
пересечения безграничного цилиндра
радиусом r0
и пластины толщиной 2δZ.
Следовательно, и безразмерную температуру
для такого тела можно записать как:
Q
= Qr
×
Qz
(12.44)
Полученные решения
для полуограниченного прямоугольного
стержня и цилиндра конечной длины
(формулы 12.43 и 12.44) справедливы и для
нахождения средних температур.
Кроме того, следует
подчеркнуть, что все решения, полученные
выше справедливы как для охлаждения,
так и для нагрева тел неограниченных и
конечных размеров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При какой температуре шар взлетит
По мере нагревания воздуха сила тяжести, действующая на шар, должна
уменьшаться, т.к. плотность воздуха, находящегося в оболочке, будет
падать. Будем, поскольку другое не оговорено в условии задачи,
считать, что находящийся вне шара воздух покоится относительно
Земли, и лабораторная система отсчета является инерциальной.
На покоящийся шар со стороны окружающего воздуха действуют силы
гидростатического давления. Величина равнодействующей этих сил,
равной согласно закону Архимеда весу вытесненного шаром воздуха, при
сделанных предположениях равна F=mg, где m — масса вытесненного воздуха, а g — величина
ускорения свободного падения. Поскольку абсолютная температура
окружающего воздуха T=273+t, то полагая, как
обычно, что воздух подчиняется уравнению состояния идеальных газов,
получим
$m=frac{PVmu}{RT}$
где R=8,31 —
универсальная газовая постоянная.
Из условия задачи следует, что нагревание происходит столь медленно
и теплопроводность оболочки столь мала, что во всех точках внутри
оболочки температура воздуха устанавливается одинаковой. При этом
можно считать, что давление воздуха в оболочке равно атмосферному.
Тогда согласно уравнению Клапейрона-Менделеева при абсолютной
температуре воздуха в оболочке, равной Т, масса
содержащегося в ней воздуха должна быть равна
$m=frac{PVmu}{RT_x}$
где m — масса, p — давление, V -объем, Tx -температура внутри шара, мю -молярная масса воздуха
Поскольку при сделанных выше предположениях шар должен начать
взлетать, когда масса груза и оболочки с находящимся в ней воздухом
станет меньше массы вытесненного шаром воздуха, то шар начнет
подниматься при выполнении условия
$M+frac{PVmu}{RT_x}<frac{PVmu}{RT}$
Следовательно, искомая температура при сделанных предположениях
определяется условием
$T_x>frac{PVmu T}{PVmu-MRT}$
2017-03-18
Дан воздушный шар с постоянным объемом $V = 1,10 м^{3}$. Масса оболочки (объемом оболочки пренебречь) составляет $m_{0}=0,187 кг$. Шар должен стартовать при окружающей температуре воздуха $t_{1} = 20^{ circ} С$ и нормальном атмосферном давлении $P_{0} = 1,013 cdot 10^{6} Па$. Плотность воздуха при этих условиях имеет следующее значение: $rho_{1} = 1,2 кг/м^{3}$.
а) Вычислите температуру $t_{2}$, которую должен иметь нагретый воздух внутри шара, чтобы он мог свободно парить в воздухе.
б) Воздух внутри привязанного на тросе шара нагревается до постоянной температуры $t_{3}=110^{ circ} С$. Вычислите силу действующую на трос.
в) Примем, что отверстие снизу шара завязано (плотность воздуха в нем остается тогда постоянной). Шар поднимается с постоянной температурой внутреннего воздуха $t_{3}=110^{ circ} С$ в изотермической атмосфере при $20^{ circ} С$ и давлении на уровне Земли $P_{0}=1,013 cdot 10^{5} Па$. Какой высоты $h$ достигнет шар при этих условиях?
г) Шар, находящийся на высоте $h$ (вопрос в)), смещается на высоту, приблизительно равную $Delta = 10 м$, из положения равновесия и затем отпускается. Опишите качественнее как он движется.
Решение:
а) Условие равновесия шара в воздухе запишем в виде
$F_{A} = F_{т}$.
где $F_{A}$ — архимедова сила, равная $F_{A} = rho_{1} Vg$, а $F_{т}$ — сила тяжести шара с воздухом: $F_{т} = rho_{2} Vg + m_{0}g$ ($rho_{1}$ и $rho_{2}$ — плотности окружающего воздуха при температуре $T_{1}$ и воздуха в шаре при температуре $T_{2}$).
Тогда условие равновесия шара в воздухе можно записать как
$rho_{1} Vg = rho_{2} Vg + m_{0}g$,
откуда
$m{0} = ( rho_{1} — rho_{2})V$. (1)
Из уравнения газового состояния:
$PV = frac{m}{M}RT, P = frac{ rho}{M} RT$
следует, что
$rho_{1} = PM/RT_{1}, rho_{2} = PM/RT_{2}$.
Отсюда
$rho_{1} / rho_{2} = T_{2}/T_{1}$. (2)
Из выражений (1) и (2) получаем
$T_{2} = frac{T_{1}}{1 — m_{0}/ rho V}$. (3)
Подстановка числовых данных приводит к результату: $T_{2} = 341 К$, или $t_{2} = 68^{ circ} С$.
б) Если воздух в шаре нагреть до температуры $T_{3} = 383 К$, то новое значение силы тяжести шара $F_{т}^{ prime}$ равно
$F_{т}^{ prime} = m_{0}g + rho_{3} Vg$.
Для удержания шара в положении равновесия необходимо, чтобы сила $F$, действующая на трос, привязанный к шару, была равна
$F = F_{A} — F_{т}^{ prime} = rho_{1} Vg — (m_{0} + rho_{3} Vg) = [( rho_{1} — rho_{3})V — m_{0}]g$. (4)
Аналогично выражению (2) записываем
$rho_{1}/ rho_{3} = T_{3}/ T_{1}$. (5)
Из выражений (4) и (5) получаем
$F = [ rho_{1} (1 — T_{1}/T_{3})V — m_{0}]g = l,2H$. (6)
в) Из условия равновесия шара на искомой высоте $h$ получаем
$F_{A}^{ prime} = F_{т}^{ prime}, rho_{h}Vg = m_{0}g + rho_{3} Vg, rho_{h} = frac{m_{0} + rho_{3}V}{V}$. (7)
где $rho_{h}$ — плотность воздуха на высоте $h$.
С другой стороны, плотности воздуха $rho_{h}$ и $rho_{1}$ в изотермической атмосфере связаны барометрической формулой:
$rho_{h} = rho_{1} e^{ — rho_{1} g h/P_{0}}$, (8)
откуда получим
$h = frac{P_{0}}{ rho_{1} g} ln frac{ rho_{1}}{ rho_{h}}$,
а с учетом выражений (5) и (7) запишем:
$h = frac{P_{0}}{ rho_{1} g} ln frac{ rho_{1}V}{m_{0} + rho_{3} V} = frac{P_{0}}{ rho_{1} g} ln frac{ rho_{1}V}{ m_{0} + rho_{1} T_{1} V/T_{2}}$. (9)
Подстановка числовых значений приводит к результату: $h approx 843 м$.
г) При небольшой разности высот $Delta h = 10 м$ по сравнению с высотой $h=843 м$ барометрическую формулу (8) можно представить в виде линейной функции:
$rho_{h+ Delta h} = rho_{1} e^{ — rho_{1} g ( h + Delta h) / P_{0}} = rho_{h} e^{ — rho_{1} g Delta h/P_{0}} approx rho_{h} (1 — rho_{1} g Delta h / P_{0}) $.
Следовательно, для шара, у которого отверстие закрыто, архимедова сила, действующая на него, равна
$F_{A} = rho_{h + Delta h} Vg$.
Изменение этой силы при малых изменениях высоты $Delta h$ нетрудно рассчитать:
$frac{ Delta F_{A}}{ Delta h} = — frac{ rho_{h} rho_{1} g}{P_{0}} Vg$,
откуда
$Delta F_{A} = — frac{ rho_{h} rho_{1} g^{2}}{P_{0}} V Delta h$.
Так как сила, действующая на шар, прямо пропорциональна смещению шара, то он совершает гармонические колебания, период которых равен
$T = 2 pi sqrt{ frac{(m_{0} + rho_{3} V)P_{0}}{ rho_{h} rho_{1} g^{2} V}} = frac{2 pi}{g} sqrt{ frac{(m_{0} + rho_{3} V)P_{0}}{(m_{0} + rho_{3} V) rho_{1}}} = frac{2 pi}{g} sqrt{ frac{P_{0}}{ rho_{1}}} approx 186 с approx 3 мин$.
При получении этого результата мы не учитывали сопротивление воздуха, которое, с одной стороны, приведет к тому, что колебания будут затухающими, а с другой стороны, период реальных колебаний будет несколько больше рассчитанного.
Отметим, что в связи с большим периодом колебаний шара (3 мин.) указанные поправки к полученному значению будут незначительными, так как сила сопротивления, зависящая от скорости, будет невелика.
Примечание. При решении этой части задачи мы не учитывали эффекта «присоединенной массы» воздуха.