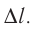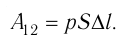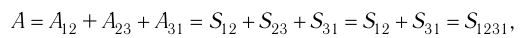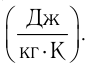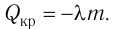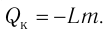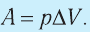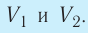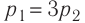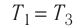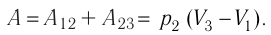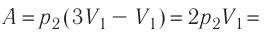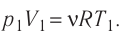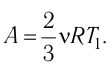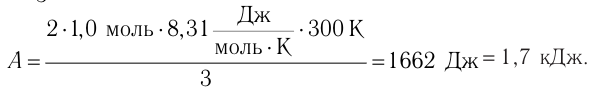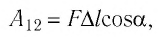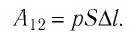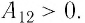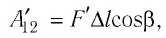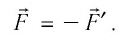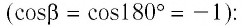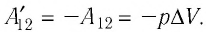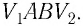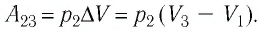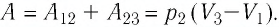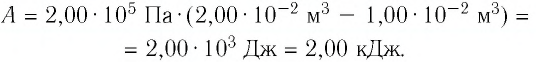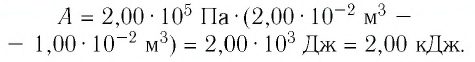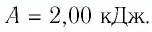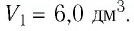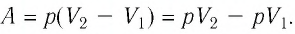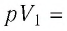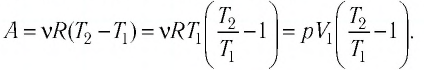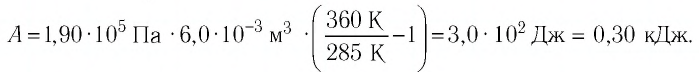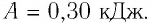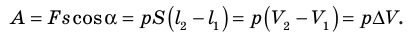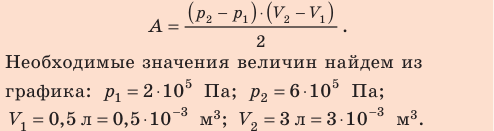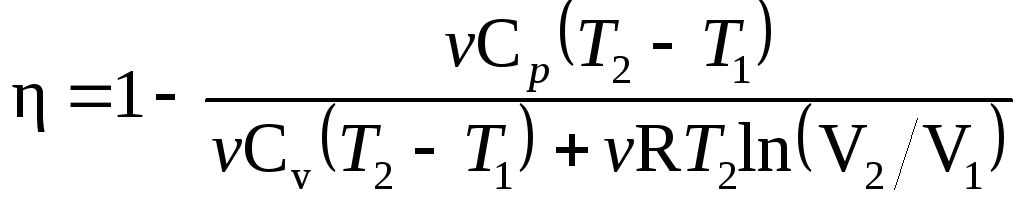Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
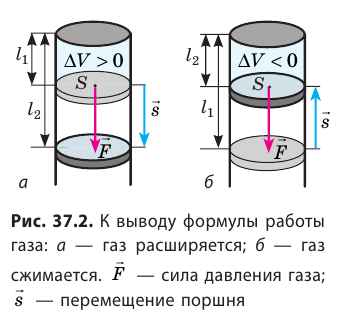
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
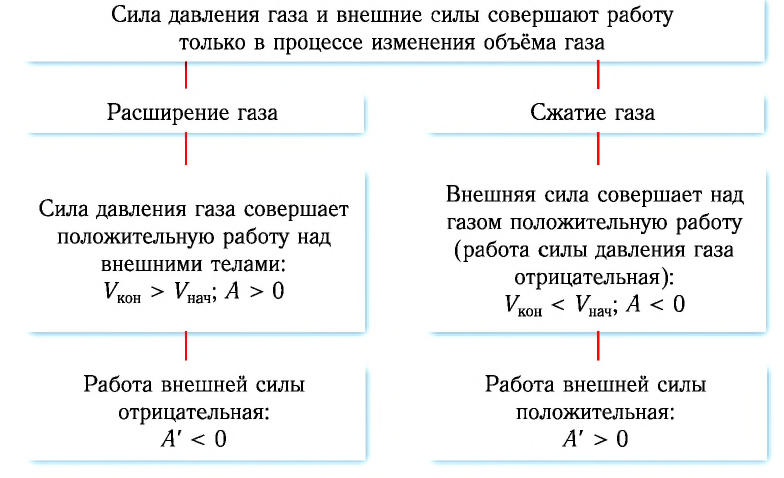
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
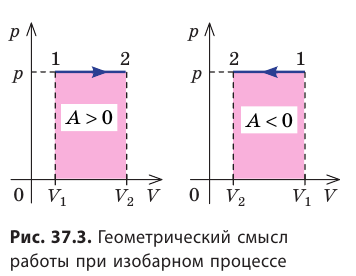
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
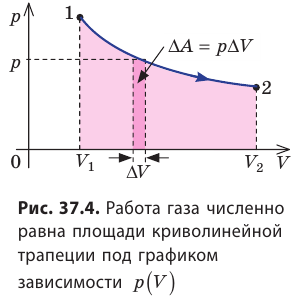
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
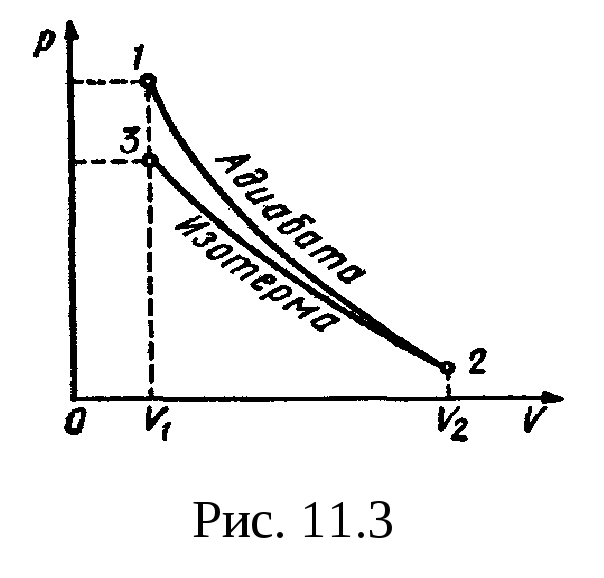
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Содержание:
Работа в термодинамике:
В 9 классе вы узнали, что работа силы (механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. Работу силы рассматривают как меру изменения энергии физической системы. А как определить работу в термодинамике? Как может быть выражена эта работа через макроскопические параметры — давление и об1
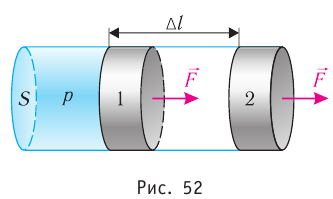
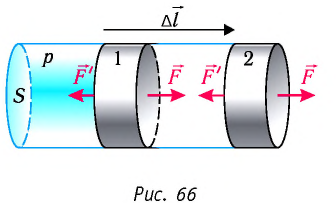
Рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, закрытом подвижным поршнем (рис. 52).
Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением р, которое газ оказывает на них. Допустим, что в результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние
Модуль силы давления газа, действующей на поршень, F = pS. Эта сила совершает работу по перемещению поршня
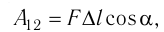
где а — угол между направлениями силы и перемещения. В рассматриваемом примере а = 0, тогда
Произведение 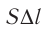
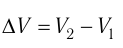
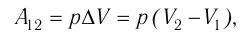
где 
Так как давление р газа всегда величина положительная, из формулы (10.2) следует, что, если газ расширяется 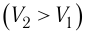
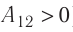
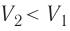
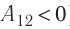
Процесс медленного изобарного сжатия газа из состояния 2 с начальным объёмом 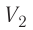
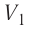
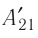
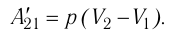
Из сравнения равенств (10.2) и (10.3) вытекает соотношение между работой 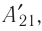
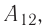
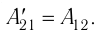
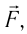
направление, противоположное силе давления 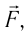
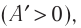
Если газ расширяется 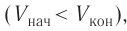
Геометрическое толкование работы
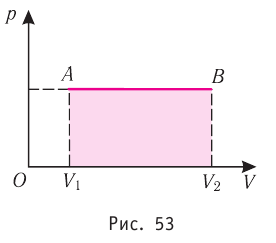
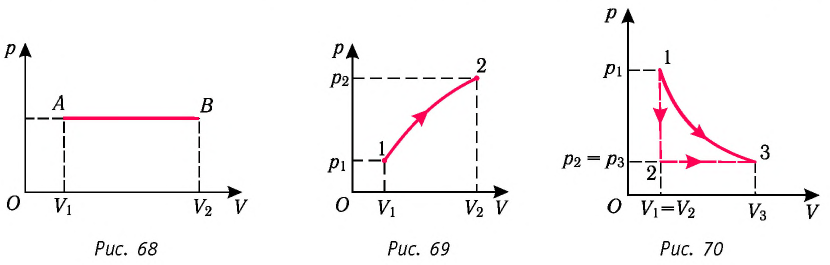
Построим график зависимости давления газа от его объёма при р = const. Как видно из рисунка 53, при изобарном расширении газа работа, совершённая силой давления газа, численно равна площади прямоугольника
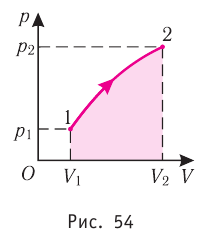
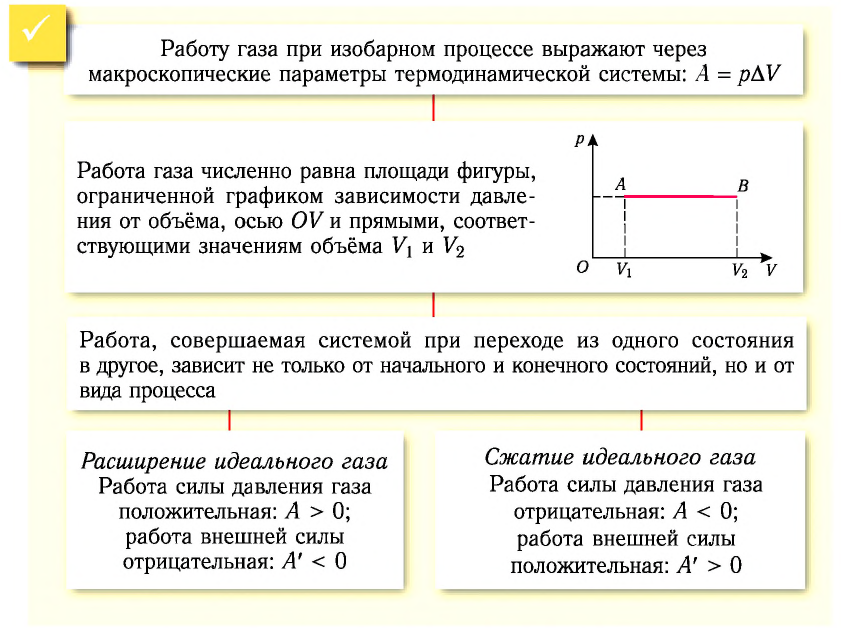
Если процесс перехода газа из начального состояния в конечное не является изобарным, то работа, совершённая силой давления газа при изменении его объёма от 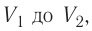
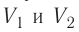
Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, снова возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 55). Работа, совершаемая системой при циклическом процессе, или работа цикла, равна площади фигуры, ограниченной линиями, которые изображают цикл:
где
Если «кривая расширения» (изобара
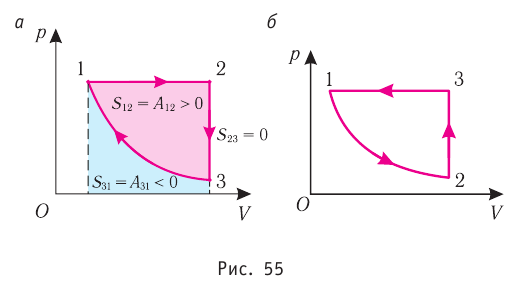
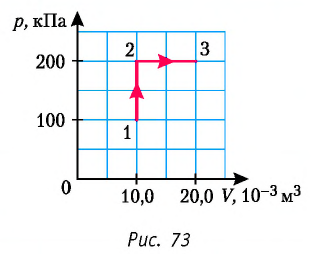
Из рисунка 56 видно, что численное значение работы цикла определяется не только начальным и конечным состояниями системы, но и видом процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения, либо сначала изохорно понизив его давление до значения 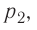
Как видно из рисунка 56, в первом случае работа, совершённая силами давления газа, больше, чем во втором. Следовательно, работа, совершаемая при переходе термодинамической системы из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Количество теплоты и удельная теплоёмкость
Итак, существуют два способа передачи энергии от одного тела к другому. Первый характеризуется передачей энергии в процессе механического взаимодействия тел — механическая энергия одного тела переходит в энергию хаотического движения частиц вещества другого тела или, наоборот, убыль энергии хаотического движения частиц вещества одного тела сказывается на увеличении механической энергии другого тела. Такую форму передачи энергии в термодинамике (как и в механике) называют работой. Так, например, в рассмотренной нами ранее термодинамической системе (газ в цилиндрическом сосуде под поршнем) расширение газа приводит к перемещению поршня. При этом убыль внутренней энергии газа равна работе, совершённой силой давления газа, под действием которой поршень переместился.
Второй способ передачи энергии осуществляется при непосредственном обмене энергией между хаотически движущимися частицами взаимодействующих тел. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей энергии частицам более холодного тела. В результате внутренняя энергия первого тела уменьшается, а второго тела увеличивается. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей. Как вы уже знаете, существуют три вида теплопередачи: теплопроводность, конвекция и излучение.
Количественной мерой энергии, переданной телу в процессе теплопередачи, является количество теплоты Q. В СИ единицей количества теплоты является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию (1 кал = 4,19Дж).
Если процесс теплопередачи не сопровождается изменением агрегатного состояния вещества, то
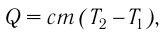
где m — масса тела, 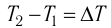
теплоемкость измеряют в джоулях, деленных на килограмм, кельвин
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкости тела. Обозначают теплоёмкость тела С и измеряют в джоулях на кельвин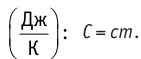
Удельная теплота плавления
Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления 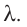
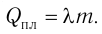
Удельная теплота парообразования
Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Количество теплоты, необходимое для превращения жидкости массой m, предварительно нагретой до температуры кипения, в пар, определяют по формуле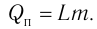
Удельная теплота сгорания топлива
Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания топлива q. Количество теплоты, выделившееся при полном сгорании некоторой массы m топлива, определяют по формуле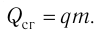
Отметим, что в результате теплопередачи могут изменяться как обе составляющие внутренней энергии тела, так и одна из них. При нагревании (охлаждении) изменяются кинетическая энергия хаотического движения частиц, которые составляют тело, и потенциальная энергия их взаимодействия. При плавлении (кристаллизации), кипении (конденсации) изменяется только потенциальная энергия взаимодействия частиц вещества.
При совершении работы также может изменяться как кинетическая, так и потенциальная энергия частиц вещества. Следовательно, как при теплопередаче, так и при совершении работы происходит изменение кинетической и потенциальной энергий частиц вещества, что приводит к изменению внутренней энергии тела.
1. Работу газа при изобарном процессе выражают через макроскопические параметры термодинамической системы:
2. Работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёмов
3. Работа, совершаемая при переходе системы из одного состояния в другое, зависит не только от начального и конечного состояний, но и от вида процесса.
4. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей.
Пример №1
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 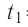
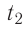
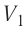
Дано:
Пример №2
Состояние идеального газа, взятого в количестве v=l,0 моль при температуре 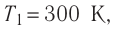
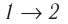
Дано:
v = 1,0 моль
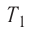
А — ?
Решение. Работа Л газа в ходе всего процесса равна сумме работ на участках 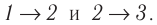
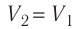
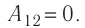
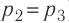
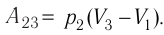
Так как по условию 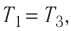
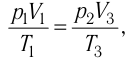
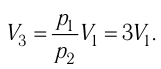
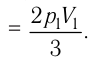
Тогда
Ответ: А = 1,7 кДж.
Работа в термодинамике
В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.
Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.
Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.
Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре 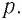
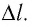
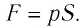
где 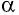
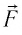
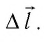
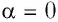
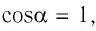
Произведение 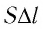
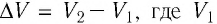
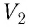
Таким образом, работа силы давления газа при его изобарном расширении:
Так как давление р газа — величина положительная, то из формулы (12.1) следует, что
При изобарном расширении газа из состояния 1 в состояние 2 работа силы 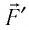
где 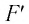
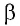
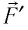
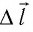
Перемещение 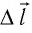
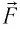
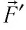
Следовательно, работы 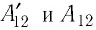
Таким образом, можно сделать следующие выводы.
Геометрическое толкование работы:
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при 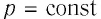
Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от 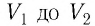
Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения 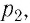
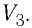
Следовательно, работа, совершаемая термодинамическом системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Пример №3
Определите работу, совершаемую силой давления идеального газа определённой 200 массы при переходе из состояния 1 в состояние 3 (рис. 73).
Решение. 1 способ. Работа А газа в ходе всего процесса равна сумме работ на участках 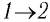
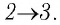
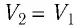
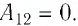
Тогда при переходе из состояния 1 в состояние 3 работа
2 способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёма 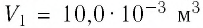
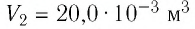
Ответ:
Пример №4
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 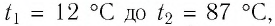
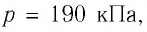
Решение. Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
Согласно уравнению Клапейрона—Менделеева,
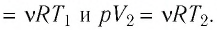
Ответ:
Как определить работу в термодинамике
В конце XVIII в. английский физик Бенджамин Томпсон (граф Румфорд) исследовал тепло, выделяющееся при сверлении бронзовых пушек. Румфорд успевал вскипятить поставленные на пушки котлы с водой за счет тепла, которое выделялось, пока лошади приводили в движение очень тупое сверло. В данном случае энергия механического движения сверла превращалась в энергию хаотического движения молекул бронзы и воды. А можно ли сделать наоборот?
Почему при изменении объема газа изменяется его внутренняя энергия
Внутренняя энергия газа может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ сжимают (газ совершает отрицательную работу) (рис. 37.1) и он при этом не отдает энергию окружающей среде, то скорость движения молекул газа, а соответственно, и внутренняя энергия, и температура газа увеличиваются. И наоборот: если газ расширяется (то есть совершает положительную работу), то скорость движения молекул, температура и внутренняя энергия газа уменьшаются.
Рис. 37.1. При сжатии газа скорость его молекул после столкновения с поршнем увеличивается (v > 
Как вычислить работу газа
Вычислим работу, которую совершает сила давления газа при изменении его объема от 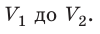
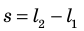
Таким образом, работа газа при его изобарном расширении равна:
Работе газа при изобарном расширении (или сжатии) можно дать простое геометрическое толкование: работа газа численно равна площади прямоугольника под графиком зависимости p(V) (рис. 37.3).
Пусть некоторый газ переходит из состояния 1 в состояние 2 (рис. 37.4). Если изменение объема газа (∆V) достаточно мало, то давление газа можно считать неизменным. Тогда работа газа численно равна площади выделенной на рисунке полосы. Полная работа при изменении объема от 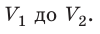
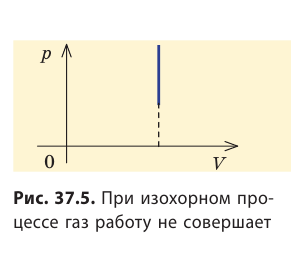
Очевидно, что при изохорном процессе (V = const) площадь фигуры под графиком зависимости p (V) равна нулю (рис. 37.5), — газ работу не совершает (A = 0) . Работа газа зависит от того, каким образом происходил переход газа из начального состояния в конечное (рис. 37.6).
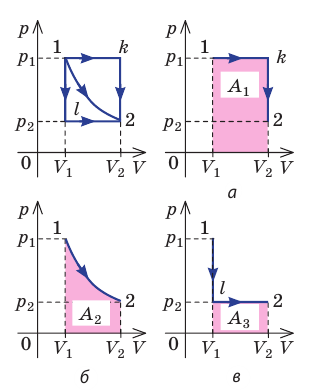
Рис. 37.6. три пути перехода газа из состояния 1 в состояние 2: а — газ изобарно расширяется (участок 1k), затем изохорно охла ждается (участок k2); б — газ изотермически расширяется; в — газ изохорно охлаждается (участок 1l), затем изобарно расширяется (участок l2). сравнив площади фигур под графиками, видим, что:
Пример №5
На рисунке графически изображен циклический процесс, совершаемый идеальным газом. Определите работу газа за цикл.
Решение:
Полная работа за цикл равна сумме работ, совершенных газом в ходе каждого процесса цикла. Работа газа в ходе процесса 1–2 численно равна площади трапеции, основания которой равны 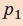
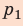
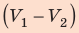
Выводы:
- При отсутствии теплообмена с окружающей средой, если над газом совершают работу, внутренняя энергия газа увеличивается; если газ сам совершает работу, его внутренняя энергия уменьшается.
- Если объем газа увеличивается, то газ совершает положительную работу. Если объем газа уменьшается, то работа газа отрицательна.
- Работа газа численно равна площади фигуры под графиком зависимости p (V). При изобарном процессе работу газа можно определить по формуле A=p∆V, при изохорном процессе работа газа равна нулю: A = 0.
- Первый закон термодинамики
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Термодинамика — основные понятия, формулы и определения
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория
Связь между
молярной (Cm)
и удельной (с) теплоемкостями газа
Cm=cM,
где М
— молярная
масса газа.
Молярные
теплоемкости*
при
постоянном объеме и постоянном давлении
соответственно равны
Cv=iR/2;
Cp=(i+2)R/2
где i
— число
степеней свободы; R
— молярная
газовая постоянная.
Удельные
теплоемкости при постоянной объеме и
постоянном давлении соответственно
равны
,
.
Уравнение Майера
Cр—Сv=R.
Показатель
адиабаты
,
или
,
или.
Внутренняя
энергия идеального газа
U=N<>
или U=vCvT,
где <>—средняя
кинетическая энергия молекулы;
N—число
молекул газа;
v
— количество
вещества.
Работа, связанная
с изменением объема газа, в общем случае
вычисляется по формуле
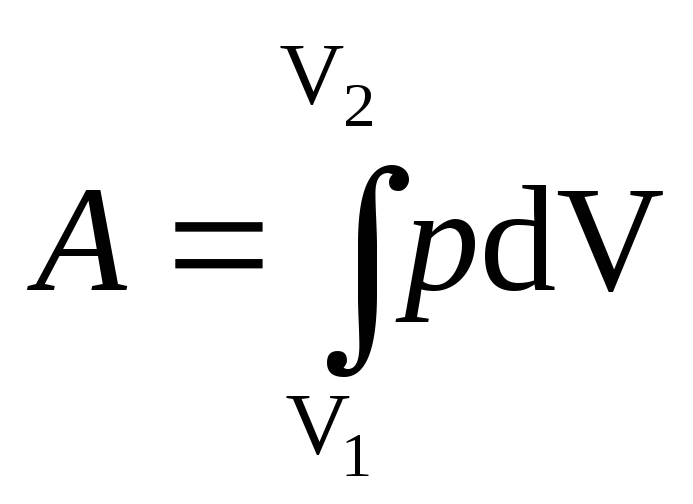
где V1
— начальный
объем газа; V2
— его
конечный объем.
Работа газа:
а) при изобарном
процессе (p=const)
A=p(V2
—
V1);
б) при изотермическом
процессе (T=const)
;
*
Здесь и далее
в целях упрощения записи в индексах
обозначений молярной теплоемкости при
постоянном давлении и постоянном объеме
букву «m»
будем опускать.
в) при адиабатном
процессе
,
или
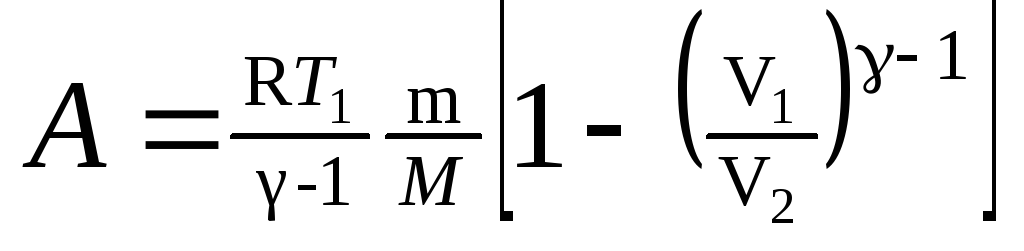
где T1
— начальная
температура газа; T2
— его
конечная температура.
Уравнение Пуассона
(уравнение газового состояния при
адиабатном процессе)
.
Связь между
начальным и конечным значениями
параметров состояний газа при адиабатном
процессе:
.
Первое начало
термодинамики в общем случае записывается
в виде
Q=U+A,
где Q
– количество теплоты, сообщённое газу;
U—изменение
его внутренней энергии; А
—
работа, совершаемая газом против внешних
сил.
Первое начало
термодинамики:
а) при изобарном
процессе
б) при изохорном
процессе (A=0)
;
в) при изотермическом
процессе (U=0)
,
г) при адиабатном
процессе (Q=0)
.
Термический
коэффициент полезного действия (КПД)
цикла
в
общем случае
,
где Q1—количество
теплоты, полученное рабочим телом
(газом) от нагревателя; Q2—количество
теплоты, переданное рабочим телом
охладителю.
КПД цикла Карно
,
или
,
где T1
— температура
нагревателя; T2
— температура
охладителя.
Изменение энтропии
где A
и B
— пределы
интегрирования, соответствующие
начальному и конечному состояниям
системы. Так как процесс равновесный,
то
интегрирование проводится по любому
пути.
Формула Больцмана
S=klnW,
где
S — энтропия
системы;
W
—
термодинамическая вероятность ее
состояния; k
—
постоянная Больцмана.
Примеры решения задач
Пример
1. Вычислить
удельные теплоемкости неона и водорода
при постоянных объеме (сv)
и давлении (cp),
принимая эти газы за идеальные.
Решение.
Удельные теплоемкости идеальных газов
выражаются формулами
; (1)
. (2)
Для неона (одноатомный
газ) i1=3,
M1=2010-з
кг/моль.
Подставив в формулы
(1) и
(2) значения
i1,
M1
и R
и произведя вычисления, найдем:
сv1=
624
Дж/(кгК);
сp1=1,04
кДж/(кгК).
Для водорода
(двухатомный газ) i2=5,
M2=210-3
кг/моль.
Вычисление по
формулам
(1) и
(2) дает
следующие значения удельных теплоемкостей
водорода:
сv2=10,4
кДж/(кгK);
сp2=14,6
кДж/(кгK).
Пример
2. Вычислить
удельные теплоемкости сv
и сp
смеси неона и водорода. Массовые доли
газов соответственно равны 1=0,8
и 2=0,2.
Значения удельных теплоемкостей газов
взять из примера
1.
Решение.
Удельную теплоемкость смеси при
постоянном объеме сv
найдем из следующих рассуждений. Теплоту,
необходимую для нагревания смеси на
T,
выразим двумя соотношениями:
Q=сv(m1+m2)T
(1)
где сv
— удельная
теплоемкость смеси; m1
— масса
неона; m2
— масса
водорода, и
Q=(сv1m1+
сv2m2)T (2)
где сv1
и сv2
— удельные
теплоемкости неона и водорода
соответственно.
Приравняв правые
части выражений
(1) и
(2) и разделив
обе части полученного равенства на
T,
найдем
сv(m1+m2)=
сv1m1+
сv2m2,
откуда
Отношения
1=m1/(m1+m2)
и 1=m2/(m1+m2)
выражают массовые доли соответственно
неона и водорода. С учетом этих обозначений
последняя формула, примет вид
сv=сv11+
сv22.
Подставив в эту
формулу числовые значения величин,
найдем
сv=2,58
кДж/(кгК).
Рассуждая
таким
же
образок, получим формулу для вычисления
удельной теплоёмкости смеси при
постоянном давлении:
cp=сp11+
сp22
Произведя вычисления
по этой формуле, найдем
cp=3,73
кДж/(кгК).
Пример
3. Определить
количество теплоты, поглощаемой
водородом массой m=0,2
кг при нагревании его от температуры
t1=0°С
до температуры t2=100
°С при постоянном давлении. Найти также
изменение внутренней энергии газа и
совершаемую им работу.
Решение.
Количество теплоты Q,
поглощаемое газом при изобарном
нагревании, определяется по формуле
Q=mcpT,
(1)
где m
— масса
нагреваемого газа; cp
— его
удельная теплоемкость при постоянном
давлении; T
— изменение температуры газа.
Как известно,
.
Подставив это выражение cp
в формулу
(1), получим
Произведя вычисления
по этой формуле, найдем
Q=291
кДж.
Внутренняя энергия
выражается формулой
,
следовательно, изменение внутренней
энергии
.
После подстановки
в эту формулу числовых значений величин
и вычислений получим U=208
кДж.
Работу расширения газа
определим по формуле, выражающей первое
начало термодинамики: Q=U+A,
откуда
A=Q — U.
Подставив значения
Q и U,
найдем
А
=83 кДж.
Пример
4. Кислород
занимает объем V1=1
м3
и находится под давлением р1=200
кПа. Газ нагрели сначала при постоянном
давлении до объема V2=3
м2,
a
затем при постоянном объеме до давления
Рис
11.1 р2=500
кПа. Построить график процесса и найти:
1) изменение
U
внутренней энергии газа; 2)
совершенную им работу A;
3) количество
теплоты
Q,
переданное
газу.
Решение.
Построим график процесса (рис.
11.1). На
графике точками
1, 2, 3
обозначены состояния газа, характеризуемые
параметрами (р1,
V1,
T1),
(р1,
V2,
T2),
(р2,
V2,
T3).
1.
Изменение внутренней энергии газа при
переходе его из состояния
1 в состояние
3 выражается
формулой
U=cvmT,
где cv
— удельная
теплоемкость газа при постоянном объеме;
m
— масса
газа; T
— разность
температур, соответствующих конечному
3 и
начальному 1 состояниям, т. е. T=T3—
T1.
Так как
;
где М
— молярная
масса газа, то
.
(1)
Температуры T1
и T3
выразим из уравнения Менделеева
— Клапейрона
():
С учетом этого
равенство
(1) перепишем
в виде
U=(i/2)(p2V2—p1V1).
Подставим сюда
значения величин (учтем, что для кислорода,
как двухатомного газа, i=5)
и произведем вычисления:
U=3,25
МДж.
2.
Полная работа, совершаемая газом, равна
A=A1+A2,
где A1
— работа
на участке
1—2; A2
— работа
на участке
2—3,
На участке
1—2 давление
постоянно (p=const).
Работа в этом случае выражается формулой
A1=p1V=p1(V2—V1).
На участке 2—3
объем газа не изменяется и, следовательно,
работа газа на этом участке равна нулю
(A2=0).
Таким образом,
A=A1=p1(V2—V1).
Подставив в эту
формулу значения физических величин,
произведем вычисления:
A=0,4
МДж
3.
Согласно первому началу термодинамики,
количество теплоты Q,
переданное газу, равно сумме работы
A,
совершенной газом, и изменению U
внутренней энергии:
Q=A+U,
или
Q=3,65 МДж.
Пример
5. Идеальный
двухатомный газ, содержащий количество
вещества v=l
моль, находится под давлением p1=250кПа
и занимает объем V1==10
л. Сначала газ изохорно нагревают до
температуры T2=400
К. Далее, изотермически расширяя, доводят
его до первоначального давления.
После этого путем изобарного сжатия
возвращают газ в начальное состояние.
Определить термический КПД
цикла.
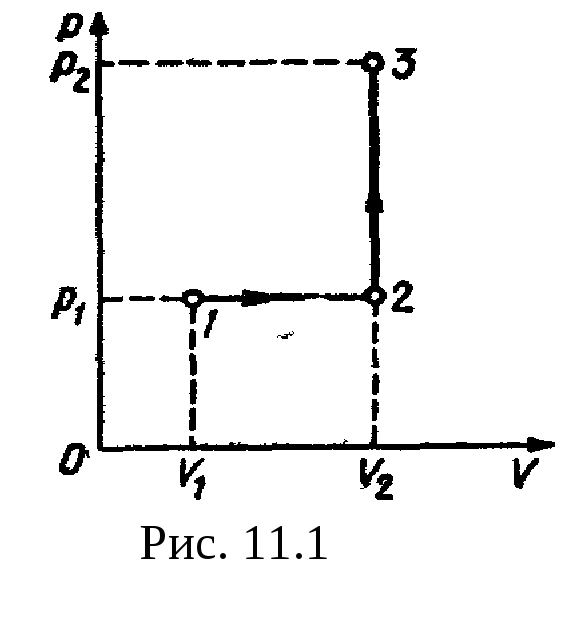
Решение.
Для наглядности построим сначала график
цикла, который состоит из изохоры,
изотермы и изобары. В координатах р,
Vэтот
цикл имеет вид. представленный на рис.
11.2. Характерные
точки цикла обозначим
1, 2, 3.
Термический КПД
любого цикла определяется выражением
=(Q1
– Q2)/Q1,
или =l
– Q2/Q1,
(1) где
Q1
—
количество теплоты, полученное газом
за цикл от нагревателя; Q2
— количество теплоты, отданное газом
за цикл охладителю.
Заметим, что разность
количеств теплоты Q1
– Q2
равна работе A,
совершаемой газом за цикл.
Эта
работа на графике в координатах р,
V (рис.
11.2)
изображается площадью цикла (площадь
цикла заштрихована).
Рабочее вещество
(газ) получает количество теплоты
Q1
на двух участках: Q1-2
на участке
1—2 (изохорный
процесс) и Q2-3
на участке
2—3
(изотермический процесс). Таким образом,
Q1=Q1-2+Q2-3.
Количество теплоты,
полученное газом при изохорном процессе,
равно
Q1-2=Cvv(T2
–
T1),
где Cv
— молярная
теплоемкость газа при постоянном объеме;
v
— количестве вещества. Температуру T1
начального состояния газа найдем,
воспользовавшись уравнением Клапейрона
— Менделеева:
T1=p1V1/(vR).
Подставив числовые
значения и произведя вычисления, получим
Количество теплоты,
полученное газом при изотермическом
процессе, равно
Q2-3=vRT2ln(V2/V1),
где V2
—
объем, занимаемый газом при температуре
T2
и давлении p1
(точка
3 на графике).
На участке
3—1 газ
отдает количество теплоты Q2,
равное
Q2=Q3-1=Cpv(T2
–T1),
где Cp
— молярная
теплоемкость газа при изобарном процессе.
Подставим найденные
значения
Q1
и Q2
в формулу
(1):
В полученном
выражении заменим отношение объемов
V2/V1,
согласно закону Гей-Люссака, отношением
температур (V2/V1=T2/T1)
и выразим Cv
и Cp
через число степеней свободы молекулы
[Cv=iR/2,
Cp=(i+2)R/2].
Тогда после сокращения на
v
и R/2
получим
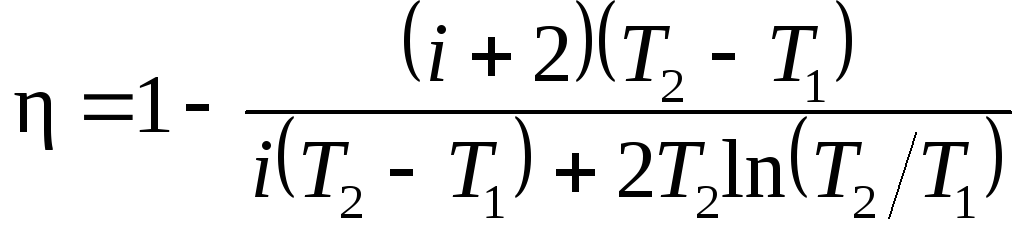
Подставив значения
i,
T1,
T2
и R
и произведя вычисления, найдем
Пример 6.
В цилиндре под поршнем находится водород
массой m=0,02
кг при температуре T1=300K.
Водород начал расширяться адиабатно,
увеличив свой объем в пять раз, а затем
был сжат изотермически, причем объем
газа уменьшился в пять раз. Найти
температуру Т2,
в конце адиабатного расширения и работу
А,
совершенную газом. Изобразить процесс
графически.
Решение.
Температуры и объемы газа, совершающего
адиабатный процесс, связаны между
собой соотношением
,
где —
показатель адиабаты (для водорода как
двухатомного газа =1,4).
Отсюда получаем
выражение для конечной температуры T2:
.
Подставляя числовые
значения заданных величин, находим
.
Прологарифмируем
обе части полученного выражения:
lgT2=lg300+0,4(lgl
— lg5)=2,477+0,4( -0,699)=2,477—0,280=2,197.
Зная lgT2,
по таблицам антилогарифмов находим
искомое значение T2:
T2=157
К.
Работа A1
газа при адиабатном расширении
определяется по формуле
.
Подставив сюда
числовые значения величин, после
вычисления получим
Работа A2
газа при изотермическом сжатии выражается
формулой
A2=RT2(m/M)ln(V2/V1).
Произведя вычисления
по этой формуле, найдем
A2=
-21 кДж.
Знак минус показывает,
что при сжатии газа работа совершена
внешними силами.
Общая работа,
совершенная газом при рассмотренных
процессах, А=A1+A2=29,8кДж
+ (-21 кДж)=8,8 кДж.
График процесса
приведен на рис.
11.3.
Пример
7. Нагреватель
тепловой машины, работающей по обратимому
циклу Карно, имеет температуру
t1==200°С.
Определить температуру Т2,
охладителя, если при получении от
нагревателя количества теплоты Q1=
1 Дж машина
совершает работу A=0,4
Дж? Потери на трение и теплоотдачу не
учитывать.
Решение.Температуру охладителя найдем, использовав
выражение для термического КПД машины,
работающей по циклу Карно,=(T1—
T2)/T1.
Отсюда
T2=
T1(1-).
(1)
Термический КПД
тепловой машины выражает отношение
количества теплоты, которое превращено
в механическою работу A,
к количеству теплоты Q1,
которое получено рабочим телом тепловой
машины из внешней среды (от нагревателя),
т. е. =A/Q1.
Подставив это выражение в формулу
(1), найдем
T2=
T1(1-A/Q).
(2)
Учтя, что T1=473
К, после вычисления по формуле
(2) получим
T2=284
К.
Пример
8. Найти
изменение S
энтропии при нагревании воды массой
m=100
г от температуры t1=0°C
до температуры
t2=100
°С и последующем превращении воды в пар
той же температуры.
Решение.
Найдем отдельно изменение энтропии S’
при нагревании воды и изменение энтропии
S»
при превращении ее в пар. Полное изменение
энтропии выразится суммой S’
и S».
Как известно,
изменение энтропии выражается общей
формулой
(1)
При бесконечно
малом изменении dT
температуры нагреваемого тела
затрачивается количество теплоты
dQ=mcdT,
где m
— масса
тела; с
— его
удельная теплоемкость. Подставив
выражение dQ
в равенство
(1), найдем
формулу для вычисления изменения
энтропии при нагревании воды:
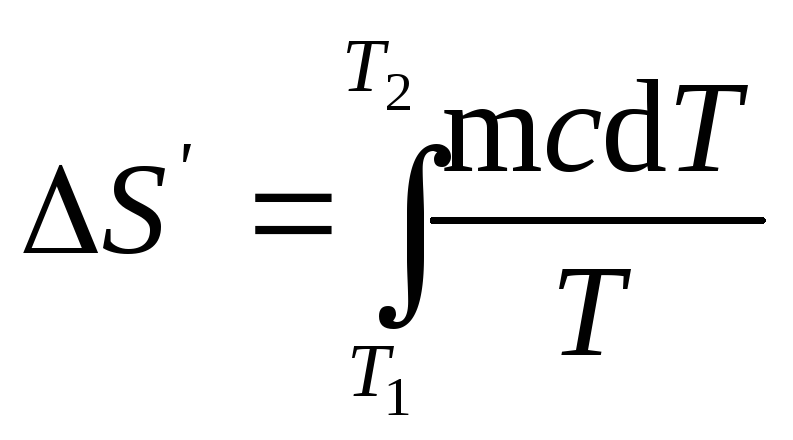
Вынесем за знак
интеграла постоянные величины и
произведем интегрирование, тогда получим
S’=mcln(T2/T1).
После вычислений
найдем S’=132
Дж/К.
При вычислении по
формуле
(1) изменения
энтропии во время превращения воды в
пар той же температуры постоянная
температуpa
T
‘выносится
за знак интеграла. Вычислив интеграл,
найдем
(2)
где Q
—
количество теплоты, переданное при
превращении нагретой воды в пар той
же температуры.
Подставив в равенство
(2) выражение
количества теплоты Q=m,
где
— удельная
теплота парообразования, получим
(3)
Произведя вычисления
по формуле
(3), найдем
S»=605
Дж/К.
Полное изменение
энтропии при нагревании воды и последующем
превращении ее в пар S=S’+S»=737
Дж/К.
Пример
9. Определить
изменение S
энтропии при изотермическом расширении
кислорода массой m=10
г от объема V1=25
л до объема V2=100
л.
Решение.
Так как процесс изотермический, то в
общем выражении энтропии
температуру выносят за знак интеграла.
Выполнив это, получим
(1)
Количество теплоты
Q, полученное
газом, найдем по первому началу
термодинамики: Q=U+A.
Для изотермического процесса U=0,
следовательно,
Q=A,
(2) а
работа А для этого процесса определяется
по формуле
A=(m/M)RT
ln(V2/V1).
(3)
С учетом
(2) и
(3) равенство
(1) примет
вид
S=(m/M)R
ln(V2/V1).
(4)
Подставив в
(4) числовые
значения и произведя вычисления, получим
S=(1010-3/(3210-3))
8,31
ln(10010-3/(2510-3))
Дж/К=3,60
Дж/К.
2010-03-24 22:39
В предыдущем параграфе мы установили, что при работе против сил трения трущиеся тела нагреваются. Было сделано много различных опытов с целью точно измерить то изменение температуры, которое получается ври совершении определенной работы. Такие опыты в середине XIX века одним из первых осуществил Джоуль. Его прибор изображен на рис. 365. Разрез прибора показан в упрощенном виде на рис. 366. В сосуде с водой вращаются лопасти 1, приводимые в движение с помощью груза массы
, который подвешен на шнуре, перекинутом через блок 2. При опускании груза лопасти вращаются, проходя при этом сквозь отверстия в перегородках 3, и, увлекая воду, вызывают трение одних слоев воды о другие. При трении вода и сосуд нагреваются; никаких других изменений ни вода, ни другие части прибора не испытывают. При опускании груза с высоты
действующая на него сила тяжести
совершает работу, равную
. В начале и в конце опыта все части прибора — груз, лопасти, вода — находятся в покое, так что в результате опускания груза кинетическая энергия всех этих тел не изменяется.
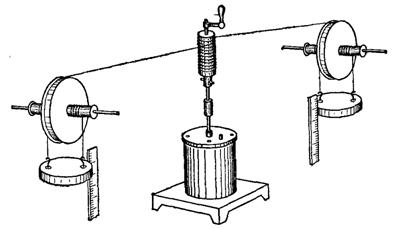
Рис. 365. Прибор Джоуля
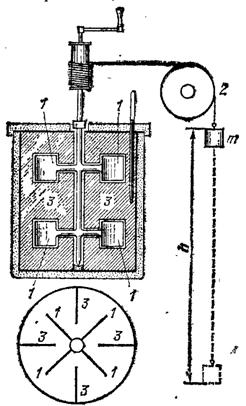
Рис. 366. Разрез прибора Джоуля
Таким образом, вся совершенная работа вызывает только нагревание воды, лопастей и других частей прибора. Это дает возможность подсчитать, какую работу нужно затратить, чтобы повысить температуру единицы массы воды на один кельвин. При этом Джоуль учел, что кроме воды нагреваются также и лопасти и сосуд. Как учитывается это нагревание, мы рассмотрим далее.
Опыты Джоуля повторялись неоднократно, причем условия опыта подвергались разнообразным изменениям. Менялось количество наливавшейся воды, масса грузов и высота их поднятия, моменты действующих сил и т. д. При всех этих измерениях всегда получался один и тот же результат: для нагревания одного килограмма воды на один кельвин надо произвести работу, равную 4,18 килоджоуля.
Кроме описанного опыта, и самим Джоулем и другими исследователями было выполнено много других опытов, также имевших целью установить связь между изменением температуры и совершенной работой. Наблюдалось нагревание газа, возникающее за счет работы, совершенной при сжатии; определялось разогревание трущихся друг о друга металлических дисков при одновременном определении работы, совершенной при преодолении трения, и т. д. Сравнение результатов этих опытов представляет некоторую трудность, так как в разных опытах нагреванию подвергались весьма различные тела.
Мы увидим дальше (§209), каким образом можно каждый раз свести полученное нагревание к нагреванию одного и того же вещества, например воды. Если произвести такое сравнение, то из всех описанных и многих аналогичных опытов можно вывести крайне важное заключение: если при исчезновении механической энергии не происходит никаких изменений в состоянии тел (например, плавления, испарения и т. д.), кроме изменения температуры, то за счет энергии 4,18 килоджоуля температура одного килограмма воды повышается всегда на один кельвин.
Таким образом, опыты Джоуля дают подтверждение закона сохранения энергии в расширенном смысле. При всех движениях, как происходящих без трения, так и сопровождающихся трением, сумма кинетической, потенциальной и внутренней энергий всех участвующих тел не изменяется. Эту сумму мы будем называть полной энергией тел или просто их энергией.
Рассмотрим пример. Пусть над свинцовой пластинкой висит на некоторой высоте свинцовый шарик. Энергия этой системы состоит из: а) потенциальной энергии шарика; б) внутренней энергии шарика и пластинки. Пусть теперь шарик упадет на пластинку и своим ударом вызовет нагревание. Потенциальная энергия шарика уменьшится, зато увеличится внутренняя энергия пластинки и шарика. Полная энергия остается неизменной.
203.1.
В приборе Джоуля, как это видно на рис. 365 и 366, скорость опускающихся грузов во много раз меньше скорости лопаток. Какая цель преследовалась таким устройством?
Примеры решения задач
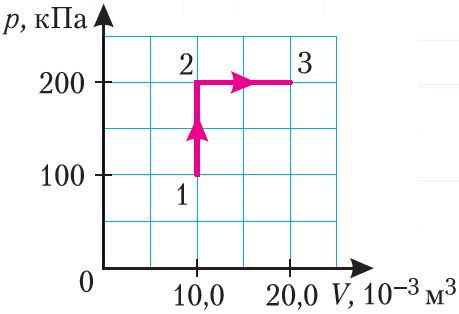
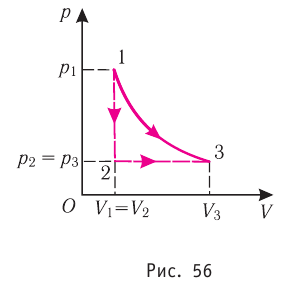
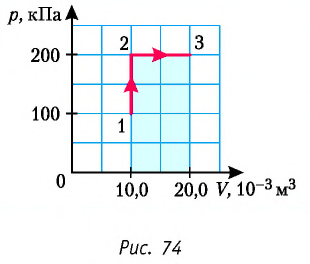
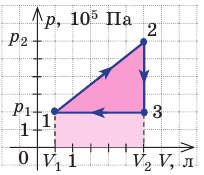
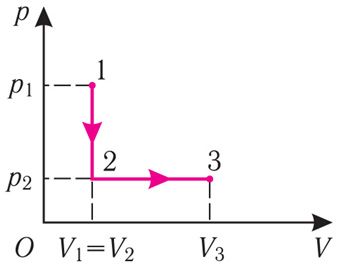
Пример 1. Определите работу, совершаемую силой давления идеального газа определённой массы при переходе из состояния 1 в состояние 3 (рис. 73).
Решение. I способ. Работа А газа в ходе всего процесса равна сумме работ на участках 12 и 2
3. Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс V2 = V1), то работа, совершаемая силой давления газа, А12 = 0. В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу
A23 = p2ΔV = p2(V3 – V1).
Тогда при переходе из состояния 1 в состояние 3 работа
А = А12 + А23 = p2(V3–V1).
А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.
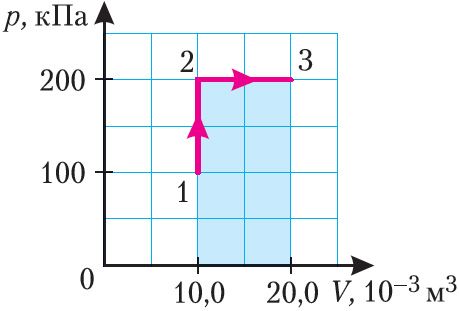
II способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью ОV и прямыми, соответствующими значениям объёма V1 = 10,0 · 10–3 м3 и V2 = 20,0 · 10–3 м3 (закрашенная область на рисунке 74).
А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.
Ответ: А = 2,00 кДж.
Пример 2. Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от t1 = 12 °С до t2 = 87 °С, если давление газа p = 190 кПа, а его начальный объём V1 = 6,0 дм3.
Дано:
Т1 = 285 К
Т2 = 360 К
p = 190 кПа = 1,90 · 105 Па
V1 = 6,0 дм3 = 6,0 · 10–3 м3
А — ?
Решение: Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
.
Согласно уравнению Клапейрона–Менделеева, и
. Следовательно,
.
.
Ответ: .
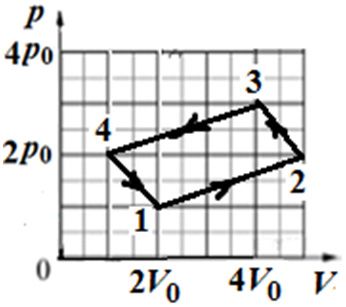
Пример 3. На рисунке 74.1 изображен процесс изменения состояния идеального газа определённой массы. На каком участке сила давления газа совершила наименьшую положительную работу? На каком участке внешняя сила совершила наибольшую положительную работу?
Решение. Работе силы давления газа соответствует площадь под графиком процесса. При расширении газа сила давления совершает положительную работу, а внешняя сила — отрицательную. При сжатии газа наоборот: сила давления совершает отрицательную работу, а внешняя сила — положительную. Анализ графика позволяет сделать вывод, что в процессе перехода из состояния 4 в состояние 1 сила давления газа совершила минимальную положительную работу (газ расширялся, а площадь под графиком минимальна). Максимальную же положительную работу внешняя сила совершает при сжатии, когда площадь под графиком максимальна (это процесс перехода из состояния 3 в состояние 4).
Пример 4. Состояние идеального газа, взятого в количестве ν = 1,0 моль при абсолютной температуре Т1 = 300 К, изменяется так, как изображено на рисунке 74.2. Определите работу газа в ходе всего процесса, если на изохоре 12 его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.
Дано:
ν = 1,0 моль
Т1 = 300 К
p1 = 3p2
Т1 = Т3
A – ?
Решение: Работа А газа в ходе всего процесса равна сумме значений работы на участках 12 и 2
3 (рис. 74.2). Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный V2 = V1), то работа газа А12 = 0. Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (р2 = р3), следовательно, работа газа А23 = p2(V3 − V1). Тогда А = А12 + А23 = p2(V3 − V1). Так как по условию Т1 = Т3, то воспользуемся уравнением Клапейрона:
, откуда
. Следовательно,
.
Согласно уравнению Клапейрона‒Менделеева, p1V1 = νRT1. Тогда .
Ответ: А = 1,7 кДж.