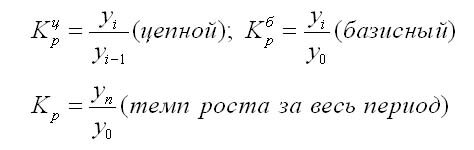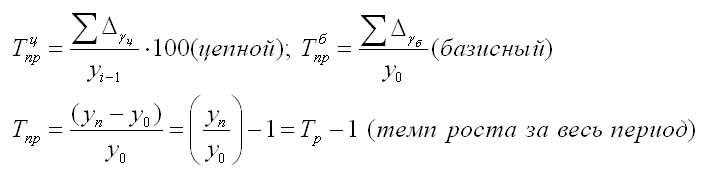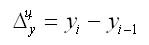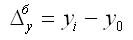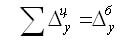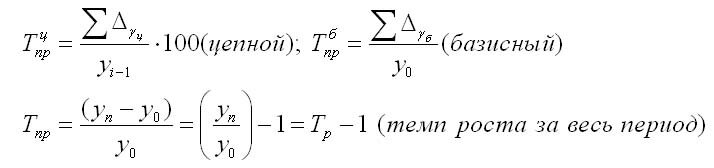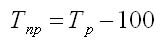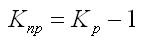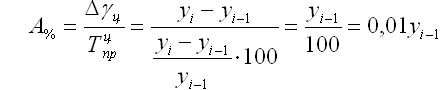Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Показатели динамического ряда
Для углубленного
изучения процессов во времени рассчитывают
показатели динамического ряда.
1.
Для
характеристики скорости изменения
процесса
применяются такие показатели, как
абсолютный прирост (убыль), темп прироста
(убыли).
• Абсолютный
прирост (убыль) характеризует
скорость изменения процесса (абсолютную
величину прироста/убыли в единицу
времени). Абсолютный прирост рассчитывается
как разность между данным уровнем и
предыдущим; обозначается знаком » +
«, характеризуя прирост, или знаком
«-«, характеризуя убыль.
• Темп
прироста (убыли) характеризует
величину прироста (убыли) в относительных
показателях в % и определяется как
процентное отношение абсолютного
прироста (убыли) к предыдущему уровню
ряда; обозначается знаком «+»
(прирост) или знаком «-» (убыль).
2.
Темп
роста (снижения)
– применяется для
характеристики
изменения процесса одного периода по
отношению к предыдущему периоду;
рассчитывается
как процентное отношение последующего
уровня к предыдущему.
3.
Значение
1% прироста (убыли) — используется
при
сравнении динамических рядов с разными
исходными уровнями (например,
средними, интенсивными, абсолютными),
который рассчитывается как отношение
абсолютного прироста к темпу прироста
за каждый период.
4.
Средний
темп прироста (снижения) – используется
для
обобщенной количественной оценки
тенденций динамического ряда, при
его расчете для большинства рядов можно
использовать следующую формулу:
Т пр.сн.
=

где
К = 1 при нечетном
числе уровней ряда;
К = 2 при четном
числе уровней ряда;
А и В показатели
линейной зависимости, используемые при
выравнивании
ряда методом наименьших квадратов.
Задача-эталон
Условие
задачи: в
Н-ском районе изучена заболеваемость
населения ветряной оспой за 10 лет
(табл. 13):
Таблица
13. Заболеваемость
населения Н-ского района ветряной оспой
за 10 лет
(на 10 000 населения)
|
Годы |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
Показатель |
3,5 |
4,9 |
3,6 |
5,7 |
6,5 |
5,5 |
8,1 |
7,2 |
5,0 |
7,3 |
Задание:
на
основании данного динамического ряда
требуется:
1. Выровнять ряд
с применением скользящей средней;
2.
Рассчитать показатели динамического
ряда (абсолютный прирост, темп прироста,
темп роста, значение 1%
прироста);
3. Сделать выводы
о динамике явления по выровненным
уровням;
4. Охарактеризовать
скорость изменения явлений.
Решение:
Таблица 14. Методика расчета
скользящей средней:
|
Годы |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
Показатель |
3,5 |
4,9 |
3,6 |
5,7 |
6,5 |
5,5 |
8,1 |
7,2 |
5,0 |
7,3 |
|
Скользящая средняя |
— |
4,0 |
4,7 |
5,3 |
5,9 |
6,7 |
6,9 |
6,8 |
6,5 |
— |
1. Найти среднюю
величину из данного уровня и двух
соседних с ним:
Заболеваемость
ветряной оспой в 1991 году: (3,5 + 4,9 + 3,6) : 3
= 4,0
Заболеваемость
ветряной оспой в 1992 году: (4,9 + 3,6 + 5,7) : 3
= 4,7
Заболеваемость
ветряной оспой в 1993 году: (3,6 + 5,7 + 6,5) : 3
= 5,3 и т.д.
Расчет
показателей динамического ряда (табл.
15):
1.
Абсолютный
прирост: разность
уровней данного и предыдущего года.
1991 год: 4,9 – 3,5 = +
1,4
1992 год: 3,6 – 4,9 = —
1,3
1993 год: 5,7 – 3,6 = +
2,1 и т.д.
2. Темп
прироста: процентное
отношение абсолютного прироста в % к
предыдущему уровню.
1991 год: (+ 1,4 : 3,5) х
100% = + 40,0 %
1992 год: (- 1,3 : 4,9) х
100% = — 27,0 %
1993 год: (+2,1 : 3,6) х
100% = + 58,0 % и т.д.
3. Темп
роста: процентное
отношение последующего уровня к
предыдущему уровню.
1991 год: (4,9 : 3,5) х
100% = 140 %
1992 год: (3,6 : 4,9) х
100 % = 73%
1993 год: (5,7 : 3,6) х
100 % = 158 % и т.д.
4.
Значение 1% прироста:
отношение абсолютного прироста к темпу
прироста за тот же период.
1991 год: + 1,4 : 40,0% =
0,04%
1992 год: — 1,3 : (-27,0%)
= 0,05 %
1993 год: +2,1 : 58,0% =
0,04% и т.д.
Таблица 15. Расчет показателей
динамического ряда
|
Год |
Заболеваемость оспой |
Абсолютный |
Темп % |
Темп % |
Значение 1% |
|
1990 |
3,5 |
— |
— |
— |
— |
|
1991 |
4,9 |
+ |
+ |
140 |
0,04 |
|
1992 |
3,6 |
— |
— |
73 |
0,05 |
|
1993 |
5,7 |
+ |
+ |
158 |
0,04 |
|
1994 |
6,5 |
+ |
+ |
114 |
0,06 |
|
1995 |
5,5 |
— |
— |
85 |
0,07 |
|
1996 |
8,1 |
+ |
+ |
147 |
0,06 |
|
1997 |
7,2 |
— |
+ |
89 |
0,08 |
|
1998 |
5,0 |
— |
+ |
69 |
0,07 |
|
1999 |
7,3 |
+ |
+ |
146 |
0,05 |
Выводы:
Заболеваемость
населения Н-ского района ветряной оспой
за 10 лет неравномерна. Скорость изменений
показателей заболеваемости различна,
наибольший темп прироста отмечается в
1993 году. При выравнивании показателей
динамического ряда с 1990 по 1996 год
отмечается тенденция увеличения
заболеваемости ветряной оспой, за период
с 1996 по 1999 год уровень заболеваемости
имеет тенденцию к снижению.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Гражданское право — работа с недвижимостью. договорная работа, наследственное право, банкротство.
Важнейшим показателем эффективности производства в анализе финансовой ситуации компании является показатель темпа роста. Поговорим об особенностях его расчета.
Как рассчитать темп роста: формула
Что называют снижением темпа роста цен?
Подробнее
Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.
Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.
Как рассчитать темп роста в процентах — формула:
ТР = Пт / Пб х 100%,
где Пк и Пб – показатели значений текущего и базового периодов.
Узнайте, может ли темп роста быть отрицательной величиной.
Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:
-
ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;
-
ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;
-
ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.
Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:
|
Объем выпуска в тыс. руб. |
Расчет (Пт / Пб х 100%) |
|
|
2017 (Пб) |
2018 (Пт) |
|
|
600 |
800 |
133,3% |
|
600 |
600 |
100% |
|
600 |
400 |
66,7% |
Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.
Узнайте, чем отличается темп роста от темпа прироста.
Как рассчитать цепные темпы роста
Рассмотрим пример расчета базисного и цепного темпов роста:
|
Период |
Объем в тыс.руб. |
Темп роста в % |
|
|
базисный |
цепной |
||
|
1 кв. |
300 |
100 |
— |
|
2 кв. |
310 |
103,3 (310 / 300) |
103,3 (310 / 300) |
|
3 кв. |
280 |
93,3 (280 / 300) |
90,3 (280 / 310) |
|
4 кв. |
360 |
120 (360 / 300) |
128,6 (360 / 280) |
Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).
Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.
Как рассчитать темпы прироста
Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:
∆ ТР = (Птек – Пбаз) / Пбаз х 100%
Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:
∆ ТР = (Птек – Ппр.п) / Ппр. п х 100%.
Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.
Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:
|
Период |
Темпы прироста |
|
|
базисные |
цепные |
|
|
1 кв. |
— |
— |
|
2 кв. |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
|
3 кв. |
— 6,7% (93,3 – 100) или ((280 – 300) / 300 х 100) |
-9,7% (90,3 – 100) или ((280 – 310) / 310 х 100) |
|
4 кв. |
20% (120 – 100) или (( 360 – 300) / 300 х 100) |
28,6% (128,6 – 100) или ((360 – 280) / 280 х 100) |
Анализируя результаты вычислений, экономист может сделать вывод:
-
Прирост объемов наблюдался во 2-м и 4-м кварталах, причем во 2-м он был наименьшим (3,3%). В 3-м квартале объем выпуска сократился на 6,7% в сравнении с показателями начала года;
-
Цепные темпы прироста обнаружили более глубокие колебания: объемы 3-го квартала снизились по отношению к показателям 2-го на 9,7%. Зато выпуск товаров в 4-м квартале вырос почти на треть в сравнении с итогами 3-го квартала. Столь существенные изменения в объемах производства могут свидетельствовать о сезонности выпускаемых продуктов, перебоях в снабжении необходимым сырьем или других причинах, которые исследует аналитик.
Как рассчитать средний темп роста
Средний темп роста – обобщающая характеристика уровня изменений. Расчет средних темпов роста и прироста также разграничивают на базисные и цепные. Для определения среднего темпа роста расчетные показатели по периодам складывают и делят на количество периодов. Таким же образом находят и средние темпы приростов. Вернемся к предыдущему примеру, рассчитав средние значения базисных темпов роста и прироста, а также аналогичных цепных показателей.
|
Показатель |
Значение в % |
Расчет |
|
Средний темп роста (базисный) |
105,5 |
(103,3 + 93,3 + 120) / 3 |
|
Средний темп прироста (базисный) |
5,5 |
(3,3 – 6,7 + 20) / 3 |
|
Средний темп роста (цепной) |
107,4 |
(103,3 + 90,3 + 128,6) / 3 |
|
Средний темп прироста (цепной) |
7,4 |
(3,3 – 9,7 + 28,6) / 3 |
Полученные цифры свидетельствуют о том, что в среднем с начала года объемы выпуска выросли на 5,5%, а в поквартальной привязке рост составил 7,4%.
Читайте также: Экспресс-анализ финансового состояния предприятия

Специализация: Гражданское право — работа с недвижимостью. договорная работа, наследственное право, банкротство.
Окончила в 2005 г. Тверской государственный университет, юридический факультет, специальность-юриспруденция.
Юрист в сфере недвижимости:составление договоров, регистрация в Росреестре прав и сделок,оформление наследственных прав,
сопровождение сделок с недвижимым имуществом,судебный опыт по делам,связанным с признанием прав на недвижимость.
Имеется опыт работы помощником арбитражного управляющего.
Показатели динамики: темп роста и темп прироста
Темп роста
Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр). Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.
Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста
Коэффициент роста может быть рассчитан по формулам:
Также темп роста может определяться так:
Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.
Абсолютный прирост
Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:
1. Абсолютный прирост (цепной):
2. Абсолютный прирост (базисный):
где уi — уровень сравниваемого периода;
Уi-1 — Уровень предшествующего периода;
У0 — уровень базисного периода.
Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:
Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.
Темп прироста
Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:
Темп прироста можно получить из темпа роста:
Коэффициент прироста может быть получен таким образом:
Абсолютное значение 1%-го прироста
Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:
Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.
Примеры расчетов показателей динамики
Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики
Пример 1. Расчет среднемесячного темп роста объема продаж
Пример 2. Определение всех показателей динамики (подробный расчет)
Пример 3. Расчет цепных, базисных и средних показателей динамики
О показателях динамики
При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.
Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста. Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения. Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.
Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем. В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными. Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Среднегодовой темп роста применяется при анализе рядов динамики для выявления общей тенденции изменения показателя во времени.
Как видно из названия – это усредненный показатель. Его значение говорит о том, что если бы каждый год темп роста был одинаковым и равен среднему, то общий рост показателя был равен фактическому.
Среднегодовой темп роста можно определить двумя способами:
- Tp‾=yny1n−1∗100%overline{T_p}=sqrt[n-1]{frac{y_n}{y_1}}*100%,
где yny_n — значение показателя отчетного периода;
y1y_1 — значение показателя базового периода;
nn — количество лет.
- Tp‾=Kp2∗Kp3∗…∗Kpnn−1∗100%overline{T_p}=sqrt[n-1]{K_p^2*K_p^3*…*K_p^n}*100%,
где KpiK_p^i — цепной коэффициент роста за i-й период.
Примеры решения задач
Пример 1
В 2010 году на предприятии было выпущено продукции на 3650 тыс. руб., а в 2017 — на 4251 тыс. руб. Найти среднегодовой темп роста выпуска продукции.
Решение
Tp‾=425136508−1∗100%=102,2%overline{T_p}=sqrt[8-1]{frac{4251}{3650}}*100%=102,2%
В среднем за год выпуск продукции возрастал на 2,2%.
Ответ: Tp‾=102,2%overline{T_p}=102,2%
Пример 2
Рассчитать среднегодовой темп роста с использованием коэффициентов роста.
| Год | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Объем выпуска, тыс. шт. | 1020 | 1021 | 1300 | 1250 | 1280 | 1310 | 1390 | 1460 |
Решение
Решим данную задачу средствами MS Excel.
Коэффициент роста определяется как отношение показателя текущего года к предыдущему.
Получаем
Далее необходимо получить произведение этих коэффициентов.
Извлекаем корень 7-й степени. Это возможно двумя путями
Или
Также среднегодового темпа роста при помощи средней геометрической
Получили
Ответ: 105,26%.
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат