Что такое Тау в физике?
Тау это буква греческого алфавита выглядит вот так — τ. В физики ей принято обозначать время. Обычно τ используют для времени когда буква t занята для другой величены, к примеру, температуры.
Чему равно число Тау?
Число Тау — это очень просто: отношение длины окружности к радиусу. Оно ровно в два раза больше числа Пи (там вместо радиуса — диаметр).
Как пишется буква Тау?
ταῦ) — 19-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 300. Происходит от финикийской буквы 𐤕 — тав. От буквы тау произошли латинская буква T и кириллическая Т.
Что значит слово Тау?
В системе греческой алфавитной записи чисел имеет числовое значение 300. Происходит от финикийской буквы — тав. От буквы «тау» произошли латинская буква T и кириллическая Т. Буква τ… ТАУ — символ символов, скрытая мудрость, символ жизни, знак доброты, так называемый «ключ Нила», т.
Что это табу?
Табу́ — термин, заимствованный из религиозно-обрядовых установлений Полинезии и ныне принятый в этнографии и социологии для обозначения системы специфических запретов — системы, черты которой под различными названиями найдены у всех народов, стоящих на определённой ступени развития. …
Как пишется буква сигма?
Строчное начертание сигмы двояко: в начале и середине слов пишется σ, в конце же ς. …
Как пишется буква эта?
Η, η (название: э́та, греч. ήτα, др. … ἦτα) — 7-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 8.
Как пишется буква эпсилон?
Эпсилон
| Буква греческого алфавита эпсилон | |
|---|---|
| Изображения[показать] | |
| ◄ Α Β Γ Δ Ε Ζ Η Θ Ι ► ◄ α β γ δ ε ζ η θ ι ► ◄ ϱ ϲ ϳ ϴ ϵ ϶ Ϸ ϸ Ϲ ► | |
| Характеристики | |
| Название | Ε: greek capital letter epsilon ε: greek small letter epsilon ϵ: greek lunate epsilon symbol |
Как пишется буква дзета?
Ζ, ζ (название: дзе́та, греч. ζήτα, др. -греч. ζῆτα) — 6-я буква греческого алфавита.
Как пишется буква лямбда?
Λ, λ (название: ля́мбда (ла́мбда), греч. λάμδα, λάμβδα) — 11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30. Происходит от финикийской буквы 𐤋 — ламд.
Как пишется буква гамма?
Γ, γ (название: га́мма, греч. γάμμα) — 3-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 3. Происходит от финикийской буквы 𐤂 — гамл.
Как пишется буква альфа?
Альфа (буква) Вики ἄλφα) — первая буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 1. Происходит от финикийской буквы — алеф, которая в переводе означает «бык» и своим начертанием изображает голову быка.
Как пишутся буквы Альфа и Омега?
Альфа и Омега (ΑΩ, Αω, αω) — сочетание первой и последней букв классического (ионического) греческого алфавита, которое является наименованием Бога в Книге Откровения Иоанна Богослова, символами Бога как начала и конца всего сущего. Се, гряду скоро, и возмездие Мое со Мною, чтобы воздать каждому по делам его.
Как пишется буква бета?
βῆτα) — 2-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 2. Происходит от финикийской буквы 𐤁 — бет, что в переводе означает «дом». От буквы бета произошли латинская буква B и кириллические Б и В.
Как пишется буква омега?
ὦ μέγα) — 24-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 800. От буквы омега произошла кириллическая буква Ѡ, известная под названиями «от» и «омега». В древнегреческом омега обозначала долгий звук [oː], в то время как омикрон (ο) обозначал краткий [o].
Сколько букв в греческом алфавите?
Греческий алфавит состоит из 24 букв, из которых 17 согласных и 7 гласных: α, ε, η, ι, ο, υ, ω.
Какая письменность стала основой для греческого алфавита?
Западно-греческое письмо стало основой для этрусского, а следовательно латинского и рунического германского письма. Первоначально греческий алфавит состоял из 27 букв, и в таком виде сложился к 5 в. до н. э.
Как называются буквы греческого алфавита?
Греческий алфавит. Все 24 буквы в таблице транскрипцией.
| № | Греческая буква. (Прописная — строчная) | Название буквы (на русском) |
|---|---|---|
| 2 | Β — β | Бета |
| 3 | Γ — γ | Гамма |
| 4 | Δ — δ | Дельта |
| 5 | Ε — ε | Эпсилон |
Сколько государственных языков в Бельгии?
В стране три официальных языка — фламандский (близок к голландскому, имеет несколько диалектов), немецкий и французский (отличается характерным местным произношением и большим количеством диалектных слов).
В физике и инженерии, постоянная времени, обычно обозначаемый греческой буквой τ (тау), является параметром, характеризующим реакцию на ступенчатый ввод первого порядка, линейный, неизменный во времени ( LTI) система. Постоянная времени является основной единицей характеристики LTI-системы первого порядка.
Во временной области обычный выбор для изучения временной характеристики — это переход от переходной характеристики к ступенчатому входу или импульсной характеристики на вход дельта-функции Дирака. В частотной области (например, глядя на преобразование Фурье переходной характеристики или используя вход, который является простой синусоидальной функцией времени) постоянная времени также определяет полосу пропускания инвариантной во времени системы первого порядка, то есть частота, на которой мощность выходного сигнала падает до половины значения, которое она имеет на низких частотах.
Постоянная времени также используется для характеристики частотной характеристики различных систем обработки сигналов — магнитных лент, радиопередатчиков и приемники, оборудование для записи и воспроизведения, и цифровые фильтры, которые могут быть смоделированы или аппроксимированы системами LTI первого порядка. Другие примеры включают постоянную времени, используемую в системах управления для регуляторов интегрального и производного действия, которые часто пневматические, а не электрические.
Постоянные времени — это особенность анализа сосредоточенных систем (метод анализа сосредоточенной емкости) для тепловых систем, который используется, когда объекты равномерно охлаждают или нагреваются под влиянием конвективного охлаждения или нагревания.
Физически постоянная времени представляет собой время, необходимое для того, чтобы отклик системы упал до нуля, если бы система продолжала распадаться с начальной скоростью, из-за постепенного изменения скорости распада отклик фактически уменьшился. по значению до 1 / e ≈ 36,8% { displaystyle 1 / e приблизительно 36,8 , %}

Содержание
- 1 Дифференциальное уравнение
- 1.1 Пример решения
- 1.1.1 Обсуждение
- 1.1.2 Особые случаи
- 1.1 Пример решения
- 2 Связь постоянной времени с полосой пропускания
- 3 Отклик на скачок с произвольным начальным значением условия
- 4 Примеры
- 4.1 Постоянные времени в электрических цепях
- 4.2 Тепловая постоянная времени
- 4.3 Постоянные времени в неврологии
- 4.4 Экспоненциальный спад
- 4.5 Метеорологические датчики
- 5 См. также
- 6 Примечания
- 7 Ссылки
- 8 Внешние ссылки
Дифференциальное уравнение
LTI-системы первого порядка характеризуются дифференциальным уравнением
- τ d V dt + V = f (t) { displaystyle { tau} {dV over dt} + V = f (t)}
где τ представляет собой константу экспоненциального затухания, а V является функцией времени t
- V = V (т). { displaystyle V = V (t).}
В правой части находится функция принуждения f (t), описывающая внешнюю движущую функцию времени, которую можно рассматривать как вход системы, для которой V (t) это ответ или вывод системы. Классическими примерами для f (t) являются:
ступенчатая функция Хевисайда, часто обозначаемая u (t):
- u (t) = {0, t < 0 1, t ≥ 0 {displaystyle u(t)={begin{cases}0,t<0\1,tgeq 0end{cases}}}
the импульсная функция, часто обозначаемая δ (t), а также синусоидальная входная функция:
- f (t) = A sin (2 π ft) { displaystyle f (t) = A sin (2 pi ft)}
или
- f (t) = A ej ω t, { displaystyle f (t) = Ae ^ {j omega t},}
где A — амплитуда вынуждающей функции, f — частота в герцах, а ω = 2π f — частота в радианах в секунду.
Пример решения
Пример решения дифференциального уравнения с начальным значением V 0 и без функции принуждения:
- V (t) = V oe — t / τ { displaystyle V (t) = V_ {o} e ^ {- t / tau}}
где
- V o = V (t = 0) { displaystyle V_ {o} = V (t = 0)}
— начальное значение V. Таким образом, ответ представляет собой экспоненциальный спад с постоянной времени τ.
Обсуждение
Предположим,
- V (t) = V 0 e — t / τ { displaystyle V (t) = V_ {0} e ^ {- t / tau} }
.
Такое поведение называется «убывающей» экспоненциальной функцией. Время τ { displaystyle tau}
Здесь:
- t = время (обычно t>0 { displaystyle t>0}
в системе управления)
- V0= начальное значение (см. «Особые случаи» ниже).
Конкретные случаи
- 1) Пусть t = 0 { displaystyle t = 0}
; тогда V = V 0 e 0 { displaystyle V = V_ {0} e ^ {0 }}
, и поэтому V = V 0 { displaystyle V = V_ {0}}
- 2) Пусть t = τ { displaystyle t = tau}
; тогда V = V 0 e — 1 ≈ 0,37 V 0 { displaystyle V = V_ {0} e ^ {- 1} приблизительно 0,37V_ {0}}
- 3) Пусть V = е (t) = V 0 e — t τ { displaystyle V = f (t) = V_ {0} e ^ {- {t over tau}}}
, и поэтому lim t → ∞ е (t) = 0 { displaystyle lim _ {t to infty} f (t) = 0}
- 4) Пусть t = 5 τ { displaystyle t = 5 tau}
; тогда V = V 0 e — 5 ≈ 0,0067 V 0 { displaystyle V = V_ {0} e ^ {- 5} приблизительно 0,0067V_ {0} }
После периода, равного одной постоянной времени, функция n достигает e = примерно 37% от своего начального значения. В случае 4 после пяти постоянных времени функция достигает значения менее 1% от исходного. В большинстве случаев этот порог в 1% считается достаточным, чтобы предположить, что функция упала до нуля — как показывает опыт, в технике управления стабильная система — это система, которая демонстрирует такое общее затухающее поведение.
Связь постоянной времени с полосой пропускания
τ { displaystyle tau}


Предположим, что функция форсирования выбрана синусоидальной так:
- τ d V dt + V = f (t) = A ej ω t. { displaystyle tau {dV over dt} + V = f (t) = Ae ^ {j omega t}.}
(Ответ на ввод действительной косинусной или синусоидальной волны можно получить, взяв действительную или мнимая часть окончательного результата в силу формулы Эйлера.) Общее решение этого уравнения для времен t ≥ 0 с, предполагая V (t = 0) = V 0 :
- В (т) знак равно В 0 е — t / τ + А е — t / τ τ ∫ 0 tdt ′ et ′ / τ ej ω t ′ { displaystyle V (t) = V_ {0} e ^ { -t / tau} + {Ae ^ {- t / tau} over tau} int _ {0} ^ {t} , dt ‘ e ^ {t’ / tau} e ^ {j omega t ‘}}
- = V 0 e — t / τ + 1 / τ j ω + 1 / τ A (ej ω t — e — t / τ). { displaystyle = V_ {0} e ^ {- t / tau} + { frac {1 / tau} {j omega + 1 / tau}} A left (e ^ {j omega t} -e ^ {- t / tau} right).}
- = V 0 e — t / τ + 1 / τ j ω + 1 / τ A (ej ω t — e — t / τ). { displaystyle = V_ {0} e ^ {- t / tau} + { frac {1 / tau} {j omega + 1 / tau}} A left (e ^ {j omega t} -e ^ {- t / tau} right).}
В течение долгого времени убывающие экспоненты становятся незначительными и стационарное решение или долгосрочное решение:
- V ∞ (t) = 1 / τ j ω + 1 / τ A ej ω t. { displaystyle V _ { infty} (t) = { frac {1 / tau} {j omega + 1 / tau}} Ae ^ {j omega t}.}
Величина этого ответа это:
- | V ∞ (t) | = A 1 τ (ω 2 + (1 / τ) 2) 1/2 = A 1 1 + (ω τ) 2. { displaystyle | V _ { infty} (t) | = A { frac {1} { tau left ( omega ^ {2} + (1 / tau) ^ {2} right) ^ {1 / 2}}} = A { frac {1} { sqrt {1 + ( omega tau) ^ {2}}}}.}
По соглашению, полоса пропускания этой системы — это частота, где | V ∞ | падает до половинного значения, или где ωτ = 1. Это обычное соглашение о полосе пропускания, определяемое как частотный диапазон, в котором мощность падает менее чем наполовину (не более -3 дБ). Использование частоты в герцах, а не в радианах / с (ω = 2πf):
- f 3 d B = 1 2 π τ. { displaystyle f_ {3dB} = { frac {1} {2 pi tau}}.}
Обозначение f 3dB происходит от выражения мощности в децибелах и наблюдение, что половинная мощность соответствует падению значения | V ∞ | на коэффициент 1 / √2 или на 3 децибела.
Таким образом, постоянная времени определяет полосу пропускания этой системы.
Переходная характеристика с произвольными начальными условиями

τ { displaystyle tau}

Предположим, что функция принуждения выбрана в качестве пошагового входа, поэтому:
- d V dt + 1 τ V = f (t) = A u (t), { displaystyle {dV over dt} + { frac {1} { tau}} V = f (t) = Au (t),}
с u (t) шагом Хевисайда функция. Общее решение этого уравнения для времен t ≥ 0 с при условии, что V (t = 0) = V 0 :
- V (t) = V 0 e — t / τ + A τ ( 1 — е — t / τ). { Displaystyle V (t) = V_ {0} e ^ {- t / tau} + A tau left (1-e ^ {- t / tau} right).}
(Может Следует отметить, что этот отклик является пределом ω → 0 указанного выше отклика на синусоидальный вход.)
Решение для длительного времени не зависит от времени и от начальных условий:
- V ∞ = A τ. { displaystyle V _ { infty} = A tau.}
Постоянная времени остается неизменной для той же системы независимо от начальных условий. Проще говоря, система приближается к своей конечной устойчивой ситуации с постоянной скоростью, независимо от того, насколько она близка к этому значению в любой произвольной начальной точке.
Например, рассмотрим электродвигатель, запуск которого хорошо моделируется системой LTI первого порядка. Предположим, что при запуске из состояния покоя двигателю требуется секунды, чтобы достичь 63% его номинальной скорости 100 об / мин, или 63 об / мин, то есть меньше 37 об / мин. Затем будет обнаружено, что после следующих секунды двигатель ускорился еще на 23 об / мин, что составляет 63% от этой разницы в 37 об / мин. Это доводит его до 86 об / мин, что все еще составляет 14 об / мин. Через треть ⅛ секунды двигатель наберет дополнительные 9 оборотов в минуту (63% от этой разницы в 14 оборотов в минуту), установив его на 95 оборотов в минуту.
Фактически, при любой начальной скорости с ≤ 100 об / мин, через ⅛ секунды этот конкретный двигатель получит дополнительные 0,63 × (100 — с ) Об / мин.
Примеры
Постоянные времени в электрических цепях


В цепи RL составлен для одного резистора и катушки индуктивности постоянная времени τ { displaystyle tau}
- τ = LR { displaystyle tau = { L over R}}
, где R — сопротивление (в Ом ), а L — индуктивность (в Henrys ).
Аналогично, в RC-цепи, состоящей из одного резистора и конденсатора, постоянная времени τ { displaystyle tau}
- τ = RC { displaystyle tau = RC}
где R — сопротивление (в Ом ), а C — емкость (в фарадах ).
Электрические цепи часто более сложны, чем эти примеры, и могут иметь несколько постоянных времени (см. Переходная характеристика и Разделение полюсов для некоторых примеров.) В случае, когда обратная связь присутствует, система может показывать нестабильные, увеличивающиеся колебания. Вдобавок физические электрические цепи редко являются действительно линейными системами, за исключением возбуждений с очень низкой амплитудой; однако широко используется приближение линейности.
В цифровых электронных схемах часто используется другая мера, FO4. Это можно преобразовать в единицы постоянной времени с помощью уравнения 5 τ = FO4 { displaystyle 5 tau = { text {FO4}}}
Тепловая постоянная времени
Постоянные времени — это характеристика анализа сосредоточенных систем (метод анализа сосредоточенной емкости) для тепловых систем, используемых, когда объекты равномерно охлаждаются или нагреваются под влиянием конвективного охлаждения или нагревания. В этом случае передача тепла от тела к окружающей среде в данный момент времени пропорциональна разнице температур между телом и окружающей средой:
- F = h A s (T (t) — T a), { displaystyle F = hA_ {s} left (T (t) -T_ {a} right),}
, где h — коэффициент теплопередачи, а A s — площадь поверхности, T (t) = температура тела в момент времени t, а T a — постоянная температура окружающей среды. Положительный знак указывает на то, что F является положительным, когда тепло выходит из тела, потому что его температура выше, чем температура окружающей среды (F — поток наружу). Если тепло теряется в окружающую среду, эта теплопередача приводит к падению температуры тела, определяемой по формуле:
- ρ cp V d T dt = — F, { displaystyle rho c_ {p} V { frac { dT} {dt}} = — F,}
где ρ = плотность, c p= удельная теплоемкость, а V — объем тела. Отрицательный знак указывает на падение температуры при передаче тепла наружу от тела (то есть, когда F>0). Приравнивая эти два выражения для теплопередачи,
- ρ c p V d T d t = — h A s (T (t) — T a). { displaystyle rho c_ {p} V { frac {dT} {dt}} = — hA_ {s} left (T (t) -T_ {a} right).}
Очевидно, это система LTI первого порядка, которая может быть представлена в виде:
- d T dt + 1 τ T = 1 τ T a, { displaystyle { frac {dT} {dt}} + { frac {1} { tau}} T = { frac {1} { tau}} T_ {a},}
с
- τ = ρ cp V h A s. { displaystyle tau = { frac { rho c_ {p} V} {hA_ {s}}}.}
Другими словами, постоянная времени говорит, что большие массы ρV и большая теплоемкость c p приводят к более медленным изменениям температуры, в то время как большие площади поверхности A s и лучшая теплопередача h приводят к более быстрым изменениям температуры.
Сравнение с вводным дифференциальным уравнением предлагает возможное обобщение для изменяющихся во времени температур окружающей среды T a. Однако, сохраняя простой пример окружающего константы, подставляя переменную ΔT ≡ (T — T a), получаем:
- d Δ T dt + 1 τ Δ T = 0. { Displaystyle { frac {d Delta T} {dt}} + { frac {1} { tau}} Delta T = 0.}
Системы, для которых охлаждение удовлетворяет вышеуказанному экспоненциальному уравнению, говорят, что удовлетворяют Закон охлаждения Ньютона. Решение этого уравнения предполагает, что в таких системах разница между температурой системы и ее окружения ΔT как функция времени t определяется как:
- Δ T (t) = Δ T 0 e — t / τ, { displaystyle Delta T (t) = Delta T_ {0} e ^ {- t / tau},}
, где ΔT 0 — начальная разница температур в момент времени t = 0. На словах, тело принимает ту же температуру, что и окружающая среда, с экспоненциально медленной скоростью, определяемой постоянной времени.
Постоянные времени в неврологии
В возбудимой клетке, такой как мышца или нейрон, постоянная времени мембранного потенциала τ { displaystyle tau}
- τ = rmcm { displaystyle tau = r_ {m} c_ {m}}
, где r m — это сопротивление через мембрану, а c m — емкость мембраны.
Сопротивление через мембрану является функцией количества открытых ионных каналов, а емкость — функцией свойств липидного бислоя.
Постоянная времени равна используется для описания роста и падения мембранного напряжения, где рост описывается как
- V (t) = V max (1 — e — t / τ) { displaystyle V (t) = V _ { textrm {max }} (1-e ^ {- t / tau})}
и падение описывается как
- V (t) = V max e — t / τ { displaystyle V (t) = V_ { textrm {max}} e ^ {- t / tau}}
где напряжение в милливольтах, время в секундах, а τ { displaystyle tau}
Vmax определяется как максимальное изменение напряжения от потенциала покоя, где
- V max = rm I { displaystyle V _ { textrm {max}} = r_ {m} I}
, где r m — сопротивление через мембрану, а I — ток через мембрану.
Настройка для t = τ { displaystyle tau}
Установка для t = τ { displaystyle tau}
Чем больше время константа, тем медленнее растет или падает потенциал нейрона. Длительная постоянная времени может привести к временному суммированию или алгебраическому суммированию повторяющихся потенциалов. Короткая постоянная времени дает скорее детектор совпадений через пространственное суммирование.
Экспоненциальный распад
В экспоненциальном распаде, например, радиоактивного изотоп, постоянная времени может интерпретироваться как среднее время жизни. период полураспада THLсвязан с экспоненциальной постоянной времени τ { displaystyle tau}
- THL = τ ⋅ ln 2. { displaystyle T_ {HL } = tau cdot mathrm {ln} , 2.}
Величина, обратная постоянной времени, называется постоянной распада и обозначается λ = 1 / τ. { displaystyle lambda = 1 / tau.}
Метеорологические датчики
A постоянная времени — это количество времени, которое требуется метеорологическому датчику, чтобы отреагировать на быстрое изменение измеряемой величины, пока он не начнет измерять значения. в пределах допуска точности, обычно ожидаемого от датчика.
Это чаще всего применяется к измерениям температуры, температуры точки росы, влажности и давления воздуха. Радиозонды особенно страдают из-за их быстрого увеличения высоты.
См. Также
Примечания
Ссылки
Внешние ссылки
| На Викискладе есть материалы, связанные с Постоянная времени. |
Угловое ускорение – что это?
Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.
Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})
Угловая скорость
Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.
При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).
Вектор угловой скорости направлен вдоль оси вращения.
Основные формулы для вычисления угловой скорости
Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):
- (omega=frac nt), где (n) – количество оборотов за единицу времени (t).
- (omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
- (omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
- (omega=2pinu), где (nu) – числом оборотов в единицу времени.
Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)
Связь между угловой скоростью и нормальным (центростремительным) ускорением
Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.
Центростремительное ускорение определяется по формуле:
(a_n=frac{V^2}R),
где (V) – скорость движения, (R) – радиус окружности.
Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})
Итак, формула связывающая эти две величины:
(a_n=omega^2R)
Основные формулы для расчета углового ускорения
Значение углового ускорения в определенный момент времени вычисляется как первая производная от угловой скорости или вторая производная от угла поворота по времени.
(varepsilon=lim_{triangle trightarrow0}frac{triangleomega}{triangle t}=frac{domega}{dt}=frac{d^2varphi}{dt}=overset.omega=overset{..}varphi)
Угловое ускорение маховика
(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).
Среднее угловое ускорение
Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.
(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})
Тангенциальное ускорение
Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.
(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) – радиус кривизны траектории в заданной точке.
Мгновенное угловое ускорение
Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.
(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})
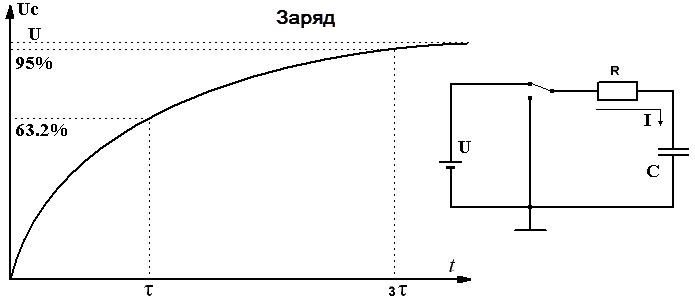
Электрическая цепь RC
Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе,
согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.
Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и
противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:
Решаем дифференциальное уравнение C(dU/dt)= -U/R

Из таблицы интегралов здесь используем преобразование
Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e-t/RC * eConst.
Решение примет вид:
U = e-t/RC * Const.
Здесь Const — константа, величина, определяемая начальными условиями.
Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону
e-t/RC.
Экспонента — функция exp(x) = ex
e – Математическая константа, приблизительно равная 2.718281828…
Постоянная времени τ
Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U,
в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения UC и определится выражением:

Тогда напряжение UC на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:
UC = U(1 — e-t/RC)
При t = RC, напряжение на конденсаторе составит UC = U(1 — e-1) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.
Постоянная времени τ = RC
За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e3)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e5)*100% ≈ 99% значения U.
Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R,
тогда в цепи пойдёт ток разряда конденсатора.
Напряжение на конденсаторе при разряде будет составлять UC = Ue-t/τ = U/et/τ.
За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e3)*100% ≈ 5% от значения U.
За время 5τ до (1/e5)*100% ≈ 1% значения U.
Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.
Замечания и предложения принимаются и приветствуются!
Физика, 11 класс
Урок №20. Постулаты специальной теории относи-тельности (СТО)
Основные вопросы, рассматриваемые в теме: событие, постулат, собственная инерциальная система отсчёта, собственное время, собственная длина тела, масса покоя, инвариант; причины появления СТО; постулаты СТО: инвариантность модуля скорости света в вакууме, принцип относительности Эйнштейна.
Глоссарий:
Специальная теория относительности (СТО) – физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физических процессов.
Событие — физическое явление, которое происходит в определённый момент времени в данной точке пространства.
События могут происходить в одно и тоже время и их называют одновременными. Если координаты событий совпадают, то события называют одноместными.
Инерциальные системы отсчёта (ИСО) – это системы отсчёта, в которых выполняется первый закон Ньютона – закон инерции.
Два постулата теории:
1. Все физические явления протекают одинаково во всех инерциальных системах отсчёта.
2. Скорость света в вакууме одинакова во всех инерциальных системах отсчёта.
Постулат – это основное положение, которое не может быть логически доказано, а является результатом обобщения всех опытов.
Время, отсчитываемое покоящимися в ИСО часами, называется собственным временем.
Длину тела L0, относительно которого оно в ИСО находится в покое называют собственной длиной.
Массой покоя m0, называют массу тела в состоянии покоя относительно ИСО.
Скорость света c и собственное время Δτ инвариантны в любых ИСО.
Список основной и дополнительной литературы по теме:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 229 – 238.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 147 – 148
- Анциферов Л.И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 242-253.
- Айзексон У., Эйнштейн. Жизнь гения; пер. с анг. А.Ю. Каннуниковой. – М: АСТ, 2016 – С.16-25
Теоретический материал для самостоятельного изучения
Человек, открывший новый взгляд на пространство и время мыслил образами. Альберт Эйнштейн всегда твёрдо верил, что именно воображение способно проникнуть в суть, в глубину, в основу сущего. Он никогда не заучивал теорию, он представлял её образами. В детстве Эйнштейну привили интерес к математике, естествознанию. Одной из любимых книг Альберта была книга Аарона Бернштейна «Популярные книги по естественной истории». От описаний научных историй у 12 летнего Эйнштейна захватывало дух. Мысленные эксперименты были самым занимательным в книгах Бернштейна.
В 1895 году Эйнштейну повезло, в 16-летнем возрасте, провалив экзамены в Цюрихский политехникум по французскому языку, литературе, политике и зоологии, но легко справившись с математикой и естествознанием, он поступил в сельскую школу Арау. Образование здесь строилось на методах, разработанных Иоганном Песталоцци, на проведении мысленных экспериментов, на более глубоком понимании явлений и ситуаций. Это были первые шаги на пути формирования специальной теории относительности (СТО).
Теория относительности – физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физических процессов.
В теории относительности часто будет использовано понятие «событие». Событием будем называть физическое явление, которое происходит в определённый момент времени в данной точке пространства.
В движущемся поезде, вывешенная в центре, вспыхивает лампочка в точке О – это одно событие. Свет от лампочки достигает точку А в одном конце помещения – это другое событие, а также достигает противоположного конца помещения в точке В – то третье событие.
События могут происходить в одно и тоже время и их называют одновременными. Если координаты событий совпадают, то события называют одноместными. При этом учитываем, что реальные тела имеют размеры и события разворачиваются во времени.
Одновременно ли достигнет свет две противолежащие точки А и В? Ведь корабль движется со скоростью в одном направлении и одна стенка приближается к летящему свету, а другая отдаляется.
Классический закон сложения скоростей не работает в описании распространения электромагнитного излучения от источника света.
Чтобы ответить на эти вопросы, необходимо выяснить, меняются ли основные законы электродинамики при переходе одной инерциальной системы отсчёта к другой, или же подобно принципам относительности Галилея и законам Ньютона, они остаются неизменными.
Принцип относительности Галилея.
Инерциальные системы отсчёта (ИСО) – это системы отсчёта, в которых выполняется первый закон Ньютона – закон инерции. Системы, которые ускоряются или вращаются называют неинерциальными. Система отсчёта, движущаяся равномерно и прямолинейна относительно ИСО, также инерциальная. Земля не совсем инерциальная система отсчёта, так как она вращается, но для большинства наших примеров, будем считать её инерциальной.
К началу XX века в физике накопилось много наблюдений и опытов, которые не могли быть объяснены классическими теориями. В XVII – XIX веках большое место в теории отводилось гипотезе о существовании эфира. Эфир представляли себе, как занимающая всё пространство упругая среда, с помощью которой осуществляется взаимодействие между телами, благодаря которой распространяются волны звуковые, световые, электромагнитные. Считалось естественным связывать абсолютную систему отсчёта с мировым эфиром. Этой теории придерживался и основатель электронной теории Х. Лоренц и Г.Герц. Однако эксперименты, поставленные в 1881 году учёными А. Майкельсоном, Э.Морли и А.Физо об изотропности света, приводили к противоположным результатам. В опытах по изучению распространения света, А.Физо с помощью оптических приборов находил подтверждение, существования эфира. Опыты Майкельсона существование «эфирного ветра», то есть преимущественной системы отсчёта или «светового эфира» не подтверждали, за что подверглись критике со стороны прославленного учёного Х.Лоренца.
Но противоречия в опытах классическими законами уже невозможно было объяснить. Эйнштейн, изменяя классические законы механики, а не законы электродинамики Максвелла, предложил наиболее революционный способ описания явлений в пространстве и времени. Из теории Максвелла следовало, что электромагнитные волны, в отличие от механических волн, могут распространяться в вакууме и подчиняются законам электромагнетизма, что свет – это электромагнитная волна и скорость света:
У Максвелла не было оговорок по поводу относительности скорости света.
И в 1905 году появилась работа А. Эйнштейна «К электродинамике движущихся сред», в которой излагались идеи новой теории – специальной теории относительности.
В основу теории были положены два постулата*:
- Все физические явления протекают одинаково во всех инерциальных системах отсчёта, или никакими опытами, проводимыми в инерциальной системе отсчёта, невозможно установить её движение относительно других инерциальных систем.
- Скорость света в вакууме одинакова во всех инерциальных системах отсчёта. Она не зависит от ни от скорости источника света, ни от скорости светового приёмника сигнала.
Постулат – это основное положение, которое не может быть логически доказано, а является результатом обобщения всех опытов. В физической теории выполняет ту же роль, что и аксиома в математике.
Скорость света занимает особое положение в этой теории, распространение света в вакууме является максимально возможной скоростью передачи взаимодействий в природе.

С точки зрения классической физики первый и второй постулаты входят в противоречия друг с другом. По первому постулату законы механики (как частный случай законов физики) справедливы во всех ИСО. Следовательно, справедлив и закон сложения скоростей. Однако второй постулат противоречит классическому закону сложения скоростей. Значит, в СТО нельзя пользоваться преобразованиями Галилея. Заменив преобразования Галилея на преобразования Лоренца, Эйнштейн устранил кажущееся противоречие между постулатами, что позволило объяснить многие опыты по электродинамике и оптике.
Независимость скорости света от источника много раз проверялись на опытах. Советские учёные А.М. Бонч-Бруевич и В.А. Молчанов в 1955 году проводили опыты, измеряя скорости света от правого и левого краёв Солнца (один из которых из-за осевого вращения Солнца приближается к нам со скоростью 2,3 км/с, а другой с такой же скоростью удаляется). Учёные, проведя расчёты, пришли к выводу, что скорости распространения света с обоих концов одинаковы.
Преобразования Лоренца, которые использовал Эйнштейн, заменив преобразования Галилея, для описания распространения света в системе координат:

Если скорость намного меньше скорости света 



Новая теория раскрыла более глубокую физическую реальность и включает старую как предельный (частный) случай, который называют принципом соответствия.
Иначе это можно объяснить так: классическая механика (механика Ньютона) является частным случаем более общей механики, описывающих процессы в разных инерциальных системах отсчёта с учётом преобразований Лоренца.
Мы ещё неоднократно убедимся, что при малых скоростях, намного меньших, чем скорость света законы СТО переходят в законы классической механики.
Существование предельной конечной скорости изменяет наши привычные представления о пространстве и времени. Представление об абсолютном времени, которое течёт с навсегда заданным темпом, оказывается неверным.
Следствия постулатов относительности:
- Относительность одновременности
Рассмотрим простой метод синхронизации часов. Допустим, что космонавт хочет узнать, одинаково ли идут часы в разных концах корабля в точках А и В. С помощью источника света в центре корабля производят вспышку света, если часы идут синхронно, по показания на часах будут одинаковы при приёме света. Но так будет только в движущейся системе отсчёта К1, связанной с кораблём. И так же, как и в первом случае, вспышка для наблюдателя, находящегося в системе отсчёта К (неподвижная система), часы будут удалятся от вспышки света, и излучению нужно пройти большее расстояние, значит и время должно зафиксироваться отличное от часов в точке В. Вывод наблюдателя в системе отсчёта К: сигналы достигают часов не одновременно.
Время, отсчитываемое покоящимися в ИСО часами, называется собственным временем и обозначают буквой τ (тау). Промежуток времени 
Это означает, что часы, движущиеся относительно ИСО идут медленнее, неподвижных часов и показывают меньший промежуток времени между событиями (замедление времени).
Преобразовав выражение Δt, получим:
А так как скорость света c постоянна и собственное время Δτ неизменно для данного события, то есть инвариантны, то получим:
Наряду с протонами и нейтронами в природе существуют мюоны – элементарные частицы. Мюоны могут образовываться в атмосфере Земли. Но мюоны не стабильны и довольно быстро распадаются, превращаясь в другие элементарные частицы. В лаборатории, где мюоны практически покоятся, среднее время их жизни Δτ =2·10-6с. Вычисляя скорость и другие параметры мюонов, физики обнаружили, что мюоны в атмосфере Земли (без распада) могут пройти расстояние 6 км за время Δt =2·10-5с. Это означает, что время жизни движущегося мюона в системе «Земля» в 10 раз больше собственного времени жизни Δτ.
Рассмотрим ещё один парадокс: относительность расстояний или размеров тела. Допустим, что в космическом корабле измеряют длину стержня, расположенного вдоль направления скорости. Длину стержня внутри корабля, относительно которого он находится в покое обозначим L0 и назовём собственной длиной. При этом расчёты показывают, что линейный размер тела, движущегося относительно ИСО уменьшается в направлении движения.
Закон сложения скоростей в СТО записывается так:
𝟅 – скорость тела, относительно неподвижной системы отсчёта,
𝟅´ — скорость относительно подвижной системы отсчёта,
v – скорость подвижной системы отсчёта относительно неподвижной,
c – скорость света.
При скоростях движения намного меньших, чем скорость света закон сложения скоростей переходит в классический, а длина тела и интервал времени становятся одинаковыми в неподвижной и движущейся системах отсчёта.
Даже масса, такое непоколебимое в нашем представлении значение, меняет свои параметры в движущейся системе относительно неподвижной ИСО. Собственную массу тела, находящегося в состоянии покоя, относительно ИСО, называют m0 массой покоя.
Сам А. Эйнштейн говорил о том, что правильнее было бы называть его теорию относительности теорией абсолютности, так как в основе её заложена идея абсолютности во всех инерциальных системах отсчёта.
Примеры и разбор заданий
1. Две частицы удаляются друг от друга, имея скорость 0,6с каждая, относительно земного наблюдателя. Относительная скорость частиц составляет ______скорости света.
Решение:
Дано: 𝟅´ = 0,6 с, v = — 0,6 с.
Найти: 𝟅.
Решение:
Для решения задачи, необходимо перейти в ИСО, связанную с одной из частиц. Пусть частицы движутся вдоль одной прямой, в противоположные стороны. Используем закон сложения скоростей СТО:
𝟅 – скорость частицы, относительно неподвижной системы отсчёта,
𝟅´ — скорость частицы относительно подвижной системы отсчёта,
v – скорость подвижной системы отсчёта относительно неподвижной,
c – скорость света.
Примем скорость v = — 0,6с одной частицы за положительное значение, скорость 𝟅´ = 0,6с. Тогда формула примет вид:
Ответ значения скорости частицы будет корректен относительно скорости света, а не в м/с или км/с.
Ответ: 0,882 с.
1. Масса протона, летящего со скоростью 1,3·108 м/с, составляет_____ а.е.м. Массу покоя протона считать равной 1 а.е.м.
Решение:
Дано:
𝟅 = 1,3·108 м/с,
m0 = 1а.е.м.
Найти: m.
Решение:
В атомной и ядерной физике для выражения массы пользуются специальной внесистемной единицей – атомной единицей массы (а.е.м.), равной 1/12 массы атома углерода.
1 а.е.м. = 1,66057·10-27кг.
Подставим числовые значения в формулу определения массы частицы, движущейся относительно неподвижной ИСО:
Ответ: 1,11 а.е.м.








 .
. в системе управления)
в системе управления) ; тогда V = V 0 e 0 { displaystyle V = V_ {0} e ^ {0 }}
; тогда V = V 0 e 0 { displaystyle V = V_ {0} e ^ {0 }} , и поэтому V = V 0 { displaystyle V = V_ {0}}
, и поэтому V = V 0 { displaystyle V = V_ {0}}
 ; тогда V = V 0 e — 1 ≈ 0,37 V 0 { displaystyle V = V_ {0} e ^ {- 1} приблизительно 0,37V_ {0}}
; тогда V = V 0 e — 1 ≈ 0,37 V 0 { displaystyle V = V_ {0} e ^ {- 1} приблизительно 0,37V_ {0}}
 , и поэтому lim t → ∞ е (t) = 0 { displaystyle lim _ {t to infty} f (t) = 0}
, и поэтому lim t → ∞ е (t) = 0 { displaystyle lim _ {t to infty} f (t) = 0}
 ; тогда V = V 0 e — 5 ≈ 0,0067 V 0 { displaystyle V = V_ {0} e ^ {- 5} приблизительно 0,0067V_ {0} }
; тогда V = V 0 e — 5 ≈ 0,0067 V 0 { displaystyle V = V_ {0} e ^ {- 5} приблизительно 0,0067V_ {0} }