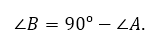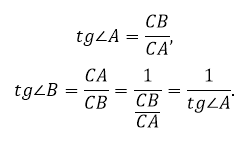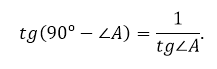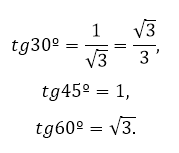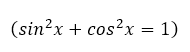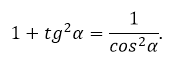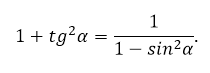Как найти тангенс угла в равностороннем треугольнике - AvtoShod.ru

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Тангенс — это отношение.

Итак, есть два определения:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

Тангенс – это отношение синуса к косинусу.

Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

» alt=»»>

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

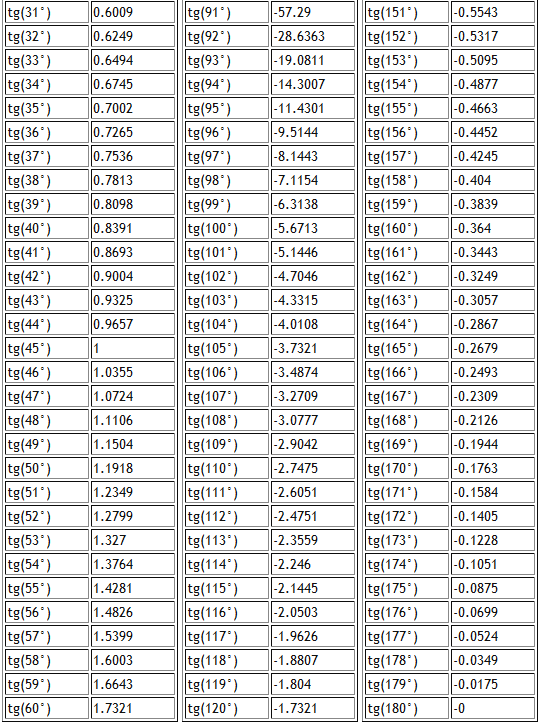
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

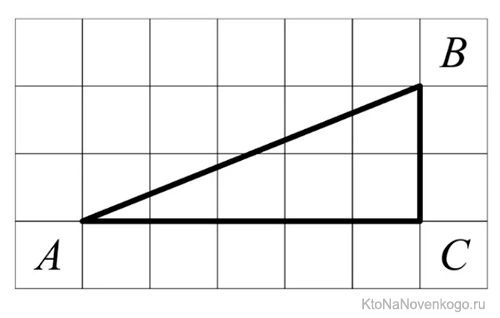
Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (5)

Я Очень Люблю Правила, Теоремы, Формулы по Предмету «Математика», «Алгебра».

Прочитал статью и остался один главный вопрос, а собственно без вспомогательных таблиц найти угол В ГРАДУСАХ вообще возможно и есть ли у вас статья, где рассказыввается как это сделать? Спасибо.

Я ни разу не математик, но почему у вас сумма углов прямоугольного треугольника равна 90 градусов. А так все хорошо начиналось. Объясняете хорошо, но после таких ошибок у меня сомнения что информация верная.

Спасибо. Уточнил в тексте, что это сумма двух непрямых углов прямоугольного треугольника.

Пишу стихи. Востребован тангенс для решения жизненных ситуаций поскольку состоит из тех же функций,как-то, касающийся,прилежащий, трогающий. Куда без них денешься.

Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

R – радиус описанной окружности;
r – радиус вписанной окружности;
R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Тангенс — что это такое (отношение чего к чему) и как его найти (по формулам и по клеточкам)

Как пользоваться таблицей Брадиса.

На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса.

sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.

sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.

Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.

Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:

sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо

sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654

Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.

cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо

Решение уравнения tg x = a

Обычная форма записи решения:
Более удобная форма записи решения
Ограничения на число a	Ограничений нет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:

Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.

Частные случаи решения уравнений tg x = a

Уравнение	Решение

tg x = – 1

tg x = 0

tg x = 1

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса , косинуса (это что?) , тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Тригонометрические функции и их значение в изучении геометрии

В геометрии особую роль имеют тригонометрические функции, при помощи которых определяют, как относятся между собой стороны и углы прямоугольного треугольника. Конечно, тригонометрия не стоит на месте и со времен Евклида она намного шагнула вперёд и теперь может эти функции могут выражаться через решение дифференциальных уравнений.

В данный момент используются шесть обозначений для основных тригонометрических функций, причем четыре функции из шести, они стоят в ряду последними, можно определять не только с помощью геометрии.

Синус (sin)

Косинус (cos)

Тангенс (tg/tan)

Котангенс (ctg/cot)

Секанс (sec)

Косеканс (cosec/csc) .

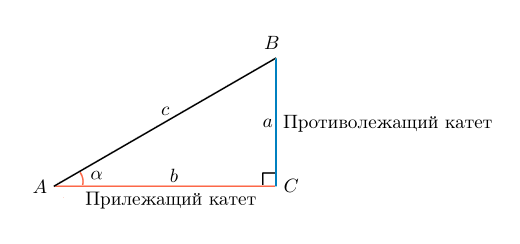
Рассмотрим сам прямоугольный треугольник, обозначения его сторон и углов во всех справочниках, как обычно, стандартные, какой бы стороной он не лежал бы на плоскости.

В этом треугольнике различают три угла, обозначаемые α, β, γ, при этом γ всегда 90°. Сторона, лежащая напротив прямого угла γ, называется гипотенузой, она обозначается буквой С. Угол α, с него начинаются все расчеты, находится напротив стороны а / ВС/, называемой противолежащей к этому углу, и сторона b /АС/, которая находится рядом, подлежит к этому углу и называется прилежащей.

По Евклидовой теории, которая верна до сих пор (и будет верна всегда), суммы углов такого треугольника, который находится в одной плоскости, будет равна 180 или числу π. И значение любого угла будут находиться в пределах между 0 и π /2.

Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.

Синус α выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть sin α = а: с.
Косинус α выражается через отношение катета, который прилежит к углу α, и гипотенузы с, cos α = b: с. Кстати, sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α.
Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
Котангенс угла α в соответствии равен ctg α = b : а.
Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b.
Косеканс угла α составляет отношение гипотенузы треугольника к катету, который противостоит углу, cosecα = с : a.

Эти функции можно выразить и через окружность путем задания системы координат. Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.

Тогда тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Следовательно, если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.

Тангенс — это отношение…

Итак, есть два определения:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Тангенс – это отношение синуса к косинусу.

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Применение функции тангенса для решения задач

Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.

Пример: есть два катета ВС = 7 см и АС = 12 см. Нам нужно узнать все остальные данные о треугольнике.

Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.

Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.

Нам осталось найти гипотенузу с.

Можем найти её через sin α, который равен а: с, тогда с = а : sin α.

Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.

Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.

Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875. Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.

Для удобства есть рассчитанная таблица основных углов через значение π.

Значение угла α (градусов)	Значение угла α в радианах	tg (тангенс)
Тангенс 0	0	0
Тангенс 15	π/12	0.2679
Тангенс 30	π/6	0.5774
Тангенс 45	π/4	1
Тангенс 50	5π/18	5114
Тангенс 60	π/3	1.7321
Тангенс 65	13π/36	2.1445
Тангенс 70	7π/18	2.7475
Тангенс 75	5π/12	3.7321
Тангенс 90	π/2	–
Тангенс 105	5π/12	-3.7321
Тангенс 120	2π/3	-1.7321
Тангенс 135	3π/4	-1
Тангенс 140	7π/9	-0.8391
Тангенс 150	5π/6	-0.5774
Тангенс 180	π	0
Тангенс 270	3π/2	–
Тангенс 360	2π	0

Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.

источники:

Свойства равностороннего треугольника: теория и пример задачи

http://exceltut.ru/tangens-chto-eto-takoe-otnoshenie-chego-k-chemu-i-kak-ego-najti-po-formulam-i-po-kletochkam/

Источник

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Тангенс — это отношение…

Итак, есть два определения:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.

Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

Приняты обозначения:

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Получается, что

В частности,

Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Из формулы тангенсов, записывающей кратко второе определение

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:

Источник

Определение тангенса угла

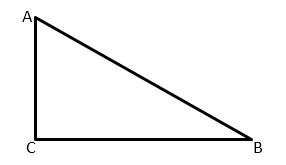
Тангенсом угла в прямоугольном треугольнике называют отношение противолежащего катета к прилежащему.

Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.

Для простоты запоминания можно дать такое определение: тангенс угла — это отношение дальнего от рассматриваемого угла катета к ближнему катету.

В случае с рисунком, описанным выше: tg⁡α=abtgalpha=frac{a}{b}

Тангенс можно найти напрямую пользуясь данной формулой, а можно и через тригонометрические тождества. Разберем подробнее задачи.

Задача 1

В прямоугольном треугольнике катеты равны 6 см6text{ см} и 8 см8text{ см}. Найдите тангенс угла, близлежащего к меньшей стороне.

Решение

a=8a=8
b=6b=6

tg⁡α=ab=86≈1.33tgalpha=frac{a}{b}=frac{8}{6}approx1.33

Ответ

1.331.33

Формулу:

tg⁡α=abtgalpha=frac{a}{b}

Можно записать в следующем виде:

tg⁡α=sin⁡αcos⁡αtgalpha=frac{sinalpha}{cosalpha}

Проверим истинность данного выражения. Подставим вместо синуса и косинуса их определения:

tg⁡α=sin⁡αcos⁡α=acbc=abtgalpha=frac{sinalpha}{cosalpha}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{b}

Получили первичное равенство, значит выражение для тангенса через отношение синуса к косинусу верно.

Решим задачу, пользуясь этой формулой.

Задача 2

По условию задачи известен косинус угла, равный 32frac{sqrt{3}}{2} и синус того же угла, равный 12frac{1}{2}. Найдите тангенс данного угла.

Решение

cos⁡α=32cosalpha=frac{sqrt{3}}{2}

sin⁡α=12sinalpha=frac{1}{2}

tg⁡α=sin⁡αcos⁡α=1232=13tgalpha=frac{sinalpha}{cosalpha}=frac{frac{1}{2}}{frac{sqrt{3}}{2}}=frac{1}{sqrt{3}}

Ответ

13frac{1}{sqrt{3}}

Еще одно тождество помогает решить задачи, связанные с тангенсом:

1+tg⁡2α=1cos⁡2α1+tg^2alpha=frac{1}{cos^2alpha}

Оно появляется путем деление каждого слагаемого основного тождества тригонометрии на квадрат косинуса.

Задача 3

Известен квадрат косинуса угла в прямоугольном треугольнике, равный 0.80.8. Нужно найти тангенс этого угла.

Решение

cos⁡2α=0.8cos^2alpha=0.8

1+tg⁡2α=1cos⁡2α1+tg^2alpha=frac{1}{cos^2alpha}

1+tg⁡2α=10.81+tg^2alpha=frac{1}{0.8}

1+tg⁡2α=1.251+tg^2alpha=1.25

tg⁡2α=0.25tg^2alpha=0.25

tg⁡α=0.25tgalpha=sqrt{0.25}

tg⁡α=0.5tgalpha=0.5

Ответ

0.50.5

У вас есть трудности с вычислением тангенса? Можете заказать задачу по математике у наших экспертов!

Тест по теме “Вычисление тангенса”

Источник

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

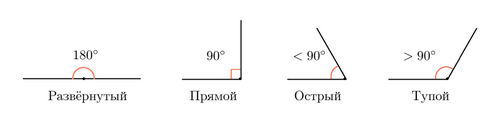
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой alpha .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла alpha , называется противолежащим (по отношению к углу alpha ). Другой катет , который лежит на одной из сторон угла alpha , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.$

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A $=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.$

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.$

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A $=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.$

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A $=genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.$

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin $displaystyle alpha = frac{a}{c}$	sin ${}^2 alpha +$ cos $displaystyle {}^2 alpha =1$	$alpha + beta = 90 ^{circ}$
cos $displaystyle alpha = frac{b}{c}$	1+tg $displaystyle {}^2 alpha =frac{1}{cos ^2 alpha}$	cos = sin
tg $displaystyle alpha = frac{a}{b}$	1+ctg $displaystyle {}^2 alpha =frac{1}{sin ^2 alpha}$	sin = cos
ctg $displaystyle alpha = frac{b}{a}$		tg = ctg

Давайте докажем некоторые из них.

Сумма углов любого треугольника равна $180^{circ}$ . Значит, сумма двух острых углов прямоугольного треугольника равнa $90^{circ}$ .
С одной стороны, $sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ как отношение противолежащего катета к гипотенузе. С другой стороны, $cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, $cos left( 90^{circ}-A right) = sin A$ .
Возьмем теорему Пифагора: . Поделим обе части на получаем $displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 ,$ то есть
Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на , получим: $1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }.$ Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично, $1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.$

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна $180^{circ}$ .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от $0^{circ}$ до $90^{circ}$ .

	0	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}$
sin	0	$displaystyle frac{1}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{sqrt{3}}{2}$
cos		$displaystyle frac{sqrt{3}}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{1}{2}$	0
tg	0	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$			−
ctg	−			$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$	0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и C_1 и равными острыми углами А и A_1.

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому $displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .$

Из этих равенств следует, что $displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} ,$ т. е. sin А = sin A_1.

Аналогично, $displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1},$ т. е. cos А = cos A_1, и $displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1},$ т. е. tg A = tg A_1.

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен $90^{circ}$ , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку $A+B = 90^{circ}$ , sin A = cos B = 0,1.

Задача 2. В треугольнике ABC угол равен $90^{circ}$ , AB=5 , $sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}$ .

Найдите .

Решение:

$sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.$

Отсюда

$BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.$

Найдем AC по теореме Пифагора.

$AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.$

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A $displaystyle = frac{BC}{AB}= frac{5}{13}.$

Катет, прилежащий к angle A – это катет АС, следовательно, cos⁡ А $displaystyle = frac{AC}{AB}=frac{AC}{13}.$

Длину катета АС найдем по теореме Пифагора:

Тогда $AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.$

cos⁡ А $displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;$

tg A $displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.$

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A= $displaystyle frac{sqrt{17}}{17} .$

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A $displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17},$ $displaystyle frac{a}{c} = frac{sqrt{17}}{17} ,$ $displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.$

По теореме Пифагора получим

$a^2+2^2=(sqrt{17} a)^2;$

$displaystyle a= frac{1}{2}=0,5;$

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен AC = 4, tg A = $displaystyle frac{33}{4sqrt{33}} .$ Найдите AB.

Решение:

AC = b = 4, tg A $displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},$

$displaystyle frac{a}{4}=frac{33}{4sqrt{33}},$ $displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},$

$AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.$

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = $displaystyle frac{1}{5} .$ Найдите AH.

Решение:

AВ = с = 13, tg A = $displaystyle frac{a}{b}=frac{1}{5} ,$ тогда b = 5a.

По теореме Пифагора ABC:

$displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}},$ тогда $displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.$

(по двум углам), следовательно $displaystyle frac{AH}{AC}=frac{AC}{AB} ,$ откуда

$displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.$

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A = $displaystyle frac{1}{6} .$

Найдите AH.

Решение:

Так как sin A = $displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6},$ тогда $displaystyle frac{3}{c} = frac{1}{6} ,$ c = АВ = 18.

sin A = $displaystyle frac{a}{c}$ = cos⁡ B = $displaystyle frac{1}{6} .$

Рассмотрим BHC:

${cos B= }displaystyle frac{BH}{BC}$ = $displaystyle frac{1}{6} ,$ получим $displaystyle frac{BH}{3}=displaystyle frac{1}{6},$

тогда BH = $displaystyle frac{3}{6}=displaystyle frac{1}{2}$ = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BC = 3, cos A = $displaystyle frac{sqrt{35}}{6}.$

Найдите АH.

Решение:

Так как для АВС: cos A = $displaystyle frac{AC}{AB}=$ sin В = $displaystyle frac{sqrt{35}}{6},$

а для ВНС: sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{sqrt{35}}{6}$ , откуда СН = $displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},$

По теореме Пифагора найдем ВН:

$BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=$

$=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.$

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:

${CH}^2=AH cdot BH,$ тогда $AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.$

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ =

Рассмотрим BHC : ${cos B= }displaystyle frac{BH}{BC}.$

ВС найдем по теореме Пифагора:

ВС= $sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,$

тогда ${cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28,$ а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ = cos A = $displaystyle frac{b}{c}$ = $displaystyle frac{AC}{AB}$ =

тогда tg A = $displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB,$ который найдем из BHC:

$ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.$

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, tg A = $displaystyle frac{2}{3}.$ Найдите АН.

Решение:

По определению tg A= $displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.$

Для BHC: $ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3}$ , значит $displaystyle frac{12}{CH}=displaystyle frac{2}{3},$ СН = $displaystyle frac{12 cdot 3}{2}=18.$

Для АHC: tg A= $displaystyle frac{CH}{AH}=displaystyle frac{2}{3},$ то $displaystyle frac{18}{AH}=displaystyle frac{2}{3},$ AH = $displaystyle frac{18 cdot 3}{2}=27.$

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, sin A = $displaystyle frac{2}{3}.$ Найдите АВ.

Решение:

Так как cos В = $displaystyle frac{BC}{AB}$ = sin A = $displaystyle frac{2}{3}.$

Из СВН имеем cos В = $displaystyle frac{HB}{BC}$ = $displaystyle frac{2}{3},$ тогда ВС = $displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.$

В АВС имеем sinA = $displaystyle frac{BC}{AB}$ = $displaystyle frac{2}{3},$ тогда AВ = $displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.$

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 ${}^circ,$ из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

$HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=$

sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{12}{20}=displaystyle frac{3}{5}.$

Для АВС: cos A = $displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5},$ получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = $displaystyle frac{AC}{AB}=displaystyle frac{3}{5},$ то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора ${AC}^2+{BC}^2= {AB}^2,$ получим ${(3x)}^2+{(20)}^2= {(5x)}^2$
${25x}^2-{9x}^2= {20}^2 ,$

${16x}^2= {20}^2,$

$x^2= {left(displaystyle frac{20}{4}right)}^2,$
х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит $displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB}$ или $displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,$

k = $displaystyle frac{16}{20}=displaystyle frac{4}{5} ,$ тогда $displaystyle frac{12}{AC}=displaystyle frac{4}{5},$ АС = $displaystyle frac{12 cdot 5}{4}=15$ ; $displaystyle frac{20}{AB}=displaystyle frac{4}{5},$ АВ = $displaystyle frac{20 cdot 5}{4}=25.$

3-й способ.

${CH}^2=AH cdot HB$ (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда ${12}^2=AH cdot 16,$ АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)}$ =

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = $sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}$ =

cos C = $displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.$

Для АВС: sin А = $displaystyle frac{BC}{AC}$ = cos C = $displaystyle frac{3}{5}.$

Для АНВ: sin А = $displaystyle frac{BH}{AB}$ = $displaystyle frac{3}{5},$ то $displaystyle frac{24}{AB}$ = $displaystyle frac{3}{5},$ АВ = $displaystyle frac{24 cdot 5}{3}=40.$

Из основного тригонометрического тождества найдем

cos A = $sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.$

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = $displaystyle frac{7}{25}.$

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А = $displaystyle frac{CE}{AC},$

значит $displaystyle frac{7}{25}$ = 14.

Второй катет найдем, используя теорему Пифагора: $AE= sqrt{{AC}^2-{CE}^2};$

$AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.$

Площадь прямоугольного треугольника равна S = $displaystyle frac{1}{2}ab,$

поэтому $S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.$

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, $angle AKC=angle ACB=90{}^circ$ ),

значит sin $angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.$

Найдем АС по теореме Пифагора из САВ:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=$

Тогда sin $angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.$

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = $displaystyle frac{12}{13}.$ Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = $displaystyle frac{1}{2}AB=36.$

Поскольку АСН — прямоугольный,

cos A = $displaystyle frac{AH}{AC}=$ $displaystyle frac{12}{13},$ то есть $displaystyle frac{36}{AC}=$ $displaystyle frac{12}{13}$ АС = $displaystyle frac{36 cdot 13}{12}=39.$

По теореме Пифагора ${AH}^2+{CH}^2={AC}^2,$ тогда

$CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=$

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 ${}^circ,$ sin A = $displaystyle frac{11}{14},$ AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = $displaystyle frac{BC}{AB}=$ $displaystyle frac{11}{14},$ то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора $AC^2+{BC}^2={AB}^2;$

${(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;$

${(14x)}^2-{(11x)}^2 = 3 cdot 100;$

(14х- 11х)(14х + 11х) = 3 cdot 100;

x^2=4, учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 cdot 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством ${sin}^2A+{cos}^2A=1;$

cos A = $sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.$

По определению cos A = $displaystyle frac{AC}{AB},$ значит $displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.$

Так как АС=10 то $displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14},$ откуда АВ = $displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}}$ = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 sqrt{3} и 4.

Решение:

Пусть angle ВАО = alpha .

Диагонали ромба делят его углы пополам, значит, = alpha .

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = $displaystyle frac{1}{2} AC=2sqrt{3},$ а катет ВО = $displaystyle frac{1}{2}BD =2.$

Поэтому tg $alpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}},$ откуда $alpha =30{}^circ .$

$angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .$

Ответ: ${60}^circ,$ ${120}^circ,$ ${60}^circ,$ ${120}^circ .$

Часто в задачах встречаются треугольники с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ или с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ катет, лежащий напротив угла в $30^{circ}$ , равен половине гипотенузы.

Треугольник с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ — равнобедренный. В нем гипотенуза в sqrt{2} раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 ${}^circ,$ угол А равен 30 ${}^circ,$ АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла ${30}^circ,$ имеем ВС = $displaystyle frac{1}{2}$ АВ =

В BHC: $angle BHC=90{}^circ ,; angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно, ВН = $displaystyle frac{1}{2}$ BC = $displaystyle frac{sqrt{3}}{2}.$

По теореме Пифагора найдем НС:

$HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=$

$=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.$

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, АВ = 2, $angle A=30{}^circ .$ Найдите АH.

Решение:

Из АВС найдем ВС = $displaystyle frac{1}{2}$ АВ = 1 (по свойству катета, лежащего против угла 30 ${}^circ$ ),

$angle A=30{}^circ ,$ то $angle B=60{}^circ .$

Из ВСН: $angle BHC=90{}^circ , angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно,

ВН = $displaystyle frac{1}{2}$ ВС = $displaystyle frac{1}{2}.$

АН = АВ — НВ = 2 — $displaystyle frac{1}{2}$ = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

В этой статье мы разберем такое понятие, как тангенс угла. Начнем с понятия прямого угла. Прямым углом называется угол равный 90⁰. Угол в котором меньше 90 градусов — называется острым. Угол в котором больше 90 градусов — называется тупым. В развернутом угле 180 градусов.

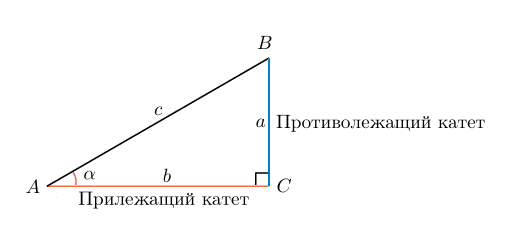
Изображаем треугольник с прямым углом С , при этом противолежащая сторона будет имеет такое же обозначение (с -будет гипотенузой), аналогично поступаем и с другими углами. Сторона находящаяся противоположно от острого угла — называется катетом.

Синус и косинус находятся с помощью катета и гипотенузы, а именно:

sinA = a/c
cosA = b/c

Формула тангенса

tg A = a/b

другими словами определение тангенса — это деление противоположного катета на прилежащий
Существует ещё одна равносильная формула тангенса

tg A = sinA/cosA

расшифровывается как деление sin на cos.

Котангенс находится практически аналогично, лишь значения поменяются местами.

ctg A = cosA/sinA

Внимание! В помощь родителям и учителям гдз по математики 5 класс (http://spisaly.ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.

Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.

Обозначения для основных углов:
тангенс 30 — 0,577

тангенс 45 — 1,000
тангенс 60 — 1,732

Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.

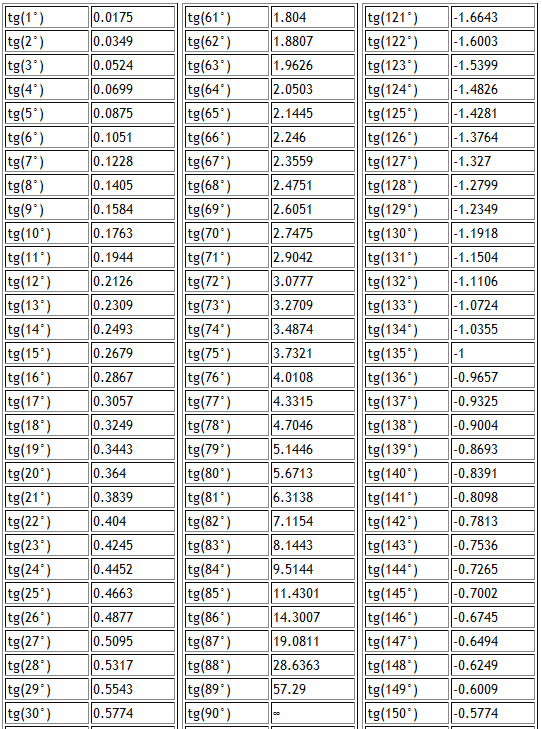
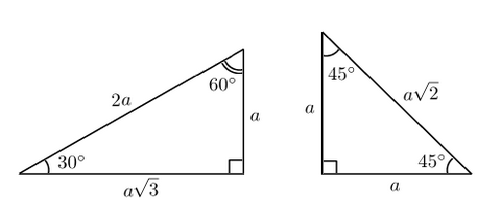
Есть очень много задач в которых у треугольника углы равны 90, 30, 60 градусам. либо 90, 45, 45 градусам. Для таких фигур лучше заучить их соотношение , что бы потом было проще.

В первом случае катет противоположный 30 градусам равняется 1/2 от гипотенузы.
Во втором случае гипотенуза превышает катет в ?2 раз.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Источник

Что такое тангенс угла и как его найти

Тангенс угла

Тангенс — это отношение.

Как найти тангенс угла (формулы)

Как найти тангенс по клеточкам

Комментарии и отзывы (5)

Свойства равностороннего треугольника: теория и пример задачи

Определение равностороннего треугольника

Свойства равностороннего треугольника

Свойство 1

Свойство 2

Свойство 3

Свойство 4

Свойство 5

Свойство 6

Пример задачи

Тангенс — что это такое (отношение чего к чему) и как его найти (по формулам и по клеточкам)

Как пользоваться таблицей Брадиса.

Решение уравнения tg x = a

Тангенс угла

Тригонометрические функции и их значение в изучении геометрии

Тангенс — это отношение…

Применение функции тангенса для решения задач

Тангенс угла

Тангенс — это отношение…

Как найти тангенс угла (формулы)

Как найти тангенс по клеточкам

Тест по теме “Вычисление тангенса”

Синус, косинус и тангенс острого угла прямоугольного треугольника

Не пропустите также: