Арифметические действия
- Запись, знаки и результат
Арифметическое действие — это процесс нахождения по двум данным числам одного нового числа. Найденное число называется результатом этого действия.
Например, возьмём число 4, добавим к нему единицу, получим новое число — 5. Таким образом, мы из двух данных чисел 4 и 1, составили одно новое число: 5, то есть произвели арифметическое действие над данными числами.
Арифметических действий всего четыре:
- сложение
- вычитание
- умножение
- деление
Возведение в степень и извлечение корня относятся к элементарной алгебре.
Каждое арифметическое действие имеет свои свойства, которые помогают упрощать вычисления.
Запись, знаки и результат
Любое арифметическое действие подразумевает взаимодействие двух или более чисел. Числа записываются друг за другом и между ними ставится знак, показывающий какое именно арифметическое действие будет над ними производиться.
Знаки арифметических действий:
- Сложение:
+
. - Вычитание:
—
. - Умножение:
*
,·
илиx
.Пример.
2 * 3
2 · 3
2 x 3
- Деление:
:
.
Выполнение любого арифметического действия подразумевает получение какого-либо результата от произведённых вычислений. Результат каждого арифметического действия имеет своё название, которое также распространяется и на запись данного выражения. Результат вычислений записывается после знака равенства =
, который ставится после выражения.
Обратите внимание, что каждое число в выражении имеет название.
Запиши на карточках такие знаки арифметических действий, чтобы записи были верными.
6 * 4 = 16 _ 8
81 _ 9 = 27 : 3
14 _ 8 = 48 : 8
72 : 9 = 0 _ 8
36 : 4 = 27 _ 3
40 _ 8 = 25 : 5
14 _ 7 = 100 _ 98
6 _ 8 = 2 _ 7
reshalka.com
ГДЗ учебник по математике 2 класс (часть 2) Рудницкая. Нахождение нескольких частей числа. Номер №16*
Решение
6 * 4 = 16 + 8
81 : 9 = 27 : 3
14 — 8 = 48 : 8
72 : 9 = 0 + 8
36 : 4 = 27 : 3
40 : 8 = 25 : 5
14 : 7 = 100 — 98
6 + 8 = 2 * 7
Вычисления:
6 * 4 = 16 + 8
6 * 4 = 24
16 + 8 = 24
81 : 9 = 27 : 3
81 : 9 = 9
27 : 3 = 9
14 — 8 = 48 : 8
14 − 8 = 6
48 : 8 = 6
72 : 9 = 0 + 8
72 : 9 = 8
0 + 8 = 8
36 : 4 = 27 : 3
36 : 4 = 9
27 : 3 = 9
40 : 8 = 25 : 5
40 : 8 = 5
25 : 5 = 5
14 : 7 = 100 — 98
14 : 7 = 2
100 − 98 = 2
6 + 8 = 2 * 7
6 + 8 = 14
2 * 7 = 14
Порядок действий в математике
Какое действие выполнить в первую очередь: сложение или умножение? Простые для внимательного школьника примеры вида 2 + 2 × 2 не всякий взрослый решит правильно. Разберемся вместе, как без ошибок решать числовые выражения со скобками и без.
Решайте математические и логические задачи и примеры на ЛогикЛайк!
Выберите возраст для старта

Более 5500 увлекательных заданий для развития математических
способностей и логического мышления — в онлайн‑курсе ЛогикЛайк.
Для чего нужен порядок действий?
Большинство действий, которые мы выполняем в жизни имеют свой порядок. Согласитесь, чтобы пойти в магазин вы сначала одеваетесь, а затем выходите на улицу, а не наоборот. Так же и в математике, у арифметических действий есть своя очередность, которую необходимо соблюдать.
Вы уже решали простые примеры на сложение, вычитание, умножение или деление. Более сложные примеры называют числовыми выражениями, они содержат два, три и даже больше действий.
7 — 4 + 10
6 + 4 ∙ 5 — 3
60 — 24 : 8 + 2 × 4
Чтобы правильно решить подобные примеры, нужно знать какое действие выполняется раньше других.
Кто придумал порядок действий?
В 1560 году французский логик и математик Пьер де ла Раме в своей книге «Алгебра» впервые применил определенный способ выполнения последовательности действий.
Порядок действий в примерах и картинках
Вам задали решить длинный пример – не паникуйте, это проще простого, если знать порядок действий.
Порядок действий – это определенная последовательность выполнения цепочки арифметических действий.
В каком порядке выполнять действия?
Первыми всегда выполняются действия в скобках с учетом приоритетности. Приоритет действий: умножение или деление выполняются раньше, чем сложение или вычитание. При равном приоритете действия выполняются слева направо.
- Скобки (если они есть)
- Умножение или деление
- Сложение или вычитание
Порядок действий в выражениях без скобок
Вычислим значение выражения, применяя порядок выполнения действий.
Порядок выполнения равнозначных действий
- Умножение и деление равнозначны. Если умножение стоит слева от деления, то умножение выполняется первым. Если деление находится слева от умножения, сначала выполняется деление.
- Сложение и вычитание равнозначны. Если сложение стоит слева от вычитания, то сложение выполняется первым. Если вычитание находится слева от сложения, сначала выполняется вычитание.
Равнозначные действия выполняются по очереди слева направо.
Пример: 12 + 6 — 8
В данном выражении нет скобок и знаки равнозначные по очередности (сложение, вычитание), значит выполнять их мы будем по очереди слева направо.
12 + 6 — 8
18 — 8 = 10
Получаем результат 10.
Пример: 6 + 4 × 8 — 7
В данном выражении нет скобок, значит сначала мы будем выполнять умножение.
6 + 4 × 8 — 7
6 + 32 — 7
Когда остается два равнозначных действия, мы будем их выполнять слева направо по порядку. В данном случае сначала выполним сложение, а затем вычитание.
6 + 32 — 7
38 — 7
Получаем результат 31.
Если действия записаны в скобках, выполнение порядка действий сохраняется внутри скобок.
Как ЛогикЛайк может помочь родителям?
Выберите основную цель занятий
Порядок действий в выражениях со скобками
Пример: (4 + 3 × 2) ÷ (12 ÷ 4 — 3)
Начнем со скобок. В каждой скобке мы должны начинать с самой важной операции.
(4 + 3 × 2) ÷ (12 ÷ 4 — 3)
Если в примере две или более скобок – начинаем их решать слева направо. В левой скобке есть сложение и умножение. Начинаем с умножения, которое приоритетнее, «главнее» сложения.
(4 + 3 × 2) ÷ (16 ÷ 2 — 3)
В правой скобке в первую очередь выполним деление – оно приоритетнее, чем вычитание.
(4 + 6) ÷ (16 ÷ 2 — 3)
(4 + 6) ÷ (8 — 3)
Заканчиваем решение в каждой скобке.
(4 + 6) ÷ (8 — 3)
Остается только разделить.
10 ÷ 5 = 2
Получаем результат 2.
Решите выражения, расставляя порядок действий над знаками:
5 · 8 + 4 · 6 + 15 – 14 =
9 · 5 – 19 + 6 · 6 – 3 · 4 =
32 : 4 · 6 : 8 + 6 · 3 – 17 =
27 + 7 · 8 – 35 : 35 =
6 · 5 – 12 : 6 · 3 + 49 =
42 : 6 + 28 – 3 · 6 =
32 : 4 · 6 : 8 + 6 · 3 – 17 =
9 · 7 – 3 · 7 + 29 – 24 : 4 =
48 : 6 + 33 – 54 : 9 + 7 · 4 =
Подключайтесь к ЛогикЛайк!
Развивайте логику, интеллект и расширяйте
кругозор на сайте Logiclike.com.

План урока:
Действие сложение. Знак «+». Название компонентов действия сложения. Переместительное свойство сложения
Действие вычитание. Знак «–». Название компонентов действия вычитания
Взаимосвязь между действием сложения и действием вычитания
Действие сложение. Знак +
Название компонентов действия сложения. Переместительное свойство сложения
Добрый день! Готов к новому уроку? Сегодня у нас будет очень важное занятие. Мы получим самые драгоценные и сокровенные знания. Без этих знаний невозможно существование науки математики!
В таком сложном деле нам нужны помощники. Мы их найдем в сказочном лесу.
— Догадался? В этом лесу живут настоящие профессионалы по поиску драгоценностей и сокровищ. Это сказочные гномики.
Посмотри на них, какие они веселые и доброжелательные. Гномики улыбаются тебе и желают хорошего настроения на весь урок. Улыбнись им в ответ и давай приступим к занятию.
Гномики целый день работали в шахте. Они искали драгоценные камни.
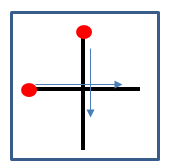
Посмотри, сколько камней собрал гном Том и гном Тим. Посчитай.
Гном Том собрал 4 камня.
А гном Тим собрал 3 камня.
Чтобы не нести эту тяжесть в руках, они сложили все свои камни в тачку.
Теперь в тачке лежат и камни, которые собрал Том, и камни, которые собрал Тим. Давай-ка мы их все достанем и пересчитаем.
В тачке оказалось 7 камней.
Ого, как много! Как ты думаешь, почему?
Верно, потому что в тачку сложили камни оба гномика. А это всегда будет больше, чем у каждого по отдельности.
Итак, что сделали гномики?
Точно, они сложили свои камни вместе. В математике такое действие тоже называется сложение. Его суть в том, что элементы двух множеств объединяются в одно целое.
Смотри, множество камней Тома и множество камней Тима объединились в тачке в одно множество. При этом в объединенном множестве количество элементов становится больше.
Чтобы узнать результат сложения чисел, нужно пересчитать все элементы и первого, и второго множества вместе.
Гномики сложили камни вместе. А какие еще действия приводят к тому, что предметов становится больше?
Таких действий довольно много. Например, если в добавок к тому, что уже есть, кто-то:
- еще что-то даст или подарит;
- купит;
- принесет или привезет;
- смастерит еще несколько предметов;
- еще кто-то придет или прилетит.
Любое действие, которое ведет к увеличению количества предметов, подразумевает выполнение действия сложения. Часто это действие еще называют «прибавление».
Чтобы записать действие сложение в виде математического выражения, используется специальный знак. Знак сложения выглядит так.
Посмотри, в этом знаке тоже произошло объединение: две палочки соединились в одно целое. Этот знак называется «плюс».
Посмотри, как знак «плюс» пишется в тетради.
Порядок написания следующий.
- Начинаем чуть ниже середины верхней границы клетки. Ведем прямую линию вниз и останавливаемся, немного не дописав до середины нижней границы клетки.
- Вторую линию начинаем писать чуть правее середины левой границы клетки. Ведем ее вправо и останавливаемся, немного не дописав до середины правой границы клетки.
Потренируйся писать знак плюс в тетради.
Теперь разберемся, как именно надо составлять математическое выражение, описывающее действие сложения. Давай вспомним, что было сначала.
Том собрал 4 камня и Тим собрал 3 камня.
Они вместе высыпали свои камни в тачку, т.е. объединили их. Поэтому мы ставим между числами знак «+».
В результате объединения все камни оказались в тачке. Мы их все пересчитали – в тачке 7 камней. Их ровно столько, сколько было у обоих гномиков вместе. Поэтому между левой и правой частью выражения нужно поставить знак равенства «=».
В тетради надо записать так.
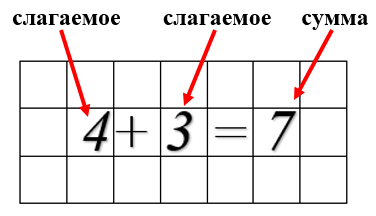
Теперь я расскажу, как называются компоненты действия сложения. Числа, которые обозначают количество элементов в каждом отдельном множестве, называются слагаемые. А число, которое обозначает результат, полученный при объединении этих множеств, называется сумма.
Поскольку левая сторона записи равна правой, то и само выражение тоже называют «сумма». Читают так «сумма чисел 4 и 3».
Поэтому, когда говорят «найди сумму», нужно выполнить действие сложение.
Итак, наше выражение можно прочитать несколькими способами:
- Четыре плюс три равно семь.
- К четырем прибавить три получим семь.
- Первое слагаемое – четыре, второе слагаемое – три, а сумма – семь.
- Сумма чисел четыре и три равна семи.
Идем дальше. Нам нужно выучить очень важное правило для действия сложения. Давай вернемся к нашим гномикам. Ты же помнишь, что каждый из них положил свои камни в тачку и потом мы их посчитали вместе, т.е. нашли сумму. Как ты думаешь, кто из гномиков первый положил камушки в тачку?
Мы записали, что первое слагаемое четыре. Получается, что первым был гномик Том, а потом гномик Тим.
Теперь давай представим, что порядок был другой. Сначала в тачку положил свои камушки Тим, а потом Том. Значит первое слагаемое – это три, а второе – четыре. Изменится ли от этого общее количество камней в тачке, т.е. наша сумма?
Теперь в тачке три камня Тима и четыре камня Тома. Посчитай их вместе.
Всего камней семь. Ровно столько же, сколько был и первый раз.
Получается, что не важно, кто из гномиков положил камушки первый, а кто второй. Их общее количество не меняется. Значит, сумма не меняется.
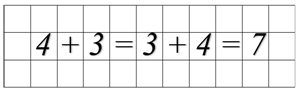
Посмотри. И четыре плюс три будет семь, и три плюс четыре тоже будет семь.
В математике это называется переместительное свойство сложения. Оно звучит так: от перестановки слагаемых местами сумма не изменяется. Запишем.
Это переместительное свойство очень пригодится тебе при изучении таблиц сложения. Запомни его!
Чтобы закрепить все, что мы узнали о действии сложения, потренируемся составлять примеры по картинкам.
Посчитай, сколько синих фигур на картинке. Запиши.
Правильно, 3.
Теперь посчитай красные фигуры и запиши.
Их 2.
Нам нужно посчитать их вместе. Это подразумевает объединение всех фигур. А значит, надо выполнить действие сложение. Поэтому поставим между нашими числами знак «плюс».
3 + 2
Теперь нужно пересчитать ВСЕ фигуры ВМЕСТЕ. Сколько у тебя получится?
У меня вышло 5. Уверена, у тебя тоже. Запишем это, поставив сначала знак равенства.
3 + 2 = 5
Вот и все. Ничего сложного.
Теперь рассмотрим, как нужно решать примеры на сложение. Давай прочитаем это выражение.
2 + 4
Можно так «два плюс четыре».
Чтобы найти результат, нужно следовать алгоритму выполнения действия сложения.
- Посмотри, какой знак используется в выражении.
Это знак «плюс», значит нужно объединить, посчитать все вместе.
- Назови первое слагаемое и положи перед собой нужное количество кружочков (можно взять палочки, спички, кубики или любые другие предметы).
- Теперь назови второе слагаемое и положи необходимое количество кружочков рядом с предыдущими.
- Пересчитай все кружочки вместе и запиши полученный результат.
2 + 4 = 6
Вот и все. Теперь ты знаешь, что такое действие сложение, как называются компоненты сложения, а также как составлять и решать примеры, в которых нужно выполнить это действие.
Действие вычитание. Знак-
Название компонентов действия вычитания
Давай продолжим раскрывать тайны науки математики. Ведь есть еще одно очень важное математическое действие, с которым нам обязательно нужно познакомиться.
Итак, гномики закончили свою работу и возвращаются домой.
Дома их ждет Белоснежка.
Она приготовила для гномиков угощение – испекла пирожные. Посчитай, сколько их получилось.
У тебя тоже получилось девять пирожных? Значит, ты посчитал правильно!
Когда гномики пришли домой, каждый из них съел по пирожному. Помнишь, сколько было гномов у Белоснежки? Точно, семь. Они съели столько же пирожных, т.е. тоже семь.
Давай зачеркнем съеденные пирожные.
Мы видим, что осталось совсем мало – всего два пирожных. Наверное, они достанутся Белоснежке.
В математике действие, которое ведет к уменьшению количества предметов, называется вычитание. Его смысл в следующем. Из целого множества удаляется его часть. В итоге остается меньше элементов, чем их было в целом множестве.
Чтобы узнать результат действия вычитания, нужно пересчитать элементы, которые остались.
Давай подумаем, в каких случаях предметов станет меньше. Пирожных стало меньше, потому что гномики съели часть из них. Еще могут быть такие ситуации:
- отдали;
- забрали;
- улетели (ушли, уехали);
- продали;
- использовали;
- сломали.
Для того, чтобы записать действие вычитания в виде математического выражения используют специальный знак. Знак вычитания выглядит так.
Он называется «минус».
В тетради знак «минус» пишется так.
Порядок написания знака «минус» следующий.
- Ставим ручку чуть правее середины левой границы клетки.
- Ведем горизонтальную прямую линию вправо.
- Останавливаемся, немного не доходя до середины правой границы клетки.
Потренируйся писать знак «минус» в тетради.
А теперь я расскажу, как составлять математическое выражение, которое описывает действие вычитание.
Вспомни, сколько пирожных было сначала?
Правильно, 9. Запиши.
9
Гномики съели пирожные и их стало меньше, поэтому ставим знак «минус».
9 –
Они съели 7 пирожных. Запишем это число.
9 – 7
Ставим знак равенства и запишем количество пирожных, которые остались. Их оставалось 2.
9 – 7 = 2
В тетради запись выглядит так.
Названия компонентов действия вычитания запомнить довольно легко.
- Первое число в результате вычитания станет меньше. Поэтому его называют уменьшаемое.
- Второе число показывает, сколько надо вычесть. Значит оно вычитаемое.
- В результате мы определяем какая разница между тем, что было и тем, что осталось. Поэтому результат действия вычитания называется разность.
Левая сторона этого выражения тоже называется разность.
Если в задании говорится, что нужно «найти разность чисел», значит, следует составить математическое выражение с действием вычитания.
Такое выражение можно прочитать по-разному.
- Из девяти вычесть семь будет два.
- Девять минус семь получим два.
- Уменьшаемое девять, вычитаемое семь, разность два.
- Разность чисел девять и семь равна двум.
Закрепим все, что ты узнал о действии вычитания и составим математическое выражение по такой картинке.
Посмотри, сколько всего было шариков у гномика сначала? Запиши.
Правильно, пять.
Что случилось с некоторыми шариками? Сколько таких шаров?
Верно, два шарика сдулись и у гномика шариков осталось меньше. Значит нужно написать «минус два».
5 – 2
Ставим знак равенства и пересчитаем, сколько осталось целых шариков.
Их три.
5 – 2 = 3
Вот мы и составили выражение.
А теперь разберемся, как нужно решать примеры на вычитание. Например, посчитаем, сколько будет:
6 — 4
Назови уменьшаемое. Выложи столько же кружочков. Их должно быть 6.
Теперь назови вычитаемое. Убери (отодвинь, зачеркни) четыре кружочка.
Пересчитай кружочки, которые остались, и ты узнаешь ответ. Запиши его после знака равенства.
6 – 4 = 2
Мы решили пример на вычитание. Теперь ты знаешь, что обозначает это математическое действие, как называются компоненты вычитания, и как нужно составлять и решать математические выражения с действием вычитания.
Взаимосвязь между действием сложения и действием вычитания
Итак, ты выучил два математических действия: сложение и вычитание. Одно из них используется при объединении предметов в единое множество, а другое при удалении из целого множества его части.
Ты вспомнил, что обозначает каждое действие?
Эти действия связаны между собой, но имеют противоположное значение. При сложении мы получаем больший результат, а при вычитании предметов становится меньше. Вот, например, представь, что у тебя было несколько конфет и тебе дадут еще пару штук. Что получится?
Правильно, у тебя конфет станет больше.
А если ты съешь несколько конфет? Что у тебя останется?
Правильно, у тебя останется меньше конфет.
А теперь давай проверим, какая именно взаимосвязь между действиями сложения и вычитания. Разберем одну ситуацию и составим по ней математическое выражение.
У Белоснежки День рождения. Гномики решили устроить для нее праздник. Посчитай, сколько их всех на картинке.
Правильно, их трое.
К Белоснежке на День рождения пришли зверята. Посчитай, сколько их.
Верно, пять зверят.
Подумай, какое действие мы должны использовать, чтобы составить выражение?
Ну конечно, действие сложение. Ведь теперь их всех вместе стало больше.
Было три, пришло еще пять. Посчитай, сколько теперь всех вместе.
Правильно, восемь.
Запишем в виде выражения.
3 + 5 = 8
3 – это первое слагаемое, оно показывает, сколько элементов было в первом множестве.
5 – это второе слагаемое, оно показывает, сколько элементов было во втором множестве.
8 – это сумма, она обозначает количество элементов в общем множестве.
Теперь на полянке и гномики с Белоснежкой (это наше первое множество), и зверята (это второе множество). Они все вместе.
Получается, что на празднике веселились 8 друзей. Когда праздник закончился, зверята ушли домой. Как ты думаешь, какое математическое действие надо использовать в этом случае?
Правильно, действие вычитание. Ведь зверята ушли и на полянке останется меньше друзей.
Итак, 5 зверят ушло. Кто остался? Сколько их?
Верно, остались гномики с Белоснежкой. Их 3.
Составим математическое выражение.
8 – 5 = 3
Мы видим, что если из общего множества (суммы) убрать элементы второго множества (второе слагаемое), то останутся только элементы первого множества (первое слагаемое).
А если было наоборот, из 8 друзей первыми с полянки ушли гномики с Белоснежкой (их 3). Кто на ней останется?
Правильно, останутся зверята. Их 5.
Посмотри, как это запишем.
8 – 3 = 5
Теперь мы из общего множества (суммы) убрали элементы первого множества (первое слагаемое) и остались только элементы второго множества (второе слагаемое).
Итак, у нас получается, что мы при сложении два множества объединяем в одно целое. А если из этого общего множества убрать какое-то одно из составляющих множеств, то останется другое.
В математике это правило взаимосвязи между компонентами сложения звучит так: если из суммы вычесть одно слагаемое, то получим другое слагаемое.
Мы видим, что в примере на сложение есть два слагаемых. Поэтому можно сделать следующий вывод: из одного математического выражения с действием сложения можно составить два выражения с действием вычитания.
8 – 3 = 5
8 – 5 = 3
Это очень важное правило, которое поможет тебе в дальнейшем быстро и легко учить таблицы вычитания.
А на сегодня все. Гномики помогли нам получить очень важные и ценные знания. Нужно обязательно поблагодарить их за это.
В материалах урока использованы кадры из а/ф «Белоснежка и семь гномов», 1937
Арифметическое действие — это такая операция, которая удовлетворяет ряд свойств и позволяет с помощью нескольких чисел, данных по условию, найти новое число.
Основные арифметические действия и знаки арифметических действий:
- Сложение
Сложением именуется прибавление одного числа к другому. То есть увеличение одного числа на несколько единиц.
Знак сложения + (плюс)
Пример: 15 + 27 = 42
Компоненты сложения имеют свои названия. В приведённом примере
15 — это первое слагаемое;
27 — второе слагаемое;
42 — третье слагаемое.
- Вычитание
Вычитание — это обратное сложению действие. С его помощью мы уменьшаем одно число на несколько единиц.
Знак вычитания — (минус)
Пример: 30 — 8 = 22
Компоненты вычитания называются:
30 — уменьшаемое;
8 — вычитаемое;
22 — разность.
- Умножение
Сложение одинаковых слагаемых называется умножением.
Условно, если Вам надо сложить 5 + 5 + 5 + 5, вовсе не обязательно записывать цепочку одинаковых слагаемых. Можно заменить её на на действие умножение. Число 5 умножить на количество повторяемых раз (4 раза).
Знак умножения (умножить)
Пример: 7 4 = 28
Компоненты умножения называются:
7 — первый множитель;
4 — второй множитель;
28 — произведение.
- Деление
Противоположное умножению действие называется делением. С его помощью мы делим число на равные части.
Знак деления : (разделить)
Пример: 35 : 5 = 7
Компоненты деления называются:
35 — делимое;
5 делитель;
7 — частное.
Вот и всё! Мы с Вами изучили основные арифметические действия. Но это была теория. А на практику приглашаем Вашего ребёнка в школу математики World of Math. Первое занятие бесплатное, Вы можете выбрать любую тему и тщательно изучить её вместе с педагогом.
Уроки в World of Math проходят дистанционно. Мы онлайн-школа, поэтому преподавание проходит на базе интерактивной платформы. Ребёнок находится в комфортной домашней обстановке, воспринимает урок как познавательную игру, и в то же время за ним приглядывает учитель, который задаёт ход занятия. Пока Ваше чадо познаёт Мир Математики, у Вас, родители, есть свободное время!
Взгляните на математику по-новому в World of Math! Записаться на бесплатное занятие можно здесь.