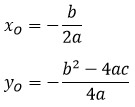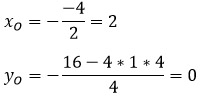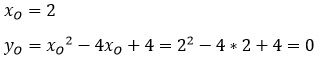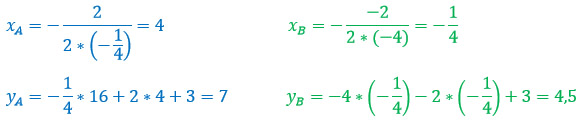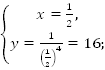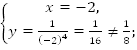Как найти свойства квадратичной функции - AvtoShod.ru

	(a > 0) (коэффициент (a) положительный)	(a < 0) (коэффициент (a) отрицательный)

	Ветви параболы направлены вверх	Ветви параболы направлены вниз
	Функция убывает, если x∈(−∞;0 , возрастает, если x∈0;+∞	Функция возрастает, если x∈(−∞;0 , убывает, если x∈0;+∞
	Наибольшее значение функции: нет	Наибольшее значение функции: (y = 0)
	Наименьшее значение функции: (y = 0)	Наименьшее значение функции: нет
	Функция положительная ((y > 0)), если x∈(−∞;0)∪(0;+∞) (график находится выше оси (Ox))	Интервалы, в которых значение функции положительное: нет
	Интервалы, в которых значение функции отрицательное: нет	Функция отрицательная ((y < 0)), если x∈(−∞;0)∪(0;+∞) (график находится ниже оси (Ox))

Источник

Функция вида , где называется квадратичной функцией.

График квадратичной функции – парабола.

Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА

, то есть , ,

Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай , , , то есть , то мы получим параболу, симметричную относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:

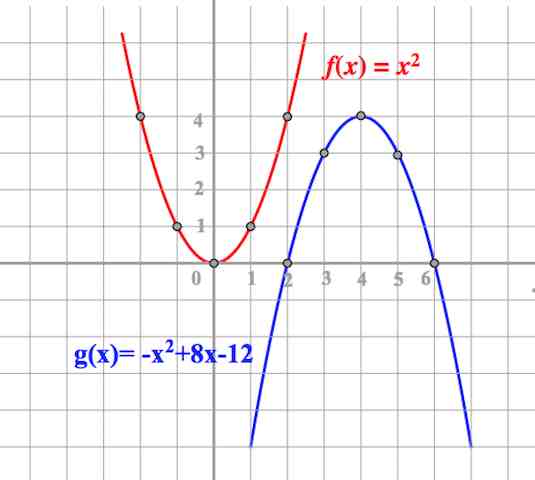
II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать , , ? Как изменится поведение параболы? При парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях ордината каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при парабола «станет шире» параболы :

Давайте подитожим:

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»

Теперь давайте введем в игру (то есть рассматриваем случай, когда ), будем рассматривать параболы вида . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы вдоль оси вверх или вниз в зависимости от знака :

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда перестанет быть равным .

Здесь для построения параболы нам понадобится формула для вычисления вершины: $x_o=frac{-b}{2a}$ , .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы :

$x_o=frac{4}{2}=2$ , . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы , ведь в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку . Действительно, подставив в формулу x=0, получим, что . То есть ордината точки пересечения параболы с осью (оу), это . В нашем примере (выше), парабола пересекает ось ординат в точке , так как .

2) осью симметрии параболы является прямая $x=frac{-b}{2a}$ , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая к , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение . В зависимости от дискриминанта, будем получать одну (, $x=-frac{b}{2a}$ ), две (, $x_{1,2}=frac{-bpmsqrt{b^2-4ac}}{2a}$ ) или нИсколько () точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана в виде

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины параболы по формуле $x_o=frac{-b}{2a}$ , .

3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если , то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение

Пример 1

Пример 2

Замечание 1. Если же парабола изначально нам задана в виде , где – некоторые числа (например, ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины . Почему?

Возьмем квадратный трехчлен и выделим в нем полный квадрат: $ax^2+bx+c=a(x^2+frac{b}{a}x+frac{c}{a})=a((x^2+2frac{b}{2a}x+frac{b^2}{4a^2})-frac{b^2}{4a^2}+frac{c}{a})=a(x+frac{b}{2a})^2-frac{b^2}{4a}+c.$ Посмотрите, вот мы и получили, что $m=frac{-b}{2a}$ , $n=-frac{b^2}{4a}+c=y(frac{-b}{2a})$ . Мы с вами ранее называли вершину параболы , то есть теперь , .

Например, $y=-frac{1}{3}{(x+2)}^2+6$ . Отмечаем на плоскости вершину параболы , понимаем, что ветви направлены вниз, парабола расширена (относительно ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

Источник

На координатной плоскости отмечаем эти точки и чертим параболу.

Вершина этой параболы находится в точке (0; 0). И не забудь про то, что ветви параболы бесконечно поднимаются ввысь и не ограничены точками с координатами (3; 9) и (3; -9).

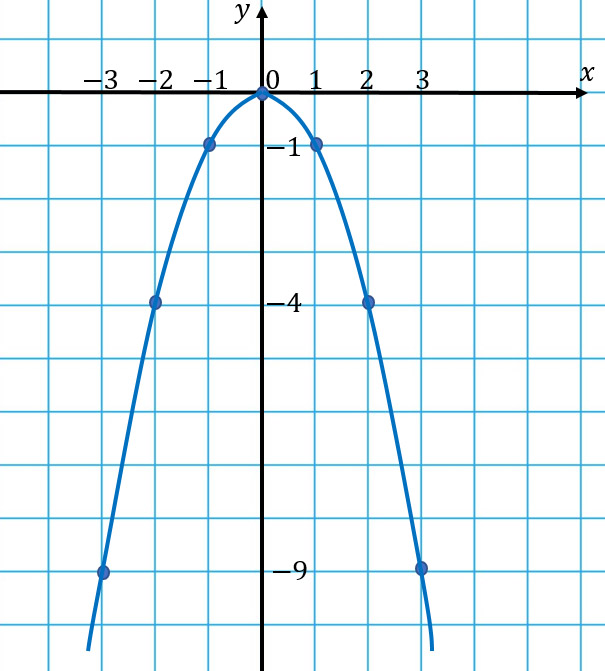
Еще одна стандартная парабола задается функцией y = —x²(в этом случае а = -1). Для этого графика я тоже напишу табличку:

x	-3	-2	-1	0	1	2	3
y	-9	-4	-1	0	-1	-4	-9

Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:

Сразу напрашивается вывод: если перед х² стоит положительное число, то ветви параболы направлены вверх, если отрицательное — то вниз.

Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя «на ура».

Параболы со смещенной вершиной.

Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции y = ±x² + bx + c (обязательно коэффициент перед х² должен равняться ±1) является стандартной параболой, только вот вершины этих парабол не будут находится в начале координат.

Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.

Пусть вершиной параболы будет точка О с координатами (x₁; y₁). Тогда найти эти координаты можно по формулам:

Кстати, можно найти координаты вершины и другим способом.

Координату х_О находим по той же формуле, а координату у_О можно найти подстановкой координаты х_О в функцию.

Без примера не обойтись)

Пример 1.

Дана функция y = x² — 4x + 4. Найдите вершину параболы и постройте график.

Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.

1 способ: по формулам.

2 способ: подстановкой.

Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.

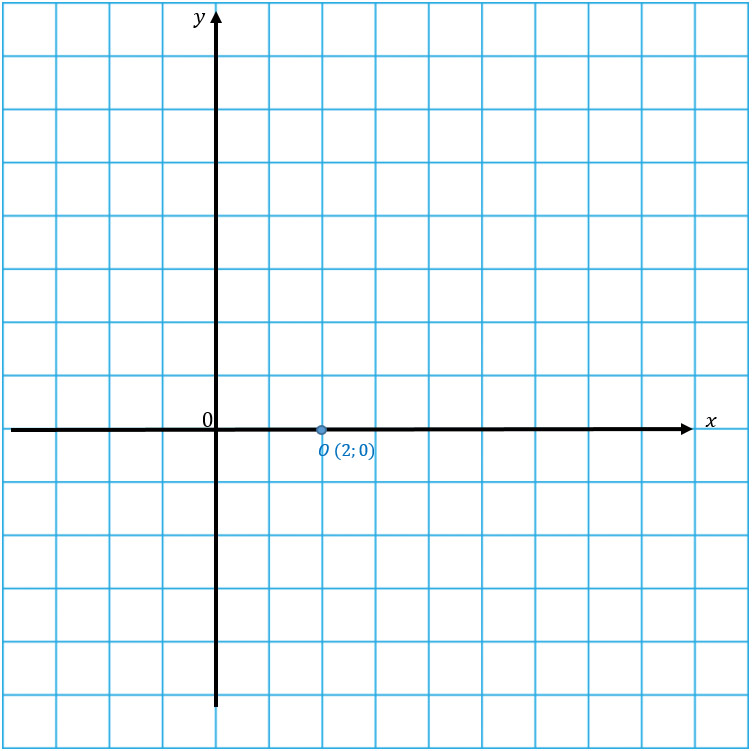
Итак, получили, что О(2; 0) — вершина параболы. Отмечаем ее на координатной плоскости.

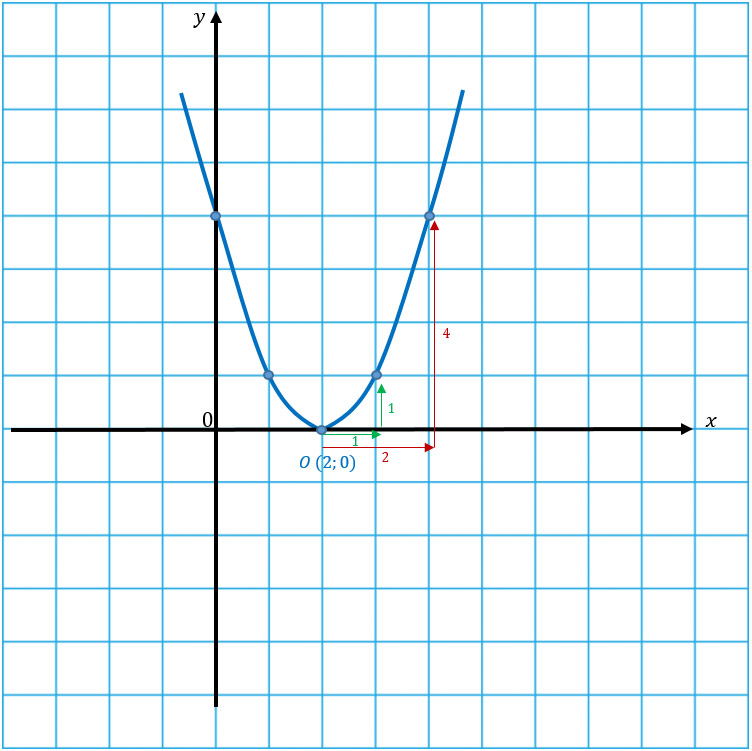
Перед х² стоит положительное число, значит ветви параболы направлены вверх. Наша задача: нарисовать стандартную параболу, представив, что точка О — начало координат. Если тебе это сложно сделать, то необходимо начертить таблицу значений и уже по ней рисовать параболу.

Параболы-стройняшки и параболы-пухляшки.

Удивительно, но числовой коэффициент перед х² оказывается влияет на стройность и полноту парабол.

Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.

А если числовой коэффициент лежит в промежутке (-∞; -1) ∪ (1; +∞), то парабола будет прижиматься к оси Оу и занимать меньше места на плоскости.

Не веришь? Давай проверим! Для примера возьмем две функции:

К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.

Пусть вершиной первой параболы будет точка А(х_А; у_А), а вершиной второй параболы — точка B(х_B; у_B). Вершины буду находить по второму способу (см. выше).

Переходим к таблицам значений.

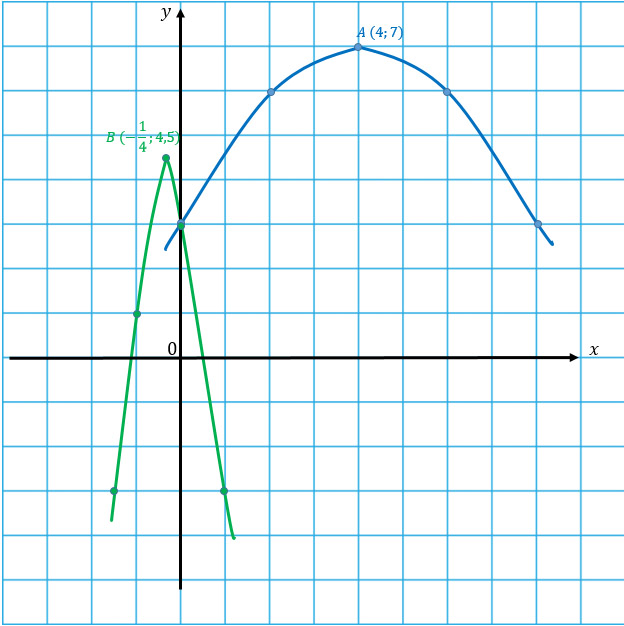
Голубая парабола.

x	0	2	4	6	8
y	3	6	7	6	3

Зеленая парабола.

x	-1,5	-1	-0,25	0	1
y	-3	1	4,5	3	-3

Чертим обе параболы по получившимся координатам.

Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.

А ты заметил, что свободный член в уравнении функции — это точка пересечения графика с осью Оу? В обеих функциях свободный член равен 3 и графики пересекают ось Оу в точке с координатами (0; 3).

Практикум по параболам.

Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.

Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.

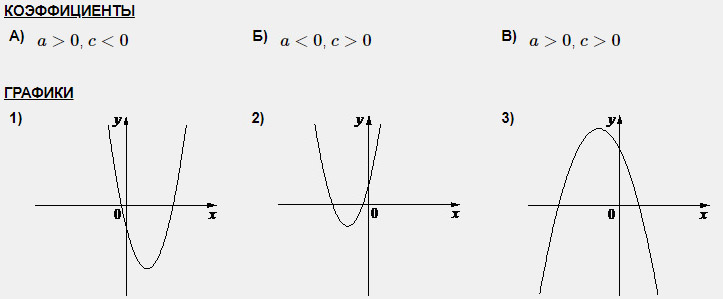
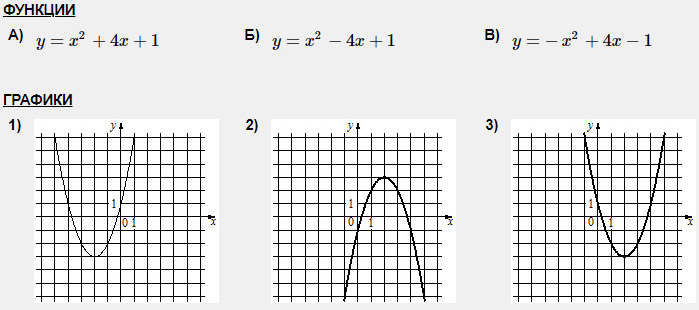
Задание 1. На рисунке изображены графики функций вида y = ax²+ bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.

Решение. Коэффициент а, стоящий перед х², отвечает за направление ветвей параболы, а свободный член с — за пересечение графика с осью Оу.

А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.

Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.

В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 2.

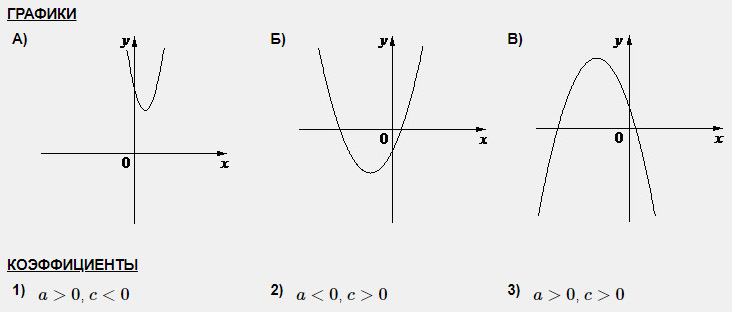
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax²+ bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.

А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.

Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с < 0. Подходит вариант под номером 1.

В) Ветви направлены вниз, значит а < 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 2.

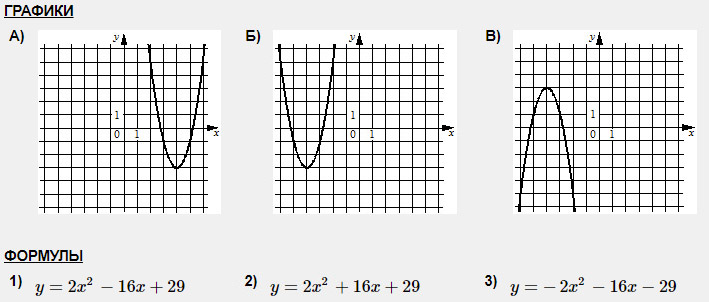
Задание 3. Установите соответствие между графиками и их функциями.

График В отличается от остальных тем, что его ветви направлены вниз. За направление ветвей отвечает коэффициент перед х² — он отрицательный. Отрицательный коэффициент только в функции под номером 3. Значит В-3.

Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)

Итак, рассматриваем график А и выбираем на нем точку с красивыми координатами (красивые значит не дробные). Мне нравится тут вершина. Ее координаты (4; -3). Даже не спрашивайте почему не прорисованы оси; эти задания взяты с сайта ФИПИ)

Теперь эти координаты подставляем в оставшиеся функции: вместо у подставляем -3, а вместо х подставляем 4.

Подставляем в первую функцию: -3 = 2 · 4² — 16 · 4 + 29; -3 = -3 — верно. Значит, А-1.

И остается Б-2.

Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.

Очевидно, что В-2.

На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!

Подставляем в функцию А: 1 = (-4)² + 4 · (-4) + 1; 1 = 1 — верно. Значит, А-1.

Соответственно, Б-3.

Если ты считаешь, что чего-то не хватает или у тебя есть ещё задания из первой части, связанные с параболами, — напиши мне в VK)

Источник

Свойства квадратичной функции

Здесь
рассматриваются
свойства квадратичной
функции вида ,график
квадратичной функции и
решаются задачи на чтение
графиков и задачи с
параметром.

Напоминание

Определение. Квадратичной
функцией называется
функция вида

,
где .

График
– парабола (см. Рис. 1) с вершиной
в точке ,
где.

Рис.
1. График функции ,
где

.
Функция непрерывна на всей .

Свойства
функции

в
случае .

Пусть .

Свойства:

1. ;

2. ;

3. убывает
при;возрастает
при;

4. —
не существует;

5.
Непрерывна;

6.
Выпукла вниз.

Свойства
функции

в
случае .

Пусть .

Свойства
(см. Рис. 2):

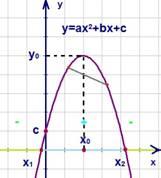
Рис.
2. График функции в случае.

1. ;

2. ;

3. возрастает
при;убывает
при;

4. —
не существует;

5.
Непрерывна;

6.
Выпукла вверх.

Задача
1 на нахождение пределов изменения
конкретной квадратичной функции

Найдите
пределы изменения функции,
прочитайте график.

а.

Ответ: ;убывает
при;возрастает
при.

б.

Ответ: ;убывает
при;возрастает
при.

Задача
2 на нахождение пределов изменения
конкретной квадратичной функции

Найдите
пределы изменения функции,
прочитайте график.

а.

Ответ: ;возрастает
при;убывает
при.

б.

Ответ: ;возрастает
при;убывает
при.

Задача
1 с параметром

Найдите
число корней уравнения с
параметром,
где,.

Ответ
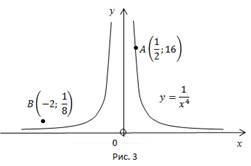
(см. Рис. 3):

Рис.
3. График функции ,
рассеченный прямыми,
гдеи.

1.
Корней нет при ;

2.
Уравнение имеет

—
один корень при ;

—
два корня при .

Задача
2 с параметром

Найдите
все значения параметра ,
при каждом из которых уравнение,
где,,
имеет хотя бы один корень (см. Рис.
4).

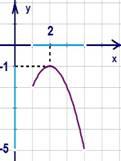
Ответ: .

Задача
на построение и чтение графика функции

Постройте
и прочитайте график функции

Ответ:
(см. Рис. 5)

Рис.
5. График функции

1.
Возрастает при ;

2.
Убывает при .

Задача
3 с параметром

Найдите
число корней уравнения ,
где.

Ответ:
уравнение имеет (см. Рис. 6)

Рис.
6. График функции ,

рассеченный
прямыми ,
гдеи.

1.
Один корень при ;

2.
Два корня при ;

3.
Три корня при .

Задачи на степенные функции

Здесь
вспомним свойства степенных
функций с целым отрицательным
показателем и используем
их при решении задач на
степенную функцию.

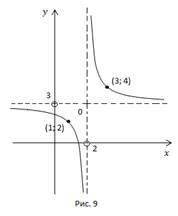
Напоминание:
график и свойства функции

Функция

Основные
свойства:

3.
Функция четная.

4.
Две характерные фиксированные
точки для всех кривых:

5.
Асимптоты: прямые

6.
Если тоy возрастает,

Если тоy убывает,

Напоминание:
график и свойства функции

Функция

Основные
свойства:

3.
Функция нечетная.

4.
Две фиксированные характерные
точки для всех кривых:

5.
Асимптоты: прямые

6.
Если тоy убывает,

Если тоy убывает,

Решение
задач

Рассмотрим
типовые задачи:

1.
Какая из точек – А или В – принадлежит
графику функции если

Решение:

т.
А:

т.
А принадлежит графику.

т.
В:

т.
В не принадлежит графику.

Ответ:
т. А.

2.
Какая из точек А, В, С принадлежит
графику функции если

Решение:

т.
А:

т.
В:

т.
С:

Ответ:
т. В принадлежит графику.

3.
Постройте график функции и
прочтите его.

Решение:

Построим
график функции (Рис.
5). Его асимптоты – прямыеи.

Чтобы
получить график функции необходимо
графиксдвинуть
на 1 вверх по осиyи
на 1 единицу влево по оси x (Рис.
6).

Асимптоты
полученного графика –
прямые и,
характерные точки

Если тоy возрастает,

Если тоy убывает,

4.
Найдите все значения
параметра m,
при каждом из которых уравнение

имеет
хотя бы одно решение.

Решение:

Нам
необходимо построить
график функции ,
пересечь его семейством
прямых,
найти точки пересечения и
записать ответ (Рис. 7).

Ответ:

5.
Найти все значения параметра m,
при каждом из которых уравнение

1.
Не имеет решений.

2.
Имеет только отрицательные
решения.

3.
Имеет два корня разных знаков.

Решение:

Ответ:

6.
Постройте график функции и
прочитайте его.

Решение:

Построим
график функции (Рис.
8).

Теперь
чтобы получить график
функции сдвинем
кривуюна
2 вправо вдоль осиx,
и на 3 вверх по осиy (Рис.
9).

Прямые иявляются
асимптотами.

Характерные
точки –

Если тоy убывает,

7.
Найти все значения параметра m,
при каждом из которых уравнение

имеет
решения

1.
На луче

2.
На луче

Решение:

Изобразим
график функции и
пересечем его семейством
прямых(Рис.
10).

Ответ:

8.
Решите графически
неравенство

Решение:

Построим
в одной системе координат
график функции и
график функции(Рис.
11).

Графики
пересекаются в точке

Чтобы
выполнялось
неравенство криваядолжна
располагаться выше прямой

Ответ:

9.
Даны две функции, и,
где

Докажите,
что

Доказательство:

Тождество
доказано.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Свойства квадратичной функции

1) Область определения квадратичной функции (значения которые может принимать «

«)

D(f)=(-∞;+∞)

Область значений квадратичной функции (значения которые может принимать «у«)

Е(f)=(-∞;+∞)

2) Нули функции

Для того чтобы найти нули функции необходимо «y» прировнять к нулю. Получим квадратное уравнение стандартного вида, следовательно количество точек пересечения графика с осью ОХ зависит от дискриминанта:

Если D<0, то уравнение не имеет корней и график не имеет точек пересечения с осью ОХ, то есть находится выше оси ОХ при a>0 и ниже оси ОХ при a<0
Если D=0, то уравнение имеет один корень и одну точку пересечения с ОХ, исходя из этого делаем вывод о том, что вершина параболы находится на оси ОХ
Если D<0, то уравнение имеет 2 корня и соответственно 2 точки пересечения с ОХ

3) Промежутки знакопостоянства квадратичной функции

Рассмотрим несколько случаев, которые зависят от знаков коэффициентов и количества нулей функции:

1 случай

a) a>0, D<0

Ветви параболы направлены вверх, точек пересечения с ОХ нет, следовательно f(x) >0, при любых «х», таким образом f(x) >0 при х ∈ (-∞;+∞)

б) a>0, D=0

Ветви параболы направлены вверх, одна точка пересечения с ОХ , следовательно f(x) >0, при любых «х», кроме вершины параболы, где f(x)=0, таким образом f(x) >0 при х ∈ (-∞;хв) U (хв;+∞)
в) a>0, D>0
Ветви параболы направлены вверх, две точки пересечения с ОХ, следовательно
f(x) >0, при х ∈ (-∞;х1) U (х2;+∞)
f(x) <0, при х ∈ (х1;х2)
На рисунке красным цветом выделены положительные части графика, синим отрицательные

Источник

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА

II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Свой­ства квад­ра­тич­ной функ­ции

За­да­чи на сте­пен­ные функ­ции

Не пропустите также:

Свойства квадратичной функции

Задачи на степенные функции